Prediction of Human Brucellosis in China Based on Temperature and NDVI
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Sources
2.1.1. Human Brucellosis Data
2.1.2. Land Surface Temperature Data
2.1.3. Normalized Difference Vegetation Index Data
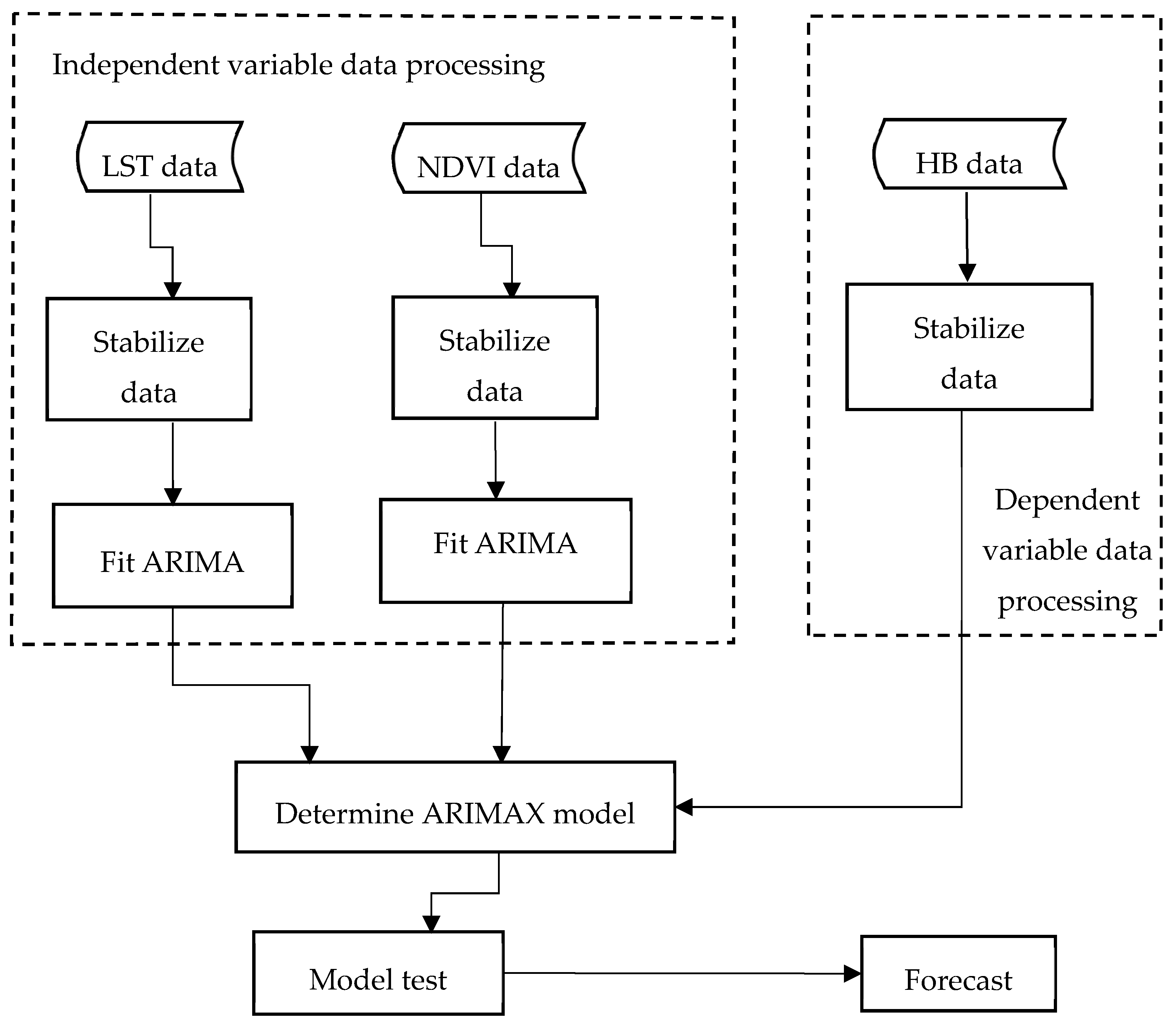
2.2. Methods
2.2.1. General Concepts
2.2.2. Seasonal Autoregressive Integrated Moving Average with Exogenous Variables (SARIMAX) Models
2.2.3. Model Test
3. Results
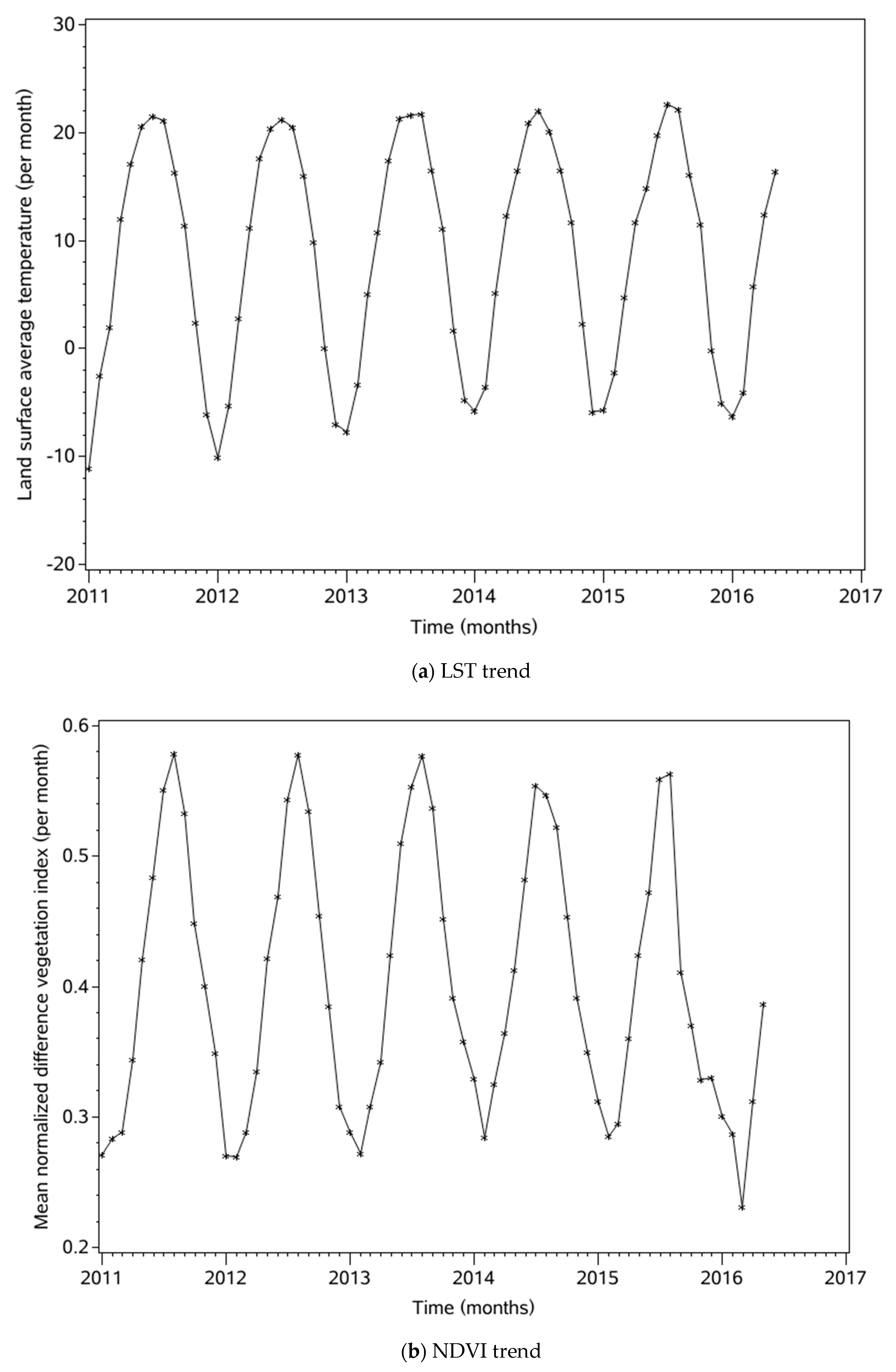
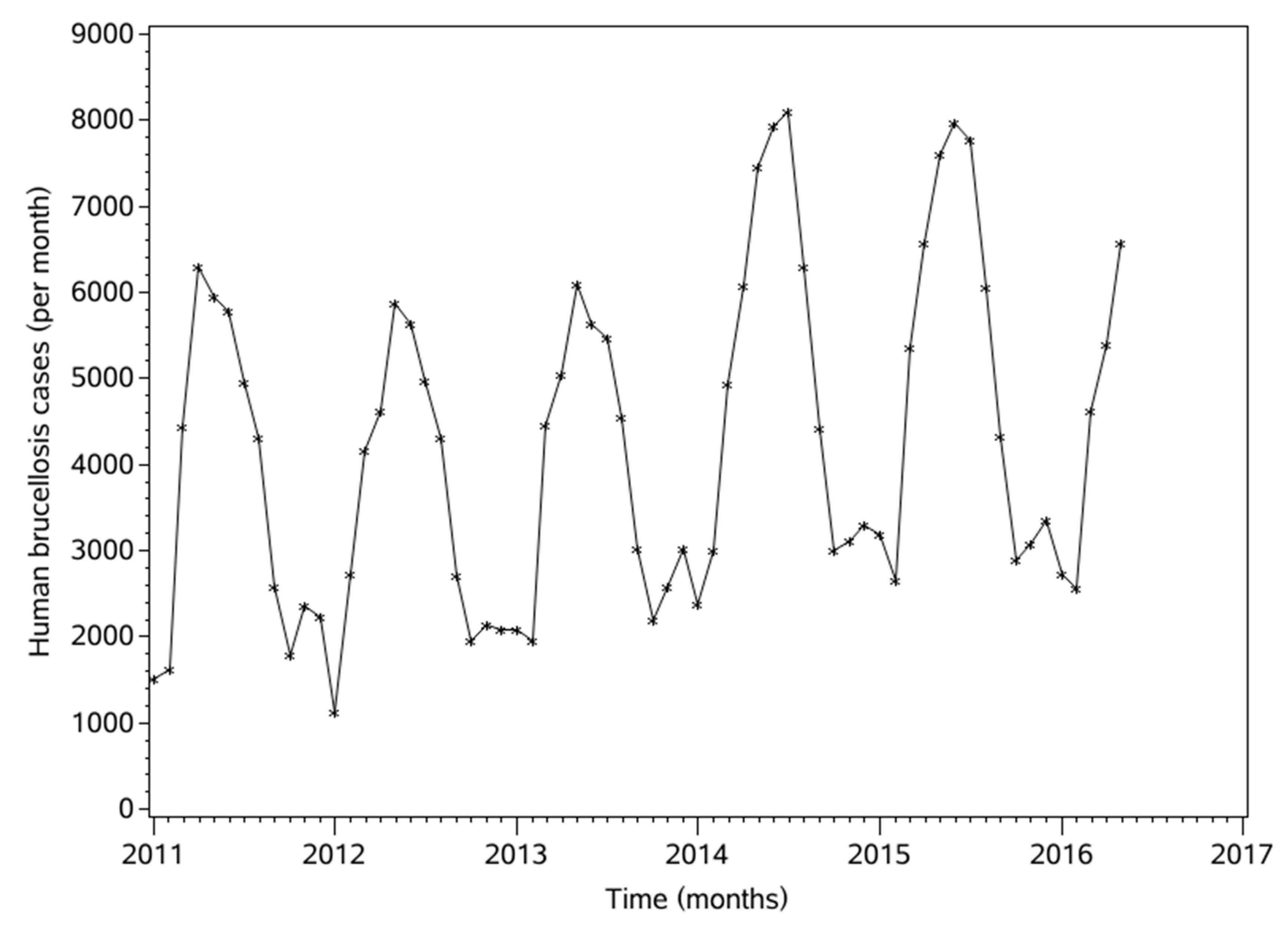
3.1. General Characteristics
3.2. HB Data Stationarity
3.3. LST and NDVI Models
3.4. SARIMAX Model
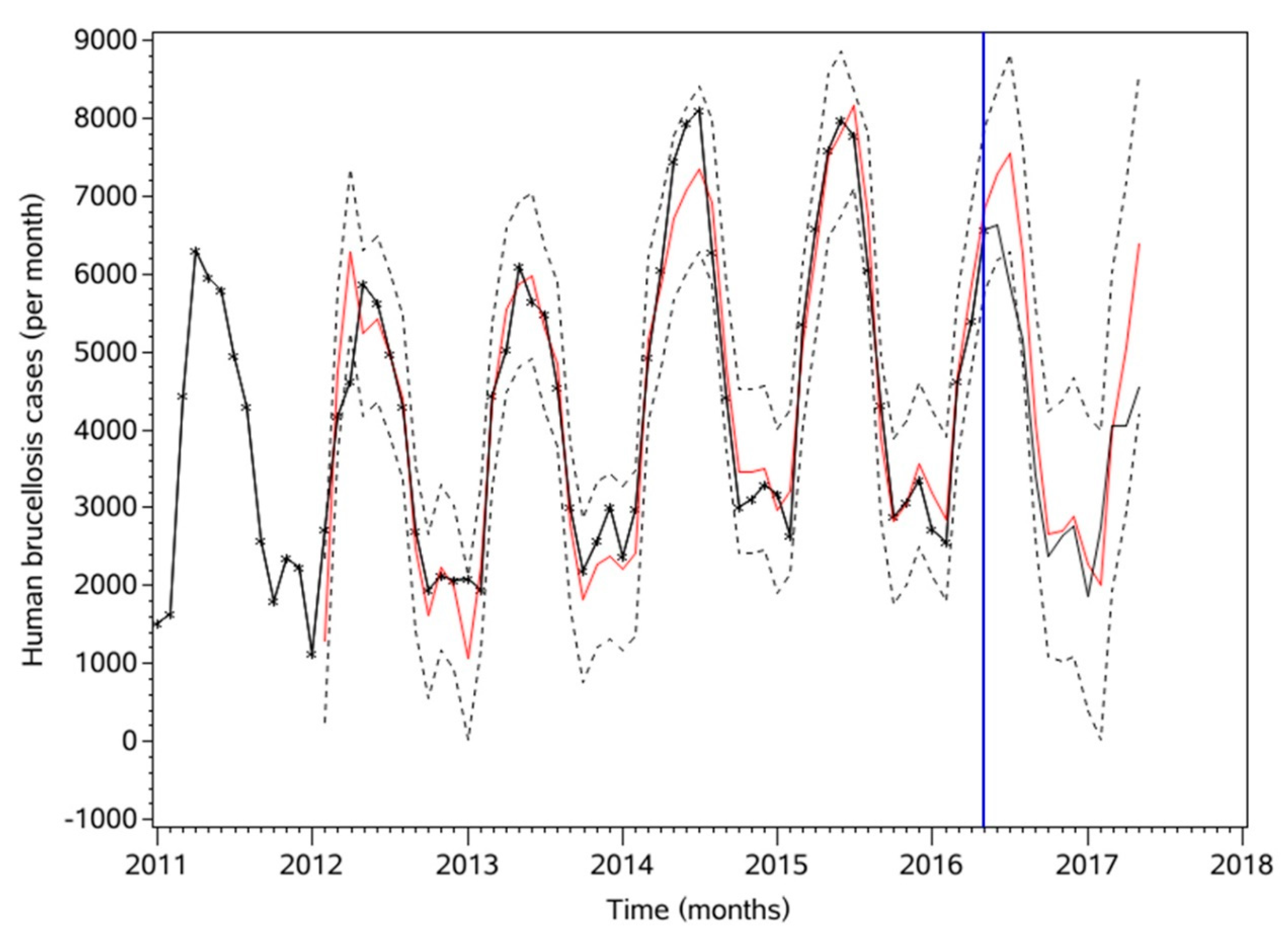
3.5. Assessing Model Performance
4. Discussion
4.1. Trends and Seasonal Periodicity
4.2. The Interrelations of Variables and Their Significance
4.3. Other Factors
4.4. Limitations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pappas, G.; Papadimitriou, P.; Akritidis, N.; Christou, L.; Tsianos, E.V. The new global map of human brucellosis. Lancet Infect. Dis. 2006, 6, 91–99. [Google Scholar] [CrossRef]
- Zhong, Z.; Yu, S.; Wang, X.; Dong, S.; Xu, J.; Wang, Y.; Chen, Z.; Ren, Z.; Peng, G. Human brucellosis in the People’s Republic of China during 2005–2010. Int. J. Infect. Dis. 2013, 17, e289–e292. [Google Scholar] [CrossRef] [PubMed]
- Asiimwe, B.B.; Kansiime, C.; Rwego, I.B. Risk factors for human brucellosis in agro-pastoralist communities of south western Uganda: A case-control study. BMC Res. Notes 2015, 8, 405. [Google Scholar] [CrossRef] [PubMed]
- Abdullayev, R.; Kracalik, I.; Ismayilova, R.; Ustun, N.; Talibzade, A.; Blackburn, J.K. Analyzing the spatial and temporal distribution of human brucellosis in Azerbaijan (1995–2009) using spatial and spatio-temporal statistics. BMC Infect. Dis. 2012, 12, 185. [Google Scholar] [CrossRef] [PubMed]
- Zinsstag, J.; Roth, F.; Orkhon, D.; Chimed-Ochir, G.; Nansalmaa, M.; Kolář, J.; Vounatsou, P. A model of animal–human brucellosis transmission in Mongolia. Prev. Vet. Med. 2005, 69, 77–95. [Google Scholar] [CrossRef] [PubMed]
- De Massis, F.; Di Girolamo, A.; Petrini, A.; Pizzigallo, E.; Giovannini, A. Correlation between animal and human brucellosis in Italy during the period 1997–2002. Clin. Microbiol. Infect. 2005, 11, 632–636. [Google Scholar] [CrossRef]
- Marianelli, C.; Graziani, C.; Santangelo, C.; Xibilia, M.T.; Imbriani, A.; Amato, R.; Neri, D.; Cuccia, M.; Rinnone, S.; Di Marco, V.; et al. Molecular Epidemiological and Antibiotic Susceptibility Characterization of Brucella Isolates from Humans in Sicily, Italy. J. Clin. Microbiol. 2007, 45, 2923–2928. [Google Scholar] [CrossRef]
- Memish, Z.A.; Balkhy, H.H. Brucellosis and International Travel. J. Travel Med. 2004, 11, 49–55. [Google Scholar] [CrossRef] [Green Version]
- Punda-Polić, V.; Cvetnić, Ž. Human brucellosis in Croatia. Lancet Infect. Dis. 2006, 9, 540–541. [Google Scholar] [CrossRef]
- Bossi, P.; Tegnell, A.; Baka, A.; Van Loock, F.; Hendriks, J.; Werner, A.; Maidhof, H.; Gouvras, G. Bichat guidelines for the clinical management of brucellosis and bioterrorism-related brucellosis. Eurosurveillance 2004, 9, 33–34. [Google Scholar] [CrossRef]
- Corbel, M.J. Brucellosis: An Overview. Emerg. Infect. Dis. 1997, 3, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Earhart, K.; Vafakolov, S.; Yarmohamedova, N.; Michael, A.; Tjaden, J.; Soliman, A. Risk factors for brucellosis in Samarqand Oblast, Uzbekistan. Int. J. Infect. Dis. 2009, 13, 749–753. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shang, D.Q.; Xiao, D.L.; Yin, J.M. Epidemiology and control of brucellosis in China. Vet. Microbiol. 2002, 90, 165–182. [Google Scholar]
- Sohn, A.H.; Probert, W.S.; Glaser, C.A.; Gupta, N.; Bollen, A.W.; Wong, J.D.; Grace, E.M.; McDonald, W.C. Human Neurobrucellosis with Intracerebral Granuloma Caused by a Marine Mammal Brucella spp. Emerg. Infect. Dis. 2003, 9, 485–488. [Google Scholar] [CrossRef]
- Jia, P.; Joyner, A. Human brucellosis occurrences in inner mongolia, China: A spatio-temporal distribution and ecological niche modeling approach. BMC Infect. Dis. 2015, 15, 36. [Google Scholar] [CrossRef]
- Mufinda, F.C.; Boinas, F.; Nunes, C. Prevalence and factors associated with human brucellosis in livestock professionals. Rev. Saúde Pública 2017, 51, 57. [Google Scholar] [CrossRef]
- Sanjuan-Jimenez, R.; Colmenero, J.D.; Morata, P. Lessons learned with molecular methods targeting the BCSP-31 membrane protein for diagnosis of human brucellosis. Clin. Chim. Acta 2017, 469, 1–9. [Google Scholar] [CrossRef]
- Jain-Gupta, N.; Contreras-Rodriguez, A.; Vemulapalli, R.; Witonsky, S.G.; Boyle, S.M.; Sriranganathan, N. Pluronic P85 enhances the efficacy of outer membrane vesicles as a subunit vaccine against Brucella melitensis challenge in mice. FEMS Immunol. Med. Microbiol. 2012, 66, 436–444. [Google Scholar] [CrossRef]
- Banai, M. Control of small ruminant brucellosis by use of Brucella melitensis Rev.1 vaccine: Laboratory aspects and field observations. Vet. Microbiol. 2002, 90, 497–519. [Google Scholar] [CrossRef]
- Godfroid, J.; Käsbohrer, A. Brucellosis in the European Union and Norway at the turn of the twenty-first century. Vet. Microbiol. 2002, 90, 135–145. [Google Scholar] [CrossRef]
- Carneiro, P.A.; Kaneene, J.B. Bovine tuberculosis control and eradication in Brazil: Lessons to learn from the US and Australia. Food Control 2018, 93, 61–69. [Google Scholar] [CrossRef]
- Chen, J.-D.; Ke, C.-W.; Deng, X.; Jiang, S.; Liang, W.; Ke, B.-X.; Li, B.; Tan, H.; Liu, M. Brucellosis in Guangdong Province, People’s Republic of China, 2005–2010. Emerg. Infect. Dis. 2013, 19, 817–818. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, W.; Ke, Y.; Zhen, Q.; Yuan, X.; Zou, W.; Li, S.; Sun, Y.; Cui, B.; Song, H.; et al. Human Brucellosis, a Heterogeneously Distributed, Delayed, and Misdiagnosed Disease in China. Clin. Infect. Dis. 2013, 56, 750–751. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lai, S.J.; Zhou, H.; Xiong, W.Y.; Gilbert, M.; Huang, Z.J.; Yu, J.X.; Yin, W.W.; Wang, L.P.; Chen, Q.L.; Li, Y.; et al. Changing Epidemiology of Human Brucellosis, China, 1955–2014. Emerg. Infect. Dis. 2017, 2, 184–194. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, F.; Zhang, T.; Yang, C.; Zhang, X.; Feng, Z.; Li, X. Spatial analysis on human brucellosis incidence in mainland China: 2004–2010. BMJ Open 2014, 4, 004470. [Google Scholar] [CrossRef]
- Wang, J.; Jia, P.; Cuadros, D.F.; Xu, M.; Wang, X.; Guo, W.; Portnov, B.A.; Bao, Y.; Chang, Y.; Song, G.; et al. A Remote Sensing Data Based Artificial Neural Network Approach for Predicting Climate-Sensitive Infectious Disease Outbreaks: A Case Study of Human Brucellosis. Remote Sens. 2017, 9, 1018. [Google Scholar] [CrossRef]
- Li, Y.-J.; Li, X.-L.; Liang, S.; Fang, L.-Q.; Cao, W.-C. Epidemiological features and risk factors associated with the spatial and temporal distribution of human brucellosis in China. BMC Infect. Dis. 2013, 13, 547. [Google Scholar] [CrossRef]
- Guan, P.; Wu, W.; Huang, D. Trends of reported human brucellosis cases in mainland China from 2007 to 2017: An exponential smoothing time series analysis. Environ. Heal. Prev. Med. 2018, 1, 23. [Google Scholar] [CrossRef]
- Yang, L.; Bi, Z.W.; Kou, Z.Q.; Li, X.J.; Zhang, M.; Wang, M.; Zhang, L.Y.; Zhao, Z.T. Time-series analysis on human brucellosis during 2004-2013 in Shandong Province, China. Zoonoses Public Health 2015, 3, 228–235. [Google Scholar] [CrossRef]
- Lee, H.S.; Her, M.; Levine, M.; Moore, G.E. Time series analysis of human and bovine brucellosis in South Korea from 2005 to 2010. Prev. Vet. Med. 2013, 2, 190–197. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, C.; Zhang, S.; Wang, Z.; Zhu, Y.; Yuan, J. Temporal trends analysis of human brucellosis incidence in mainland China from 2004 to 2018. Sci. Rep. 2018, 8, 15901. [Google Scholar] [CrossRef] [PubMed]
- Akhtar, S.; Rozi, S. An autoregressive integrated moving average model for short-term prediction of hepatitis C virus seropositivity among male volunteer blood donors in Karachi, Pakistan. World J. Gastroenterol. 2009, 15, 1607–1612. [Google Scholar] [CrossRef] [PubMed]
- Wangdi, K.; Singhasivanon, P.; Silawan, T.; Lawpoolsri, S.; White, N.J.; Kaewkungwal, J. Development of temporal modelling for forecasting and prediction of malaria infections using time-series and ARIMAX analyses: A case study in endemic districts of Bhutan. Malar. J. 2010, 9, 251. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.Y.; Liu, X.D.; Jiang, B.F.; Yang, W.Z. Forecasting incidence of hemorrhagic fever with renal syndrome in China using ARIMA model. BMC Infect. Dis. 2011, 11, 218. [Google Scholar] [CrossRef] [PubMed]
- Martinez, E.Z.; Da Silva, E.A.S.; Fabbro, A.L.D. A SARIMA forecasting model to predict the number of cases of dengue in Campinas, State of São Paulo, Brazil. Rev. Soc. Bras. Med. Trop. 2011, 44, 436–440. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Li, R.; Qiu, J.; Sun, X.; Yuan, R.; Shi, Y.; Qu, Y.; Niu, Y. Geographical Environment Factors and Risk Mapping of Human Cystic Echinococcosis in Western China. Int. J. Environ. Res. Public Health 2018, 15, 1729. [Google Scholar] [CrossRef] [PubMed]
- Bastiaanssen, W.G.; Molden, D.J.; Makin, I.W. Remote sensing for irrigated agriculture: Examples from research and possible applications. Agric. Water Manag. 2000, 46, 137–155. [Google Scholar] [CrossRef]
- Jia, P.; Nie, Y.; Song, G. Detection of underground remains by remote sensing and geophysics. In Proceedings of the 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010. [Google Scholar]
- Jia, P.; Nie, Y.P.; Yang, L. Recognition and extraction of the ancient sites covered by thick vegetation in Hainan Province of China. In Proceedings of the 30th IEEE International Geoscience and Remote Sensing Symposium (IGARSS) on Remote Sensing—Global Vision for Local Action, Honolulu, HI, USA, 25–30 June 2010; pp. 3898–3901. [Google Scholar]
- Zhu, J.F.; Peng, J.; Nie, Y.P. Analysis of the ancient river system in Loulan period in Lop Nur region. In Proceedings of the 17th China Conference on Remote Sensing—Remote Sensing of the Environment, Hangzhou, China, 27–31 August 2010. [Google Scholar]
- Xu, M.; Cao, C.; Li, Q.; Jia, P.; Zhao, J. Ecological Niche Modeling of Risk Factors for H7N9 Human Infection in China. Int. J. Environ. Res. Public Health 2016, 13, 600. [Google Scholar] [CrossRef]
- Jia, P.; Stein, A. Using remote sensing technology to measure environmental determinants of non-communicable diseases. Int. J. Epidemiol. 2017, 46, 1343–1344. [Google Scholar] [CrossRef] [Green Version]
- Jia, P.; Joyner, A.; Sun, Y.L. Short-term Associations between Accumulated Rainfall and Atmospheric Moisture during Landfall of Three Atlantic Hurricanes. Geogr. Bull. 2014, 55, 49–62. [Google Scholar]
- Ahani, I.K.; Salari, M.; Shadman, A. Statistical models for multi-step-ahead forecasting of fine particulate matter in urban areas. Atmos. Pollut. Res. 2019, 10, 689–700. [Google Scholar] [CrossRef]
- Kim, M.; Chemere, B.; Sung, K. Effect of Heavy Rainfall Events on the Dry Matter Yield Trend of Whole Crop Maize (Zea mays L.). Agriculture 2019, 4, 75. [Google Scholar] [CrossRef]
- Aekphachaisawat, N.; Sawanyawisuth, K.; Khamsai, S.; Chattakul, P.; Takahashi, K.; Chotmongkol, V.; Tiamkao, S.; Limpawattana, P.; Senthong, V.; Chindaprasirt, J.; et al. An ecological study of eosinophilic meningitis caused by the nematode, Angiostrongylus cantonensis (Chen, 1935) (Nematoda: Metastrongylidae). Parasitol. Int. 2019, 72, 101944. [Google Scholar] [CrossRef] [PubMed]
- Chinese Center for Disease Control and Prevention (CDC). Available online: http://www.nhc.gov.cn/jkj/s2907/new_list.shtml (accessed on 20 August 2019).
- International Scientific & Technical Data Mirror Site, Computer Network Information Center, Chinese Academy of Sciences. Available online: http://www.gscloud.cn (accessed on 20 August 2019).
- Briet, O.J.; Vounatsou, P.; Gunawardena, D.M.; Galappaththy, G.N.; Amerasinghe, P.H. Models for short term malaria prediction in Sri Lanka. Malar. J. 2008, 7, 76. [Google Scholar] [CrossRef] [PubMed]
- Moghram, l.; Rahrnan, S. Analysis and evaluation of five short-term load forecasting techniques. IEEE Trans. Power Syst. 1989, 4, 1484–1491. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Yang, M.; Zhang, T.; Young, A.A.; Li, X. Comparative Study of Four Time Series Methods in Forecasting Typhoid Fever Incidence in China. PLoS ONE 2013, 8, e63116. [Google Scholar] [CrossRef]
- National Development and Reform Commission of China. National Beef and Mutton Production Development Plan (2013–2020). Available online: http://www.ndrc.gov.cn/zcfb/zcfbghwb/201402/P020140221362074574291.pdf (accessed on 20 August 2019).
| Type | Lags | Rho | Pr < Rho | Tau | Pr < Tau | F | Pr > F |
|---|---|---|---|---|---|---|---|
| Zero Mean | 0 | −69.6921 | <0.0001 | −11.03 | <0.0001 | ||
| 1 | −110.947 | 0.0001 | −7.51 | <0.0001 | |||
| 2 | −90.4384 | <0.0001 | −5.33 | <0.0001 | |||
| 3 | −76.5233 | <0.0001 | −3.75 | 0.0004 | |||
| Single Mean | 0 | −69.7764 | 0.0004 | −10.96 | 0.0001 | 60.15 | 0.001 |
| 1 | −111.796 | 0.0001 | −7.46 | 0.0001 | 27.81 | 0.001 | |
| 2 | −90.5227 | 0.0004 | −5.26 | 0.0001 | 13.91 | 0.001 | |
| 3 | −77.2761 | 0.0004 | −3.71 | 0.0067 | 6.89 | 0.0042 | |
| Trend | 0 | −70.1527 | <0.0001 | −10.87 | <0.0001 | 59.35 | 0.001 |
| 1 | −116.393 | 0.0001 | −7.56 | <0.0001 | 28.57 | 0.001 | |
| 2 | −107.518 | 0.0001 | −5.74 | 0.0001 | 17.26 | 0.001 | |
| 3 | −112.044 | 0.0001 | −4.11 | 0.0113 | 8.59 | 0.0126 |
| Variable | Model | AIC Value | SBC Value | Optimization Model |
|---|---|---|---|---|
| LST | ARMA (2, 1) | 340.43 | 349.13 | ARMA (2, 1) |
| NDVI | ARMA (2, 0) | 237.51 | 230.99 | ARMA (2,1) |
| ARMA (2, 1) | 253.63 | 244.94 | ||
| ARMA (3, 2) | 249.83 | 236.79 |
| Parameter | Estimate | Standard Error | t-Value | Approx | Lag | Variable | Shift |
|---|---|---|---|---|---|---|---|
| Pr > |t| | |||||||
| MA1,1 | 0.53724 | 0.12945 | 4.15 | 0.0001 | 1 | HB | 0 |
| MA2,1 | 0.57166 | 0.14307 | 4.00 | 0.0002 | 12 | HB | 0 |
| NUM1 | −36.80113 | 16.58224 | −2.22 | 0.0314 | 0 | LST | 0 |
| NUM1,1 | −25.29822 | 12.04109 | −2.10 | 0.0412 | 1 | LST | 0 |
| NUM2 | 5000.2 | 1720.1 | 2.91 | 0.0056 | 0 | NDVI | 0 |
| NUM1,1 | 4680.1 | 1571.9 | 2.98 | 0.0046 | 1 | NDVI | 0 |
| Lag | χ 2 | df | Pr > χ 2 | Autocorrelations | |||||
|---|---|---|---|---|---|---|---|---|---|
| 6 m | 1.12 | 4 | 0.8908 | 0.052 | −0.118 | 0.022 | 0.047 | −0.009 | −0.020 |
| 12 m | 3.26 | 10 | 0.9746 | −0.036 | 0.063 | −0.099 | −0.058 | 0.117 | −0.007 |
| 18 m | 7.37 | 16 | 0.9654 | −0.081 | −0.015 | 0.038 | 0.153 | 0.144 | 0.019 |
| 24 m | 10.26 | 22 | 0.9837 | −0.079 | 0.002 | −0.051 | −0.097 | −0.092 | 0.066 |
| Time | Forecast | 95% Confidence Limits | |
|---|---|---|---|
| June 2016 | 7270.13 | 6170.46 | 8372.49 |
| July 2016 | 7512.87 | 6285.99 | 8820.31 |
| August 2016 | 6194.6 | 4859.57 | 7645.41 |
| September 2016 | 4070.9 | 2598.44 | 5576.09 |
| October 2016 | 2621.38 | 1086.38 | 4242.86 |
| November 2016 | 2712.06 | 1017.16 | 4374.35 |
| December 2016 | 2948.77 | 1096.85 | 4673.4 |
| January 2017 | 2285.18 | 382.38 | 4166.83 |
| February 2017 | 1988.04 | 33.07 | 3989.59 |
| March 2017 | 3884.78 | 1925.2 | 6020.5 |
| April 2017 | 5013.8 | 2947.99 | 7172.93 |
| May 2017 | 6347.48 | 4193 | 8560.69 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Li, R.; Qiu, J.; Sun, X.; Gao, L.; Wu, M. Prediction of Human Brucellosis in China Based on Temperature and NDVI. Int. J. Environ. Res. Public Health 2019, 16, 4289. https://doi.org/10.3390/ijerph16214289
Zhao Y, Li R, Qiu J, Sun X, Gao L, Wu M. Prediction of Human Brucellosis in China Based on Temperature and NDVI. International Journal of Environmental Research and Public Health. 2019; 16(21):4289. https://doi.org/10.3390/ijerph16214289
Chicago/Turabian StyleZhao, Yongqing, Rendong Li, Juan Qiu, Xiangdong Sun, Lu Gao, and Mingquan Wu. 2019. "Prediction of Human Brucellosis in China Based on Temperature and NDVI" International Journal of Environmental Research and Public Health 16, no. 21: 4289. https://doi.org/10.3390/ijerph16214289






