Sun Exposure of Body Districts: Development and Validation of an Algorithm to Predict the Erythemal Ultra Violet Dose
Abstract
1. Introduction
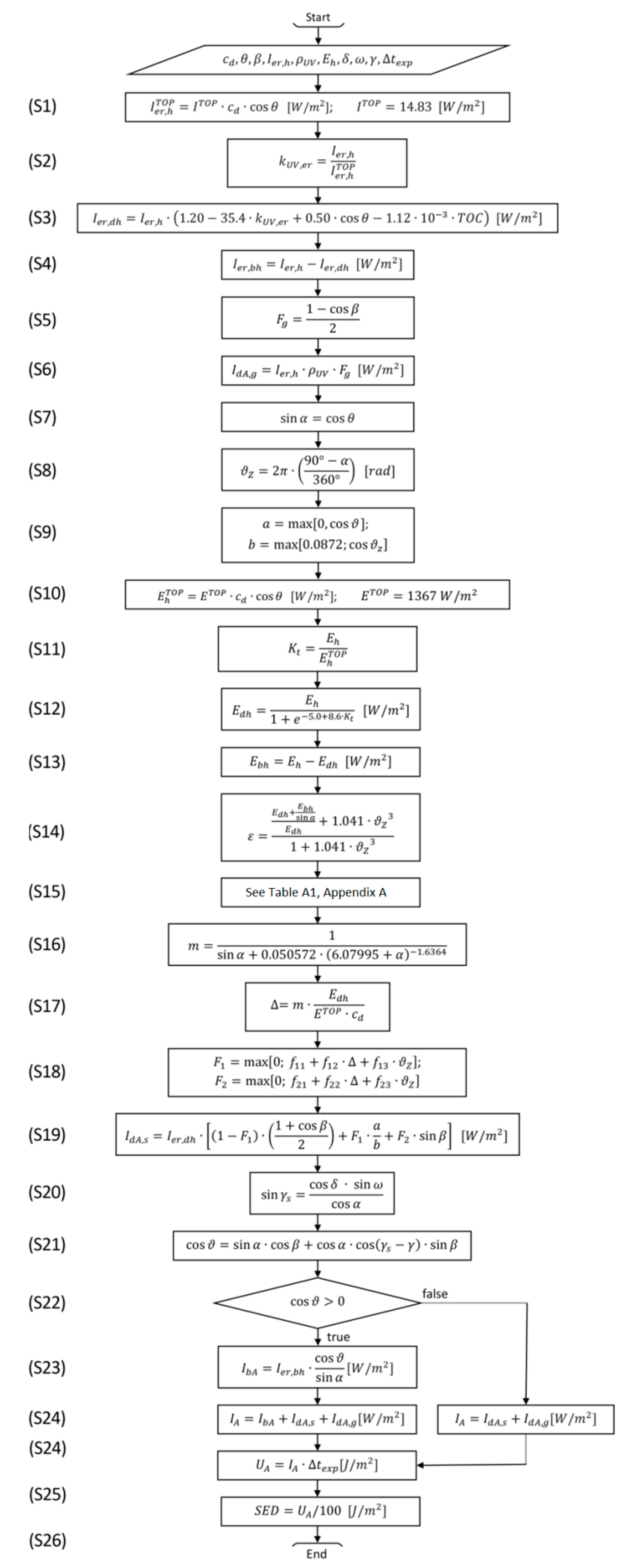
2. Algorithm for the Calculation of the Erythemal UV Dose on Sloped Surfaces
3. Use of the Algorithm: Numerical Examples
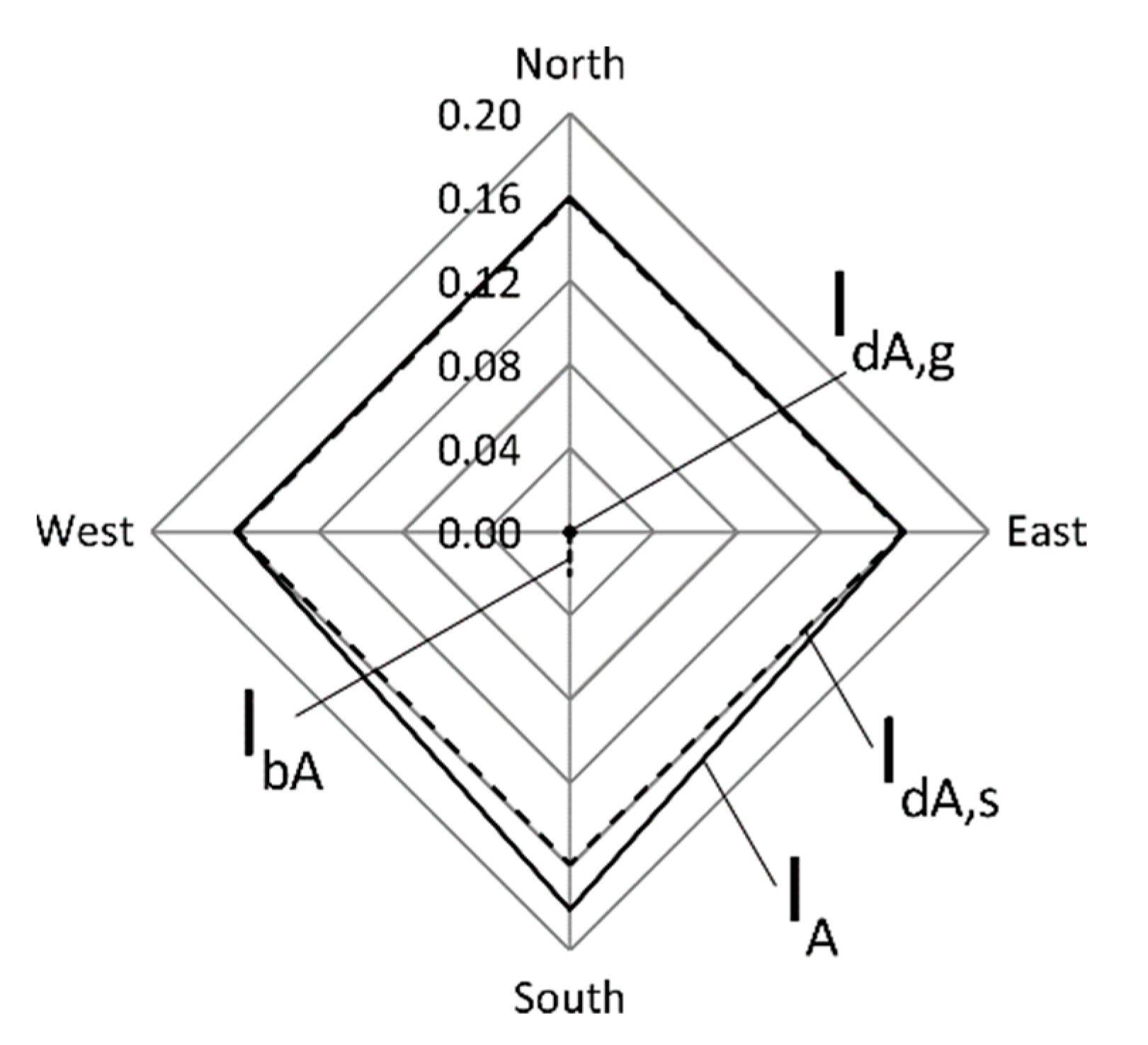
3.1. Case A: Assessment of Erythemal UV Dose on Different Vertical Surfaces Facing the Four Cardinal Points
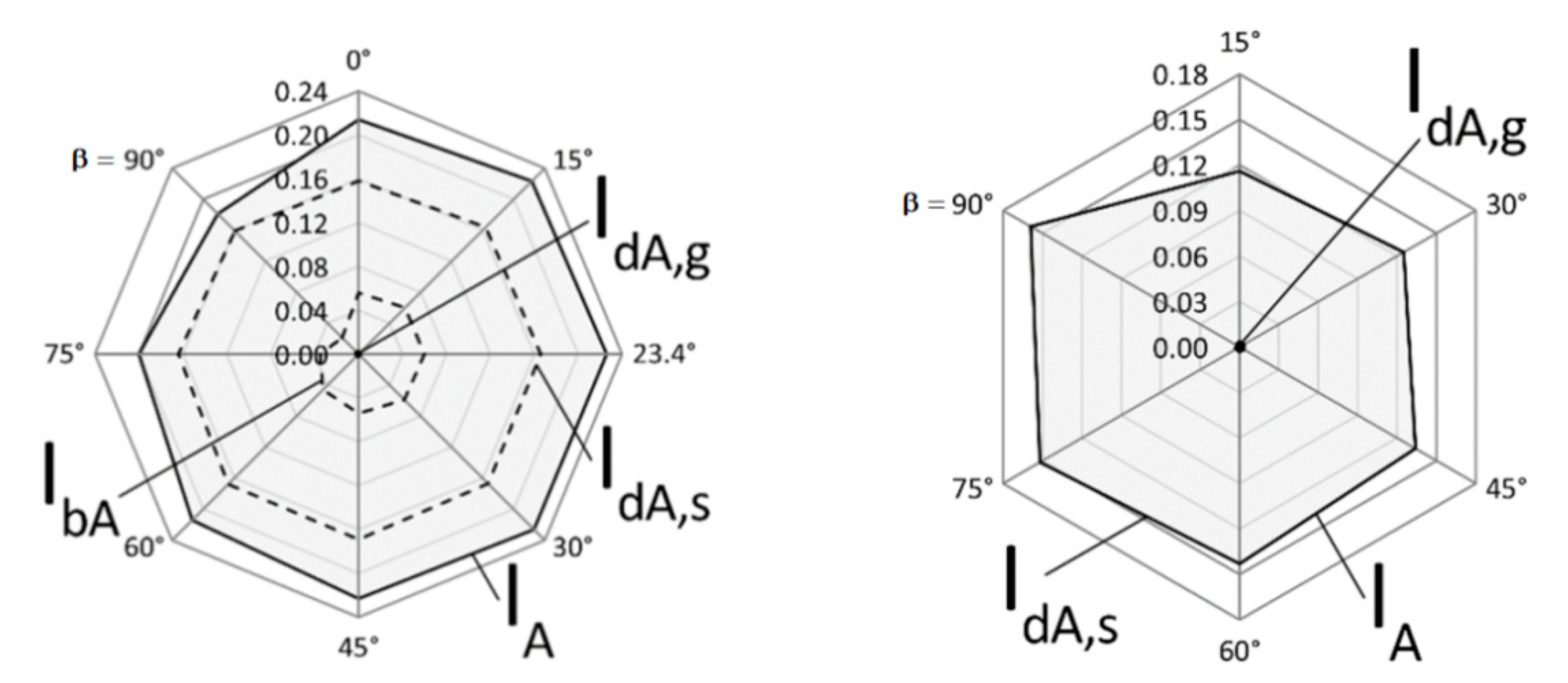
3.2. Case B: Assessment of Erythemal UV Dose on Different Sloped Surfaces Facing South and North
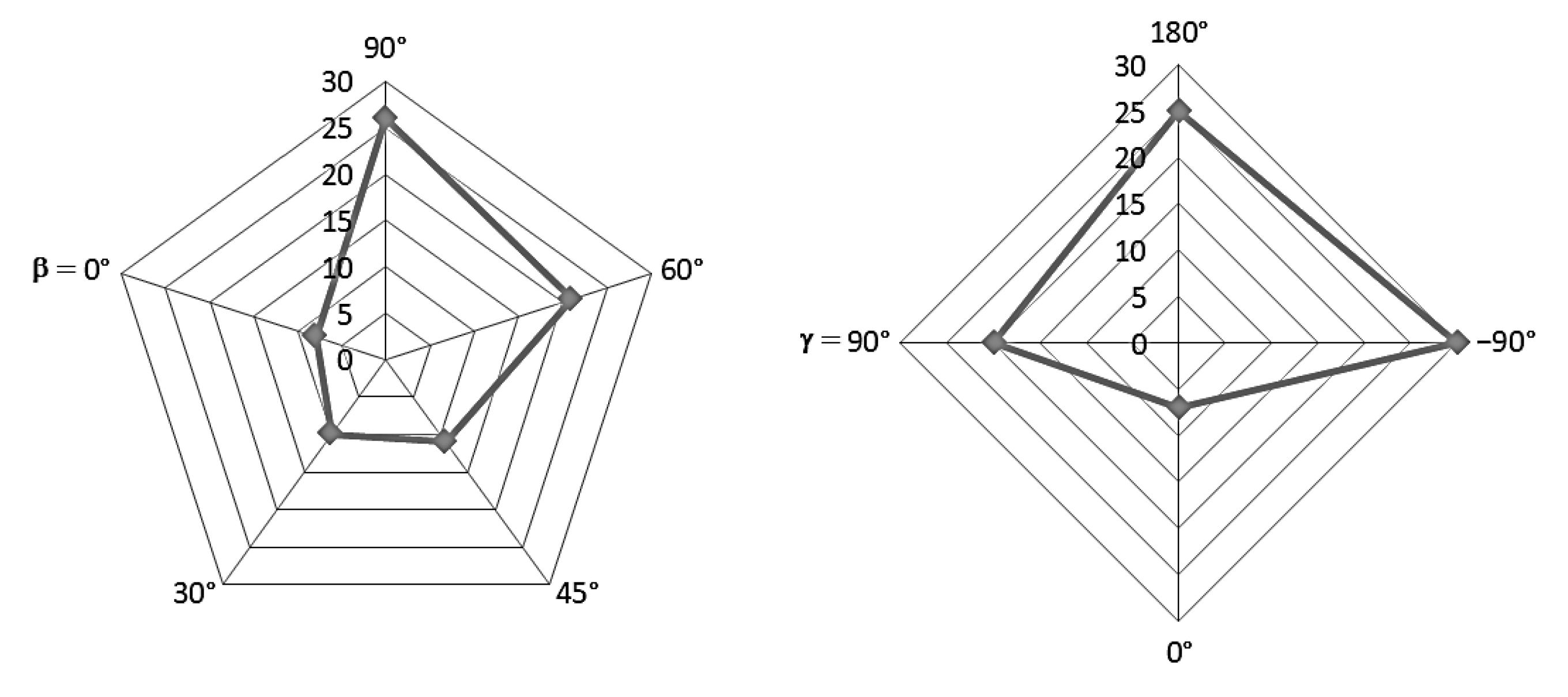
4. Validation of the Algorithm
4.1. Field Measurements of Erythemal UV Dose
4.2. Application of the Algorithm to the Measured Conditions
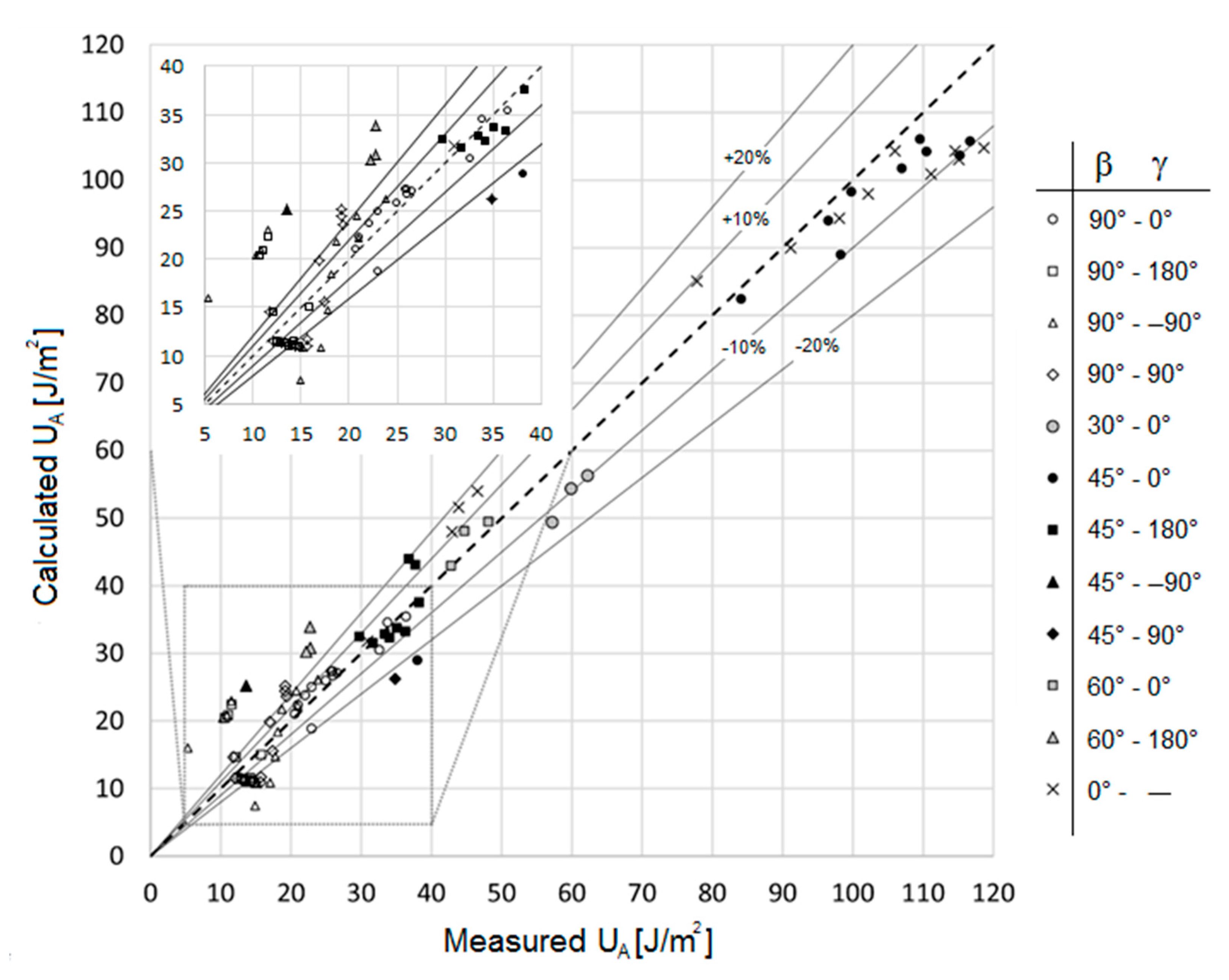
4.3. Comparison between Measured and Calculated Values of the Erythemal UV Dose
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| ε | 1.000–1.065 | 1.065–1.230 | 1.230–1.500 | 1.500–1.950 | 1.950–2.800 | 2.800–4.500 | 4.500–6.200 | >6.200 |
|---|---|---|---|---|---|---|---|---|
| f11 | −0.0083 | 0.1299 | 0.3297 | 0.5682 | 0.8730 | 1.1326 | 1.0602 | 0.6777 |
| f12 | 0.5877 | 0.6826 | 0.4869 | 0.1875 | −0.3920 | −1.2367 | −1.5999 | −0.3273 |
| f13 | −0.0621 | −0.1514 | −0.2211 | −0.2951 | −0.3616 | −0.4118 | −0.3589 | −0.2504 |
| f21 | −0.0596 | −0.0189 | 0.0554 | 0.1089 | 0.2256 | 0.2878 | 0.2642 | 0.1561 |
| f22 | 0.0721 | 0.0660 | −0.0640 | −0.1519 | −0.4620 | −0.8230 | −1.1272 | −1.3765 |
| f23 | −0.0220 | −0.0289 | −0.0261 | −0.0140 | 0.0012 | 0.0559 | 0.1311 | 0.2506 |
| Symbol | Unit | Description |
|---|---|---|
| a, b | - | coefficients considering the angle of incidence of Sun rays on the investigated surface |
| cd | - | eccentricity correction factor of Earth’s orbit |
| Ebh | W/m2 | direct component of the solar total irradiance on a horizontal surface |
| Edh | W/m2 | diffuse component of the solar total irradiance on a horizontal surface |
| Eh | W/m2 | solar total irradiance on a horizontal surface |
| ETOP | W/m2 | solar total irradiance at the top of the atmosphere, equal to 1367 W/m2 |
| Fg | - | view-factor between the visible portion of the ground and the considered surface |
| F1 | - | coefficient for the circumsolar irradiance |
| F2 | - | coefficient for the horizon irradiance |
| IA | W/m2 | Erythemal UV irradiance arriving on the investigated surface |
| IbA | W/m2 | direct component of Erythemal UV irradiance |
| Ier,h | W/m2 | Erythemal UV irradiance on a horizontal surface |
| IdA,g | W/m2 | Erythemal UV irradiance reflected from the ground |
| IdA,s | W/m2 | Erythemal UV irradiance diffused from the sky |
| Ier,bh | W/m2 | direct component of the Erythemal UV irradiance on a horizontal surface |
| Ier,dh | W/m2 | diffuse component of the Erythemal UV irradiance on a horizontal surface |
| Ier,hTOP | W/m2 | Erythemal UV irradiance at the top of the atmosphere |
| ITOP | W/m2 | UV solar constant erythemally weighted, equal to 14.83 W/m2 |
| Kt | - | Clearness index |
| kUV,er | - | UV clearness index |
| m | - | air optic mass |
| SED | J/m2 | Standard Erythemal Dose received by a plane during the time of exposure Δtexp |
| UA | J/m2 | Erythemal UV dose arriving on the investigated surface during an exposure time of Δtexp |
| α | ° | angle of elevation of the Sun |
| β | ° | inclination angle (angle between the horizontal and the investigated surface) |
| γ | ° | azimuth angle (angle between the perpendicular projection on a horizontal plane of the investigated surface and the south direction, positive in the direction from south to west) |
| γs | ° | solar azimuth angle |
| δ | ° | solar declination angle |
| Δ | - | coefficient of brightness |
| Δtexp | s | time of exposure of the investigated surface between the instant ti and the instant ti+1 |
| ε | - | coefficient of transparency of the sky |
| θ | ° | solar zenith angle |
| ϑZ | rad | solar zenith angle |
| ϑ | ° | angle of incidence of the Sun rays on the investigated surface |
| ρUV | - | ground albedo in the UV wavelengths |
| ω | ° | hour angle |
References
- CIE 209. Rationalizing Nomenclature for UV Doses and Effects on Humans; International Commission of Illumination: Wien, Austria, 2014. [Google Scholar]
- Ghetti, F.; Checcucci, G.; Bornman, J.F. Environmental UV Radiation: Impact on Ecosystems and Human Health and Predictive Models, 1st ed.; Springer: Dordrecht, The Netherlands, 2001; pp. 1–288. [Google Scholar]
- Militello, A.; Borra, M.; Bisegna, F.; Burattini, C.; Grandi, C. Smart technologies: Useful tools to assess the exposure to solar ultra violet radiation for general population and outdoor workers. In Proceedings of the Fotonica 2016—18th Italian National Conference on Photonic Technologies, Rome, Italy, 6–8 June 2016; pp. 1–4. [Google Scholar]
- IARC 55. Evaluation of Carcinogenic Risks to Humans—Solar and Ultraviolet Radiation; International Agency for Research on Cancer: Lyon, France, 1992. [Google Scholar]
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Guidelines on limits of exposure to Ultraviolet Radiation of wavelengths between 180 nm and 400 nm (incoherent optical radiation). Health Phys. 2004, 87, 171–186. [Google Scholar] [CrossRef] [PubMed]
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Statement on protection of workers against ultraviolet radiation. Health Phys. 2010, 99, 66–87. [Google Scholar] [CrossRef] [PubMed]
- Modenese, A.; Bisegna, F.; Borra, M.; Grandi, C.; Gugliermetti, F.; Militello, A.; Gobba, F. Outdoor work and solar radiation exposure: Evaluation method for epidemiological studies. Med. Pr. 2016, 26, 577–587. [Google Scholar] [CrossRef] [PubMed]
- Modenese, A.; Korpinen, L.; Gobba, F. Solar radiation exposure and outdoor work: An underestimated occupational risk. Int. J. Environ. Res. Public Health 2018, 15, 2063. [Google Scholar] [CrossRef] [PubMed]
- Chubarova, N.; Zhdanova, Y. Ultraviolet resources over Northern Eurasia. J. Photochem. Photobiol. B Biol. 2013, 127, 38–51. [Google Scholar] [CrossRef] [PubMed]
- Lucas, R.; McMichael, T.; Smith, W.; Armstrong, B. Solar Ultraviolet Radiation: Global Burden of Disease from Solar Ultraviolet Radiation; Environmental Burden of Disease Series, No. 13; World Health Organization: Geneva, Switzerland, 2006. [Google Scholar]
- WHO. INTERSUN—The Global UV Project: A Guide and Compendium; World Health Organization: Geneva, Switzerland, 2003; pp. 1–258. [Google Scholar]
- ISO/CIE 17166. Erythema Reference Action Spectrum and Standard Erythema Dose; International Organization for Standardization: Geneva, Switzerland, 2019. [Google Scholar]
- D’Orazio, J.; Jarrett, S.; Amaro-Ortiz, A.; Scott, T. UV Radiation and the Skin. Int. J. Mol. Sci. 2013, 14, 12222–12248. [Google Scholar] [CrossRef] [PubMed]
- WHO. Global Solar UV Index: A Practical Guide; World Health Organization: Geneva, Switzerland, 2002. [Google Scholar]
- Leccese, F.; Salvadori, G.; Lista, D.; Burattini, C. Outdoor workers exposed to UV radiation: Comparison of UV Index forecasting methods. In Proceedings of the IEEE 2018—18th International Conference on Environment and Electrical Engineering, Palermo, Italy, 12–15 June 2018; pp. 1–5. [Google Scholar]
- Siani, A.M.; Casale, G.R.; Sisto, R.; Colosimo, A.; Lang, C.A.; Kimlin, M.G. Occupational Exposures to Solar Ultraviolet Radiation of Vineyard Workers in Tuscany (Italy). Photochem. Photobiol. 2011, 87, 925–934. [Google Scholar] [CrossRef] [PubMed]
- Serrano, M.A.; Cañada, J.; Moreno, J.C. Erythemal Ultraviolet Exposure in two Groups of Outdoor workers in Valencia, Spain. Photochem. Photobiol. 2009, 85, 1468–1473. [Google Scholar] [CrossRef] [PubMed]
- De Backer, H.; Koepke, P.; Bais, A.; de Cabo, X.; Frei, T.; Gillotay, D. Comparison of measured and modelled UV indices for the assessment of health risks. Meteorol. Appl. 2001, 8, 267–277. [Google Scholar] [CrossRef]
- Jacklitsch, B.; Williams, J.; Musolin, K.; Coca, A.; Kim, J.H.; Turner, N. Occupational Exposure to Heat and Hot Environments; U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, NIOSH: Cincinnati, OH, USA, 2016; pp. 1–159.
- Marini, A.; Ciribolla, C.; Lazzeri, L.; d’Errico, F. Redox-Phen solution: A water equivalent dosimeter for UVA, UVB and Xrays radiation. Radiat. Phys. Chem. 2018, 147, 7–12. [Google Scholar] [CrossRef]
- Wainwright, L.; Parisi, A.V.; Downs, N. Dual calibrated dosimeter for simultaneous measurements of erythemal and vitamin D effective solar ultraviolet radiation. J. Photochem. Photobiol. B Biol. 2016, 157, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Wainwright, L.; Parisi, A.V. Characterisation and evaluation of a miniaturised polyphenylene oxide dosimeter for ultraviolet exposures. J. Photochem. Photobiol. B Biol. 2013, 120, 98–103. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Schouten, P.W.; Parisi, A.V.; Turnbull, D.J. Usage of the polyphenylene oxide dosimeter to measure annual solar erythemal exposures. Photochem. Photobiol. 2010, 86, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Wittlich, M.; Westerhausen, S.; Kleinespel, P.; Rifer, G.; Stöppelmann, W. An approximation of occupational lifetime UVR exposure: Algorithm for retrospective assessment and current measurements. J. Eur. Acad. Dermatol. Venereol. 2016, 30, 27–33. [Google Scholar] [CrossRef] [PubMed]
- Borra, M.; Grandi, C.; Militello, A.; Burattini, C.; Gugliermetti, L.; Mangione, A.; Bisegna, F.; Modenese, A.; Gobba, F. Developing an algorithm to assess the Erythemal UV dose for outdoor workers. In Proceedings of the IEEE 2018—18th International Conference on Environment and Electrical Engineering, Palermo, Italy, 12–15 June 2018; pp. 1–5. [Google Scholar]
- Park, D.H.; Oh, S.T.; Lim, J.H. Development of UVB LED Lighting System Based on UV Dose Calculation Algorithm to Meet Individual Daily UV Dose. Appl. Sci. 2019, 9, 2479. [Google Scholar] [CrossRef]
- Gugliermetti, L.; Burattini, C.; Militello, A.; Asdrubali, F.; Salvadori, G.; Leccese, F.; Bisegna, F. Real time UV erythemal personal exposure monitoring in outdoor workplaces. In Proceedings of the IEEE 2019–19th International Conference on Environment and Electrical Engineering, Genoa, Italy, 11–14 June 2019; pp. 1–5. [Google Scholar]
- Vanicek, K.; Frei, T.; Litynska, Z.; Schmalwieser, A. UV Index for the Public, COST-713 Action Final Report, Brusselles. 1999. Available online: https://publications.europa.eu/en/publication-detail/-/publication/ed2d6032-860f-4237-bb16-c34a7daceb17/language-en (accessed on 17 September 2019).
- Al-Mostafa, Z.A.; Elminir, H.K.; Abulwfa, A.; Al-Shehri, S.M.; Alshehri, F.A.; Al-Rougy, I.M.; Bazyad, A.A. Evaluation of erythemal ultraviolet solar radiation over Saudi Arabia. Sol. Energy 2015, 113, 258–271. [Google Scholar] [CrossRef]
- Piazena, H. The effect of altitude upon the solar UV-B and UV-A Irradiance in the tropical Chilean Andes. Sol. Energy 1996, 57, 133–140. [Google Scholar] [CrossRef]
- Dvorkin, A.Y.; Steinberger, E.H. Modelling the altitude effect on solar UV radiation. Sol. Energy 1999, 65, 181–187. [Google Scholar] [CrossRef]
- Calbó, J.; Pagès, D.; González, J.A. Empirical studies of cloud effects on UV radiation: A review. Rev. Geophys. 2004, 43, 1–28. [Google Scholar] [CrossRef]
- Lovengreen, C.; Fuenzalida, H.A.; Videla, L. On the spectral dependency of UV radiation enhancements due to clouds in Valdivia, Chile. J. Geophys. Res. Atmos. 2005, 110, 1–7. [Google Scholar] [CrossRef]
- Tiba, C.; da Silva Leal, S. Enhancement of UV radiation by cloud effect in NE of Brazil. Int. J. Photoenergy 2017, 2017, 8107435. [Google Scholar] [CrossRef]
- Chadyšienė, R.; Girgždys, A. Ultraviolet radiation albedo of natural surfaces. J. Environ. Eng. Landsc. Manag. 2008, 16, 83–88. [Google Scholar] [CrossRef]
- De Paula Corrêa, M.; Ceballos, J.C. UVB surface albedo measurements using biometers. Revis. Bras. Geofís. 2008, 26, 411–416. [Google Scholar] [CrossRef]
- Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Diffuse fraction correlations. Sol. Energy 1990, 45, 1–7. [Google Scholar] [CrossRef]
- Sanchez, G.; Serrano, A.; Cancillo, M.L. Modelling the erythemal surface diffuse irradiance fraction for Badajoz, Spain. Atmos. Chem. Phys. 2017, 17, 12697–12708. [Google Scholar] [CrossRef]
- Serrano, D.; Marín, M.J.; Utrillas, M.P.; Tena, F.; Martinez-Lozano, J.A. Measurement and modelling of global erythemal irradiance on inclined planes. J. Mediterr. Meteorol. Climatol. 2010, 7, 57–66. [Google Scholar] [CrossRef]
- UNI 10349-1. Heating and Cooling of Buildings—Climatic Data—Part 1: Monthly Means for Evaluation of Energy Need for Space Heating and Cooling and Methods for Splitting Global Solar Irradiance into the Direct and Diffuse Parts and for Calculate the Solar Irradiance on Tilted Planes; Ente Nazionale Italiano di Unificazione: Milan, Italy, 2016. (In Italian) [Google Scholar]
- Serrano, D.; Marín, M.J.; Utrillas, M.P.; Tena, F.; Martinez-Lozano, J.A. Modelling of the UV Index on vertical and 40° tilted planes for different orientations. Photochem. Photobiol. Sci. 2012, 11, 333–344. [Google Scholar] [CrossRef]
- Perez, R.; Seals, R.; Ineichen, P.; Stewart, R.; Menicucci, D. A new simplified version of the Perez diffuse irradiance model for tilted surfaces. Sol. Energy 1987, 39, 221–231. [Google Scholar] [CrossRef]
- Perez, R.; Stewart, R.; Seals, R.; Guertin, T. The Development and Verification of the Perez Diffuse Radiation Model; SAND88-7030 Contractor Report; Sandia National Laboratories: Albuquerque, NM, USA, 1988; pp. 1–176. [Google Scholar]
- Utrillas, M.P.; Martínez-Lozano, J.A. Performance evaluation of several versions of the Perez tilted diffuse irradiance model. Sol. Energy 1994, 53, 155–162. [Google Scholar] [CrossRef]
- Utrillas, M.P.; Marín, M.J.; Esteve, A.R.; Estellés, V.; Tena, F.; Cañada, J.; Martínez-Lozano, J.A. Diffuse ultraviolet erythemal irradiance on inclined planes: A comparison of experimental and modelled data. Photochem. Photobiol. 2009, 85, 1245–1253. [Google Scholar] [CrossRef]
| Skin Phototype | Cutaneous Response to UV | Cancer Risk | MED (J/m2) |
|---|---|---|---|
| I—Extremely sensitive | Always burns | ++++ | 150 |
| II—Very sensitive | Burns easily | +++/++++ | 250 |
| III—Sensitive | Burns moderately | +++ | 300 |
| IV—Mildly sensitive | Burns minimally | ++ | 400 |
| V—Resistant skin | Rarely burns | + | 600 |
| VI—Very resistant | Almost never burns | +/− | 900 |
| TOC = 329 DU | Total Ozone Column (Value from: https://ozoneaq.gsfc.nasa.gov) |
| β = 90° | inclination angle of the vertical surface (case A) |
| β = variable | from 0° to 90° (case B) |
| Ier,h = 0.214 W/m2 | Erythemal UV irradiance on a horizontal surface, estimated with the TUV software (https://www2.acom.ucar.edu/modeling/tropospheric-ultraviolet-and-visible-tuv-radiation-model) |
| δ = 23.45° | solar declination angle (value from [40]) |
| ω = 0° | hour angle (value from [40]) |
| θ = 20.27° | solar zenith angle (value from [40]) |
| ρUV = 0.011 | ground albedo in the UV wavelengths (e.g., green grass, value from [35]) |
| Eh = 931.6 W/m2 | solar total irradiance (value from: http://soda-pro.com/web-services) |
| γ = −90°, 0°, 90°, 180° | azimuth angles of the surfaces facing east, south, west, north directions respectively |
| Δtexp = 3600 s | time of exposure |
| South | West | East | North | ||
|---|---|---|---|---|---|
| Ier,dh | [W/m2] | 0.158 | 0.158 | 0.158 | 0.158 |
| Ier,bh | [W/m2] | 0.056 | 0.056 | 0.056 | 0.056 |
| IdA,g | [W/m2] | 0.001 | 0.001 | 0.001 | 0.001 |
| IdA,s | [W/m2] | 0.159 | 0.159 | 0.159 | 0.159 |
| cosϑ | - | 0.346 | 0 | 0 | −0.346 |
| IbA | [W/m2] | 0.021 | 0 | 0 | 0 |
| IA | [W/m2] | 0.181 | 0.160 | 0.160 | 0.160 |
| UA | [J/m2] | 652 | 576 | 576 | 576 |
| SED | - | 6.5 | 5.8 | 5.8 | 5.8 |
| β | [°] | 0 | 15 | 30 | 45 | 60 | 75 | 90 | 23.4 |
|---|---|---|---|---|---|---|---|---|---|
| Ier,dh | [W/m2] | 0.158 | 0.158 | 0.158 | 0.158 | 0.158 | 0.158 | 0.158 | 0.158 |
| Ier,bh | [W/m2] | 0.056 | 0.056 | 0.056 | 0.056 | 0.056 | 0.056 | 0.056 | 0.056 |
| IdA,g | [W/m2] | 0 | 4.01 × 10−5 | 1.58 × 10−4 | 3.45 × 10−4 | 5.89 × 10−4 | 8.72 × 10−4 | 1.18 × 10−3 | 9.72 × 10−5 |
| IdA,s | [W/m2] | 0.158 | 0.164 | 0.167 | 0.169 | 0.168 | 0.164 | 0.159 | 0.166 |
| cosϑ | - | 0.938 | 0.996 | 0.986 | 0.908 | 0.769 | 0.577 | 0.346 | 1.000 |
| IbA | [W/m2] | 0.056 | 0.059 | 0.059 | 0.054 | 0.046 | 0.035 | 0.021 | 0.060 |
| IA | [W/m2] | 0.214 | 0.223 | 0.226 | 0.223 | 0.214 | 0.200 | 0.181 | 0.226 |
| UA | [J/m2] | 770 | 803 | 814 | 803 | 770 | 720 | 652 | 814 |
| SED | - | 7.7 | 8.0 | 8.1 | 8.0 | 7.7 | 7.2 | 6.5 | 8.1 |
| β | [°] | 15 | 30 | 45 | 60 | 75 | 90 |
|---|---|---|---|---|---|---|---|
| Ier,dh | [W/m2] | 0.158 | 0.158 | 0.158 | 0.158 | 0.158 | 0.158 |
| Ier,bh | [W/m2] | 0.056 | 0.056 | 0.056 | 0.056 | 0.056 | 0.056 |
| IdA,g | [W/m2] | 2.31 × 10−3 | 2.20 × 10−3 | 2.01 × 10−3 | 1.77 × 10−3 | 1.48 × 10−3 | 1.02 × 10−3 |
| IdA,s | [W/m2] | 0.116 | 0.125 | 0.134 | 0.143 | 0.152 | 0.159 |
| cosϑ | - | −0.996 | −0.986 | −0.908 | −0.769 | −0.577 | −0.346 |
| IbA | [W/m2] | 0 | 0 | 0 | 0 | 0 | 0 |
| IA | [W/m2] | 0.119 | 0.127 | 0.136 | 0.145 | 0.153 | 0.160 |
| UA | [J/m2] | 428 | 457 | 490 | 522 | 551 | 576 |
| SED | - | 4.3 | 4.6 | 4.9 | 5.2 | 5.5 | 5.8 |
| Rome | Guadagnolo | Pisa | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Day | 21 February 2019 | 25 February 2019 | 16 May 2019 | ||||||||
| Time band (GMT+1) | 11:30–13:00 | 13:00–13:30 | 11:30–13:30 | ||||||||
| Solar Zenith Angle [°] | 58.62–52.75 | 51.26–51.05 | 32.95–24.83 | ||||||||
| Weather | Sunny | Sunny with some clouds | Sunny | ||||||||
| Type of floor | Red brick | Gravel | Asphalt | ||||||||
| Surface of measure | β [°] | 90 | 45 | 0 | 90 | 60 | 30 | 0 | 90 | 45 | 0 |
| γ [°] | 90 0 −90 | 90 0 −90 | - | 180 90 0 −90 | 180 0 | 0 | - | 180 90 0−90 | 180 0 | - | |
| h [m] | 1.5 | ||||||||||
| Site (Day) | Hour | β [°] | γ [°] | UA [J/m2] | Site (Day) | Hour | β [°] | γ [°] | UA [J/m2] |
|---|---|---|---|---|---|---|---|---|---|
| Rome (2019-02-21) | 11:30 | 90 | 0 | 12.96 | Pisa (2019-05-16) | 12:00 | 90 | 180 | 12.90 |
| 11:45 | 90 | 17.40 | 90 | 12.96 | |||||
| 12:00 | −90 | 15.31 | 0 | 22.02 | |||||
| 12:15 | 0 | - | 30.93 | −90 | 20.94 | ||||
| 12:30 | 45 | 0 | 38.02 | 45 | 180 | 34.08 | |||
| 12:45 | 90 | 34.82 | 0 | 96.54 | |||||
| 13:00 | −90 | 22.61 | 0 | - | 98.10 | ||||
| Guadagnolo (2019-02-25) | 13:00 | 90 | 180 | 11.59 | 12:15 | 90 | 180 | 13.38 | |
| 90 | 19.21 | 90 | 13.32 | ||||||
| 0 | 36.42 | 0 | 22.98 | ||||||
| −90 | 11.51 | −90 | 18.72 | ||||||
| 60 | 180 | 22.71 | 45 | 180 | 33.36 | ||||
| 0 | 48.11 | 0 | 99.78 | ||||||
| 30 | 0 | 62.27 | 0 | - | 102.18 | ||||
| 0 | - | 46.58 | 12:30 | 90 | 180 | 14.10 | |||
| 13:15 | 90 | 180 | 11.10 | 90 | 14.34 | ||||
| 90 | 19.21 | 0 | 24.96 | ||||||
| 0 | 33.77 | −90 | 18.12 | ||||||
| −90 | 10.91 | 45 | 180 | 36.30 | |||||
| 60 | 180 | 22.75 | 0 | 106.98 | |||||
| 0 | 44.70 | 0 | - | 111.12 | |||||
| 30 | 0 | 58.90 | 12:45 | 90 | 180 | 13.68 | |||
| 0 | - | 43.88 | 90 | 14.40 | |||||
| 13:30 | 90 | 180 | 10.66 | 0 | 25.98 | ||||
| 90 | 19.37 | −90 | 17.76 | ||||||
| 0 | 32.57 | 45 | 180 | 37.74 | |||||
| −90 | 10.30 | 0 | 110.52 | ||||||
| 60 | 180 | 22.20 | 0 | - | 115.08 | ||||
| 0 | 42.79 | 13:00 | 90 | 180 | 14.82 | ||||
| 30 | 0 | 57.22 | 90 | 15.66 | |||||
| 0 | - | 42.96 | 0 | 26.58 | |||||
| Pisa (2019-05-16) | 11:30 | 90 | 180 | 12.18 | −90 | 17.04 | |||
| 90 | 11.82 | 45 | 180 | 35.10 | |||||
| 0 | 20.58 | 0 | 116.70 | ||||||
| −90 | 23.82 | 0 | - | 114.54 | |||||
| 45 | 180 | 29.76 | 13:15 | 90 | 180 | 14.22 | |||
| 0 | 84.12 | 90 | 15.72 | ||||||
| 0 | - | 77.82 | 0 | 25.74 | |||||
| 11:45 | 90 | 180 | 12.42 | −90 | 14.88 | ||||
| 90 | 12.06 | 45 | 180 | 36.78 | |||||
| 0 | 21.00 | 0 | 109.56 | ||||||
| −90 | 20.76 | 0 | - | 118.68 | |||||
| 45 | 180 | 31.68 | 13:30 | 90 | 180 | 15.78 | |||
| 0 | 98.28 | 90 | 16.98 | ||||||
| 0 | - | 91.14 | 0 | 25.92 | |||||
| −90 | 15.18 | ||||||||
| 45 | 180 | 38.28 | |||||||
| 0 | 115.26 | ||||||||
| 0 | - | 106.02 | |||||||
| Hour | Eh [W/m2] | ||
|---|---|---|---|
| Rome | Guadagnolo | Pisa | |
| 11:30 | 160.99 | - | 851.92 |
| 11:45 | 159.60 | 874.68 | |
| 12:00 | 157.04 | 894.84 | |
| 12:15 | 153.27 | 911.96 | |
| 12:30 | 148.57 | 925.72 | |
| 12:45 | 142.96 | 935.56 | |
| 13:00 | 136.48 | 100.08 | 940.20 |
| 13:15 | - | 102.12 | 922.20 |
| 13:30 | 103.77 | 911.88 | |
| Site (Day) | Hour | β [°] | γ [°] | UA [J/m2] | Site (Day) | Hour | β [°] | γ [°] | UA [J/m2] |
|---|---|---|---|---|---|---|---|---|---|
| Rome (2019-02-21) | 11:30 | 90 | 0 | 18.85 | Pisa (2019-05-16) | 12:00 | 90 | 180 | 11.42 |
| 11:45 | 90 | 15.57 | 90 | 11.42 | |||||
| 12:00 | −90 | 15.99 | 0 | 23.79 | |||||
| 12:15 | 0 | - | 31.80 | −90 | 22.23 | ||||
| 12:30 | 45 | 0 | 28.96 | 45 | 180 | 32.26 | |||
| 12:45 | 90 | 26.22 | 0 | 94.02 | |||||
| 13:00 | −90 | 25.20 | 0 | - | 94.34 | ||||
| Guadagnolo (2019-02-25) | 13:00 | 90 | 180 | 22.39 | 12:15 | 90 | 180 | 11.27 | |
| 90 | 25.15 | 90 | 11.28 | ||||||
| 0 | 35.43 | 0 | 24.98 | ||||||
| −90 | 22.99 | −90 | 21.74 | ||||||
| 60 | 180 | 33.89 | 45 | 180 | 32.82 | ||||
| 0 | 49.48 | 0 | 98.24 | ||||||
| 30 | 0 | 56.28 | 0 | - | 97.95 | ||||
| 0 | - | 54.00 | 12:30 | 90 | 180 | 11.11 | |||
| 13:15 | 90 | 180 | 20.86 | 90 | 11.15 | ||||
| 90 | 24.46 | 0 | 25.96 | ||||||
| 0 | 34.54 | −90 | 18.39 | ||||||
| −90 | 14.86 | 45 | 180 | 33.24 | |||||
| 60 | 180 | 30.79 | 0 | 101.70 | |||||
| 0 | 48.07 | 0 | - | 100.89 | |||||
| 30 | 0 | 54.32 | 12:45 | 90 | 180 | 10.97 | |||
| 0 | - | 51.60 | 90 | 11.02 | |||||
| 13:30 | 90 | 180 | 20.44 | 0 | 26.67 | ||||
| 90 | 23.61 | −90 | 14.73 | ||||||
| 0 | 30.51 | 45 | 180 | 43.11 | |||||
| −90 | 20.44 | 0 | 104.23 | ||||||
| 60 | 180 | 30.22 | 0 | - | 103.02 | ||||
| 0 | 42.94 | 13:00 | 90 | 180 | 10.92 | ||||
| 30 | 0 | 49.34 | 90 | 10.98 | |||||
| 0 | - | 48.00 | 0 | 27.11 | |||||
| Pisa (2019-05-16) | 11:30 | 90 | 180 | 14.62 | −90 | 10.89 | |||
| 90 | 14.62 | 45 | 180 | 33.72 | |||||
| 0 | 21.04 | 0 | 105.76 | ||||||
| −90 | 26.14 | 0 | - | 104.33 | |||||
| 45 | 180 | 32.48 | 13:15 | 90 | 180 | 11.51 | |||
| 0 | 82.41 | 90 | 11.70 | ||||||
| 0 | - | 85.05 | 0 | 27.28 | |||||
| 11:45 | 90 | 180 | 11.52 | −90 | 7.48 | ||||
| 90 | 11.52 | 45 | 180 | 43.96 | |||||
| 0 | 22.37 | 0 | 106.05 | ||||||
| −90 | 24.43 | 0 | - | 104.76 | |||||
| 45 | 180 | 31.50 | 13:30 | 90 | 180 | 14.99 | |||
| 0 | 88.98 | 90 | 19.86 | ||||||
| 0 | - | 89.97 | 0 | 27.33 | |||||
| −90 | 10.83 | ||||||||
| 45 | 180 | 37.52 | |||||||
| 0 | 103.68 | ||||||||
| 0 | - | 104.31 | |||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salvadori, G.; Lista, D.; Burattini, C.; Gugliermetti, L.; Leccese, F.; Bisegna, F. Sun Exposure of Body Districts: Development and Validation of an Algorithm to Predict the Erythemal Ultra Violet Dose. Int. J. Environ. Res. Public Health 2019, 16, 3632. https://doi.org/10.3390/ijerph16193632
Salvadori G, Lista D, Burattini C, Gugliermetti L, Leccese F, Bisegna F. Sun Exposure of Body Districts: Development and Validation of an Algorithm to Predict the Erythemal Ultra Violet Dose. International Journal of Environmental Research and Public Health. 2019; 16(19):3632. https://doi.org/10.3390/ijerph16193632
Chicago/Turabian StyleSalvadori, Giacomo, Davide Lista, Chiara Burattini, Luca Gugliermetti, Francesco Leccese, and Fabio Bisegna. 2019. "Sun Exposure of Body Districts: Development and Validation of an Algorithm to Predict the Erythemal Ultra Violet Dose" International Journal of Environmental Research and Public Health 16, no. 19: 3632. https://doi.org/10.3390/ijerph16193632
APA StyleSalvadori, G., Lista, D., Burattini, C., Gugliermetti, L., Leccese, F., & Bisegna, F. (2019). Sun Exposure of Body Districts: Development and Validation of an Algorithm to Predict the Erythemal Ultra Violet Dose. International Journal of Environmental Research and Public Health, 16(19), 3632. https://doi.org/10.3390/ijerph16193632








