Impact of Farmland Change on Soybean Production Potential in Recent 40 Years: A Case Study in Western Jilin, China
Abstract
1. Introduction
2. Materials and Methods
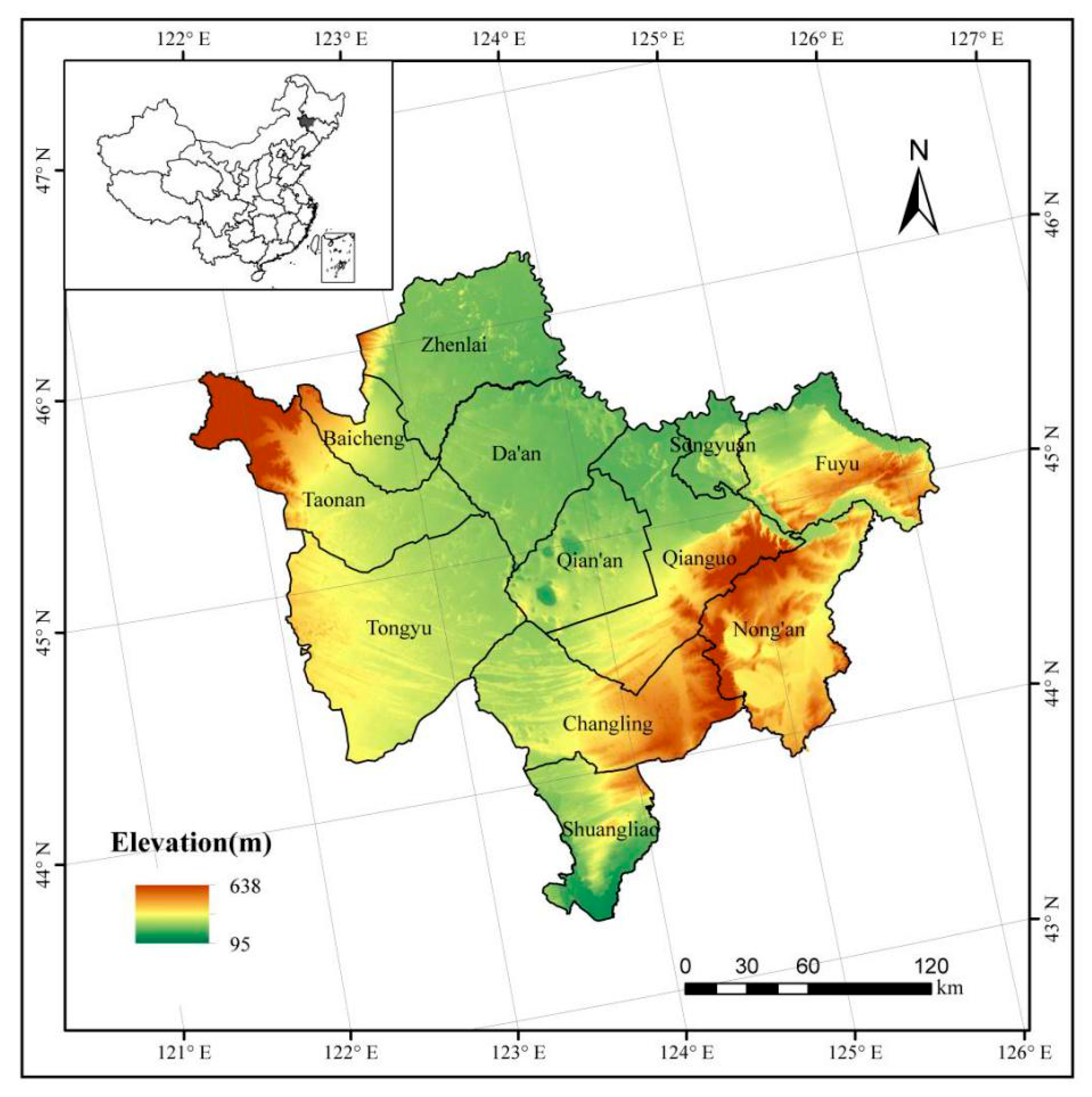
2.1. Study Area
2.2. Data Source
2.3. Methodology
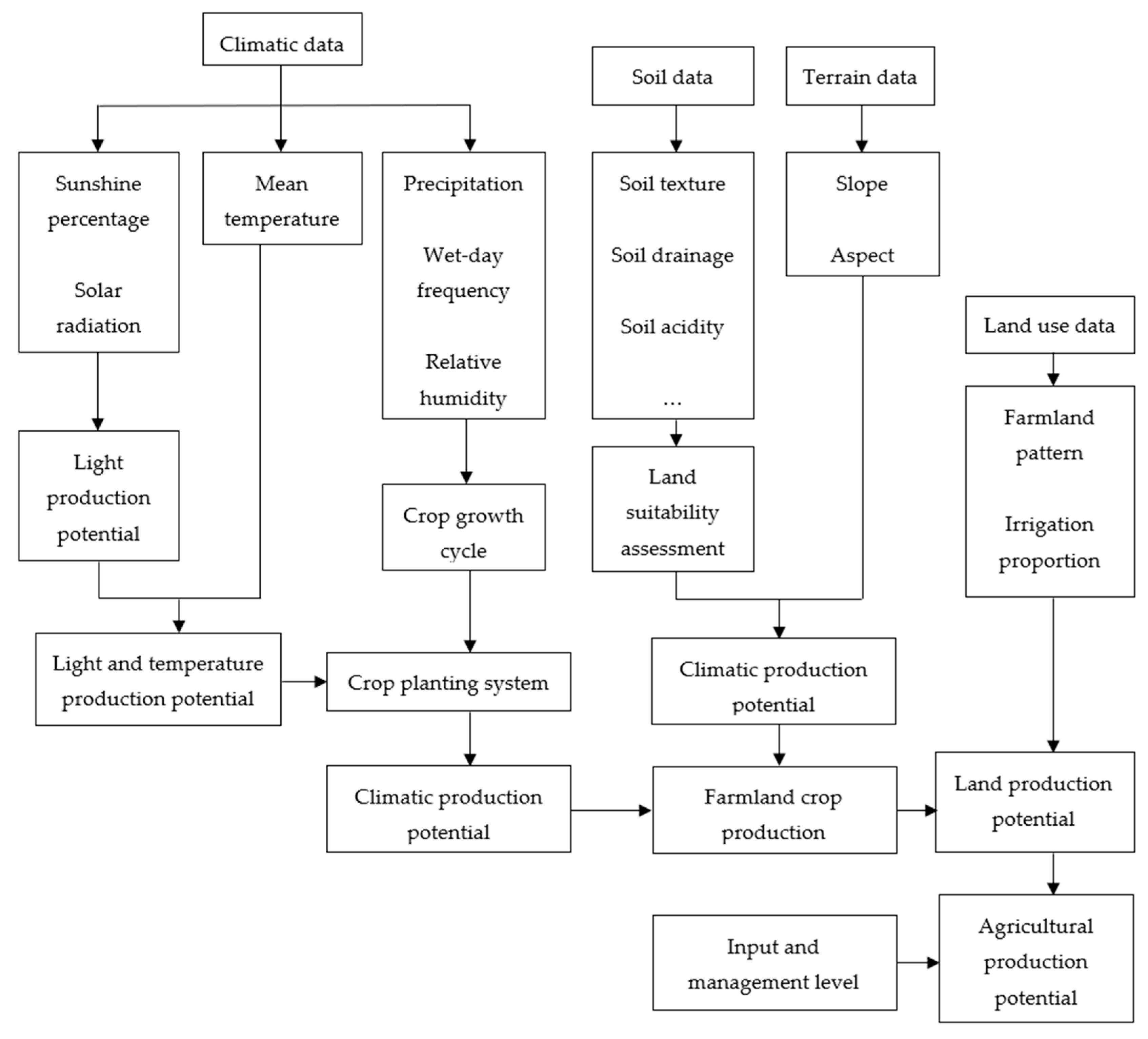
2.3.1. Crop Production Potential Simulation Method
- Module1: Climatic data analysis and compilation of general agro-climatic indicators. In Module1, seven climatic data of a specific year are input to the GAEZ model, and then the module calculates and stores climate-related variables and indicators for each grid-cell.
- Module2: Grain-specific agro-climatic assessment and potential water-limited yield calculation. Module2 calculates the yield of all crop types with the specific climate conditions, considering the limit of water supply.
- Module3: Yield-reduction due to agro-climatic constraints. This step is carried out to make explicit the effect of limitations due to soil workability, pest and diseases, and then revises the calculation results of Module2.
- Module4: Edaphic assessment and yield reduction due to soil and topography limitations. This module evaluates yield reduction due to limitations imposed by soil and topography conditions.
- Module5: Integration of results from Module1–4 into crop-specific grid-cell databases. This module reads the results of the agro-climatic evaluation for yield calculated in Module2/3 for different soil classes and it uses the edaphic rating produced for each soil/slope combination in Module4.
- Module6: Actual yield and production. This module estimates actual yield and production of specific crop types according to the percentage of farmland area to each grid-cell area and shares of rain-fed and irrigated farmland within each grid-cell, using a downscaling method.
2.3.2. Farmland Change Impact Analysis on Soybean Production Potential
3. Results and Analysis
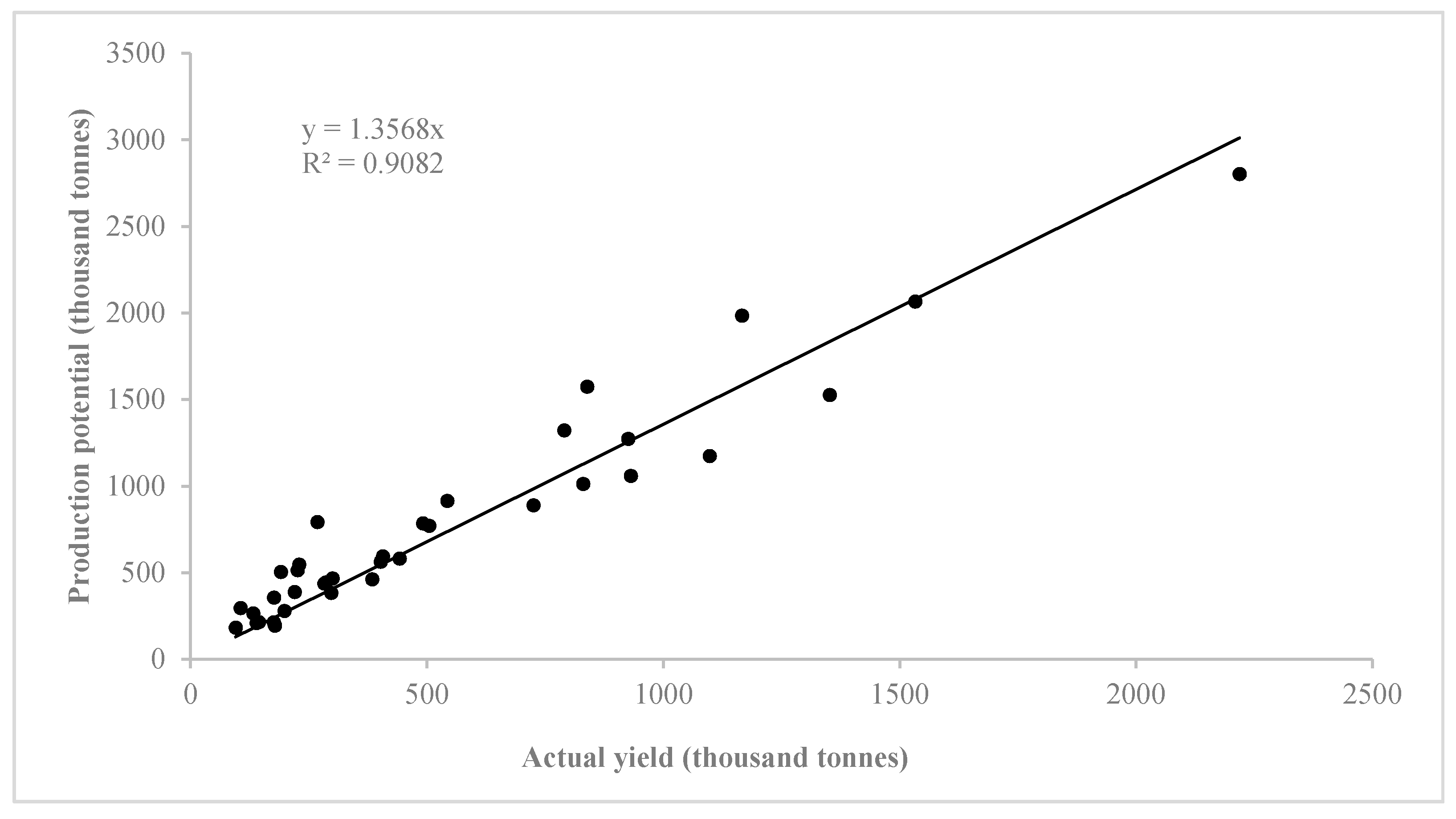
3.1. Results Validation
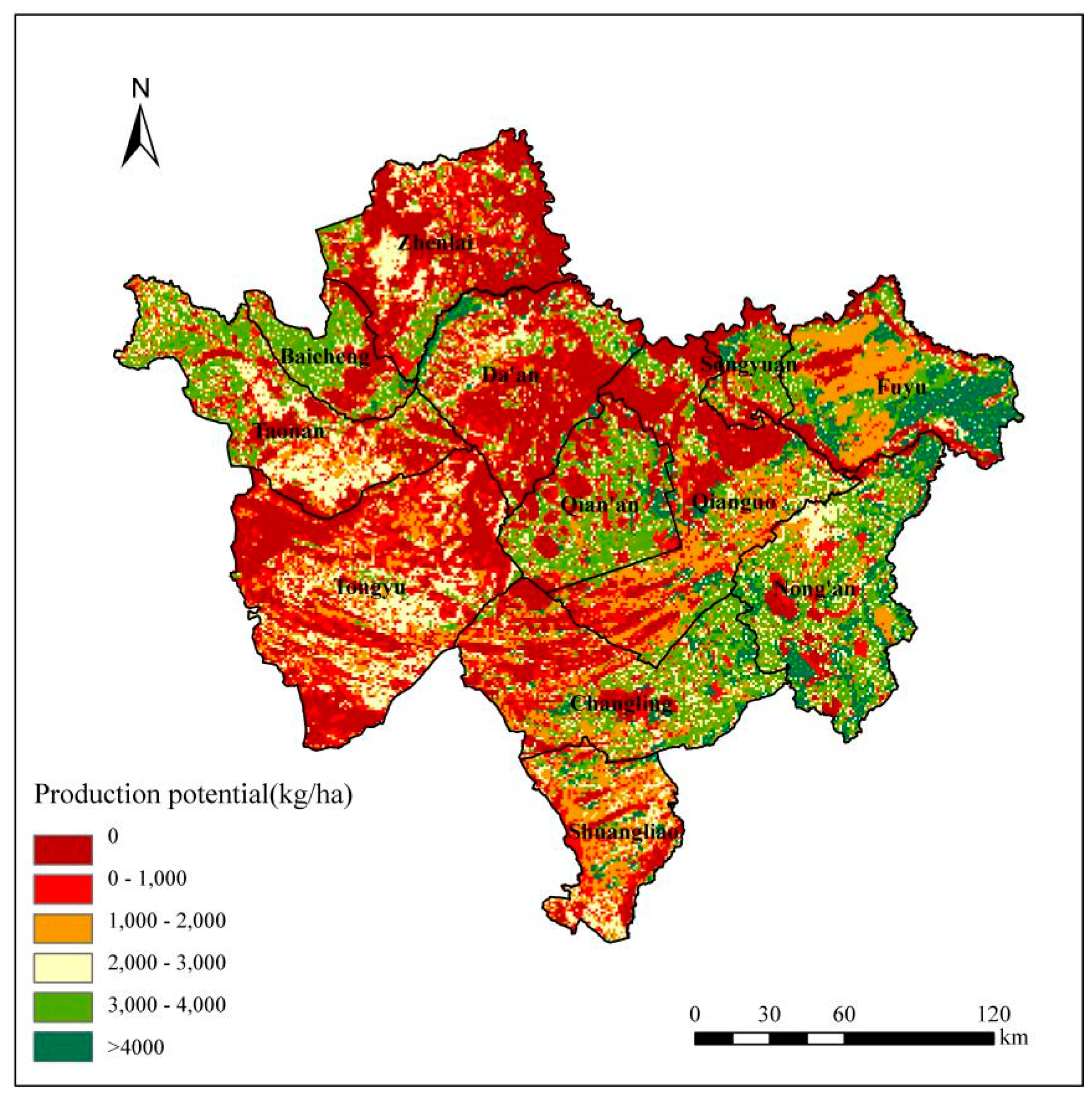
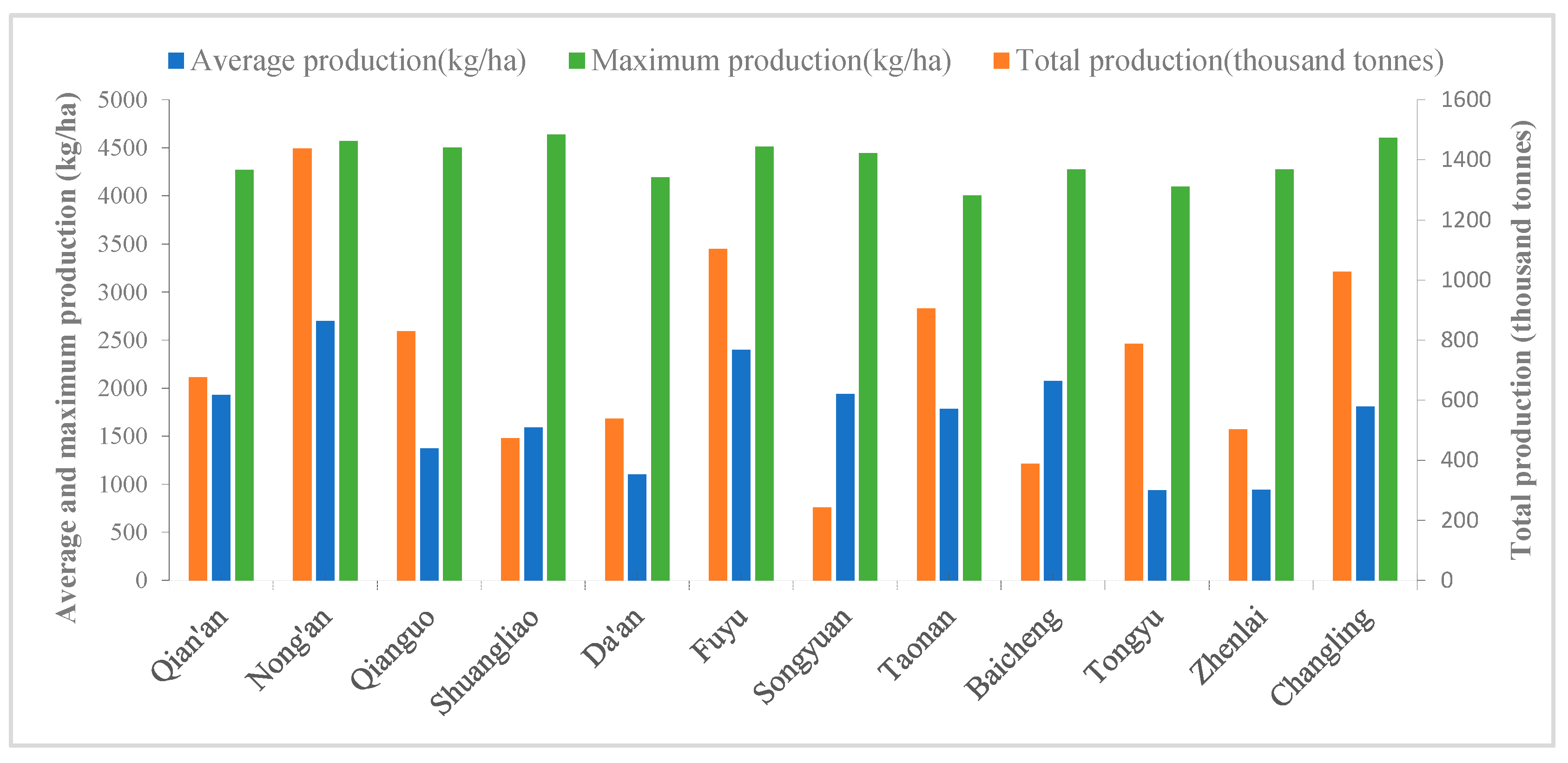
3.2. Spatial Contribution Characteristics of Soybean Production Potential in Western Jilin in 2013
3.3. Impact of Farmland Change on Soybean Production Potential
3.3.1. Characteristics of Farmland Change in Western Jilin between 1975–2013
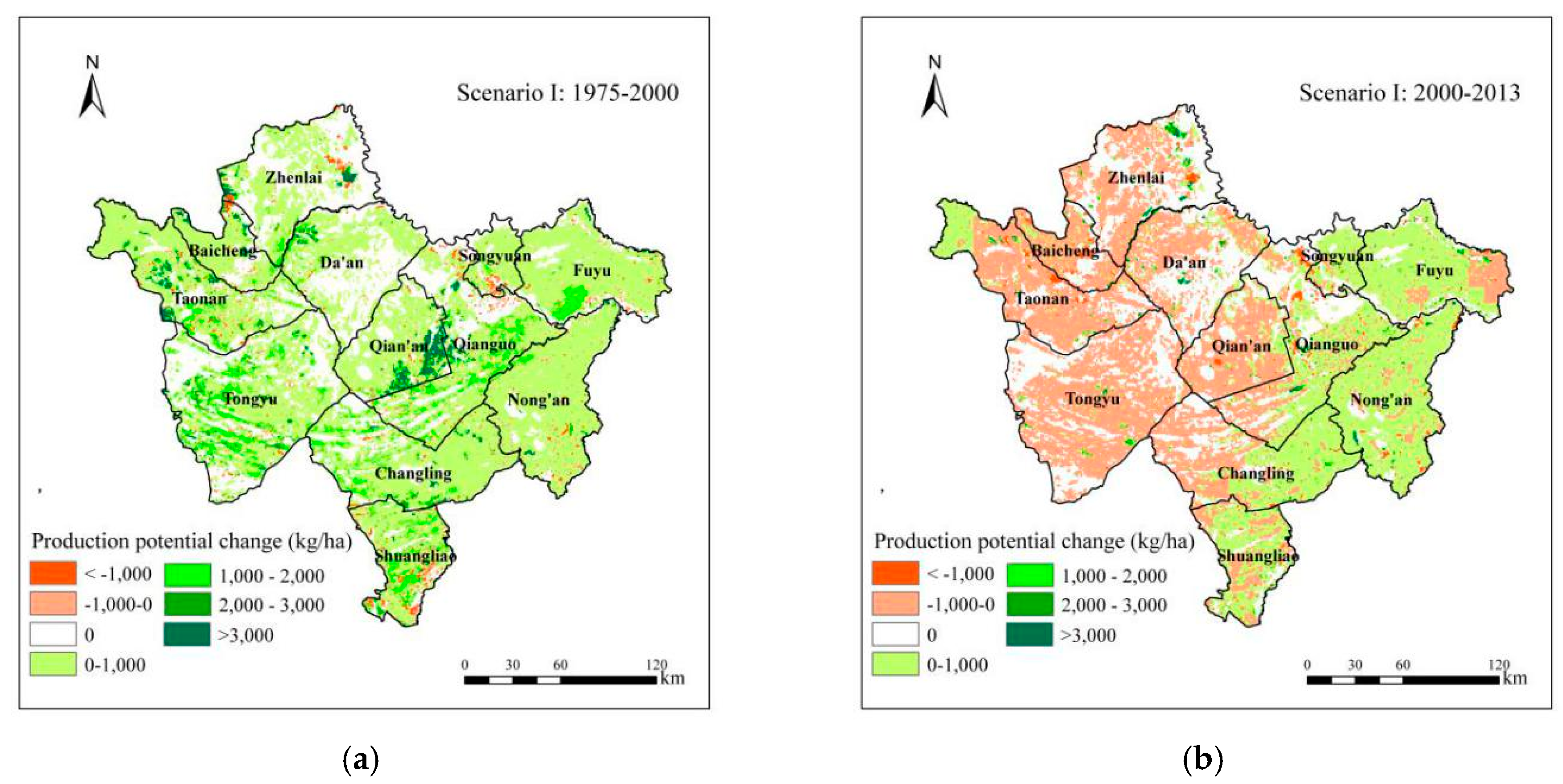
3.3.2. Impact of Farmland Change on Soybean Production Potential from 1975 to 2013
4. Discussions
4.1. Impact of Two Situations of Farmland Change on Soybean Production Potential
4.1.1. Impact of the Conversion between Dryland and Other Categories
4.1.2. Impact of the Change of Irrigation Percentage
4.2. Comparison between the GAEZ Model and Other Methods
4.3. Limitations of the GAEZ Model
4.4. Advantage of Impact of Farmland Change on Production Potential Analysis Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Tmax maximum daily temperature (°C) |
| Tmin minimum daily temperature (°C) |
| RH mean daily relative humidity (%) |
| U2 wind speed measurement (ms−1) |
| SD bright sunshine hours per day (hours) |
| A elevation (m) |
| L latitude (deg) |
| J Julian date, i.e., number of day in year |
- Ta average daily temperature (°C)
- ea saturation vapor pressure (kPa)
- ed vapor pressure at dew point (kPa)
- vapor pressure deficit (kPa)
- Rn net radiation flux at surface (MJ m−2 d−1)
- G soil heat flux (MJ m−2 d−1)
- (i)
- Adequate soil water availability (Eta = ETm)
- (ii)
- Limiting soil water availability (Eta < ETm)
- ks = 0.0 when Tx < Ts; Ts is assumed as 0 °C in GAEZ
- ks = 0.1 when Tx > Ts and Ta < 0 °C
- ks = 0.2 when Tx > Ts and 0 °C < Ta < 5 °C
- F =
- the fraction of the daytime the sky is clouded, F = (Ac − 0.5 Rg)/(0.8 Ac), where Ac (or PAR) is the maximum active incoming short-wave radiation on clear days (de Wit, 1965), and Rg is incoming short-wave radiation (both are measured in cal cm−2 day−1)
- bo =
- gross dry mater production rate of a standard crop for a given location and time of the year on a completely overcast day, (kg ha−1 day−1) (de Wit, 1965)
- bc =
- gross dry mater production rate of a standard crop for a given location and time of the year on a perfectly clear day, (kg ha−1 day−1) (de Wit, 1965)
- bgm = maximum rate of gross biomass production at leaf area index (LAI) of 5
- L = growth ratio, equal to the ratio of bgm at actual LAI to bgm at LAI of 5
- N = length of normal growth cycle
- ct = maintenance respiration, dependent on both crop and temperature according to Equation (A8)
- Hi = harvest index, i.e., proportion of the net biomass of a crop that is economically useful
- (1)
- Land utilization type, LUT
- (2)
- Thermal climate
- (3)
- Input level
- (4)
- Length of the growing period, LGP, length of the equivalent LGP (LGPeq), and the frost-free period (LGPt=10)
- (1)
- Reading agro-climatic yields calculated for separate crop water balances of six broad soil AWC classes (from Module II/III);
- (2)
- Applying AEZ rules for water-collecting sites (defined as Fluvisols and Gleysols on flat terrain);
- (3)
- Applying reduction factors due to edaphic evaluation for the specific combinations of soil types/slope classes making up a grid-cell;
- (4)
- Aggregating results over component land units (soil type/slope combinations), and calculating applicable fallow requirement factors depending on climate characteristics, soil type and crop group.
- (1)
- Estimation of shares of rain-fed or irrigated cultivated land by 5 arc-minute grid cell;
- (2)
- Estimation of crop specific harvested area, yield and production of crops within the rain-fed and irrigated cultivated land of each grid cell.
References and Note
- Liu, L.; Xu, X.; Liu, J.; Chen, X.; Ning, J. Impact of farmland changes on production potential in China during 1990–2010. J. Geogr. Sci. 2015, 25, 19–34. [Google Scholar] [CrossRef]
- Li, F.; Zhang, S.; Xu, X.; Yang, J.; Wang, Q.; Bu, K.; Chang, L. The Response of grain potential productivity to land use change: A case study in Western Jilin, China. Sustainability 2015, 7, 14729–14744. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Liu, L.; Xu, X. Spatial-temporal characteristics of soybean production potential change under the background of climate change over the past 50 years in China. Prog. Geogr. 2014, 33, 1414–1423. [Google Scholar]
- Ren, M. Geographical distribution of crop productivity in Sichuan Province. Acta Geogr. Sin. 1950, 16, 1–22. [Google Scholar]
- Grace, J. Simulation of ecological processes. By C. T. de Wit and J. Goudriaan. Centre for Agricultural Publishing and Documentation, Wageningen 1978. ISBN 90-220-0652-2. Q. J. R. Meteorol. Soc. 2010, 106, 223. [Google Scholar] [CrossRef]
- Fischer, R.; Mature, R. Crop temperature modification and yield potential in a dwarf spring wheat. Crop. Sci. 1976, 16, 855–859. [Google Scholar] [CrossRef]
- Gifford, R.; Thorne, J.; Hitz, W. Crop productivity and photo assimilate partitioning. Science 1984, 225, 801–808. [Google Scholar] [CrossRef] [PubMed]
- Amthor, J. Respiration and crop productivity. Plant. Growth Regul. 1989, 10, 271–273. [Google Scholar]
- Li, J.; Wang, L.; Shao, M.; Fan, T. Simulation of wheat potential productivity on Loess Plateau region of China. J. Nat. Resour. 2001, 16, 161–165. [Google Scholar]
- Wang, Z.; Liang, Y. The application of EPIC model to calculate crop productive potentialities in Loessic yuan region. J. Nat. Resour. 2002, 4, 481–487. [Google Scholar]
- Wang, T.; Lv, C.; Yu, B. Assessing the potential productivity of winter wheat using WOFOST in the Beijing-Tianjin-Hebei region. J. Nat. Resour. 2010, 25, 475–487. [Google Scholar]
- Fischer, G.; Velthuizen, H.V.; Shah, M.; Nachtergaele, F. Global agro-ecological assessment for agriculture in the 21st century. J. Henan Vocat.-Tech. Teacher’s Coll. 2002, 11, 371–374. [Google Scholar]
- Fischer, G.; Shah, M.; Velthuizen, H.V.; Nachtergaele, F. Agro-ecological zones assessments. Land Use Land Cover Soil Sci. 2006, 3, 1–9. [Google Scholar]
- Fischer, G.; Teixeira, E.; Hizsnyik, E. Land use dynamics and sugarcane production. In Sugarcane Ethanol: Contribution to Climate Change Mitigation and the Environment; Wageningen Academic: Wageningen, The Netherlands, 2008; pp. 29–62. [Google Scholar]
- Fischer, G.; Velthuizen, H.V.; Hizsnyik, E.; Wiberg, D. Potentially obtainable yields in the semi-arid tropics. In Global Theme on Agroecosystems Report No. 54; ICRISAT: Andhra Pradesh, India, 2009. [Google Scholar]
- Cai, C. Analysis of China’s farming and wheat yield potential based on AEZ model. J. Wheat Res. 2006, 1, 10–14. [Google Scholar]
- Cai, C. Rape yield potential analysis of cropping system regions in China based on AEZ model. Chin. J. Agric. Resour. Reg. Plan. 2007, 1, 34–37. [Google Scholar]
- Yu, D.; Liu, C.; Xu, W. Analysis on the potential productivity of maize in Gansu Province based on the AEZ model. J. Gansu Agric. Univ. 2012, 47, 73–77. [Google Scholar]
- Zhan, J.; Yu, R.; Shi, Q. Dynamic assessment of the grain productivity in China based on the enhances AEZ model. China Popul. Resour. Environ. 2013, 23, 102–109. [Google Scholar]
- Pan, P.; Yang, G.; Su, W.; Wang, X. Impact of land use change on cultivated land productivity in Taihu Lake Plain. Sci. Geogr. Sin. 2015, 35, 990–998. [Google Scholar]
- Alan, V.; Page, K.; William, D. What are the effects of Agro-Ecological Zones and land use region boundaries on land resource projection using the Global Change Assessment Model. Environ. Model. Softw. 2016, 85, 246–265. [Google Scholar]
- Rachidatou, S.; Fenton, B.; Vincent, E.; Josephine, H.; Sally, A. Distribution, pathological and biochemical characterization of Ralstonia solanacearum in Benin. Ann. Agric. Sci. 2017, 62, 83–88. [Google Scholar]
- Nazrul, M.; Hasan, M.; Mondal, M. Production potential and economics of mung bean in rice based cropping pattern in Sylhet region under AEZ 20. Bangladesh J. Agric. Res. 2017, 42, 413. [Google Scholar] [CrossRef]
- Wang, L.; Lv, Y.; Li, Q.; Hu, Z.; Wu, D.; Zhang, Y.; Wang, T. Spatial-temporal analysis of winter wheat yield gaps in Henan Province using AEZ model. Chin. J. Eco-Agric. 2018, 26, 547–558. [Google Scholar]
- Pu, L.; Zhang, S.; Li, F.; Wang, R.; Wang, Q.; Chang, L.; Yang, J. Study on land use change in Western Jilin Province based on topographic factors. J. Northeast Norm. Univ. 2016, 48, 133–140. [Google Scholar]
- Shortridge, A.; Messina, J. Spatial structure and landscape associations of SRTM error. Remote Sens. Environ. 2011, 115, 1576–1587. [Google Scholar] [CrossRef]
- Hutchinson, M.F. Interpolating mean rainfall using thin plate smoothing splines. Int. J. Geogr. Inf. Syst. 1995, 9, 385–403. [Google Scholar] [CrossRef]
- Hutchinson, M.F. Interpolation of rainfall data with thin plate smoothing splines. Part I: Two dimensional smoothing of data with short range correlation. J. Geogr. Inf. Decis. Anal. 1998, 2, 139–151. [Google Scholar]
- Hutchinson, M.F. Interpolation of rainfall data with thin plate smoothing splines. Part II: Analysis of topographic dependence. J. Geogr. Inf. Decis. Anal. 1998, 2, 152–167. [Google Scholar]
- Seo, S.N. assessment of the Agro-Ecological Zone methods for the study of climate change with micro farming decisions in sub-Saharan Africa. Eur. J. Agron. 2014, 52, 57–165. [Google Scholar] [CrossRef]
- Van Wart, J.; van Bussel, L.G.; Wolf, J.; Licker, R.; Grassini, P.; Nelson, A.; Boogaard, H.; Gerber, J.; Mueller, N.D.; Claessens, L.; et al. Use of agro-climatic zones to upscale simulated crop yield potential. Field Crops Res. 2013, 143, 44–55. [Google Scholar] [CrossRef]
- Cai, C.; Harrij, V.; Guenther, F.; Sylvia, P. Analysis of China’s farming and rice yield potential based on AEZ model. Seed 2006, 2, 6–9. [Google Scholar]
- Brouwer, F.; Mccarl, B. Agriculture and climate beyond 2015. In Environment Policy; Springer: Dordrecht, The Netherlands, 2006; Volume 46. [Google Scholar]
- Peltonensainio, P.; Hakala, K.; Ojanen, H.; Vanhatalo, A.; Alakukku, L. Climate change and prolongation of growing season: Changes in regional potential for field crop production in Finland. Agric. Food Sci. 2009, 18, 171–190. [Google Scholar] [CrossRef]
- Adejuwon, J. Food crop production in Nigeria. II. Potential effects of climate change. Clim. Res. 2006, 32, 229–245. [Google Scholar] [CrossRef]
- Williamson, D.; Moffat, A. Tree crop production systems: A change in land use with the potential to reduce inputs. J. Sci. Food Agric. 1990, 53, 113–115. [Google Scholar]
- Gardner, W.; Velthuis, R.; Amor, R. Field crop production in southwest Victoria. I. Area description, current land use and potential for crop production. J. Educ. Behav. Stat. 1983, 39, 426–451. [Google Scholar]
- Tscharntke, T.; Clough, Y.; Wanger, T.; Jackson, L.; Motzke, I. Global food security, biodiversity conservation and the future of agricultural intensification. Biol. Conserv. 2012, 151, 53–59. [Google Scholar] [CrossRef]
- Fischer, G.; Sun, L.X. model based analysis of future land-use development in China. Agric. Ecosyst. Environ. 2001, 85, 163–176. [Google Scholar] [CrossRef]
- International Institute for Applied Systems Analysis (IIASA). Global Agro-Ecological Zones. Available online: http://www.gaez.iiasa.ac.at/ (accessed on 22 October 2015).
- Tatsumi, K.; Yamashiki, Y.; Valmir da Silva, R.; Takara, K.; Matsuoka, Y.; Takahashi, K.; Maruyama, K.; Kawahara, N. Estimation of potential changes in cereals production under climate change scenarios. Hydrol. Process. 2011, 25, 2715–2725. [Google Scholar] [CrossRef]
- Li, F. Land Use Optimization under the Perspective of Restoration Ecology: A Case Study of Western Jilin; Jilin University: Changchun, China, 2016. [Google Scholar]
- Diepen, C.; Wolf, J.; Keulen, H. WOFOST: A simulation model of crop production. Soil Use Manag. 2010, 5, 16–24. [Google Scholar] [CrossRef]
- Supit, I.; Hooijer, A.; Van, D. System Description of the WOFOST 6.0 Crop Simulation Model Implemente in CGMS. The CGMS. 1994. Available online: https://www.researchgate.net/publication/282287246_System_description_of_the_Wofost_60_crop_simulation_model_implemented_in_CGMS_Volume_1_Theory_and_Algorithms (accessed on 22 October 2015).
- Williams, J. The EPIC crop growth model. Trans. ASAE 1989, 32, 497–511. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, S.; Yang, J.; Pu, L.; Yang, C.; Yu, L.; Chang, L.; Bu, K. Integrated Use of GCM, RS, and GIS for the Assessment of Hillslope and Gully Erosion in the Mushi River Sub-Catchment, Northeast China. Sustainability 2016, 8, 317. [Google Scholar] [CrossRef]
- McCree, K. Equations for rate of dark respiration of white clover and grain sorghum, as functions of dry weight, photosynthesis rate and temperature. Crop Sci. 1974, 14, 509–514. [Google Scholar] [CrossRef]
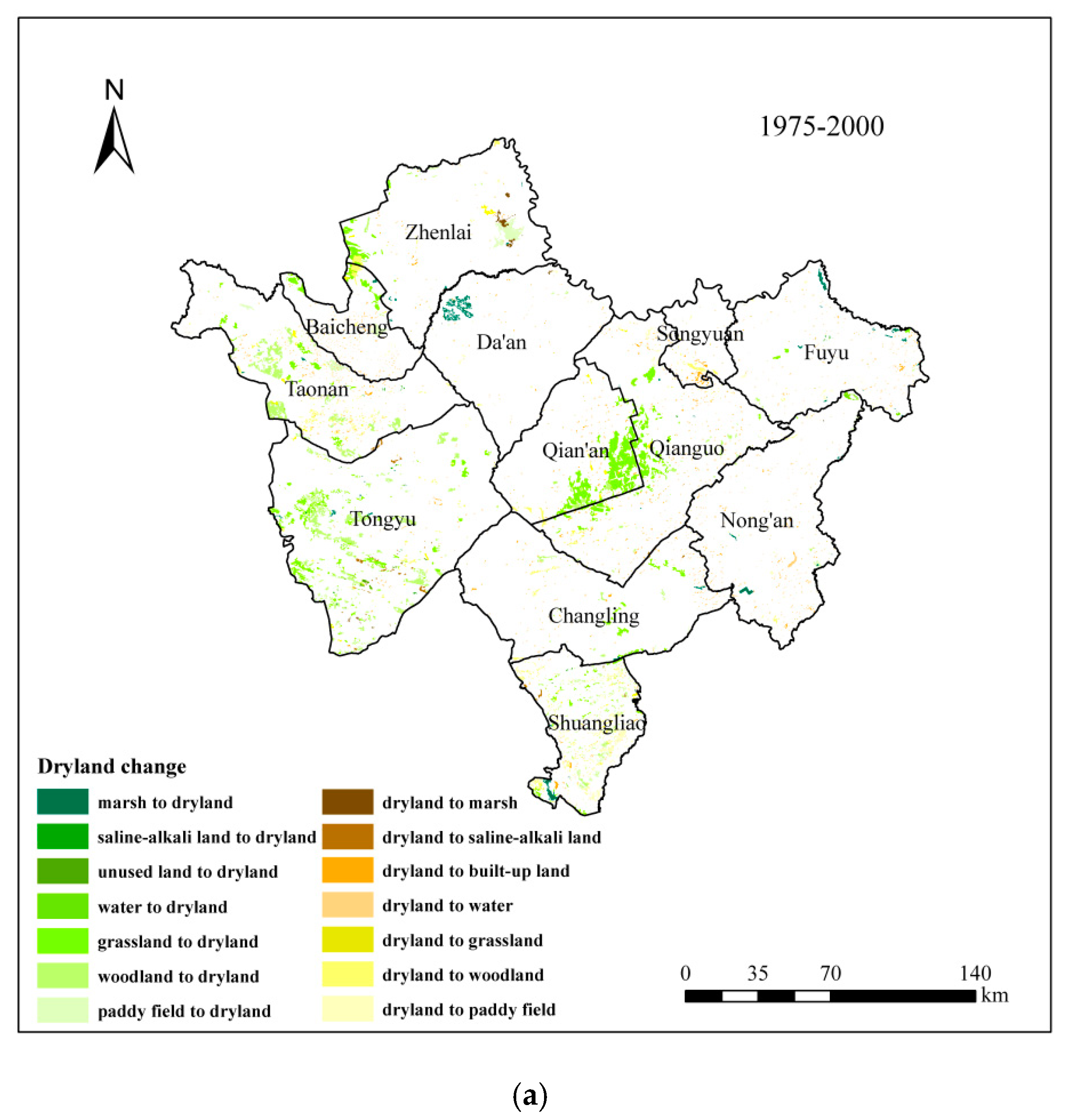
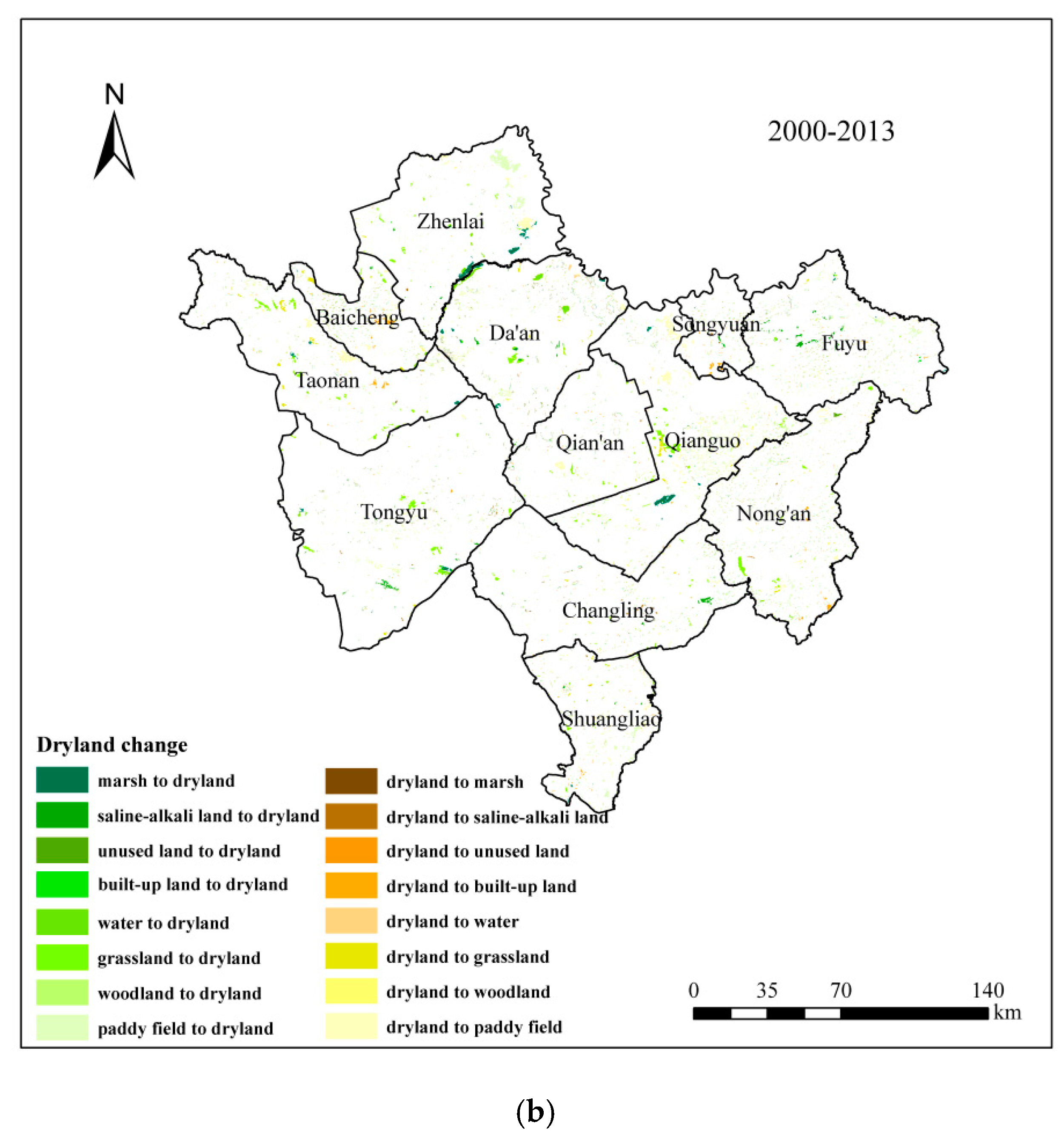

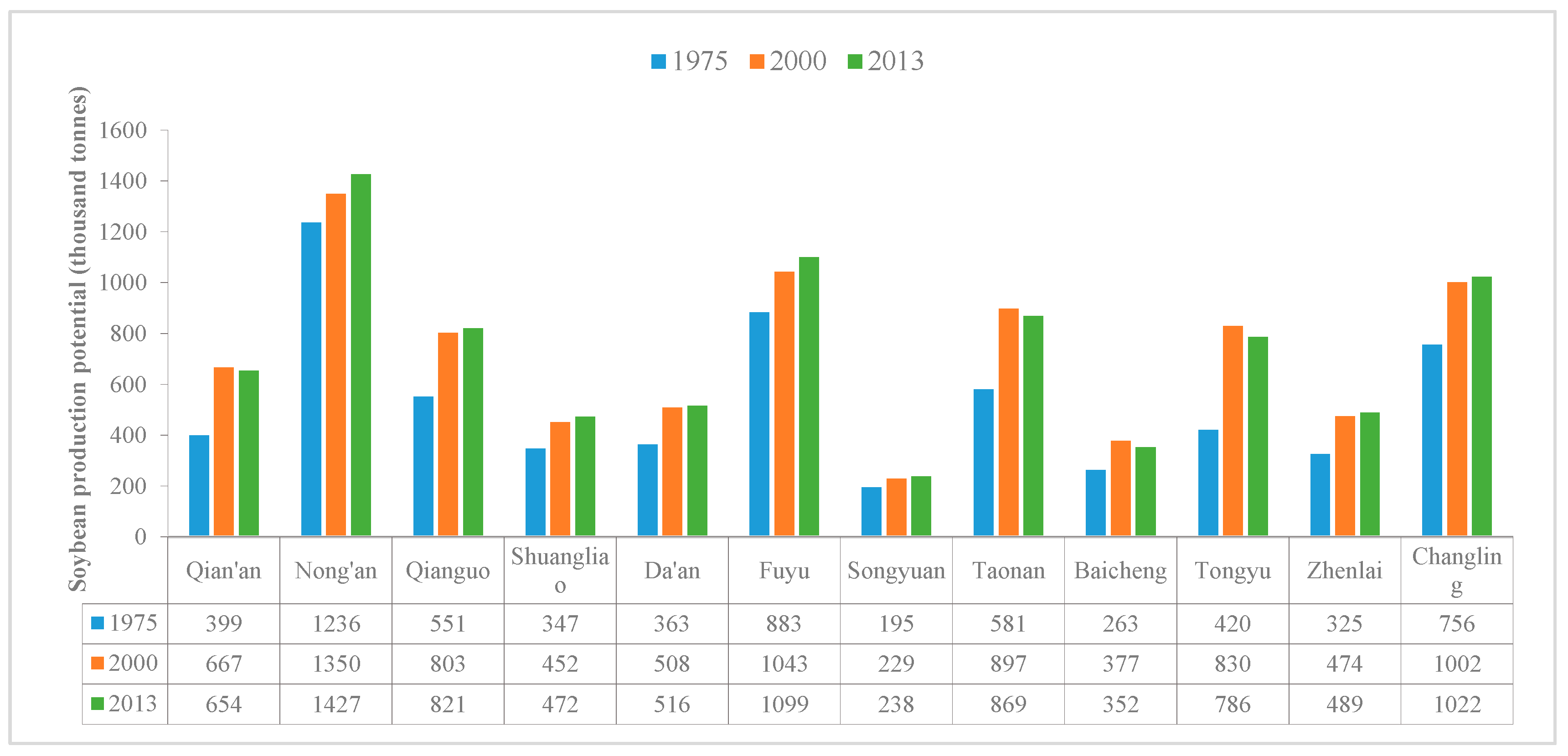
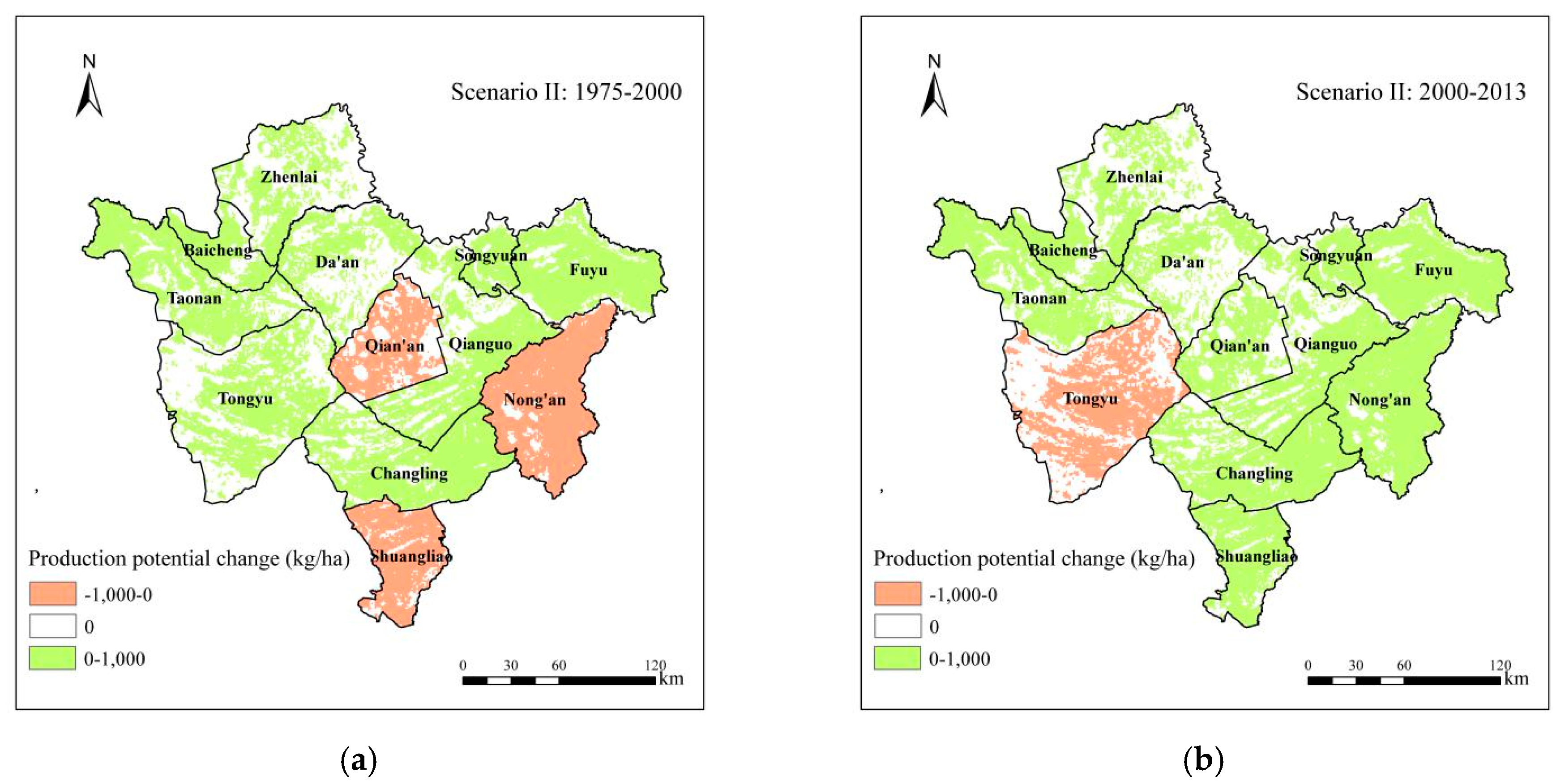
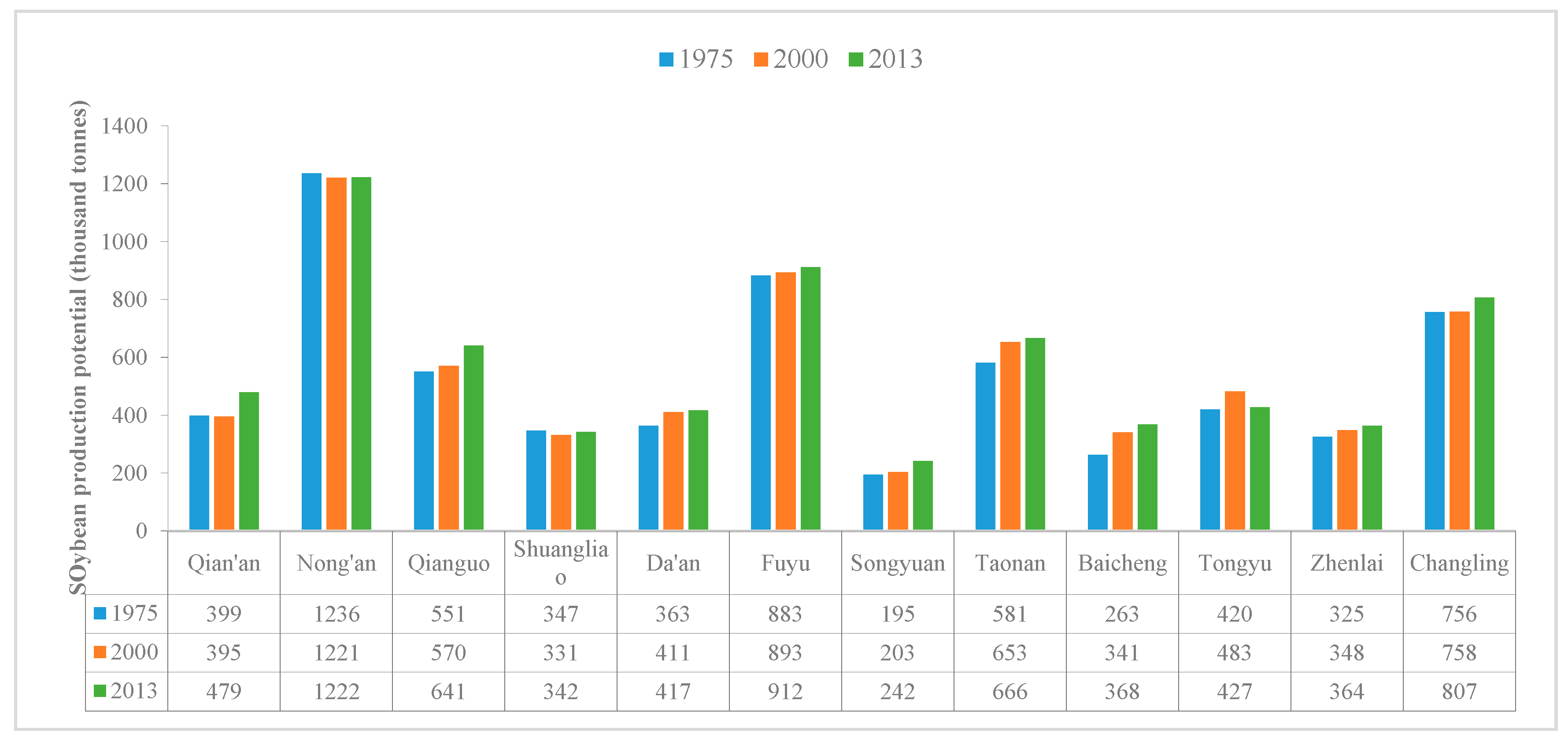
| Dryland Change | Dryland Change Types | 1975–2000 | 2000–2013 |
|---|---|---|---|
| Dryland decrease | Dryland to paddy field | 104.67 | 310.46 |
| Dryland to woodland | 352.16 | 126.26 | |
| Dryland to grassland | 77.75 | 81.10 | |
| Dryland to water | 12.54 | 9.94 | |
| Dryland to built-up land | 303.94 | 168.75 | |
| Dryland to saline-alkali land | 43.39 | 46.37 | |
| Dryland to marsh | 29.91 | 3.27 | |
| Dryland to unused land | 0.00 | 1.52 | |
| Total decrease | 924.36 | 747.67 | |
| Dryland increase | Paddy field to dryland | 159.58 | 157.49 |
| Woodland to dryland | 717.72 | 127.09 | |
| Grassland to dryland | 1218.45 | 261.35 | |
| Water to dryland | 15.43 | 80.69 | |
| Built-up land to dryland | 0.00 | 124.35 | |
| Unused land to dryland | 9.63 | 5.20 | |
| Saline-alkali land to dryland | 10.09 | 112.66 | |
| Marsh to dryland | 154.37 | 103.54 | |
| Total increase | 2285.27 | 972.37 | |
| Total change | 1360.91 | 224.70 | |
| Dryland Change | Dryland Change Types | Qian’an | Nong’an | Qianguo | Shuangliao | Da’an | Fuyu | Songyuan | Taonan | Baicheng | Tongyu | Zhenlai | Changling | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Decrease | Returning dryland to paddy field | −11 | 0 | 0 | −27 | −11 | −31 | −21 | 0 | 0 | 0 | 0 | 0 | −101 |
| Returning forests | 0 | 0 | −22 | −21 | −45 | −21 | −33 | −71 | −46 | −37 | −34 | −22 | −352 | |
| Returning grassland | −26 | 0 | −25 | −33 | 0 | 0 | 0 | −13 | −47 | −71 | −42 | 0.00 | −257 | |
| Returning water | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Urban expansion | −11 | −69 | −29 | −34 | −28 | −13 | −22 | −40 | −36 | −45 | 0 | −42 | −369 | |
| Returning dryland to saline-alkali land | 0 | −26 | −2 | 0 | 0 | 0 | 0 | −22 | 0 | −12 | 0 | 0 | −62 | |
| Returning dryland to marsh | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −13 | −13 | 0.00 | −26 | |
| Total decrease | −48 | −95 | −78 | −115 | −84 | −65 | −76 | −147 | −129 | −178 | −89 | −64 | −1168 | |
| Increase | Returning paddy field to dryland | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 9 | 9 | 0 | 25 | 0 | 46 |
| Woodland reclamation | 797 | 179 | 58 | 14 | 57 | 6 | 0 | 78 | 49 | 52 | 11 | 16 | 1317 | |
| Grassland reclamation | 913 | 59 | 446 | 98 | 123 | 12 | 0 | 13 | 241 | 337 | 60 | 677 | 2979 | |
| Returning water to dryland | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| Unused land reclamation | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
| Returning saline-alkali land to dryland | 0 | 0 | 2 | 8 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 14 | |
| Returning marsh to dryland | 0 | 16 | 18 | 25 | 13 | 23 | 0 | 5 | 1 | 7 | 1 | 1 | 110 | |
| Total increase | 1710 | 257 | 527 | 145 | 193 | 44 | 0 | 105 | 300 | 399 | 97 | 694 | 4471 | |
| Net change | 1662 | 162 | 449 | 30 | 109 | −21 | −76 | −42 | 171 | 221 | 8 | 630 | 3303 |
| Dryland Change | Dryland Change Types | Qian’an | Nong’an | Qianguo | Shuangliao | Da’an | Fuyu | Songyuan | Taonan | Baicheng | Tongyu | Zhenlai | Changling | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Decrease | Returning dryland to paddy field | 0 | −13 | −11 | −24 | −21 | 0 | −43 | 0 | 0 | −21 | 0 | 0 | −133 |
| Returning forests | −31 | −32 | 0 | −36 | −54 | −47 | −35 | −69 | −56 | −43 | −39 | −47 | −489 | |
| Returning grassland | −56 | −41 | −31 | −34 | −12 | −21 | −31 | −39 | −27 | −74 | −45 | −43 | −454 | |
| Returning water | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Urban expansion | −32 | −74 | −41 | −45 | −31 | −55 | −47 | −42 | −45 | −36 | −41 | −29 | −518 | |
| Returning dryland to saline-alkali land | −1 | −23 | 0 | 0 | −2 | 0 | 0 | −29 | 0 | −28 | 0 | 0 | −83 | |
| Returning dryland to marsh | 0 | 0 | 0 | 0 | 0 | −11 | 0 | 0 | 0 | −3 | −16 | 0 | −30 | |
| Total decrease | −120 | −183 | −83 | −139 | −120 | −134 | −156 | −179 | −128 | −205 | −141 | −119 | −1707 | |
| Increase | Returning paddy field to dryland | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 5 | 4 | 0 | 17 | 0 | 28 |
| Woodland reclamation | 48 | 24 | 13 | 15 | 24 | 0 | 0 | 51 | 24 | 25 | 7 | 30 | 231 | |
| Grassland reclamation | 51 | 21 | 74 | 51 | 32 | 0 | 0 | 2 | 27 | 32 | 45 | 32 | 367 | |
| Returning water to dryland | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Unused land reclamation | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| Returning saline-alkali land to dryland | 0 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 6 | |
| Returning marsh to dryland | 0 | 0 | 8 | 15 | 3 | 13 | 0 | 2 | 0 | 2 | 0 | 1 | 44 | |
| Total increase | 99 | 45 | 97 | 83 | 59 | 15 | 0 | 60 | 56 | 61 | 69 | 63 | 707 | |
| Net change | −21 | −138 | 14 | −56 | −61 | −119 | −156 | −119 | −72 | −144 | −72 | −56 | −1000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, L.; Zhang, S.; Li, F.; Wang, R.; Yang, J.; Chang, L. Impact of Farmland Change on Soybean Production Potential in Recent 40 Years: A Case Study in Western Jilin, China. Int. J. Environ. Res. Public Health 2018, 15, 1522. https://doi.org/10.3390/ijerph15071522
Pu L, Zhang S, Li F, Wang R, Yang J, Chang L. Impact of Farmland Change on Soybean Production Potential in Recent 40 Years: A Case Study in Western Jilin, China. International Journal of Environmental Research and Public Health. 2018; 15(7):1522. https://doi.org/10.3390/ijerph15071522
Chicago/Turabian StylePu, Luoman, Shuwen Zhang, Fei Li, Ranghu Wang, Jiuchun Yang, and Liping Chang. 2018. "Impact of Farmland Change on Soybean Production Potential in Recent 40 Years: A Case Study in Western Jilin, China" International Journal of Environmental Research and Public Health 15, no. 7: 1522. https://doi.org/10.3390/ijerph15071522
APA StylePu, L., Zhang, S., Li, F., Wang, R., Yang, J., & Chang, L. (2018). Impact of Farmland Change on Soybean Production Potential in Recent 40 Years: A Case Study in Western Jilin, China. International Journal of Environmental Research and Public Health, 15(7), 1522. https://doi.org/10.3390/ijerph15071522





