Multi-Objective Drug Molecule Optimization Based on Tanimoto Crowding Distance and Acceptance Probability
Abstract
1. Introduction
2. Results and Discussion
2.1. Benchmark Evaluation of MOGA-TA
2.1.1. Test Tasks for Molecular Optimization
- Task 1 (Fexofenadine): Tanimoto similarity (AP), TPSA, logP.
- Task 2 (Pioglitazone): Tanimoto similarity (ECFP4), molecular weight, number of rotatable bonds.
- Task 3 (Osimertinib): Tanimoto similarity (FCFP4), Tanimoto similarity (FCFP6), polar surface area (TPSA), logP.
- Task 4 (Ranolazine): Tanimoto similarity (AP), polar surface area (TPSA), logP, number of fluorine atoms.
- Task 5 (Cobimetinib): Tanimoto similarity (FCFP4), Tanimoto similarity (ECFP6), number of rotatable bonds, number of aromatic rings, CNS [34].
- Task 6 (DAP kinases): DAPk1, DRP1, ZIPk, QED, logP.
2.1.2. Evaluation Metrics
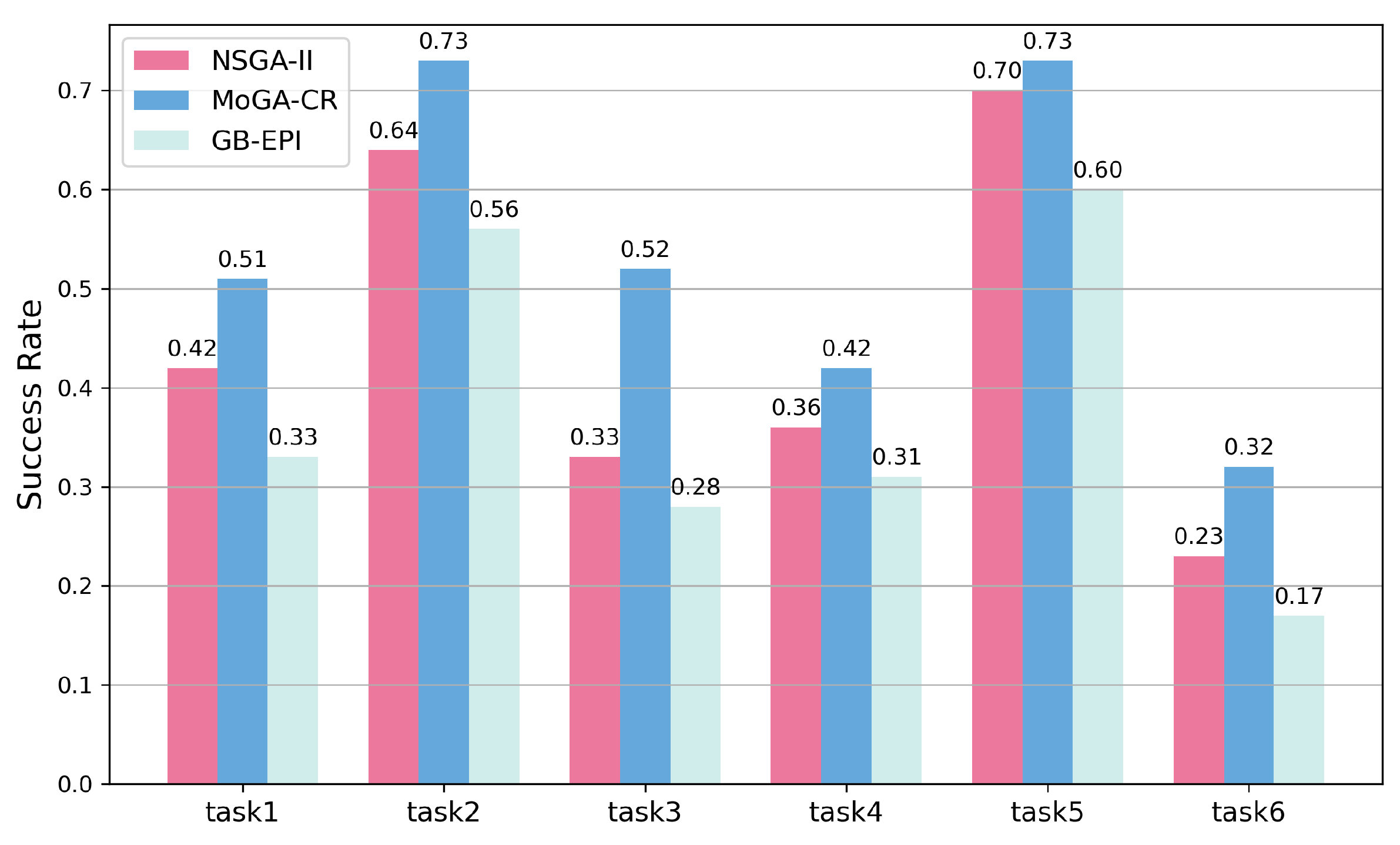
2.2. Comparisons on Test Tasks
2.3. Ablation Experiment
3. Materials and Methods
3.1. Related Work
3.1.1. Non-Dominated Sorting Genetic Algorithm II (NSGA-II)
3.1.2. Multi-Objective Molecular Optimization
| Algorithm 1 The framework of the algorithm for NSGA-II. |
|
3.1.3. Crossover and Mutation Operations
3.2. Method
3.2.1. Problem Definition
- Chemical rationality assessment: including synthetic accessibility (SA score), drug similarity (QED), LogP (lipid solubility), etc.
- Total polar surface area (TPSA): used to predict the ability of a molecule to cross a cell membrane [39].
- Molecular structure characteristics: including the number of aromatic rings (Number of Aromatic Rings), the number of rotatable bonds (Number of Rotatable Bonds), etc.
- Bioactivity: refers to the ability of a molecule to interact with a biological target (such as an enzyme, receptor, or ion channel).
3.2.2. Framework of MOGA-TA
| Algorithm 2 The framework of the algorithm for MoGA-TA |
|
3.2.3. Crowding Distance Based on Tanimoto Similarity
3.2.4. Population Update
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hsu, H.-H.; Hsu, Y.-C.; Chang, L.-J.; Yang, J.-M. An integrated approach with new strategies for QSAR models and lead optimization. BMC Genom. 2017, 18, 104. [Google Scholar] [CrossRef]
- Zhavoronkov, A. Artificial intelligence for drug discovery, biomarker development, and generation of novel chemistry. Mol. Pharm. 2018, 15, 4311–4313. [Google Scholar] [CrossRef]
- DiMasi, J.A.; Grabowski, H.G.; Hansen, R.W. Innovation in the pharmaceutical industry: New estimates of R&D costs. J. Health Econ. 2016, 47, 20–33. [Google Scholar]
- Polishchuk, P.G.; Madzhidov, T.I.; Varnek, A. Estimation of the size of drug-like chemical space based on GDB-17 data. J. Comput.-Aided Mol. Des. 2013, 27, 675–679. [Google Scholar] [CrossRef]
- Grantham, K.; Mukaidaisi, M.; Ooi, H.K.; Ghaemi, M.S.; Tchagang, A.; Li, Y. Deep evolutionary learning for molecular design. IEEE Comput. Intell. Mag. 2022, 17, 14–28. [Google Scholar] [CrossRef]
- Liu, X.; Ye, K.; van Vlijmen, H.W.T.; Emmerich, M.T.M.; IJzerman, A.P.; van Westen, G.J.P. DrugEx v2: De novo design of drug molecules by Pareto-based multi-objective reinforcement learning in polypharmacology. J. Cheminform. 2021, 13, 85. [Google Scholar] [CrossRef] [PubMed]
- Blaschke, T.; Olivecrona, M.; Engkvist, O.; Bajorath, J. Application of generative autoencoder in de novo molecular design. Mol. Inform. 2018, 37, 1700123. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Bombarelli, R.; Wei, J.N.; Duvenaud, D.; Hernández-Lobato, J.M.; Sánchez-Lengeling, B.; Sheberla, D.; Aguilera-Iparraguirre, J.; Hirzel, T.D.; Adams, R.P. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent. Sci. 2018, 4, 268–276. [Google Scholar] [CrossRef]
- Kotsias, P.-C.; Arús-Pous, J.; Chen, H.; Engkvist, O.; Tyrchan, C. Direct steering of de novo molecular generation using descriptor conditional recurrent neural networks (cRNNs). J. Cheminform. 2019, 16, 64. [Google Scholar]
- Prykhodko, O.; Johansson, S.V.; Kotsias, P.-C.; Arús-Pous, J.; Bjerrum, E.J.; Engkvist, O.; Chen, H. A de novo molecular generation method using latent vector based generative adversarial network. J. Cheminform. 2019, 11, 74. [Google Scholar] [CrossRef]
- Jin, W.; Yang, K.; Barzilay, R.; Jaakkola, T. Learning multimodal graph-to-graph translation for molecular optimization. arXiv 2018, arXiv:1812.01070. [Google Scholar]
- Fu, T.; Xiao, C.; Li, X.; Glass, L.M.; Sun, J. Mimosa: Multi-constraint molecule sampling for molecule optimization. Proc. AAAI Conf. Artif. Intell. 2021, 35, 125–133. [Google Scholar] [CrossRef]
- Lee, M.; Min, K. MCVAE: Multi-objective inverse design via molecular graph conditional variational autoencoder. J. Chem. Inf. Model. 2022, 62, 2943–2950. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Min, M.R.; Parthasarathy, S.; Ning, X. A deep generative model for molecule optimization via one fragment modification. Nat. Mach. Intell. 2021, 3, 1040–1049. [Google Scholar] [CrossRef] [PubMed]
- Winter, R.; Montanari, F.; Steffen, A.; Briem, H.; Noé, F.; Clevert, D.A. Efficient multi-objective molecular optimization in a continuous latent space. Chem. Sci. 2019, 10, 8016–8024. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Fu, T.; Sun, J.; Coley, C. Sample efficiency matters: A benchmark for practical molecular optimization. Adv. Neural Inf. Process. Syst. 2022, 35, 21342–21357. [Google Scholar]
- Xie, Y.; Shi, C.; Zhou, H.; Yang, Y.; Zhang, W.; Yu, Y.; Li, L. Mars: Markov molecular sampling for multi-objective drug discovery. arXiv 2021, arXiv:2103.10432. [Google Scholar]
- Hoffman, S.C.; Chentham, V.; Wadhawan, K.; Chen, P.-Y.; Das, P. Optimizing molecules using efficient queries from property evaluations. Nat. Mach. Intell. 2022, 4, 21–31. [Google Scholar] [CrossRef]
- Jensen, J.H. A graph-based genetic algorithm and generative model/Monte Carlo tree search for the exploration of chemical space. Chem. Sci. 2019, 10, 3567–3572. [Google Scholar] [CrossRef]
- Nigam, A.K.; Friederich, P.; Krenn, M.; Aspuru-Guzik, A. Augmenting genetic algorithms with deep neural networks for exploring the chemical space. arXiv 2019, arXiv:1909.11655. [Google Scholar]
- Kwon, Y.; Lee, J. MolFinder: An evolutionary algorithm for the global optimization of molecular properties and the extensive exploration of chemical space using SMILES. J. Cheminform. 2021, 13, 24. [Google Scholar] [CrossRef] [PubMed]
- Leguy, J.; Cauchy, T.; Glavatskikh, M.; Du Mota, B. EvoMol: A flexible and interpretable evolutionary algorithm for unbiased de novo molecular generation. J. Cheminform. 2020, 12, 55. [Google Scholar] [CrossRef] [PubMed]
- Thomas, M.; O’Boyle, N.M.; Bender, A.; De Graaf, C. MolScore: A scoring, evaluation and benchmarking framework for generative models in de novo drug design. J. Cheminform. 2024, 16, 64. [Google Scholar] [CrossRef] [PubMed]
- Barshatski, G.; Radinsky, K. Unpaired generative molecule-to-molecule translation for lead optimization. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 2554–2564. [Google Scholar]
- Tian, Y.; Cheng, R.; Jin, Y.; Zhang, X. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- van der Horst, E.; Marqués-Gallego, P.; Mulder-Krieger, T. Multi-objective evolutionary design of adenosine receptor ligands. J. Chem. Inf. Model. 2012, 52, 1713–1721. [Google Scholar] [CrossRef]
- Ekins, S.; Honeycutt, J.D.; Metz, J.T. Evolving molecules using multi-objective optimization: Applying to ADME/Tox. Drug Discov. Today 2010, 15, 451–460. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; MeyarivanTAM, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- López-Pérez, K.; Avellaneda-Tamayo, J.F.; Chen, L.; López-López, E. Molecular similarity: Theory, applications, and perspectives. Artif. Intell. Chem. 2024, 2, 100077. [Google Scholar] [CrossRef]
- Bajusz, D.; Rácz, A.; Héberger, K. Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations? J. Cheminform. 2015, 7, 20. [Google Scholar] [CrossRef]
- Slowik, A.; Kwasnicka, H. Evolutionary algorithms and their applications to engineering problems. Neural Comput. Appl. 2020, 32, 12363–12379. [Google Scholar] [CrossRef]
- Brown, N.; Fiscato, M.; Segler, M.H.S.; Vaucher, A.C. GuacaMol: Benchmarking models for de novo molecular design. J. Chem. Inf. Model. 2019, 59, 1096–1108. [Google Scholar] [CrossRef]
- Verhellen, J. Graph-based molecular Pareto optimisation. Chem. Sci. 2022, 13, 7526–7535. [Google Scholar] [CrossRef] [PubMed]
- Wager, T.T.; Hou, X.; Verhoest, P.R.; Villalobos, A.; Will, Y. Central Nervous System Multiparameter Optimization Desirability: Application in Drug Discovery. ACS Chem. Neurosci. 2016, 7, 767–775. [Google Scholar] [CrossRef] [PubMed]
- Verhellen, J.; Van den Abeele, J. Illuminating elite patches of chemical space. Chem. Sci. 2020, 11, 11485–11491. [Google Scholar] [CrossRef] [PubMed]
- Guerreiro, A.P.; Fonseca, C.M.; Paquete, L. The hypervolume indicator: Problems and algorithms. arXiv 2020, arXiv:2005.00515. [Google Scholar]
- Lipkus, A.H. A proof of the triangle inequality for the Tanimoto distance. J. Math. Chem. 1999, 26, 263–265. [Google Scholar] [CrossRef]
- Xia, X.; Liu, Y.; Zheng, C.; Zhang, X.; Wu, Q.; Gao, X.; Zeng, X. Evolutionary Multiobjective Molecule Optimization in an Implicit Chemical Space. J. Chem. Inf. Model. 2024, 64, 5161–5174. [Google Scholar] [CrossRef]
- Ertl, P.; Rohde, B.; Selzer, P. Fast calculation of molecular polar surface area as a sum of fragment-based contributions and its application to the prediction of drug transport properties. J. Med. Chem. 2000, 43, 3714–3717. [Google Scholar] [CrossRef]
- Rogers, D.; Hahn, M. Extended-connectivity fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef]
- Bento, A.P.; Hersey, A.; Félix, E.; Landrum, G.; Gaulton, A. An open source chemical structure curation pipeline using RDKit. J. Cheminform. 2020, 12, 51. [Google Scholar] [CrossRef]
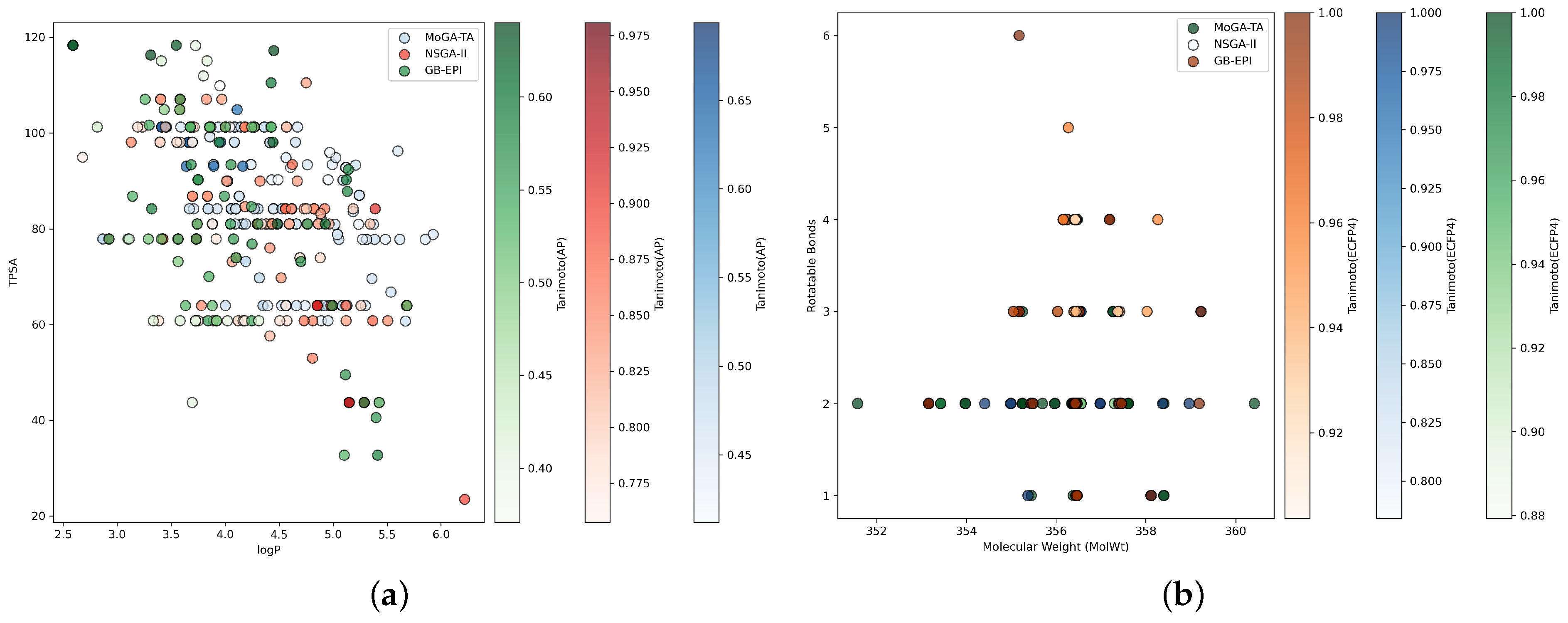
| Benchmark Name | Scoring Functions | Modifier |
|---|---|---|
| Fexofenadine | Tanimoto (AP) | Thresholded (0.8) |
| TPSA | MaxGaussian (90, 10) | |
| logP | MinGaussian (4, 2) | |
| Pioglitazone | Tanimoto(ECFP4) | Gaussian (0, 0.1) |
| Molecular weight | Gaussian (356, 10) | |
| Number of rotatable bonds | Gaussian (2, 0.5) | |
| Osimertinib | Tanimoto(FCFP4) | Thresholded (0.8) |
| Tanimoto(ECFP6) | MinGaussian (0.85, 2) | |
| TPSA | MaxGaussian (95, 20) | |
| logP | MinGaussian (1, 2) | |
| Ranolazine | Tanimoto (AP) | Thresholded (0.7) |
| TPSA | MaxGaussian (95, 20) | |
| logP | MaxGaussian (7, 1) | |
| Number of fluorine count | Gaussian (1, 1) | |
| Cobimetinib | Tanimoto(FCFP4) | Thresholded (0.7) |
| Tanimoto(ECFP6) | MinGaussian (0.75, 0.1) | |
| Number of rotatable bonds | MinGaussian (3, 1) | |
| Number of aromatic rings | MaxGaussian (3, 1) | |
| CNS (0.5) | — | |
| DAP kinases | DAPk1 | Thresholded (0.8) |
| DRP1 | Thresholded (0.8) | |
| ZIPk | Thresholded (0.8) | |
| QED | Gaussian (0.8, 0.1) | |
| logP | MaxGaussian (3, 1) |
| Algorithm | Task | HV | Success Rate | Geometric Mean | Internal Similarity |
|---|---|---|---|---|---|
| GB-EPI | Fexofenadine | 0.67 | 0.33 | 0.87 | 0.50 |
| Pioglitazone | 0.98 | 0.55 | 0.99 | 0.50 | |
| Osimertinib | 0.54 | 0.28 | 0.85 | 0.50 | |
| Ranolazine | 0.46 | 0.31 | 0.81 | 0.50 | |
| Cobimetinib | 0.77 | 0.60 | 0.93 | 0.50 | |
| DAP kinases | 0.04 | 0.17 | 0.50 | 0.51 | |
| NSGA-II | Fexofenadine | 0.78 | 0.42 | 0.92 | 0.52 |
| Pioglitazone | 1.00 | 0.64 | 1.00 | 0.51 | |
| Osimertinib | 0.66 | 0.33 | 0.89 | 0.52 | |
| Ranolazine | 0.68 | 0.36 | 0.87 | 0.51 | |
| Cobimetinib | 0.94 | 0.70 | 0.94 | 0.51 | |
| DAP kinases | 0.04 | 0.23 | 0.48 | 0.51 | |
| MoGA-TA | Fexofenadine | 0.85 | 0.51 | 0.94 | 0.51 |
| Pioglitazone | 1.00 | 0.73 | 1.00 | 0.50 | |
| Osimertinib | 0.70 | 0.52 | 0.90 | 0.52 | |
| Ranolazine | 0.75 | 0.42 | 0.89 | 0.51 | |
| Cobimetinib | 0.96 | 0.73 | 0.94 | 0.50 | |
| DAP kinases | 0.06 | 0.32 | 0.51 | 0.50 |
| Algorithm | Task | HV | Success Rate | Geometric Mean | Internal Similarity |
|---|---|---|---|---|---|
| MoGA-T | Fexofenadine | 0.81 | 0.46 | 0.93 | 0.51 |
| Pioglitazone | 1.00 | 0.67 | 1.00 | 0.50 | |
| Osimertinib | 0.68 | 0.44 | 0.89 | 0.51 | |
| Ranolazine | 0.71 | 0.35 | 0.88 | 0.51 | |
| Cobimetinib | 0.94 | 0.71 | 0.95 | 0.51 | |
| DAP kinases | 0.05 | 0.26 | 0.49 | 0.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Dai, C.; Lei, X. Multi-Objective Drug Molecule Optimization Based on Tanimoto Crowding Distance and Acceptance Probability. Pharmaceuticals 2025, 18, 1227. https://doi.org/10.3390/ph18081227
Wang Y, Dai C, Lei X. Multi-Objective Drug Molecule Optimization Based on Tanimoto Crowding Distance and Acceptance Probability. Pharmaceuticals. 2025; 18(8):1227. https://doi.org/10.3390/ph18081227
Chicago/Turabian StyleWang, Yuxin, Cai Dai, and Xiujuan Lei. 2025. "Multi-Objective Drug Molecule Optimization Based on Tanimoto Crowding Distance and Acceptance Probability" Pharmaceuticals 18, no. 8: 1227. https://doi.org/10.3390/ph18081227
APA StyleWang, Y., Dai, C., & Lei, X. (2025). Multi-Objective Drug Molecule Optimization Based on Tanimoto Crowding Distance and Acceptance Probability. Pharmaceuticals, 18(8), 1227. https://doi.org/10.3390/ph18081227






