A Novel Workflow for Non-Animal PBK Modelling of UV Filters: Oxybenzone as a Case Study
Abstract
1. Introduction
2. Results
2.1. In Vitro Skin Absorption and Evaluation of the TCAT Model for In Vitro Skin Absorption
2.2. Prediction of Human Plasma Concentrations
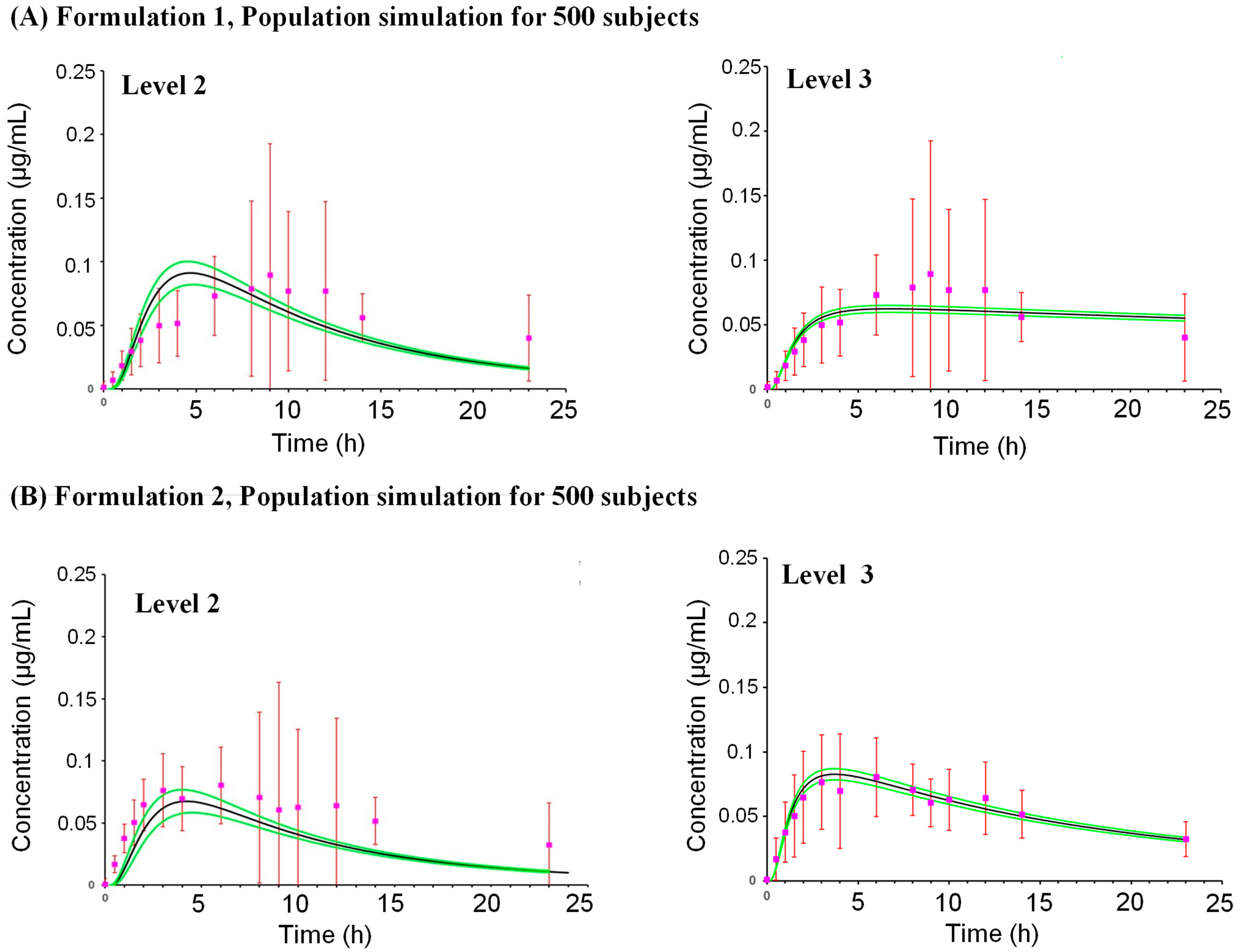
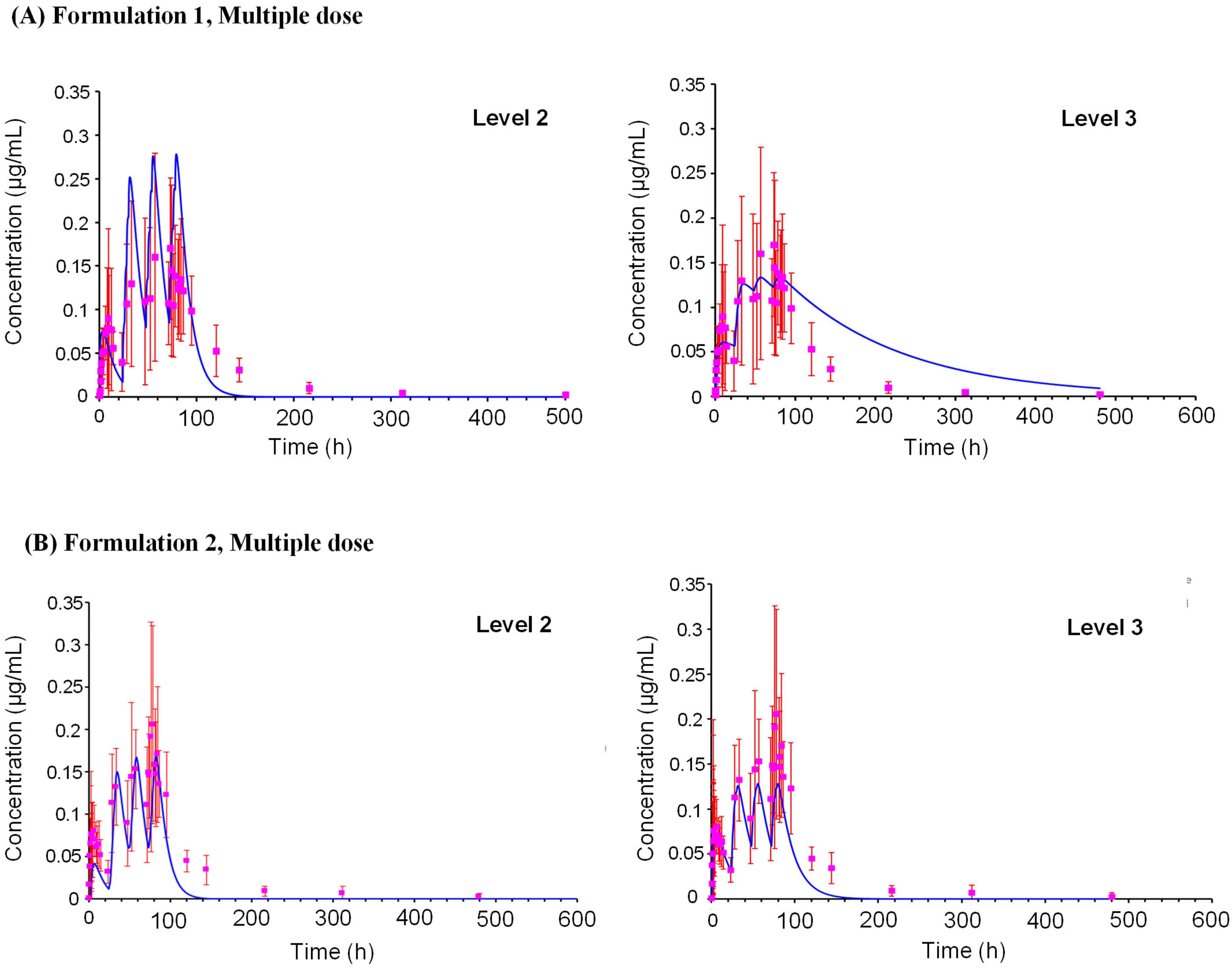
2.3. Model Performance
2.3.1. Formulation 1
2.3.2. Formulation 2
3. Discussion
3.1. Development of the Skin Module
3.2. Evaluation of the Sensitivity Analysis
3.3. Uncertainty Evaluation
3.4. Formulation Effects
3.5. Use of In Silico, In Vitro and Clinical Data
3.6. Use of PBK Models in NGRAs
4. Materials and Methods
4.1. Test Chemical Properties and Available Clinical Data
4.2. Dermal Disposition and Absorption Data
4.2.1. In Vitro (Ex Vivo) Skin Absorption Data
4.2.2. Kinetics in Isolated Dermis
4.2.3. Thickness and Volume of Skin Layers
4.2.4. Residual Volume Fraction
4.2.5. Skin Metabolism Data
4.3. In Vitro Data Related to Distribution, and Metabolism
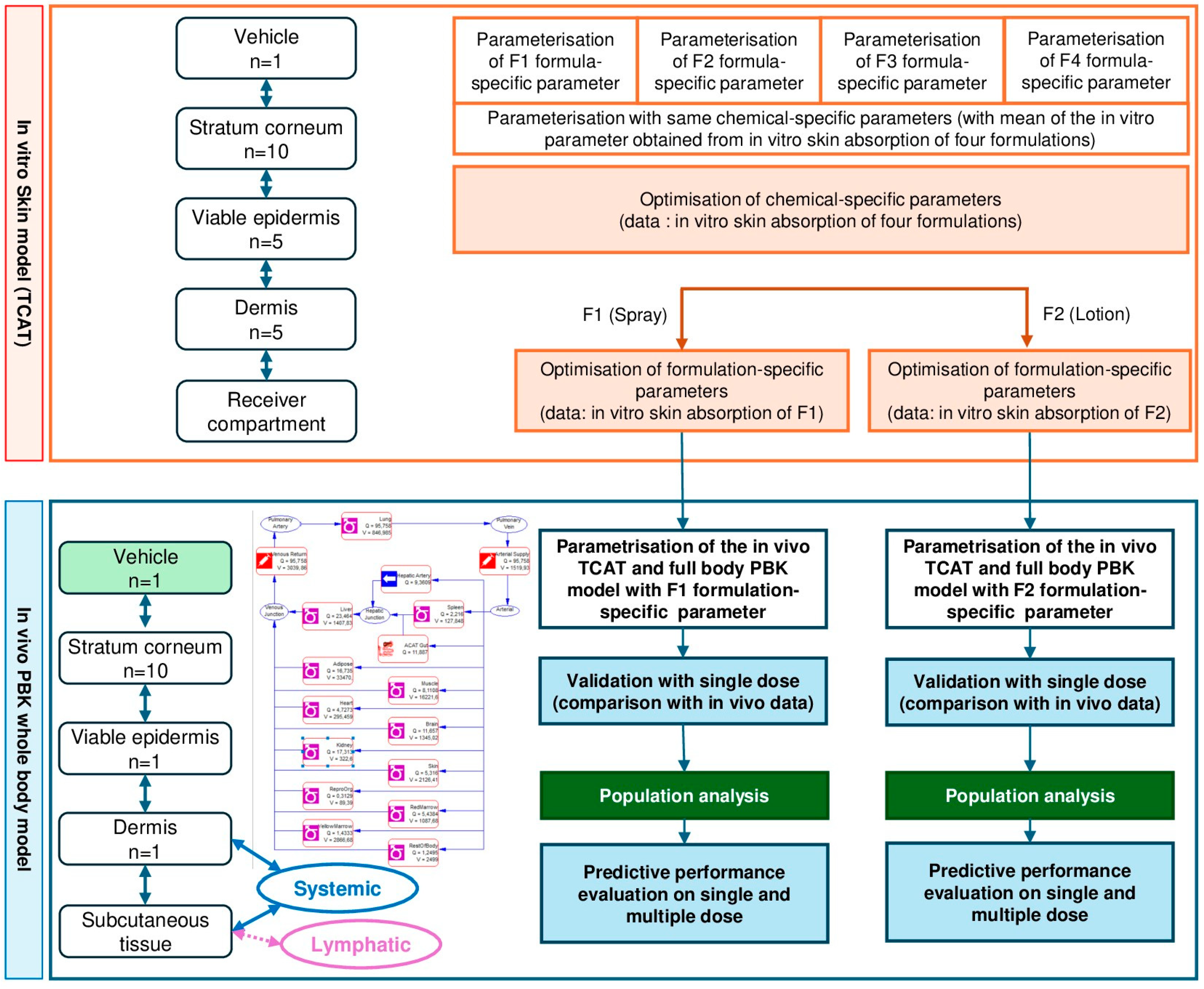
4.4. Model Development
4.4.1. Dermal Model
4.4.2. Refinement of Chemical-Specific Parameters
4.4.3. Refinement of Formulation-Specific Parameters
4.4.4. Human Full Body PBK Model
Application Scenarios
PBK Model Parameterization
4.4.5. PBK Model Performance
Sensitivity Analysis
Uncertainty Analysis
Reliability
Simulation for Human Population
PBK Model External Validation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- EPA, U. Next Generation Risk Assessment: Incorporation of Recent Advances In Molecular, Computational, And Systems Biology (Final Report); U.S. Environmental Protection Agency: Washington, DC, USA, 2014.
- Rogiers, V.; Benfenati, E.; Bernauer, U.; Bodin, L.; Carmichael, P.; Chaudhry, Q.; Coenraads, P.J.; Cronin, M.T.D.; Dent, M.; Dusinska, M.; et al. The way forward for assessing the human health safety of cosmetics in the EU—Workshop proceedings. Toxicology 2020, 436, 152421. [Google Scholar] [CrossRef]
- Bessems, J.G.; Loizou, G.; Krishnan, K.; Clewell, H.J., 3rd; Bernasconi, C.; Bois, F.; Coecke, S.; Collnot, E.M.; Diembeck, W.; Farcal, L.R.; et al. PBTK modelling platforms and parameter estimation tools to enable animal-free risk assessment: Recommendations from a joint EPAA--EURL ECVAM ADME workshop. Regul. Toxicol. Pharmacol. 2014, 68, 119–139. [Google Scholar] [CrossRef]
- Coecke, S.; Pelkonen, O.; Leite, S.B.; Bernauer, U.; Bessems, J.G.; Bois, F.Y.; Gundert-Remy, U.; Loizou, G.; Testai, E.; Zaldívar, J.M. Toxicokinetics as a key to the integrated toxicity risk assessment based primarily on non-animal approaches. Toxicol. In Vitro 2013, 27, 1570–1577. [Google Scholar] [CrossRef] [PubMed]
- Berggren, E.; Amcoff, P.; Benigni, R.; Blackburn, K.; Carney, E.; Cronin, M.; Deluyker, H.; Gautier, F.; Judson, R.S.; Kass, G.E.; et al. Chemical Safety Assessment Using Read-Across: Assessing the Use of Novel Testing Methods to Strengthen the Evidence Base for Decision Making. Environ. Health Perspect. 2015, 123, 1232–1240. [Google Scholar] [CrossRef]
- Cable, S.; Baltazar, M.T.; Bunglawala, F.; Carmichael, P.L.; Contreas, L.; Dent, M.P.; Houghton, J.; Kukic, P.; Malcomber, S.; Nicol, B.; et al. Advancing systemic toxicity risk assessment: Evaluation of a NAM-based toolbox approach. Toxicol. Sci. 2025, 204, 79–95. [Google Scholar] [CrossRef]
- Paul Friedman, K.; Thomas, R.S.; Wambaugh, J.F.; Harrill, J.A.; Judson, R.S.; Shafer, T.J.; Williams, A.J.; Lee, J.J.; Loo, L.H.; Gagné, M.; et al. Integration of new approach methods for the assessment of data-poor chemicals. Toxicol. Sci. 2025, 205, 74–105. [Google Scholar] [CrossRef] [PubMed]
- Andersen, M.E. Toxicokinetic modeling and its applications in chemical risk assessment. Toxicol. Lett. 2003, 138, 9–27. [Google Scholar] [CrossRef]
- Yuan, Y.; He, Q.; Zhang, S.; Li, M.; Tang, Z.; Zhu, X.; Jiao, Z.; Cai, W.; Xiang, X. Application of Physiologically Based Pharmacokinetic Modeling in Preclinical Studies: A Feasible Strategy to Practice the Principles of 3Rs. Front. Pharmacol. 2022, 13, 895556. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Zhang, L.; Grillo, J.A.; Liu, Q.; Bullock, J.M.; Moon, Y.J.; Song, P.; Brar, S.S.; Madabushi, R.; Wu, T.C.; et al. Applications of physiologically based pharmacokinetic (PBPK) modeling and simulation during regulatory review. Clin. Pharmacol. Ther. 2011, 89, 259–267. [Google Scholar] [CrossRef]
- Ellison, C.A.; Wu, S. Application of structural and functional pharmacokinetic analogs for physiologically based pharmacokinetic model development and evaluation. Regul. Toxicol. Pharmacol. 2020, 114, 104667. [Google Scholar] [CrossRef]
- Thompson, C.V.; Firman, J.W.; Goldsmith, M.R.; Grulke, C.M.; Tan, Y.-M.; Paini, A.; Penson, P.E.; Sayre, R.R.; Webb, S.; Madden, J.C. A Systematic Review of Published Physiologically-based Kinetic Models and an Assessment of their Chemical Space Coverage. ALTA 2021, 49, 197–208. [Google Scholar] [CrossRef]
- EU. Regulation (EC) No 1223/2009 of the European Parliament and of the Council. 2009. Available online: https://www.legislation.gov.uk/eur/2009/1223/contents (accessed on 10 March 2025).
- SCCS (Scientific Committee on Consumer Safety). SCCS Notes of Guidance for the Testing of Cosmetic Ingredients and their Safety Evaluation 11th revision, 30–31 March 2021, SCCS/1628/21. Regul. Toxicol. Pharmacol. 2021, 127, 105052. [Google Scholar] [CrossRef]
- SCCS. The SCCS notes of Guidance for the Testing of Cosmetic Ingredients and their Safety Evaluation 12th Revision; SCCS/1647/22; Publications Office of the European Union: Luxembourg, 2023; pp. 1–203. [Google Scholar]
- WHO. Harmonization Project Document No. 9: Characterization and Application of Physiologically Based Pharmacokinetic Models; IPCS-WHO: Geneva, Switzerland, 2010. [Google Scholar]
- OECD. Guidance Document on the Characterisation, Validation and Reporting of Physiologically Based Kinetic (PBK) Models for Regulatory Purposes; OECD Series on Testing and Assessment, No. 331, Environment, Health and Safety, Environment Directorate; OECD: Paris, France, 2021. [Google Scholar]
- Matta, M.K.; Florian, J.; Zusterzeel, R.; Pilli, N.R.; Patel, V.; Volpe, D.A.; Yang, Y.; Oh, L.; Bashaw, E.; Zineh, I.; et al. Effect of Sunscreen Application on Plasma Concentration of Sunscreen Active Ingredients: A Randomized Clinical Trial. JAMA 2020, 323, 256–267. [Google Scholar] [CrossRef]
- Matta, M.K.; Zusterzeel, R.; Pilli, N.R.; Patel, V.; Volpe, D.A.; Florian, J.; Oh, L.; Bashaw, E.; Zineh, I.; Sanabria, C.; et al. Effect of Sunscreen Application Under Maximal Use Conditions on Plasma Concentration of Sunscreen Active Ingredients: A Randomized Clinical TrialEffect of Sunscreen Application on Plasma Concentration of Active IngredientsEffect of Sunscreen Application on Plasma Concentration of Active Ingredients. JAMA 2019, 321, 2082–2091. [Google Scholar] [CrossRef]
- van Osdol, W.W.; Novakovic, J.; Le Merdy, M.; Tsakalozou, E.; Ghosh, P.; Spires, J.; Lukacova, V. Predicting Human Dermal Drug Concentrations Using PBPK Modeling and Simulation: Clobetasol Propionate Case Study. AAPS PharmSciTech 2024, 25, 39. [Google Scholar] [CrossRef]
- Mukhedkar, P.; Marfatia, A.; DiBella, J. Mechanistic TCAT, a novel PBPK modeling of dermal drug absorption. Pharma Times 2018, 50, 52–56. [Google Scholar]
- Ellison, C.A.; Tankersley, K.O.; Obringer, C.M.; Carr, G.J.; Manwaring, J.; Rothe, H.; Duplan, H.; Géniès, C.; Grégoire, S.; Hewitt, N.J.; et al. Partition coefficient and diffusion coefficient determinations of 50 compounds in human intact skin, isolated skin layers and isolated stratum corneum lipids. Toxicol. In Vitro 2020, 69, 104990. [Google Scholar] [CrossRef]
- Wang, T.F.; Kasting, G.B.; Nitsche, J.M. A multiphase microscopic model for stratum corneum permeability. I.Formulation, solution and illustrative results for representative compounds. J. Pharm. Sci. 2006, 95, 620–648. [Google Scholar] [CrossRef]
- Nitsche, J.M.; Wang, T.F.; Kasting, G.B. A two-phase analysis of solute partitioning into the stratum corneum. J. Pharm. Sci. 2006, 95, 649–666. [Google Scholar] [CrossRef]
- Potts, R.O.; Guy, R.H. Predicting Skin Permeability. Pharm. Res. 1992, 9, 663–669. [Google Scholar] [CrossRef]
- Wilschut, A.; ten Berge, W.F.; Robinson, P.J.; McKone, T.E. Estimating skin permeation. The validation of five mathematical skin permeation models. Chemosphere 1995, 30, 1275–1296. [Google Scholar] [CrossRef]
- Bunge, A.L.; Cleek, R.L. A new method for estimating dermal absorption from chemical exposure: 2. Effect of molecular weight and octanol-water partitioning. Pharm. Res. 1995, 12, 88–95. [Google Scholar] [CrossRef]
- Ibrahim, R.; Nitsche, J.M.; Kasting, G.B. Dermal clearance model for epidermal bioavailability calculations. J. Pharm. Sci. 2012, 101, 2094–2108. [Google Scholar] [CrossRef]
- Wester, R.C.; Maibach, H.I. Percutaneous absorption of drugs. Clin. Pharmacokinet. 1992, 23, 253–266. [Google Scholar] [CrossRef]
- Middleton, A.M.; Reynolds, J.; Cable, S.; Baltazar, M.T.; Li, H.; Bevan, S.; Carmichael, P.L.; Dent, M.P.; Hatherell, S.; Houghton, J.; et al. Are Non-animal Systemic Safety Assessments Protective? A Toolbox and Workflow ? A Toolbox and Workflow. Toxicol. Sci. 2022, 189, 124–147. [Google Scholar] [CrossRef]
- Hamadeh, A.; Nash, J.F.; Bialk, H.; Styczynski, P.; Troutman, J.; Edginton, A. Mechanistic skin modeling of plasma concentrations of sunscreen active ingredients following facial application. J. Pharm. Sci. 2023, 113, 806–825. [Google Scholar] [CrossRef]
- Yang, Y.; Ako-Adounvo, A.-M.; Wang, J.; Coelho, S.G.; Adah, S.A.; Matta, M.K.; Strauss, D.; Michele, T.M.; Wang, J.; Faustino, P.J.; et al. In Vitro Testing of Sunscreens for Dermal Absorption: Method Comparison and Rank Order Correlation with In Vivo Absorption. AAPS PharmSciTech 2022, 23, 121. [Google Scholar] [CrossRef]
- Grégoire, S.; Sorrell, I.; Lange, D.; Najjar, A.; Schepky, A.; Ellison, C.; Troutman, J.; Fabian, E.; Duplan, H.; Genies, C.; et al. Cosmetics Europe evaluation of 6 in silico skin penetration models. Comput. Toxicol. 2021, 19, 100177. [Google Scholar] [CrossRef]
- Grégoire, S.; Ribaud, C.; Benech, F.; Meunier, J.R.; Garrigues-Mazert, A.; Guy, R.H. Prediction of chemical absorption into and through the skin from cosmetic and dermatological formulations. Br. J. Dermatol. 2009, 160, 80–91. [Google Scholar] [CrossRef]
- Hansen, S.; Lehr, C.M.; Schaefer, U.F. Improved input parameters for diffusion models of skin absorption. Adv. Drug Deliv. Rev. 2013, 65, 251–264. [Google Scholar] [CrossRef]
- Moxon, T.E.; Li, H.; Lee, M.Y.; Piechota, P.; Nicol, B.; Pickles, J.; Pendlington, R.; Sorrell, I.; Baltazar, M.T. Application of physiologically based kinetic (PBK) modelling in the next generation risk assessment of dermally applied consumer products. Toxicol. In Vitro 2020, 63, 104746. [Google Scholar] [CrossRef]
- Romanhole, R.C.; Fava, A.L.M.; Tundisi, L.L.; Macedo, L.M.; Santos É, M.D.; Ataide, J.A.; Mazzola, P.G. Unplanned absorption of sunscreen ingredients: Impact of formulation and evaluation methods. Int. J. Pharm. 2020, 591, 120013. [Google Scholar] [CrossRef]
- Frechen, S.; Rostami-Hodjegan, A. Quality Assurance of PBPK Modeling Platforms and Guidance on Building, Evaluating, Verifying and Applying PBPK Models Prudently under the Umbrella of Qualification: Why, When, What, How and By Whom? Pharm. Res. 2022, 39, 1733–1748. [Google Scholar] [CrossRef]
- Scheuplein, R.J.; Blank, I.H. Permeability of the skin. Physiol. Rev. 1971, 51, 702–747. [Google Scholar] [CrossRef]
- Najjar, A.; Schepky, A.; Krueger, C.T.; Dent, M.; Cable, S.; Li, H.; Grégoire, S.; Roussel, L.; Noel-Voisin, A.; Hewitt, N.J.; et al. Use of Physiologically-Based Kinetics Modelling to Reliably Predict Internal Concentrations of the UV Filter, Homosalate, After Repeated Oral and Topical Application. Front. Pharmacol. 2022, 12, 802514. [Google Scholar] [CrossRef]
- Dancik, Y.; Miller, M.A.; Jaworska, J.; Kasting, G.B. Design and performance of a spreadsheet-based model for estimating bioavailability of chemicals from dermal exposure. Adv. Drug Deliv. Rev. 2012, 65, 221–236. [Google Scholar] [CrossRef]
- Géniès, C.; Jacques-Jamin, C.; Duplan, H.; Rothe, H.; Ellison, C.; Cubberley, R.; Schepky, A.; Lange, D.; Klaric, M.; Hewitt, N.J.; et al. Comparison of the metabolism of 10 cosmetics-relevant chemicals in EpiSkin™ S9 subcellular fractions and in vitro human skin explants. J. Appl. Toxicol. 2020, 40, 313–326. [Google Scholar] [CrossRef]
- Sintov, A.C.; Zhang, P.J.; Michniak-Kohn, B.B. Cutaneous biotransformation of N-(4-bromobenzoyl)-S,S-dimethyliminosulfurane and its product, 4-bromobenzamide, leading to percutaneous penetration enhancement of drugs: Initial evidence using hydrocortisone. J. Control. Release 2009, 133, 44–51. [Google Scholar] [CrossRef]
- Mavon, A.; Jacques-Jamin, C. The Effect of Skin Metabolism on the Absorption of Chemicals. Cosmet. Toilet. 2013, 128, 98–103. [Google Scholar]
- SCCS (Scientific Committee on Consumer Safety). Opinion on Benzophenone-3 (CAS No 131-57-7, EC No 205-031-5), Preliminary Version of 15 December 2020, Final Version of 30–31 March 2021, SCCS/1625/20. 2021. Available online: https://health.ec.europa.eu/latest-updates/sccs-final-opinion-benzophenone-3-2021-04-15_en (accessed on 10 March 2025).
- Nakamura, N.; Inselman, A.L.; White, G.A.; Chang, C.W.; Trbojevich, R.A.; Sephr, E.; Voris, K.L.; Patton, R.E.; Bryant, M.S.; Harrouk, W.; et al. Effects of maternal and lactational exposure to 2-hydroxy-4-methoxybenzone on development and reproductive organs in male and female rat offspring. Birth Defects Res. Part B-Dev. Reprod. Toxicol. 2015, 104, 35–51. [Google Scholar] [CrossRef]
- Desprez, B.; Dent, M.; Keller, D.; Klaric, M.; Ouédraogo, G.; Cubberley, R.; Duplan, H.; Eilstein, J.; Ellison, C.; Grégoire, S.; et al. A strategy for systemic toxicity assessment based on non-animal approaches: The Cosmetics Europe Long Range Science Strategy programme. Toxicol. In Vitro 2018, 50, 137–146. [Google Scholar] [CrossRef]
- US-EPA, CompTox Chemicals Dashboard v.2.2.1. Available online: https://www.epa.gov/comptox-tools/comptox-chemicals-dashboard (accessed on 10 March 2025).
- OECD. OECD Guideline for the Testing of Chemicals, N° 428. Skin Absorption: In Vitro Method; OECD: Paris, France, 2004; p. 8. [Google Scholar]
- OECD. Test No. 428: Skin Absorption: In Vitro Method; OECD: Paris, France, 2004. [Google Scholar] [CrossRef]
- Hummer, J.; Schwingenschuh, S.; Raml, R.; Boulgaropoulos, B.; Schwagerle, G.; Augustin, T.; Sinner, F.; Birngruber, T. OFM-recirculation and OFM-suction: Advanced in-vivo open flow microperfusion (OFM) methods for direct and absolute quantification of albumin in interstitial fluid. Biomed. Phys. Eng. Express 2021, 6, 065031. [Google Scholar] [CrossRef]
- Todo, H.; Oshizaka, T.; Kadhum, W.R.; Sugibayashi, K. Mathematical model to predict skin concentration after topical application of drugs. Pharmaceutics 2013, 5, 634–651. [Google Scholar] [CrossRef]
- Fruhstorfer, H.; Abel, U.; Garthe, C.D.; Knüttel, A. Thickness of the stratum corneum of the volar fingertips. Clin. Anat. 2000, 13, 429–433. [Google Scholar] [CrossRef]
- Peress, J. Estimate evaporative losses from spills. Chem. Eng. Prog. 2003, 99, 32–34. [Google Scholar]
- Eilstein, J.; Grégoire, S.; Fabre, A.; Arbey, E.; Géniès, C.; Duplan, H.; Rothe, H.; Ellison, C.; Cubberley, R.; Schepky, A.; et al. Use of human liver and EpiSkin™ S9 subcellular fractions as a screening assays to compare the in vitro hepatic and dermal metabolism of 47 cosmetics-relevant chemicals. J. Appl. Toxicol. 2020, 40, 416–433. [Google Scholar] [CrossRef]
- Yu, S.; Li, S.; Yang, H.; Lee, F.; Wu, J.T.; Qian, M.G. A novel liquid chromatography/tandem mass spectrometry based depletion method for measuring red blood cell partitioning of pharmaceutical compounds in drug discovery. Rapid Commun. Mass Spectrom. 2005, 19, 250–254. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Reynolds, J.; Sorrell, I.; Sheffield, D.; Pendlington, R.; Cubberley, R.; Nicol, B. PBK modelling of topical application and characterisation of the uncertainty of Cmax estimate: A case study approach. Toxicol. Appl. Pharmacol. 2022, 442, 115992. [Google Scholar] [CrossRef] [PubMed]
- Varma, M.V.; Steyn, S.J.; Allerton, C.; El-Kattan, A.F. Predicting Clearance Mechanism in Drug Discovery: Extended Clearance Classification System (ECCS). Pharm. Res. 2015, 32, 3785–3802. [Google Scholar] [CrossRef]
- Lukacova, V.; Parrott, N.; Lave, T.; Fraczkiewicz, G.; Bolger, M.; Woltosz, W. General approach to calculation of tissue: Plasma partition coefficients for physiologically based pharmacokinetic (PBPK) modeling. In Proceedings of the 2008 AAPS National Annual Meeting and Exposition, Boston, MA, USA, 5–8 April 2008. [Google Scholar]
- Evans, M.V.; Andersen, M.E. Sensitivity analysis of a physiological model for 2,3,7,8-tetrachlorodibenzo-p-dioxin (TCDD): Assessing the impact of specific model parameters on sequestration in liver and fat in the rat. Toxicol. Sci. 2000, 54, 71–80. [Google Scholar] [CrossRef]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef] [PubMed]
- Najjar, A.; Hamadeh, A.; Krause, S.; Schepky, A.; Edginton, A. Global sensitivity analysis of Open Systems Pharmacology Suite physiologically based pharmacokinetic models. CPT Pharmacomet. Syst. Pharmacol. 2024, 13, 2052–2067. [Google Scholar] [CrossRef] [PubMed]



| (A) Formulation 1 | |||||
| Dosing Schedule | Output parameter | Observed | Predicted L1 | Predicted L2 | Predicted L3 |
| Single dose 1 app/day (Day 1) (1710 in 28.5 mL) | Cmax (µg/mL) | 0.0894 | 0.06524 | 0.0633 | 0.0627 |
| Tmax (h) | 9.00 | 23 | 5.75 | 6.82 | |
| AUC0–∞ (µg·h/mL) | 2.37 | NA * | 0.97294 | 9.69 | |
| AUC0–23 (µg·h/mL) | 1.29 | 0.96534 | 0.8147 | 1.30 | |
| Cmax Pred/Obs ratio | 0.729754 | 0.708054 | 0.701 | ||
| AUC0–23 Prd/Obs ratio | 0.746 | 0.630 | 1.01 | ||
| CLsys(L/h) | 5.299 | 64.669 | 27.319 | ||
| Vss (L) | 400.327 | 138.201 | 82.008 | ||
| Sim Pop 1 app/day (Day 1) (1710 in 28.5 mL) | Number of subjects | - | 500 | 500 | |
| Cmax (µg/mL) mean | - | 0.0982 | 0.063 | ||
| CV% | - | 150.99 | 59.8 | ||
| min | - | 0.00224 | 0.00698 | ||
| max | - | 1.6827 | 0.231 | ||
| CI 90% | - | 0.087 to 0.109 | 0.060 to 0.0650 | ||
| AUC0–23 (µg·h/mL) | 1.0526 | 1.28 | |||
| CV% | 114.05 | 58.0 | |||
| min | 0.03435 | 0.150 | |||
| max | 10.824 | 4.56 | |||
| CI 90% | 0.964 to 1.141 | 1.22 to 1.33 | |||
| Multiple dose 1 app/day 1 4 app/day 2-3-4 2 h of interval (1710 in 28.5 mL) | Cmax (µg/mL) | 0.170 | - | 0.278 | 0.134 |
| Tmax (h) | 73.0 | - | 79.2 | 80.4 | |
| AUC0–∞ (µg·h/mL) | 16.4 | - | 14.6 | 28.4 | |
| AUC0–23 (µg·h/mL) | 15.6 | - | 14.6 | 27.1 | |
| Cmax Pred/Obs ratio | 1.64 | 0.788 | |||
| AUC0–t Prd/Obs ratio | 0.936 | 1.74 | |||
| (B) Formulation 2 | |||||
| Dosing Schedule | Output parameter | Observed | Predicted L1 | Predicted L2 | Predicted L3 |
| Single dose 1 app/day (Day 1) (1140 in 28.5 mL) | Cmax (µg/mL) | 0.0800 | 0.05082 | 0.047 | 0.084 |
| Tmax (h) | 6.00 | 23 | 5.6733 | 3.760 | |
| AUC0–∞ (µg·h/mL) | 1.89 | NA * | 0.70546 | 1.820 | |
| AUC0–23 (µg·h/mL) | 1.26 | 0.75961 | 0.5965 | 1.270 | |
| Cmax Pred/Obs ratio | 0.632877 | 0.585 | 1.05 | ||
| AUC0–23 Prd/Obs ratio | 0.603 | 0.473 | 1.01 | ||
| CLsys(L/h) | 5.299 | 64.669 | 59.570 | ||
| Vss (L) | 400.327 | 138.201 | 81.683 | ||
| Sim Popm 1 app/day (Day 1) (1140 in 28.5 mL) | Number of subjects | - | 500 | 500 | |
| Cmax (µg/mL) mean | - | 0.07788 | 0.084 | ||
| CV% | - | 153.79 | 72.500 | ||
| min | - | 0.0009136 | 0.00657 | ||
| max | - | 1.5748 | 0.381 | ||
| CI 90% | - | 0.069 to 0.087 | 0.0800 to 0.0890 | ||
| AUC0–23 (µg·h/mL) | 0.81645 | 1.26 | |||
| CV% | 115.56 | 66.7 | |||
| min | 0.009218 | 0.129 | |||
| max | 9.3286 | 5.28 | |||
| CI 90% | 0.747 to 0.886 | 1.20 to 1.32 | |||
| Multiple dose 1 app/day 1 4 app/day 2-3-4 2 h of interval (1140 mg in 28.5 mL) | Cmax (µg/mL) | 0.210 | - | 0.169 | 0.128 |
| Tmax (h) | 78.0 | - | 82.1 | 79.7 | |
| AUC0–∞ (µg·h/mL) | 17.3 | - | 9.02 | 9.2 | |
| AUC0–23 (µg·h/mL) | 16.8 | - | 9.02 | 9.2 | |
| Cmax Pred/Obs ratio | 0.805 | 0.610 | |||
| AUC0–23 Prd/Obs ratio | 0.537 | 0.549 | |||
| (A) Formulation 1 | ||||
| Uncertainty in variability of the input parameter estimates | ||||
| High | Medium | Low | ||
| SENSITIVITY | High | KVH/w | Rbp | |
| Medium | DSTCOR, DDE, KDE/w | |||
| Low | KSTCOR/w | Fup, DVH, DVE, KVE/w, Solvent Residual Volume Fraction, Kevap | ||
| (B) Formulation 2 | ||||
| Uncertainty in variability of the input parameter estimates | ||||
| High | Medium | Low | ||
| SENSITIVITY | High | DSTCOR | Rbp, KVH/w, KSTCOR/w, DDE, KDE/w | |
| Medium | ||||
| Low | Fup, DVH, KVE/w, DVE, Solvent Residual Volume Fraction, Kevap | |||
| PBK Model | Formulation 1 | Formulation 2 |
|---|---|---|
| Species | Human | Human |
| Population | American | American |
| Gender | Male | Male |
| Age (year) | 41 | 45 |
| Weight (kg) | 76 | 76,3 |
| Height (cm) | 176.23 | 176.01 |
| Dose (mg) | 1710 | 1140 |
| Volume (ml) | 28.5 | 28.5 |
| Application surface area (cm2) | 14,250 | 14,250 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Golbamaki, N.; Moustié, A.; Hewitt, N.J.; Lereaux, G.; Burbank, M.; Ben Yahya, E.M.; Grégoire, S.; Roussel-Berlier, L. A Novel Workflow for Non-Animal PBK Modelling of UV Filters: Oxybenzone as a Case Study. Pharmaceuticals 2025, 18, 1607. https://doi.org/10.3390/ph18111607
Golbamaki N, Moustié A, Hewitt NJ, Lereaux G, Burbank M, Ben Yahya EM, Grégoire S, Roussel-Berlier L. A Novel Workflow for Non-Animal PBK Modelling of UV Filters: Oxybenzone as a Case Study. Pharmaceuticals. 2025; 18(11):1607. https://doi.org/10.3390/ph18111607
Chicago/Turabian StyleGolbamaki, Nazanin, Anne Moustié, Nicola J. Hewitt, Guillaume Lereaux, Matthew Burbank, El Mehdi Ben Yahya, Sébastien Grégoire, and Laurène Roussel-Berlier. 2025. "A Novel Workflow for Non-Animal PBK Modelling of UV Filters: Oxybenzone as a Case Study" Pharmaceuticals 18, no. 11: 1607. https://doi.org/10.3390/ph18111607
APA StyleGolbamaki, N., Moustié, A., Hewitt, N. J., Lereaux, G., Burbank, M., Ben Yahya, E. M., Grégoire, S., & Roussel-Berlier, L. (2025). A Novel Workflow for Non-Animal PBK Modelling of UV Filters: Oxybenzone as a Case Study. Pharmaceuticals, 18(11), 1607. https://doi.org/10.3390/ph18111607







