Enhancing the Solubility of Indomethacin: A Breakthrough with Cocrystal Formation
Abstract
1. Introduction
1.1. Cocrystal Intermolecular Interactions
1.2. Crystallization as a Tool for Optimizing Drug Properties
1.3. Solubility and Methods of Cocrystals Formation
1.4. Theorical Solubility
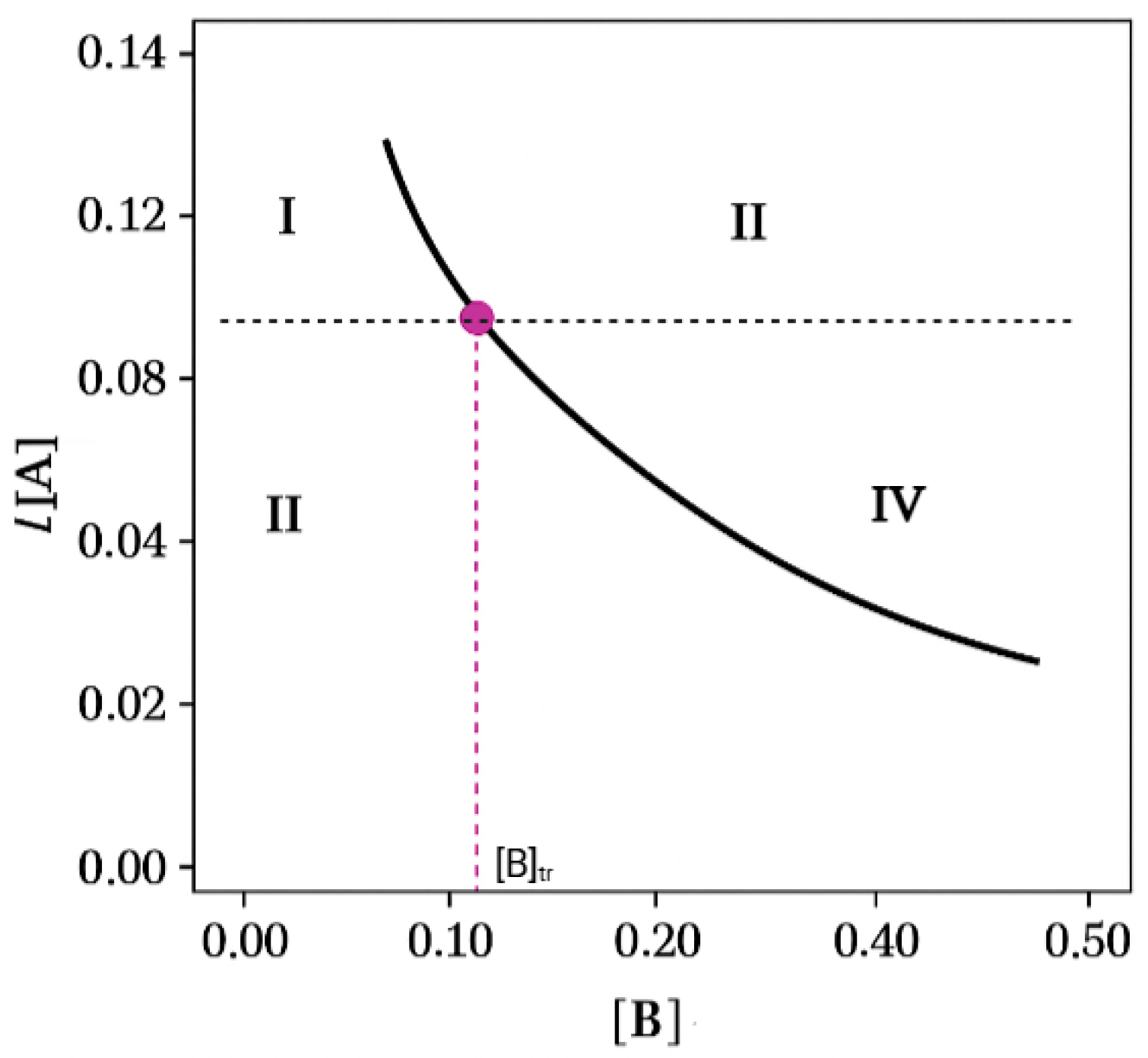
1.4.1. Determination of the Phase Solubility Diagram (PSD)
1.4.2. Determination of the Triangular Diagram Phases (TPD)
2. Results and Discussion
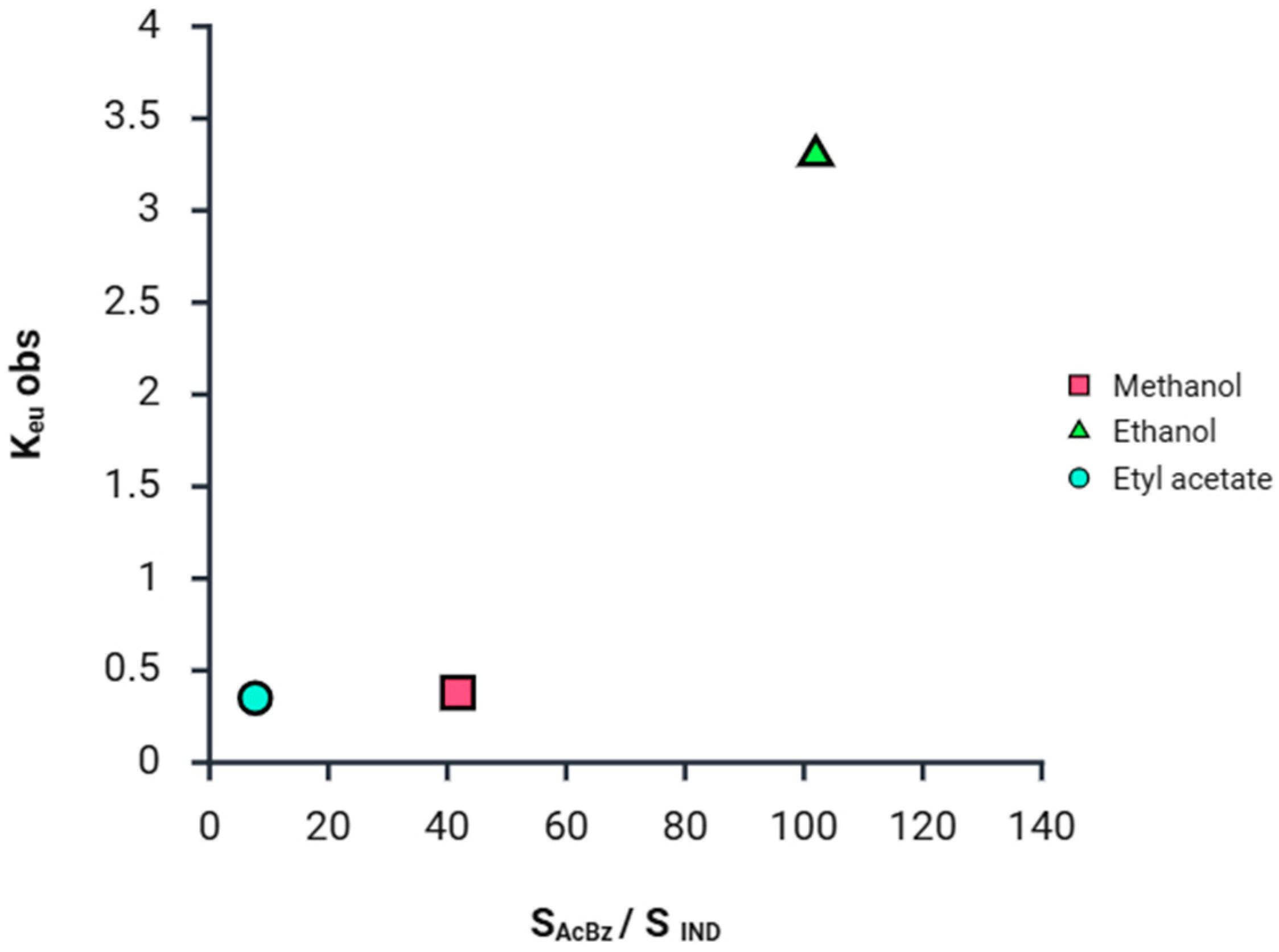
2.1. Eutectics Concentrations of the IND-AcBZ Cocrystal
2.2. Ternary Diagrams
2.3. Physical Properties of Cocrystals
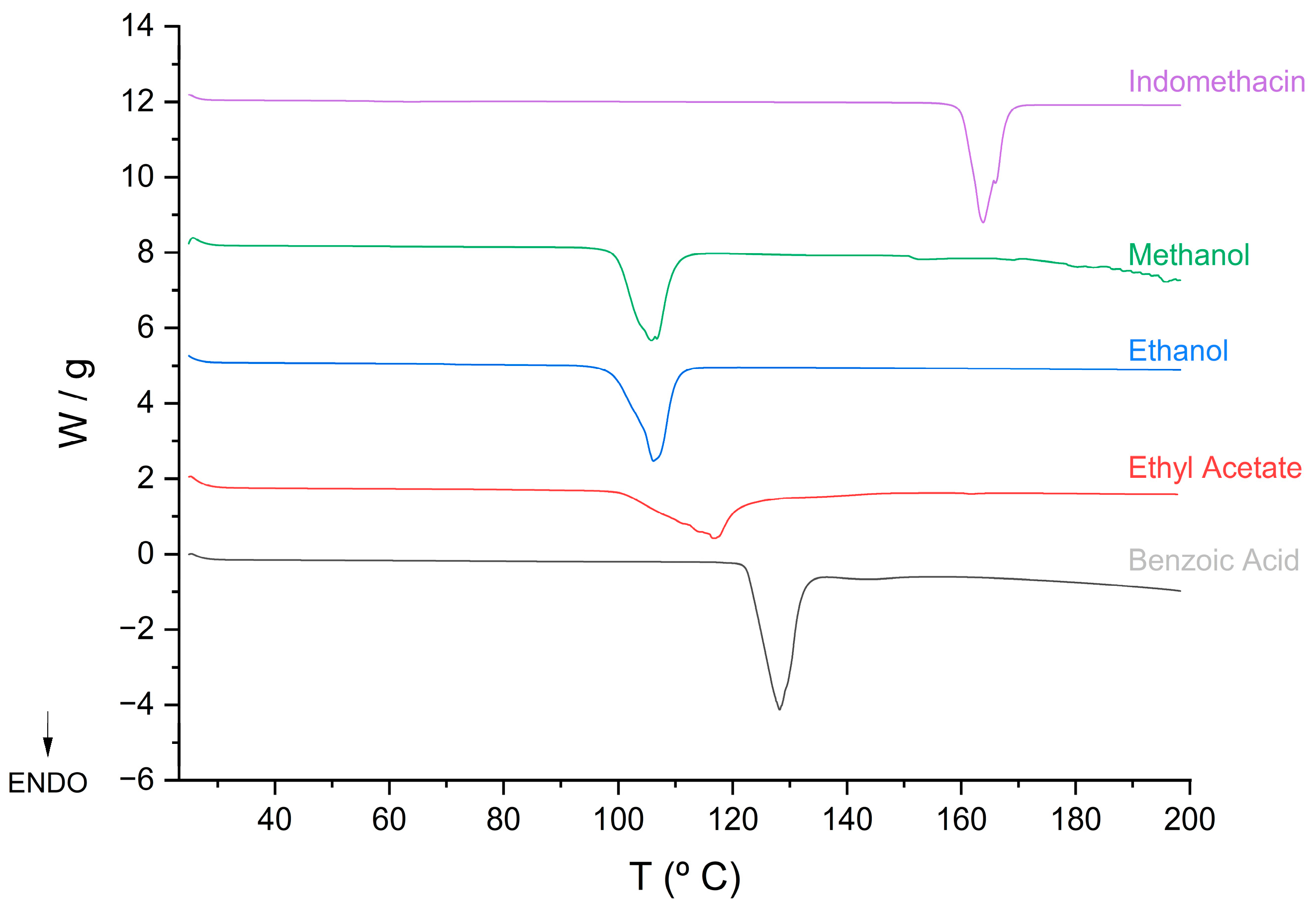
2.3.1. Differential Scanning Calorimeter (DSC)
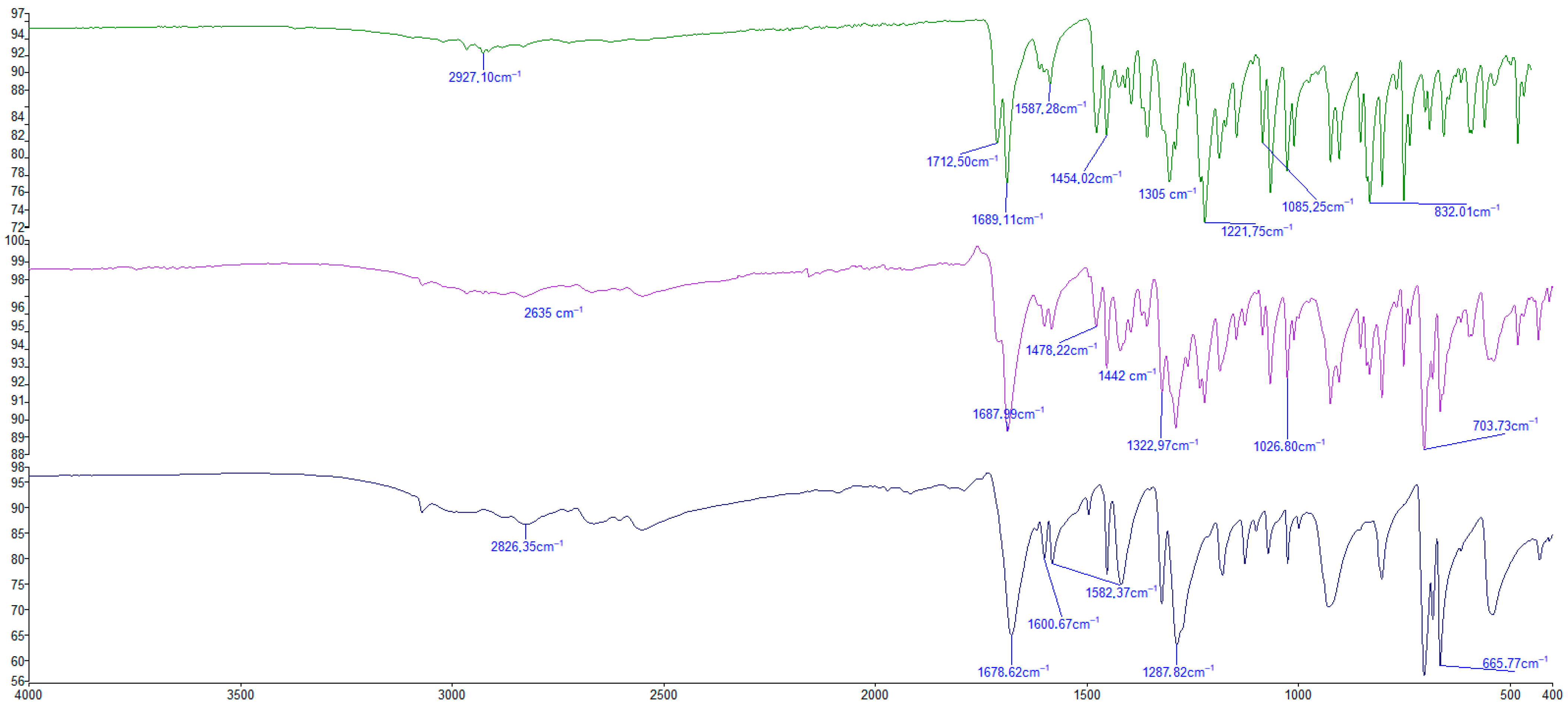
2.3.2. Fourier Transformation Infrared Absorption Spectroscopy (FT-IR)
3. Materials and Methods
3.1. Indomethacin/Benzoic Acid Cocrystal Preparation
3.2. Solubility
Solubility Determination of Cocrystal of Indomethacin in Different Solvents
3.3. Indomethacin/Benzoic Acid Cocrystal Characterization
3.3.1. Differential Scanning Calorimeter (DSC)
3.3.2. Fourier Transform Infrared Absorption Spectroscopy (FT-IR)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alvarado López, K. Uso de cocristales para mejorar la solubilidad y velocidad de disolución de los fármacos Using cocrystals to improve the solubility and dissolution rate of drugs. Med. Mater. Sci. Chem. 2015, 15, 207–215. [Google Scholar]
- Karagianni, A.; Malamatari, M.; Kachrimanis, K. Pharmaceutical cocrystals: New solid phase modification approaches for the formulation of APIs. Pharmaceutics 2018, 10, 18. [Google Scholar] [CrossRef]
- Shan, N.; Zaworotko, M.J. The role of cocrystals in pharmaceutical science. Drug Discov. Today 2008, 13, 440–446. [Google Scholar] [CrossRef] [PubMed]
- Guo, M.; Sun, X.; Chen, J.; Cai, T. Pharmaceutical cocrystals: A review of preparations, physicochemical properties and applications. Acta Pharm. Sin. B 2021, 11, 2537–2564. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Nanda, A. In-silico methods of cocrystal screening: A review on tools for rational design of pharmaceutical cocrystals. J. Drug Deliv. Sci. Technol. 2021, 63, 102527. [Google Scholar] [CrossRef]
- Hickey, M.B.; Peterson, M.L.; Scoppettuolo, L.A.; Morrisette, S.L.; Vetter, A.; Guzmán, H.; Remenar, J.F.; Zhang, Z.; Tawa, M.D.; Haley, S.; et al. Performance comparison of a co-crystal of carbamazepine with marketed product. Eur. J. Pharm. Biopharm. 2007, 67, 112–119. [Google Scholar] [CrossRef]
- Schultheiss, N.; Newman, A. Pharmaceutical Cocrystals and Their Physicochemical Properties. Cryst. Growth Des. 2009, 9, 2950–2967. [Google Scholar] [CrossRef]
- Karimi-Jafari, M.; Padrela, L.; Walker, G.M.; Croker, D.M. Creating cocrystals: A review of pharmaceutical cocrystal preparation routes and applications. Cryst. Growth Des. 2018, 18, 6370–6387. [Google Scholar] [CrossRef]
- Childs, S.L.; Rodríguez-Hornedo, N.; Reddy, L.S.; Jayasankar, A.; Maheshwari, C.; McCausland, L.; Shipplett, R.; Stahly, B.C. Screening strategies based on solubility and solution composition generate pharmaceutically acceptable cocrystals of carbamazepine. CrystEngComm 2008, 10, 856. [Google Scholar] [CrossRef]
- Qiao, N.; Li, M.; Schlindwein, W.; Malek, N.; Davies, A.; Trappitt, G. Pharmaceutical cocrystals: An overview. Int. J. Pharm. 2011, 419, 1–11. [Google Scholar] [CrossRef]
- Vyas, A.J.; Jadav, C.D.; Patel, A.I.; Patel, A.B.; Shah, S.R.; Sheth, D.; Dholakia, S. Review on stability indicating assay method or forced degradation study: Strategy and regulatory consideration. Asian J. Pharm. Anal. 2023, 13, 131–139. [Google Scholar] [CrossRef]
- Alvani, A.; Shayanfar, A. Solution Stability of Pharmaceutical Cocrystals. Cryst. Growth Des. 2022, 22, 6323–6337. [Google Scholar] [CrossRef]
- Bandaru, R.K.; Rout, S.R.; Kenguva, G.; Gorain, B.; Alhakamy, N.A.; Kesharwani, P.; Dandela, R. Recent advances in pharmaceutical cocrystals: From bench to Market. Front. Pharmacol. 2021, 12, 780582. [Google Scholar] [CrossRef] [PubMed]
- Aitipamula, S.; Chow, P.S.; Tan, R.B.H. Polymorphism in cocrystals: A review and assessment of its significance. CrystEngComm 2014, 16, 3451. [Google Scholar] [CrossRef]
- Ma, K.; Wang, N.; Cheng, L.; Wei, Y.; Zhang, J.; Gao, Y.; Qian, S. Identification of novel adefovir dipivoxil-saccharin cocrystal polymorphs and their thermodynamic polymorphic transformations. Int. J. Pharm. 2019, 566, 361–370. [Google Scholar] [CrossRef]
- O’sUllivan, A.; Kelly, S.; Bhattacharya, S.; Ryan, K.M.; Collins, M.N.; Padrela, L. Polymorph selection of pharmaceutical cocrystals via bench-top and continuous production techniques. Int. J. Pharm. 2024, 663, 124596. [Google Scholar] [CrossRef]
- Baptista, J.A.; Castro, R.A.E.; Rosado, M.T.S.; Maria, T.M.R.; Silva, M.R.; Canotilho, J.; Eusébio, M.E.S. Polymorphic Cocrystals of the Antimalarial Drug Pyrimethamine: Two Case Studies. Cryst. Growth Des. 2021, 21, 3699–3713. [Google Scholar] [CrossRef]
- Inoue, D.; Furubayashi, T.; Tanaka, A.; Sakane, T.; Sugano, K. Quantitative estimation of drug permeation through nasal mucosa using in vitro membrane permeability across Calu-3 cell layers for predicting in vivo bioavailability after intranasal administration to rats. Eur. J. Pharm. Biopharm. 2020, 149, 145–153. [Google Scholar] [CrossRef]
- Yunta, M.J.R. It is important to compute intramolecular hydrogen bonding in drug design? Am. J. Model. Optim. 2017, 5, 24–57. [Google Scholar] [CrossRef]
- Sathisaran, I.; Dalvi, S.V. Engineering cocrystals of poorly water-soluble drugs to enhance dissolution in aqueous medium. Pharmaceutics 2018, 10, 108. [Google Scholar] [CrossRef]
- Alahalaweh, A. Pharmaceutical Cocrystals (Formation Mechanisms, Solubility Behaviour and Solid-State Properties). Available online: www.ltu.se (accessed on 1 September 2025).
- Ji, C.; Hoffman, M.C.; Mehta, M.A. Catalytic effect of solvent vapors on the spontaneous formation of caffeine–malonic acid cocrystal. Cryst. Growth Des. 2017, 17, 1456–1459. [Google Scholar] [CrossRef]
- Pawar, N.; Saha, A.; Nandan, N.; Parambil, J.V. Solution cocrystallization: A scalable approach for cocrystal production. Crystals 2021, 11, 303. [Google Scholar] [CrossRef]
- Santos, J.A.V.; Baptista, J.A.; Santos, I.C.; Maria, T.M.R.; Canotilho, J.; Castro, R.A.E.; Eusébio, M.E.S. Pharmaceutical nanococrystal synthesis: A novel grinding approach. CrystEngComm 2022, 24, 947–961. [Google Scholar] [CrossRef]
- Nitin Sanjay, A. Pharmaceutical Cocrystallization: A Review. Available online: www.japer.in (accessed on 1 September 2025).
- Ahuja, D.; Ramisetty, K.A.; Sumanth, P.K.; Crowley, C.M.; Lusi, M.; Rasmuson, Å.C. Microwave assisted slurry conversion crystallization for manufacturing of new co-crystals of sulfamethazine and sulfamerazine. CrystEngComm 2020, 22, 1381–1394. [Google Scholar] [CrossRef]
- Trask, A.V.; Motherwell, W.D.S.; Jones, W. Solvent-drop grinding: Green polymorph control of cocrystallisation. Chem. Commun. 2004, 7, 890–891. [Google Scholar] [CrossRef]
- Cuadra, I.A.; Cabañas, A.; Cheda, J.A.; Pando, C. Polymorphism in the co-crystallization of the anticonvulsant drug carbamazepine and saccharin using supercritical CO2 as an anti-solvent. J. Supercrit. Fluids 2018, 136, 60–69. [Google Scholar] [CrossRef]
- Daurio, D.; Medina, C.; Saw, R.; Nagapudi, K.; Alvarez-Núñez, F. Application of twin screw extrusion in the manufacture of cocrystals, part I: Four case studies. Pharmaceutics 2011, 3, 582–600. [Google Scholar] [CrossRef]
- Daurio, D.; Nagapudi, K.; Li, L.; Quan, P.; Nunez, F.A. Application of twin screw extrusion to the manufacture of cocrystals: Scale-up of AMG 517–sorbic acid cocrystal production. Faraday Discuss. 2014, 170, 235–249. [Google Scholar] [CrossRef]
- Sládková, V.; Dammer, O.; Sedmak, G.; Skořepová, E.; Kratochvíl, B. Ivabradine hydrochloride (s)-mandelic acid co-crystal: In situ preparation during formulation. Crystals 2017, 7, 13. [Google Scholar] [CrossRef]
- Nehm, S.J.; Rodríguez-Spong, B.; Rodríguez-Hornedo, N. Phase solubility diagrams of cocrystals are explained by solubility product and solution complexation. Cryst. Growth Des. 2006, 6, 592–600. [Google Scholar] [CrossRef]
- Good, D.J.; Rodríguez-Hornedo, N. Solubility advantage of pharmaceutical cocrystals. Cryst. Growth Des. 2009, 9, 2252–2264. [Google Scholar] [CrossRef]
- Alhalaweh, A.; Sokolowski, A.; Rodríguez-Hornedo, N.; Velaga, S.P. Solubility behavior and solution chemistry of indomethacin cocrystals in organic solvents. Cryst. Growth Des. 2011, 11, 3923–3929. [Google Scholar] [CrossRef]
- Sun, X.; Yin, Q.; Ding, S.; Shen, Z.; Bao, Y.; Gong, J.; Hou, B.; Hao, H.; Wang, Y.; Wang, J.; et al. (Solid + liquid) phase diagram for (indomethacin + nicotinamide)-methanol or methanol/ethyl acetate mixture and solubility behavior of 1:1 (indomethacin + nicotinamide) co-crystal at T = (298.15 and 313.15) K. J. Chem. Thermodyn. 2015, 85, 171–177. [Google Scholar] [CrossRef]
- Huang, Y.; Sun, X.; Zhou, L.; Zhang, Z.; Zhang, S.; Yin, Q. Investigation of ternary phase diagrams of carbamazepine–nicotinamide cocrystal in ethanol and ethanol/ethyl acetate mixtures at 298.15 K and 313.15 K. J. Solut. Chem. 2020, 49, 117–132. [Google Scholar] [CrossRef]
- Lee, M.-J.; Chun, N.-H.; Wang, I.-C.; Liu, J.J.; Jeong, M.-Y.; Choi, G.J. Understanding the formation of indomethacin–saccharin cocrystals by anti-solvent crystallization. Cryst. Growth Des. 2013, 13, 2067–2074. [Google Scholar] [CrossRef]
- Alhalaweh, A.; Velaga, S.P. Formation of cocrystals from stoichiometric solutions of incongruently saturating systems by spray drying. Cryst. Growth Des. 2010, 10, 3302–3305. [Google Scholar] [CrossRef]
- Vasoya, J.M.; Shah, A.V.; Serajuddin, A.T. Investigation of possible solubility and dissolution advantages of cocrystals, I: Aqueous solubility and dissolution rates of ketoconazole and its cocrystals as functions of pH. ADMET DMPK 2019, 7, 106–130. [Google Scholar] [CrossRef]
- Di Salvo, F.; Suarez, S. Polimorfismo cristalino: Aplicaciones en fármacos y técnicas de caracterización. SAFIBY 2020, 166, 53–57. [Google Scholar]
- Malwade, C.R.; Qu, H. Cooling crystallization of indomethacin: Effect of supersaturation, temperature, and seeding on polymorphism and crystal size distribution. Org. Process Res. Dev. 2018, 22, 697–706. [Google Scholar] [CrossRef]
- Dallos, L.J.; Manzo, R.H.; Baena, Y. Análisis por FTIR y DSC de complejos polielectrolito entre Eudragit® E100 y ácido benzoico como evidencia de hidrólisis de los grupos éster del polímero. Rev. Colomb. De Cienc. Químico-Farm. 2019, 48, 700–721. [Google Scholar] [CrossRef]
- da Silva, C.C.; Guimarães, F.F.; Ribeiro, L.; Martins, F.T. Salt or cocrystal of salt? Probing the nature of multicomponent crystal forms with infrared spectroscopy. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2016, 167, 89–95. [Google Scholar] [CrossRef]
- Ali, H.R.H.; Alhalaweh, A.; Velaga, S.P. Vibrational spectroscopic investigation of polymorphs and cocrystals of indomethacin. Drug Dev. Ind. Pharm. 2013, 39, 625–634. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Zeitler, J.A.; Tomerini, D.; Parrott, E.P.J.; Gladden, L.F.; Day, G.M. A study into the effect of subtle structural details and disorder on the terahertz spectrum of crystalline benzoic acid. Phys. Chem. Chem. Phys. 2010, 12, 5329. [Google Scholar] [CrossRef] [PubMed]
- Grossjohann, C.; Serrano, D.R.; Paluch, K.J.; O’connell, P.; Vella-Zarb, L.; Manesiotis, P.; McCabe, T.; Tajber, L.; Corrigan, O.I.; Healy, A.M. Polymorphism in sulfadimidine/4-aminosalicylic acid cocrystals: Solid-state characterization and physicochemical properties. J. Pharm. Sci. 2015, 104, 1385–1398. [Google Scholar] [CrossRef] [PubMed]
- Costa, W.S.; de Oliveira, Y.S.; Ayala, A.P. Polymorphism in cocrystals of metronidazole benzoate. CrystEngComm 2023, 25, 4716–4728. [Google Scholar] [CrossRef]

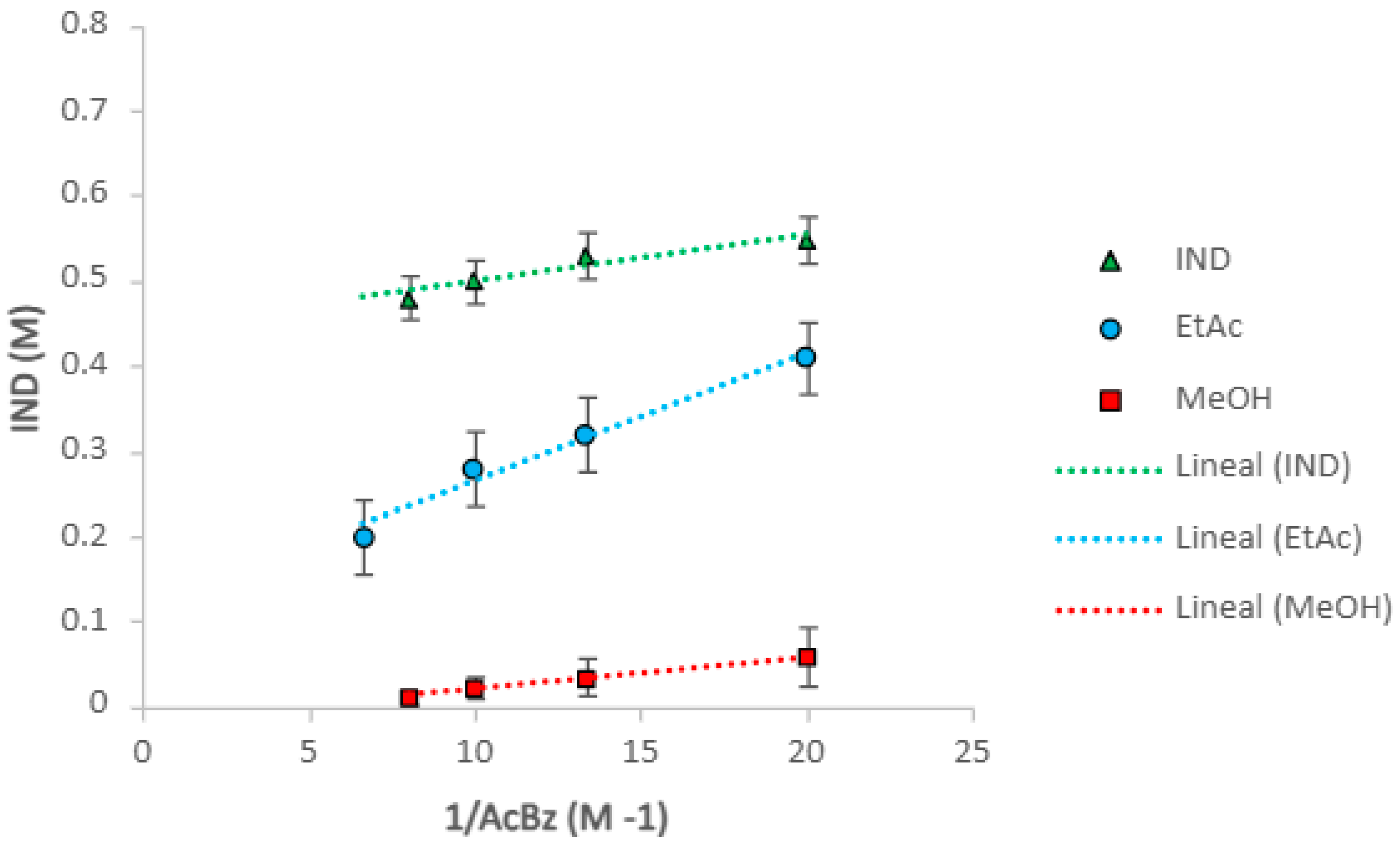
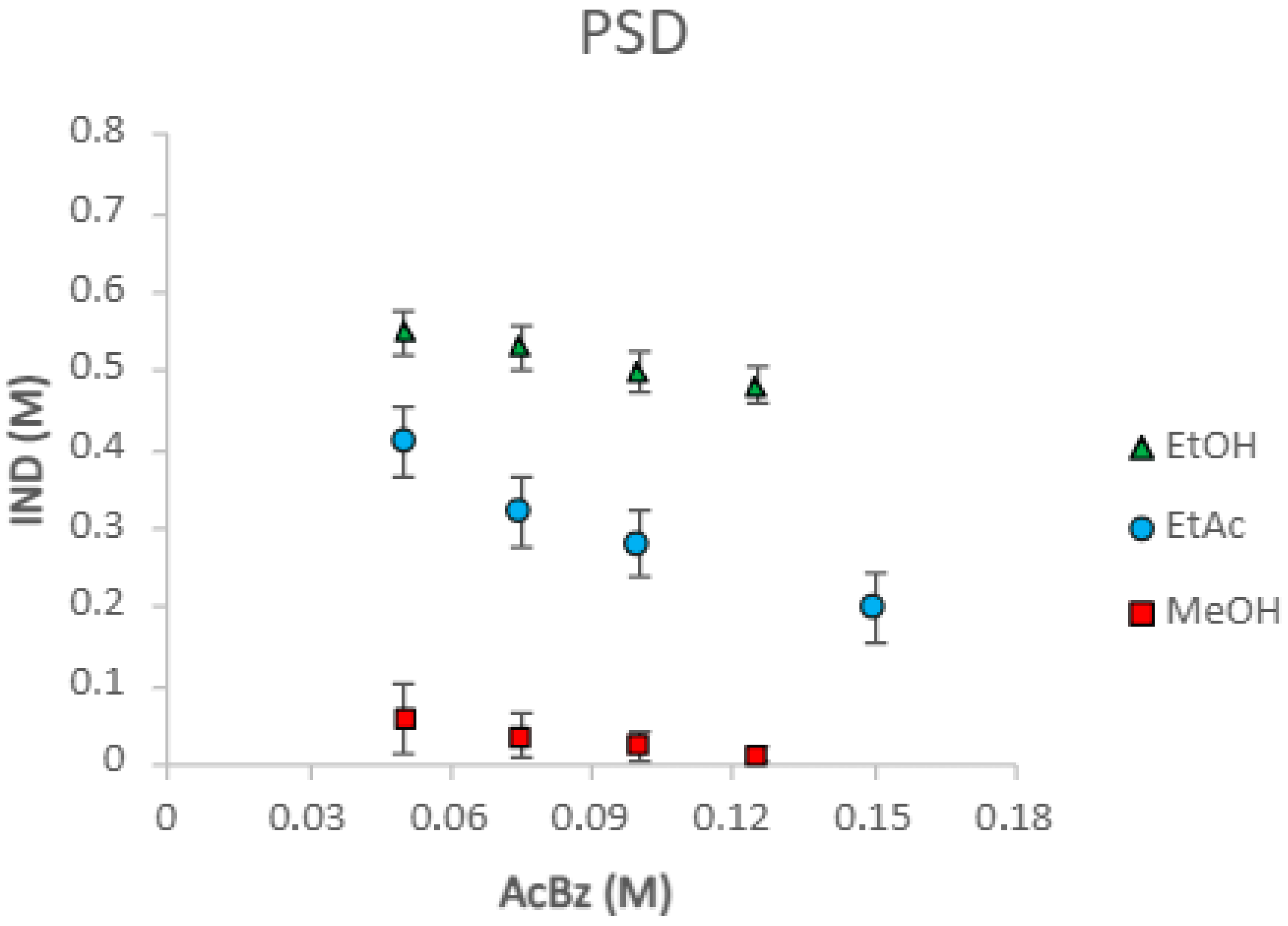

| Solvent | Equation of Line | R2 Value | Ksp (M2) | K11 (M−1) |
|---|---|---|---|---|
| Ethanol | 0.96 | 5.2 × 10−3 | 92.19 | |
| Methanol | 0.99 | 3.8 × 10−3 | 0 | |
| Ethyl acetate | 0.99 | 1.5 × 10−2 | 4.24 |
| Solvent | Ksp (M2) | K11 (M−1) |
|---|---|---|
| Ethanol | 5.2 × 10−3 | 92.19 |
| Methanol | 3.8 × 10−3 | 0 |
| Ethyl acetate | 1.5 × 10−2 | 4.24 |
| Solvent | [IND] (M) | [AcBz] (M) | [IND-AcBZ] (M) | [AcBz]/[IND] | [IND]eu (M) | [AcBz] eu (M) | Keu | Scc |
|---|---|---|---|---|---|---|---|---|
| Ethanol | 0.01 | 1.02 | 0.47 | 101.50 | 0.05 | 0.16 | 3.30 | 0.09 |
| Methanol | 0.067 | 2.80 | 0 | 41.79 | 0.09 | 0.04 | 0.38 | 0.06 |
| Etyl Acetate | 0.23 | 1.77 | 0.0636 | 7.69 | 0.28 | 0.10 | 0.35 | 0.16 |
| Samples | DSC | Reported Melting Point | Ref | ||
|---|---|---|---|---|---|
| Tonset (fusion)/°C | Tpeak(fusion)/°C | ΔHfusion/Jg−1 | |||
| IND (γ form) | 160.67 | 162.69 | 91.051 | 162 | [41] |
| IND (α form) | - | - | - | 154.5–155.5 | [41] |
| Cocrystals EtOH | 102.21 | 105.25 | 99.606 | - | |
| Cocrystal MeOH | 99.87 | 105.18 | 100.13 | - | |
| Cocrystal EtAc | 109.85 | 116.65 | 82.60 | - | |
| Benzoic Acid | 122.75 | 125.53 | 124.20 | 122 | [42] |
| IND | Cocrystal | AcBz | Assigned Functional Group |
|---|---|---|---|
| 2927.10 | 2826.37 | W (OH) | |
| 2635 | W (C=O modified) | ||
| 1713 | 1687 | 1687.12 | S (COOH) |
| 1689 | S (C=O amide) | ||
| 1600 | W (C=C) | ||
| 1587 | 1582 | W (c=c) aromatic | |
| 1454 | 1442 | 1452 | M (C=C) aromatic |
| 1305 | 1323 | M (C-H in plane) | |
| 1221 | 1287 | S (C-O) | |
| 1028 | m (C-C in plane) | ||
| 1085 | m(C-Cl) | ||
| 832 | C-H out of plane | ||
| 703 | Ring deformation | ||
| 665 | C-H out of plane |
| Sample | Ethanol (M) | Methanol (M) | Etyl Acetate (M) |
|---|---|---|---|
| AcBz | 1.015 | 2.800 | 1.77 |
| IND | 0.010 | 0.067 | 0.23 |
| IND/AcBz (1:1) | 0.089 | 0.056 | 0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pardo, H.; Guarnizo-Herrero, V.; Martínez-Alonso, B.; Peña Fernández, M.Á. Enhancing the Solubility of Indomethacin: A Breakthrough with Cocrystal Formation. Pharmaceuticals 2025, 18, 1610. https://doi.org/10.3390/ph18111610
Pardo H, Guarnizo-Herrero V, Martínez-Alonso B, Peña Fernández MÁ. Enhancing the Solubility of Indomethacin: A Breakthrough with Cocrystal Formation. Pharmaceuticals. 2025; 18(11):1610. https://doi.org/10.3390/ph18111610
Chicago/Turabian StylePardo, Hugo, Víctor Guarnizo-Herrero, Borja Martínez-Alonso, and Mª Ángeles Peña Fernández. 2025. "Enhancing the Solubility of Indomethacin: A Breakthrough with Cocrystal Formation" Pharmaceuticals 18, no. 11: 1610. https://doi.org/10.3390/ph18111610
APA StylePardo, H., Guarnizo-Herrero, V., Martínez-Alonso, B., & Peña Fernández, M. Á. (2025). Enhancing the Solubility of Indomethacin: A Breakthrough with Cocrystal Formation. Pharmaceuticals, 18(11), 1610. https://doi.org/10.3390/ph18111610








