PK Modeling of L-4-Boronophenylalanine and Development of Bayesian Predictive Platform for L-4-Boronophenylalanine PKs for Boron Neutron Capture Therapy
Abstract
1. Introduction
2. Materials and Methods
- Construction of a PK model for blood boron (10B)
- A user-friendly predictive interface consisting of a master R script, sub-R scripts for individual specific NONMEM dataset generation using the Shiny package, execution of NONMEM, and summation and graphical display of the NONMEM results
- Sensitivity analyses to evaluate the predictive performance of the platform and identify the optimal PK sampling time for blood (10B)
2.1. PK Modeling of Blood (10B)
2.2. Validation of Population PK Model
2.3. Bayesian Predictive Model
2.4. Optimal Sampling Schedule Determination for Blood Boron Concentration Prediction
3. Results
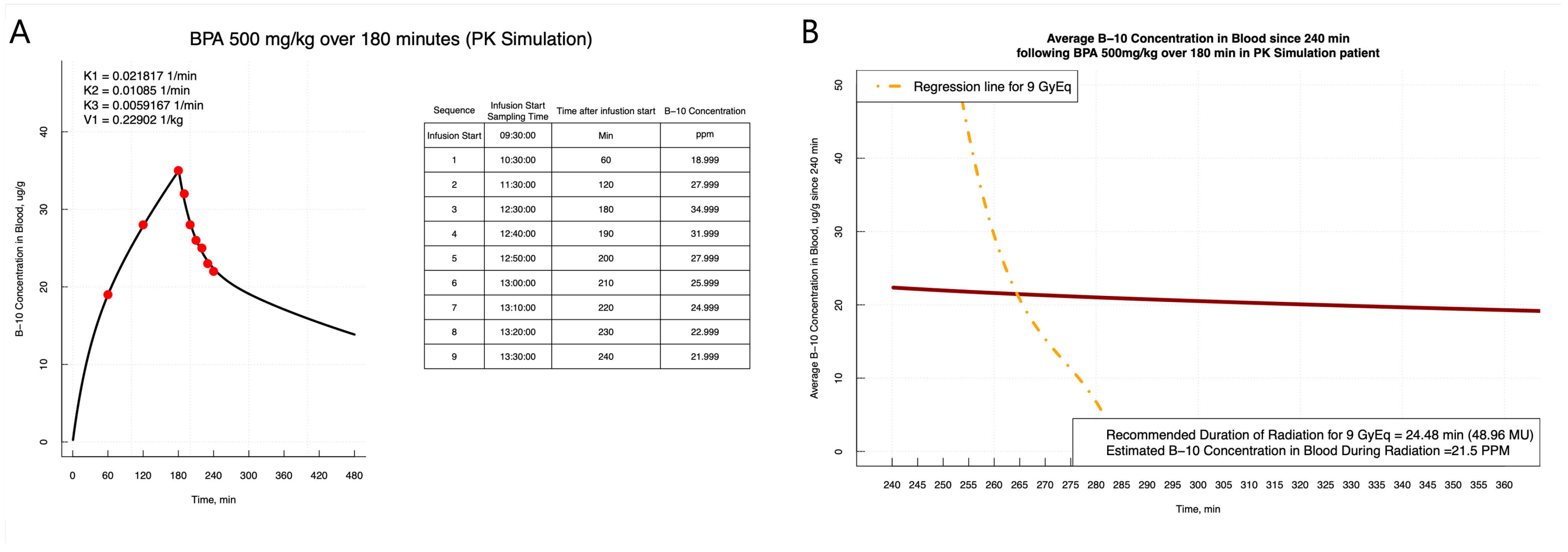
3.1. PK Modeling
| Parameter | Estimates | 95% Confidence Interval |
|---|---|---|
| , 1/min | 0.023 | 0.018–0.028 |
| IIV (CV %) | 0.071 (27.2) | 0.005–0.137 |
| , 1/min | 0.012 | 0.009–0.014 |
| IIV (CV %) | 0.037 (19.4) | 0.012–0.061 |
| , 1/min | 0.006 | 0.005–0.007 |
| IIV (CV %) | 0.050 (22.6) | −0.002–0.102 |
| , L | 0.252 | 0.216–0.288 |
| IIV (CV %) | 0.061 (25.0) | 0.029–0.092 |
| (additive)*, g/g | 0.540 | 0.054–1.026 |
| (proportional)* | 0.001 | 0.000–0.003 |
3.2. Optimal Sampling Schedule Determination
3.3. User-Friendly Prediction Platform for Boron Concentration Estimation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BNCT | Boron Neutron Capture Therapy |
| BPA | L-4-Boronophenylalanine |
| CI | Confidence Interval |
| CV | Coefficient of Variation |
| Residual Error | |
| FOCE | First-Order Conditional Estimation |
| ICRU | International Commission on Radiation Units and Measurements |
| IIV | Inter-Individual Variation |
| IPRED | Individual Predictions |
| MAP | Maximum a Posteriori Probability |
| NTCP | Normal Tissue Complication Probability |
| PRED | Population Prediction |
| PD | Pharmacodynamics |
| PK | Pharmacokinetics |
| TCP | Tumor Control Probability |
| VD | Volume of Distribution |
References
- Burnet, N.G.; Thomas, S.J.; Burton, K.E.; Jefferies, S.J. Defining the tumour and target volumes for radiotherapy. Cancer Imaging 2004, 4, 153–161. [Google Scholar] [CrossRef]
- Mohan, R. Intensity-modulated radiation therapy—You can have your cake and eat it too! Med. Phys. 2023, 50 (Suppl. 1), 74–79. [Google Scholar] [CrossRef] [PubMed]
- Hegde, J.V.; Chen, A.M.; Chin, R.K. Advances in Radiation Oncology: What to Consider. Otolaryngol. Clin. N. Am. 2017, 50, 755–764. [Google Scholar] [CrossRef] [PubMed]
- Blanchard, P.; Frank, S.J. Place de la protonthérapie en cancérologie ORL. Cancer Radiother. 2017, 21, 515–520. [Google Scholar] [CrossRef] [PubMed]
- Malouff, T.D.; Seneviratne, D.S.; Ebner, D.K.; Stross, W.C.; Waddle, M.R.; Trifiletti, D.M.; Krishnan, S. Boron Neutron Capture Therapy: A Review of Clinical Applications. Front. Oncol. 2021, 11, 601820. [Google Scholar] [CrossRef] [PubMed]
- International Atomic Energy Agency. Advances in Boron Neutron Capture Therapy. In Advances in Boron Neutron Capture Therapy; IAEA: Vienna, Austria, 2023; p. 29. [Google Scholar]
- Coderre, J.A.; Morris, G.M. The Radiation Biology of Boron Neutron Capture Therapy. Radiat. Res. 1999, 151, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Ryynänen, P.M.; Kortesniemi, M.; Coderre, J.A.; Diaz, A.Z.; Hiismäki, P.; Savolainen, S.E. Models for estimation of the (10)B concentration after BPA-fructose complex infusion in patients during epithermal neutron irradiation in BNCT. Int. J. Radiat. Oncol. Biol. Phys. 2000, 48, 1145–1154. [Google Scholar] [CrossRef] [PubMed]
- Palmer, M.R.; Goorley, J.T.; Kiger, W.S.; Busse, P.M.; Riley, K.J.; Harling, O.K.; Zamenhof, R.G. Treatment planning and dosimetry for the Harvard-MIT Phase I clinical trial of cranial neutron capture therapy. Int. J. Radiat. Oncol. Biol. Phys. 2002, 53, 1361–1379. [Google Scholar] [CrossRef]
- Kiger, W.S., 3rd; Palmer, M.R.; Riley, K.J.; Zamenhof, R.G.; Busse, P.M. A pharmacokinetic model for the concentration of 10B in blood after boronophenylalanine-fructose administration in humans. Radiat. Res. 2001, 155, 611–618. [Google Scholar] [CrossRef]
- Kiger, W.S., 3rd; Palmer, M.R.; Riley, K.J.; Zamenhof, R.G.; Busse, P.M. Pharamacokinetic modeling for boronophenylalanine-fructose mediated neutron capture therapy: 10B Concentration predictions and dosimetric consequences. J. Neurooncol. 2003, 62, 171–186. [Google Scholar] [CrossRef]
- Yong, Z.; Song, Z.; Zhou, Y.; Liu, T.; Zhang, Z.; Zhao, Y.; Chen, Y.; Jin, C.; Chen, X.; Lu, J.; et al. Boron neutron capture therapy for malignant melanoma: First clinical case report in China. Chin. J. Cancer Res. 2016, 28, 634–640. [Google Scholar] [CrossRef] [PubMed]
- Koivunoro, H.; Hippeläinen, E.; Auterinen, I.; Kankaanranta, L.; Kulvik, M.; Laakso, J.; Seppälä, T.; Savolainen, S.; Joensuu, H. Biokinetic analysis of tissue boron (10B) concentrations of glioma patients treated with BNCT in Finland. Appl. Radiat. Isot. 2015, 106, 189–194. [Google Scholar] [CrossRef] [PubMed]
- Wittig, A.; Collette, L.; Appelman, K.; Bührmann, S.; Jäckel, M.C.; Jöckel, K.H.; Schmid, K.W.; Ortmann, U.; Moss, R.; Sauerwein, W.A.G. EORTC trial 11001: Distribution of two 10B-compounds in patients with squamous cell carcinoma of head and neck, a translational research/phase 1 trial. J. Cell. Mol. Med. 2009, 13, 1653–1665. [Google Scholar] [CrossRef] [PubMed]
- Fukuda, H.; Hiratsuka, J.; Honda, C.; Kobayashi, T.; Yoshino, K.; Karashima, H.; Takahashi, J.; Abe, Y.; Kanda, K.; Ichihashi, M.; et al. Boron neutron capture therapy of malignant melanoma using 10B-paraboronophenylalanine with special reference to evaluation of radiation dose and damage to the normal skin. Radiat. Res. 1994, 138, 435–442. [Google Scholar] [CrossRef] [PubMed]
- Thwaites, D. Accuracy required and achievable in radiotherapy dosimetry: Have modern technology and techniques changed our views? J. Phys. Conf. Ser. 2013, 444, 012006. [Google Scholar] [CrossRef]
- Chanana, A.D.; Capala, J.; Chadha, M.; Coderre, J.A.; Diaz, A.Z.; Elowitz, E.H.; Iwai, J.; Joel, D.D.; Liu, H.B.; Ma, R.; et al. Boron neutron capture therapy for glioblastoma multiforme: Interim results from the phase I/II dose-escalation studies. Neurosurgery 2000, 44, 1182–1192. [Google Scholar]
- Elowitz, E.H.; Bergland, R.M.; Coderre, J.A.; Joel, D.D.; Chadha, M.; Chanana, A.D. Biodistribution of p-boronophenylalanine in patients with glioblastoma multiforme for use in boron neutron capture therapy. Neurosurgery 1998, 42, 463–468; discussion 468–469. [Google Scholar]
- Coderre, J.A.; Chanana, A.D.; Joel, D.D.; Elowitz, E.H.; Micca, P.L.; Nawrocky, M.M.; Chadha, M.; Gebbers, J.O.; Shady, M.; Peress, N.S.; et al. Biodistribution of boronophenylalanine in patients with glioblastoma multiforme: Boron concentration correlates with tumor cellularity. Radiat. Res. 1998, 149, 163–170. [Google Scholar] [CrossRef]
- Murata, I.; Mukai, T.; Nakamura, S.; Miyamaru, H.; Kato, I. Development of a thick CdTe detector for BNCT-SPECT. Appl. Radiat. Isot. 2011, 69, 1706–1709. [Google Scholar] [CrossRef]
- Ito, M.; Murata, I.; Miyamaru, H.; Mukai, T.; Yoshida, S. Feasibility study on BNCT-SPECT using a CdTe detector. Prog. Nucl. Sci. Technol. 2015, 1, 267–270. [Google Scholar]
- Murata, I.; Kusaka, S.; Minami, K.; Saraue, N.; Tamaki, S.; Kato, I.; Sato, F. Design of SPECT for BNCT to measure local boron dose with GAGG scintillator. Appl. Radiat. Isot. 2022, 181, 110056. [Google Scholar] [CrossRef] [PubMed]
- Lo, Y.W.; Lee, J.C.; Hu, Y.S.; Li, C.Y.; Chen, Y.L.; Lin, C.S.; Huang, W.S.; Lin, K.H.; Chen, Y.W. The importance of optimal ROIs delineation for FBPA-PET before BNCT. Appl. Radiat. Isot. 2020, 163, 109219. [Google Scholar] [CrossRef] [PubMed]
- Ishiwata, K. 4-Borono-2-18F-fluoro-L-phenylalanine PET for boron neutron capture therapy-oriented diagnosis: Overview of a quarter century of research. Ann. Nucl. Med. 2019, 33, 223–236. [Google Scholar] [CrossRef]
- Isohashi, K.; Kanai, Y.; Aihara, T.; Hu, N.; Fukushima, K.; Baba, I.; Hirokawa, F.; Kakino, R.; Komori, T.; Nihei, K.; et al. Exploration of the threshold SUV for diagnosis of malignancy using 18F-FBPA PET/CT. Eur. J. Hybrid Imaging 2022, 6, 35. [Google Scholar] [CrossRef]
- Hanaoka, K.; Watabe, T.; Naka, S.; Kanai, Y.; Ikeda, H.; Horitsugi, G.; Kato, H.; Isohashi, K.; Shimosegawa, E.; Hatazawa, J. FBPA PET in boron neutron capture therapy for cancer: Prediction of (10)B concentration in the tumor and normal tissue in a rat xenograft model. EJNMMI Res. 2014, 4, 70. [Google Scholar] [CrossRef] [PubMed]


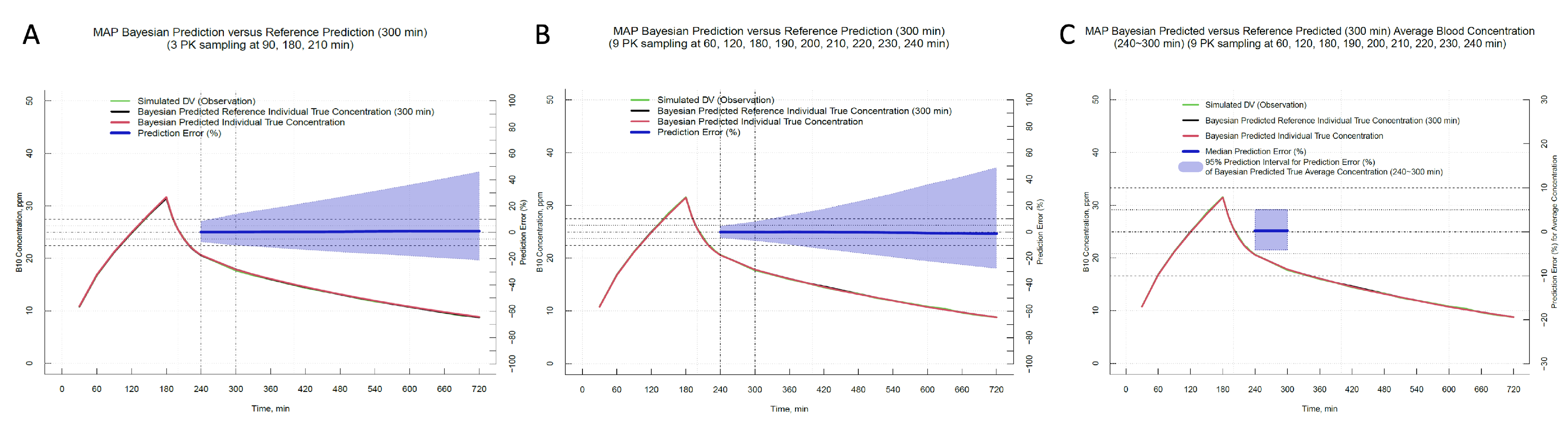
| No. | Number of Blood Samplings and Timepoints per Schedule |
|---|---|
| I | 3 PK samplings at 90, 180, 210 min |
| II | 4 PK samplings at 90, 180, 210, 240 min |
| III | 4 PK samplings at 90, 180, 200, 220 min |
| IV | 5 PK samplings at 90, 180, 200, 220, 240 min |
| V | 4 PK samplings at 90, 180, 195, 210 min |
| VI | 5 PK samplings at 90, 180, 195, 210, 240 min |
| VII | 6 PK samplings at 90, 180, 190, 200, 210, 220 min |
| VIII | 8 PK samplings at 90, 180, 190, 200, 210, 220, 230, 240 min |
| IX | 4 PK samplings at 60, 120, 180, 210 min |
| X | 5 PK samplings at 60, 120, 180, 210, 240 min |
| XI | 5 PK samplings at 60, 120, 180, 200, 220 min |
| XII | 6 PK samplings at 60, 120, 180, 200, 220, 240 min |
| XIII | 5 PK samplings at 60, 120, 180, 195, 210 min |
| XIV | 7 PK samplings at 60, 120, 180, 195, 210, 225, 240 min |
| XV | 7 PK samplings at 60, 120, 180, 190, 200, 210, 220 min |
| XVI | 9 PK samplings at 60, 120, 180, 190, 200, 210, 220, 230, 240 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, W.; Won, J.Y.; Yi, J.; Choi, S.C.; Lee, S.M.; Mun, K.; Lim, H.-S. PK Modeling of L-4-Boronophenylalanine and Development of Bayesian Predictive Platform for L-4-Boronophenylalanine PKs for Boron Neutron Capture Therapy. Pharmaceuticals 2024, 17, 301. https://doi.org/10.3390/ph17030301
Kim W, Won JY, Yi J, Choi SC, Lee SM, Mun K, Lim H-S. PK Modeling of L-4-Boronophenylalanine and Development of Bayesian Predictive Platform for L-4-Boronophenylalanine PKs for Boron Neutron Capture Therapy. Pharmaceuticals. 2024; 17(3):301. https://doi.org/10.3390/ph17030301
Chicago/Turabian StyleKim, Woohyoung, Ji Yeong Won, Jungyu Yi, Seung Chan Choi, Sang Min Lee, Kyungran Mun, and Hyeong-Seok Lim. 2024. "PK Modeling of L-4-Boronophenylalanine and Development of Bayesian Predictive Platform for L-4-Boronophenylalanine PKs for Boron Neutron Capture Therapy" Pharmaceuticals 17, no. 3: 301. https://doi.org/10.3390/ph17030301
APA StyleKim, W., Won, J. Y., Yi, J., Choi, S. C., Lee, S. M., Mun, K., & Lim, H.-S. (2024). PK Modeling of L-4-Boronophenylalanine and Development of Bayesian Predictive Platform for L-4-Boronophenylalanine PKs for Boron Neutron Capture Therapy. Pharmaceuticals, 17(3), 301. https://doi.org/10.3390/ph17030301







