Recent Advances in Translational Pharmacokinetics and Pharmacodynamics Prediction of Therapeutic Antibodies Using Modeling and Simulation
Abstract
1. Introduction
2. Traditional Model-Based Prediction of Human PKPD
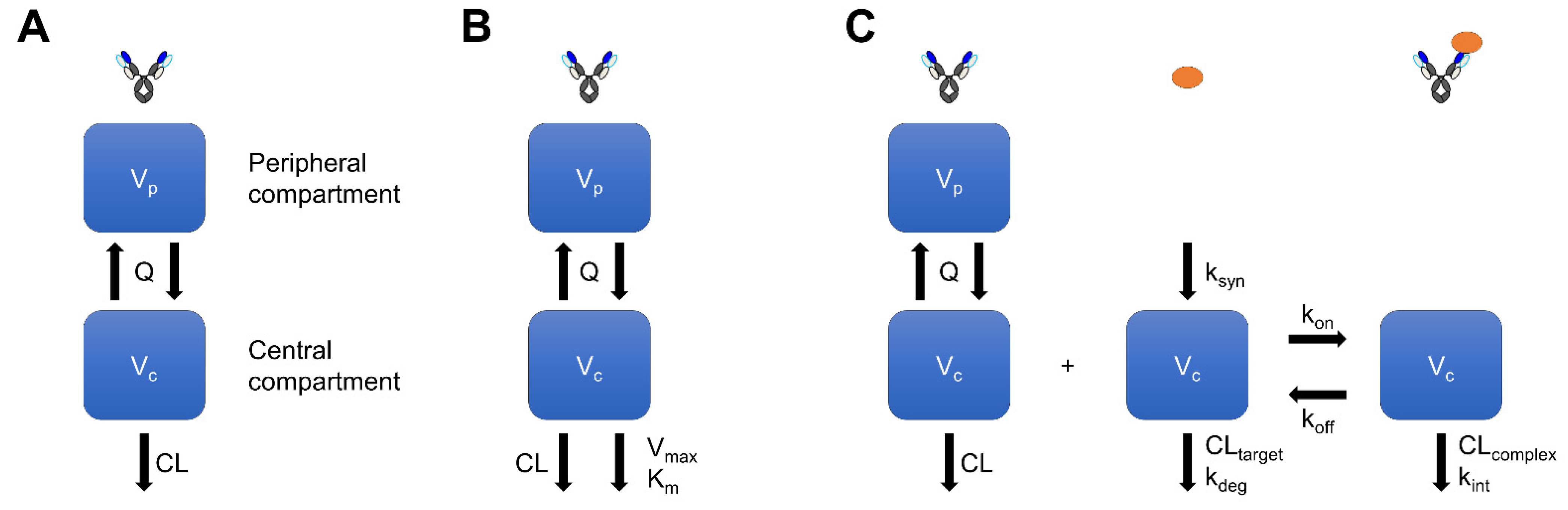
2.1. Compartment-Model-Based Prediction of Linear Pharmacokinetics
2.2. Michaelis–Menten-Model-Based Prediction of Nonlinear Pharmacokinetics
2.3. Traditional Model-Based Prediction of Pharmacodynamics
3. TMDD-Model-Based Prediction of Human PKPD
3.1. TMDD-Model-Based Prediction of Nonlinear Pharmacokinetics
3.2. TMDD-Model-Based Prediction of Pharmacodynamics
4. PBPK-Model-Based Prediction of Human PKPD
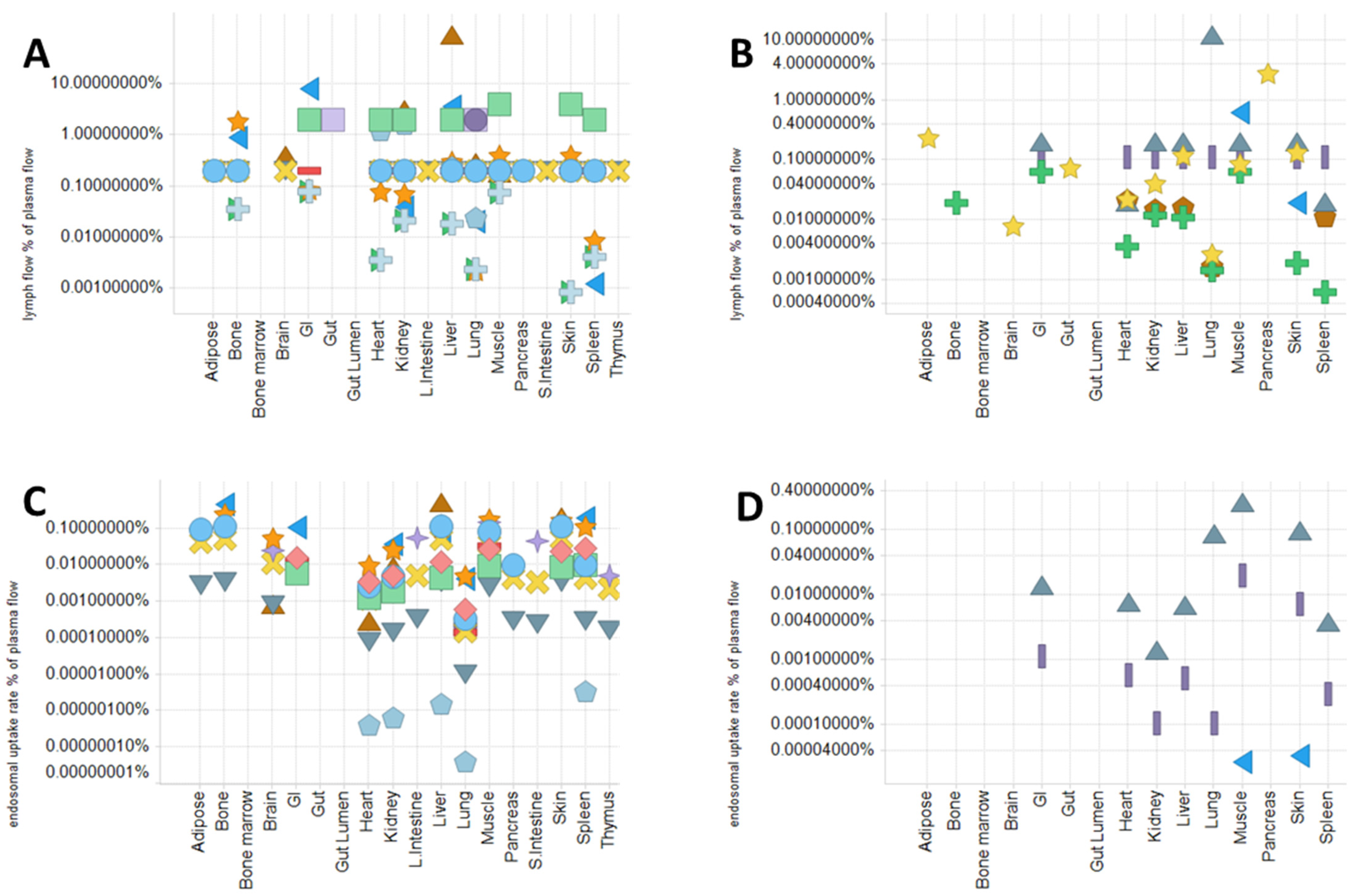
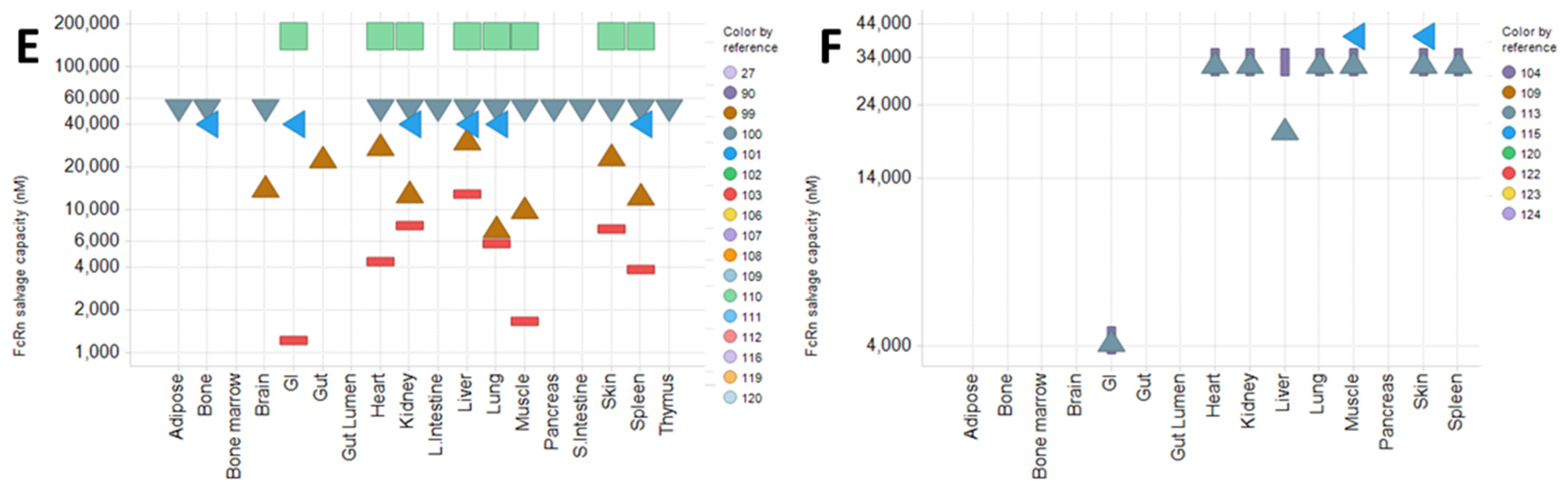
4.1. Physiological Parameters and Model Structure in PBPK Model
- Plasma and lymph flow rate
- 2.
- Rate of pinocytosis, lysosomal degradation, and FcRn-related parameters
- 3.
- Recirculation flow rate (for the two-pore model) and lymphatic/vascular reflection coefficients
- 4.
- Volumes of tissues and sub-tissue compartments
4.2. Use of PBPK Model to Mechanistically Describe and Predict mAb PK and PD
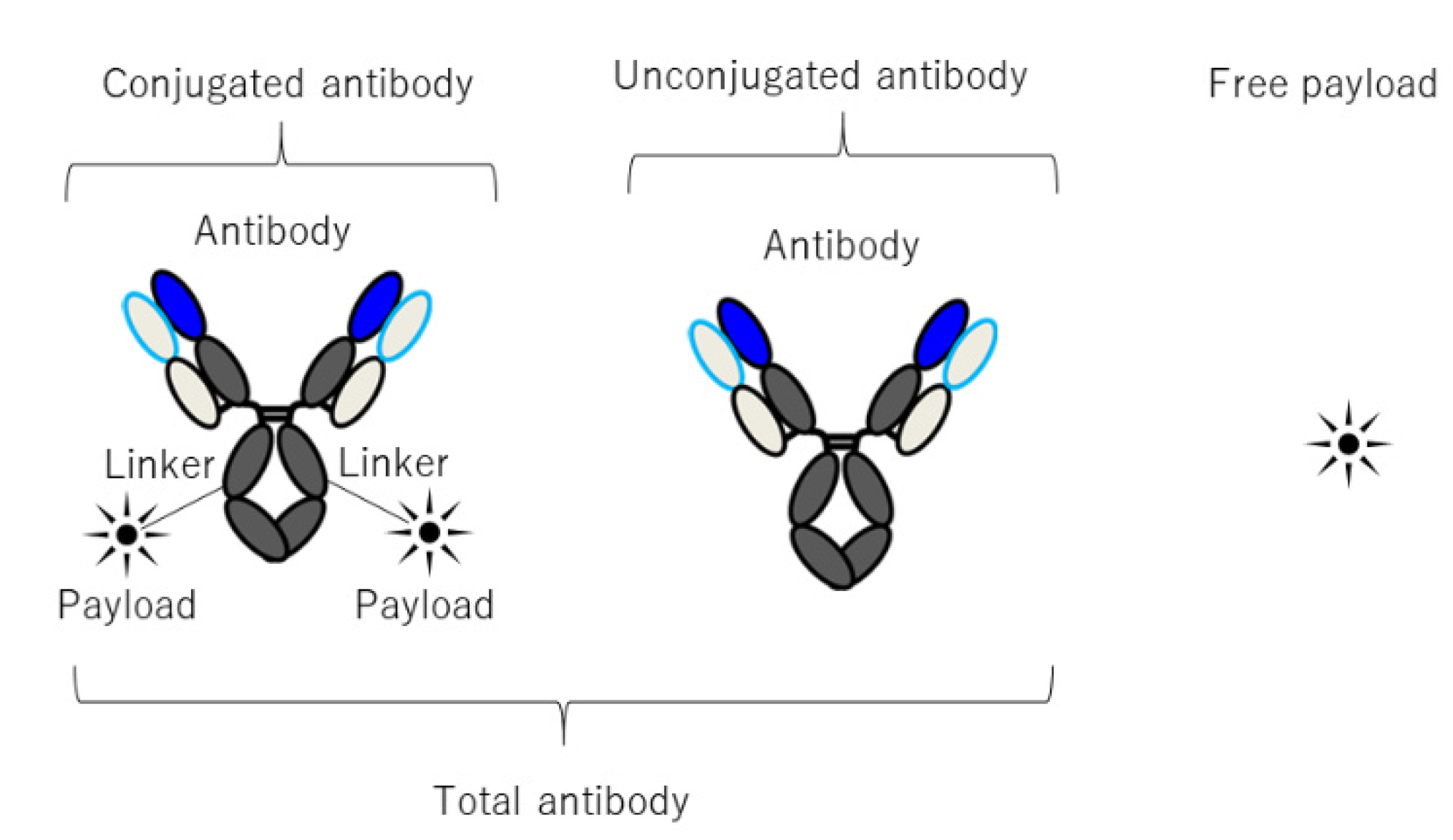
5. Prediction of Human PKPD of ADC Using M&S
5.1. PKPD Modeling of ADC
5.2. Translational PKPD Prediction and Clinical Model Analysis of ADC
6. QSP-Model-Based Prediction of Human PKPD
6.1. QSP-Model-Based Prediction of Pharmacodynamics for Masked Tumor-Activated Antibody
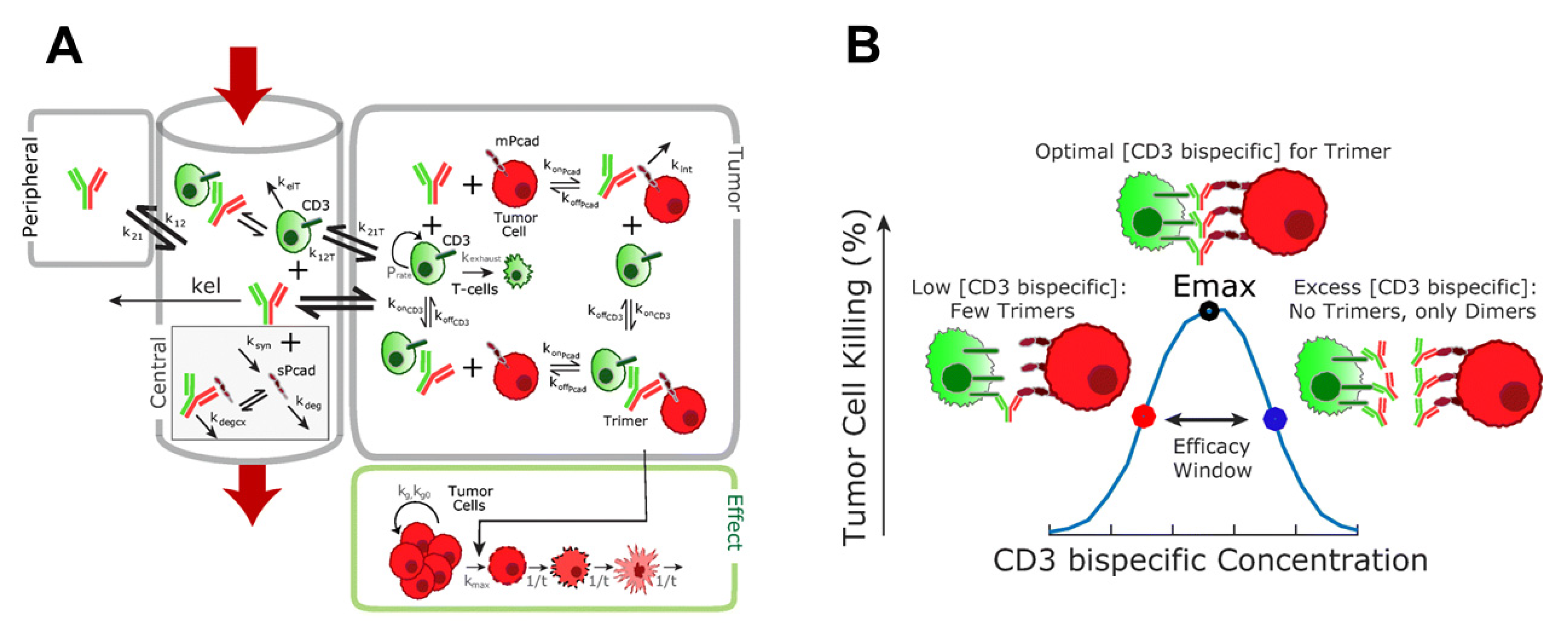
6.2. QSP-Model-Based Prediction of Pharmacodynamics for Bispecific T Cell Engager
6.3. Future Perspectives for QSP-Model-Based Prediction of Pharmacodynamics
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kitazawa, T.; Igawa, T.; Sampei, Z.; Muto, A.; Kojima, T.; Soeda, T.; Yoshihashi, K.; Okuyama-Nishida, Y.; Saito, H.; Tsunoda, H.; et al. A bispecific antibody to factors IXa and X restores factor VIII hemostatic activity in a hemophilia A model. Nat. Med. 2012, 18, 1570–1574. [Google Scholar] [CrossRef] [PubMed]
- Khongorzul, P.; Ling, C.J.; Khan, F.U.; Ihsan, A.U.; Zhang, J. Antibody-Drug Conjugates: A Comprehensive Review. Mol. Cancer Res. 2020, 18, 3–19. [Google Scholar] [CrossRef] [PubMed]
- Igawa, T.; Ishii, S.; Tachibana, T.; Maeda, A.; Higuchi, Y.; Shimaoka, S.; Moriyama, C.; Watanabe, T.; Takubo, R.; Doi, Y.; et al. Antibody recycling by engineered pH-dependent antigen binding improves the duration of antigen neutralization. Nat. Biotechnol. 2010, 28, 1203–1207. [Google Scholar] [CrossRef] [PubMed]
- Igawa, T.; Haraya, K.; Hattori, K. Sweeping antibody as a novel therapeutic antibody modality capable of eliminating soluble antigens from circulation. Immunol. Rev. 2016, 270, 132–151. [Google Scholar] [CrossRef] [PubMed]
- Haraya, K.; Tachibana, T.; Igawa, T. Improvement of pharmacokinetic properties of therapeutic antibodies by antibody engineering. Drug Metab. Pharmacokinet. 2019, 34, 25–41. [Google Scholar] [CrossRef] [PubMed]
- Mimoto, F.; Tatsumi, K.; Shimizu, S.; Kadono, S.; Haraya, K.; Nagayasu, M.; Suzuki, Y.; Fujii, E.; Kamimura, M.; Hayasaka, A.; et al. Exploitation of Elevated Extracellular ATP to Specifically Direct Antibody to Tumor Microenvironment. Cell Rep. 2020, 33, 108542. [Google Scholar] [CrossRef] [PubMed]
- Autio, K.A.; Boni, V.; Humphrey, R.W.; Naing, A. Probody Therapeutics: An Emerging Class of Therapies Designed to Enhance On-Target Effects with Reduced Off-Tumor Toxicity for Use in Immuno-Oncology. Clin. Cancer Res. 2020, 26, 984–989. [Google Scholar] [CrossRef]
- Kamata-Sakurai, M.; Narita, Y.; Hori, Y.; Nemoto, T.; Uchikawa, R.; Honda, M.; Hironiwa, N.; Taniguchi, K.; Shida-Kawazoe, M.; Metsugi, S.; et al. Antibody to CD137 Activated by Extracellular Adenosine Triphosphate Is Tumor Selective and Broadly Effective In Vivo without Systemic Immune Activation. Cancer Discov. 2021, 11, 158–175. [Google Scholar] [CrossRef]
- Han, C.; Mayer, C.L. Prediction of Human Pharmacokineticsfor Protein-Based Biologic Therapeutics. In Pharmaceutical Sciences Encyclopedia; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 1–16. [Google Scholar]
- Lobo, E.D.; Hansen, R.J.; Balthasar, J.P. Antibody pharmacokinetics and pharmacodynamics. J. Pharm. Sci. 2004, 93, 2645–2668. [Google Scholar] [CrossRef]
- Qi, T.; Cao, Y. In Translation: FcRn across the Therapeutic Spectrum. Int. J. Mol. Sci. 2021, 22, 3048. [Google Scholar] [CrossRef]
- Keizer, R.J.; Huitema, A.D.; Schellens, J.H.; Beijnen, J.H. Clinical pharmacokinetics of therapeutic monoclonal antibodies. Clin. Pharm. 2010, 49, 493–507. [Google Scholar] [CrossRef] [PubMed]
- Yeung, Y.A.; Wu, X.; Reyes, A.E., 2nd; Vernes, J.M.; Lien, S.; Lowe, J.; Maia, M.; Forrest, W.F.; Meng, Y.G.; Damico, L.A.; et al. A therapeutic anti-VEGF antibody with increased potency independent of pharmacokinetic half-life. Cancer Res. 2010, 70, 3269–3277. [Google Scholar] [CrossRef] [PubMed]
- Maeda, A.; Iwayanagi, Y.; Haraya, K.; Tachibana, T.; Nakamura, G.; Nambu, T.; Esaki, K.; Hattori, K.; Igawa, T. Identification of human IgG1 variant with enhanced FcRn binding and without increased binding to rheumatoid factor autoantibody. mAbs 2017, 9, 844–853. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Scheerens, H.; Davis, J.C., Jr.; Deng, R.; Fischer, S.K.; Woods, C.; Fielder, P.J.; Stefanich, E.G. Translational pharmacokinetics and pharmacodynamics of an FcRn-variant anti-CD4 monoclonal antibody from preclinical model to phase I study. Clin. Pharmacol. Ther. 2011, 89, 283–290. [Google Scholar] [CrossRef] [PubMed]
- Robbie, G.J.; Criste, R.; Dall’acqua, W.F.; Jensen, K.; Patel, N.K.; Losonsky, G.A.; Griffin, M.P. A novel investigational Fc-modified humanized monoclonal antibody, motavizumab-YTE, has an extended half-life in healthy adults. Antimicrob. Agents Chemother. 2013, 57, 6147–6153. [Google Scholar] [CrossRef]
- Gaudinski, M.R.; Coates, E.E.; Houser, K.V.; Chen, G.L.; Yamshchikov, G.; Saunders, J.G.; Holman, L.A.; Gordon, I.; Plummer, S.; Hendel, C.S.; et al. Safety and pharmacokinetics of the Fc-modified HIV-1 human monoclonal antibody VRC01LS: A Phase 1 open-label clinical trial in healthy adults. PLoS Med. 2018, 15, e1002493. [Google Scholar] [CrossRef]
- Griffin, M.P.; Khan, A.A.; Esser, M.T.; Jensen, K.; Takas, T.; Kankam, M.K.; Villafana, T.; Dubovsky, F. Safety, Tolerability, and Pharmacokinetics of MEDI8897, the Respiratory Syncytial Virus Prefusion F-Targeting Monoclonal Antibody with an Extended Half-Life, in Healthy Adults. Antimicrob. Agents Chemother. 2017, 61, e01714-16. [Google Scholar] [CrossRef]
- Igawa, T.; Tsunoda, H.; Tachibana, T.; Maeda, A.; Mimoto, F.; Moriyama, C.; Nanami, M.; Sekimori, Y.; Nabuchi, Y.; Aso, Y.; et al. Reduced elimination of IgG antibodies by engineering the variable region. Protein Eng. Des. Sel. 2010, 23, 385–392. [Google Scholar] [CrossRef]
- Leabman, M.K.; Meng, Y.G.; Kelley, R.F.; DeForge, L.E.; Cowan, K.J.; Iyer, S. Effects of altered FcgammaR binding on antibody pharmacokinetics in cynomolgus monkeys. mAbs 2013, 5, 896–903. [Google Scholar] [CrossRef]
- Gordon, M.S.; Margolin, K.; Talpaz, M.; Sledge, G.W., Jr.; Holmgren, E.; Benjamin, R.; Stalter, S.; Shak, S.; Adelman, D. Phase I safety and pharmacokinetic study of recombinant human anti-vascular endothelial growth factor in patients with advanced cancer. J. Clin. Oncol. 2001, 19, 843–850. [Google Scholar] [CrossRef]
- Weisman, M.H.; Moreland, L.W.; Furst, D.E.; Weinblatt, M.E.; Keystone, E.C.; Paulus, H.E.; Teoh, L.S.; Velagapudi, R.B.; Noertersheuser, P.A.; Granneman, G.R.; et al. Efficacy, pharmacokinetic, and safety assessment of adalimumab, a fully human anti-tumor necrosis factor-alpha monoclonal antibody, in adults with rheumatoid arthritis receiving concomitant methotrexate: A pilot study. Clin. Ther. 2003, 25, 1700–1721. [Google Scholar] [CrossRef]
- Tsukamoto, N.; Takahashi, N.; Itoh, H.; Pouliquen, I. Pharmacokinetics and pharmacodynamics of mepolizumab, an anti-interleukin 5 monoclonal antibody, in healthy Japanese male subjects. Clin. Pharmacol. Drug Dev. 2016, 5, 102–108. [Google Scholar] [CrossRef] [PubMed]
- Emu, B.; Luca, D.; Offutt, C.; Grogan, J.L.; Rojkovich, B.; Williams, M.B.; Tang, M.T.; Xiao, J.; Lee, J.H.; Davis, J.C. Safety, pharmacokinetics, and biologic activity of pateclizumab, a novel monoclonal antibody targeting lymphotoxin alpha: Results of a phase I randomized, placebo-controlled trial. Arthritis Res. Ther. 2012, 14, R6. [Google Scholar] [CrossRef] [PubMed]
- Low, J.G.; Ng, J.H.J.; Ong, E.Z.; Kalimuddin, S.; Wijaya, L.; Chan, Y.F.Z.; Ng, D.H.L.; Tan, H.C.; Baglody, A.; Chionh, Y.H.; et al. Phase 1 Trial of a Therapeutic Anti-Yellow Fever Virus Human Antibody. N. Engl. J. Med. 2020, 383, 452–459. [Google Scholar] [CrossRef] [PubMed]
- Kakkar, T.; Ma, M.; Zhuang, Y.; Patton, A.; Hu, Z.; Mounho, B. Pharmacokinetics and safety of a fully human hepatocyte growth factor antibody, AMG 102, in cynomolgus monkeys. Pharm. Res. 2007, 24, 1910–1918. [Google Scholar] [CrossRef]
- Mo, G.; Baldwin, J.R.; Luffer-Atlas, D.; Ilaria, R.L., Jr.; Conti, I.; Heathman, M.; Cronier, D.M. Population Pharmacokinetic Modeling of Olaratumab, an Anti-PDGFRalpha Human Monoclonal Antibody, in Patients with Advanced and/or Metastatic Cancer. Clin. Pharmacokinet. 2018, 57, 355–365. [Google Scholar] [CrossRef]
- Hotzel, I.; Theil, F.P.; Bernstein, L.J.; Prabhu, S.; Deng, R.; Quintana, L.; Lutman, J.; Sibia, R.; Chan, P.; Bumbaca, D.; et al. A strategy for risk mitigation of antibodies with fast clearance. mAbs 2012, 4, 753–760. [Google Scholar] [CrossRef]
- Haraya, K.; Tachibana, T.; Nezu, J. Predicting pharmacokinetic profile of therapeutic antibodies after iv injection from only the data after sc injection in cynomolgus monkey. Xenobiotica 2017, 47, 194–201. [Google Scholar] [CrossRef]
- Haraya, K.; Tachibana, T. Estimation of Clearance and Bioavailability of Therapeutic Monoclonal Antibodies from Only Subcutaneous Injection Data in Humans Based on Comprehensive Analysis of Clinical Data. Clin. Pharmacokinet. 2021, 60, 1325–1334. [Google Scholar] [CrossRef]
- Covell, D.G.; Barbet, J.; Holton, O.D.; Black, C.D.; Parker, R.J.; Weinstein, J.N. Pharmacokinetics of monoclonal immunoglobulin G1, F(ab’)2, and Fab’ in mice. Cancer Res. 1986, 46, 3969–3978. [Google Scholar]
- Khawli, L.A.; Goswami, S.; Hutchinson, R.; Kwong, Z.W.; Yang, J.; Wang, X.; Yao, Z.; Sreedhara, A.; Cano, T.; Tesar, D.; et al. Charge variants in IgG1: Isolation, characterization, in vitro binding properties and pharmacokinetics in rats. mAbs 2010, 2, 613–624. [Google Scholar] [CrossRef] [PubMed]
- Higel, F.; Seidl, A.; Demelbauer, U.; Viertlboeck-Schudy, M.; Koppenburg, V.; Kronthaler, U.; Sorgel, F.; Friess, W. N-glycan PK Profiling Using a High Sensitivity nanoLCMS Work-Flow with Heavy Stable Isotope Labeled Internal Standard and Application to a Preclinical Study of an IgG1 Biopharmaceutical. Pharm. Res. 2015, 32, 3649–3659. [Google Scholar] [CrossRef] [PubMed]
- Tabrizi, M.; Neupane, D.; Elie, S.E.; Shankaran, H.; Juan, V.; Zhang, S.; Hseih, S.; Fayadat-Dilman, L.; Zhang, D.; Song, Y.; et al. Pharmacokinetic Properties of Humanized IgG1 and IgG4 Antibodies in Preclinical Species: Translational Evaluation. AAPS J. 2019, 21, 39. [Google Scholar] [CrossRef] [PubMed]
- Dowall, S.; Taylor, I.; Yeates, P.; Smith, L.; Rule, A.; Easterbrook, L.; Bruce, C.; Cook, N.; Corbin-Lickfett, K.; Empig, C.; et al. Catheterized guinea pigs infected with Ebola Zaire virus allows safer sequential sampling to determine the pharmacokinetic profile of a phosphatidylserine-targeting monoclonal antibody. Antivir. Res. 2013, 97, 108–111. [Google Scholar] [CrossRef]
- Iwasaki, K.; Uno, Y.; Utoh, M.; Yamazaki, H. Importance of cynomolgus monkeys in development of monoclonal antibody drugs. Drug Metab. Pharmacokinet. 2019, 34, 55–63. [Google Scholar] [CrossRef]
- Yeung, Y.A.; Leabman, M.K.; Marvin, J.S.; Qiu, J.; Adams, C.W.; Lien, S.; Starovasnik, M.A.; Lowman, H.B. Engineering human IgG1 affinity to human neonatal Fc receptor: Impact of affinity improvement on pharmacokinetics in primates. J. Immunol. 2009, 182, 7663–7671. [Google Scholar] [CrossRef]
- Abdiche, Y.N.; Yeung, Y.A.; Chaparro-Riggers, J.; Barman, I.; Strop, P.; Chin, S.M.; Pham, A.; Bolton, G.; McDonough, D.; Lindquist, K.; et al. The neonatal Fc receptor (FcRn) binds independently to both sites of the IgG homodimer with identical affinity. mAbs 2015, 7, 331–343. [Google Scholar] [CrossRef]
- Ling, J.; Zhou, H.; Jiao, Q.; Davis, H.M. Interspecies scaling of therapeutic monoclonal antibodies: Initial look. J. Clin. Pharmacol. 2009, 49, 1382–1402. [Google Scholar] [CrossRef]
- Deng, R.; Iyer, S.; Theil, F.P.; Mortensen, D.L.; Fielder, P.J.; Prabhu, S. Projecting human pharmacokinetics of therapeutic antibodies from nonclinical data: What have we learned? mAbs 2011, 3, 61–66. [Google Scholar] [CrossRef]
- Biliouris, K.; Nestorov, I.; Naik, H.; Dai, D.; Xiao, G.; Wang, Q.; Pellerin, A.; Rabah, D.; Lesko, L.J.; Trame, M.N. A pre-clinical quantitative model predicts the pharmacokinetics/pharmacodynamics of an anti-BDCA2 monoclonal antibody in humans. J. Pharmacokinet. Pharmacodyn. 2018, 45, 817–827. [Google Scholar] [CrossRef]
- Song, L.; Xue, J.; Zhang, J.; Li, S.; Liu, D.; Zhou, T. Mechanistic prediction of first-in-human dose for bispecific CD3/EpCAM T-cell engager antibody M701, using an integrated PK/PD modeling method. Eur. J. Pharm. Sci. 2021, 158, 105584. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Shen, F.; Jones, B.; Fink, D.; Geist, B.; Nnane, I.; Zhou, Z.; Hall, J.; Malaviya, R.; Ort, T.; et al. Characterization of concurrent target suppression by JNJ-61178104, a bispecific antibody against human tumor necrosis factor and interleukin-17A. mAbs 2020, 12, 1770018. [Google Scholar] [CrossRef] [PubMed]
- Haraya, K.; Tachibana, T.; Nezu, J. Quantitative prediction of therapeutic antibody pharmacokinetics after intravenous and subcutaneous injection in human. Drug. Metab. Pharmacokinet. 2017, 32, 208–217. [Google Scholar] [CrossRef] [PubMed]
- Haraya, K.; Tachibana, T. Simple Approach to Accurately Predict Pharmacokinetics of Therapeutic Monoclonal Antibodies after Subcutaneous Injection in Humans. Clin. Pharmacokinet. 2021, 60, 111–120. [Google Scholar] [CrossRef] [PubMed]
- Shivva, V.; Fink, M.; Lowe, P.J. Improving priors for human monoclonal antibody linear pharmacokinetic parameters by using half-lives from non-human primates. J. Pharmacokinet. Pharmacodyn. 2021, 48, 295–303. [Google Scholar] [CrossRef] [PubMed]
- Haraya, K.; Tachibana, T.; Nanami, M.; Ishigai, M. Application of human FcRn transgenic mice as a pharmacokinetic screening tool of monoclonal antibody. Xenobiotica 2014, 44, 1127–1134. [Google Scholar] [CrossRef]
- Avery, L.B.; Wang, M.; Kavosi, M.S.; Joyce, A.; Kurz, J.C.; Fan, Y.Y.; Dowty, M.E.; Zhang, M.; Zhang, Y.; Cheng, A.; et al. Utility of a human FcRn transgenic mouse model in drug discovery for early assessment and prediction of human pharmacokinetics of monoclonal antibodies. mAbs 2016, 8, 1064–1078. [Google Scholar] [CrossRef]
- Reddy, J.; Madishetti, S.; Vachaspati, P.R. Fast mouse PK (Fast PK): A rapid screening method to increase pharmacokinetic throughput in pre-clinical drug discovery. Eur. J. Pharm. Sci. 2012, 47, 444–450. [Google Scholar] [CrossRef]
- Ober, R.J.; Radu, C.G.; Ghetie, V.; Ward, E.S. Differences in promiscuity for antibody-FcRn interactions across species: Implications for therapeutic antibodies. Int. Immunol. 2001, 13, 1551–1559. [Google Scholar] [CrossRef]
- Betts, A.; Keunecke, A.; van Steeg, T.J.; van der Graaf, P.H.; Avery, L.B.; Jones, H.; Berkhout, J. Linear pharmacokinetic parameters for monoclonal antibodies are similar within a species and across different pharmacological targets: A comparison between human, cynomolgus monkey and hFcRn Tg32 transgenic mouse using a population-modeling approach. mAbs 2018, 10, 751–764. [Google Scholar] [CrossRef]
- Sohn, W.; Simiens, M.A.; Jaeger, K.; Hutton, S.; Jang, G. The pharmacokinetics and pharmacodynamics of denosumab in patients with advanced solid tumours and bone metastases: A systematic review. Br. J. Clin. Pharmacol. 2014, 78, 477–487. [Google Scholar] [CrossRef] [PubMed]
- Fracasso, P.M.; Burris, H., 3rd; Arquette, M.A.; Govindan, R.; Gao, F.; Wright, L.P.; Goodner, S.A.; Greco, F.A.; Jones, S.F.; Willcut, N.; et al. A phase 1 escalating single-dose and weekly fixed-dose study of cetuximab: Pharmacokinetic and pharmacodynamic rationale for dosing. Clin. Cancer Res. 2007, 13, 986–993. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ricart, A.D.; Tolcher, A.W.; Liu, G.; Holen, K.; Schwartz, G.; Albertini, M.; Weiss, G.; Yazji, S.; Ng, C.; Wilding, G. Volociximab, a chimeric monoclonal antibody that specifically binds alpha5beta1 integrin: A phase I, pharmacokinetic, and biological correlative study. Clin. Cancer Res. 2008, 14, 7924–7929. [Google Scholar] [CrossRef] [PubMed]
- Byrd, J.C.; O’Brien, S.; Flinn, I.W.; Kipps, T.J.; Weiss, M.; Rai, K.; Lin, T.S.; Woodworth, J.; Wynne, D.; Reid, J.; et al. Phase 1 study of lumiliximab with detailed pharmacokinetic and pharmacodynamic measurements in patients with relapsed or refractory chronic lymphocytic leukemia. Clin. Cancer Res. 2007, 13, 4448–4455. [Google Scholar] [CrossRef] [PubMed]
- Zonder, J.A.; Mohrbacher, A.F.; Singhal, S.; van Rhee, F.; Bensinger, W.I.; Ding, H.; Fry, J.; Afar, D.E.; Singhal, A.K. A phase 1, multicenter, open-label, dose escalation study of elotuzumab in patients with advanced multiple myeloma. Blood 2012, 120, 552–559. [Google Scholar] [CrossRef] [PubMed]
- Atzori, F.; Tabernero, J.; Cervantes, A.; Prudkin, L.; Andreu, J.; Rodriguez-Braun, E.; Domingo, A.; Guijarro, J.; Gamez, C.; Rodon, J.; et al. A phase I pharmacokinetic and pharmacodynamic study of dalotuzumab (MK-0646), an anti-insulin-like growth factor-1 receptor monoclonal antibody, in patients with advanced solid tumors. Clin. Cancer Res. 2011, 17, 6304–6312. [Google Scholar] [CrossRef]
- Rosen, L.S.; Hurwitz, H.I.; Wong, M.K.; Goldman, J.; Mendelson, D.S.; Figg, W.D.; Spencer, S.; Adams, B.J.; Alvarez, D.; Seon, B.K.; et al. A phase I first-in-human study of TRC105 (Anti-Endoglin Antibody) in patients with advanced cancer. Clin. Cancer Res. 2012, 18, 4820–4829. [Google Scholar] [CrossRef]
- LoRusso, P.M.; Krishnamurthi, S.; Youssoufian, H.; Hall, N.; Fox, F.; Dontabhaktuni, A.; Grebennik, D.; Remick, S. Icrucumab, a fully human monoclonal antibody against the vascular endothelial growth factor receptor-1, in the treatment of patients with advanced solid malignancies: A Phase 1 study. Investig. New Drugs 2014, 32, 303–311. [Google Scholar] [CrossRef]
- Wisniacki, N.; Amaravadi, L.; Galluppi, G.R.; Zheng, T.S.; Zhang, R.; Kong, J.; Burkly, L.C. Safety, tolerability, pharmacokinetics, and pharmacodynamics of anti-TWEAK monoclonal antibody in patients with rheumatoid arthritis. Clin. Ther. 2013, 35, 1137–1149. [Google Scholar] [CrossRef]
- Uhl, W.; Zuhlsdorf, M.; Koernicke, T.; Forssmann, U.; Kovar, A. Safety, tolerability, and pharmacokinetics of the novel alphav-integrin antibody EMD 525797 (DI17E6) in healthy subjects after ascending single intravenous doses. Investig. New Drugs 2014, 32, 347–354. [Google Scholar] [CrossRef]
- Salinger, D.H.; Endres, C.J.; Martin, D.A.; Gibbs, M.A. A semi-mechanistic model to characterize the pharmacokinetics and pharmacodynamics of brodalumab in healthy volunteers and subjects with psoriasis in a first-in-human single ascending dose study. Clin. Pharmacol. Drug Dev. 2014, 3, 276–283. [Google Scholar] [CrossRef] [PubMed]
- Oitate, M.; Nakayama, S.; Ito, T.; Kurihara, A.; Okudaira, N.; Izumi, T. Prediction of human plasma concentration-time profiles of monoclonal antibodies from monkey data by a species-invariant time method. Drug Metab. Pharmacokinet. 2012, 27, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.Q.; Salinger, D.H.; Endres, C.J.; Gibbs, J.P.; Hsu, C.P.; Stouch, B.J.; Hurh, E.; Gibbs, M.A. Quantitative prediction of human pharmacokinetics for monoclonal antibodies: Retrospective analysis of monkey as a single species for first-in-human prediction. Clin. Pharmacokinet. 2011, 50, 131–142. [Google Scholar] [CrossRef] [PubMed]
- Tabuchi, H.; Katsurabara, T.; Mori, M.; Aoyama, M.; Obara, T.; Yasuda, N.; Kawano, T.; Imai, T.; Ieiri, I.; Kumagai, Y. Pharmacokinetics, Pharmacodynamics, and Safety of E6011, a Novel Humanized Antifractalkine (CX3CL1) Monoclonal Antibody: A Randomized, Double-Blind, Placebo-Controlled Single-Ascending-Dose Study. J. Clin. Pharmacol. 2019, 59, 688–701. [Google Scholar] [CrossRef] [PubMed]
- de Vries Schultink, A.H.M.; Doornbos, R.P.; Bakker, A.B.H.; Bol, K.; Throsby, M.; Geuijen, C.; Maussang, D.; Schellens, J.H.M.; Beijnen, J.H.; Huitema, A.D.R. Translational PK-PD modeling analysis of MCLA-128, a HER2/HER3 bispecific monoclonal antibody, to predict clinical efficacious exposure and dose. Investig. New Drugs 2018, 36, 1006–1015. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Kong, D.; Yao, Y.; Yang, L.; Yao, Q.; Zhu, Y.; Ding, Y.; Yang, F.; Gong, J.; Shen, L.; et al. Prediction of Human Pharmacokinetics and Clinical Effective Dose of SI-B001, an EGFR/HER3 Bi-specific Monoclonal Antibody. J. Pharm. Sci. 2020, 109, 3172–3180. [Google Scholar] [CrossRef]
- Singh, R.; Moreno, M.; Stanimirovic, D. Comparison of Various Approaches to Translate Non-Linear Pharmacokinetics of Monoclonal Antibodies from Cynomolgus Monkey to Human. Eur. J. Drug Metab. Pharmacokinet. 2021, 46, 555–567. [Google Scholar] [CrossRef]
- Xiang, H.; Bender, B.C.; Reyes, A.E., 2nd; Merchant, M.; Jumbe, N.L.; Romero, M.; Davancaze, T.; Nijem, I.; Mai, E.; Young, J.; et al. Onartuzumab (MetMAb): Using nonclinical pharmacokinetic and concentration-effect data to support clinical development. Clin. Cancer Res. 2013, 19, 5068–5078. [Google Scholar] [CrossRef]
- Xiang, H.; Reyes, A.E., 2nd; Eppler, S.; Kelley, S.; Damico-Beyer, L.A. Death receptor 5 agonistic antibody PRO95780: Preclinical pharmacokinetics and concentration-effect relationship support clinical dose and regimen selection. Cancer Chemother. Pharmacol. 2013, 72, 405–415. [Google Scholar] [CrossRef]
- Mordenti, J.; Thomsen, K.; Licko, V.; Chen, H.; Meng, Y.G.; Ferrara, N. Efficacy and concentration-response of murine anti-VEGF monoclonal antibody in tumor-bearing mice and extrapolation to humans. Toxicol. Pathol. 1999, 27, 14–21. [Google Scholar] [CrossRef]
- Lledo-Garcia, R.; Dixon, K.; Shock, A.; Oliver, R. Pharmacokinetic-pharmacodynamic modelling of the anti-FcRn monoclonal antibody rozanolixizumab: Translation from preclinical stages to the clinic. CPT Pharmacomet. Syst. Pharmacol. 2021, 11, 116–128. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.; Rong, H.; Gordi, T.; Bosley, J.; Bhattacharya, I. Translational Pharmacokinetic/Pharmacodynamic Analysis of MYO-029 Antibody for Muscular Dystrophy. Clin. Transl. Sci. 2016, 9, 302–310. [Google Scholar] [CrossRef] [PubMed]
- Luu, K.T.; Bergqvist, S.; Chen, E.; Hu-Lowe, D.; Kraynov, E. A model-based approach to predicting the human pharmacokinetics of a monoclonal antibody exhibiting target-mediated drug disposition. J. Pharmacol. Exp. Ther. 2012, 341, 702–708. [Google Scholar] [CrossRef] [PubMed]
- Parng, C.; Singh, P.; Pittman, D.D.; Wright, K.; Leary, B.; Patel-Hett, S.; Rakhe, S.; Stejskal, J.; Peraza, M.; Dufield, D.; et al. Translational Pharmacokinetic/Pharmacodynamic Characterization and Target-Mediated Drug Disposition Modeling of an Anti-Tissue Factor Pathway Inhibitor Antibody, PF-06741086. J. Pharm. Sci. 2018, 107, 1995–2004. [Google Scholar] [CrossRef] [PubMed]
- Park, W.S.; Han, S.; Lee, J.; Hong, T.; Won, J.; Lim, Y.; Lee, K.; Byun, H.Y.; Yim, D.S. Use of a Target-Mediated Drug Disposition Model to Predict the Human Pharmacokinetics and Target Occupancy of GC1118, an Anti-epidermal Growth Factor Receptor Antibody. Basic Clin. Pharmacol. Toxicol. 2017, 120, 243–249. [Google Scholar] [CrossRef]
- Liang, M.; Wang, B.; Schneider, A.; Vainshtein, I.; Roskos, L. A Novel Pharmacodynamic Biomarker and Mechanistic Modeling Facilitate the Development of Tovetumab, a Monoclonal Antibody Directed Against Platelet-Derived Growth Factor Receptor Alpha, for Cancer Therapy. AAPS J. 2020, 23, 4. [Google Scholar] [CrossRef]
- Kwak, E.Y.; Kim, M.J.; Park, J.H.; Jung, H.W.; Jung, M.E. Target-mediated drug disposition modeling of an anti-TFPI antibody (MG1113) in cynomolgus monkeys to predict human pharmacokinetics and pharmacodynamics. J. Thromb. Haemost. 2021, 19, 1425–1435. [Google Scholar] [CrossRef]
- Betts, A.M.; Clark, T.H.; Yang, J.; Treadway, J.L.; Li, M.; Giovanelli, M.A.; Abdiche, Y.; Stone, D.M.; Paralkar, V.M. The application of target information and preclinical pharmacokinetic/pharmacodynamic modeling in predicting clinical doses of a Dickkopf-1 antibody for osteoporosis. J. Pharmacol. Exp. Ther. 2010, 333, 2–13. [Google Scholar] [CrossRef]
- Li, H.; Kock, K.; Wisler, J.A.; Rees, W.A.; Prince, P.J.; Reynhardt, K.O.; Hsu, H.; Yu, Z.; Borie, D.C.; Salinger, D.H.; et al. Prediction of clinical pharmacokinetics of AMG 181, a human anti-alpha 4 beta 7 monoclonal antibody for treating inflammatory bowel diseases. Pharmacol. Res. Perspect. 2015, 3, e00098. [Google Scholar] [CrossRef]
- Vugmeyster, Y.; Rohde, C.; Perreault, M.; Gimeno, R.E.; Singh, P. Agonistic TAM-163 antibody targeting tyrosine kinase receptor-B: Applying mechanistic modeling to enable preclinical to clinical translation and guide clinical trial design. mAbs 2013, 5, 373–383. [Google Scholar] [CrossRef][Green Version]
- Dudal, S.; Subramanian, K.; Flandre, T.; Law, W.S.; Lowe, P.J.; Skerjanec, A.; Genin, J.C.; Duval, M.; Piequet, A.; Cordier, A.; et al. Integrated pharmacokinetic, pharmacodynamic and immunogenicity profiling of an anti-CCL21 monoclonal antibody in cynomolgus monkeys. mAbs 2015, 7, 829–837. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Krzyzanski, W.; Martin, S.W.; Weber, G.; Betts, A.; Ahmad, A.; Abraham, A.; Zutshi, A.; Lin, J.; Singh, P. Quantitative prediction of human pharmacokinetics for mAbs exhibiting target-mediated disposition. AAPS J. 2015, 17, 389–399. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Prasad, B.; Salphati, L.; Chu, X.; Gupta, A.; Hop, C.E.; Evers, R.; Unadkat, J.D. Interspecies variability in expression of hepatobiliary transporters across human, dog, monkey, and rat as determined by quantitative proteomics. Drug Metab. Dispos. 2015, 43, 367–374. [Google Scholar] [CrossRef]
- Chu, X.; Bleasby, K.; Evers, R. Species differences in drug transporters and implications for translating preclinical findings to humans. Expert Opin. Drug Metab. Toxicol. 2013, 9, 237–252. [Google Scholar] [CrossRef] [PubMed]
- Ahlberg, J.; Giragossian, C.; Li, H.; Myzithras, M.; Raymond, E.; Caviness, G.; Grimaldi, C.; Brown, S.E.; Perez, R.; Yang, D.; et al. Retrospective analysis of model-based predictivity of human pharmacokinetics for anti-IL-36R monoclonal antibody MAB92 using a rat anti-mouse IL-36R monoclonal antibody and RNA expression data (FANTOM5). mAbs 2019, 11, 956–964. [Google Scholar] [CrossRef] [PubMed]
- de Sousa Abreu, R.; Penalva, L.O.; Marcotte, E.M.; Vogel, C. Global signatures of protein and mRNA expression levels. Mol. Biosyst. 2009, 5, 1512–1526. [Google Scholar] [CrossRef]
- Mager, D.E.; Jusko, W.J. General pharmacokinetic model for drugs exhibiting target-mediated drug disposition. J. Pharmacokinet. Pharmacodyn. 2001, 28, 507–532. [Google Scholar] [CrossRef]
- Mager, D.E. Target-mediated drug disposition and dynamics. Biochem. Pharmacol. 2006, 72, 1–10. [Google Scholar] [CrossRef]
- Mager, D.E.; Krzyzanski, W. Quasi-equilibrium pharmacokinetic model for drugs exhibiting target-mediated drug disposition. Pharm. Res. 2005, 22, 1589–1596. [Google Scholar] [CrossRef]
- Gibiansky, L.; Gibiansky, E.; Kakkar, T.; Ma, P. Approximations of the target-mediated drug disposition model and identifiability of model parameters. J. Pharmacokinet. Pharmacodyn. 2008, 35, 573–591. [Google Scholar] [CrossRef]
- Gibbs, J.P.; Yuraszeck, T.; Biesdorf, C.; Xu, Y.; Kasichayanula, S. Informing Development of Bispecific Antibodies Using Physiologically Based Pharmacokinetic-Pharmacodynamic Models: Current Capabilities and Future Opportunities. J. Clin. Pharmacol. 2020, 60 (Suppl S1), S132–S146. [Google Scholar] [CrossRef] [PubMed]
- An, B.; Zhang, M.; Pu, J.; Qu, Y.; Shen, S.; Zhou, S.; Ferrari, L.; Vazvaei, F.; Qu, J. Toward Accurate and Robust Liquid Chromatography-Mass Spectrometry-Based Quantification of Antibody Biotherapeutics in Tissues. Anal. Chem. 2020, 92, 15152–15161. [Google Scholar] [CrossRef] [PubMed]
- Karaoglu Hanzatian, D.; Schwartz, A.; Gizatullin, F.; Erickson, J.; Deng, K.; Villanueva, R.; Stedman, C.; Harris, C.; Ghayur, T.; Goodearl, A. Brain uptake of multivalent and multi-specific DVD-Ig proteins after systemic administration. mAbs 2018, 10, 765–777. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zhan, Y.; O’Neil, S.P.; Harris, S.; Henson, C.; McEwen, A.; Webster, R.; O’Hara, D.M. Quantitative biodistribution of biotherapeutics at whole body, organ and cellular levels by autoradiography. Bioanalysis 2018, 10, 1487–1500. [Google Scholar] [CrossRef]
- Conner, K.P.; Rock, B.M.; Kwon, G.K.; Balthasar, J.P.; Abuqayyas, L.; Wienkers, L.C.; Rock, D.A. Evaluation of near infrared fluorescent labeling of monoclonal antibodies as a tool for tissue distribution. Drug Metab. Dispos. 2014, 42, 1906–1913. [Google Scholar] [CrossRef]
- Urva, S.R.; Yang, V.C.; Balthasar, J.P. Physiologically based pharmacokinetic model for T84.66: A monoclonal anti-CEA antibody. J. Pharm. Sci. 2010, 99, 1582–1600. [Google Scholar] [CrossRef]
- Yip, V.; Palma, E.; Tesar, D.B.; Mundo, E.E.; Bumbaca, D.; Torres, E.K.; Reyes, N.A.; Shen, B.Q.; Fielder, P.J.; Prabhu, S.; et al. Quantitative cumulative biodistribution of antibodies in mice: Effect of modulating binding affinity to the neonatal Fc receptor. mAbs 2014, 6, 689–696. [Google Scholar] [CrossRef]
- Dewulf, J.; Adhikari, K.; Vangestel, C.; Wyngaert, T.V.D.; Elvas, F. Development of Antibody Immuno-PET/SPECT Radiopharmaceuticals for Imaging of Oncological Disorders-An Update. Cancers 2020, 12, 1868. [Google Scholar] [CrossRef]
- Gessel, M.M.; Norris, J.L.; Caprioli, R.M. MALDI imaging mass spectrometry: Spatial molecular analysis to enable a new age of discovery. J. Proteom. 2014, 107, 71–82. [Google Scholar] [CrossRef]
- Liu, X.; Lukowski, J.K.; Flinders, C.; Kim, S.; Georgiadis, R.A.; Mumenthaler, S.M.; Hummon, A.B. MALDI-MSI of Immunotherapy: Mapping the EGFR-Targeting Antibody Cetuximab in 3D Colon-Cancer Cell Cultures. Anal. Chem. 2018, 90, 14156–14164. [Google Scholar] [CrossRef]
- Kirui, D.K.; Ferrari, M. Intravital Microscopy Imaging Approaches for Image-Guided Drug Delivery Systems. Curr. Drug Targets 2015, 16, 528–541. [Google Scholar] [CrossRef] [PubMed]
- Miller, M.A.; Weissleder, R. Imaging of anticancer drug action in single cells. Nat. Rev. Cancer 2017, 17, 399–414. [Google Scholar] [CrossRef]
- Haslene-Hox, H.; Oveland, E.; Berg, K.C.; Kolmannskog, O.; Woie, K.; Salvesen, H.B.; Tenstad, O.; Wiig, H. A new method for isolation of interstitial fluid from human solid tumors applied to proteomic analysis of ovarian carcinoma tissue. PLoS ONE 2011, 6, e19217. [Google Scholar] [CrossRef] [PubMed]
- Jadhav, S.B.; Khaowroongrueng, V.; Fueth, M.; Otteneder, M.B.; Richter, W.; Derendorf, H. Tissue Distribution of a Therapeutic Monoclonal Antibody Determined by Large Pore Microdialysis. J. Pharm. Sci. 2017, 106, 2853–2859. [Google Scholar] [CrossRef] [PubMed]
- Eigenmann, M.J.; Fronton, L.; Grimm, H.P.; Otteneder, M.B.; Krippendorff, B.F. Quantification of IgG monoclonal antibody clearance in tissues. mAbs 2017, 9, 1007–1015. [Google Scholar] [CrossRef]
- Shah, D.K.; Betts, A.M. Towards a platform PBPK model to characterize the plasma and tissue disposition of monoclonal antibodies in preclinical species and human. J. Pharmacokinet. Pharmacodyn. 2012, 39, 67–86. [Google Scholar] [CrossRef]
- Ferl, G.Z.; Wu, A.M.; DiStefano, J.J., 3rd. A predictive model of therapeutic monoclonal antibody dynamics and regulation by the neonatal Fc receptor (FcRn). Ann. Biomed. Eng. 2005, 33, 1640–1652. [Google Scholar] [CrossRef]
- Baxter, L.T.; Zhu, H.; Mackensen, D.G.; Jain, R.K. Physiologically based pharmacokinetic model for specific and nonspecific monoclonal antibodies and fragments in normal tissues and human tumor xenografts in nude mice. Cancer Res. 1994, 54, 1517–1528. [Google Scholar]
- Chen, Y.; Balthasar, J.P. Evaluation of a catenary PBPK model for predicting the in vivo disposition of mAbs engineered for high-affinity binding to FcRn. AAPS J. 2012, 14, 850–859. [Google Scholar] [CrossRef]
- Hu, S.; D’Argenio, D.Z. Predicting monoclonal antibody pharmacokinetics following subcutaneous administration via whole-body physiologically-based modeling. J. Pharmacokinet. Pharmacodyn. 2020, 47, 385–409. [Google Scholar] [CrossRef]
- Li, L.; Gardner, I.; Dostalek, M.; Jamei, M. Simulation of monoclonal antibody pharmacokinetics in humans using a minimal physiologically based model. AAPS J. 2014, 16, 1097–1109. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Shah, D.K. Two-pore physiologically based pharmacokinetic model with de novo derived parameters for predicting plasma PK of different size protein therapeutics. J. Pharmacokinet. Pharmacodyn. 2019, 46, 305–318. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, Y.; Chang, H.P.; Yu, X.; Shah, D.K. Two-pore physiologically based pharmacokinetic model validation using whole-body biodistribution of trastuzumab and different-size fragments in mice. J. Pharmacokinet. Pharmacodyn. 2021, 48, 743–762. [Google Scholar] [CrossRef] [PubMed]
- Sepp, A.; Berges, A.; Sanderson, A.; Meno-Tetang, G. Development of a physiologically based pharmacokinetic model for a domain antibody in mice using the two-pore theory. J. Pharmacokinet. Pharmacodyn. 2015, 42, 97–109. [Google Scholar] [CrossRef] [PubMed]
- Davda, J.P.; Jain, M.; Batra, S.K.; Gwilt, P.R.; Robinson, D.H. A physiologically based pharmacokinetic (PBPK) model to characterize and predict the disposition of monoclonal antibody CC49 and its single chain Fv constructs. Int. Immunopharmacol. 2008, 8, 401–413. [Google Scholar] [CrossRef]
- Abuqayyas, L.; Balthasar, J.P. Application of PBPK modeling to predict monoclonal antibody disposition in plasma and tissues in mouse models of human colorectal cancer. J. Pharmacokinet. Pharmacodyn. 2012, 39, 683–710. [Google Scholar] [CrossRef]
- Chang, H.P.; Kim, S.J.; Shah, D.K. Whole-Body Pharmacokinetics of Antibody in Mice Determined using Enzyme-Linked Immunosorbent Assay and Derivation of Tissue Interstitial Concentrations. J. Pharm. Sci. 2021, 110, 446–457. [Google Scholar] [CrossRef]
- Garg, A.; Balthasar, J.P. Physiologically-based pharmacokinetic (PBPK) model to predict IgG tissue kinetics in wild-type and FcRn-knockout mice. J. Pharmacokinet. Pharmacodyn. 2007, 34, 687–709. [Google Scholar] [CrossRef]
- Glassman, P.M.; Balthasar, J.P. Physiologically-based pharmacokinetic modeling to predict the clinical pharmacokinetics of monoclonal antibodies. J. Pharmacokinet. Pharmacodyn. 2016, 43, 427–446. [Google Scholar] [CrossRef]
- Yuan, D.; Rode, F.; Cao, Y. A Minimal Physiologically Based Pharmacokinetic Model with a Nested Endosome Compartment for Novel Engineered Antibodies. AAPS J. 2018, 20, 48. [Google Scholar] [CrossRef]
- Zhao, L.; Ji, P.; Li, Z.; Roy, P.; Sahajwalla, C.G. The antibody drug absorption following subcutaneous or intramuscular administration and its mathematical description by coupling physiologically based absorption process with the conventional compartment pharmacokinetic model. J. Clin. Pharmacol. 2013, 53, 314–325. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Niu, J.; Geist, B.; Fink, D.; Xu, Z.; Zhou, H.; Wang, W. A minimal physiologically based pharmacokinetic model to characterize colon TNF suppression and treatment effects of an anti-TNF monoclonal antibody in a mouse inflammatory bowel disease model. mAbs 2020, 12, 1813962. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B.; Haraldsson, B. Transport of macromolecules across microvascular walls: The two-pore theory. Physiol. Rev. 1994, 74, 163–219. [Google Scholar] [CrossRef]
- Perl, W. Convection and permeation and albumin between plasma and interstitium. Microvasc. Res. 1975, 10, 83–94. [Google Scholar] [CrossRef]
- Gerlowski, L.E.; Jain, R.K. Physiologically based pharmacokinetic modeling: Principles and applications. J. Pharm. Sci. 1983, 72, 1103–1127. [Google Scholar] [CrossRef] [PubMed]
- Baxter, L.T.; Zhu, H.; Mackensen, D.G.; Butler, W.F.; Jain, R.K. Biodistribution of monoclonal antibodies: Scale-up from mouse to human using a physiologically based pharmacokinetic model. Cancer Res. 1995, 55, 4611–4622. [Google Scholar] [PubMed]
- Rippe, B.; Haraldsson, B. Fluid and protein fluxes across small and large pores in the microvasculature. Application of two-pore equations. Acta Physiol. Scand. 1987, 131, 411–428. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, X.; Doddareddy, R.; Geist, B.; McIntosh, T.; Jusko, W.J.; Zhou, H.; Wang, W. Development and Translational Application of a Minimal Physiologically Based Pharmacokinetic Model for a Monoclonal Antibody against Interleukin 23 (IL-23) in IL-23-Induced Psoriasis-Like Mice. J. Pharmacol. Exp. Ther. 2018, 365, 140–155. [Google Scholar] [CrossRef]
- Gill, K.L.; Gardner, I.; Li, L.; Jamei, M. A Bottom-Up Whole-Body Physiologically Based Pharmacokinetic Model to Mechanistically Predict Tissue Distribution and the Rate of Subcutaneous Absorption of Therapeutic Proteins. AAPS J. 2016, 18, 156–170. [Google Scholar] [CrossRef]
- Jiang, X.; Chen, X.; Jaiprasart, P.; Carpenter, T.J.; Zhou, R.; Wang, W. Development of a minimal physiologically-based pharmacokinetic/pharmacodynamic model to characterize target cell depletion and cytokine release for T cell-redirecting bispecific agents in humans. Eur. J. Pharm. Sci. 2020, 146, 105260. [Google Scholar] [CrossRef]
- Cao, Y.; Balthasar, J.P.; Jusko, W.J. Second-generation minimal physiologically-based pharmacokinetic model for monoclonal antibodies. J. Pharmacokinet. Pharmacodyn. 2013, 40, 597–607. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Jusko, W.J. Survey of monoclonal antibody disposition in man utilizing a minimal physiologically-based pharmacokinetic model. J. Pharmacokinet. Pharmacodyn. 2014, 41, 571–580. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Jusko, W.J. Incorporating target-mediated drug disposition in a minimal physiologically-based pharmacokinetic model for monoclonal antibodies. J. Pharmacokinet. Pharmacodyn. 2014, 41, 375–387. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, X.; Jusko, W.J.; Zhou, H.; Wang, W. Minimal physiologically-based pharmacokinetic (mPBPK) model for a monoclonal antibody against interleukin-6 in mice with collagen-induced arthritis. J. Pharmacokinet. Pharmacodyn. 2016, 43, 291–304. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Jusko, W.J.; Cao, Y. Role of Interstitial Fluid Turnover on Target Suppression by Therapeutic Biologics Using a Minimal Physiologically Based Pharmacokinetic Model. J. Pharmacol. Exp. Ther. 2018, 367, 1–8. [Google Scholar] [CrossRef]
- Varkhede, N.; Forrest, M.L. Understanding the Monoclonal Antibody Disposition after Subcutaneous Administration using a Minimal Physiologically based Pharmacokinetic Model. J. Pharm. Pharm. Sci. 2018, 21, 130s–148s. [Google Scholar] [CrossRef]
- Supersaxo, A.; Hein, W.R.; Steffen, H. Effect of molecular weight on the lymphatic absorption of water-soluble compounds following subcutaneous administration. Pharm. Res. 1990, 7, 167–169. [Google Scholar] [CrossRef]
- Glassman, P.M.; Chen, Y.; Balthasar, J.P. Scale-up of a physiologically-based pharmacokinetic model to predict the disposition of monoclonal antibodies in monkeys. J. Pharmacokinet. Pharmacodyn. 2015, 42, 527–540. [Google Scholar] [CrossRef]
- Shebley, M.; Sandhu, P.; Emami Riedmaier, A.; Jamei, M.; Narayanan, R.; Patel, A.; Peters, S.A.; Reddy, V.P.; Zheng, M.; de Zwart, L.; et al. Physiologically Based Pharmacokinetic Model Qualification and Reporting Procedures for Regulatory Submissions: A Consortium Perspective. Clin. Pharmacol. Ther. 2018, 104, 88–110. [Google Scholar] [CrossRef]
- Friedrich, S.W.; Lin, S.C.; Stoll, B.R.; Baxter, L.T.; Munn, L.L.; Jain, R.K. Antibody-directed effector cell therapy of tumors: Analysis and optimization using a physiologically based pharmacokinetic model. Neoplasia 2002, 4, 449–463. [Google Scholar] [CrossRef]
- Advani, A.; Coiffier, B.; Czuczman, M.S.; Dreyling, M.; Foran, J.; Gine, E.; Gisselbrecht, C.; Ketterer, N.; Nasta, S.; Rohatiner, A.; et al. Safety, pharmacokinetics, and preliminary clinical activity of inotuzumab ozogamicin, a novel immunoconjugate for the treatment of B-cell non-Hodgkin’s lymphoma: Results of a phase I study. J. Clin. Oncol. 2010, 28, 2085–2093. [Google Scholar] [CrossRef]
- Dowell, J.A.; Korth-Bradley, J.; Liu, H.; King, S.P.; Berger, M.S. Pharmacokinetics of gemtuzumab ozogamicin, an antibody-targeted chemotherapy agent for the treatment of patients with acute myeloid leukemia in first relapse. J. Clin. Pharmacol. 2001, 41, 1206–1214. [Google Scholar] [CrossRef]
- Cilliers, C.; Guo, H.; Liao, J.; Christodolu, N.; Thurber, G.M. Multiscale Modeling of Antibody-Drug Conjugates: Connecting Tissue and Cellular Distribution to Whole Animal Pharmacokinetics and Potential Implications for Efficacy. AAPS J. 2016, 18, 1117–1130. [Google Scholar] [CrossRef] [PubMed]
- Wagner-Rousset, E.; Janin-Bussat, M.C.; Colas, O.; Excoffier, M.; Ayoub, D.; Haeuw, J.F.; Rilatt, I.; Perez, M.; Corvaia, N.; Beck, A. Antibody-drug conjugate model fast characterization by LC-MS following IdeS proteolytic digestion. mAbs 2014, 6, 273–285. [Google Scholar] [CrossRef] [PubMed]
- Khera, E.; Cilliers, C.; Bhatnagar, S.; Thurber, G.M. Computational transport analysis of antibody-drug conjugate bystander effects and payload tumoral distribution: Implications for therapy. Mol. Syst. Des. Eng. 2018, 3, 73–88. [Google Scholar] [CrossRef]
- Anderl, J.; Faulstich, H.; Hechler, T.; Kulke, M. Antibody–Drug Conjugate Payloads. In Antibody-Drug Conjugates; Ducry, L., Ed.; Humana Press: Totowa, NJ, USA, 2013; pp. 51–70. [Google Scholar]
- Li, C.; Menon, R.; Walles, M.; Singh, R.; Upreti, V.V.; Brackman, D.; Lee, A.J.; Endres, C.J.; Kumar, S.; Zhang, D.; et al. Risk-Based Pharmacokinetic and Drug–Drug Interaction Characterization of Antibody–Drug Conjugates in Oncology Clinical Development: An International Consortium for Innovation and Quality in Pharmaceutical Development Perspective. Clin. Pharmacol. Ther. 2021. [Google Scholar] [CrossRef]
- Bender, B.; Leipold, D.D.; Xu, K.; Shen, B.Q.; Tibbitts, J.; Friberg, L.E. A mechanistic pharmacokinetic model elucidating the disposition of trastuzumab emtansine (T-DM1), an antibody-drug conjugate (ADC) for treatment of metastatic breast cancer. AAPS J. 2014, 16, 994–1008. [Google Scholar] [CrossRef]
- Sukumaran, S.; Gadkar, K.; Zhang, C.; Bhakta, S.; Liu, L.; Xu, K.; Raab, H.; Yu, S.F.; Mai, E.; Fourie-O’Donohue, A.; et al. Mechanism-Based Pharmacokinetic/Pharmacodynamic Model for THIOMAB Drug Conjugates. Pharm. Res. 2015, 32, 1884–1893. [Google Scholar] [CrossRef] [PubMed]
- Kaur, S.; Xu, K.; Saad, O.M.; Dere, R.C.; Carrasco-Triguero, M. Bioanalytical assay strategies for the development of antibody-drug conjugate biotherapeutics. Bioanalysis 2013, 5, 201–226. [Google Scholar] [CrossRef]
- Shah, D.K.; Haddish-Berhane, N.; Betts, A. Bench to bedside translation of antibody drug conjugates using a multiscale mechanistic PK/PD model: A case study with brentuximab-vedotin. J. Pharmacokinet. Pharmacodyn. 2012, 39, 643–659. [Google Scholar] [CrossRef]
- Shah, D.K.; King, L.E.; Han, X.; Wentland, J.A.; Zhang, Y.; Lucas, J.; Haddish-Berhane, N.; Betts, A.; Leal, M. A priori prediction of tumor payload concentrations: Preclinical case study with an auristatin-based anti-5T4 antibody-drug conjugate. AAPS J. 2014, 16, 452–463. [Google Scholar] [CrossRef] [PubMed]
- Jackson, D.; Atkinson, J.; Guevara, C.I.; Zhang, C.; Kery, V.; Moon, S.-J.; Virata, C.; Yang, P.; Lowe, C.; Pinkstaff, J.; et al. In Vitro and In Vivo Evaluation of Cysteine and Site Specific Conjugated Herceptin Antibody-Drug Conjugates. PLoS ONE 2014, 9, e83865. [Google Scholar] [CrossRef] [PubMed]
- Shah, D.K.; Balthasar, J.P. PK/TD modeling for prediction of the effects of 8C2, an anti-topotecan mAb, on topotecan-induced toxicity in mice. Int. J. Pharm. 2014, 465, 228–238. [Google Scholar] [CrossRef] [PubMed]
- Shah, D.K.; Balthasar, J.P. Predicting the effects of 8C2, a monoclonal anti-topotecan antibody, on plasma and tissue disposition of topotecan. J. Pharmacokinet. Pharmacodyn. 2014, 41, 55–69. [Google Scholar] [CrossRef] [PubMed]
- Gibiansky, L.; Gibiansky, E. Target-mediated drug disposition model and its approximations for antibody-drug conjugates. J. Pharmacokinet. Pharmacodyn. 2014, 41, 35–47. [Google Scholar] [CrossRef]
- Jumbe, N.L.; Xin, Y.; Leipold, D.D.; Crocker, L.; Dugger, D.; Mai, E.; Sliwkowski, M.X.; Fielder, P.J.; Tibbitts, J. Modeling the efficacy of trastuzumab-DM1, an antibody drug conjugate, in mice. J. Pharmacokinet. Pharmacodyn. 2010, 37, 221–242. [Google Scholar] [CrossRef]
- Vasalou, C.; Helmlinger, G.; Gomes, B. A mechanistic tumor penetration model to guide antibody drug conjugate design. PLoS ONE 2015, 10, e0118977. [Google Scholar] [CrossRef]
- Singh, A.P.; Seigel, G.M.; Guo, L.; Verma, A.; Wong, G.G.; Cheng, H.P.; Shah, D.K. Evolution of the Systems Pharmacokinetics-Pharmacodynamics Model for Antibody-Drug Conjugates to Characterize Tumor Heterogeneity and In Vivo Bystander Effect. J. Pharmacol. Exp. Ther. 2020, 374, 184–199. [Google Scholar] [CrossRef]
- Li, C.; Zhang, C.; Deng, R.; Leipold, D.; Li, D.; Latifi, B.; Gao, Y.; Zhang, C.; Li, Z.; Miles, D.; et al. Prediction of Human Pharmacokinetics of Antibody-Drug Conjugates from Nonclinical Data. Clin. Transl. Sci. 2019, 12, 534–544. [Google Scholar] [CrossRef]
- Liao, M.Z.; Lu, D.; Kagedal, M.; Miles, D.; Samineni, D.; Liu, S.N.; Li, C. Model-Informed Therapeutic Dose Optimization Strategies for Antibody-Drug Conjugates in Oncology: What Can We Learn from US Food and Drug Administration-Approved Antibody-Drug Conjugates? Clin. Pharmacol. Ther. 2021, 110, 1216–1230. [Google Scholar] [CrossRef]
- Sun, Q.; Seo, S.; Zvada, S.; Liu, C.; Reynolds, K. Does Hepatic Impairment Affect the Exposure of Monoclonal Antibodies? Clin. Pharmacol. Ther. 2020, 107, 1256–1262. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Chen, R.; O’Connor, O.A.; Gopal, A.K.; Ramchandren, R.; Goy, A.; Matous, J.V.; Fasanmade, A.A.; Manley, T.J.; Han, T.H. Brentuximab vedotin, an antibody-drug conjugate, in patients with CD30-positive haematologic malignancies and hepatic or renal impairment. Br. J. Clin. Pharmacol. 2016, 82, 696–705. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Lu, T.; Gibiansky, L.; Li, X.; Li, C.; Agarwal, P.; Shemesh, C.S.; Shi, R.; Dere, R.C.; Hirata, J.; et al. Integrated Two-Analyte Population Pharmacokinetic Model of Polatuzumab Vedotin in Patients with Non-Hodgkin Lymphoma. CPT Pharmacomet. Syst. Pharmacol. 2020, 9, 48–59. [Google Scholar] [CrossRef] [PubMed]
- Amadori, S.; Suciu, S.; Selleslag, D.; Aversa, F.; Gaidano, G.; Musso, M.; Annino, L.; Venditti, A.; Voso, M.T.; Mazzone, C.; et al. Gemtuzumab Ozogamicin Versus Best Supportive Care in Older Patients with Newly Diagnosed Acute Myeloid Leukemia Unsuitable for Intensive Chemotherapy: Results of the Randomized Phase III EORTC-GIMEMA AML-19 Trial. J. Clin. Oncol. 2016, 34, 972–979. [Google Scholar] [CrossRef] [PubMed]
- Castaigne, S.; Pautas, C.; Terre, C.; Raffoux, E.; Bordessoule, D.; Bastie, J.N.; Legrand, O.; Thomas, X.; Turlure, P.; Reman, O.; et al. Effect of gemtuzumab ozogamicin on survival of adult patients with de-novo acute myeloid leukaemia (ALFA-0701): A randomised, open-label, phase 3 study. Lancet 2012, 379, 1508–1516. [Google Scholar] [CrossRef]
- FDA. Application Review (Gemtuzumab Ozogamicin). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2017/761060Orig1s000Orig1Orig2s000SumR.pdf (accessed on 28 February 2022).
- FDA. Drug Approval Package (Brentuximab Vedotin). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2011/125388_adcetris_toc.cfm (accessed on 28 February 2022).
- FDA. Drug Approval Package (Ado-trastuzumab Emtansine). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2013/125427Orig1s000TOC.cfm (accessed on 28 February 2022).
- FDA. Multi-Discipline Review (Inotuzumab Ozogamicin). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2017/761040Orig1s000MultidisciplineR.pdf (accessed on 28 February 2022).
- FDA. Multi-Discipline Review (Moxetumomab Pasudotox). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2018/761104Orig1s000MultidisciplineR.pdf (accessed on 28 February 2022).
- FDA. Drug Approval Package (Polatuzumab Vedotin). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2019/761121Orig1s000TOC.cfm (accessed on 28 February 2022).
- FDA. Multi-Discipline Review (Enfortumab Vedotin). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2019/761137Orig1s000MultiDiscliplineR.pdf (accessed on 28 February 2022).
- FDA. Multi-Discipline Review (Fam-trastuzumab Deruxtecan-Nxki). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2019/761139Orig1s000MultidisciplineR.pdf (accessed on 28 February 2022).
- FDA. Multi-Discipline Review (Sacituzumab Govitecan). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2020/761115Orig1s000MultidisciplineR.pdf (accessed on 28 February 2022).
- FDA. Multi-Discipline Review (Loncastuximab Tesirine). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2021/761196Orig1s000MultidisciplineR.pdf (accessed on 28 February 2022).
- FDA. Multi-Discipline Review (Tisotumab Vedotin). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2021/761208Orig1s000MultidisciplineR.pdf (accessed on 28 February 2022).
- Nijsen, M.; Wu, F.; Bansal, L.; Bradshaw-Pierce, E.; Chan, J.R.; Liederer, B.M.; Mettetal, J.T.; Schroeder, P.; Schuck, E.; Tsai, A.; et al. Preclinical QSP Modeling in the Pharmaceutical Industry: An IQ Consortium Survey Examining the Current Landscape. CPT Pharmacomet. Syst. Pharmacol. 2018, 7, 135–146. [Google Scholar] [CrossRef]
- Stroh, M.; Sagert, J.; Burke, J.M.; Apgar, J.F.; Lin, L.; Millard, B.L.; Michael Kavanaugh, W. Quantitative Systems Pharmacology Model of a Masked, Tumor-Activated Antibody. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 676–684. [Google Scholar] [CrossRef]
- Stroh, M.; Green, M.; Millard, B.L.; Apgar, J.F.; Burke, J.M.; Garner, W.; Lu, H.; Lyman, S.K.; Desnoyers, L.R.; Richardson, J.; et al. Model-Informed Drug Development of the Masked Anti-PD-L1 Antibody CX-072. Clin. Pharmacol. Ther. 2021, 109, 383–393. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, M.; Ren, F.; Meng, X.; Yu, J. The landscape of bispecific T cell engager in cancer treatment. Biomark. Res. 2021, 9, 38. [Google Scholar] [CrossRef]
- Campagne, O.; Delmas, A.; Fouliard, S.; Chenel, M.; Chichili, G.R.; Li, H.; Alderson, R.; Scherrmann, J.M.; Mager, D.E. Integrated Pharmacokinetic/Pharmacodynamic Model of a Bispecific CD3xCD123 DART Molecule in Nonhuman Primates: Evaluation of Activity and Impact of Immunogenicity. Clin. Cancer Res. 2018, 24, 2631–2641. [Google Scholar] [CrossRef]
- Betts, A.; Haddish-Berhane, N.; Shah, D.K.; van der Graaf, P.H.; Barletta, F.; King, L.; Clark, T.; Kamperschroer, C.; Root, A.; Hooper, A.; et al. A Translational Quantitative Systems Pharmacology Model for CD3 Bispecific Molecules: Application to Quantify T Cell-Mediated Tumor Cell Killing by P-Cadherin LP DART((R)). AAPS J. 2019, 21, 66. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, I.; Gadkar, K.; Stefanich, E.; Li, C.C.; Sun, L.L.; Chu, Y.W.; Ramanujan, S. Mitigating the risk of cytokine release syndrome in a Phase I trial of CD20/CD3 bispecific antibody mosunetuzumab in NHL: Impact of translational system modeling. NPJ Syst. Biol. Appl. 2020, 6, 28. [Google Scholar] [CrossRef] [PubMed]
- Frances, N.; Bacac, M.; Bray-French, K.; Christen, F.; Hinton, H.; Husar, E.; Quackenbush, E.; Schafer, M.; Schick, E.; Vyver, A.V.; et al. Novel In Vivo and In Vitro Pharmacokinetic/Pharmacodynamic-Based Human Starting Dose Selection for Glofitamab. J. Pharm. Sci. 2021, 111, 1208–1218. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Haddish-Berhane, N.; Moore, P.; Clark, T.; Yang, Y.; Li, H.; Xuan, D.; Barton, H.A.; Betts, A.M.; Barletta, F. Mechanistic Projection of First-in-Human Dose for Bispecific Immunomodulatory P-Cadherin LP-DART: An Integrated PK/PD Modeling Approach. Clin. Pharmacol. Ther. 2016, 100, 232–241. [Google Scholar] [CrossRef]
- Karelina, T.; Lerner, S.; Stepanov, A.; Meerson, M.; Demin, O. Monoclonal antibody therapy efficacy can be boosted by combinations with other treatments: Predictions using an integrated Alzheimer’s Disease Platform. CPT Pharmacomet. Syst. Pharmacol. 2021, 10, 543–550. [Google Scholar] [CrossRef]
- Tarbell, E.D.; Van Wart, S.A.; Shah, D.K.; Walker, L.M.; Santulli, A.; Connolly, L.E.; Mager, D.E.; Brown, A.N.; Ambrose, P.G. 1088. A Whole-Body Quantitative System Pharmacology Physiologically-Based Pharmacokinetic (QSP/PBPK) Model to Support Dose Selection of ADG20: An Extended Half-Life Monoclonal Antibody Being Developed for the Treatment of Coronavirus Disease (COVID-19). Open Forum Infect. Dis. 2021, 8, S635. [Google Scholar] [CrossRef]
- Karelina, T.; Voronova, V.; Demin, O.; Colice, G.; Agoram, B.M. A Mathematical Modeling Approach to Understanding the Effect of Anti-Interleukin Therapy on Eosinophils. CPT Pharmacomet. Syst. Pharmacol. 2016, 5, 608–616. [Google Scholar] [CrossRef]
- Cheng, L.; Qiu, Y.; Schmidt, B.J.; Wei, G.W. Review of applications and challenges of quantitative systems pharmacology modeling and machine learning for heart failure. J. Pharmacokinet. Pharmacodyn. 2022, 49, 39–50. [Google Scholar] [CrossRef]
- Rogers, K.V.; Martin, S.W.; Bhattacharya, I.; Singh, R.S.P.; Nayak, S. A Dynamic Quantitative Systems Pharmacology Model of Inflammatory Bowel Disease: Part 1—Model Framework. Clin. Transl. Sci. 2021, 14, 239–248. [Google Scholar] [CrossRef]
- Roberts, P.; Spiros, A.; Geerts, H. A Humanized Clinically Calibrated Quantitative Systems Pharmacology Model for Hypokinetic Motor Symptoms in Parkinson’s Disease. Front. Pharmacol. 2016, 7, 6. [Google Scholar] [CrossRef]
- Bosley, J.R.; Maurer, T.S.; Musante, C.J. Systems Pharmacology Modeling in Type 2 Diabetes Mellitus. In Systems Pharmacology and Pharmacodynamic; Mager, D.E., Kimko, H.H.C., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 465–507. [Google Scholar]
- Lu, J.; Deng, K.; Zhang, X.; Liu, G.; Guan, Y. Neural-ODE for pharmacokinetics modeling and its advantage to alternative machine learning models in predicting new dosing regimens. iScience 2021, 24, 102804. [Google Scholar] [CrossRef] [PubMed]

| ADC Name | Approval Year | Target | Payload | Modeled Analytes in popPK Model | Model Structure and Description |
| Gemtuzumab ozogamicin | 2017;2000 | CD33 | Calicheamicin | tAb | 2-COMP, LE + TDE |
| Unconjugated Calicheamicin | 2-COMP,1stF, LE | ||||
| Brentuximab vedotin | 2011 | CD30 | MMAE | ADC | 3-COMP, LE |
| Unconjugated MMAE | 2-COMP, TDF, LE | ||||
| Ado-trastuzumab emtansine | 2013 | HER2 | DM1 | ADC | 2-COMP, LE |
| Inotuzumab ozogamicin | 2017 | CD22 | Calicheamicin | ADC | 2-COMP, LE + TDE |
| Moxetumomab pasudotox | 2018 | CD22 | Pseudomonas exotoxin A | ADC | 1-COMP, CDLE |
| Polatuzumab vedotin | 2019 | CD79 | MMAE | Conjugated MMAE | 2-COMP, LE + TDE + MME |
| Unconjugated MMAE | 2-COMP, LF + NLF, LE + MME | ||||
| Enfortumab vedotin | 2019 | Nectin-4 | MMAE | ADC | 3-COMP, LE |
| Unconjugated MMAE | 2-COMP, LE | ||||
| Fam-trastuzumab deruxtecan-nxki | 2019 | HER2 | DXd | ADC | 2-COMP, LE |
| Unconjugated DXd | 1-COMP, 1stF, LE | ||||
| Sacituzumab govitecan | 2020 | Trop-2 | SN-38 | Conjugated SN-38 | 1-COMP, LE |
| Unconjugated SN-38 | 2-COMP, 1stF, LE | ||||
| Loncastuximab tesirine | 2021 | CD19 | PBD | tAb | 2-COMP, LE + TDE |
| ADC | 2-COMP, LE + TDE | ||||
| Tisotumab vedotin | 2021 | Tissue factor | MMAE | ADC | 2-COMP, LE + MME |
| Unconjugated MMAE | 1-COMP, LE | ||||
| ADC Name | Analysis of Liver Dysfunction Patients | Analysis of Renal Dysfunction Patients | Payload DDI Risk (Perpetrator) Assessment Approach | Analytes for ER Model | Ref. |
| Gemtuzumab ozogamicin | popPK: NCI criteria | popPK: CrCL | In vitro effective concentration vs. Cp | tAb | [168] |
| Brentuximab vedotin | Clinical study: Child-Pugh | Clinical study:CrCL | In vitro effective concentration vs. Cp and clinical study | ADC, MMAE | [169] |
| Ado-trastuzumab emtansine | Clinical study: Child-Pugh | popPK: CrCL | In vitro effective concentration vs. Cp | ADC, tAb, DM1 | [170] |
| Inotuzumab ozogamicin | popPK: NCI criteria | popPK: CrCL | In vitro effective concentration vs. Cp | ADC | [171] |
| Moxetumomab pasudotox | popPK: NCI criteria | popPK: CrCL | NA | ADC | [172] |
| Polatuzumab vedotin | popPK: NCI criteria | popPK: CrCL | In vitro effective concentration vs. Cp and PBPK model | MMAE, Conjugated MMAE, tAb | [173] |
| Enfortumab vedotin | popPK: NCI criteria | popPK: CrCL and Clinical study: CrCL | In vitro effective concentration vs. Cp | ADC, MMAE | [174] |
| Fam-trastuzumab deruxtecan-nxki | popPK: NCI criteria | popPK: CrCL | In vitro effective concentration vs. Cp and clinical study | ADC, DXd | [175] |
| Sacituzumab govitecan | popPK: NCI criteria | NA | NA | IgG, total-SN-38, free-SG-38, SN-38G | [176] |
| Loncastuximab tesirine | popPK: NCI criteria | popPK: CrCL | In vitro effective concentration vs. Cp | ADC | [177] |
| Tisotumab vedotin | popPK: NCI criteria | popPK: CrCL | No dedicated study (reference to brentuximab vedotin) | ADC, MMAE | [178] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haraya, K.; Tsutsui, H.; Komori, Y.; Tachibana, T. Recent Advances in Translational Pharmacokinetics and Pharmacodynamics Prediction of Therapeutic Antibodies Using Modeling and Simulation. Pharmaceuticals 2022, 15, 508. https://doi.org/10.3390/ph15050508
Haraya K, Tsutsui H, Komori Y, Tachibana T. Recent Advances in Translational Pharmacokinetics and Pharmacodynamics Prediction of Therapeutic Antibodies Using Modeling and Simulation. Pharmaceuticals. 2022; 15(5):508. https://doi.org/10.3390/ph15050508
Chicago/Turabian StyleHaraya, Kenta, Haruka Tsutsui, Yasunori Komori, and Tatsuhiko Tachibana. 2022. "Recent Advances in Translational Pharmacokinetics and Pharmacodynamics Prediction of Therapeutic Antibodies Using Modeling and Simulation" Pharmaceuticals 15, no. 5: 508. https://doi.org/10.3390/ph15050508
APA StyleHaraya, K., Tsutsui, H., Komori, Y., & Tachibana, T. (2022). Recent Advances in Translational Pharmacokinetics and Pharmacodynamics Prediction of Therapeutic Antibodies Using Modeling and Simulation. Pharmaceuticals, 15(5), 508. https://doi.org/10.3390/ph15050508






