Abstract
Controlled drug delivery systems can provide sustained release profiles, favorable pharmacokinetics, and improved patient adherence. Here, a reservoir-style implant comprising a biodegradable polymer, poly(ε-caprolactone) (PCL), was developed to deliver drugs subcutaneously. This work addresses a key challenge when designing these implantable drug delivery systems, namely the accurate prediction of drug release profiles when using different formulations or form factors of the implant. The ability to model and predict the release behavior of drugs from an implant based on their physicochemical properties enables rational design and optimization without extensive and laborious in vitro testing. By leveraging experimental observations, we propose a mathematical model that predicts the empirical parameters describing the drug diffusion and partitioning processes based on the physicochemical properties of the drug. We demonstrate that the model enables an adequate fit predicting empirical parameters close to experimental values for various drugs. The model was further used to predict the release performance of new drug formulations from the implant, which aligned with experimental results for implants exhibiting zero-order release kinetics. Thus, the proposed empirical models provide useful tools to inform the implant design to achieve a target release profile.
1. Introduction
Sustained-release drug delivery systems can provide enhanced therapeutic efficiency with drug levels maintained at a nearly constant rate within a therapeutic window [1,2]. The advantages of these systems often include maximal drug efficacy, minimal side effects, and favorable pharmacokinetics [3]. A common controlled drug delivery system involves a reservoir-based architecture, where a drug core is surrounded by a polymer film. In this system, the drug release rate is controlled by the properties of the polymer such as composition, molecular weight, and film thickness, as well as the physicochemical properties of the enclosed drug, including solubility, drug particle size, and molecular weight [4]. Examples of reservoir-based architectures include injectable microspheres and nanospheres [5,6] with several systems approved by the FDA [7,8,9,10,11,12,13], hydrogel systems [14,15,16,17,18], and implants [19,20,21]. For implants comprising slowly degrading polymers and a constant concentration of drug within the reservoir, the driving force of the drug release is the constant diffusion through the polymer coating, which can result in zero-order release kinetics [4]. In addition, implants offer a promising approach for long-acting drug delivery since they reside under the skin, are discreet to use, and remain reversible during the therapeutic duration if removal is required. One polymer compatible with long-acting implants is semi-crystalline aliphatic polyester poly(ε-caprolactone) (PCL). This polymer is biocompatible, biodegradable by hydrolysis within physiological conditions, and has good mechanical integrity and processability for shaping and manufacture [22]. Due to these characteristics, PCL has been used in various drug delivery systems [23,24,25,26,27] and has shown promise with implants for HIV pre-exposure prophylaxis (HIV PrEP). For instance, Barrett et al. reported a matrix-style implant consisting of an antiretroviral (ARV) drug dispersed within a PCL polymer to deliver 4′-ethynyl-2-fluoro-2′deoxyadenosine (EFdA) [28], an investigational nucleoside reverse transcriptase translocation inhibitor (NRTTI) with subnanomolar antiviral activity, a long half-life, and the potential as a single agent for HIV PrEP [29].
A biodegradable subcutaneous implant with a reservoir architecture was developed by RTI International that comprises a drug formulated with an excipient and encased within a PCL tube for membrane-controlled drug release. Using this architecture, the in vitro and in vivo delivery of tenofovir alafenamide (TAF) for HIV PrEP was demonstrated for multiple months [30,31]. In addition, the long-acting and sustained co-delivery of ARVs and hormones was shown for multipurpose prevention technology (MPT) indications, where progestins and ARVs were simultaneously delivered for HIV PrEP and contraception [32,33]. These studies showed that the release rate of the drug is controlled by modifying the properties of the polymer tubes such as wall thickness, surface area, PCL molecular weight, and polymer composition (e.g., blends of PCL homopolymers of different molecular weight [34]). Specifically, PCL tubes with thin walls, large surface areas, and high molecular weights release drugs faster. The solubility of drugs in the excipient also affects the release rate, where higher rates are typically related to higher solubility of a drug within the excipient.
The use of in vitro experiments can readily inform how implant features affect the drug release rates. Without the aid of in vitro testing, however, predicting the performance of implants with new drug formulations, polymer compositions, or dimensions can prove challenging. A predictive model can inform how the properties of the drug and polymer affect performance and further guide the design of the implant to achieve a target release profile [35,36,37]. Such a predictive model will allow the rapid selection of implant parameters without the need to perform extensive in vitro testing, therefore significantly reducing the time and cost associated with in vitro product development efforts. Empirical models and parameters based on theoretical equations were previously generated for polymeric thin-film matrix and reservoir designs to predict drug release profiles [38]. Herein, we have developed an empirical model to predict drug release rates and profiles for various ARVs for HIV PrEP: the nucleoside reverse transcriptase inhibitors (NRTIs) emtricitabine (FTC), tenofovir alafenamide (TAFbase), tenofovir alafenamide hemifumarate (TAFsalt), abacavir (ABC), and lamivudine (3TC); the integrase strand transfer inhibitors (INSTIs) raltegravir potassium (RALsalt), dolutegravir sodium (DTGsalt), and bictegravir (BIC); and the NRTTI EFdA. In addition, the release characteristics of contraceptive hormones including the progestins levonorgestrel (LNG) and etonogestrel (ENG) were evaluated.
This manuscript describes a new linear regression model for predicting the empirical parameters based on the physicochemical properties of seven active pharmaceutical ingredients (APIs) (LNG, ENG, TAFsalt, TAFbase, EFdA, BIC, and FTC) based on their molecular weight (MW), solubility in excipient (CsE), solubility in PBS (CsP), pKa, and logP. The empirical model can offer a beneficial approach to inform the product development of implants without requiring excessive experimentation.
2. Results and Discussion
2.1. In Vitro Performance of PCL Reservoir Implants with Various API Formulations
The implant consists of a biodegradable PCL membrane that encapsulates an API formulated with excipient (Figure 1). To develop empirical and predictive models that describe drug release profiles from this implant, various API formulations were tested in vitro under simulated physiological conditions. Once submerged in the simulated physiological solution, the API that is encapsulated within the implant solubilizes and transports through the PCL membrane via passive diffusion. Because the biodegradation process of PCL is slow and can require several years [39], the faster process of drug delivery is decoupled from biodegradation. When the implant reservoir is saturated, a constant concentration gradient is maintained across the membrane, achieving zero-order release kinetics. A total of seven APIs (BIC, EFdA, ENG, FTC, LNG, TAFsalt, and TAFbase; (Table 1)) were each formulated with various pharmaceutical-grade excipients and evaluated using this in vitro method. Figure S1 shows exemplary cumulative release profiles of implants with different lengths and wall thicknesses over time. Linear release profiles were achieved for these APIs and the constant release rates were determined.
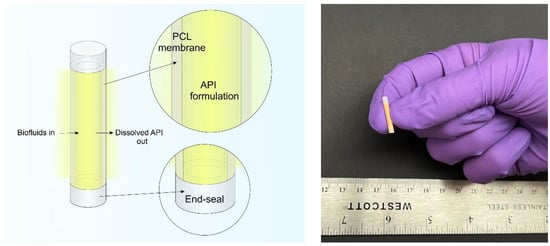
Figure 1.
(Left) A schematic of a PCL reservoir-style implant containing formulated API inside the reservoir and the dissolved drug releasing into to the surrounding medium. (Right) A digital camera image of a 10mm-long biodegradable implant containing surrogate drug formulation.

Table 1.
Physical properties and sources of APIs used to develop the model.
2.2. Predictive Models
As described in the method section, the release of a drug from a reservoir-style implant is driven by a concentration gradient across the polymeric membrane in the following steps: the diffusion of the surrounding aqueous solution into the reservoir of the implant to dissolve the drug, the partitioning of the dissolved drug into the polymer membrane, and finally the diffusion of the dissolved drug through the membrane into the surrounding aqueous media. The diffusion coefficient (D) describes the rate of a substance diffusing through the membrane, and the partition coefficient (k) determines the ratio of the concentration of a substance for the polymer membrane relative to the aqueous release media. Although D and k are separate parameters, they are calculated as a single parameter in the empirical model and were not determined independently. Here, we developed a model to predict empirical parameters based on the physicochemical properties of drugs, including MW, solubility in excipient, solubility in PBS, pKa, and logP. The solubility of the drugs within PBS (Table 1) and pharmaceutical-grade excipients (Table 2) were measured by HPLC. As shown in Table 1, the solubility of the APIs in PBS (CsP) varied, with FTC showing the highest solubility and the hormones (ENG, LNG) showing the lowest solubility. Likewise, Table 2 shows that the solubility of the APIs in excipients (CsE) varied across the different combinations. Most APIs tested here were more soluble in excipients such propylene glycol, polysorbate 80, and PEG-based compounds, as compared to excipients such as castor oil and cottonseed oil. Interestingly, LNG showed relatively low solubility in all excipients. Overall, these data were used in next steps to generate the linear regression model.

Table 2.
The solubility of the API within various pharmaceutical-grade excipients.
The fitted linear regression model for predicting in a reservoir system is:
No property variable was excluded from the model because the regression coefficient Wald test p-values were less than 0.05 for all properties. The adjusted of the prediction model was 0.75.
Figure 2 compares the predicted values directly to the experimental values. The solid red diagonal line indicates when the prediction and observation are the same, and the blue and orange dashed lines indicate the predictive values within 1 log and 0.5 log, respectively, of the observed values. For all seven APIs, most of the predicted values were in the range of 1/3 to 3 times that of the experimental values. The comparison of predicted values and experimental values for individual drugs are included in Figure S2.
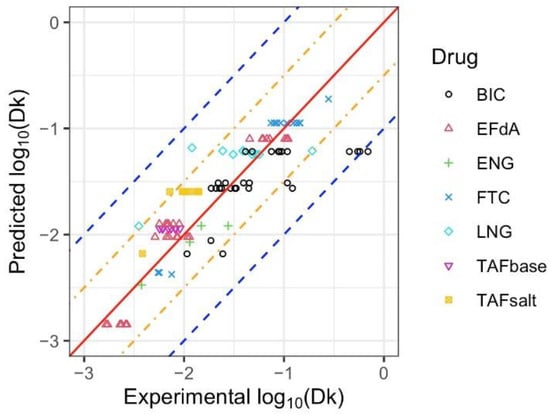
Figure 2.
Predicted and experimental values of for BIC, EFdA, ENG, FTC, LNG, TAFbase, and TAFsalt. The solid red diagonal line indicates when the prediction and observation are the same, the orange and blue dashed lines indicate predictive values within 0.5 log and 1 log of the observed values, respectively. Different symbols represent each drug, with multiple points for the same symbol representing different configurations of drug formulation or implant design tested for each drug.
To evaluate the performance of the linear regression model, machine learning prediction models (support vector machine and random forest) were also fit. The mean squared errors of the linear regression, support vector machine, and random forest models were 0.094, 0.124, and 0.089, respectively. The predicted () values from the machine learning models were compared to the experimental values in Figure S3. Overall, all models gave similar results, while the linear regression model provided a simple and explicit prediction equation.
Figure 3 shows representative cumulative release profiles of predicted and experimental fits for BIC, EFdA, ENG, FTC, LNG, and TAFsalt from the reservoir-style implants with different configurations. The approximate drug loading for these implants is 116 mg, 22 mg, 7.9 mg, 82mg, 6.9 mg, and 124 mg, respectively. The cumulative release profile represents the average values from three replicate implants and the predicted fits are based on Equation (3) and parameter calculated using Equation (4). The predicted and experimental values for and daily release rates for these implants are tabulated in Table S1. The cumulative release profiles from the in vitro dissolution assay overlapped with the results from the predictive model, indicating that the model adequately depicts the release profiles from the implants with different configurations.
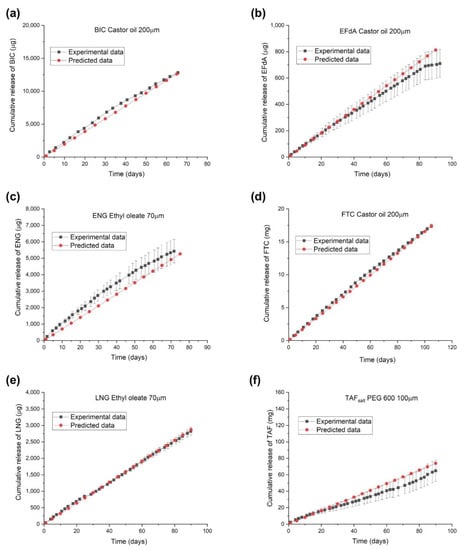
Figure 3.
Predicted and experimental release profiles of implants containing a single drug with individual configurations: (a) BIC (castor oil, PC-17, 40 mm length, 200 μm wall thickness, drug to excipient ratio: 2:1), (b) EFdA (castor oil, PC-17, 10 mm length, 200 μm wall thickness, drug to excipient ratio: 1:1), (c) ENG (ethyl oleate, Sigma, 10 mm length, 70 μm wall thickness, drug to excipient ratio: 1:4), (d) FTC (castor oil, PC-17, 40 mm length, 200 μm wall thickness, drug to excipient ratio: 1:1), (e) LNG (ethyl oleate, Sigma, 10 mm length, 70 μm wall thickness, drug to excipient ratio: 1:4), and (f) TAFsalt (PEG600, Sigma, 40 mm length, 100 μm wall thickness, drug to excipient ratio: 2:1).
2.3. Utilizing the Predictive Model
We demonstrated that the model provided an adequate fit predicting empirical parameters close to experimental values for the APIs tested above. Here, the developed model was used to predict the release rate of four additional antiretrovirals (RALsalt, 3TC, DTGsalt, and ABC), each having unique physicochemical properties as outlined in Table 3 and Table S2. Using Equation (4), the predicted values were determined and the resultant comparison of the predicted () values with the experimental values is shown in Figure 4. A good agreement exists between the experimental and predicted values, where all of the predicted values reside between two blue dashed lines, meaning that the predicted values were in the range of 1/10 and 10 times of the experimental values. The mean squared errors of the linear regression, support vector machine, and random forest models were 0.382, 0.498, 0.599, respectively, suggesting an adequate fit of the linear regression model.

Table 3.
Physical properties and sources of APIs for model validation.
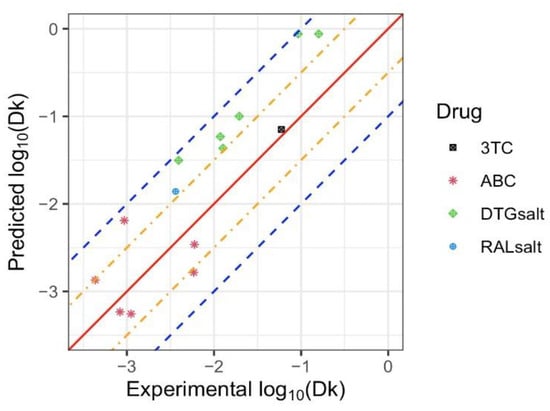
Figure 4.
Predicted and experimental values of . for 3TC, ABC, DTGsalt, and RALsalt. The solid red diagonal line indicates when the prediction and observation are the same, the orange and blue dashed lines indicate predictive values within 0.5 log and 1 log of the observed values, respectively. Different symbols represent each drug, with multiple points for the same symbol representing different implant configurations tested for each drug.
Figure 5 illustrates the predicted linear release profiles and experimental data of reservoir-style implants containing an ARV: 3TC, ABC, DTGsalt, or RALsalt. The approximate drug loading for these implants is 117 mg, 25 mg, 82 mg, and 97 mg, respectively. The proposed predictive models accurately describe the cumulative release profiles from implants containing 3TC and DTGsalt formulations, whereas discrepancies exist between experimental data and model predictions for implants containing ABC and RALsalt. Since the proposed mathematical model is ideally intended to predict the release profile of implants exhibiting constant zero-order release kinetics, the model does not account for the non-linear release profile that deviates from Fick’s first law of diffusion. As shown in Figure 5, implants containing ABC and RALsalt formulations showed non-linear release profiles due to burst release and/or drug depletion. The ABC formulation demonstrated a pronounced burst release during the first two weeks, which could be attributed to a storage effect, wherein the formulation saturates the entire PCL membrane enclosing the drug reservoir during the storage prior to use. Burst release can occur with reservoir-style implants that encapsulate hydrophilic formulations or have thin polymer walls [30,32]. In addition, the non-linear release profile of the implant with the RALsalt formulation is likely caused by drug depletion. Due to the high release rate of RALsalt, the drug concentration in the reservoir quickly falls below the solubility limit, resulting in gradually decreasing release rates over time. Therefore, the applicability of the model is limited when predicting release kinetics that are not zero-order. However, this model closely characterizes the membrane-controlled release process from a reservoir-style implants that reflects zero-order Fickian diffusion, as demonstrated for implants containing 3TC and DTGsalt.
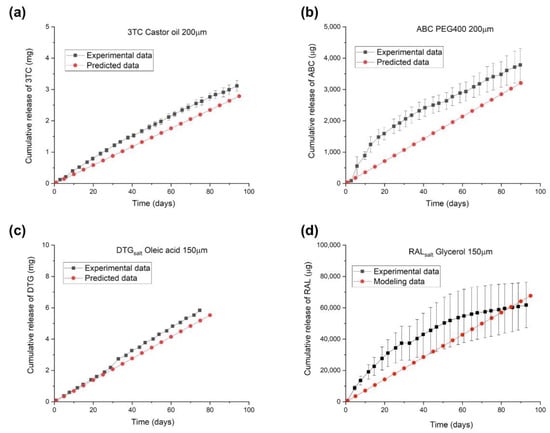
Figure 5.
Predicted and experimental release profiles of implants containing a single ARV with individual configurations: (a) 3TC (castor oil, PC-17, 40 mm length, 200 μm wall thickness, drug to excipient ratio: 2:1), (b) ABC (PEG400, PC-17, 10 mm length, 200 μm wall thickness, drug to excipient ratio: 2:1), (c) DTGsalt (oleic acid, PC-31, 10 mm length, 150 μm wall thickness, drug to excipient ratio: 2:1), and (d) RALsalt (glycerol, PC-31, 40 mm length, 150 μm wall thickness, drug to excipient ratio: 2:1).
3. Materials and Methods
3.1. Solubility and Stability Analysis of the Drug Formulations
FTC, RAL potassium (referred to as RALsalt), and DTG sodium (referred to as DTGsalt) were purchased from Boc Sciences (Shirley, NY, USA). BIC was purchased from AstaTech Inc. (Bristol, PA, USA). 3TC was purchased from Ambeed Inc. (Arlington Heights, IL, USA). ABC was purchased from ThermoFisher Scientific (Bridgewater, NJ, USA). Tenofovir alafenamide (TAFbase) and tenofovir alafenamide hemifumarate (TAFsalt) were graciously provided by Gilead Sciences (Foster City, CA, USA). ENG and LNG were procured from AdooQ® Bioscience (Irvine, CA, USA) and Selleck Chemicals LLC (Houston, TX, USA), respectively. EFdA was purchased from Pharmaron (Beijing, China) and Wuxi AppTec (Wuhan, China). To test the solubility and stability of the formulations, the individual drugs were mixed with pharmaceutical-grade, Super RefinedTM castor oil (Croda, Cat# SR40890, Snaith, UK), Super RefinedTM sesame oil (Croda, Cat# SR40294, Snaith, UK), Crodamol™ ethyl oleate (Croda, Cat# EO-LQ-(MH) ES45252, Snaith, UK), PEG300 (Croda, Cat# SR41329, Snaith, UK), PEG400 (Croda, Cat# SR40377, Snaith, UK), PEG600 (Croda, Cat# SR40269, Snaith, UK), castor oil Etocas 40-SS-(MH) (Croda, Cat# ET48333, Snaith, UK), oleic acid (Croda, Cat# SR40211, Snaith, UK), propylene glycol (Croda, Cat# SR40836, Snaith, UK), or glycerol (Sigma Aldrich, Cat#G6279, St. Louis, MO, USA). The solubility test was conducted by mixing an excess amount of drug with a specific excipient at 37 °C to create a supersaturated solution. The solutions were kept in the incubator at 37 °C for 2 days to determine the solubility of drugs within excipients and for an additional 7 days to assess the solubility and the purity of drugs. After being removed from the incubator, the solutions were then centrifuged while still warm at 1500 rpm for 3 min to separate any undissolved drugs. The supernatants were extracted and analyzed by high-performance liquid chromatography coupled with UV spectroscopy (HPLC-UV) to determine the quantity of the drug dissolved in the excipient. The solubility of the drugs within the excipients was reported as an average solubility measured on day 2 and day 9. The analysis for TAFsalt and TAFbase was performed using a Waters BEH C18 column (2.1 mm × 50 mm, 1.7 μm) under gradient, reversed-phase conditions with detection at 260 nm. The HPLC analyses of EFdA, ENG, LNG, RALsalt, DTGsalt, and ABC samples were performed using an Agilent Zorbax SB-C8 (4.6 × 150 mm) column on Agilent 1100/1200 HPLC-UV (Agilent Technologies, Santa Clara, CA, USA) with a gradient of 0.01% TFA (solvent A) and acetonitrile (solvent B). BIC samples were analyzed using a Thermo Fisher Hypersil Gold (4.6 × 150 mm) column on an Agilent 1100/1200 HPLC-UV (Agilent Technologies, Santa Clara, CA, USA) with a gradient of 0.01% trifluoroacetic acid (TFA) (solvent A) and acetonitrile (solvent B). 3TC samples were analyzed using an Agilent Zorbax SB-C8 (4.6 × 150 mm) column on Agilent 1100/1200 HPLC-UV (Agilent Technologies, Santa Clara, CA, USA) with a gradient of 0.01% TFA (solvent A) and methanol (solvent B). The saturated solutions were quantitated by linear regression analysis against a 5-point calibration curve.
3.2. Implant Fabrication
The research-grade PCL pellets were purchased from Sigma Aldrich (weight average molecular weight (Mw) = 132 kDa, Catalog# 440744, St. Louis, MO, USA). The medical-grade PCL pellets were procured from Corbion (Amsterdam, Netherlands) at different molecular weights: PURASORB PC-12 (Mw = 72 KDa), PURASORB PC-17 (Mw = 106 kDa), and PURASORB PC-41 (Mw = 136 kDa). Medical-grade PCL pellets PC-31 (Mw = 150 kDa) were also procured from Bezwada Biomedical (Hillsborough, NJ, USA). PCL tubes were fabricated via a hot-melt, single-screw extrusion process using solid PCL pellets at GenX Medical (Chattanooga, TN, USA). Before the extrusion process, all the PCL pellets were dried in a compressed air dryer at 60 °C for 4 h. All tubes measured 2.5 mm in outer diameter (OD), as determined using a 3-axis laser measurement system and light microscopy at GenX Medical.
All implants were fabricated in a biosafety cabinet under aseptic conditions using a previously reported method [34]. Prior to starting the in vitro studies, all implants were packed within amber glass vials and sterilized using gamma irradiation (dose range 18–24 kGy) at Steris (Mentor, OH, USA) via continuous exposure to a Cobalt-60 gamma-ray source (Nordion Inc., Ottawa, ON, Canada) for 8 h.
3.3. In Vitro Drug Release Studies
For in vitro drug release studies, implants were placed in polypropylene tubes containing 1X phosphate-buffered saline (PBS) (pH 7.4) and incubated at 37 °C within an incubator shaker at 100 rpm. The volume of the buffer and the time intervals for transferring the implants were selected to ensure implants were completely submerged and sink conditions were maintained. The buffer volume in tubes containing implants with LNG, ENG, and RALsalt was 200 mL and the buffer volume in tubes containing implants with TAF, BIC, EFdA, DTGsalt, 3TC, and ABC was 40 mL. The implants were transferred to fresh PBS buffer twice per week in a biosafety hood under aseptic conditions. During the transfer, a 250 µL aliquot of the release buffer was collected for UV-Vis measurement, whereas a 500 µL aliquot of release media was added to 96-well plates for HPLC analysis. The concentration of the released drug in buffer was determined using either HPLC or UV-Vis. The concentration of BIC and TAF species in the release media were measured by UV-Vis at 260 nm using the Synergy MX multi-mode plate reader (BioTek Instruments, Inc., Winooski, VT, USA). The concentrations of LNG, ENG, EFdA, RALsalt, DTGsalt, 3TC, and ABC were measured with an Agilent 1100/1200 HPLC-UV using an Agilent Zorbax SB-C8 (4.6 × 150 mm) column. The quantity of drug released into the PBS buffer during the time intervals, the cumulative mass of drug released as a function of time, and the daily release rates of drug were calculated as below:
Mass of drug (mg) at a given timepoint (tn) = concentration of drug in the release buffer (mg/mL) × volume of release buffer (mL).
Cumulative mass of released drug (mg) at a given timepoint (tn) = drug mass at t0 + drug mass at t1 + … + drug mass at tn.
Mass of drug released per day (mg/day) = cumulative mass of released drug (mg) at a given timepoint (tn)/duration of release (day).
3.4. Empirical Models
The release from a reservoir-style implant is predominantly governed by diffusional mass transport through the PCL membrane, which can be described by Fick’s first law of diffusion [57,58]:
where is the amount of drug released from the membrane per unit area per unit time (mg/day/mm2), is the diffusion coefficient, φ is the concentration, and x is the length. When the reservoir is saturated, a constant concentration gradient dφ/dx is maintained across the membrane, so the rate for drug flux J remains constant, achieving zero-order release kinetics. The constant release rate for the membrane-controlled process can be calculated according to the modified diffusion equation [35]:
where is the partition coefficient, is the saturation concentration of the substance within the excipient, and is the thickness of the PCL membrane. The cumulative mass of drug release at time can be calculated based on the following equation:
Based on the experimental data, the empirical parameter can be determined from the slope of a cumulative mass versus time plot using measured design parameters for each implant and solubility determined by HPLC.
Predictive models were developed using R version 4.2.1 for in the reservoir system as a function of drug properties: molecular weight (MW), solubility in excipient (), solubility in PBS (), pKa, and . Values for and were determined experimentally as reported under Section 2.1, whereas pKa and logP values were obtained through online databanks. Given the skewed distribution of values, linear regression models were fit with values as the outcome. Transformations (raw, reciprocal, exponential, and logarithm) of property values were considered, and the transformation which had the largest Pearson coefficient with () was chosen as the form of the predictor to be included in the model. Transformed property variables were included in the model only if the corresponding regression coefficient Wald test p-value was less than 0.05. Finally, machine learning prediction models (support vector machine and random forest), which are more robust to model misspecification yet do not provide an explicit equation to compute predicted values by hand, were also fit for comparison with the linear regression model.
4. Conclusions
Mathematical modeling is a valuable technique for predicting the release profiles of drugs from polymeric implants and for optimizing these implantable systems that exhibit zero-order release kinetics. The empirical models presented here offer a systematic approach to determine the empirical parameters that define the membrane-controlled drug release profiles from implants with a reservoir configuration. The empirical parameter, , is correlated to the key physicochemical properties of the drug (MW, solubility in excipient and in PBS, pKa, and logP) and once determined can enable the prediction of well-suited drug formulations to achieve a target release rate for a particular medical indication. The utility of the empirical model is further exemplified when designing implants containing several new ARVs for HIV treatment. In addition, we detailed the applicability for using the predictive model. Overall, the empirical model provides useful tools to guide the implant design, and the approach for developing predictive models could be extended to other drug-eluting polymeric implant systems.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ph15101226/s1, Figure S1: Cumulative release profiles APIs from PCL implants with different configurations: (a) BIC (castor oil, PC-17, 40 mm length, 200 μm wall thickness), (b) EFdA (castor oil, PC-17, 10 mm length, 200 μm wall thickness), (c) ENG (ethyl oleate, Sigma, 10 mm length, 70 μm wall thickness), (d) FTC (castor oil, PC-17, 40 mm length, 200 μm wall thickness), (e) LNG (ethyl oleate, Sigma, 10 mm length, 70 μm wall thickness), and (f) TAFsalt (PEG 600, Sigma, 40 mm length, 100 μm wall thickness); Figure S2: Predicted and experimental values of by API; Figure S3: Comparison of the linear prediction model and machine learning models; Table S1: The calculated empirical parameter Dk values for implants containing different drug formulations; Table S2: The solubility of the API within various pharmaceutical-grade excipients.
Author Contributions
Conceptualization, L.L., L.M.J., C.L. and M.G.H.; methodology, L.L., L.M.J., C.L., D.F.C., S.A.K., M.G.H. and M.L.C.; software, C.L. and M.G.H.; validation, L.L., C.L., D.F.C. and S.A.K.; formal analysis, L.L., L.M.J., C.L., D.F.C., S.A.K. and M.G.H.; investigation, L.L., L.M.J., C.L., D.F.C., S.A.K. and M.G.H.; resources, L.M.J. and M.L.C.; data curation, L.L., L.M.J., C.L., D.F.C. and S.A.K.; writing—original draft preparation, L.L., L.M.J. and D.F.C.; writing—review and editing, C.L., L.M.J., D.F.C., S.A.K., M.L.C. and M.G.H.; visualization, L.L. and C.L.; supervision, L.M.J. and M.L.C.; funding acquisition, L.M.J. and M.L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was made possible by the generous support of the American people through the U.S. President’s Emergency Plan for AIDS Relief (AID-OAA-A-17-00011, AID-OAA-A-14-00012) through the United States Agency for International Development (USAID). The contents are the responsibility of the authors and do not necessarily reflect the views of USAID, PEPFAR, or the United States Government. We would like to acknowledge support by the National Institute of Allergy and Infectious Diseases and the Eunice Kennedy Shriver National Institute of Child Health and Human Development of the National Institutes of Health (NIH) under award numbers R61AI149499/R33AI149499, R01AI152713, and R01AI154549. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. We are also thankful for support from the University of North Carolina at Chapel Hill Center for AIDS Research (P30 AI050410).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article and Supplementary Material.
Acknowledgments
We thank Gilead Sciences, Inc. for graciously providing TAF. We thank RTI team members: Chasity Norton, Ellen Luecke, Pafio Johnson, Christine Areson, Guadalupe Arce Jimenez, Patrick Gilliam, and Marza Hill. We are also grateful to Ariane van der Straten for her insights and support of this work.
Conflicts of Interest
The authors (L.L., S.A.K., and L.M.J.) are named as inventors on pending patent applications filed by their institution. The institution has a policy that grants a portion of any royalties received to named inventors. The other authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Kaur, G.; Grewal, J.; Jyoti, K.; Jain, U.K.; Chandra, R.; Madan, J. Oral controlled and sustained drug delivery systems: Concepts, advances, preclinical, and clinical status. In Drug Targeting and Stimuli Sensitive Drug Delivery Systems; Elsevier: Amsterdam, The Netherlands, 2018; pp. 567–626. [Google Scholar]
- Sanopoulou, M.; Papadokostaki, K. Controlled Drug Release Systems: Mechanisms and Kinetics. In Biomedical Membranes and (Bio) Artificial Organs; World Scientific: Singapore, 2018; pp. 1–33. [Google Scholar]
- Huynh, C.T.; Lee, D.S. Controlled Release. In Encyclopedia of Polymeric Nanomaterials; Kobayashi, S., Müllen, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 439–449. [Google Scholar]
- Yang, W.W.; Pierstorff, E. Reservoir-based polymer drug delivery systems. J. Lab. Autom. 2012, 17, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Lavan, D.A.; McGuire, T.; Langer, R. Small-scale systems for in vivo drug delivery. Nat. Biotechnol. 2003, 21, 1184–1191. [Google Scholar] [CrossRef] [PubMed]
- Freiberg, S.; Zhu, X. Polymer microspheres for controlled drug release. Int. J. Pharm. 2004, 282, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Sperry, P.; Cua, D.J.; Wetzel, S.; Moore, A.; Adler-Moore, J.P. Antimicrobial activity of AmBisome and non-liposomal amphotericin B following uptake of Candida glabrata by murine epidermal Langerhans cells. Med. Mycol. 1998, 36, 135–141. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Siena, S.; Piccart, M.J.; Holmes, F.A.; Glaspy, J.; Hackett, J.; Renwick, J.J. A combined analysis of two pivotal randomized trials of a single dose of pegfilgrastim per chemotherapy cycle and daily Filgrastim in patients with stage II-IV breast cancer. Oncol. Rep. 2003, 10, 715–724. [Google Scholar] [PubMed]
- Glue, P.; Rouzier-Panis, R.; Raffanel, C.; Sabo, R.; Gupta, S.K.; Salfi, M.; Jacobs, S.; Clement, R.P.; The Hepatitis C Intervention Therapy Group. A dose-ranging study of pegylated interferon alfa-2b and ribavirin in chronic hepatitis C. Hepatology 2000, 32, 647–653. [Google Scholar] [CrossRef] [PubMed]
- Nabhan, C.; Tallman, M.S. Early phase I/II trials with gemtuzumab ozogamicin (Mylotarg®) in acute myeloid leukemia. Clin. Lymphoma 2002, 2, S19–S23. [Google Scholar] [CrossRef] [PubMed]
- Bory, C.; Boulieu, R.; Souillet, G.; Chantin, C.; Guibaud, P.; Hershfield, M. Effect of polyethylene glycol-modified adenosine deaminase (PEG-ADA) therapy in two ADA-deficient children: Measurement of erythrocyte deoxyadenosine triphosphate as a useful tool. In Purine and Pyrimidine Metabolism in Man VII; Springer: Berlin/Heidelberg, Germany, 1991; pp. 173–176. [Google Scholar]
- Muggia, F.; Hamilton, A. Phase III data on Caelyx® in ovarian cancer. Eur. J. Cancer 2001, 37, 15–18. [Google Scholar] [CrossRef]
- Olsen, E.; Duvic, M.; Frankel, A.; Kim, Y.; Martin, A.; Vonderheid, E.; Jegasothy, B.; Wood, G.; Gordon, M.; Heald, P.; et al. Pivotal phase III trial of two dose levels of denileukin diftitox for the treatment of cutaneous T-cell lymphoma. J. Clin. Oncol. 2001, 19, 376–388. [Google Scholar] [CrossRef]
- Yamamoto, M.; Takahashi, Y.; Tabata, Y. Controlled release by biodegradable hydrogels enhances the ectopic bone formation of bone morphogenetic protein. Biomaterials 2003, 24, 4375–4383. [Google Scholar] [CrossRef]
- Piu, F.; Wang, X.; Fernandez, R.; Dellamary, L.; Harrop, A.; Ye, Q.; Sweet, J.; Tapp, R.; Dolan, D.F.; Altschuler, R.A.; et al. OTO-104: A sustained-release dexamethasone hydrogel for the treatment of otic disorders. Otol. Neurotol. 2011, 32, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Dellamary, L.; Fernandez, R.; Ye, Q.; LeBel, C.; Piu, F. Principles of inner ear sustained release following intratympanic administration. Laryngoscope 2011, 121, 385–391. [Google Scholar] [CrossRef] [PubMed]
- Casadei, M.A.; Cerreto, F.; Cesa, S.; Giannuzzo, M.; Feeney, M.; Marianecci, C.; Paolicelli, P. Solid lipid nanoparticles incorporated in dextran hydrogels: A new drug delivery system for oral formulations. Int. J. Pharm. 2006, 325, 140–146. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, T.; Sakamoto, T.; Hiraumi, H.; Kikkawa, Y.S.; Yamamoto, N.; Hamaguchi, K.; Ono, K.; Yamamoto, M.; Tabata, Y.; Teramukai, S.; et al. Topical insulin-like growth factor 1 treatment using gelatin hydrogels for glucocorticoid-resistant sudden sensorineural hearing loss: A prospective clinical trial. BMC Med. 2010, 8, 76. [Google Scholar] [CrossRef] [PubMed]
- Pons-Faudoa, F.P.; Sizovs, A.; Shelton, K.A.; Momin, Z.; Niles, J.A.; Bushman, L.R.; Xu, J.; Chua, C.Y.X.; Nichols, J.E.; Demaria, S.; et al. Preventive Efficacy of a Tenofovir Alafenamide Fumarate Nanofluidic Implant in SHIV-Challenged Nonhuman Primates. Adv. Ther. 2021, 4, 2000163. [Google Scholar] [CrossRef] [PubMed]
- Bourges, J.; Bloquel, C.; Thomas, A.; Froussart, F.; Bochot, A.; Azan, F.; Gurny, R.; BenEzra, D.; Behar-Cohen, F. Intraocular implants for extended drug delivery: Therapeutic applications. Adv. Drug Deliv. Rev. 2006, 58, 1182–1202. [Google Scholar] [CrossRef]
- Silva, G.R.d.; Fialho, S.L.; Siqueira, R.C.; Jorge, R.; Cunha Júnior, A.D.S. Implants as drug delivery devices for the treatment of eye diseases. Braz. J. Pharm. Sci. 2010, 46, 585–595. [Google Scholar] [CrossRef]
- Salerno, A. Overview of Polycaprolactone-Based Drug Delivery Systems; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Sun, H.; Mei, L.; Song, C.; Cui, X.; Wang, P. The in vivo degradation, absorption and excretion of PCL-based implant. Biomaterials 2006, 27, 1735–1740. [Google Scholar] [CrossRef]
- Hu, X.; Liu, S.; Zhou, G.; Huang, Y.; Xie, Z.; Jing, X. Electrospinning of polymeric nanofibers for drug delivery applications. J. Control. Release 2014, 185, 12–21. [Google Scholar] [CrossRef]
- Manoukian, O.S.; Marin, C.; Ahmad, A.; James, R.; Kumbar, S.G. Biodegradable injectable implants for long-term delivery of contraceptives and other therapeutics. In Proceedings of the 2015 41st Annual Northeast Biomedical Engineering Conference (NEBEC), Troy, NY, USA, 17–19 April 2015; pp. 1–2. [Google Scholar]
- Manoukian, O.S.; Arul, M.R.; Sardashti, N.; Stedman, T.; James, R.; Rudraiah, S.; Kumbar, S.G. Biodegradable polymeric injectable implants for long-term delivery of contraceptive drugs. J. Appl. Polym. Sci. 2018, 135, 46068. [Google Scholar] [CrossRef]
- Holländer, J.; Genina, N.; Jukarainen, H.; Khajeheian, M.; Rosling, A.; Mäkilä, E.; Sandler, N. Three-dimensional printed PCL-based implantable prototypes of medical devices for controlled drug delivery. J. Pharm. Sci. 2016, 105, 2665–2676. [Google Scholar] [CrossRef] [PubMed]
- Barrett, S.E.; Teller, R.S.; Forster, S.P.; Li, L.; Mackey, M.A.; Skomski, D.; Yang, Z.; Fillgrove, K.L.; Doto, G.J.; Wood, S.L.; et al. Extended-duration MK-8591-eluting implant as a candidate for HIV treatment and prevention. Antimicrob. Agents Chemother. 2018, 62, e01058-18. [Google Scholar] [CrossRef] [PubMed]
- Markowitz, M.; Sarafianos, S.G. EFdA (4′-ethynyl-2-fluoro-2′-deoxyadenosine, MK-8591): A Novel HIV-1 Reverse Transcriptase Translocation Inhibitor. Curr. Opin. HIV AIDS 2018, 13, 294. [Google Scholar] [CrossRef] [PubMed]
- Johnson, L.M.; Krovi, S.A.; Li, L.; Girouard, N.; Demkovich, Z.R.; Myers, D.; Creelman, B.; van der Straten, A. Characterization of a Reservoir-Style Implant for Sustained Release of Tenofovir Alafenamide (TAF) for HIV Pre-Exposure Prophylaxis (PrEP). Pharmaceutics 2019, 11, 315. [Google Scholar] [CrossRef]
- Li, L.; Johnson, L.M.; Krovi, S.A.; Demkovich, Z.R.; van der Straten, A. Performance and Stability of Tenofovir Alafenamide Formulations within Subcutaneous Biodegradable Implants for HIV Pre-Exposure Prophylaxis (PrEP). Pharmaceutics 2020, 12, 1057. [Google Scholar] [CrossRef]
- Li, L.; Gatto, G.J.; Brand, R.M.; Krovi, S.A.; Cottrell, M.L.; Norton, C.; van der Straten, A.; Johnson, L.M. Long-acting biodegradable implant for sustained delivery of antiretrovirals (ARVs) and hormones. J. Control. Release 2021, 340, 188–199. [Google Scholar] [CrossRef]
- Li, L.; Krovi, S.; Norton, C.; Johnson, P.; Jimenez, G.; Areson, C.; Van der Straten, A.; Johnson, L. Long-Acting Coformulated Biodegradable Implant for HIV Prevention and Contraception. In Proceedings of the Conference on Retroviruses and Opportunistic Infections (CROI), Virtual, 6–10 March 2021. [Google Scholar]
- Li, L.; Areson, C.; van der Straten, A.; Johnson, L.M. Effects of Polymer Blending on the Performance of a Subcutaneous Biodegradable Implant for HIV Pre-Exposure Prophylaxis (PrEP). Int. J. Mol. Sci. 2021, 22, 6529. [Google Scholar] [CrossRef]
- Siepmann, J.; Siepmann, F. Modeling of diffusion controlled drug delivery. J. Control. Release 2012, 161, 351–362. [Google Scholar] [CrossRef]
- Lao, L.L.; Venkatraman, S.S.; Peppas, N.A. Modeling of drug release from biodegradable polymer blends. Eur. J. Pharm. Biopharm. 2008, 70, 796–803. [Google Scholar] [CrossRef]
- Manini, G.; Benali, S.; Raquez, J.-M.; Goole, J. Proof of concept of a predictive model of drug release from long-acting implants obtained by fused-deposition modeling. Int. J. Pharm. 2022, 618, 121663. [Google Scholar] [CrossRef]
- Schlesinger, E.; Ciaccio, N.; Desai, T.A. Polycaprolactone thin-film drug delivery systems: Empirical and predictive models for device design. Mater. Sci. Eng. C 2015, 57, 232–239. [Google Scholar] [CrossRef] [PubMed]
- Pitt, C.; Chasalow, F.; Hibionada, Y.; Klimas, D.; Schindler, A. Aliphatic polyesters. I. The degradation of poly (ϵ-caprolactone) in vivo. J. Appl. Polym. Sci. 1981, 26, 3779–3787. [Google Scholar] [CrossRef]
- National Center for Biotechnology Information. PubChem Compound Summary for CID 13109, Levonorgestrel. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/Levonorgestrel (accessed on 27 June 2022).
- Toxin and Toxin Target Database. Levonorgestrel (T3D4749). Available online: http://www.t3db.ca/toxins/T3D4749 (accessed on 28 June 2022).
- National Center for Biotechnology Information. Compound Summary for CID 6917715, Etonogestrel. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/Etonogestrel (accessed on 28 June 2022).
- Toral, M.; Nacaratte, F.; Nova-Ramirez, F.; Otipka, R. Parallel determination of desogestrel and 17α-ethinylestradiol in pharmaceutical formulation by derivative spectrophotometry. J. Chil. Chem. Soc. 2013, 58, 1779–1784. [Google Scholar] [CrossRef]
- DrugBank. Tenofovir Alafenamide Fumarate. Available online: https://go.drugbank.com/salts/DBSALT002533 (accessed on 27 June 2022).
- Puri, A.; Bhattaccharjee, S.A.; Zhang, W.; Clark, M.; Singh, O.N.; Doncel, G.F.; Banga, A.K. Development of a transdermal delivery system for tenofovir alafenamide, a prodrug of tenofovir with potent antiviral activity against HIV and HBV. Pharmaceutics 2019, 11, 173. [Google Scholar] [CrossRef]
- DrugBank. Tenofovir Alafenamide. Available online: https://go.drugbank.com/drugs/DB09299 (accessed on 28 June 2022).
- Zhang, W.; Parniak, M.A.; Mitsuya, H.; Sarafianos, S.G.; Graebing, P.W.; Rohan, L.C. Preformulation studies of EFdA, a novel nucleoside reverse transcriptase inhibitor for HIV prevention. Drug Dev. Ind. Pharm. 2014, 40, 1101–1111. [Google Scholar] [CrossRef][Green Version]
- Drugbank. Islatravir. Available online: https://go.drugbank.com/drugs/DB15653 (accessed on 28 June 2022).
- ChemSpider. Bictegravir. Available online: http://www.chemspider.com/Chemical-Structure.44208822.html (accessed on 28 June 2022).
- DrugBank. Bictegravir. Available online: https://go.drugbank.com/drugs/DB11799 (accessed on 28 June 2022).
- Glilead.com. EMTRIVA® (Emtricitabine) capsule, for Oral Use. Available online: https://www.accessdata.fda.gov/drugsatfda_docs/label/2018/021500s029lbl.pdf (accessed on 28 June 2022).
- Human Metabolome Database. Lamivudine (HMDB0014847). Available online: https://hmdb.ca/metabolites/HMDB0014847 (accessed on 28 June 2022).
- Wuxi LabNetwork. [(1S,4R)-4-[2-amino-6-(cyclopropylamino)purin-9-yl]cyclopent-2-en-1-yl]methanol. Available online: https://www.labnetwork.com/frontend-app/p/#!/moleculedetails/LN01275094 (accessed on 28 June 2022).
- Drugfuture.com. Abacavir. Available online: https://www.drugfuture.com/chemdata/abacavir.html (accessed on 28 June 2022).
- Administration, T.T.G. Product Information Tivicay â (Dolutegravir) Tablets. Available online: https://www.tga.gov.au/sites/default/files/auspar-dolutegravir-140519-pi.pdf (accessed on 28 June 2022).
- DrugBank. Raltegravir. Available online: https://go.drugbank.com/drugs/DB06817 (accessed on 28 June 2022).
- Fick, A. Ueber Diffusion. Annalen Physik 1855, 170, 59–86. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975; p. 421. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).