Prediction of Antidepressant Treatment Response and Remission Using an Ensemble Machine Learning Framework
Abstract
1. Introduction
2. Results
2.1. The Study Cohort in the Taiwanese Population
2.2. Boosting Ensemble Model for Antidepressant Treatment Response
2.3. Benchmarking for Antidepressant Treatment Response
2.4. Boosting Ensemble Model for Antidepressant Remission
2.5. Benchmarking for Antidepressant Remission
3. Discussion
4. Materials and Methods
4.1. Study Population
4.2. Measurement
4.3. Genotyping Dat and Quality Controls
4.4. Key SNPs
4.5. Wrapper-Based Feature Selection Algorithm
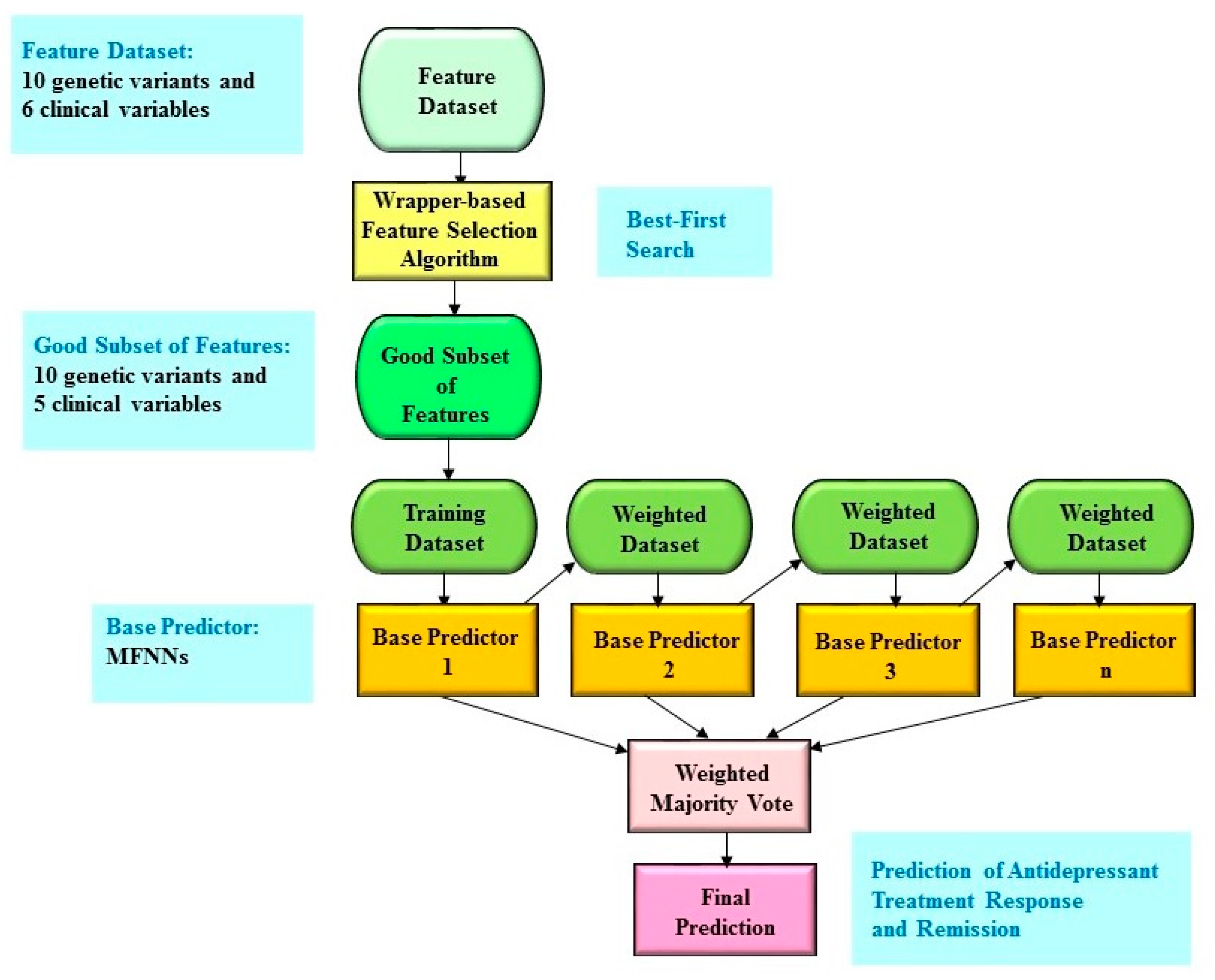
4.6. Boosting Ensemble Predictive Framework
4.7. Machine Learning Algorithms for Benchmarking
4.8. Evaluation of the Predictive Performance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lin, E.; Lin, C.-H.; Lane, H.-Y. Precision psychiatry applications with pharmacogenomics: Artificial intelligence and machine learning approaches. Int. J. Mol. Sci. 2020, 21, 969. [Google Scholar] [CrossRef]
- Bzdok, D.; Meyer-Lindenberg, A. Machine Learning for Precision Psychiatry: Opportunities and Challenges. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 2018, 3, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Gandal, M.J.; Leppa, V.; Won, H.; Parikshak, N.N.; Geschwind, D.H. The road to precision psychiatry: Translating genetics into disease mechanisms. Nat. Neurosci. 2016, 19, 1397–1407. [Google Scholar] [CrossRef] [PubMed]
- Lin, E.; Kuo, P.-H.; Liu, Y.-L.; Yu, Y.W.-Y.; Yang, A.C.; Tsai, S.-J. A deep learning approach for predicting antidepressant response in major depression using clinical and genetic biomarkers. Front. Psychiatry 2018, 9, 290. [Google Scholar] [CrossRef]
- Lin, E.; Lane, H.-Y. Machine learning and systems genomics approaches for multi-omics data. Biomark. Res. 2017, 5, 2. [Google Scholar] [CrossRef] [PubMed]
- Iniesta, R.; Stahl, D.; McGuffin, P. Machine learning, statistical learning and the future of biological research in psychiatry. Psychol. Med. 2016, 46, 2455–2465. [Google Scholar] [CrossRef]
- Dwyer, D.B.; Falkai, P.; Koutsouleris, N. Machine Learning Approaches for Clinical Psychology and Psychiatry. Annu. Rev. Clin. Psychol. 2018, 14, 91–118. [Google Scholar] [CrossRef]
- Kautzky, A.; Baldinger, P.; Souery, D.; Montgomery, S.; Mendlewicz, J.; Zohar, J.; Serretti, A.; Lanzenberger, R.; Kasper, S. The combined effect of genetic polymorphisms and clinical parameters on treatment outcome in treatment-resistant depression. Eur. Neuropsychopharmacol. 2015, 25, 441–453. [Google Scholar] [CrossRef]
- Patel, M.J.; Andreescu, C.; Price, J.C.; Edelman, K.L.; Reynolds, C.F., 3rd; Aizenstein, H.J. Machine learning approaches for integrating clinical and imaging features in late-life depression classification and response prediction. Int. J. Geriatr. Psychiatry 2015, 30, 1056–1067. [Google Scholar] [CrossRef]
- Chekroud, A.M.; Zotti, R.J.; Shehzad, Z.; Gueorguieva, R.; Johnson, M.K.; Trivedi, M.H.; Cannon, T.D.; Krystal, J.H.; Corlett, P.R. Cross-trial prediction of treatment outcome in depression: A machine learning approach. Lancet Psychiatry 2016, 3, 243–250. [Google Scholar] [CrossRef]
- Iniesta, R.; Malki, K.; Maier, W.; Rietschel, M.; Mors, O.; Hauser, J.; Henigsberg, N.; Dernovsek, M.Z.; Souery, D.; Stahl, D.; et al. Combining clinical variables to optimize prediction of antidepressant treatment outcomes. J. Psychiatr. Res. 2016, 78, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Maciukiewicz, M.; Marshe, V.S.; Hauschild, A.C.; Foster, J.A.; Rotzinger, S.; Kennedy, J.L.; Kennedy, S.H.; Muller, D.J.; Geraci, J. GWAS-based machine learning approach to predict duloxetine response in major depressive disorder. J. Psychiatr. Res. 2018, 99, 62–68. [Google Scholar] [CrossRef] [PubMed]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Galar, M.; Fernandez, A.; Barrenechea, E.; Bustince, H.; Herrera, F. A review on ensembles for the class imbalance problem: Bagging-, boosting-, and hybrid-based approaches. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2011, 42, 463–484. [Google Scholar] [CrossRef]
- Yang, P.; Hwa Yang, Y.; B Zhou, B.; Y Zomaya, A. A review of ensemble methods in bioinformatics. Curr. Bioinform. 2010, 5, 296–308. [Google Scholar] [CrossRef]
- Andreescu, C.; Mulsant, B.H.; Houck, P.R.; Whyte, E.M.; Mazumdar, S.; Dombrovski, A.Y.; Pollock, B.G.; Reynolds, M.D., III. Empirically derived decision trees for the treatment of late-life depression. Am. J. Psychiatry 2008, 165, 855–862. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, M.D.; Katon, W.J.; Russo, J.E.; Frank, E.; Barrett, J.E.; Oxman, T.E.; Williams, J.W. Patient beliefs predict response to paroxetine among primary care patients with dysthymia and minor depression. J. Am. Board Fam. Pract. 2003, 16, 22–31. [Google Scholar] [CrossRef][Green Version]
- Trivedi, M.H.; Rush, A.J.; Wisniewski, S.R.; Nierenberg, A.A.; Warden, D.; Ritz, L.; Norquist, G.; Howland, R.H.; Lebowitz, B.; McGrath, P.J. Evaluation of outcomes with citalopram for depression using measurement-based care in STAR* D: Implications for clinical practice. Am. J. Psychiatry 2006, 163, 28–40. [Google Scholar] [CrossRef]
- Lin, E.; Tsai, S.-J. Epigenetics and depression: An update. Psychiatry Investig. 2019, 16, 654. [Google Scholar] [CrossRef]
- Huang, L.-C.; Hsu, S.-Y.; Lin, E. A comparison of classification methods for predicting Chronic Fatigue Syndrome based on genetic data. J. Transl. Med. 2009, 7, 81. [Google Scholar] [CrossRef]
- Shahamat, H.; Pouyan, A.A. Feature selection using genetic algorithm for classification of schizophrenia using fMRI data. J. AI Data Min. 2015, 3, 30–37. [Google Scholar]
- Lin, K.M.; Tsou, H.H.; Tsai, I.J.; Hsiao, M.C.; Hsiao, C.F.; Liu, C.Y.; Shen, W.W.; Tang, H.S.; Fang, C.K.; Wu, C.S.; et al. CYP1A2 genetic polymorphisms are associated with treatment response to the antidepressant paroxetine. Pharmacogenomics 2010, 11, 1535–1543. [Google Scholar] [CrossRef] [PubMed]
- Kao, C.-F.; Liu, Y.-L.; Yu, Y.W.-Y.; Yang, A.C.; Lin, E.; Kuo, P.-H.; Tsai, S.-J. Gene-based analysis of genes related to neurotrophic pathway suggests association of BDNF and VEGFA with antidepressant treatment-response in depressed patients. Sci. Rep. 2018, 8, 6983. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann Publishers: Francisco, CA, USA, 2005. [Google Scholar]
- Lin, E.; Lin, C.-H.; Hung, C.-C.; Lane, H.-Y. An ensemble approach to predict schizophrenia using protein data in the N-methyl-D-aspartate receptor (NMDAR) and tryptophan catabolic pathways. Front. Bioeng. Biotechnol. 2020, 8, 569. [Google Scholar] [CrossRef]
- Lin, E.; Mukherjee, S.; Kannan, S. A deep adversarial variational autoencoder model for dimensionality reduction in single-cell RNA sequencing analysis. BMC Bioinform. 2020, 21, 1–11. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lin, E.; Hwang, Y. A support vector machine approach to assess drug efficacy of interferon-α and ribavirin combination therapy. Mol. Diagn. Ther. 2008, 12, 219–223. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Linden, A. Measuring diagnostic and predictive accuracy in disease management: An introduction to receiver operating characteristic (ROC) analysis. J. Eval. Clin. Pract. 2006, 12, 132–139. [Google Scholar] [CrossRef]
- Lin, E.; Hsu, S.-Y. A Bayesian approach to gene–gene and gene–environment interactions in chronic fatigue syndrome. Future Med. 2009, 10. [Google Scholar] [CrossRef]
| Algorithm | AUC | Sensitivity | Specificity | Number of Biomarkers |
|---|---|---|---|---|
| Boosting ensemble with feature selection | 0.8265 ± 0.0574 | 0.7651 ± 0.0574 | 0.7114 ± 0.0721 | 15 |
| Boosting ensemble | 0.8236 ± 0.0564 | 0.7517 ± 0.0602 | 0.7103 ± 0.0736 | 16 |
| Logistic regression | 0.8168 ± 0.0553 | 0.7493 ± 0.0626 | 0.7066 ± 0.0785 | 16 |
| SVM | 0.7306 ± 0.0685 | 0.7499 ± 0.0624 | 0.7113 ± 0.0785 | 16 |
| C4.5 decision tree | 0.6802 ± 0.0853 | 0.6926 ± 0.0654 | 0.6468 ± 0.0762 | 16 |
| Naïve Bayes | 0.8176 ± 0.0593 | 0.7439 ± 0.0630 | 0.6844 ± 0.0771 | 16 |
| Random forests | 0.7852 ± 0.0644 | 0.7078 ± 0.0670 | 0.6234 ± 0.0786 | 16 |
| Algorithm | AUC | Sensitivity | Specificity | Number of Biomarkers |
|---|---|---|---|---|
| Boosting ensemble with feature selection | 0.8122 ± 0.0702 | 0.7807 ± 0.0584 | 0.6589 ± 0.0872 | 15 |
| Boosting ensemble | 0.8111 ± 0.0691 | 0.7768 ± 0.0597 | 0.6529 ± 0.0875 | 16 |
| Logistic regression | 0.7985 ± 0.0772 | 0.7722 ± 0.0645 | 0.6753 ± 0.0932 | 16 |
| SVM | 0.7149 ± 0.0738 | 0.7679 ± 0.0624 | 0.6620 ± 0.0910 | 16 |
| C4.5 decision tree | 0.6276 ± 0.0955 | 0.6912 ± 0.0619 | 0.5409 ± 0.0852 | 16 |
| Naïve Bayes | 0.8078 ± 0.0709 | 0.7608 ± 0.0649 | 0.6743 ± 0.0869 | 16 |
| Random forests | 0.7733 ± 0.0766 | 0.7432 ± 0.0523 | 0.5735 ± 0.0826 | 16 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, E.; Kuo, P.-H.; Liu, Y.-L.; Yu, Y.W.-Y.; Yang, A.C.; Tsai, S.-J. Prediction of Antidepressant Treatment Response and Remission Using an Ensemble Machine Learning Framework. Pharmaceuticals 2020, 13, 305. https://doi.org/10.3390/ph13100305
Lin E, Kuo P-H, Liu Y-L, Yu YW-Y, Yang AC, Tsai S-J. Prediction of Antidepressant Treatment Response and Remission Using an Ensemble Machine Learning Framework. Pharmaceuticals. 2020; 13(10):305. https://doi.org/10.3390/ph13100305
Chicago/Turabian StyleLin, Eugene, Po-Hsiu Kuo, Yu-Li Liu, Younger W.-Y. Yu, Albert C. Yang, and Shih-Jen Tsai. 2020. "Prediction of Antidepressant Treatment Response and Remission Using an Ensemble Machine Learning Framework" Pharmaceuticals 13, no. 10: 305. https://doi.org/10.3390/ph13100305
APA StyleLin, E., Kuo, P.-H., Liu, Y.-L., Yu, Y. W.-Y., Yang, A. C., & Tsai, S.-J. (2020). Prediction of Antidepressant Treatment Response and Remission Using an Ensemble Machine Learning Framework. Pharmaceuticals, 13(10), 305. https://doi.org/10.3390/ph13100305






