Propagation of Fibrillar Structural Forms in Proteins Stopped by Naturally Occurring Short Polypeptide Chain Fragments
Abstract
:1. Introduction
2. Results
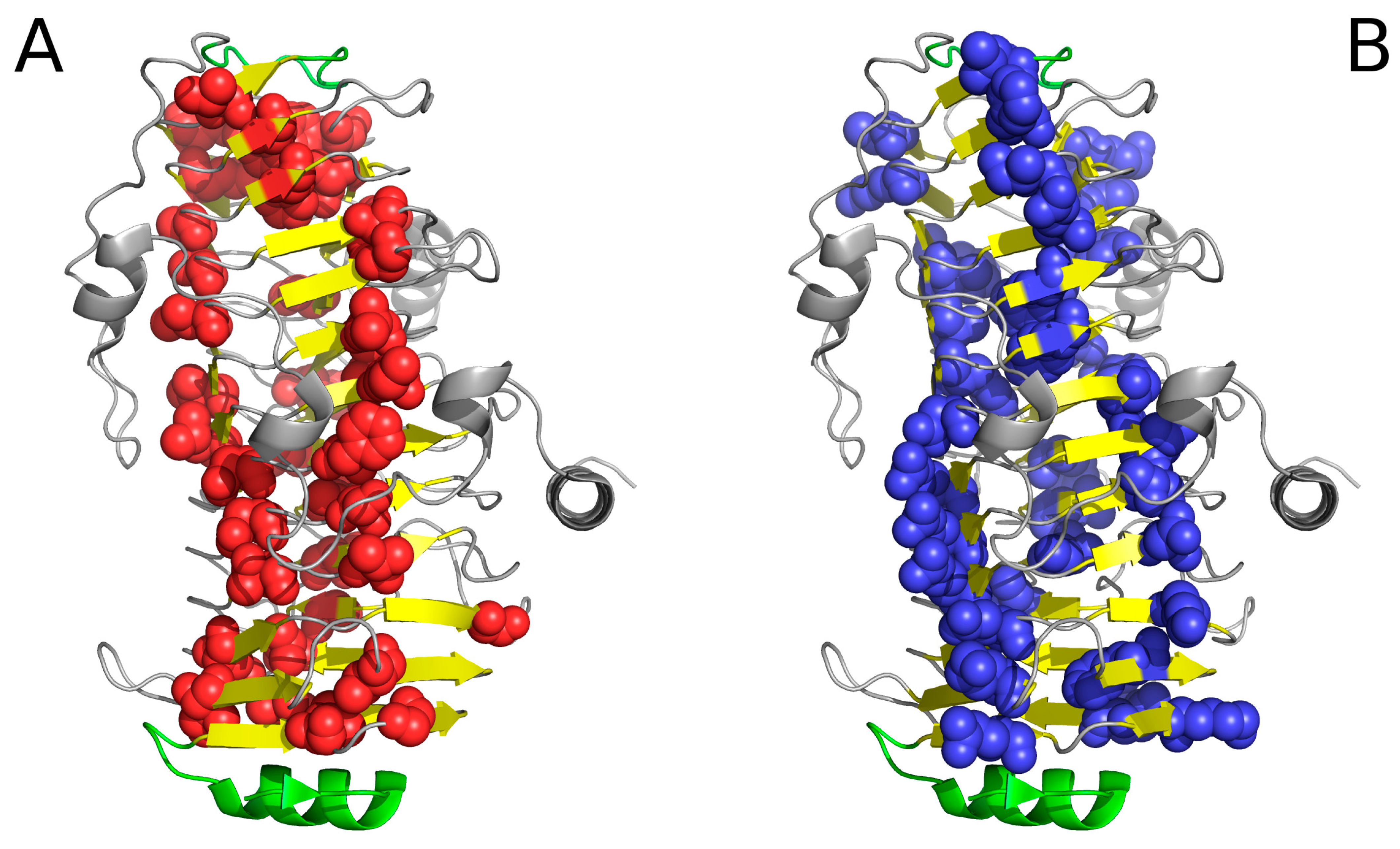
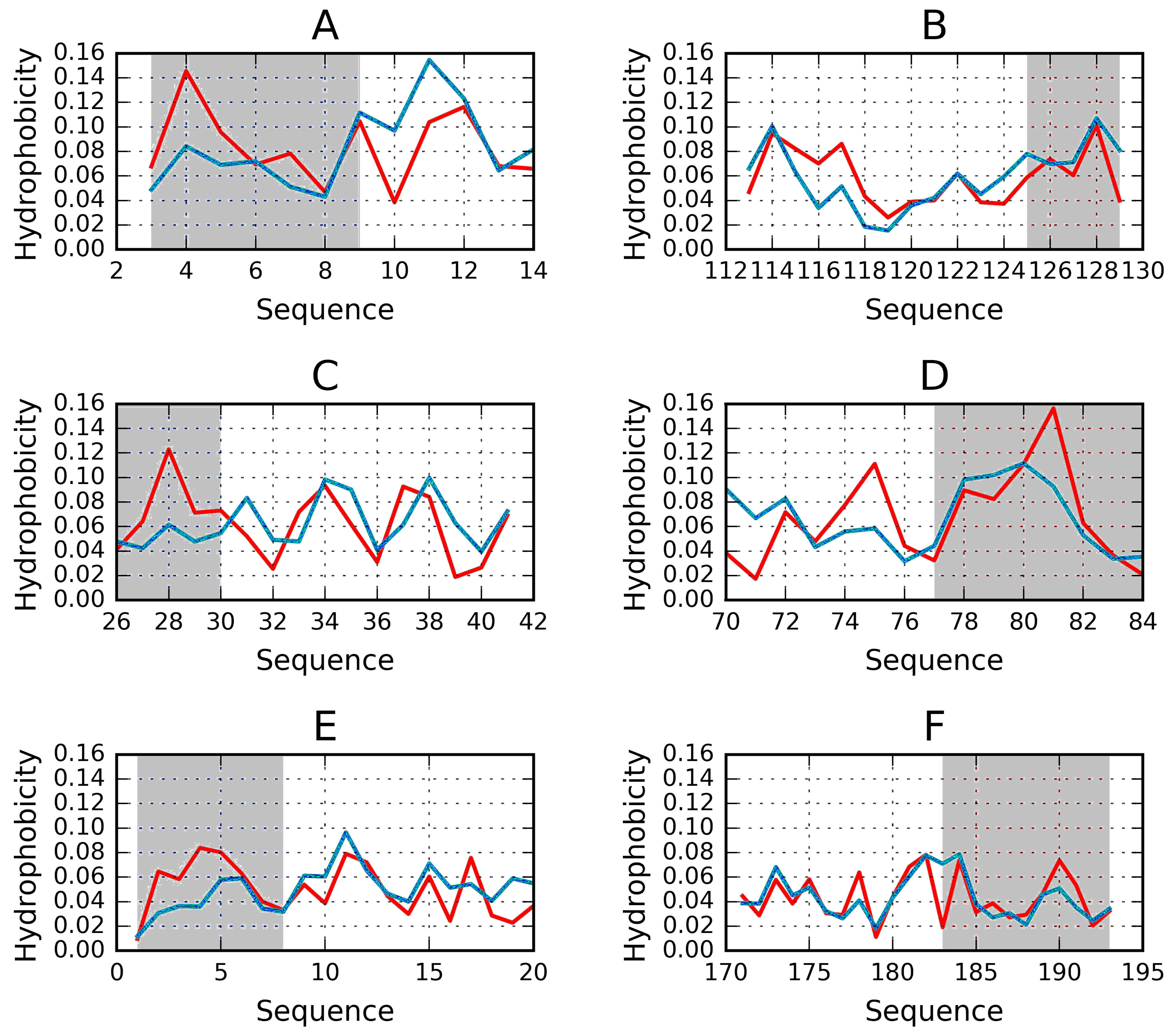
2.1. “Stop” Signals
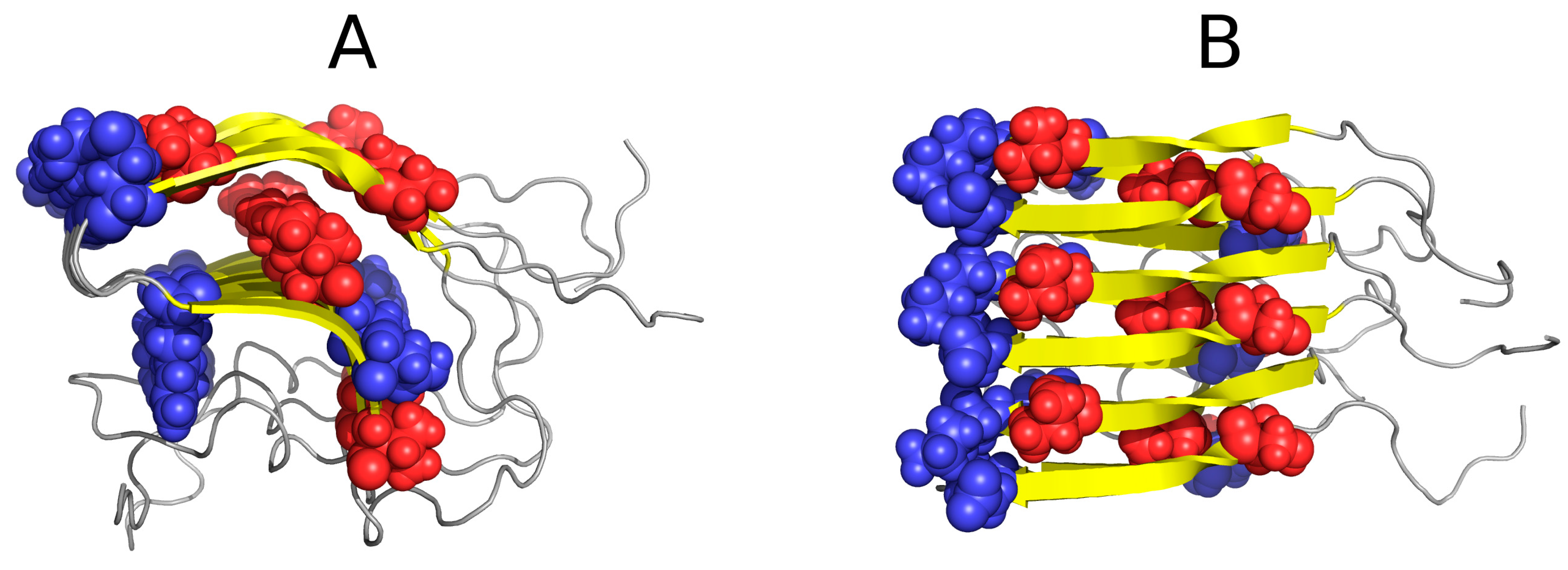
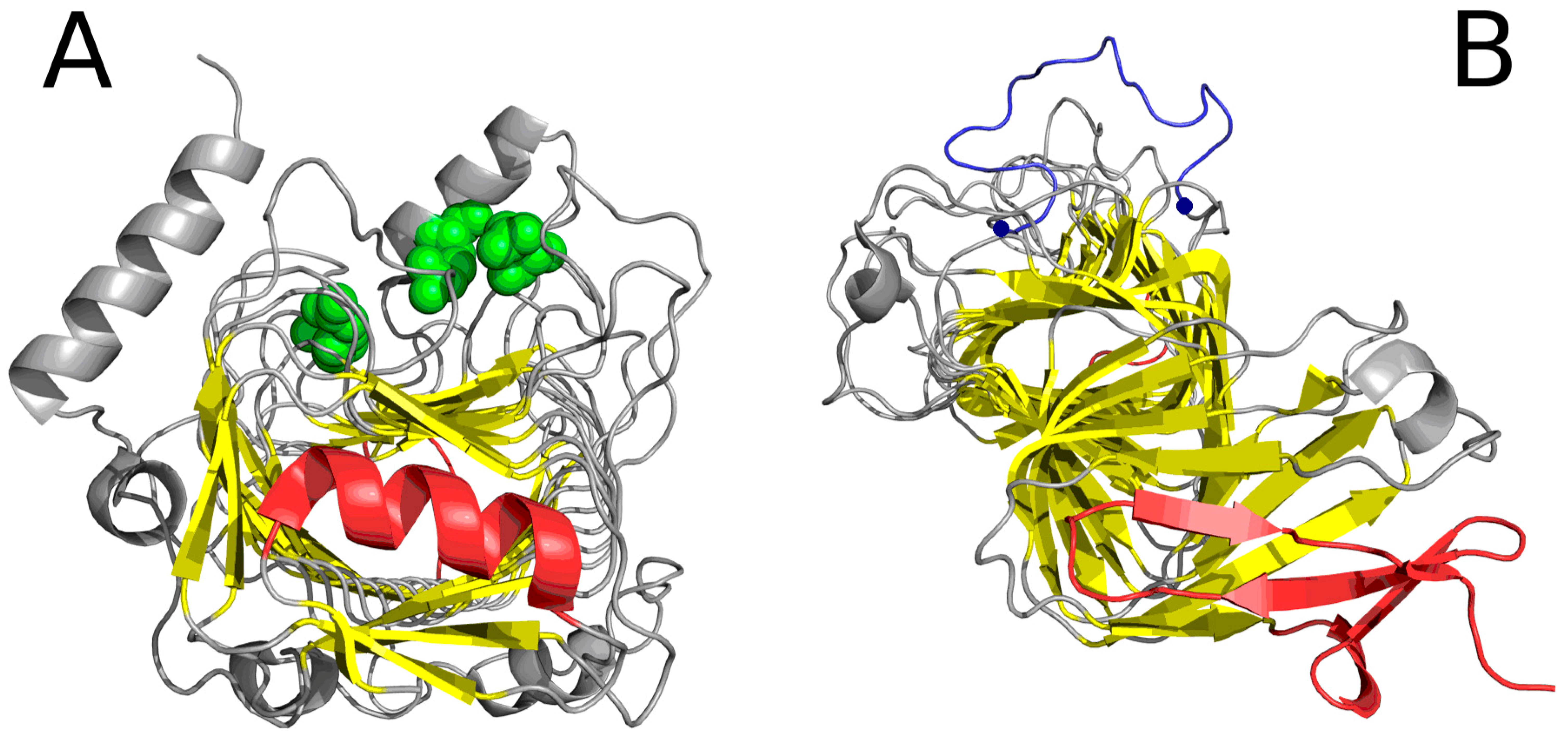
2.2. Lyase—Bacterial Chondroitinase b Pectate Lyase (PDB ID: 1DBG)
3. Description of Model
3.1. Dataset
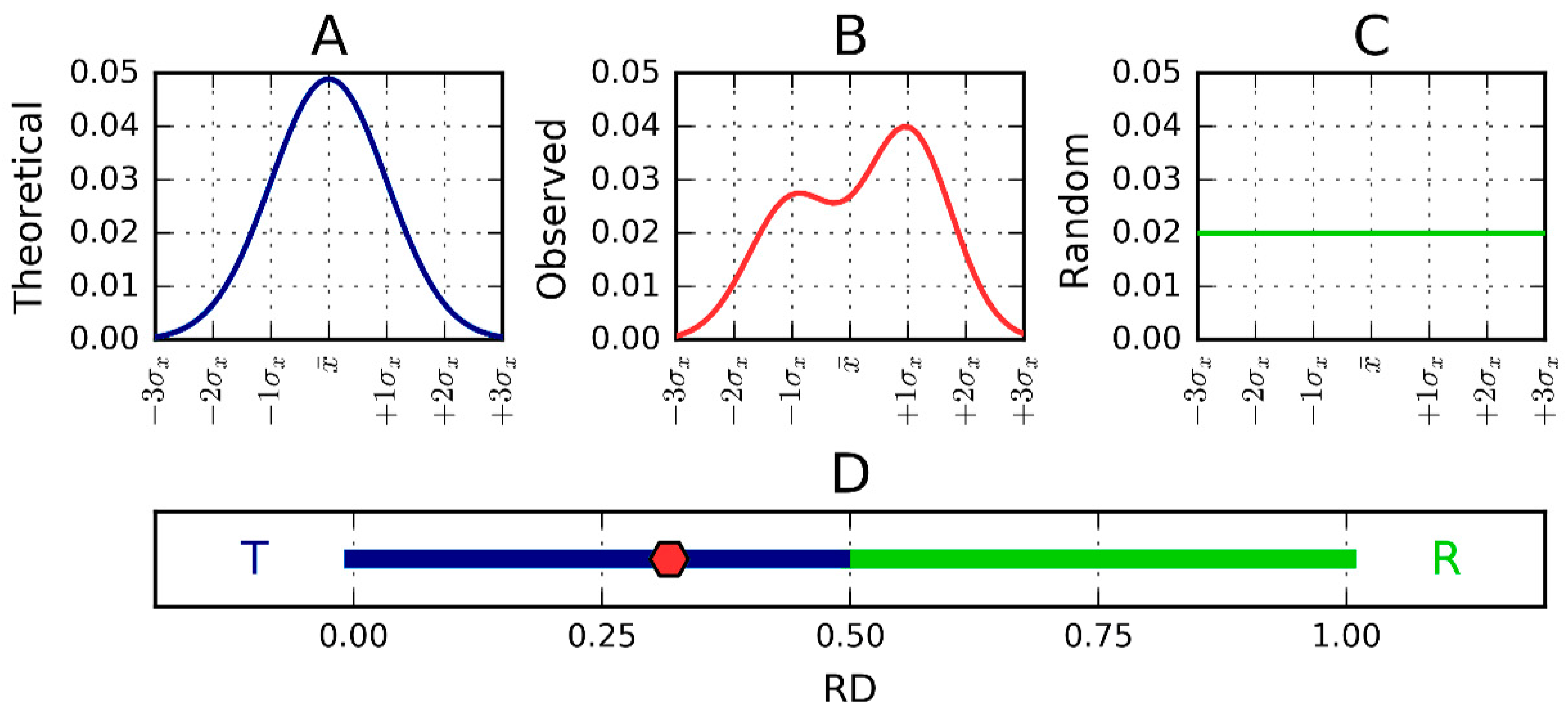
3.2. Fuzzy Oil Drop Model
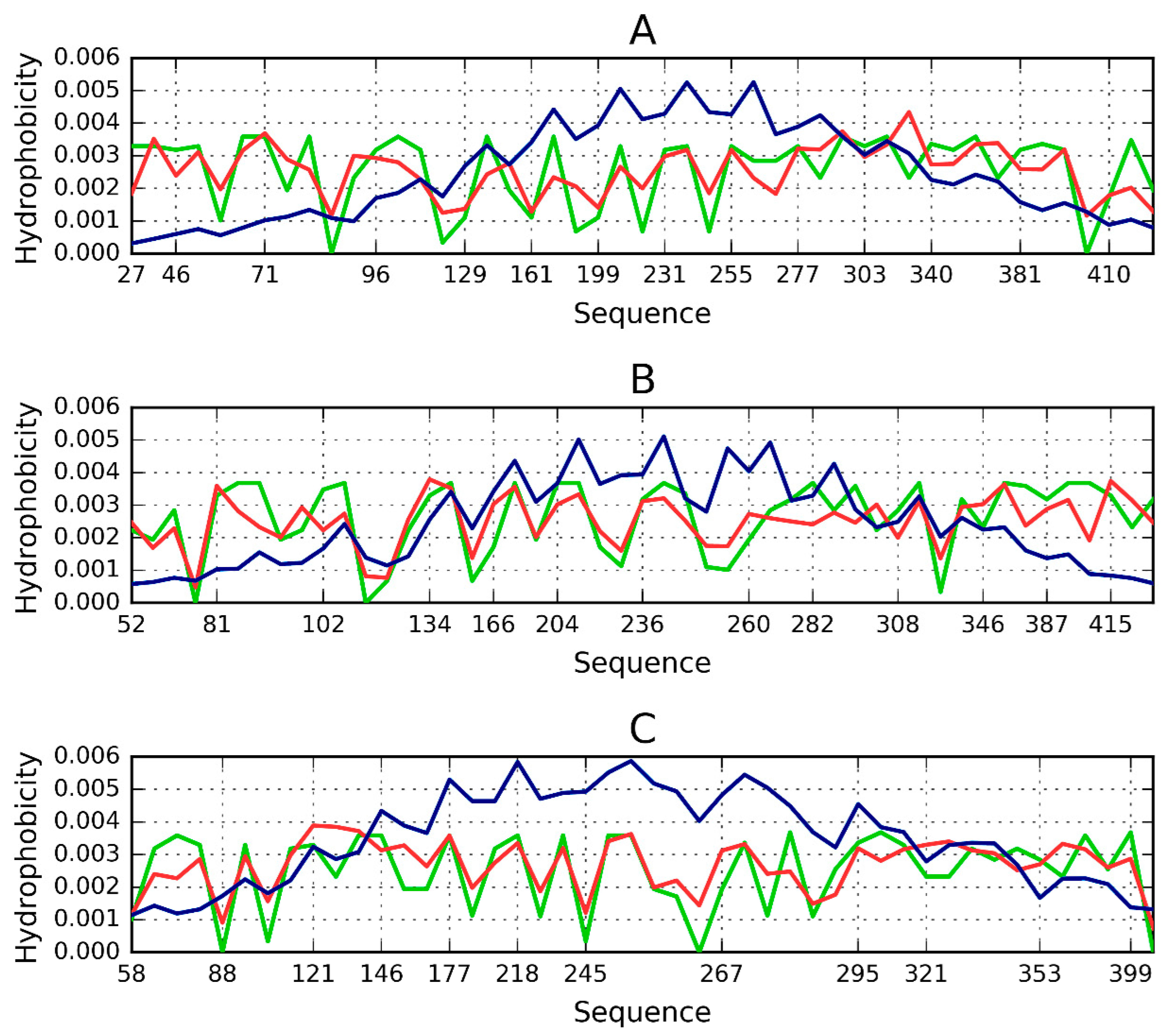
3.3. Hydrophobicity Scale
3.4. Identification of “Stop” Sequences
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Prusiner, S.B. Novel proteinaceous infectious particles cause scrapie. Science 1982, 216, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Prusiner, S.B. Detecting mad cow disease. Sci. Am. 2004, 291, 86–93. [Google Scholar] [CrossRef] [PubMed]
- Stöhr, J.; Watts, J.C.; Mensinger, Z.L.; Oehler, A.; Grillo, S.K.; DeArmond, S.J.; Prusiner, S.B.; Giles, K. Purified and synthetic Alzheimer’s amyloid beta (Aβ) prions. Proc. Natl. Acad. Sci. USA 2012, 109, 11025–11030. [Google Scholar] [CrossRef] [PubMed]
- Taubes, G. Misfolding the way to disease. Science 1996, 271, 1493–1495. [Google Scholar] [CrossRef] [PubMed]
- Purkey, H.E.; Dorrell, M.I.; Kelly, J.W. Evaluating the binding selectivity of transthyretin amyloid fibril inhibitors in blood plasma. Proc. Natl. Acad. Sci. USA 2001, 98, 5566–5571. [Google Scholar] [CrossRef] [PubMed]
- Gallardo, R.; Ramakers, M.; De Smet, F.; Claes, F.; Khodaparast, L.; Khodaparast, L.; Couceiro, J.R.; Langenberg, T.; Siemons, M.; Nyström, S.; et al. De novo design of a biologically active amyloid. Science 2016, 354. [Google Scholar] [CrossRef] [PubMed]
- Saelices, L.; Johnson, L.M.; Liang, W.Y.; Sawaya, M.R.; Cascio, D.; Ruchala, P.; Whitelegge, J.; Jiang, L.; Riek, R.; Eisenberg, D.S. Uncovering the Mechanism of Aggregation of Human Transthyretin. J. Biol. Chem. 2015, 290, 28932–28943. [Google Scholar] [CrossRef] [PubMed]
- Gibson, T.J.; Murphy, R.M. Design of peptidyl compounds that affect beta-amyloid aggregation: Importance of surface tension and context. Biochemistry 2005, 44, 8898–8907. [Google Scholar] [CrossRef] [PubMed]
- Roterman, I.; Banach, M.; Konieczny, L. Application of the fuzzy oil drop model describes amyloid as a ribbonlike micelle. Entropy 2017, 19, 167. [Google Scholar] [CrossRef]
- Banach, M.; Konieczny, L.; Roterman, I. Ligand-binding site recognition. In Protein Folding in Silico: Protein Folding versus Protein Structure Prediction; Woodhead Publishing: Cambridge, UK, 2012; pp. 79–94. [Google Scholar]
- Dygut, J.; Kalinowska, B.; Banach, M.; Piwowar, M.; Konieczny, L.; Roterman, I. Structural interface forms and their involvement in stabilization of multidomain proteins or protein complexes. Int. J. Mol. Sci. 2016, 17. [Google Scholar] [CrossRef] [PubMed]
- Pulawski, W.; Ghoshdastider, U.; Andrisano, V.; Filipek, S. Ubiquitous amyloids. Appl. Biochem. Biotechnol. 2012, 166, 1626–1643. [Google Scholar] [CrossRef] [PubMed]
- Emsley, P.; Charles, I.G.; Fairweather, N.F.; Isaacs, N.W. Structure of Bordetella pertussis virulence factor P.69 pertactin. Nature 1996, 381, 90–92. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Matte, A.; Li, Y.; Kim, Y.S.; Linhardt, R.J.; Su, H.; Cygler, M. Crystal structure of chondroitinase B from Flavobacterium heparinum and its complex with a disaccharide product at 1.7 A resolution. J. Mol. Biol. 1999, 294, 1257–1269. [Google Scholar] [CrossRef] [PubMed]
- Graether, S.P.; Kuiper, M.J.; Gagné, S.M.; Walker, V.K.; Jia, Z.; Sykes, B.D.; Davies, P.L. Beta-helix structure and ice-binding properties of a hyperactive antifreeze protein from an insect. Nature 2000, 406, 325–328. [Google Scholar] [CrossRef] [PubMed]
- Leinala, E.K.; Davies, P.L.; Jia, Z. Crystal structure of beta-helical antifreeze protein points to a general ice binding model. Structure 2002, 10, 619–627. [Google Scholar] [CrossRef]
- Daley, M.E.; Spyracopoulos, L.; Jia, Z.; Davies, P.L.; Sykes, B.D. Structure and dynamics of a beta-helical antifreeze protein. Biochemistry 2002, 41, 5515–5525. [Google Scholar] [CrossRef] [PubMed]
- Graether, S.P.; Gagné, S.M.; Spyracopoulos, L.; Jia, Z.; Davies, P.L.; Sykes, B.D. Spruce budworm antifreeze protein: changes in structure and dynamics at low temperature. J. Mol. Biol. 2003, 327, 1155–1168. [Google Scholar] [CrossRef]
- Lee, J.H.; Park, A.K.; Do, H.; Park, K.S.; Moh, S.H.; Chi, Y.M.; Kim, H.J. Structural basis for antifreeze activity of ice-binding protein from arctic yeast. J. Biol. Chem. 2012, 287, 11460–11468. [Google Scholar] [CrossRef] [PubMed]
- De Beer, T.A.; Berka, K.; Thornton, J.M.; Laskowski, R.A. PDBsum additions. Nucleic Acids Res. 2014, 42, D292–D296. [Google Scholar] [CrossRef] [PubMed]
- Howell, P.L.; Wolfram, F.; Robinson, H. Crystal structure of the alginate lyase from klebsiel pneumonia. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar]
- Alahuhta, M.; Taylor, L.E.; Brunecky, R.; Hammond, D.W.; Michener, W.; Adams, M.W.; Lunin, V. The catalytic mechanism and unique low pH optimum of Caldicellulosiruptor bescii family 3 pectate lyase. Acta Crystallogr. D Biol. Crystallogr. 2015, 71, 1946–1954. [Google Scholar] [CrossRef] [PubMed]
- Herbst, D.A.; Jakob, R.P.; Zähringer, F.; Maier, T. Mycocerosic acid synthase exemplifies the architecture of reducing polyketide synthases. Nature 2016, 531, 533–537. [Google Scholar] [CrossRef] [PubMed]
- Melckebeke, H.V.; Wasmer, C.; Lange, A.; AB, E.; Loquet, A.; Böckmann, A.; Meier, B.H. Atomic-resolution three-dimensional structure of HET-s(218–289) amyloid fibrils by solid-state NMR spectroscopy. J. Am. Chem. Soc. 2010, 132, 13765–13775. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, J.T.; Kabasakal, B.V.; Godding, D.; Kraatz, S.; Henderson, L.; Barber, J.; Freemont, P.S.; Murray, J.W. Synthetic beta-solenoid proteins with the fragment-free computational design of a β-hairpin extension. Proc. Natl. Acad. Sci. USA. 2016, 113, 10346–10351. [Google Scholar] [CrossRef] [PubMed]
- Konieczny, L.; Bryliński, M.; Roterman, I. Gauss-function-based model of hydrophobicity density in proteins. In Silico Biol. 2006, 6, 15–22. [Google Scholar] [PubMed]
- Kalinowska, B.; Banach, M.; Konieczny, L.; Roterman, I. Application of Divergence Entropy to Characterize the Structure of the Hydrophobic Core in DNA Interacting Proteins. Entropy 2015, 17, 1477–1507. [Google Scholar] [CrossRef]
- Roterman, I.; Banach, M.; Kalinowska, B.; Konieczny, L. Influence of the Aqueous Environment on Protein Structure—A Plausible Hypothesis Concerning the Mechanism of Amyloidogenesis. Entropy 2016, 18, 351. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Kyte, J.; Doolittle, R.F. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 1982, 157, 105–132. [Google Scholar] [CrossRef]
- Riek, R.; Eisenberg, D.S. The activities of amyloids from a structural perspective. Nature 2016, 539, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Kajava, A.V.; Steven, A.C. Beta-rolls, beta-helices, and other beta-solenoid proteins. Adv. Protein Chem. 2006, 73, 55–96. [Google Scholar] [PubMed]
- Hennetin, J.; Jullian, B.; Steven, A.C.; Kajava, A.V. Standard conformations of β-arches in β-solenoid proteins. J. Mol. Biol. 2006, 358, 1094–1105. [Google Scholar] [CrossRef] [PubMed]
- Vo, A.; Nguyen, N.; Huang, H. Solenoid and non-solenoid protein recognition using stationary wavelet packet transform. Bioinformatics 2010, 26, i467–i473. [Google Scholar] [CrossRef] [PubMed]
- Hrabe, T.; Jaroszewski, L.; Godzik, A. Revealing aperiodic aspects of solenoid proteins from sequence information. Bioinformatics 2016, 32, 2776–2782. [Google Scholar] [CrossRef] [PubMed]
- Peralta, M.D.; Karsai, A.; Ngo, A.; Sierra, C.; Fong, K.T.; Hayre, N.R.; Mirzaee, N.; Ravikumar, K.M.; Kluber, A.J.; Chen, X.; et al. Engineering amyloid fibrils from β-solenoid proteins for biomaterials applications. ACS Nano 2015, 9, 449–4463. [Google Scholar] [CrossRef] [PubMed]
- Squire, J.M.; Parry, D.A.D.; Kajava, A. Fibrous Proteins: Amyloids, Prions and Beta Proteins, Advances in Protein Chemistry; Elsevier Academic Press: San Diego, CA, USA, 2006. [Google Scholar]
| PDB ID | RD Protein | N-Terminal | ||||
|---|---|---|---|---|---|---|
| RD STOP | STOP Fragment | Fragment Secondary Form | RD STOP + Neighbor | STOP + Neighbor Fragment. | ||
| 1EWW | 0.522 | 0.297 | 1–8 | loop | 0.472 | 1–20 |
| 1L0S | 0.527 | 0.331 | 3–9 | β int | 0.520 | 3–14 |
| 1L1I | 0.552 | 0.426 | 1–13 | loop | 0.566 | 1–17 |
| 1N4I | 0.526 | 0.461 | 1–7 | loop | 0.565 | 1–14 |
| 3UYV | 0.610 | 0.108 | 68–72 | β-structure | 0.263 | 68–81 |
| 5B5H | 0.676 | 0.512 | 48–55 | helix | 0.542 | 48–61 |
| 2KJ3 | 0.618 | NA | NA | NA | NA | |
| 4OZX | 0.627 | 0.460 | 23–32 | helix | 0.484 | 52–58 |
| 4W8Q | 0.551 | 0.544 | 41–57 | β + loop | 0.425 | 30–60 |
| 4YFO | 0.634 | 0.481 | 21–33 | helix | 0.468 | 21–38 |
| 4YZA | 0.591 | 0.338 | −4–10 | loop | 0.543 | −4–25 |
| 4Z05 | 0.600 | 0.366 | −2–9 | β-structure | 0.628 | −2–22 |
| 5BP3 | 0.593 | 0.353 | 910–915 | β-hairpin | 0.465 | 906–927 |
| 5CU1 | 0.433 | 0.542 | 88–94 | loop | 0.513 | 82–92 |
| 1DBG | 0.651 | 0.414 | 30–41 | helix | 0.429 | 26–45 |
| 1DAB | 0.743 | 0.483 | 1–11 | β-structure | 0.619 | 1–22 |
| PDB ID | Solenoid | C-Terminal | |||||
|---|---|---|---|---|---|---|---|
| RD | FRAGM. | RD STOP | STOP Fragment | Secondary Form | RD STOP + Neighbor | Neighbor Fragment | |
| 1EWW | 0.525 | 9–73 | 0.372 | 74–78 | loop | 0.361 | 65–81 |
| 1L0S | 0.478 | 10–73 | 0.491 | 74–81 | β int | 0.502 | 72–90 |
| 1L1I | 0.479 | 14–76 | 0.211 | 77–84 | loop | 0.386 | 70–84 |
| 1N4I | 0.419 | 8–75 | 0.464 | 76–90 | loop | 0.493 | 71–90 |
| 3UYV | 0.622 | β-sheets | 0.425 | 125–129 | β + loop | 0.354 | 113–129 |
| 5B5H | 0.594 | β-sheets | 0.382 | 99–109 | β-hairpin | 0.269 | 101–113 |
| 2KJ3 | 0.618 | All residues | NA | NA | |||
| 4OZX | 0.655 | β-sheets | 0.275 | 252–261 | β + loop | 0.521 | 200–206 |
| 4W8Q | 0.551 | β-sheets | 0.377 | 255–263 | β +loop | 0.518 | 248–263 |
| 4YFO | 0.634 | 37–215 | 0.569 | 238–253 | helix | 0.719 | 223–253 |
| 4YZA | 0.591 | β-sheets | 0.479 | 183–193 | β + loop | 0.349 | 171–193 |
| 4Z05 | 0.600 | β-sheets | 0.493 | 183–193 | helix | 0.411 | 178–193 |
| 5BP3 | 0.593 | β-sheets | 0.698 | 1109–1115 | helix | 0.689 | 1109–1119 |
| 5CU1 | 0.427 | β-sheets | 0.408 | 149–156 | β-structure | 0.442 | 149–165 |
| 1DBG | 0.763 | β-sheets | 0.145 | 419–429 | loop | 0.524 | 413–435 |
| 1DAB | 0.780 | β-sheets | 0.472 | 517–525 | loop | 0.376 | 517–539 |
| PDB ID | Type | Characteristics | Ref. |
|---|---|---|---|
| 1EWW | Antifreeze | spruce budworm antifreeze protein at 30 °C | [15] |
| 1L0S | Antifreeze | Choristoneura fumiferana (spruce budworm) antifreeze protein isoform 337 | [16] |
| 1L1I | Antifreeze | Choristoneura fumiferana (spruce budworm) antifreeze protein isoform 337 | [17] |
| 1N4I | Antifreeze | Solution structure of spruce budworm antifreeze protein at 5 °C | [18] |
| 3UYV | Antifreeze | Solution structure of spruce budworm antifreeze protein at 5 °C | [19] |
| 5B5H | Antifreeze | Hydrophobic ice-binding site conferring hyperactivity on antifreeze protein from a snow mold fungus | [20] |
| 4OZX | Lyase EC4.2.2.3 | alginate lyase from Klebsiella pneumoniae | [21] |
| 4YZA | Lyase EC4.2.2.2 | Pectate lyase | [22] |
| 4Z05 | Lyase EC4.2.2.2 | Pectate lyase | [22] |
| 1DBG | LyaseEC4.2.2.19 | Chondroitinase B from Pedobacter heparinus | [14] |
| 5CU1 | Lyase E.C.4.4.1.3 Dimethylpropiothetin dethiomethylase | dmsp lyase DddQ from Regeria pomeroyi DSS3Dehydrogenase domain | [20] |
| 5BP3 | Lyase EC.2.3.1 | Dehydratase domain (dh) of a mycocerosic acid synthase-like (mas-like) pks | [23] |
| 2KJ3 | Prion | het-s (218–289) prion in its form obtained by solid-state NMR | [24] |
| 4W8Q | Toxin | truncated hemolysin A from P. Mirabilis | [20] |
| 4YFO | De novo protein | Beta1_ex1 | [25] |
| 1DAB | Cell adhesion | P.69 pertactin from Bordetella pertussis | [13] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roterman, I.; Banach, M.; Konieczny, L. Propagation of Fibrillar Structural Forms in Proteins Stopped by Naturally Occurring Short Polypeptide Chain Fragments. Pharmaceuticals 2017, 10, 89. https://doi.org/10.3390/ph10040089
Roterman I, Banach M, Konieczny L. Propagation of Fibrillar Structural Forms in Proteins Stopped by Naturally Occurring Short Polypeptide Chain Fragments. Pharmaceuticals. 2017; 10(4):89. https://doi.org/10.3390/ph10040089
Chicago/Turabian StyleRoterman, Irena, Mateusz Banach, and Leszek Konieczny. 2017. "Propagation of Fibrillar Structural Forms in Proteins Stopped by Naturally Occurring Short Polypeptide Chain Fragments" Pharmaceuticals 10, no. 4: 89. https://doi.org/10.3390/ph10040089
APA StyleRoterman, I., Banach, M., & Konieczny, L. (2017). Propagation of Fibrillar Structural Forms in Proteins Stopped by Naturally Occurring Short Polypeptide Chain Fragments. Pharmaceuticals, 10(4), 89. https://doi.org/10.3390/ph10040089






