Nonlinear Bayesian Algorithms for Gas Plume Detection and Estimation from Hyper-spectral Thermal Image Data
Abstract
:1. Introduction
2. Radiance Model
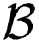 (v, T) represents the Planck spectral radiance of a blackbody at temperature. Finally, the plume transmissivity, τp is related to the chemical effluent's concentrations
(v, T) represents the Planck spectral radiance of a blackbody at temperature. Finally, the plume transmissivity, τp is related to the chemical effluent's concentrations
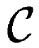 j (ppm-M) by Beer's law:
j (ppm-M) by Beer's law:
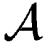 j(v) is the known absorbance spectra for effluent j, j = 1,…, J.
j(v) is the known absorbance spectra for effluent j, j = 1,…, J.- No term for solar radiation: For this model to be appropriate, one must assume that either (1) the observations are taken at night, or (2) the contribution of solar radiation is insignificant for the IR band being used.
- The atmospheric terms are known: The terms τa, Lu, and Ld are assumed to be known. This simplification is invoked to allow us to study the dominant source of variability in this problem, which is background clutter (i.e. variability in Tg and ϵg). The strategy is to include uncertainty in these atmospheric terms at a later date.
- There are no correlations or biases in the instrument errors: A well-calibrated instrument may approximate this assumption. However, periodic instrument calibrations can introduce correlations into these errors.
3. Nonlinear Bayesian Regression Model
3.1. Bayesian Methodology
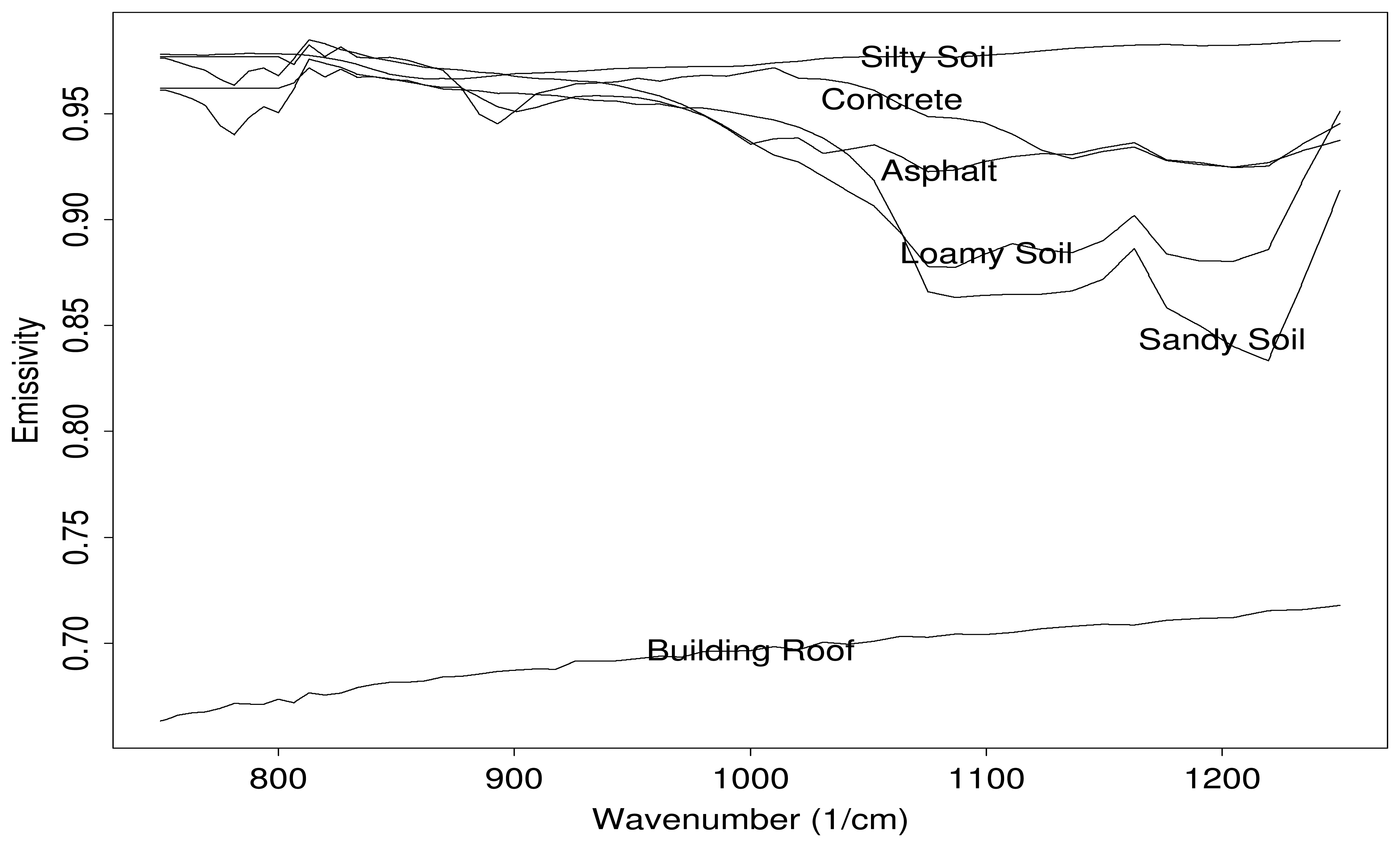
3.2. Derivation of the Prior Information
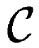 = (
= (
 1,…,
1,…,
 J).
J).4. Parameter Inference
4.1. NLMPD Algorithm
4.2. Markov Chain Monte Carlo Algorithm
- au ← (U − V))/A and al ← (L − V)/A.
- b ← max{p min{al, au}}
- b2 ← min{p max{al, au}}
- b ← b2 − b1
- ρ ← (nυ − b1) modulo 2b
- if ρ > b then ρ ← 2b − ρ
- ρ ← (ρ + b1)/nυ
5. Applications
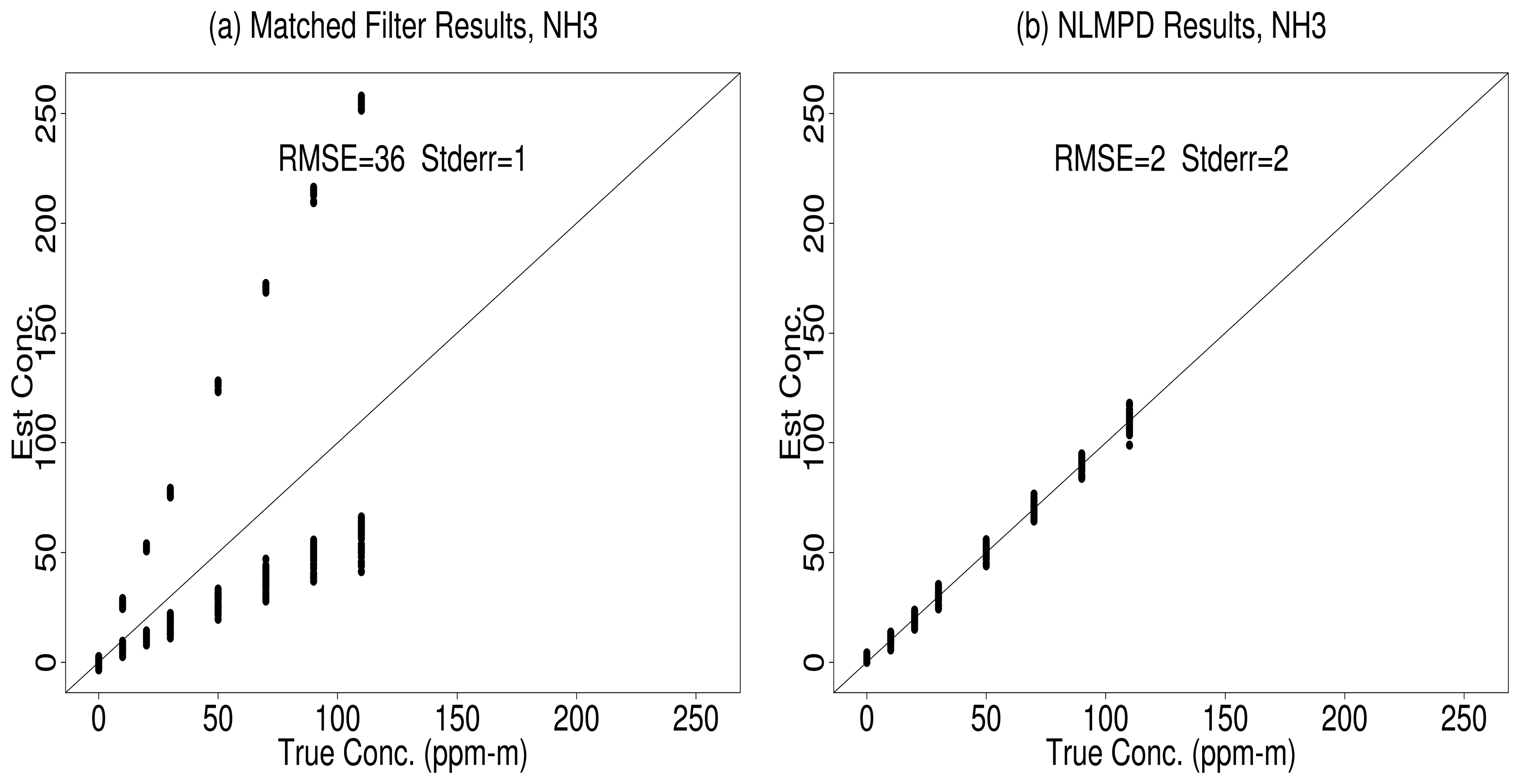
5.1. NLBR vs. Matched Filter
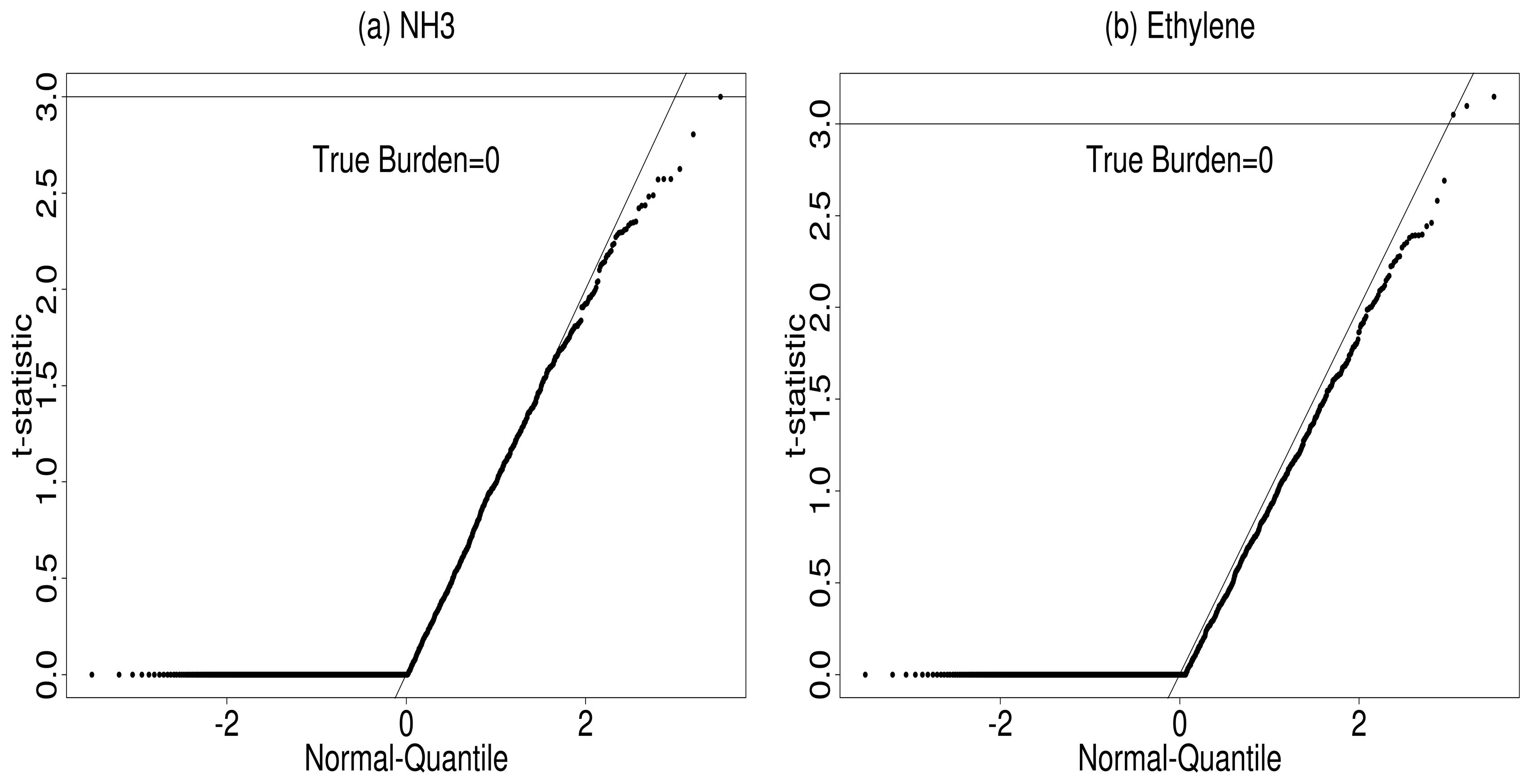
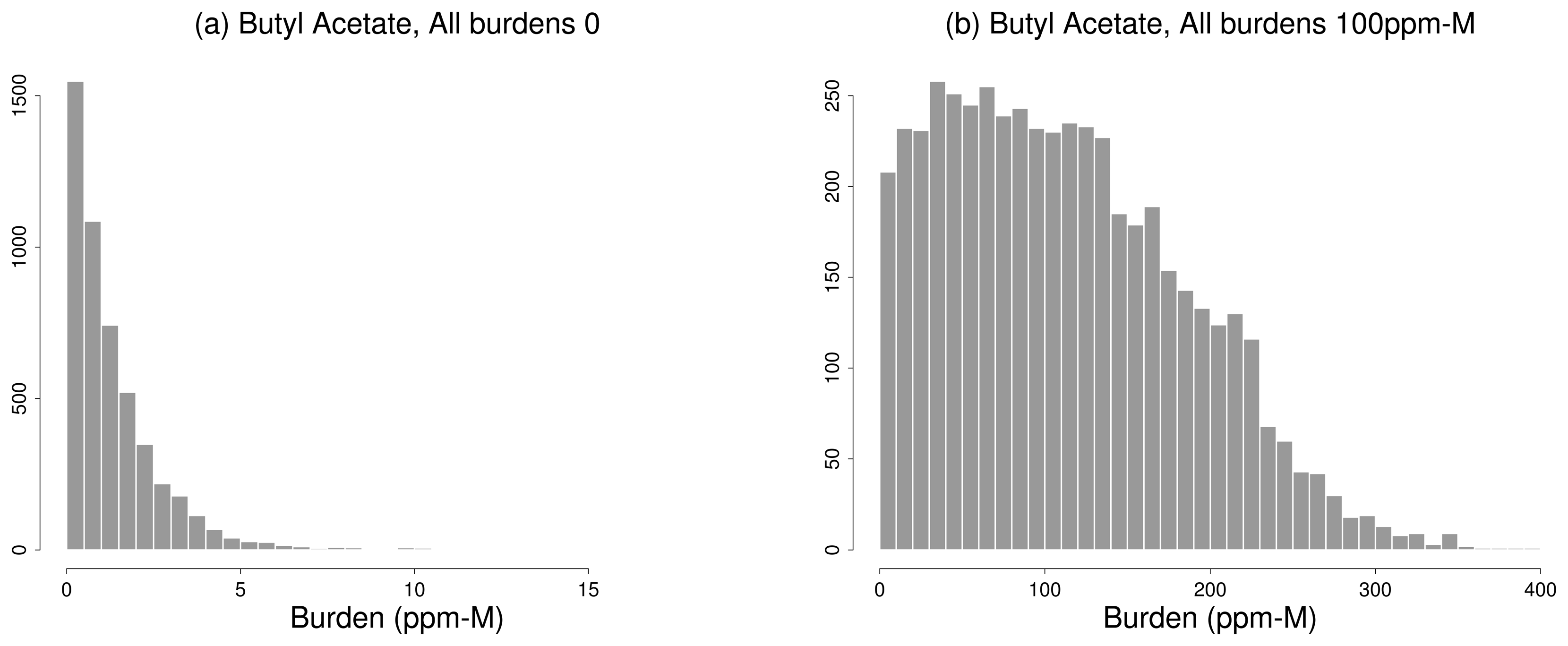
5.2. Gas Detection
6. Summary and Conclusions
Acknowledgments
References
- Funk, C.C.; Theiler, J.; Roberts, D. A.; Borel, C. C. Clustering to improve matched filter detection of weak gas plumes in hyperspectral thermal imagery. IEEE Trans. Geosci. and Remote Sensing 2001, 39, 1410–1420. [Google Scholar]
- Young, S. J. Detection and quantification of gases in industrial-stack plumes using thermal-infrared hyperspectral imaging. Aerospace Report ATR-2002(8407)-1 2002. [Google Scholar]
- Messinger, D. Gaseous plume detection in hyperspectral images: a comparison of methods. Proceedings of SPIE'04; 2004; pp. 592–603. [Google Scholar]
- ODonnell, E.; Messinger, D.; Salvaggio, C.; Schott, J. Identification and detection of gaseous effluents from hyperspectral imagery using invariant algorithms. Proceedings of SPIE'04; 2004. [Google Scholar]
- Theiler, J.; Foy, B.; Fraser, A. Characterizing non-gaussian clutter and detecting weak gaseous plumes in hyperspectral imagery. Proceedings of SPIE'05; 2005; pp. 182–193. [Google Scholar]
- Pogorzala, D. Gas plume species identification in LWIR hyperspectral imagery by regression analyses. PhD thesis, Rochester Institute of Technology, 2005. [Google Scholar]
- Hernandez-Baquero, E. D.; Schott, J. R. Atmospheric compensation for surface temperature and emissivity separation. Proceedings of the SPIE'00 Aerosense, Orlando, FL; 2000. [Google Scholar]
- Borel, C. C. Recipes for writing algorithms for atmospheric corrections and temperature/emissivity separations in the thermal regime for a multi-spectral sensor. Proceedings of the SPIE'01 Aerosense, Orlando, FL; 2001. [Google Scholar]
- Borel, C. C. Artemiss - an algorithm to retrieve temperature and emissivity from hyper-spectral thermal image data. Proceedings of the 28th Annual GOMATech Conference, Hyperspectral Imaging Session, Tampa, FL; 2003. [Google Scholar]
- Yang, Z. L.; Tse, Y. K.; Bai, Z. D. On the asymptotic effect of substituting estimators for nuisance parameters in inferential statistics; Technical report; Singapore Management University, School of Economics and Social Sciences, 2003. [Google Scholar]
- Lancaster, T. Orthogonal parameters and panel data. Review of Economic Studies 2000, 69, 647–666. [Google Scholar]
- Realmuto, V. J. Separating the effects of temperature and emissivity: Emissivity spectrum normalization. Proceedings of the 2nd TIMS Workshop, JPL Publications; 1990; 99-55, pp. 31–35. [Google Scholar]
- Milman, A. S. Mathematical Principles of Remote Sensing: Making Inferences from Noisy Dat.Taylor & Francis: New York, first edition; 2000. [Google Scholar]
- Burr, T.; McVey, B.; Sander, E. Chemical identification using bayesian model selection. Proceedings of 2002 Spring Research Conference on Statistics in Industry and Technology; 2002. [Google Scholar]
- Gelman, A.; Carlin, J. B.; Stern, H. S.; Rubin, D. B. Bayesian Data Analysis.; Chapman & Hall: London, 1995. [Google Scholar]
- Gilks, W. R.; Richardson, S.; Spiegelhalter, D. J. Markov Chain Monte Carlo.; Chapman & Hall: London, 1996. [Google Scholar]
- Hanson, K. M. Markov chain monte carlo posterior sampling with the hamiltonian method. Proceedings of SPIE Vol. 4322, Medical Imaging: Image Processing; Sonka, M., Hanson, K. M., Eds.; 2001. [Google Scholar]
- Alder, B.; Wainwright, T. Studies in molecular dynamics i, general method. Journal of Chemical Physics 1959, 31(2), 459–466. [Google Scholar]
- Berk, A.; Acharya, P. K.; Bernstein, L. S.; Anderson, G. P.; Chetwynd, J. H.; Hoke, M. L. Reformulation of the modtran band model for higher spectral resolution. Proceedings of SPIE Vol. 4049, Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VI; Shen, S., Descour, M., Eds.; 2000. [Google Scholar]
- Beer, R. Remote Sensing by Fourier Transform Spectrometry.; Wiley Interscience: New York, 1991. [Google Scholar]
- Flanigan, D. F. Prediction of the limits of detection of hazardous vapors by passive infrared with the use of modtran. Applied Optics 1996, 35, 6090–6098. [Google Scholar]
- Westlund, H. B.; Meyer, G. W. A brdf database employing the beard-maxwell reflection model. Proceedings of Graphics Interface 2002; 2002. [Google Scholar]
- Bartels, R. H.; Barsky, B. A.; Beatty, J. C. An Introduction to Splines for Use in Computer Graphics and Geometric Modellin.; Morgan Kaufman: Los Altos, CA, 1987. [Google Scholar]
- Marquardt, D. M. An algorithm for least squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar]
- Hastings, W. K. Monte carlo sampling methods using markov chains and their applications. Biometrik 1970, 97–109. [Google Scholar]
- Miller, B.; Messinger, D. The effects of atmospheric compensation upon gaseous plume signatures. Proceedings of SPIE'05; 2005. [Google Scholar]

© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Heasler, P.; Posse, C.; Hylden, J.; Anderson, K. Nonlinear Bayesian Algorithms for Gas Plume Detection and Estimation from Hyper-spectral Thermal Image Data. Sensors 2007, 7, 905-920. https://doi.org/10.3390/s7060905
Heasler P, Posse C, Hylden J, Anderson K. Nonlinear Bayesian Algorithms for Gas Plume Detection and Estimation from Hyper-spectral Thermal Image Data. Sensors. 2007; 7(6):905-920. https://doi.org/10.3390/s7060905
Chicago/Turabian StyleHeasler, Patrick, Christian Posse, Jeff Hylden, and Kevin Anderson. 2007. "Nonlinear Bayesian Algorithms for Gas Plume Detection and Estimation from Hyper-spectral Thermal Image Data" Sensors 7, no. 6: 905-920. https://doi.org/10.3390/s7060905
APA StyleHeasler, P., Posse, C., Hylden, J., & Anderson, K. (2007). Nonlinear Bayesian Algorithms for Gas Plume Detection and Estimation from Hyper-spectral Thermal Image Data. Sensors, 7(6), 905-920. https://doi.org/10.3390/s7060905



