Performance Evaluation and Calibration of Electromagnetic Field (EMF) Area Monitors Using a Multi-Wire Transverse Electromagnetic (MWTEM) Transmission Line
Abstract
1. Introduction
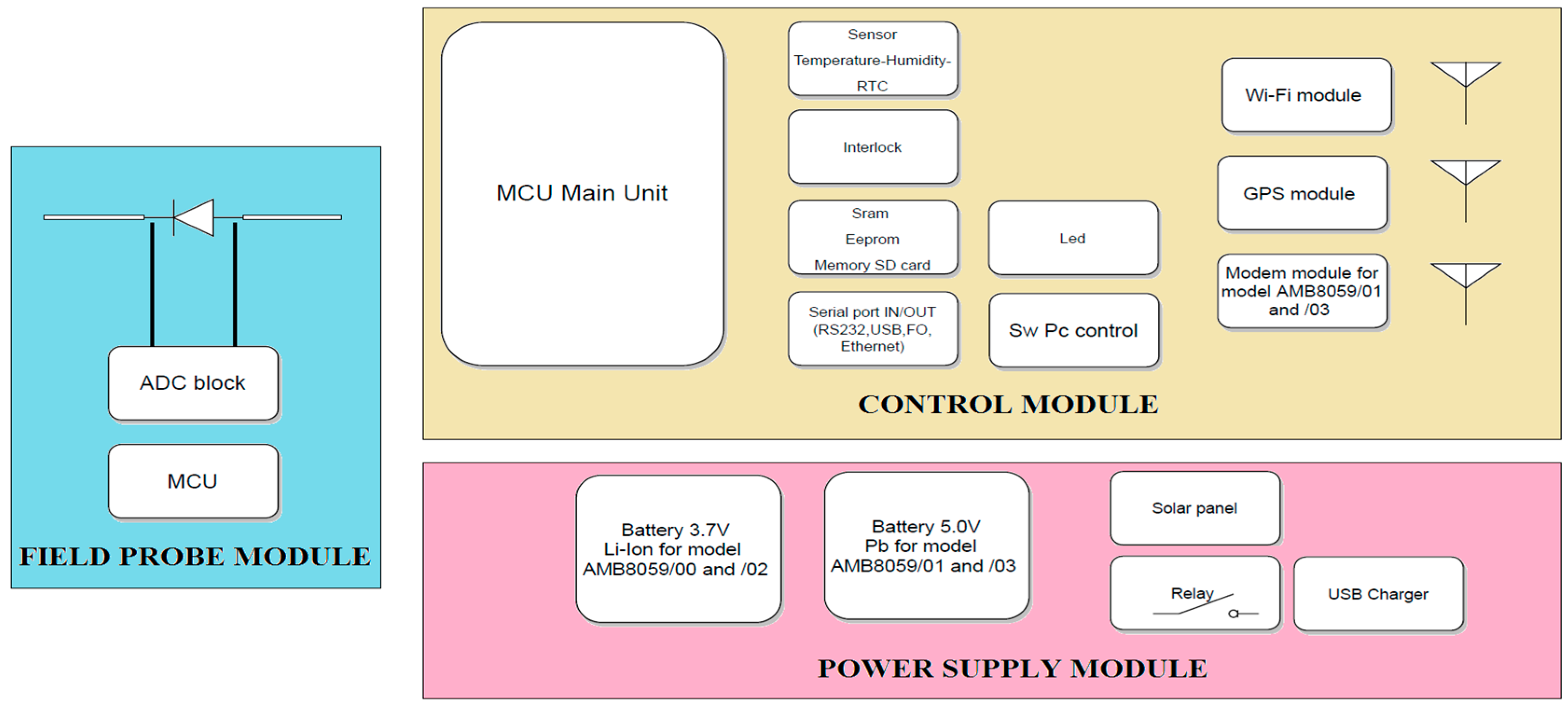
2. The Structure of an EMF Area Monitor
3. Experimental Setup
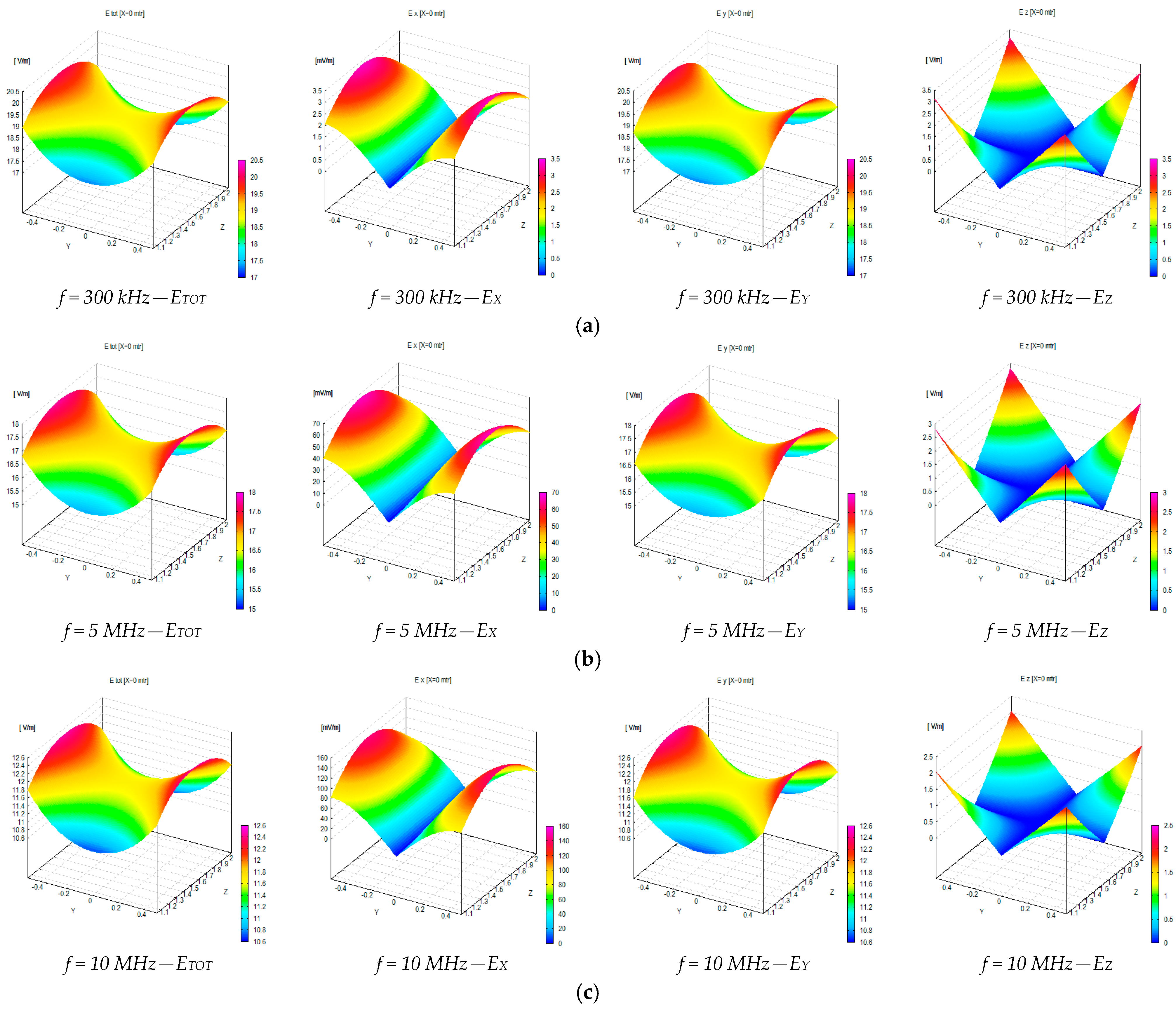
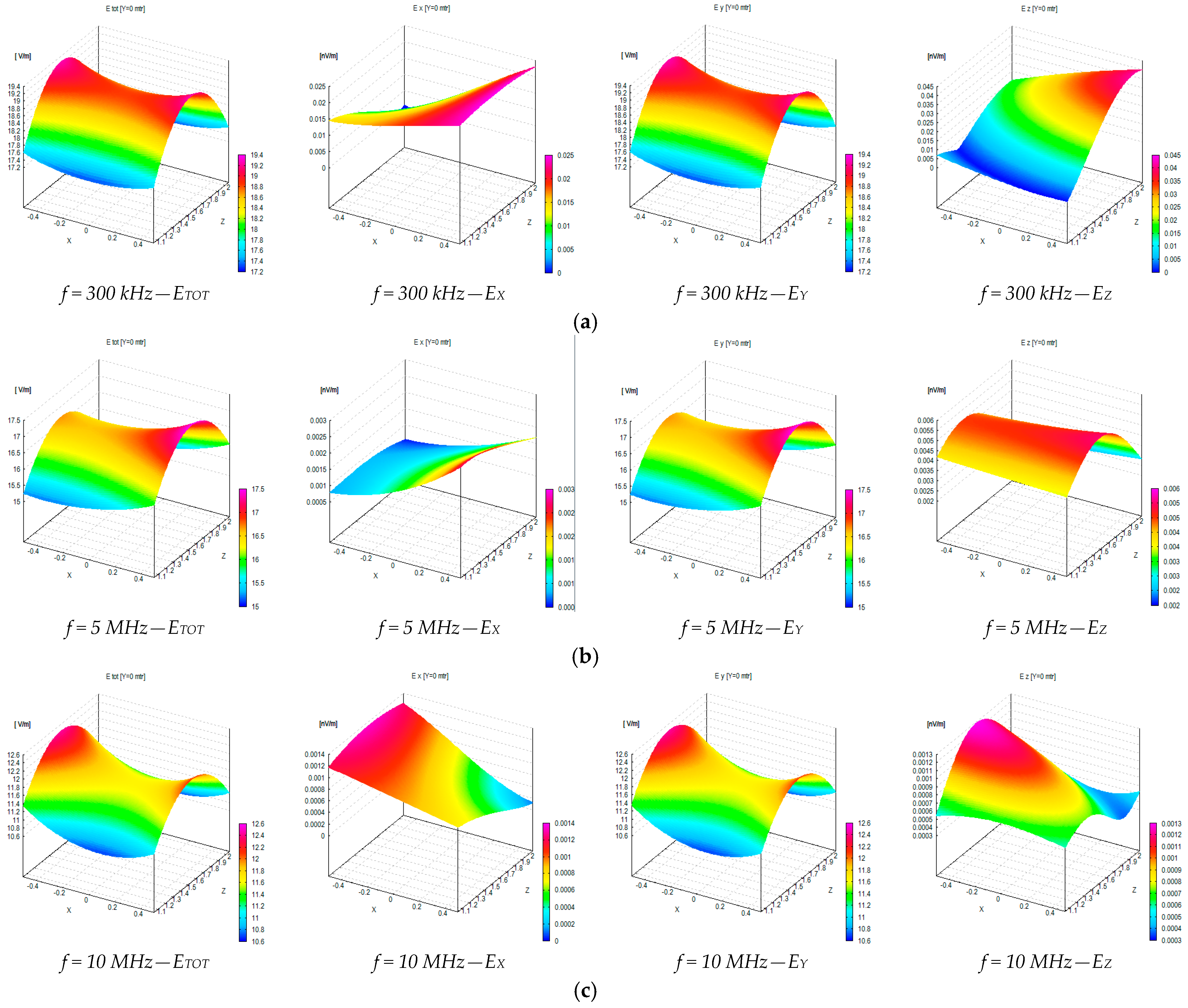
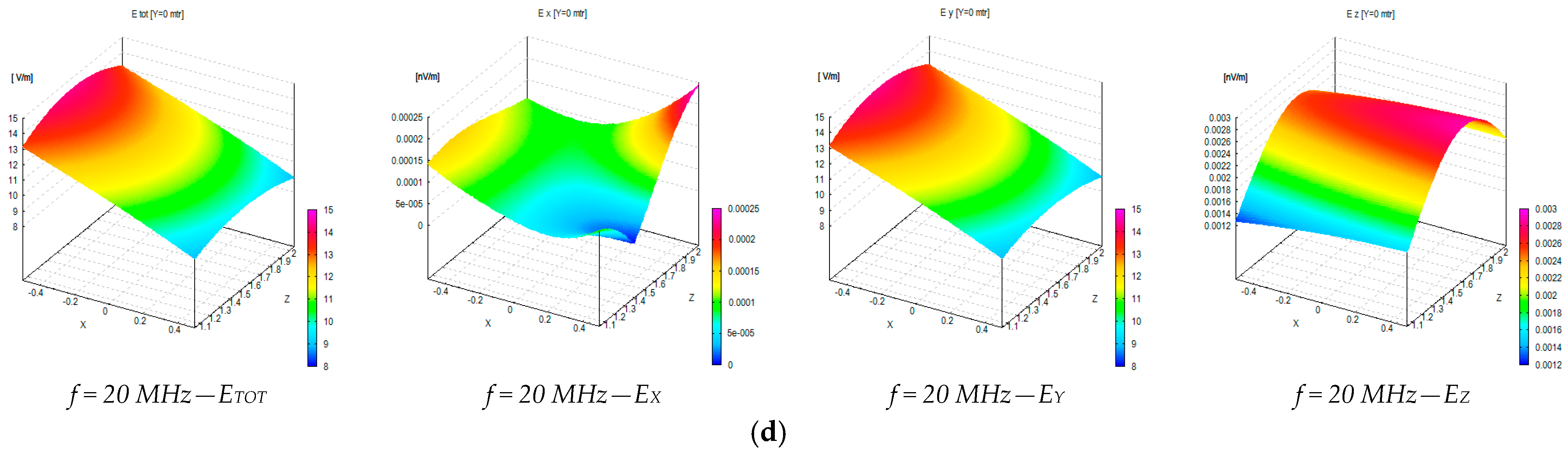
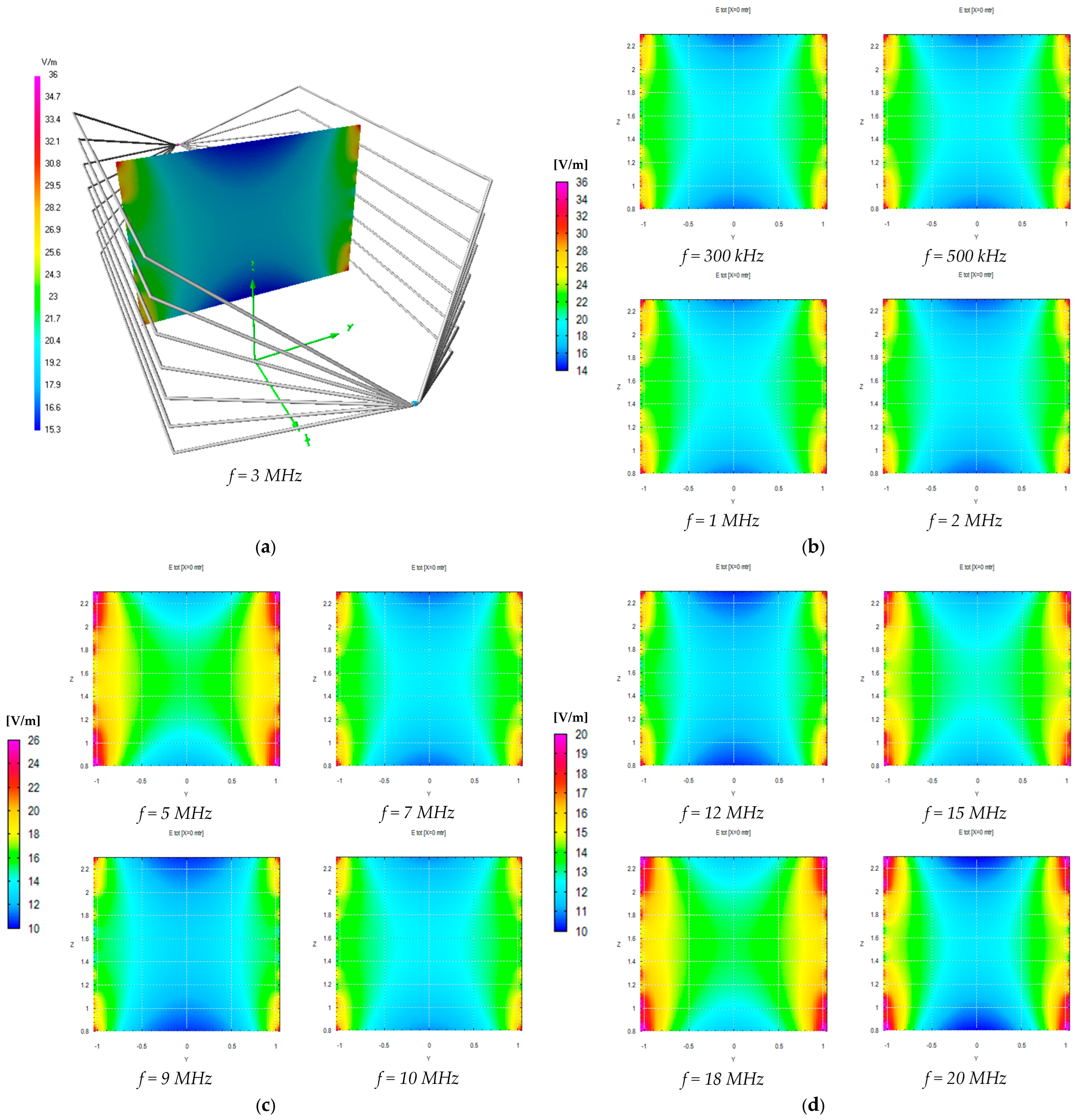
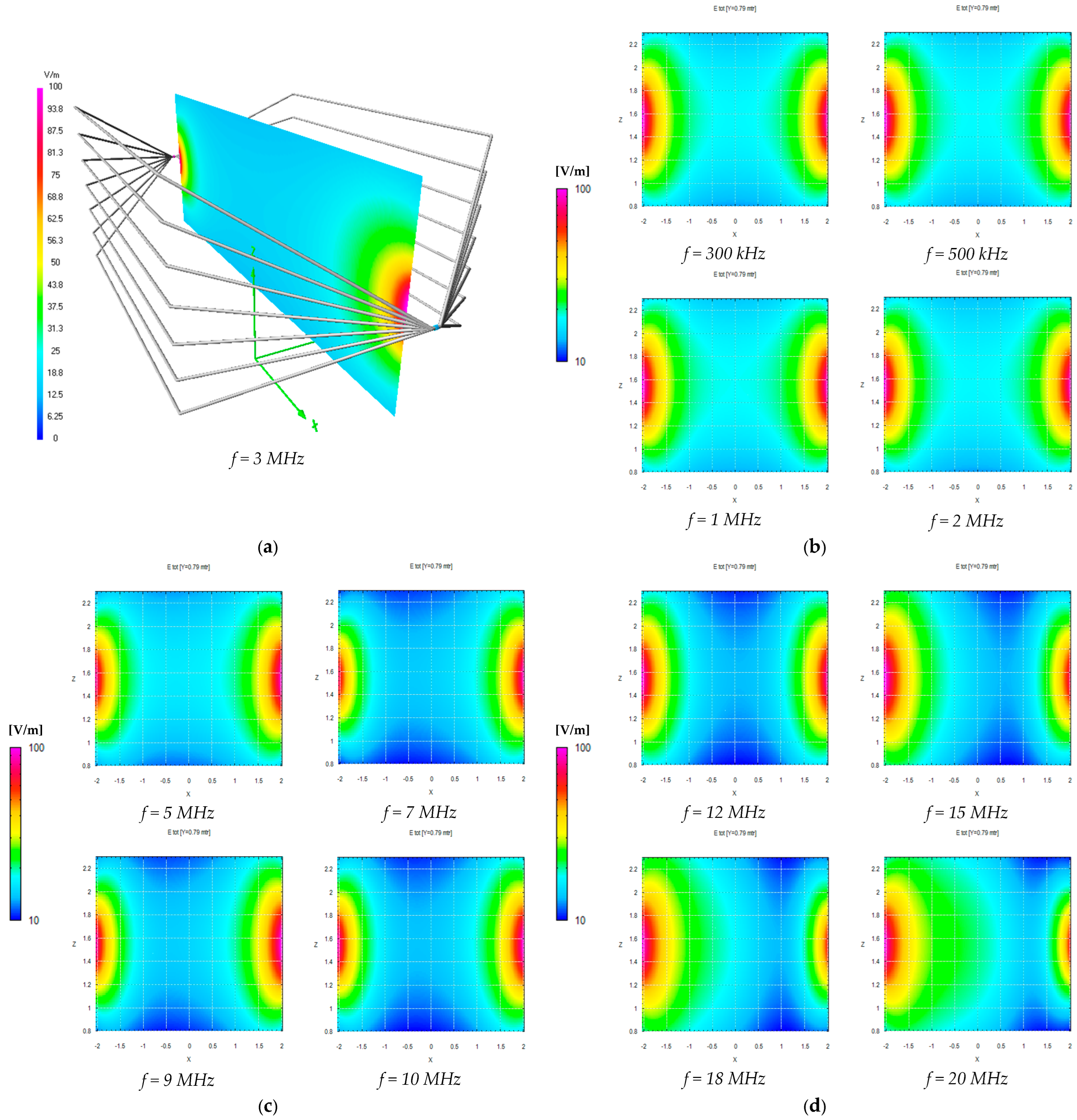
4. Numerical and Experimental Assessment of the Electric Field Generated by the MWTEM Transmission Line
5. Experimental Evaluation and Calibration of the EMF Area Monitor
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EMF | Electromagnetic field |
| HF | High frequency |
| LF | Low frequency |
| MWTEM | Multi-wire transverse electromagnetic |
| MoM | Method of moments |
Appendix A

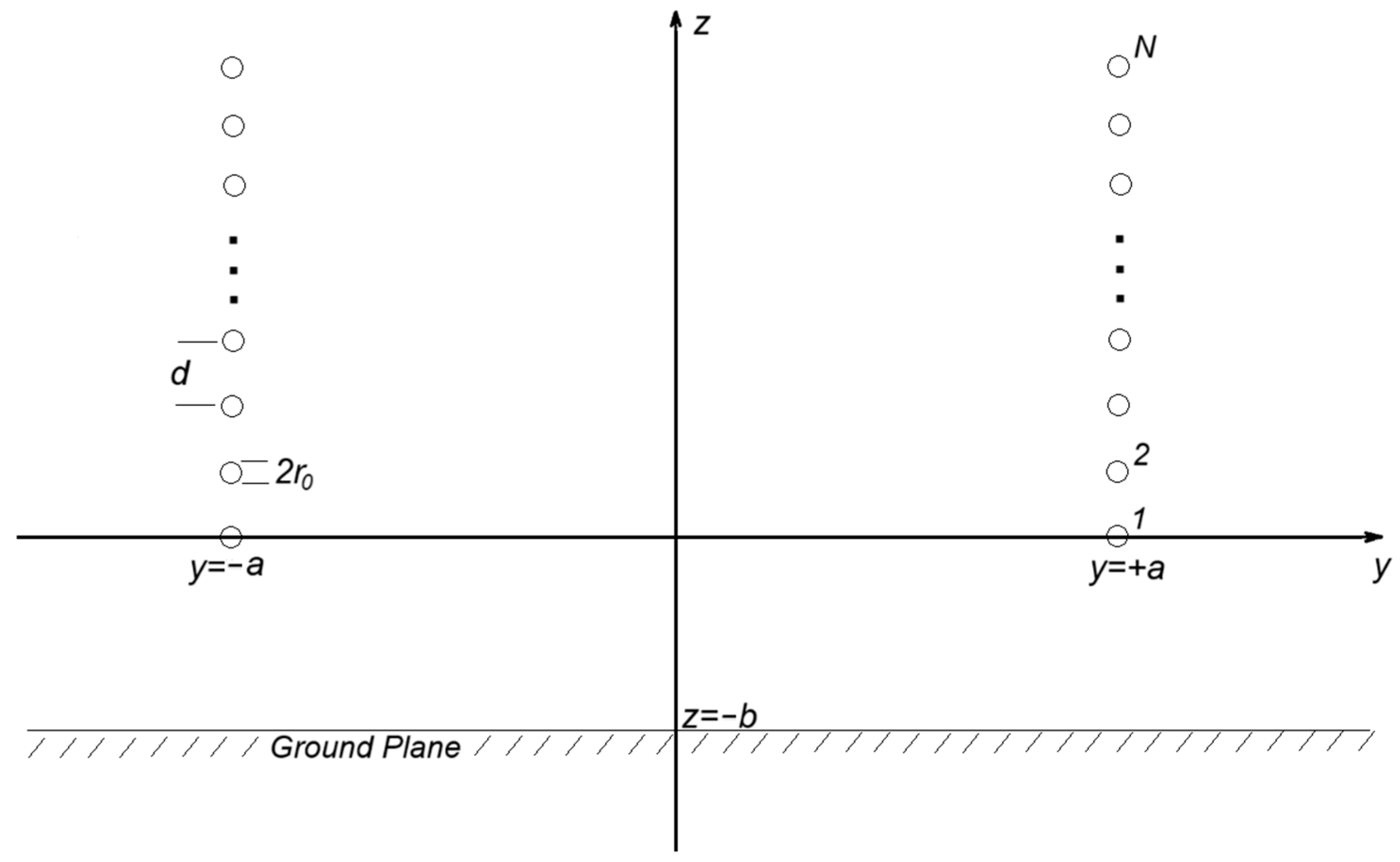
Appendix B
Appendix C
| Freq. [MHz] | Transversal Section (x = 0, −0.5 < y < 0.5, 1.05 < z < 2.05) | Longitudinal Section (−0.5 < x < 0.5, y = 0, 1.05 < z < 2.05) | ||||||
|---|---|---|---|---|---|---|---|---|
[dB] | [dB] | [dB] | [dB] | [dB] | [dB] | [dB] | [dB] | |
| 0.3 | >40 | 15.5 | >40 | 18.7 | >40 | >40 | 23.9 | >40 |
| 5 | >40 | 15.4 | 35.3 | 18.8 | >40 | >40 | 23.1 | >40 |
| 10 | 38.8 | 15.2 | 32.9 | 18.9 | >40 | >40 | 23.7 | >40 |
| 20 | >40 | 14.6 | 17.9 | 18.4 | >40 | >40 | 15.1 | >40 |




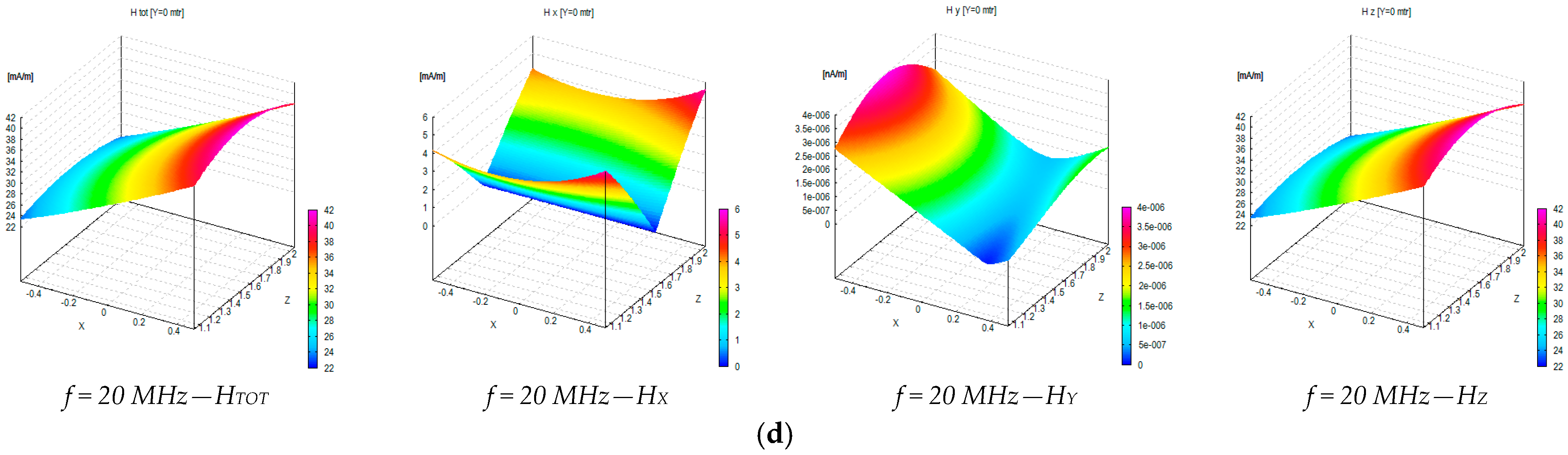
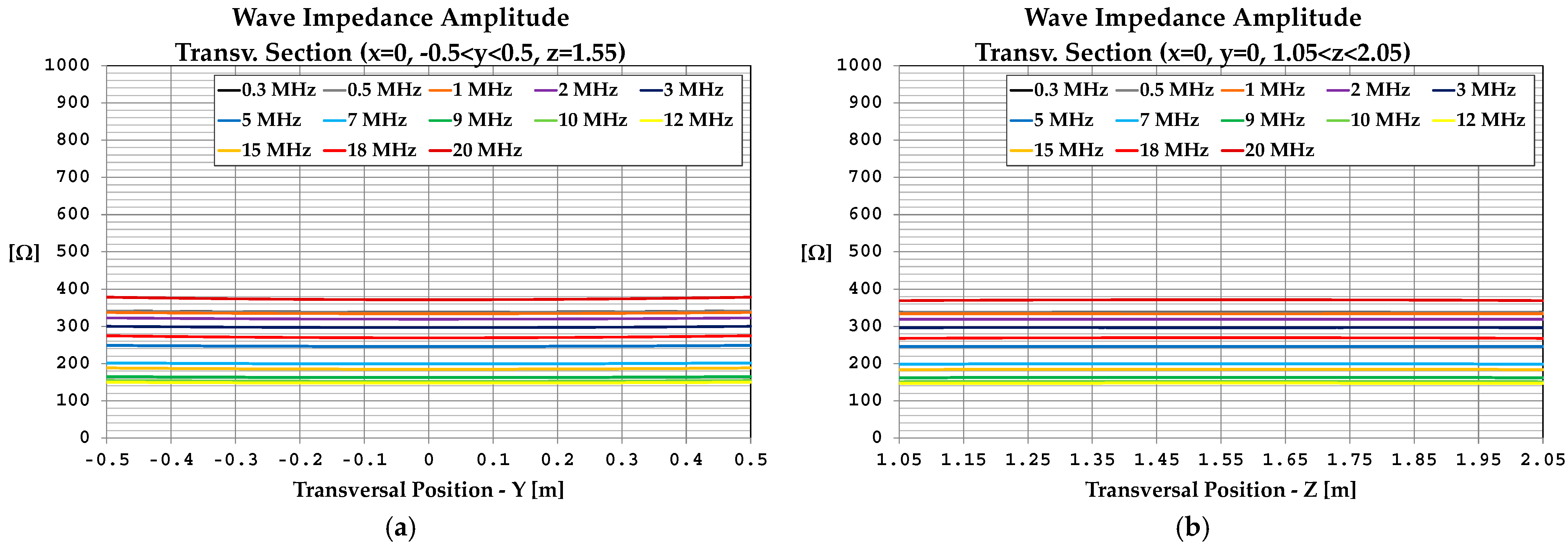
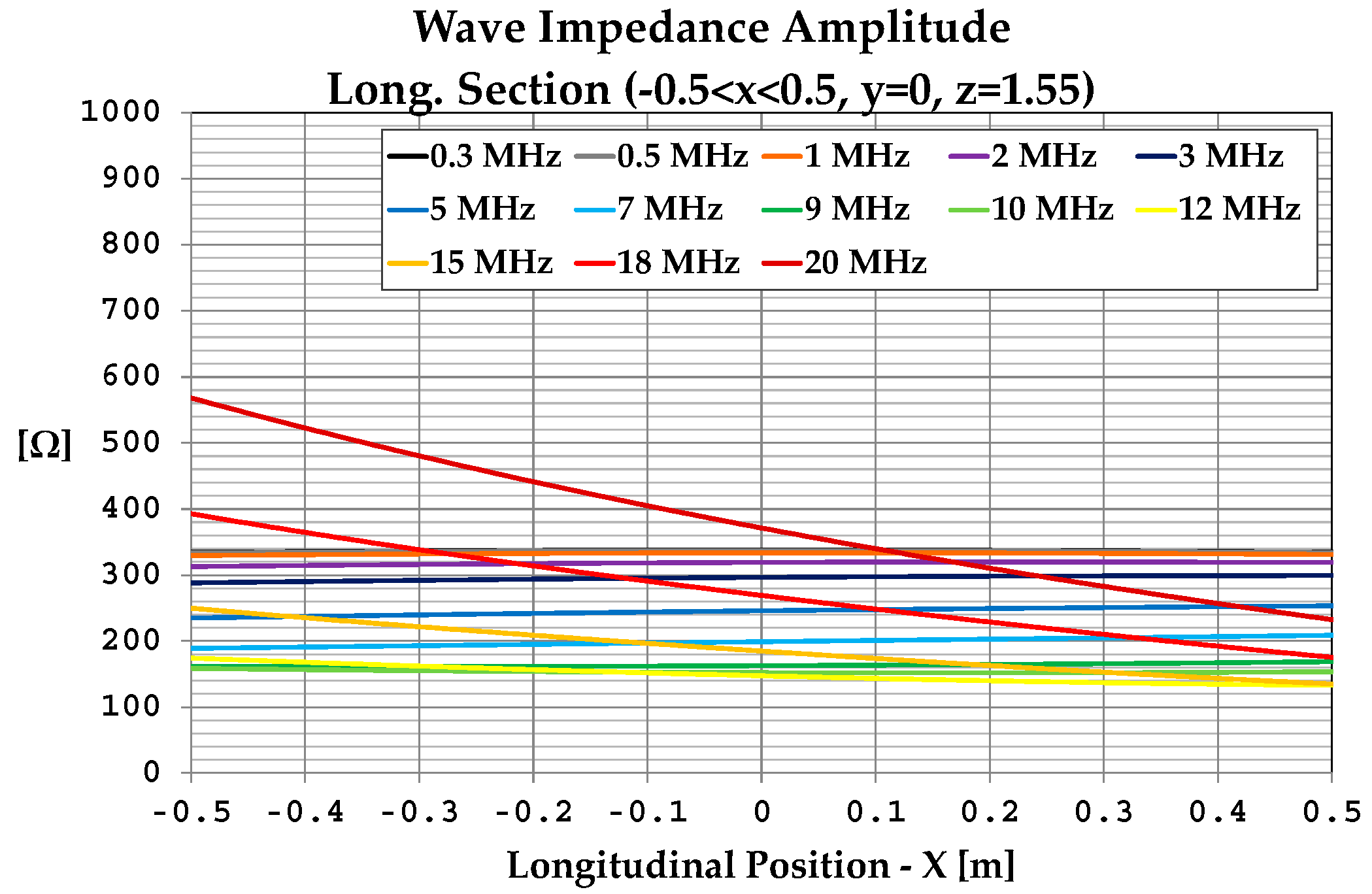
References
- International Commission on Non-Ionizing Radiation Protection. Guidelines for limiting exposure to time-varying electric and magnetic fields (1Hz–100 kHz). Health Phys. 2010, 99, 818–836. [Google Scholar] [CrossRef] [PubMed]
- International Commission on Non-Ionizing Radiation Protection. Guidelines for limiting exposure to electromagnetic fields (100 kHz to 300 GHz). Health Phys. 2020, 118, 483–524. [Google Scholar] [CrossRef] [PubMed]
- European Union. Directive 2013/35/EU on the Minimum Health and Safety Requirements Regarding the Exposure of Workers to the Risks Arising from Physical Agents (Electromagnetic Fields) and Repealing Directive 2004/40/EC; Council of the European Union: Brussels, Belgium, 2013. [Google Scholar]
- European Union (UE) Council Recommendation. Council Recommendation of 12 July 1999 on the Limitation of Exposure of the General Public to Electromagnetic Fields (0 Hz to 300 GHz)—(1999/519/EC); Council of the European Union: Brussels, Belgium, 1999. [Google Scholar]
- International Telecommunication Union (ITU). Recommendation ITU-T K.83—Monitoring Electromagnetic Field; International Telecommunication Union (ITU): Geneva, Switzerland, 2011. [Google Scholar]
- Ioriatti, L.; Martinelli, M.; Viani, F.; Benedetti, M.; Massa, A. Real-time distributed monitoring of electromagnetic pollution in urban environments. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS 2009), Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Viani, F.; Donelli, M.; Oliveri, G.; Massa, A.; Trinchero, D. A WSN-based system for real-time electromagnetic monitoring. In Proceedings of the IEEE International Symposium on Antennas and Propagation (APSURSI), Spokane, DC, USA, 3–8 July 2011. [Google Scholar]
- Viani, F.; Polo, A.; Donelli, M.; Giarola, E. A Relocable and Resilient Distributed Measurement System for Electromagnetic Exposure Assessment. IEEE Sens. J. 2016, 16, 4595–4604. [Google Scholar] [CrossRef]
- Antic, D.; Djuric, N.; Kljajic, D. Environmental EMF monitoring in the SEMONT system using quad-band AMB 8057/03 sensor. In Proceedings of the IEEE 10th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Larnaca, Cyprus, 8–10 October 2014. [Google Scholar]
- Antic, D.; Djuric, N.; Kljajic, D. The AMB 8057-03 sensor node implementation in the SEMONT EMF monitoring system. In Proceedings of the IEEE 12th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 11–13 September 2014. [Google Scholar]
- Kundacina, O.; Vincan, V.; Antic, D.; Kljajic, D.; Kasas-Lazetic, K. The AMB 8057 utilization for SEMONT’s EMF monitoring in a closed room. In Proceedings of the 24th Telecommunications Forum (TELFOR), Belgrade, Serbia, 22–23 November 2016. [Google Scholar]
- Djuric, N.; Kavecan, N.; Kljajic, D.; Mijatovic, G.; Djuric, S. Data Acquisition in Narda’s Wireless Stations based EMF RATEL Monitoring Network. In Proceedings of the 2019 International Conference on Sensing and Instrumentation in IoT Era (ISSI), Lisbon, Portugal, 29–30 August 2019. [Google Scholar]
- Djuric, N.; Kavecan, N.; Radosavljevic, N.; Djuric, S. The Wideband Approach of 5G EMF Monitoring. In Proceedings of the 12th EAI International Conference (AFRICOMM 2020), Ebène City, Mauritius, 2–4 December 2020. [Google Scholar]
- Jadhav, A.V.; Patil, A.P.; Ajwilkar, P.G.; Nadkarni, R.N.; Bhise, S. Continuous RF monitoring. In Proceedings of the 2nd International Conference on Applied and Theoretical Computing and Communication Technology (iCATccT), Bangalore, India, 21–23 July 2016. [Google Scholar]
- Carciofi, C.; Garzia, A.; Valbonesi, S.; Gandolfo, A.; Franchelli, R. RF electromagnetic field levels extensive geographical monitoring in 5G scenarios: Dynamic and standard measurements comparison. In Proceedings of the 2020 International Conference on Technology and Entrepreneurship (ICTE), Bologna, Italy, 21–23 September 2020. [Google Scholar]
- Wang, S.; Chikha, W.B.; Zhang, Y.; Liu, J.; Conil, E.; Jawad, O.; Ourak, L.; Wiart, J. RF Electromagnetic Fields Exposure Monitoring using Drive Test and Sensors in a French City. In Proceedings of the XXXVth General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS), Sapporo, Japan, 19–26 August 2023. [Google Scholar]
- Lee, A.K.; Jeon, S.; Wang, S.; Wiart, J.; Choi, H.D.; Moon, J.I. Population Density and DL EMF Exposure Levels by Region in Korea. In Proceedings of the 2024 IEEE Asia-Pacific Microwave Conference (APMC), Bali, Indonesia, 17–20 November 2024. [Google Scholar]
- Liu, S.; Tobita, K.; Onishi, T.; Taki, M.; Watanabe, S. Electromagnetic field exposure monitoring of commercial 28-GHz band 5G base stations in Tokyo. Bioelectromagnetics 2024, 45, 281–292. [Google Scholar] [CrossRef] [PubMed]
- Dikmen, I.C. Continuous Monitoring and Modeling of High-Frequency EM Pollution Using Cutting-Edge Regression Techniques. IEEE Access 2025, 13, 46627–46637. [Google Scholar] [CrossRef]
- Kiouvrekis, Y.; Psomadakis, I.; Vavouranakis, K.; Zikas, S.; Katis, I.; Tsilikas, I.; Panagiotakopoulos, T.; Filippopoulos, I. Explainable Machine Learning-Based Electric Field Strength Mapping for Urban Environmental Monitoring: A Case Study in Paris Integrating Geographical Features and Explainable AI. Electronics 2025, 14, 254. [Google Scholar] [CrossRef]
- Azaro, R.; Franchelli, R.; Gandolfo, A. Networks of EMF Area Monitor for Distributed Human Exposure Monitoring: Assessment of Performances in Simulated Realistic Scenarios. In Proceedings of the IEEE International Symposium on Measurements & Networking (M&N), Padua, Italy, 18–20 July 2022. [Google Scholar]
- Azaro, R.; Gandolfo, A. On the Electric Field Distribution in Radiated Emission Rod Antenna Test Setups: Numerical Analysis and Experimental Validation. IEEE Trans. Electromagn. Compat. 2020, 62, 1611–1618. [Google Scholar] [CrossRef]
- Crawford, M.L. Generation of Standard EM Fields Using TEM Transmission Cells. IEEE Trans. Electromagn. Compat. 1974, 16, 189–195. [Google Scholar] [CrossRef]
- Groh, C.; Karst, J.P.; Koch, M.; Garbe, H. TEM waveguides for EMC measurements. IEEE Trans. Electromagn. Compat. 1999, 41, 440–445. [Google Scholar] [CrossRef]
- Karst, J.P.; Groh, C.; Garbe, H. Calculable field generation using TEM cells applied to the calibration of a novel E-field probe. IEEE Trans. Electromagn. Compat. 2002, 44, 59–71. [Google Scholar] [CrossRef]
- Macnamara, T.M. Handbook of Antennas for EMC, 2nd ed.; Artech House: Norwood, MA, USA, 2018; pp. 273–334. [Google Scholar]
- Caorsi, S.; Azaro, R. Field Uniformity Measurements in a TEM Cell using the Modulated Scattering Technique. In Proceedings of the International Symposium on Electromagnetic Compatibility EMC 98 ROMA, Rome, Italy, 14–18 September 1998. [Google Scholar]
- Carbonini, L. Comparison of analysis of a WTEM cell with standard TEM cells for generating EM fields. IEEE Trans. Electromagn. Compat. 1993, 35, 255–263. [Google Scholar] [CrossRef]
- Burke, G.J.; Poggio, A.J. Numerical Electromagnetics Code—Method of Moments. Available online: https://apps.dtic.mil/sti/tr/pdf/ADA956129.pdf (accessed on 18 January 2025).
- Poggio, A.J.; Miller, E.K. Integral Equation Solutions of Three-Dimensional Scattering Problems. In Computer Techniques for Electromagnetics; Mittra, R., Ed.; Pergamon Press: New York, NY, USA, 2007; pp. 159–264. [Google Scholar]
- NEC Based Antenna Modeler and Optimizer. Available online: https://www.qsl.net/4nec2/ (accessed on 18 January 2025).
- Harrington, R.F. Field Computation by Moment Methods; MacMillan: New York, NY, USA, 1968. [Google Scholar]
- Ludwig, A. Wire grid modeling of surfaces. IEEE Trans. Antennas Propagat. 1987, 35, 1045–1048. [Google Scholar] [CrossRef]
- Rubinstein, A.; Rachidi, F.; Rubinstein, M. On wire-grid representation of solid metallic surfaces. IEEE Trans. Electromagn. Compat. 2005, 47, 192–195. [Google Scholar] [CrossRef]
- Rubinstein, A.; Rostamzadeh, C.; Rubinstein, M.; Rachidi, F. On the use of the equal area rule for the wire-grid representation of metallic surfaces. In Proceedings of the 7th International Zurich Symposium on Electromagnetic Compatibility, Singapore, 28 February–3 March 2006. [Google Scholar]
- Ramo, S.; Whinnery, J.R.; Van Duzer, T. Fields and Waves in Communication Electronics; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Haus, H.A.; Melcher, J.R. Electromagnetic Fields and Energy; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Higgins, D.F. A Method of Calculating Impedance and Field Distribution of a Multi-Wire Parallel Plate Transmission Line Above a Perfectly Conducting Ground. Air Force Weapons Laboratory, Sensor and Simulation Notes, Note 150, February 1972. Available online: https://summa.unm.edu/notes/SSN/note150.pdf (accessed on 10 April 2025).
- Baum, C.E.; Higgins, D.; Cummings, D.B.; Faulkner, J.E.; Heinberg, M.; Moore, P.; Nelson, E.B.; Price, M.L.; Crewson, W.F.; Naff, J.T. Electromagnetic Design Calculation for ATLAS I, Design 1. Air Force Weapons Laboratory, Sensor and Simulation Notes, Note 153, June 1972. Available online: https://summa.unm.edu/notes/SSN/note153.pdf (accessed on 10 April 2025).
- Neureuther, A.R.; Fuller, B.D.; Hakke, G.D.; Hohmann, G. A Comparison of Numerical Methods for Thin Wire Antennas. In Proceedings of the URSI Meeting, Boston, MA, USA, 10–12 September 1968. [Google Scholar]
- Miller, E.K.; Bevensee, R.M.; Poggio, A.J.; Adams, R.; Deadrick, F.J.; Landt, J.A. An Evaluation of Computer Programs Using Integral Equation for the Electromagnetics Analysis of Thin Wire Structures. Lawrence Livermore Laboratory, Interaction Notes, Note 177, March 1974. Available online: http://ece-research.unm.edu/summa/notes/In/0177.pdf (accessed on 25 February 2025).
- IEC 61000-4-20:2022-11; Electromagnetic Compatibility (EMC)—Part 4–20: Testing and Measurement Techniques—Emission and Immunity Testing in Transverse Electromagnetic (TEM) Waveguides. IEC: Geneva, Switzerland, 2022.



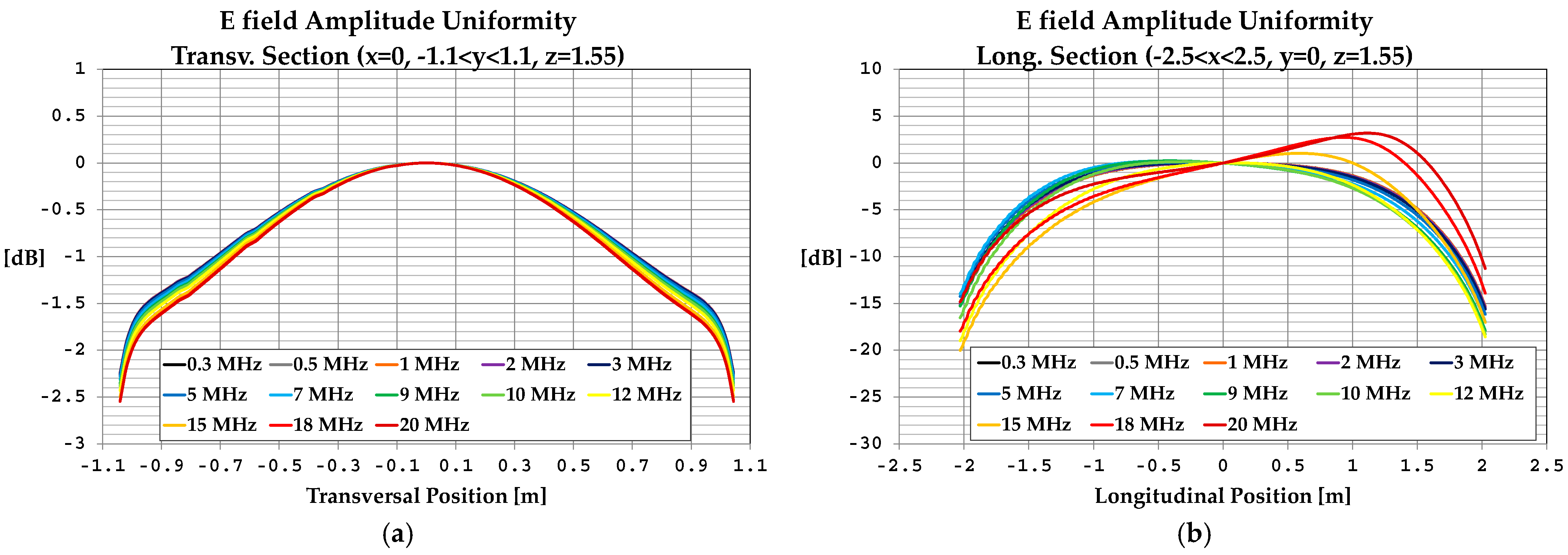
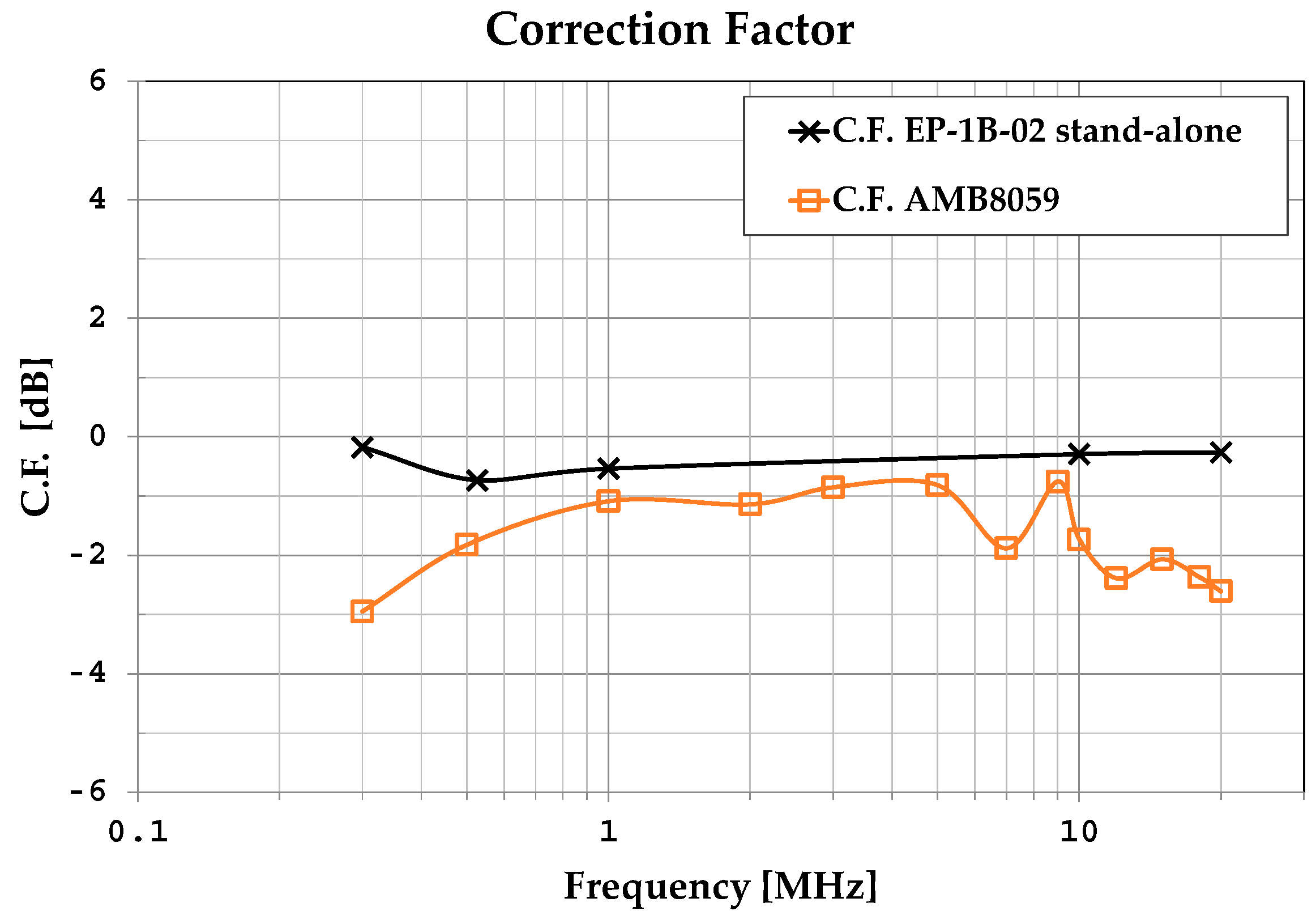
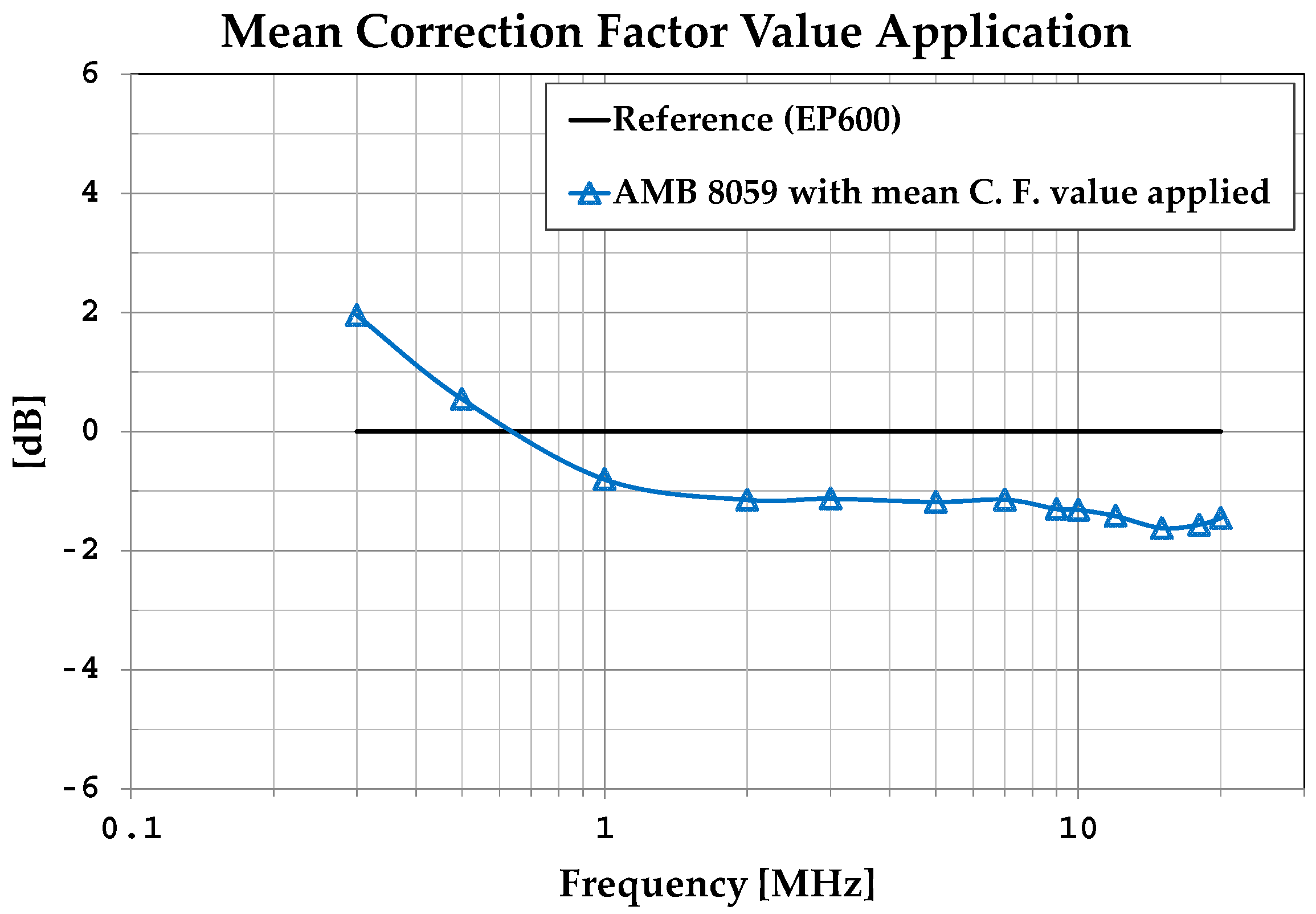
| Equipment | Manufacturer | Model | Characteristics |
|---|---|---|---|
| Shielded Chamber | Beltech | - | Dimensions: 6.1 × 4.9 × 3.6 m |
| MWTEM | Comtest | - | 7 + 7 wires balanced transm. line, 4.5 × 2.3 × 1.5 m, Z0 = 200 Ω, fmax = 20 MHz |
| MWTEM Balun | Comtest | - | Impedances levels: 50 Ω /200 Ω |
| MWTEM Load | Comtest | - | Impedance: 200 Ω (nominal value) |
| RF Signal Generator | Hewlett Packard | E4400B | Freq. band: 250 kHz–1 GHz |
| Power Amplifier | Amplifier Research | 75A250 | Freq. band: 10 kHz–250 MHz, Pmax = 75 W |
| Digital Oscilloscope | Yokogawa | DL1620 | fmax = 200 MHz |
| High Voltage Diff. Probe | Sapphire Instruments | SI-9010 | Vmax = ±7000 V, fmax = 70 MHz |
| Electric Field Probe | Narda STS | EP600 | Freq. band: 100 kHz–9.25 GHz, 0.14–140 V/m |
| Network Analyzer | Agilent | E5061B | Freq. band: 5 Hz–3 GHz |
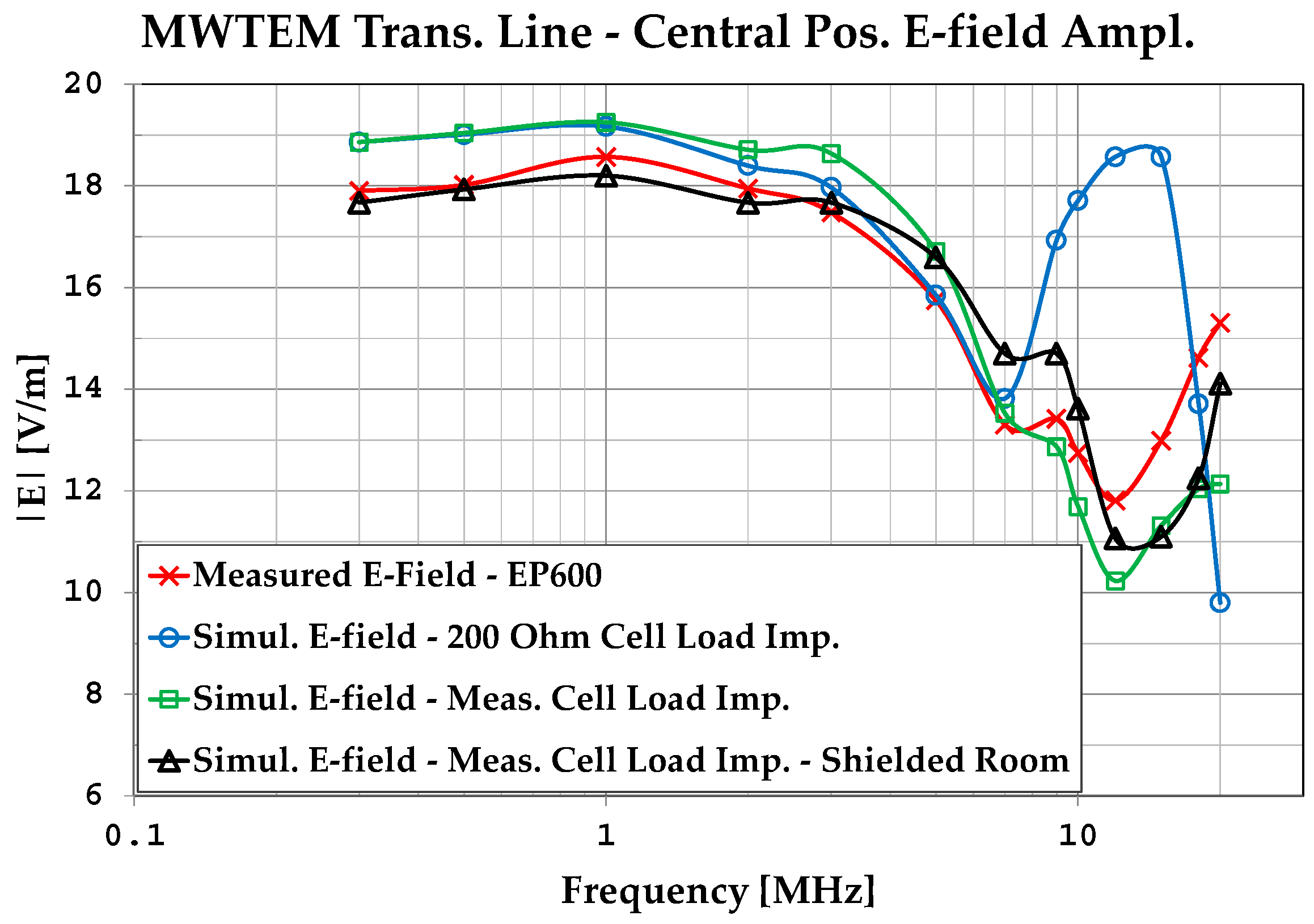
| Freq. [MHz] | Applied Voltage [Vp-p] | EP600 Meas. [V/m] | calc. 1 [V/m] | Simul. (Znom = 200 Ω) [V/m] |
|---|---|---|---|---|
| 0.3 | 162.5 | 17.93 | 24.52 | 18.86 |
| 0.5 | 162.5 | 18.02 | 24.74 | 19.01 |
| 1 | 164.5 | 18.57 | 24.91 | 19.17 |
| 2 | 158.3 | 17.95 | 23.83 | 18.40 |
| 3 | 153.1 | 17.48 | 23.18 | 17.97 |
| 5 | 133.3 | 15.75 | 20.17 | 15.85 |
| 7 | 113.3 | 13.30 | 17.37 | 13.82 |
| 9 | 139.5 | 13.42 | 21.25 | 16.93 |
| 10 | 145.8 | 12.75 | 22.37 | 17.71 |
| 12 | 160.4 | 11.81 | 24.26 | 18.57 |
| 15 | 176.1 | 12.99 | 26.81 | 18.58 |
| 18 | 150.0 | 14.62 | 22.50 | 13.71 |
| 20 | 114.5 | 15.31 | 17.37 | 9.80 |
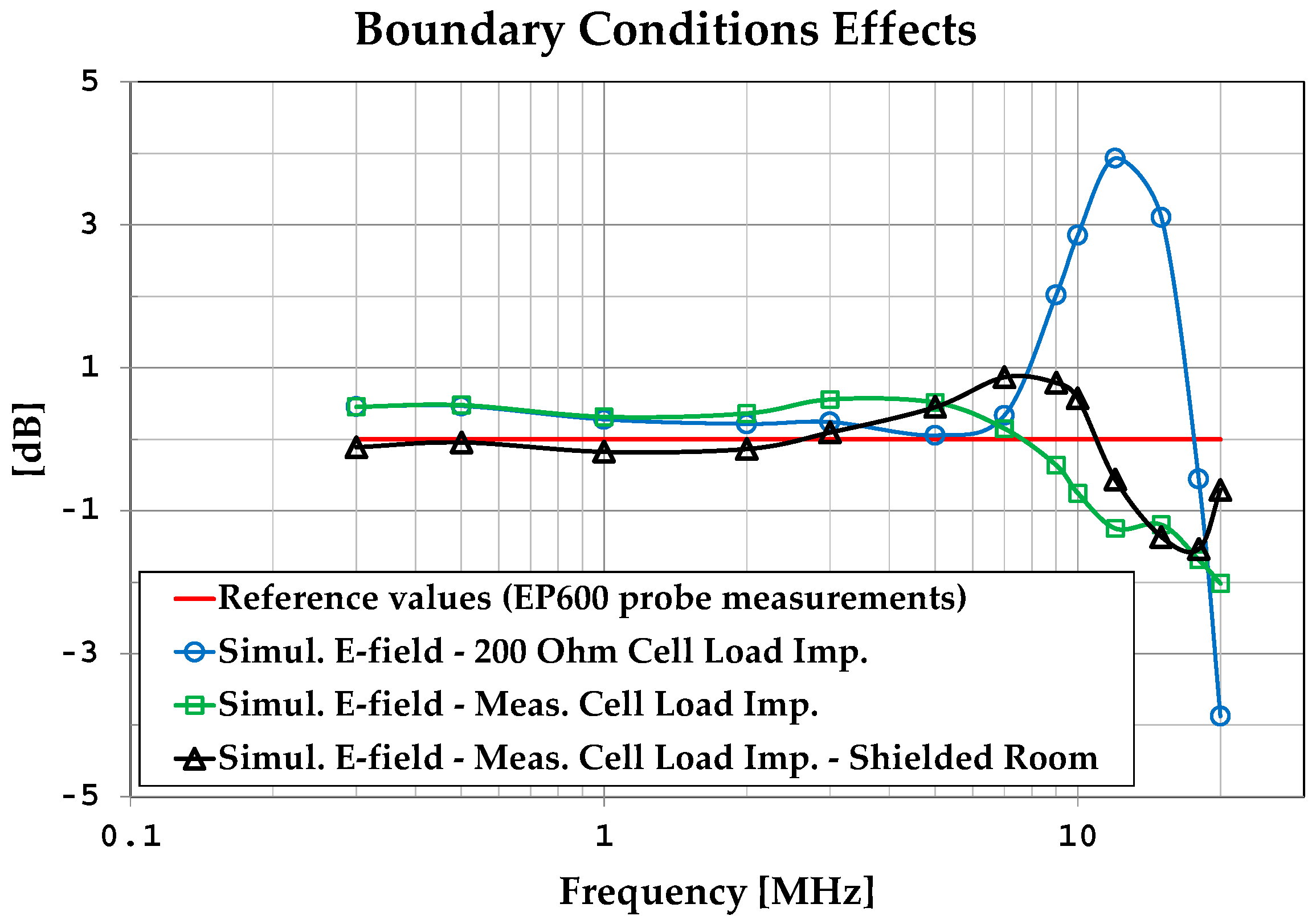
| Freq. [MHz] | Zmeas. [Ω] | Simul. [V/m] | Simul. (with Shield) [V/m] |
|---|---|---|---|
| 0.3 | 201-j5 | 18.86 | 17.67 |
| 0.5 | 201-j8 | 19.04 | 17.93 |
| 1 | 200-j15 | 19.25 | 18.20 |
| 2 | 196-j30 | 18.71 | 17.63 |
| 3 | 189-j43 | 18.64 | 17.67 |
| 5 | 171-j58 | 16.71 | 16.59 |
| 7 | 153-j72 | 13.53 | 14.70 |
| 9 | 133-j79 | 12.87 | 14.74 |
| 10 | 124-j80 | 11.69 | 13.62 |
| 12 | 107-j80 | 10.23 | 11.07 |
| 15 | 86-j74 | 11.32 | 11.10 |
| 18 | 68-j64 | 12.04 | 12.25 |
| 20 | 58-j51 | 12.14 | 14.11 |
| NEC Model | Number of Segments | Simulation Time 1 [s] |
|---|---|---|
| MWTEM in free space | 2100 | 30 |
| MWTEM inside shielded chamber | 9062 | 1743 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azaro, R.; Franchelli, R.; Gandolfo, A. Performance Evaluation and Calibration of Electromagnetic Field (EMF) Area Monitors Using a Multi-Wire Transverse Electromagnetic (MWTEM) Transmission Line. Sensors 2025, 25, 2920. https://doi.org/10.3390/s25092920
Azaro R, Franchelli R, Gandolfo A. Performance Evaluation and Calibration of Electromagnetic Field (EMF) Area Monitors Using a Multi-Wire Transverse Electromagnetic (MWTEM) Transmission Line. Sensors. 2025; 25(9):2920. https://doi.org/10.3390/s25092920
Chicago/Turabian StyleAzaro, Renzo, Roberto Franchelli, and Alessandro Gandolfo. 2025. "Performance Evaluation and Calibration of Electromagnetic Field (EMF) Area Monitors Using a Multi-Wire Transverse Electromagnetic (MWTEM) Transmission Line" Sensors 25, no. 9: 2920. https://doi.org/10.3390/s25092920
APA StyleAzaro, R., Franchelli, R., & Gandolfo, A. (2025). Performance Evaluation and Calibration of Electromagnetic Field (EMF) Area Monitors Using a Multi-Wire Transverse Electromagnetic (MWTEM) Transmission Line. Sensors, 25(9), 2920. https://doi.org/10.3390/s25092920







