Leaky Wave Generation Through a Phased-Patch Array
Abstract
1. Introduction
Phased Array
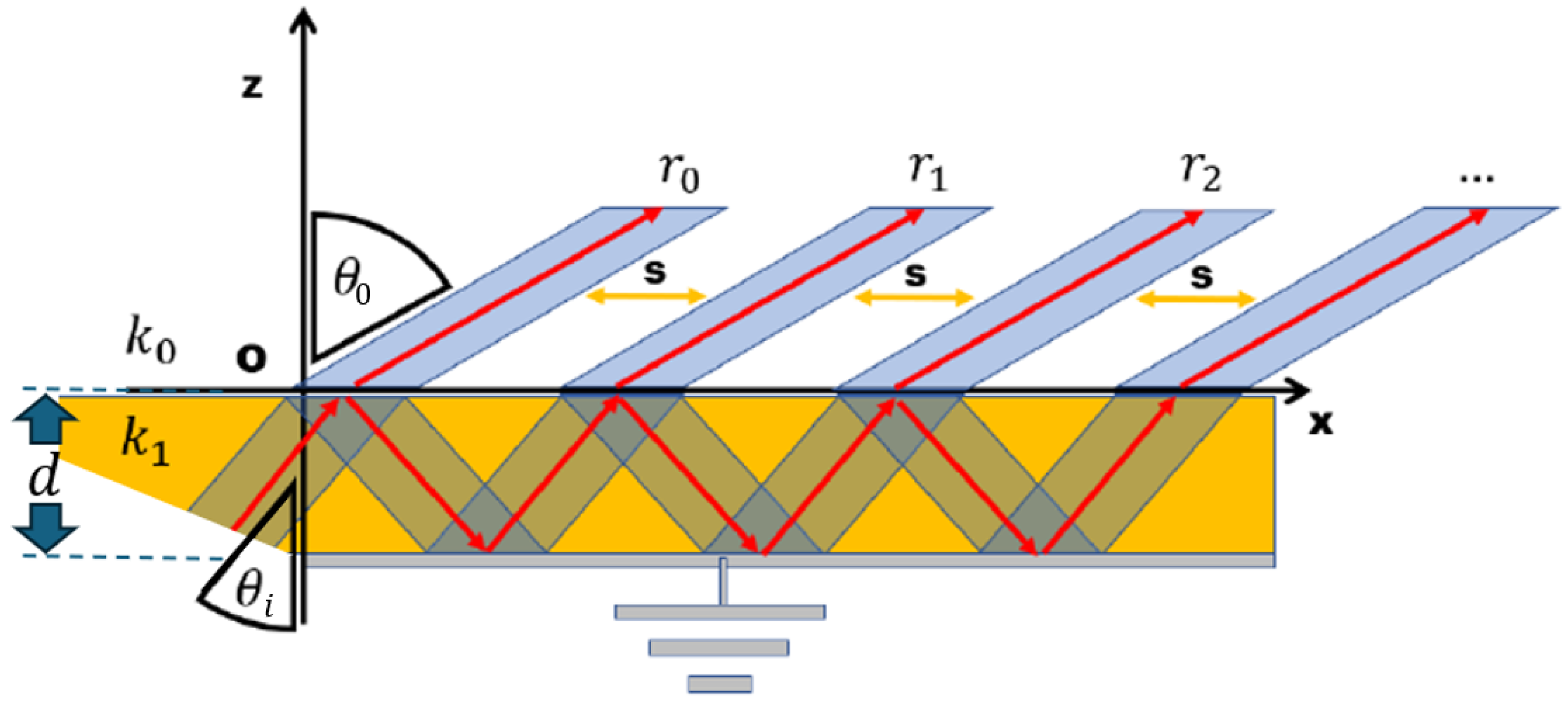
2. Materials and Methods
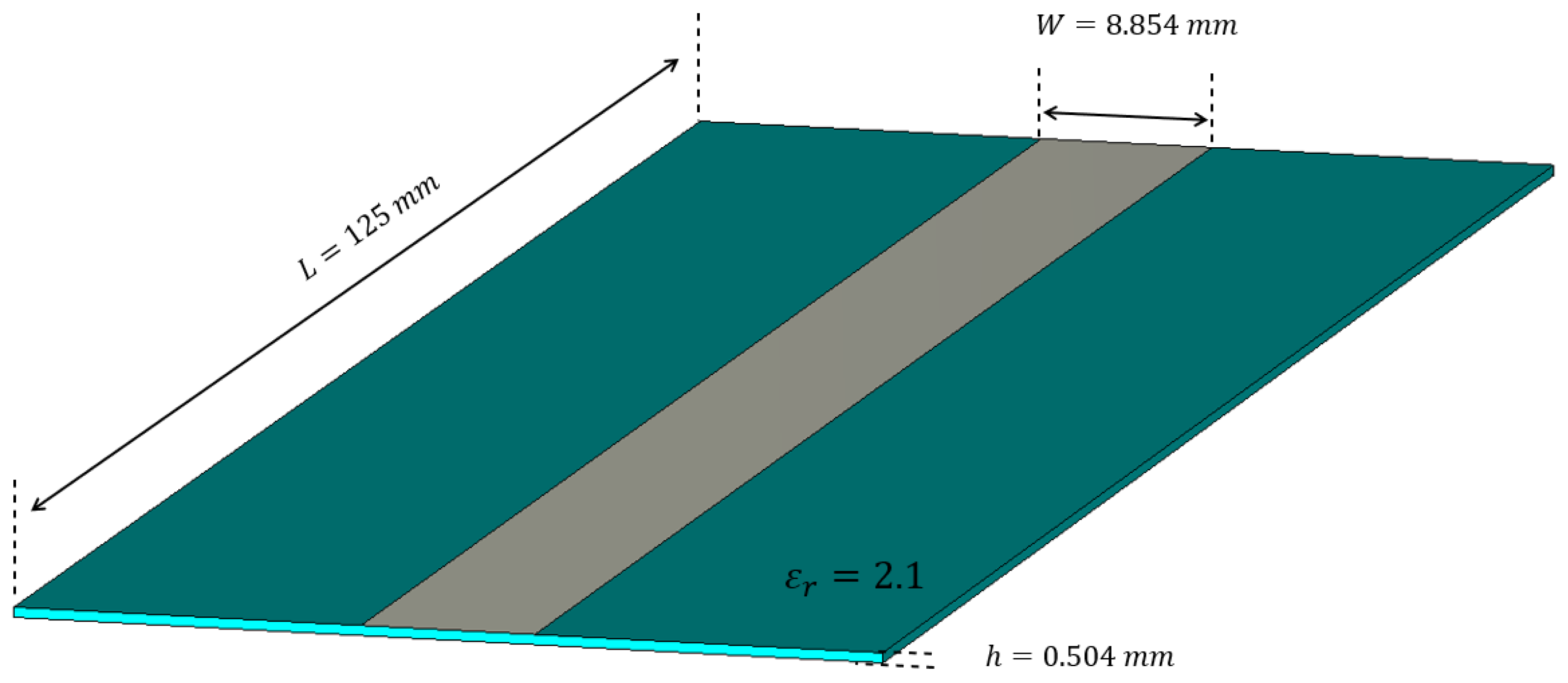
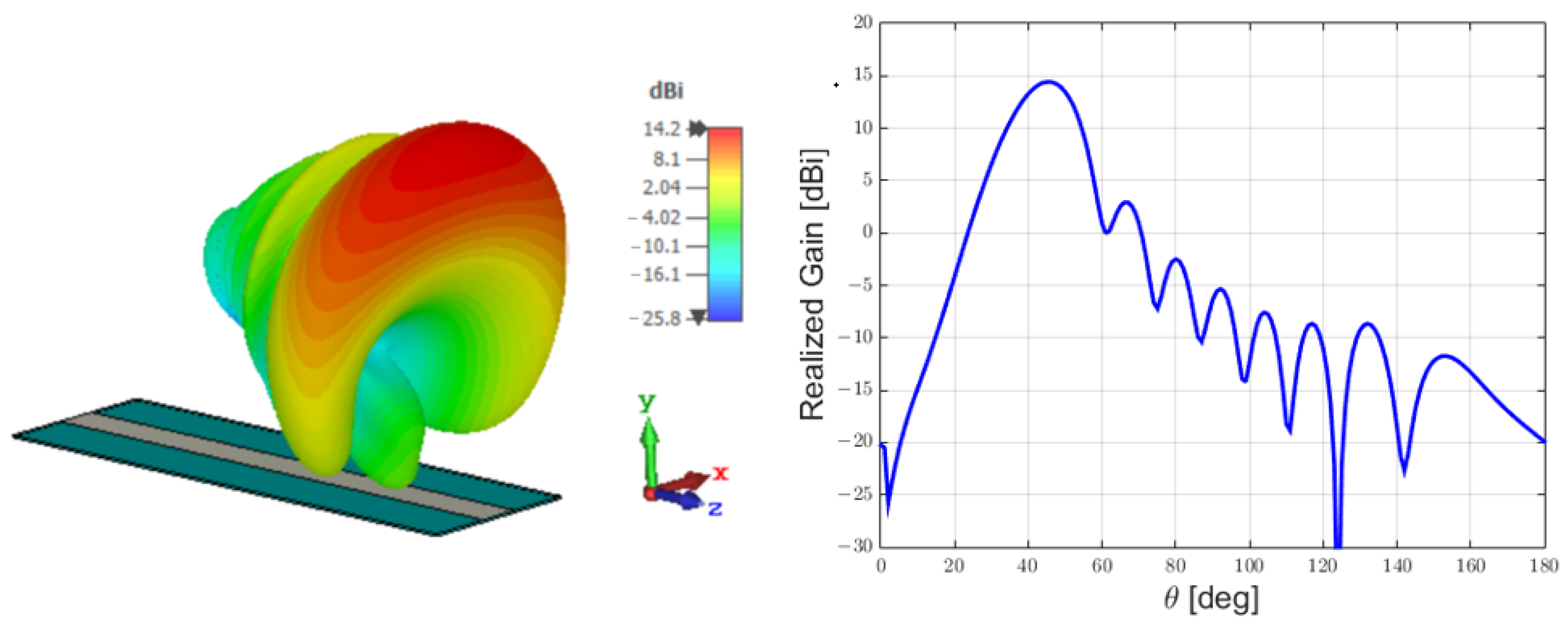
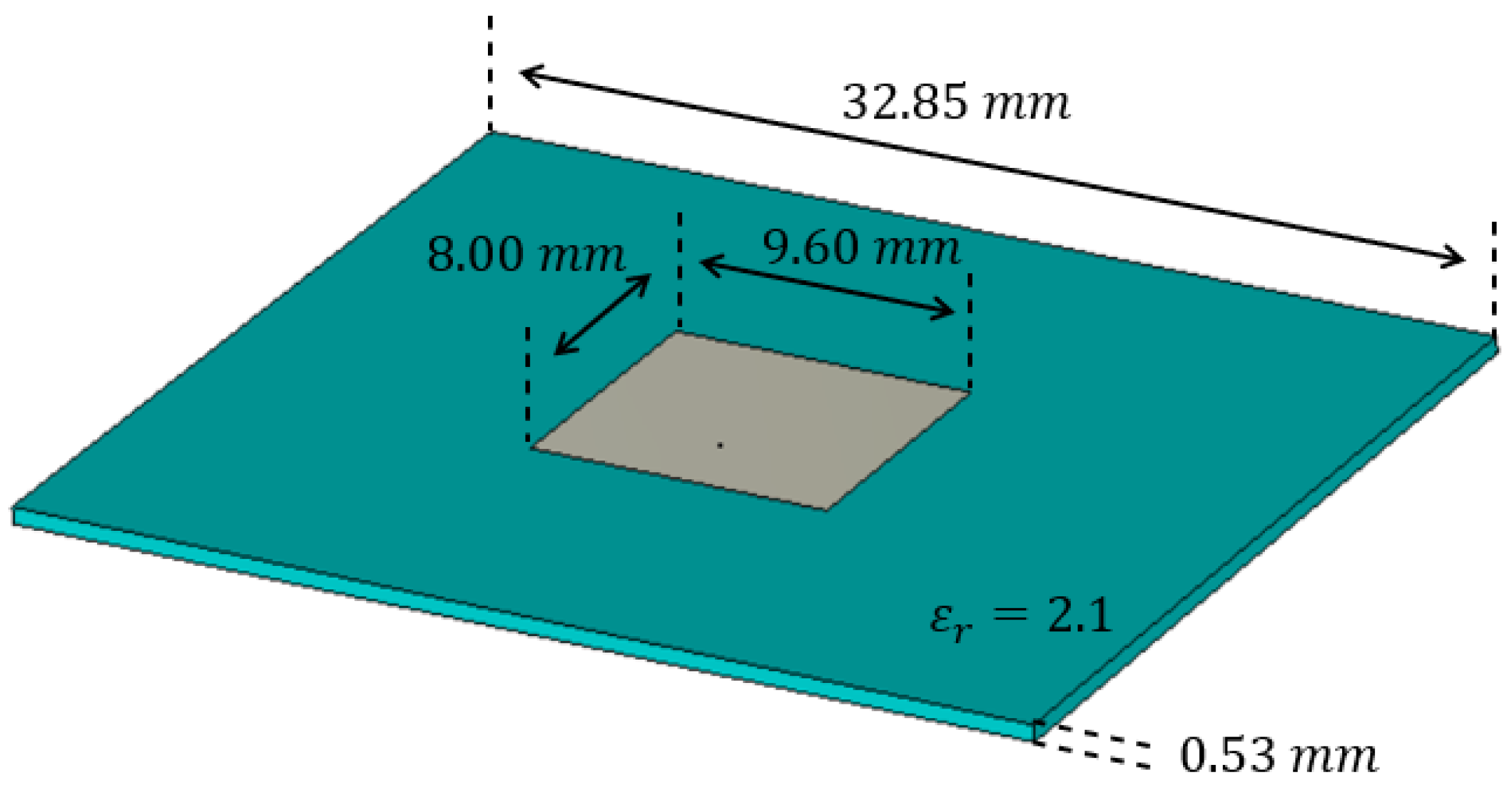
2.1. The Menzel Antenna Operating at 12 GHz
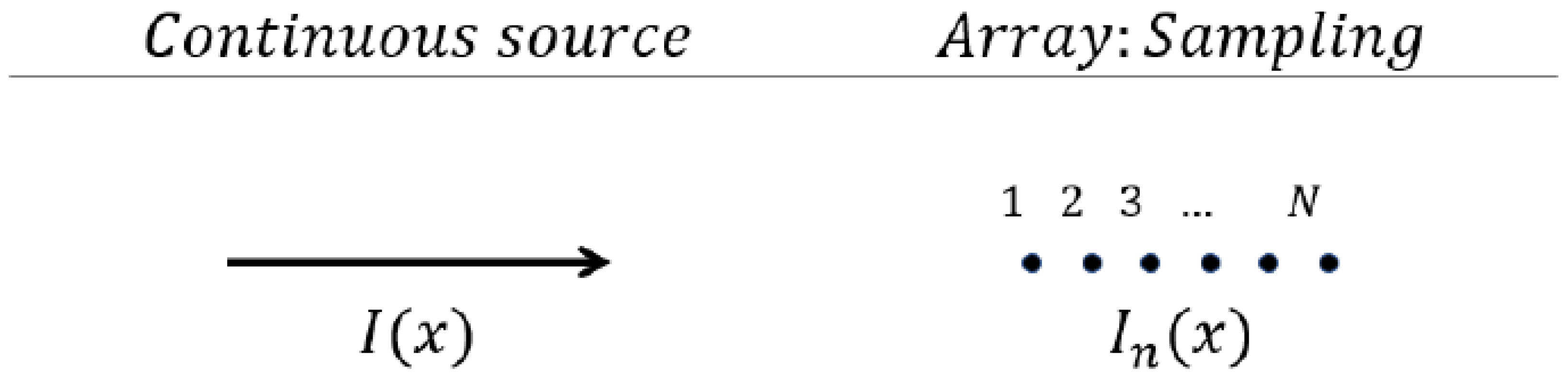
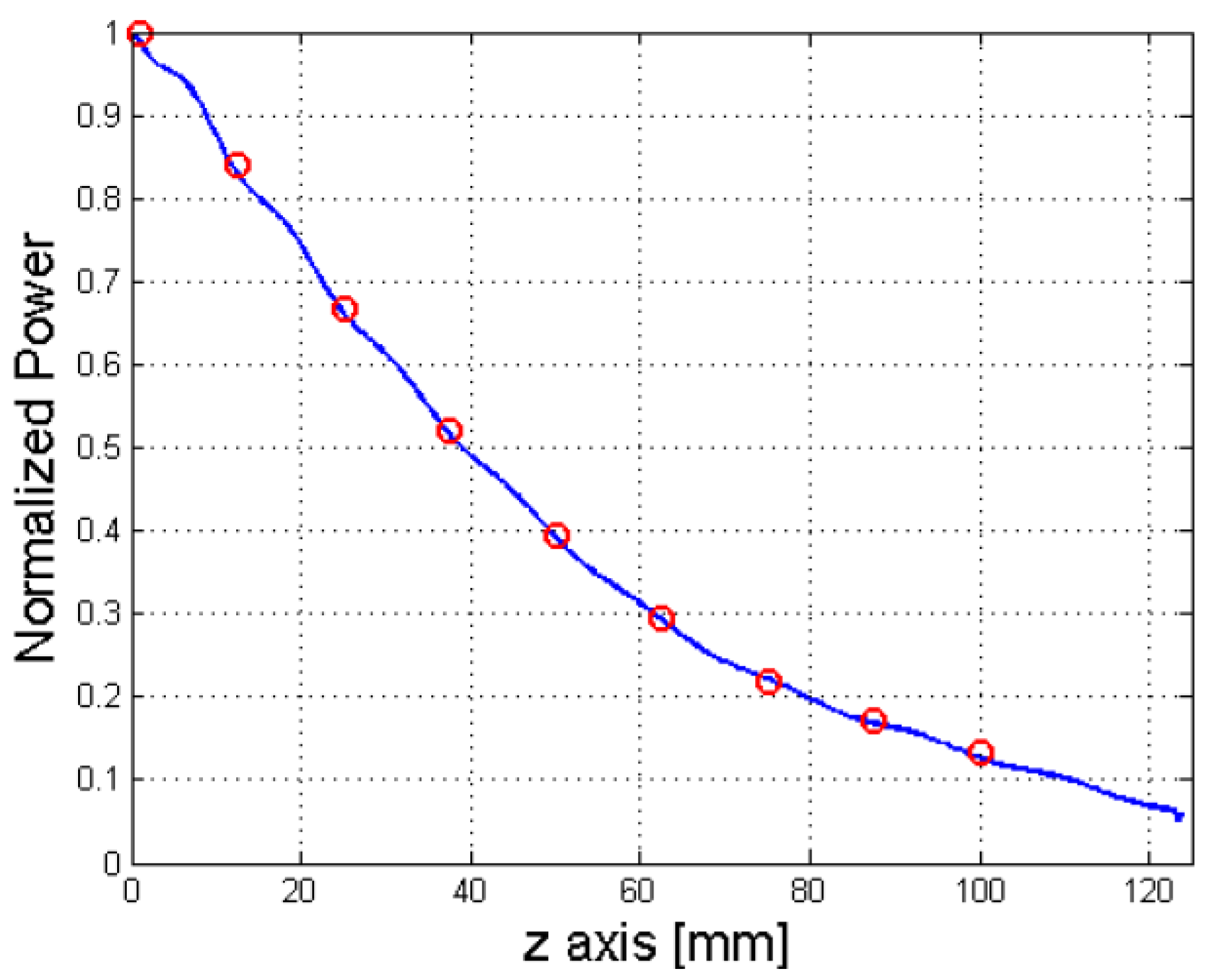
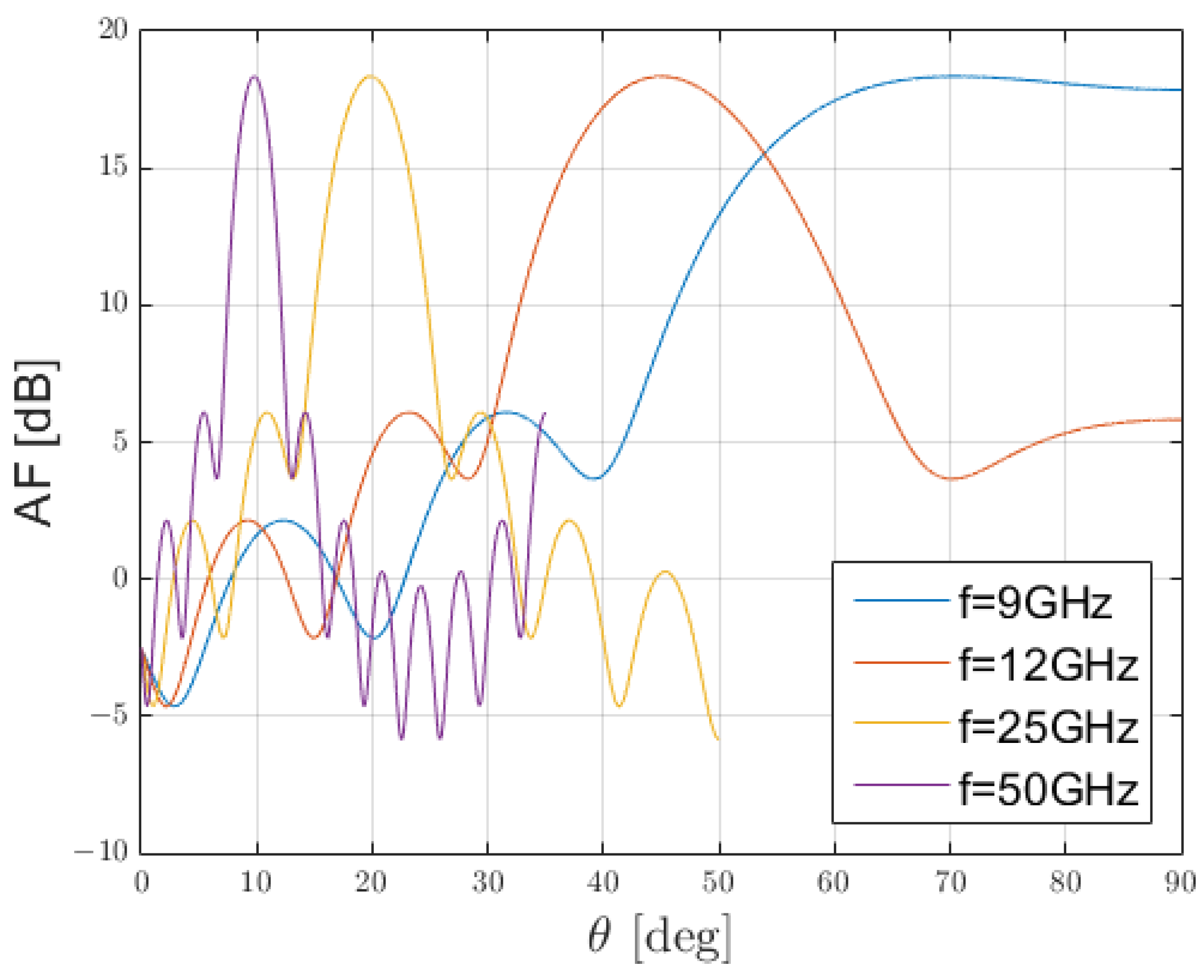
2.2. The Sampling Methodology
2.3. Analysis of an Antenna Operating at 2.4 GHz
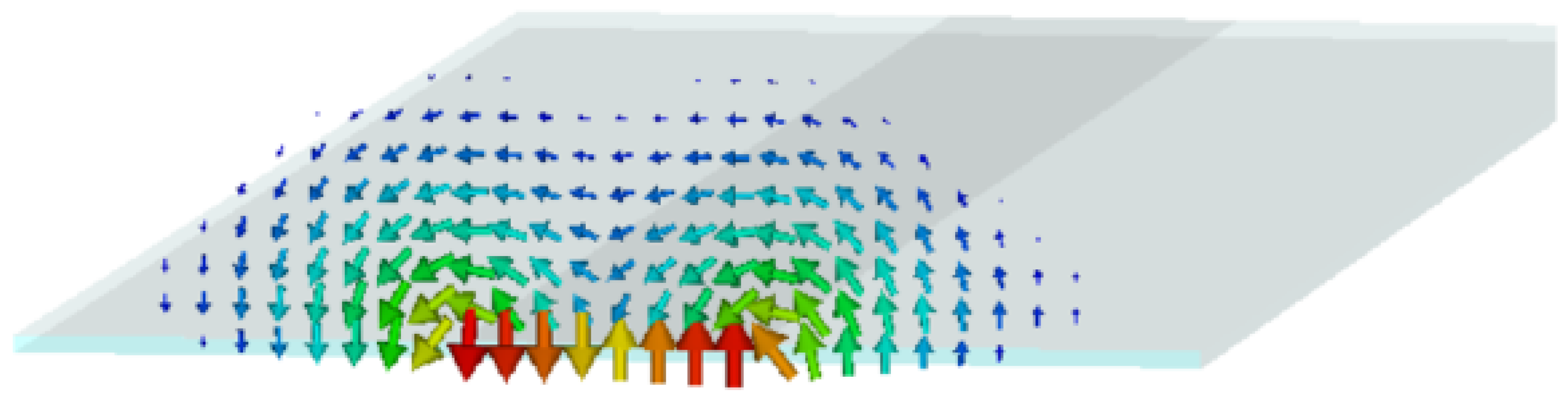
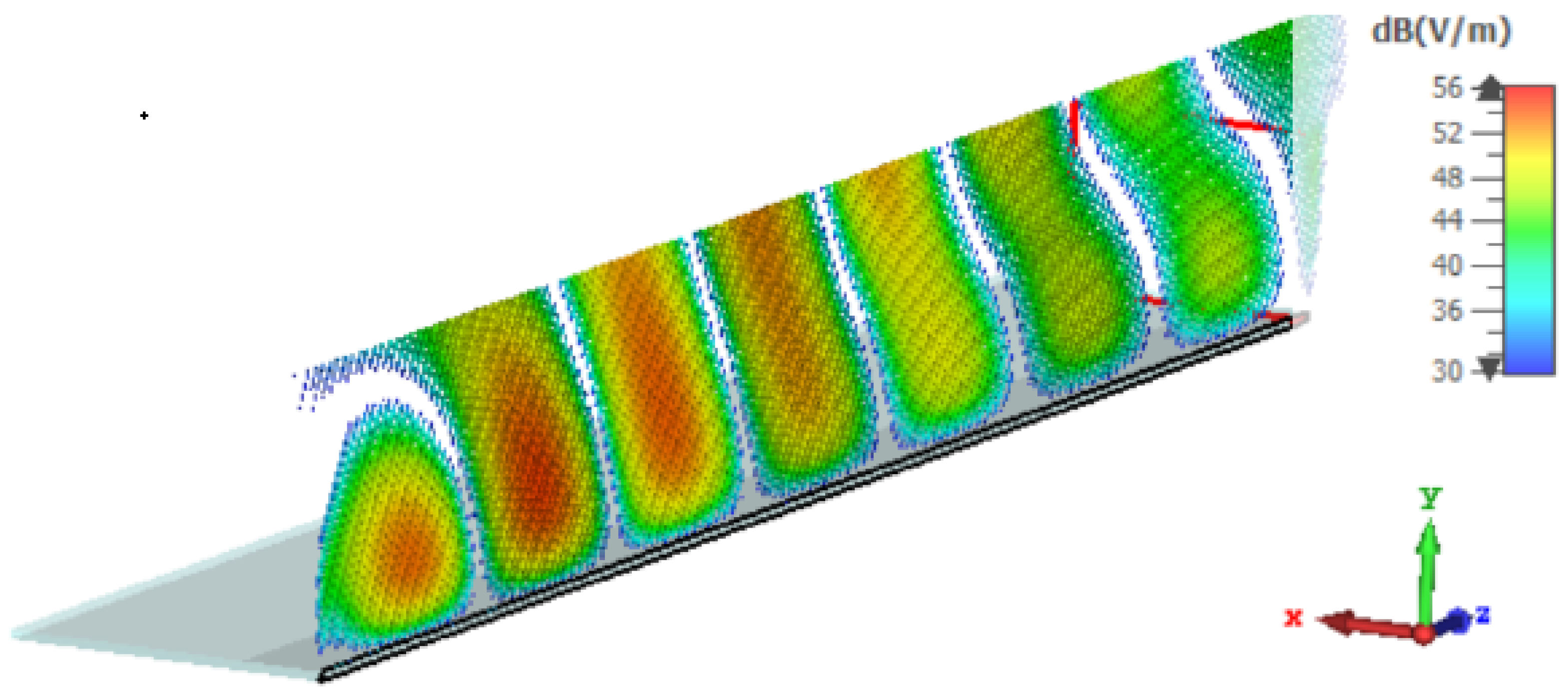
3. Results
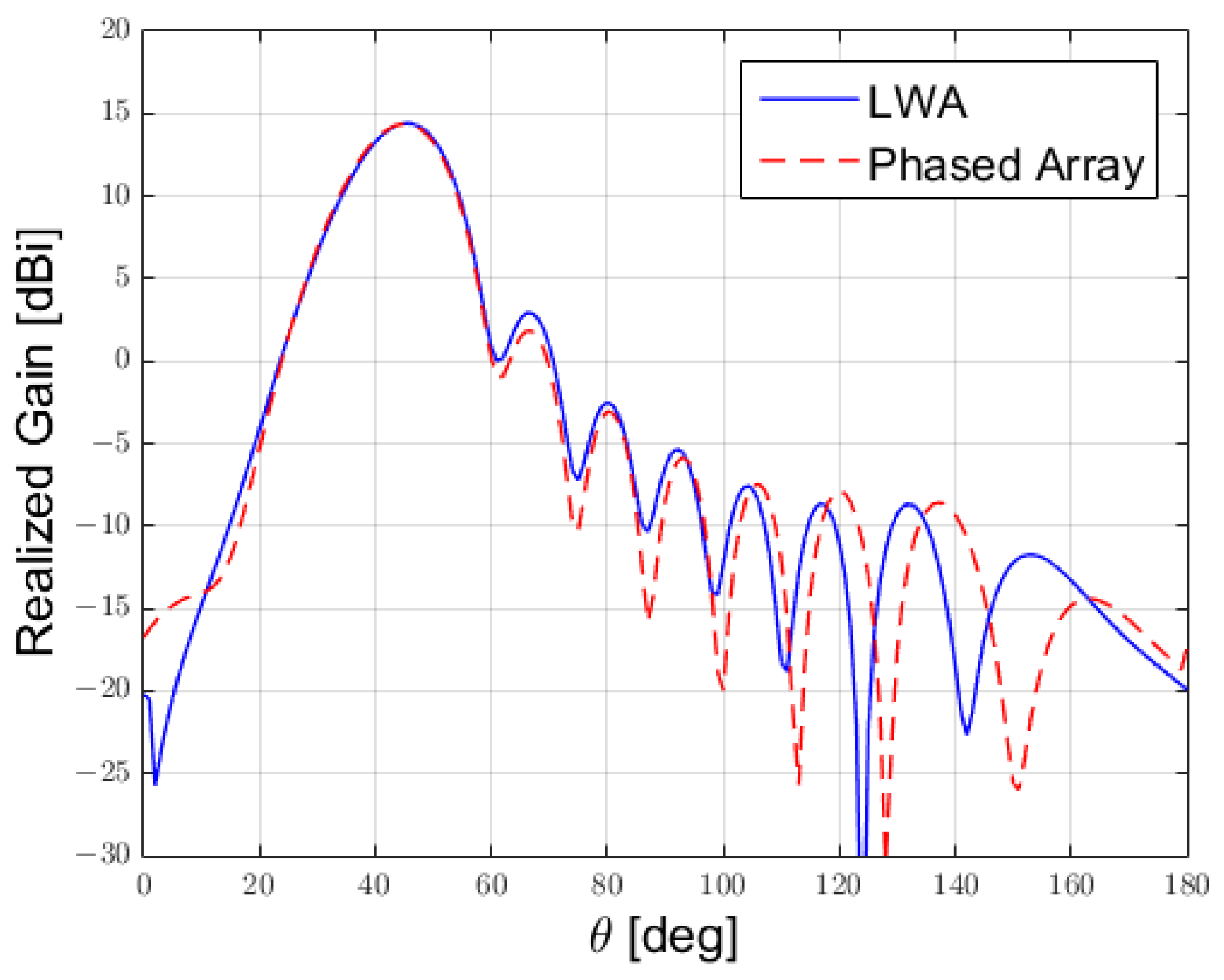
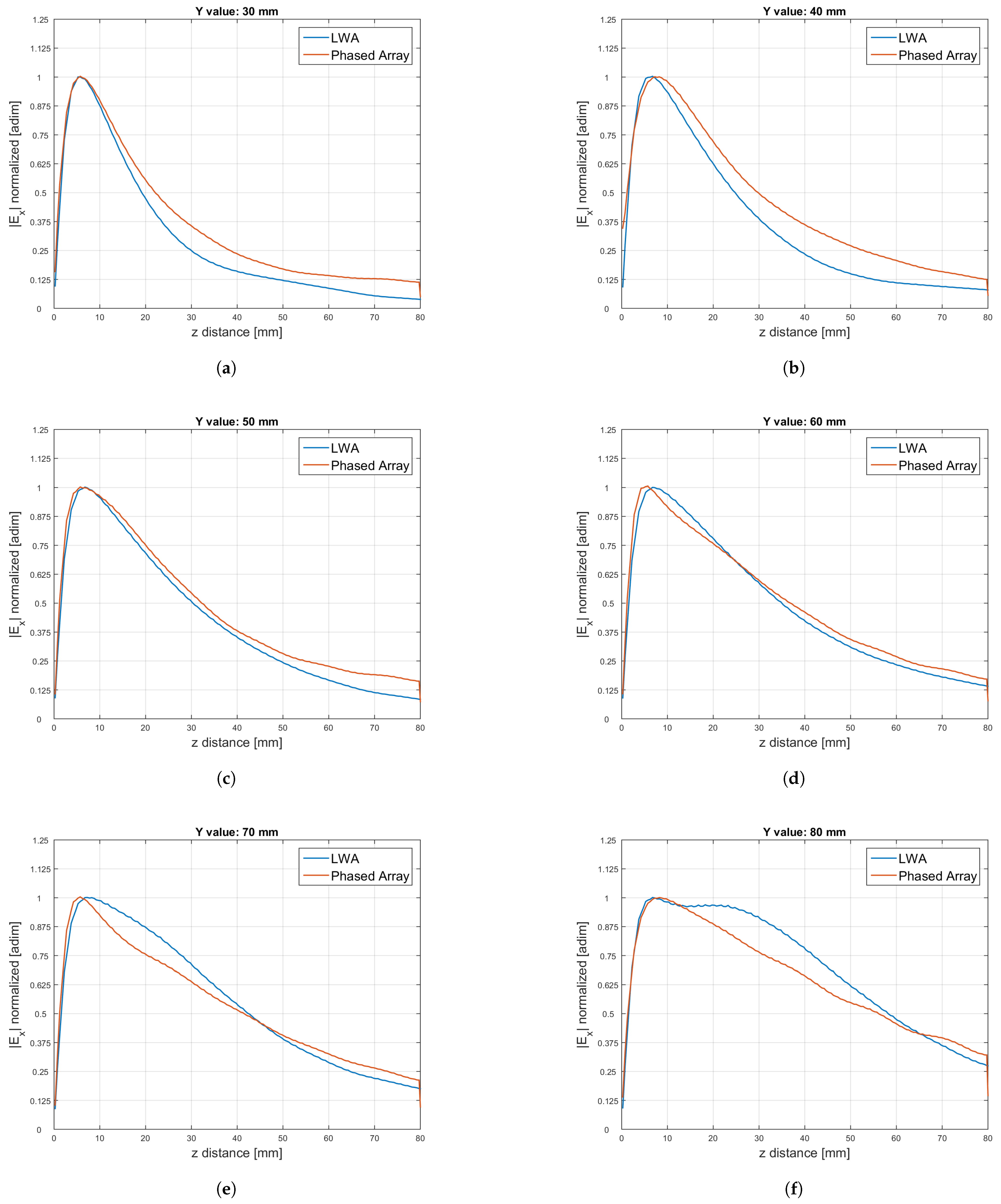
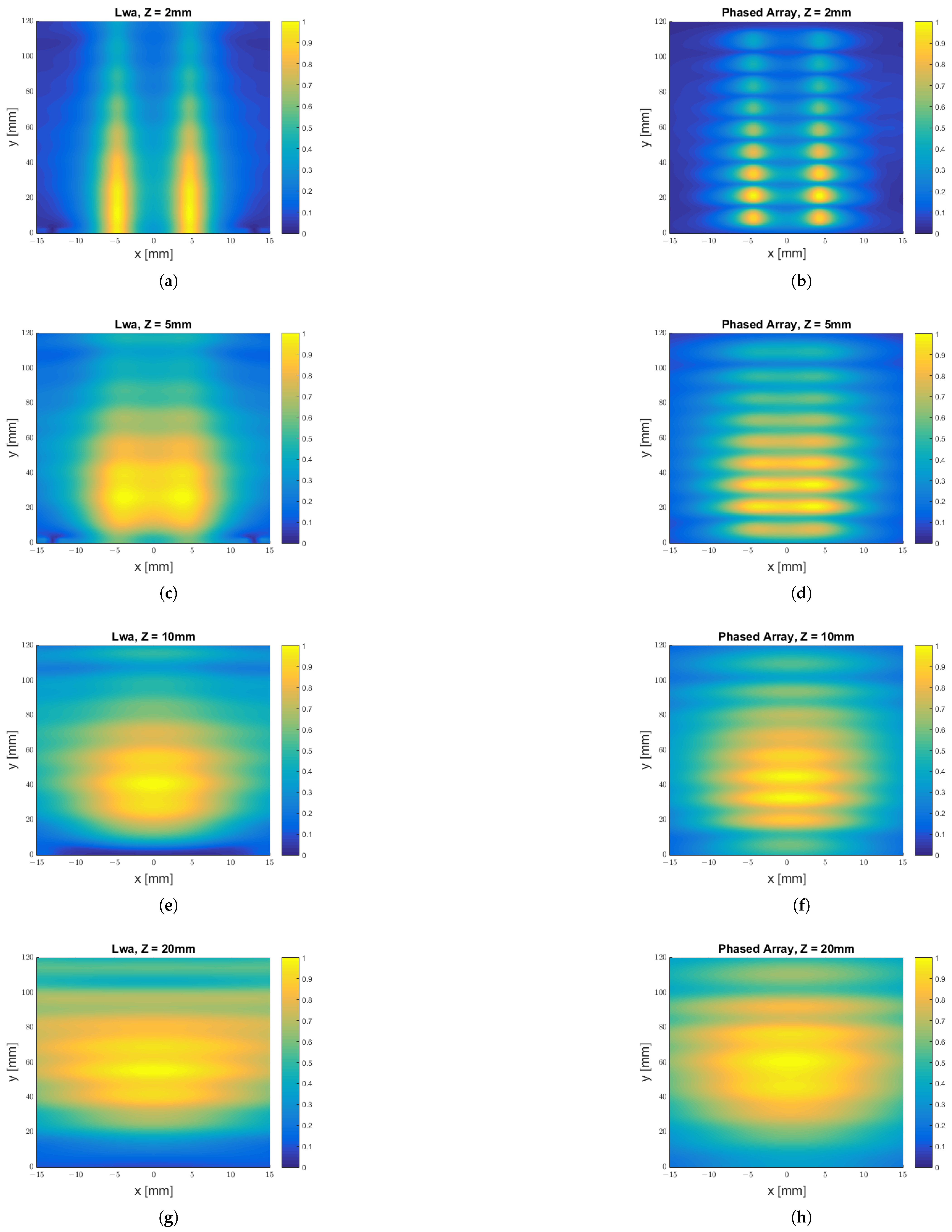
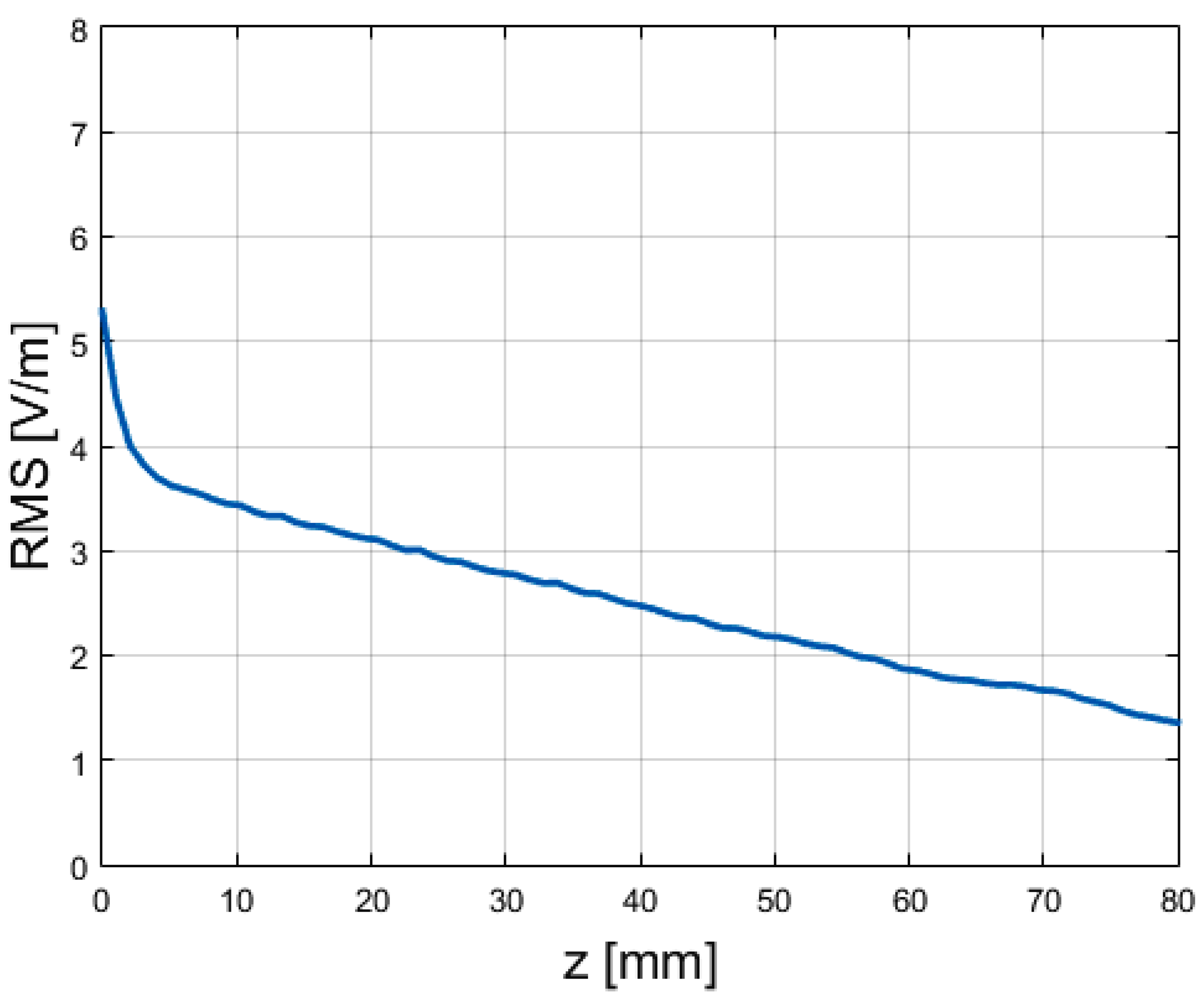
3.1. Comparison Between the Antennas Operating at 12 GHz
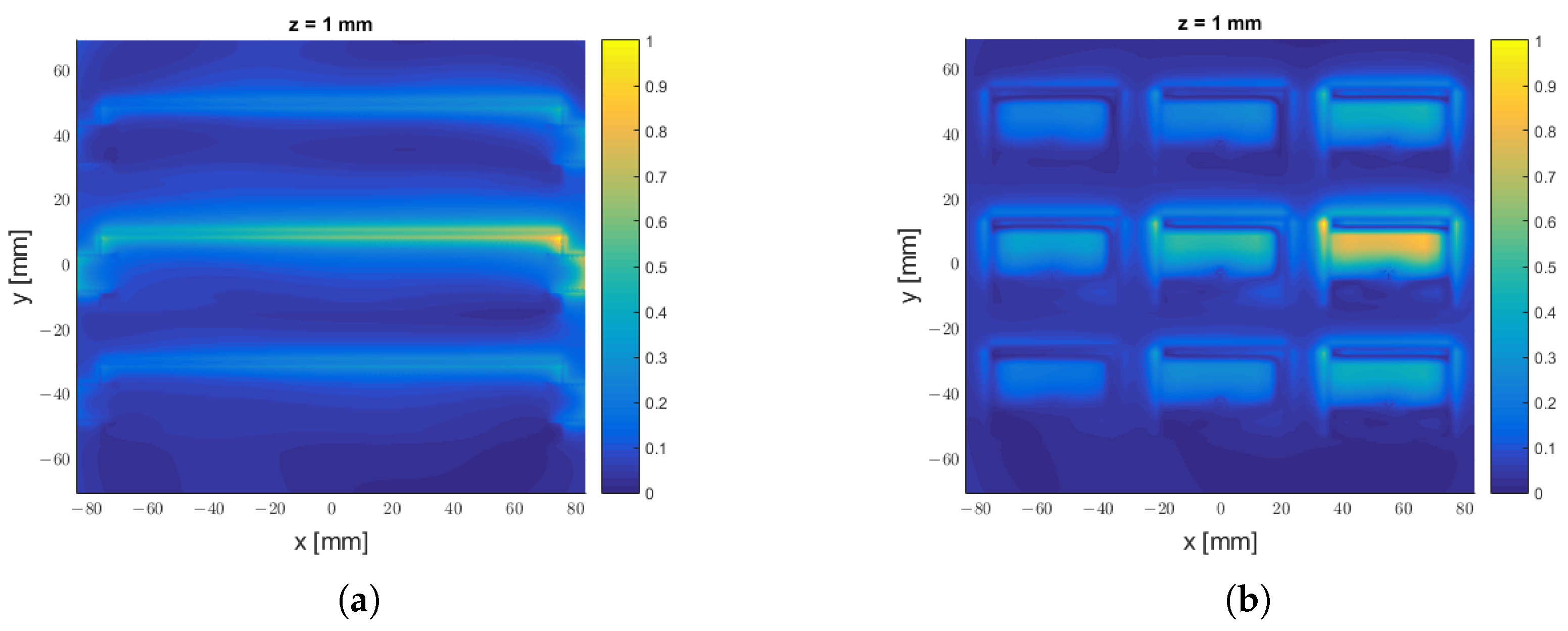
3.2. Comparison Between the Antennas Operating at 2.4 GHz
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LWA | leaky-wave antenna |
| EM | electromagnetic |
| RMS | root mean square |
References
- Baccarelli, P.; Frezza, F.; Simeoni, P.; Tedeschi, N. An Analytical Study of Electromagnetic Deep Penetration Conditions and Implications in Lossy Media through Inhomogeneous Waves. Materials 2018, 11, 1595. [Google Scholar] [CrossRef] [PubMed]
- Zenneck, J. Über die Fortpflanzung ebener elektromagnetischer Wellen längs einer ebenen Leiterfläche und ihre Beziehung zur drahtlosen Telegraphie. Ann. der Phys. 1907, 328, 846–866. [Google Scholar] [CrossRef]
- Frezza, F.; Tedeschi, N. Electromagnetic inhomogeneous waves at planar boundaries: Tutorial. J. Opt. Soc. Am. A 2015, 32, 1485–1501. [Google Scholar] [CrossRef] [PubMed]
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Elliott, R. On discretizing continuous aperture distributions. IEEE Trans. Antennas Propag. 1977, 25, 617–621. [Google Scholar] [CrossRef]
- Hodges, R.E.; Rahmat-Samii, Y. On sampling continuous aperture distributions for discrete planar arrays. IEEE Trans. Antennas Propag. 1996, 44, 1499–1508. [Google Scholar] [CrossRef]
- Calcaterra, A.; Simeoni, P.; Migliore, M.D.; Mangini, F.; Frezza, F. Optimized Leaky-Wave Antenna for Hyperthermia in Biological Tissue Theoretical Model. Sensors 2023, 23, 8923. [Google Scholar] [CrossRef] [PubMed]
- Monticone, F.; Alu, A. Leaky-wave theory, techniques, and applications: From microwaves to visible frequencies. Proc. IEEE 2015, 103, 793–821. [Google Scholar] [CrossRef]
- Oliner, A.A. Leakage from higher modes on microstrip line with application to antennas. Radio Sci. 1987, 22, 907–912. [Google Scholar] [CrossRef]
- Jackson, D.R.; Caloz, C.; Itoh, T. Leaky-Wave Antennas. Proc. IEEE 2012, 100, 2194–2206. [Google Scholar] [CrossRef]
- Oliner, A.A.; Jackson, D.R.; Volakis, J. Leaky-wave antennas. Antenna Eng. Handb. 2007, 4, 12. [Google Scholar]
- Arya, V.; Garg, T. Leaky Wave Antenna: A Historical Development. Microw. Rev. 2021, 27, 3–16. [Google Scholar]
- Balanis, C.A. Balanis’ Advanced Engineering Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Franceschetti, G. Electromagnetics: Theory, Techniques, and Engineering Paradigms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Fano, R.M.; Adler, R.B.; Chu, L.J. Electromagnetic Energy Transmission and Radiation; The M.I.T. Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Mailloux, R.J. Phased Array Antenna Handbook; Artech House: Norwood, MA, USA, 2017. [Google Scholar]
- Weiland, T. Time domain electromagnetic field computation with finite difference methods. Int. J. Numer. Model. Electron. Netw. Devices Fields 1996, 9, 295–319. [Google Scholar] [CrossRef]
- Bondeson, A.; Rylander, T.; Ingelström, P. Computational Electromagnetics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- CST Studio Suite. CST Microwave Studio (2023); Simulia: Providence, RI, USA, 2023. [Google Scholar]
- MATLAB (R2024b), The MathWorks Inc.: Natick, MA, USA, 2024.
- Microsoft PowerPoint (Version 365); Microsoft Corporation: Redmond, WA, USA, 2024.
- Menzel, W. A new travelling wave antenna in microstrip. In Proceedings of the 8th European Microwave Conference, Paris, France, 4–8 September 1978; pp. 302–306. [Google Scholar]
- Oliner, A.; Lee, K. Microstrip leaky wave strip antennas. In Proceedings of the 1986 Antennas and Propagation Society International Symposium, Philadelphia, PA, USA, 8–13 June 1986; Volume 24, pp. 443–446. [Google Scholar]
- James, J. Handbook of microstrip antennas; Peter Peregrinus Ltd.: London, UK, 1989. [Google Scholar]
- James, J.R.; Hall, P.S.; Wood, C. Microstrip Antenna: Theory and Design; IET: Stevenage, UK, 1981. [Google Scholar]
- Geng, Y.; Wang, J.; Li, Y.; Li, Z.; Chen, M.; Zhang, Z. Leaky-wave antenna array with a power-recycling feeding network for radiation efficiency improvement. IEEE Trans. Antennas Propag. 2017, 65, 2689–2694. [Google Scholar] [CrossRef]
- Poveda-García, M.; Algaba-Brazalez, A.; Cañete-Rebenaque, D.; Gómez-Tornero, J. Series Arrangement Technique for Highly-Directive PCB Leaky-Wave Antennas With Application to RFID UHF Frequency Scanning Systems. IEEE Open J. Antennas Propag. 2024, 5, 1193–1208. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Parsa, A.; Caloz, C. Power-recycling feedback system for maximization of leaky-wave antennas’ radiation efficiency. IEEE Trans. Microw. Theory Tech. 2010, 58, 1641–1650. [Google Scholar] [CrossRef]
- Barthia, P.; Bahl, I. Microstrip Antenna Design Handbook; Artech House: London, UK, 2003. [Google Scholar]
- Gupta, K.C. Microstrip Antenna Design; Artech House: London, UK, 1988. [Google Scholar]
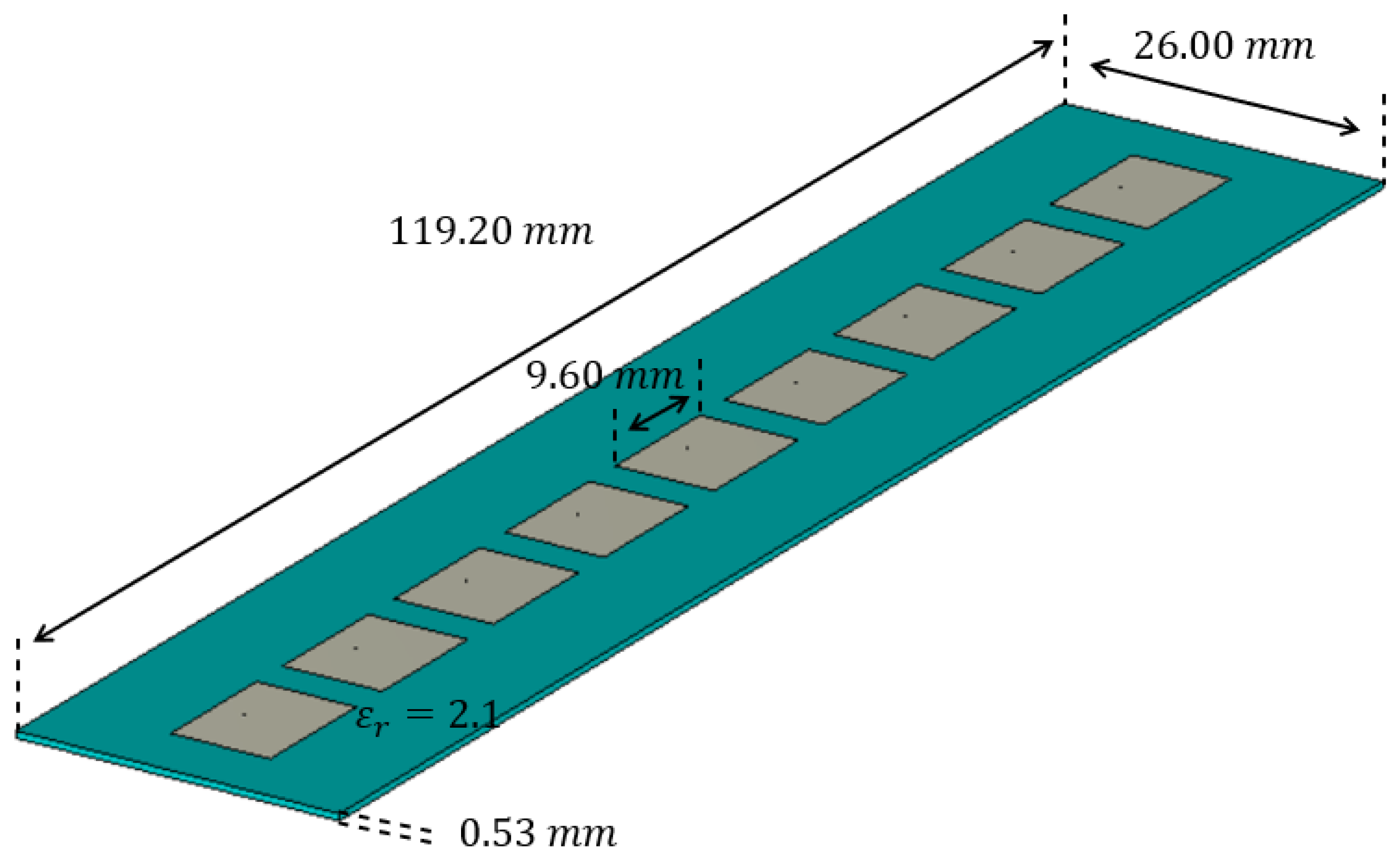
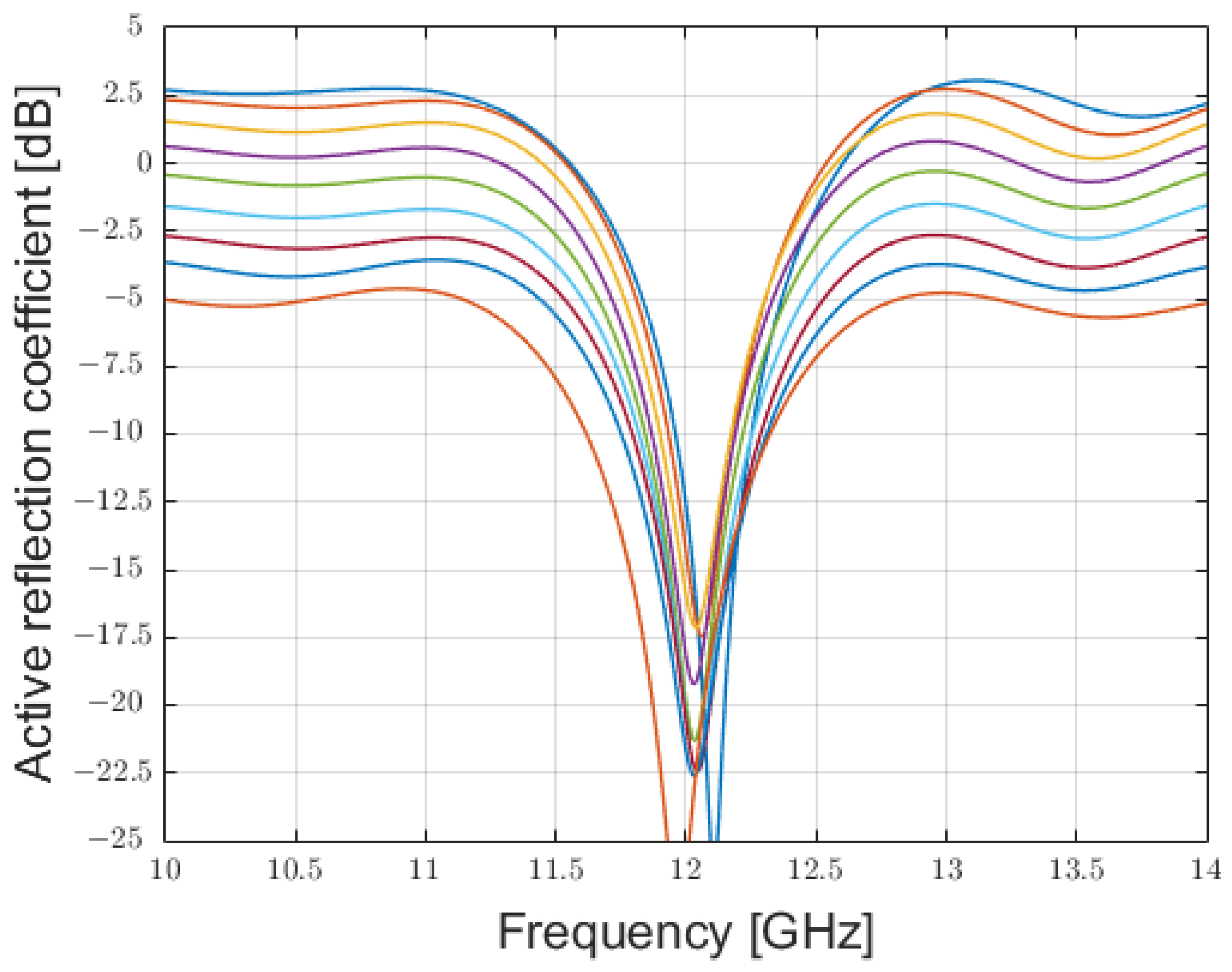
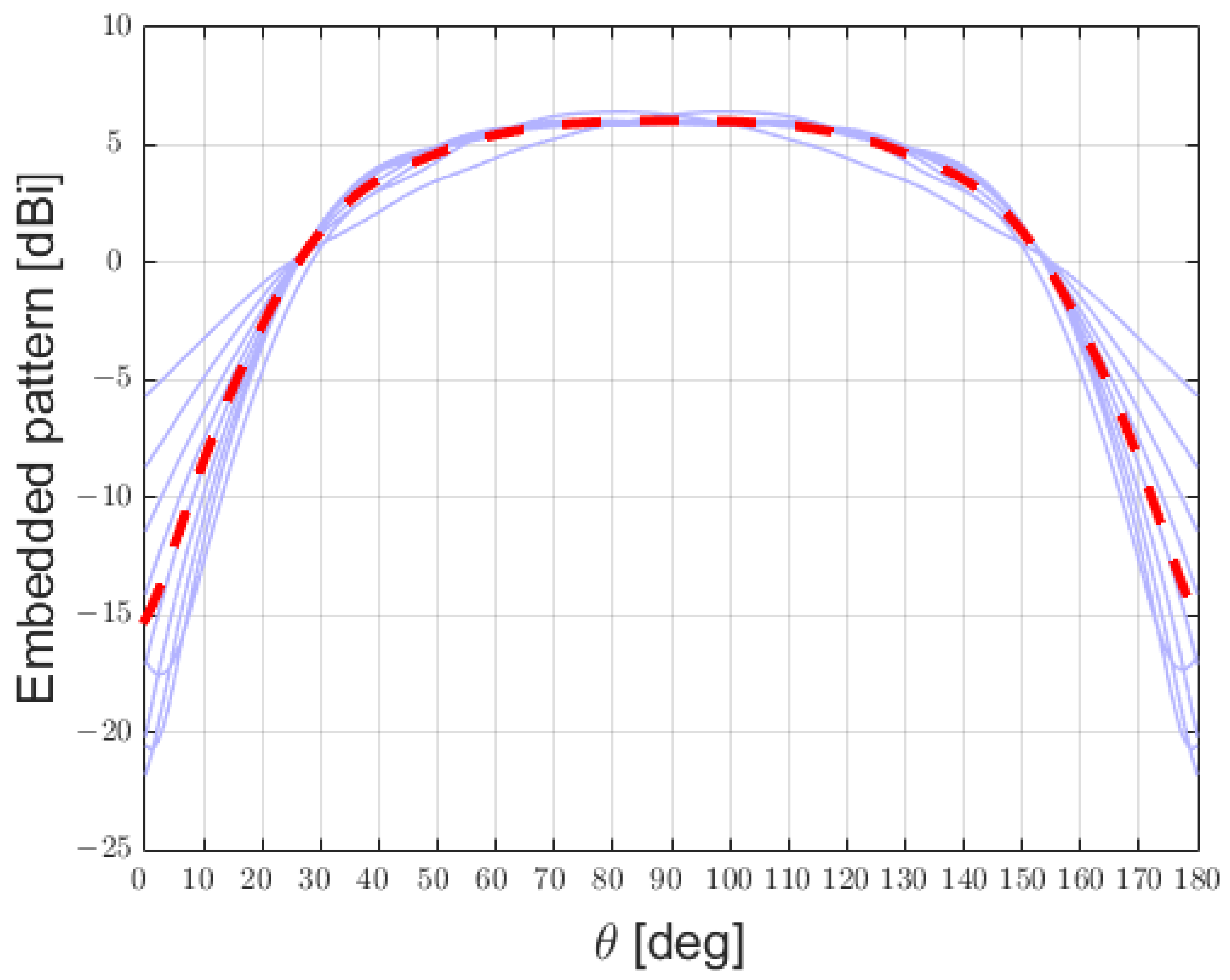
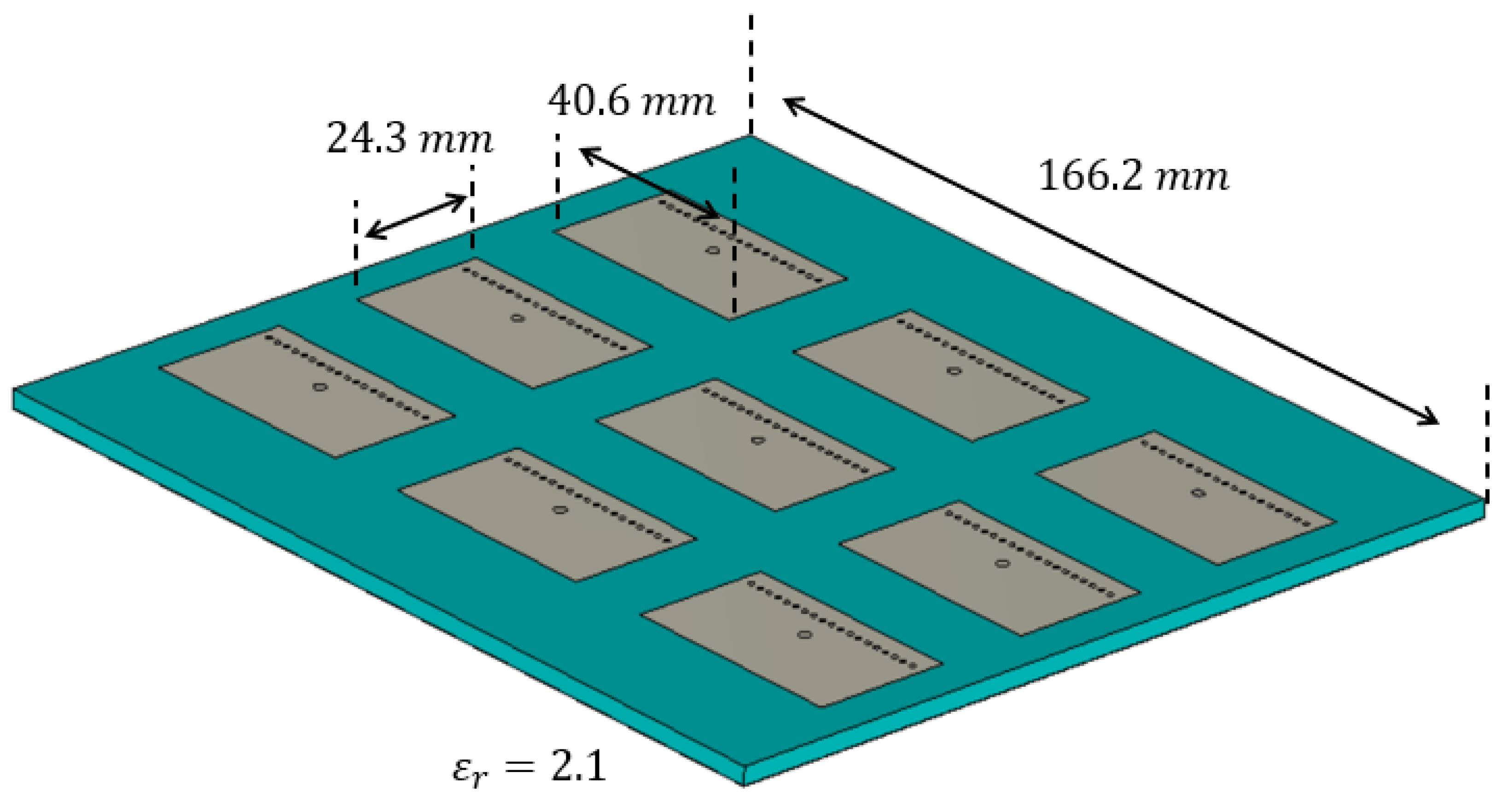



| Element | Power [W] | Amplitude [V] | Phase [deg] |
|---|---|---|---|
| 1 | 1 | 1.4142 | 0 |
| 2 | 0.8290 | 1.2876 | 127.37 |
| 3 | 0.6610 | 1.1498 | 254.74 |
| 4 | 0.5157 | 1.0155 | 382.11 |
| 5 | 0.3917 | 0.8851 | 509.48 |
| 6 | 0.2922 | 0.7645 | 636.85 |
| 7 | 0.2219 | 0.6661 | 764.22 |
| 8 | 0.1684 | 0.8504 | 891.59 |
| 9 | 0.1266 | 0.5032 | 1019.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calcaterra, A.; Simeoni, P.; Migliore, M.D.; Frezza, F. Leaky Wave Generation Through a Phased-Patch Array. Sensors 2025, 25, 2754. https://doi.org/10.3390/s25092754
Calcaterra A, Simeoni P, Migliore MD, Frezza F. Leaky Wave Generation Through a Phased-Patch Array. Sensors. 2025; 25(9):2754. https://doi.org/10.3390/s25092754
Chicago/Turabian StyleCalcaterra, Alessandro, Patrizio Simeoni, Marco Donald Migliore, and Fabrizio Frezza. 2025. "Leaky Wave Generation Through a Phased-Patch Array" Sensors 25, no. 9: 2754. https://doi.org/10.3390/s25092754
APA StyleCalcaterra, A., Simeoni, P., Migliore, M. D., & Frezza, F. (2025). Leaky Wave Generation Through a Phased-Patch Array. Sensors, 25(9), 2754. https://doi.org/10.3390/s25092754










