Intelligent Testing Method for Multi-Point Vibration Acquisition of Pile Foundation Based on Machine Learning
Abstract
1. Introduction
2. Multi-Point Traveling Wave Decomposition Method (MTWDM)
- (1)
- The reconstructed results can effectively eliminate the interference of upper structure vibrations above the measurement point while retaining all the mechanical information of the pile foundation below the measurement point;
- (2)
- The reconstructed signal is close to the results of the traditional low-strain reflected wave method, reducing the learning cost of the detection personnel;
- (3)
- The equipment is lightweight, only requiring a hammer, sensors, signal acquisition device, and a receiving terminal for detection, suitable for general surveys of high-cap service pile foundations.
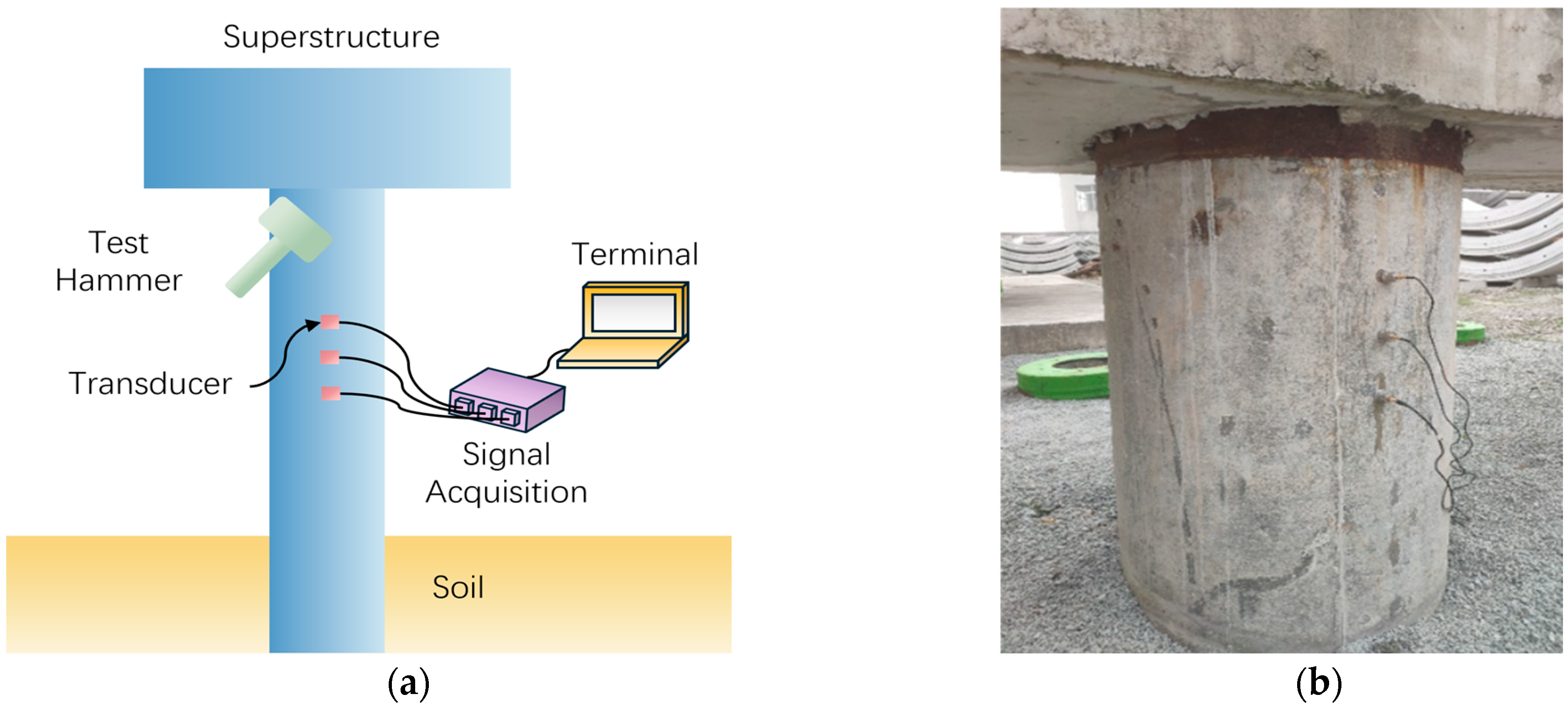
3. MTWDM Results Database
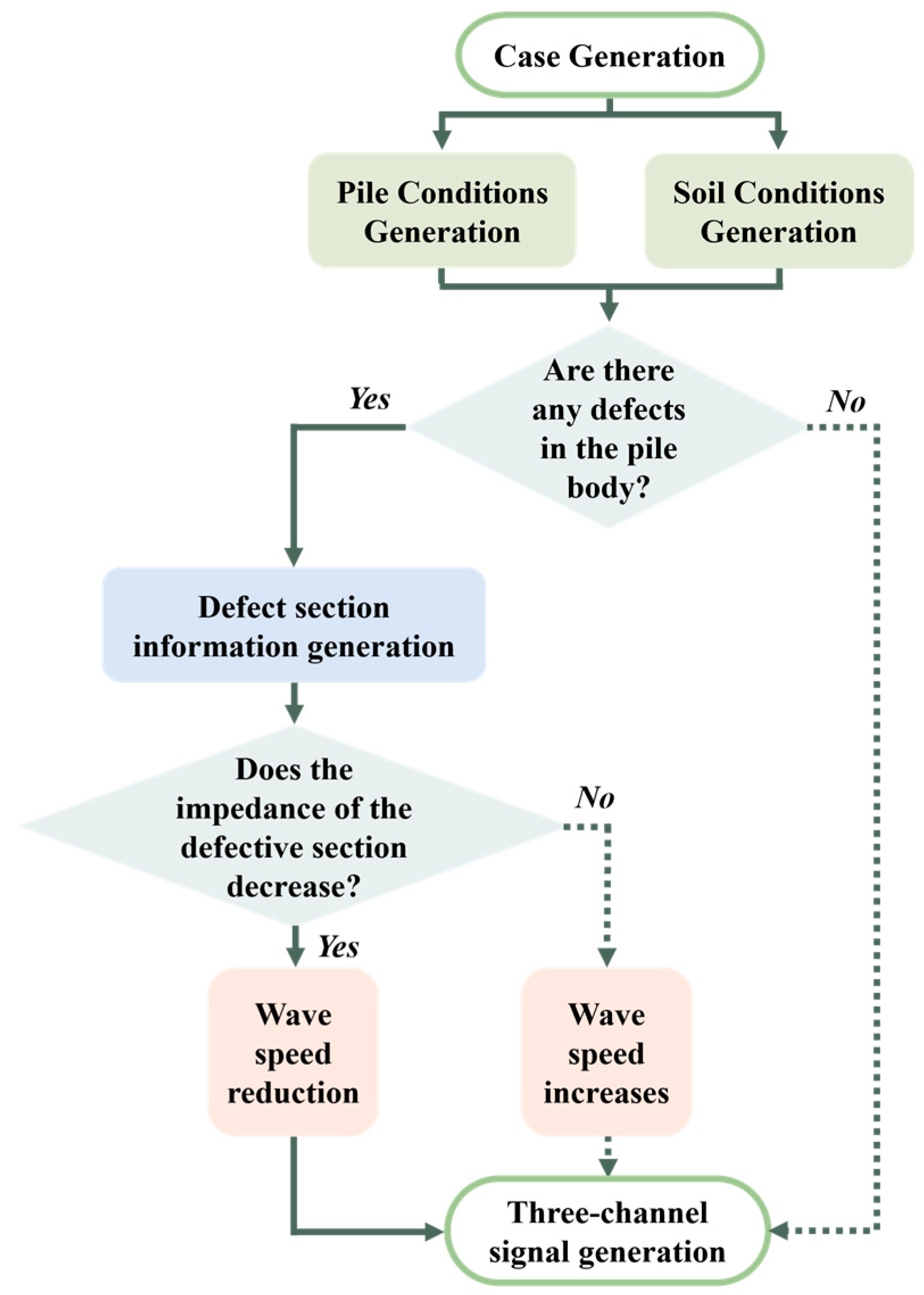
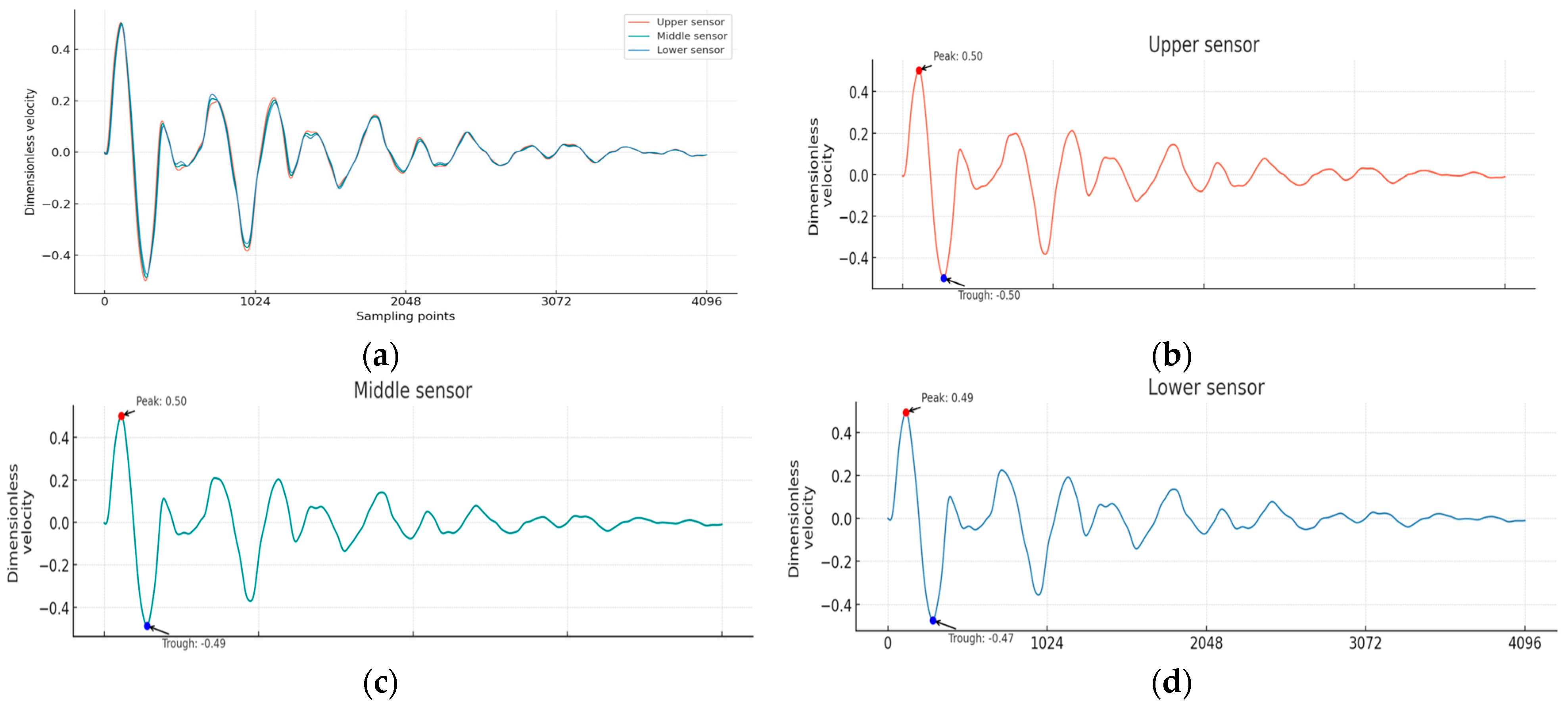
3.1. Database Generation
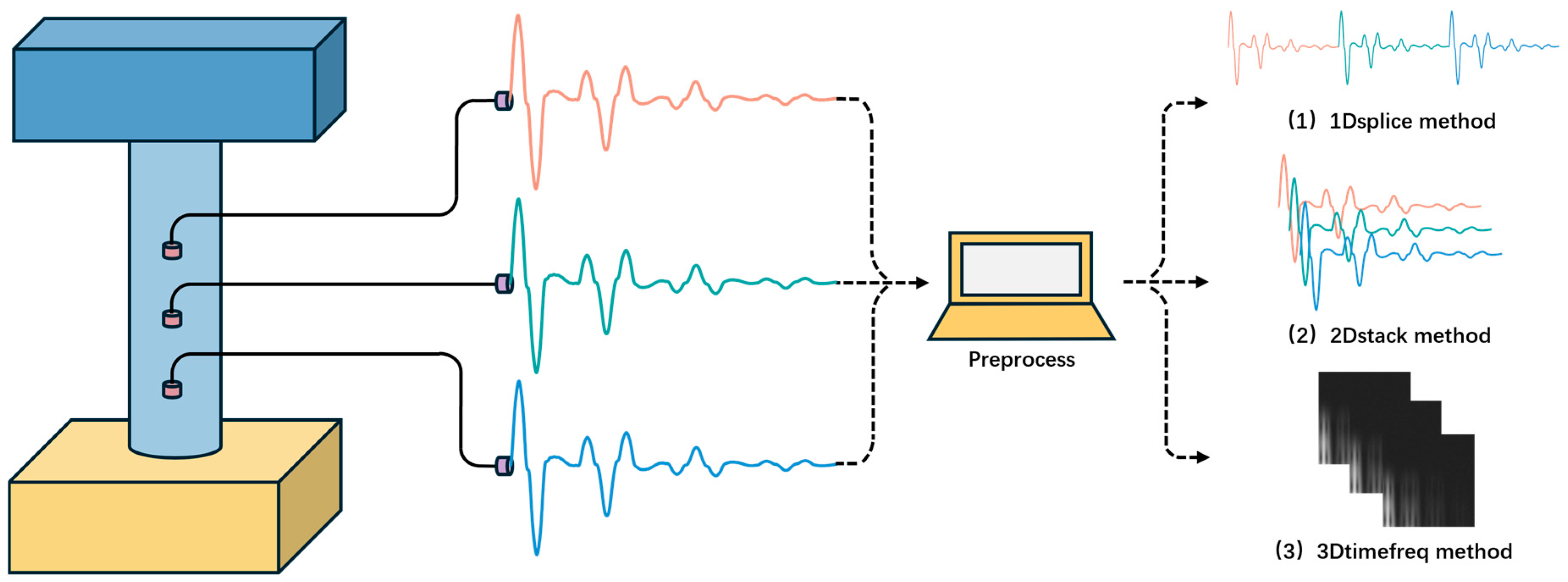
3.2. Data Preprocessing
- (1)
- Time series splicing method (1Dsplice): As shown in Figure 4 (1), the time sequence data collected by a single sensor are stored in a one-dimensional floating-point matrix with a size of [4096], and then three groups of matrices are sequentially spliced into a one-dimensional input tensor with a size of [12288]. This method has a simple integration process without requiring a large amount of data processing, but it is difficult to fully extract the complex information inherent in the system.
- (2)
- Time series stacking method (2Dstack): As shown in Figure 4 (2), the time sequence data collected by a single sensor are stored in a two-dimensional floating-point matrix with a size of [1, 4096], and then three groups of single-channel matrices are stacked into a two-dimensional input tensor with a size of [3, 4096]. This method fully retains the time-domain continuity of the pile shaft vibration signal, inputting all pile shaft information collected by the sensors into the model. However, the high-frequency multi-channel signal acquisition leads to a significant increase in the model calculation complexity, which can be effectively alleviated by the spatial down-sampling operation of the pooling layer.
- (3)
- Time-frequency stacking method (3Dtimefreq): As shown in Figure 4 (3), the time-domain pile shaft vibration signal of a single sensor is decomposed into multi-scale through continuous wavelet transform (CWT), generating a two-dimensional feature map containing scale-time spectrum information. To balance information retention and calculation efficiency, this paper uses 64 × 64 pixel resolution and only extracts grayscale features. Finally, three groups of images are stacked into a three-dimensional input tensor with a size of [3, 64, 64] along the channel direction. This method enhances the feature dimension from one-dimensional time-domain signals to three-dimensional frequency-domain tensors, facilitating the model to capture multi-scale velocity response features in the signal.
4. Calculation Model
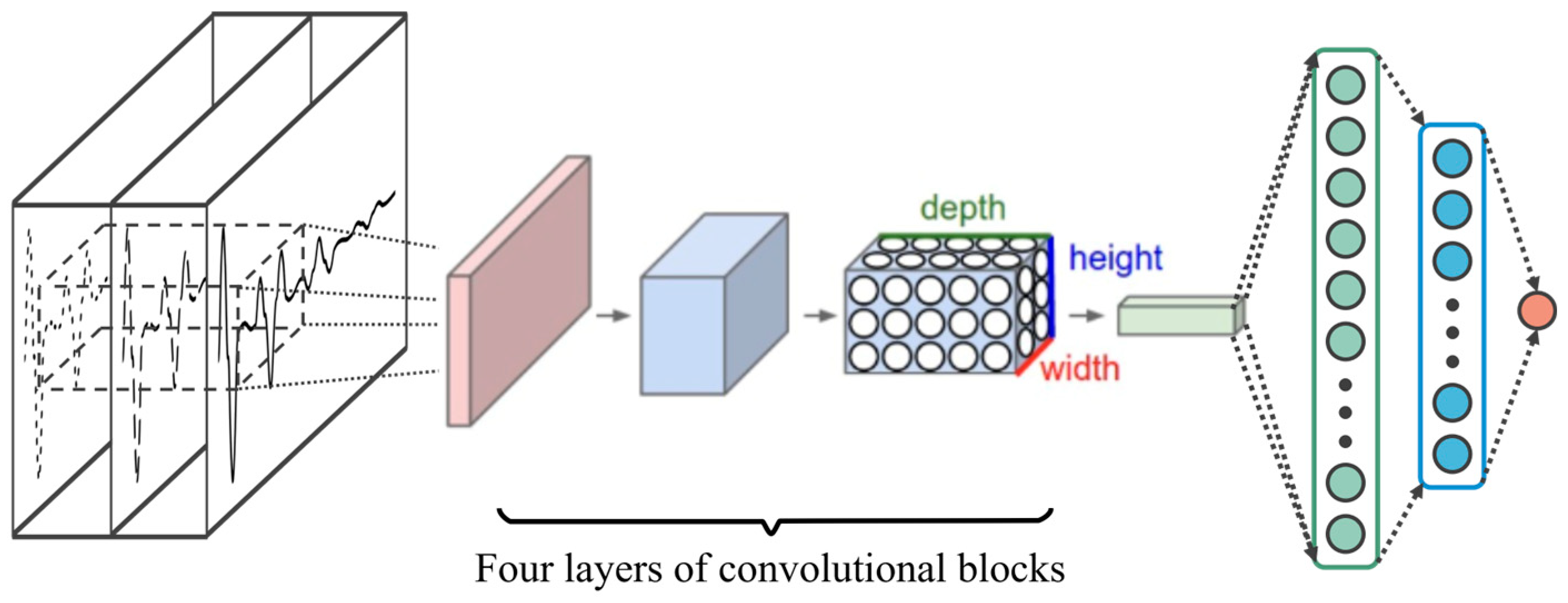
4.1. Convolutional Neural Network (CNN) Model
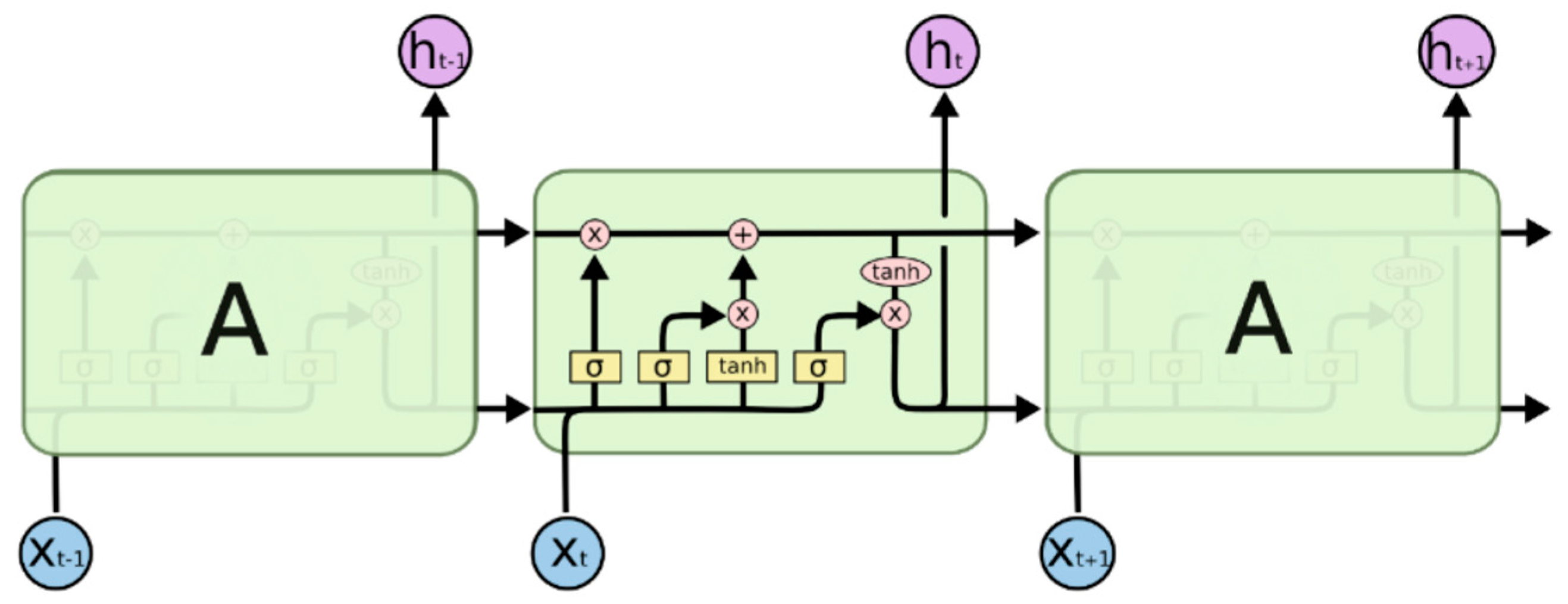
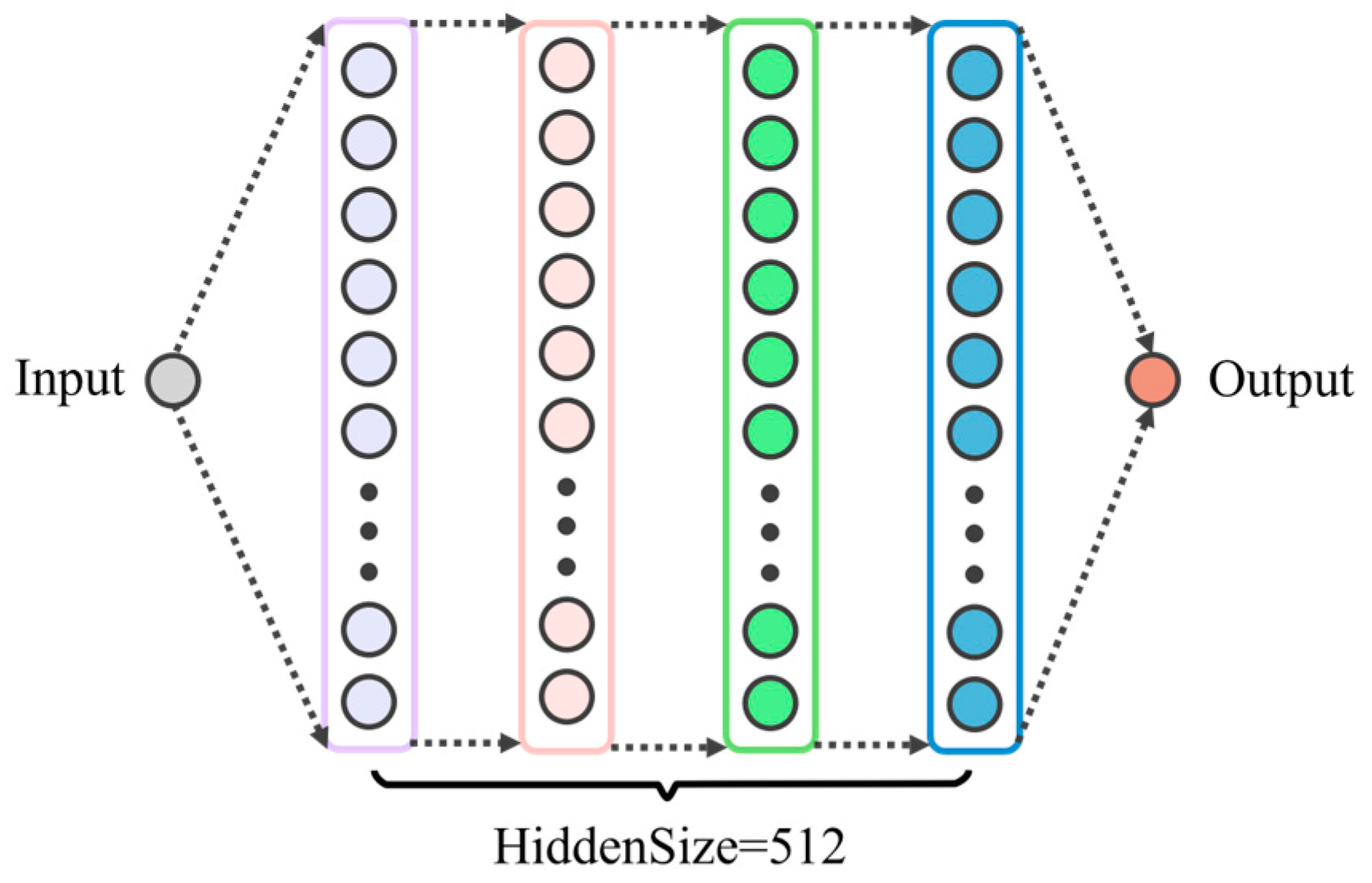
4.2. Long Short-Term Memory Neural Network (LSTM) Model
4.3. Loss Function, Optimization, Regularization, and Early Stopping Strategy
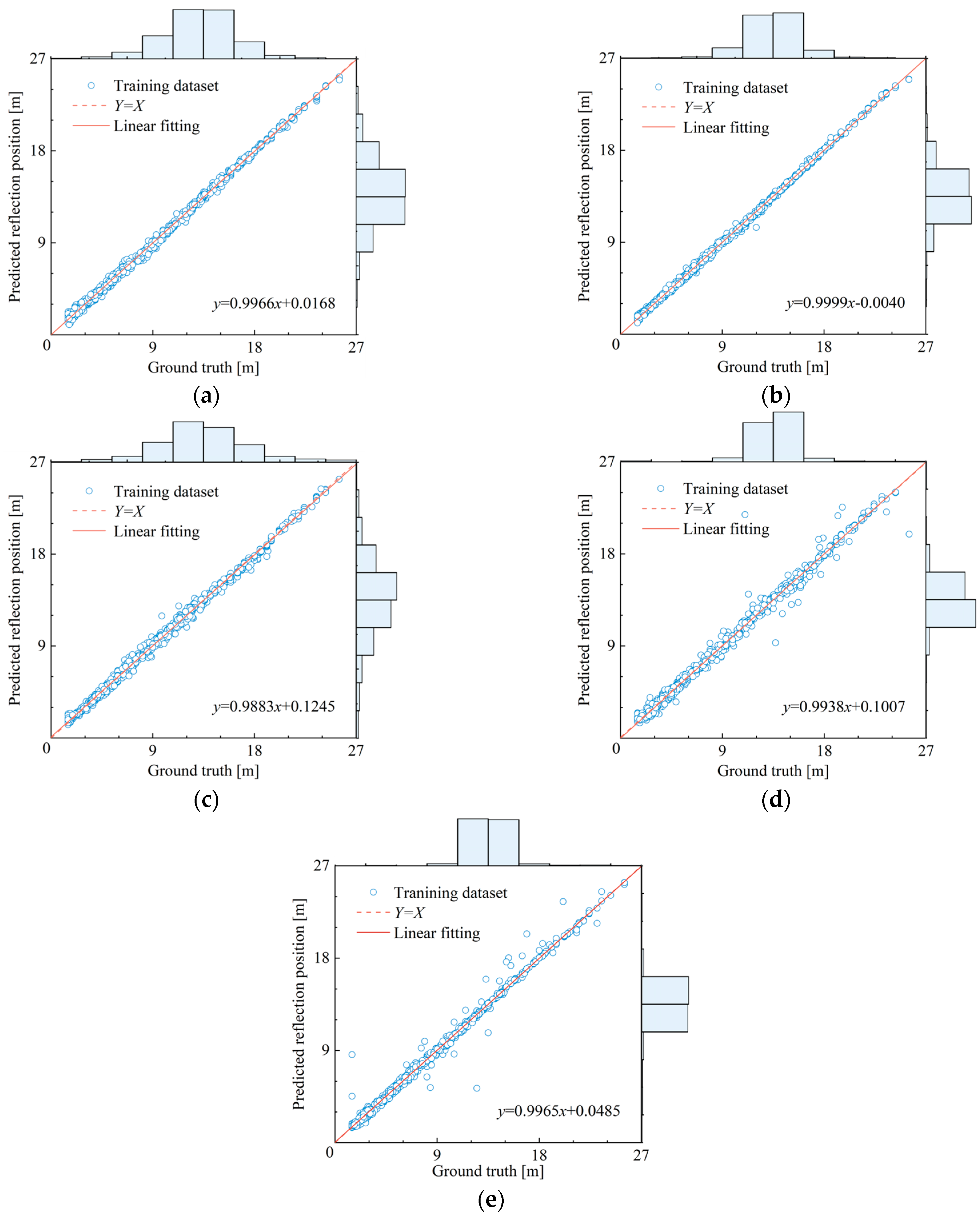
5. Model Performance Testing
6. Conclusions
- Based on the CNN model, LSTM model, and three data preprocessing methods, an intelligent detection model for damage to in-service pile foundations under existing structures based on multi-sensor data fusion and an ML algorithm is innovatively proposed, which can quantify the distance between the first reflection point in the signal and the intermediate sensor. The results show that the combination of each model framework and data preprocessing method can effectively complete the task of quantifying pile foundation damage.
- The analytical solution method is used to simulate the multi-channel pile foundation vibration response signal collected by three velocity sensors arranged at equal intervals on the exposed surface of the pile body to build a model training and verification database. The results show that the model can mine the dynamic characteristics of the pile foundation when it is forced to vibrate from the ideal data generated by the model, thereby completing the intelligent detection of pile foundation integrity.
- The calculation results of the models show that both architectures can effectively capture the main characteristic patterns in the signal, and the overall judgment results are highly accurate. Among them, the CNN model performs well in capturing fine-grained features due to its local receptive field characteristics, and its performance on the validation set is significantly better than that of the LSTM model.
- The longitudinal comparison of different data preprocessing methods under the isomorphic model shows that the input mode of the time series stacking method has a certain degree of improvement on the CNN model and the LSTM model. This significant improvement verifies the advantage of the sensor layout method of multi-point vibration detection in the intelligent detection of pile foundation damage.
- Combined with the results of horizontal and vertical comparison and error analysis, it is recommended to use a computational model based on the 2Dstack-CNN architecture to perform intelligent detection of the integrity of high-cap serving pile foundations using multi-sensor data fusion.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yi, E.; Wu, J.; El Naggar, M.H.; Wang, K.; Fu, P. Simulation of Sand-Filled Nodular Pile (SFNP) Installation Process Using DEM. Comput. Geotech. 2025, 184, 107249. [Google Scholar] [CrossRef]
- Guan, W.; Li, Q.; Jiang, G.; Liu, H.; Wu, W.; Leo, C.J. A New Non-Axisymmetric 3D Model of the Pile-Soil System for Dynamic Analysis of Large-Diameter Piles under Eccentric Excitation Load. Ocean Eng. 2023, 286, 115492. [Google Scholar] [CrossRef]
- Loseva, E.; Lozovsky, I.; Zhostkov, R. Refining Low Strain Pile Integrity Testing for Minor Flaw Detection with Complex Wavelet Transform. Civ. Eng. J. 2024, 10, 3194–3207. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, Z.; Yan, Y.; Zeng, J.; Wu, Z. Computed Tomography of Layered Defects in Large-Diameter Pile Foundation Using Transmission of Hybrid Ultrasonic Modes. Structures 2025, 74, 108545. [Google Scholar] [CrossRef]
- Ibsen, L.B.; Barari, A. Tapered Piles Responses during Large-Scale Axial Static and High-Strain Dynamic Load Testing. Acta Geotech. 2025, 1–20. [Google Scholar] [CrossRef]
- Wu, J.; El Naggar, M.H.; Wang, K. Analytical Model for Laterally Loaded Soil-Extended Pile Shaft Applied to Verifying the Applicability of Lateral PS Method. J. Geotech. Geoenviron. Eng. 2021, 147, 04021103. [Google Scholar] [CrossRef]
- Zhou, Y.; Kong, G.; Yang, Q. Field Performances of Energy Pile Based on the Secondary Utilization of Sonic Logging Pipes. Geomech. Energy Environ. 2022, 32, 100280. [Google Scholar] [CrossRef]
- Wang, K.; Wu, W.; Zhang, Z.; Leo, C.J. Vertical Dynamic Response of an Inhomogeneous Viscoelastic Pile. Comput. Geotech. 2010, 37, 536–544. [Google Scholar] [CrossRef]
- Cui, C.; Meng, K.; Liang, Z.; Xu, C.; Yang, G.; Zhang, S. Effect of Radial Homogeneity on Low-Strain Integrity Detection of a Pipe Pile in a Viscoelastic Soil Layer. Int. J. Distrib. Sens. Netw. 2018, 14, 155014771880645. [Google Scholar] [CrossRef]
- Fu, P.; Wu, J.; Jia, J.; Yi, E.; Wang, K.; Zhang, Z. Dynamic Response of Saturated Layered Soil around Defective Piles and Its Application in Engineering Testing. Soil Dyn. Earthq. Eng. 2025, 194, 109391. [Google Scholar] [CrossRef]
- Zheng, C.; Kouretzis, G.; Ding, X. Dynamic Response of Floating Piles Subjected to Axial Loads Considering Three-Dimensional Soil Deformations. Comput. Geotech. 2023, 154, 105144. [Google Scholar] [CrossRef]
- Wu, J.; El Naggar, M.H.; Wang, K. Pile Damage Detection Using Machine Learning with the Multipoint Traveling Wave Decomposition Method. Sensors 2023, 23, 8308. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; El Naggar, M.H.; Wang, K. Dynamic Response of Poroelastic Soil Adjacent to an Axially Vibrating Pile. J. Eng. Mech. 2024, 150, 04024084. [Google Scholar] [CrossRef]
- Wu, J.; El Naggar, M.H.; Ge, J.; Wang, K.; Zhao, S. Multipoint Traveling Wave Decomposition Method and Its Application in Extended Pile Shaft Integrity Test. J. Geotech. Geoenviron. Eng. 2021, 147, 04021128. [Google Scholar] [CrossRef]
- Wang, G.; Shan, Y.; Detmann, B.; Lin, W. Physics-Informed Neural Network (PINN) Model for Predicting Subgrade Settlement Induced by Shield Tunnelling beneath an Existing Railway Subgrade. Transp. Geotech. 2024, 49, 101409. [Google Scholar] [CrossRef]
- Chang, Z.; Catani, F.; Huang, F.; Liu, G.; Meena, S.R.; Huang, J.; Zhou, C. Landslide Susceptibility Prediction Using Slope Unit-Based Machine Learning Models Considering the Heterogeneity of Conditioning Factors. J. Rock Mech. Geotech. Eng. 2023, 15, 1127–1143. [Google Scholar] [CrossRef]
- Wang, Z.-F.; Peng, X.-B.; Liu, Y.; Cheng, W.-C.; Wang, Y.-Q.; Wu, C.-J. Evaluation of Ground Displacements Caused by Installing Jet Grouted Columns Using Machine Learning Methods. Adv. Civ. Eng. 2020, 2020, 8857293. [Google Scholar] [CrossRef]
- Ao, Y.; Li, H.; Zhu, L.; Ali, S.; Yang, Z. Logging Lithology Discrimination in the Prototype Similarity Space With Random Forest. IEEE Geosci. Remote Sens. Lett. 2019, 16, 687–691. [Google Scholar] [CrossRef]
- Mahadevkar, S.V.; Khemani, B.; Patil, S.; Kotecha, K.; Vora, D.R.; Abraham, A.; Gabralla, L.A. A Review on Machine Learning Styles in Computer Vision—Techniques and Future Directions. IEEE Access 2022, 10, 107293–107329. [Google Scholar] [CrossRef]
- Atha, D.J.; Jahanshahi, M.R. Evaluation of Deep Learning Approaches Based on Convolutional Neural Networks for Corrosion Detection. Struct. Health Monit. 2018, 17, 1110–1128. [Google Scholar] [CrossRef]
- Cui, D.-M.; Yan, W.; Wang, X.-Q.; Lu, L.-M. Towards Intelligent Interpretation of Low Strain Pile Integrity Testing Results Using Machine Learning Techniques. Sensors 2017, 17, 2443. [Google Scholar] [CrossRef]
- Dackermann, U.; Yu, Y.; Niederleithinger, E.; Li, J.; Wiggenhauser, H. Condition Assessment of Foundation Piles and Utility Poles Based on Guided Wave Propagation Using a Network of Tactile Transducers and Support Vector Machines. Sensors 2017, 17, 2938. [Google Scholar] [CrossRef]
- Yang, J.; Sun, X.-L.; Bian, D.-C.; Shao, J.-X. Large-Scale Model Test for Detecting Pile Defects Using the Parallel Seismic Method. Soil Dyn. Earthq. Eng. 2020, 139, 106300. [Google Scholar] [CrossRef]
- Koteleva, N.; Loseva, E. Development of an Algorithm for Determining Defects in Cast-in-Place Piles Based on the Data Analysis of Low Strain Integrity Testing. Appl. Sci. 2022, 12, 10636. [Google Scholar] [CrossRef]
- Ćosić, M.; Božić-Tomić, K.; Šušić, N. Pile Integrity and Load Testing: Methodology and Classification. Građ Mater. I Konstr. 2019, 62, 43–68. [Google Scholar] [CrossRef]
- Phellan, R.; Hachem, B.; Clin, J.; Mac-Thiong, J.; Duong, L. Real-time Biomechanics Using the Finite Element Method and Machine Learning: Review and Perspective. Med. Phys. 2021, 48, 7–18. [Google Scholar] [CrossRef]
- Wang, J.H.; Zhou, X.L.; Lu, J.F. Dynamic Response of Pile Groups Embedded in a Poroelastic Medium. Soil Dyn. Earthq. Eng. 2003, 23, 53–60. [Google Scholar] [CrossRef]
- Zhong, M.; Meng, K. Theoretical Analysis of Dynamic Response of Pipe Pile with Multi-Defects. J. Mar. Sci. Eng. 2023, 11, 83. [Google Scholar] [CrossRef]
- Lu, Z.; Sun, P.; Tan, X.; Ma, H.; Liu, S. Propagation Characteristics of Flexural Waves in Piles and the Transient Response at the Pile-Top under Lateral Excitation. Soil Dyn. Earthq. Eng. 2025, 190, 109173. [Google Scholar] [CrossRef]
- Abbasi Shanbehbazari, R.; Fakher, A. Shaking Table Test and Numerical Investigation of Seismic Response of Pile-Supported Wharves with Batter Piles. Ocean Eng. 2023, 287, 115688. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef]
- Dong, Y.; Li, X.; He, M.; Li, J. DC-BiLSTM-CNN Algorithm for Sentiment Analysis of Chinese Product Reviews. Appl. Artif. Intell. 2025, 39, 2461809. [Google Scholar] [CrossRef]
- Duan, R.; Huang, C.; Dou, P.; Hou, J.; Zhang, Y.; Gu, J. Fine-Scale Forest Classification with Multi-Temporal Sentinel-1/2 Imagery Using a Temporal Convolutional Neural Network. Int. J. Digit. Earth 2025, 18, 2457953. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent Advances in Convolutional Neural Networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Wu, K.; Sheng, H.; Cheng, Y. Remaining Useful Life Prediction Using a Hybrid Transfer Learning-Based Adaptive Wiener Process Model. Reliab. Eng. Syst. Saf. 2025, 260, 110975. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Shabani, M.; Yousefi, M. An Optimized Model Using LSTM Network for Demand Forecasting. Comput. Ind. Eng. 2020, 143, 106435. [Google Scholar] [CrossRef]
- Kouadio, L.; Deo, R.C.; Byrareddy, V.; Adamowski, J.F.; Mushtaq, S.; Phuong Nguyen, V. Artificial Intelligence Approach for the Prediction of Robusta Coffee Yield Using Soil Fertility Properties. Comput. Electron. Agric. 2018, 155, 324–338. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A Review and Analysis of Regression and Machine Learning Models on Commercial Building Electricity Load Forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Wieczorek, M.; Silka, J.; Wozniak, M.; Garg, S.; Hassan, M.M. Lightweight Convolutional Neural Network Model for Human Face Detection in Risk Situations. IEEE Trans. Ind. Inf. 2022, 18, 4820–4829. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, T.; Wang, X.; Wu, X.; Chen, A.; Chen, G.; Tang, C.; He, L.; Liu, Y.; Zeng, M.; et al. Deep Learning for the Prediction of Acute Kidney Injury after Coronary Angiography and Intervention in Patients with Chronic Kidney Disease: A Model Development and Validation Study. Ren. Fail. 2025, 47, 2474206. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Ghaderizadeh, S.; Abbasi-Moghadam, D.; Sharifi, A.; Zhao, N.; Tariq, A. Hyperspectral Image Classification Using a Hybrid 3D-2D Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7570–7588. [Google Scholar] [CrossRef]
- Jahn, T.; Jin, B. Early Stopping of Untrained Convolutional Neural Networks. SIAM J. Imaging Sci. 2024, 17, 2331–2361. [Google Scholar] [CrossRef]
- Xiong, B.; Chang, Y.; Zeng, N.; Niu, Y.; Zeng, H.; Li, H.; Mao, G.; Xu, Y. TranSEMG: A Trans-Scale Hybrid Model for High-Accurate Hip Joint Moment Prediction. IEEE Trans. Instrum. Meas. 2024, 73, 3384565. [Google Scholar] [CrossRef]


| Parameter | Unit | Variation Range | |
|---|---|---|---|
| Min | Max | ||
| Pile length (Lp) | m | 20 | 30 |
| Pile diameter | m | 0.4 | 0.6 |
| Pile material density | kg/m3 | 2400 | 2600 |
| Poisson’s ratio of soil | - | 0.25 | 0.35 |
| Soil material density | kg/m3 | 1700 | 1900 |
| Length of pile defect segment (Ld) | m | 1 | 3 |
| Defect segment location | m | 1.5 | Lp-Ld-1.5 |
| Pulse width | s | 0.0015 | 0.003 |
| Model | Dataset | R2 | MAE/(m) | VAF/% |
|---|---|---|---|---|
| 1Dsplice-CNN | Training set | 0.9980 | 0.1941 | 99.80 |
| Validation set | 0.9894 | 0.4168 | 98.94 | |
| 2Dstack-CNN | Training set | 0.9992 | 0.1251 | 99.92 |
| Validation set | 0.9988 | 0.1465 | 99.89 | |
| 3Dtimefreq-CNN | Training set | 0.9976 | 0.2169 | 99.76 |
| Validation set | 0.9896 | 0.3834 | 98.96 | |
| 1Dsplice-LSTM | Training set | 0.9967 | 0.1985 | 99.52 |
| Validation set | 0.9852 | 0.2984 | 98.57 | |
| 2Dstack-LSTM | Training set | 0.9943 | 0.2007 | 99.43 |
| Validation set | 0.9821 | 0.3136 | 98.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Zhao, W.; Wu, J.; Ma, S. Intelligent Testing Method for Multi-Point Vibration Acquisition of Pile Foundation Based on Machine Learning. Sensors 2025, 25, 2893. https://doi.org/10.3390/s25092893
Wang K, Zhao W, Wu J, Ma S. Intelligent Testing Method for Multi-Point Vibration Acquisition of Pile Foundation Based on Machine Learning. Sensors. 2025; 25(9):2893. https://doi.org/10.3390/s25092893
Chicago/Turabian StyleWang, Ke, Weikai Zhao, Juntao Wu, and Shuang Ma. 2025. "Intelligent Testing Method for Multi-Point Vibration Acquisition of Pile Foundation Based on Machine Learning" Sensors 25, no. 9: 2893. https://doi.org/10.3390/s25092893
APA StyleWang, K., Zhao, W., Wu, J., & Ma, S. (2025). Intelligent Testing Method for Multi-Point Vibration Acquisition of Pile Foundation Based on Machine Learning. Sensors, 25(9), 2893. https://doi.org/10.3390/s25092893







