Detection of Elusive Rogue Wave with Cross-Track Interferometric Synthetic Aperture Radar Imaging Approach
Abstract
1. Introduction
2. Synthesis of Rogue Waves
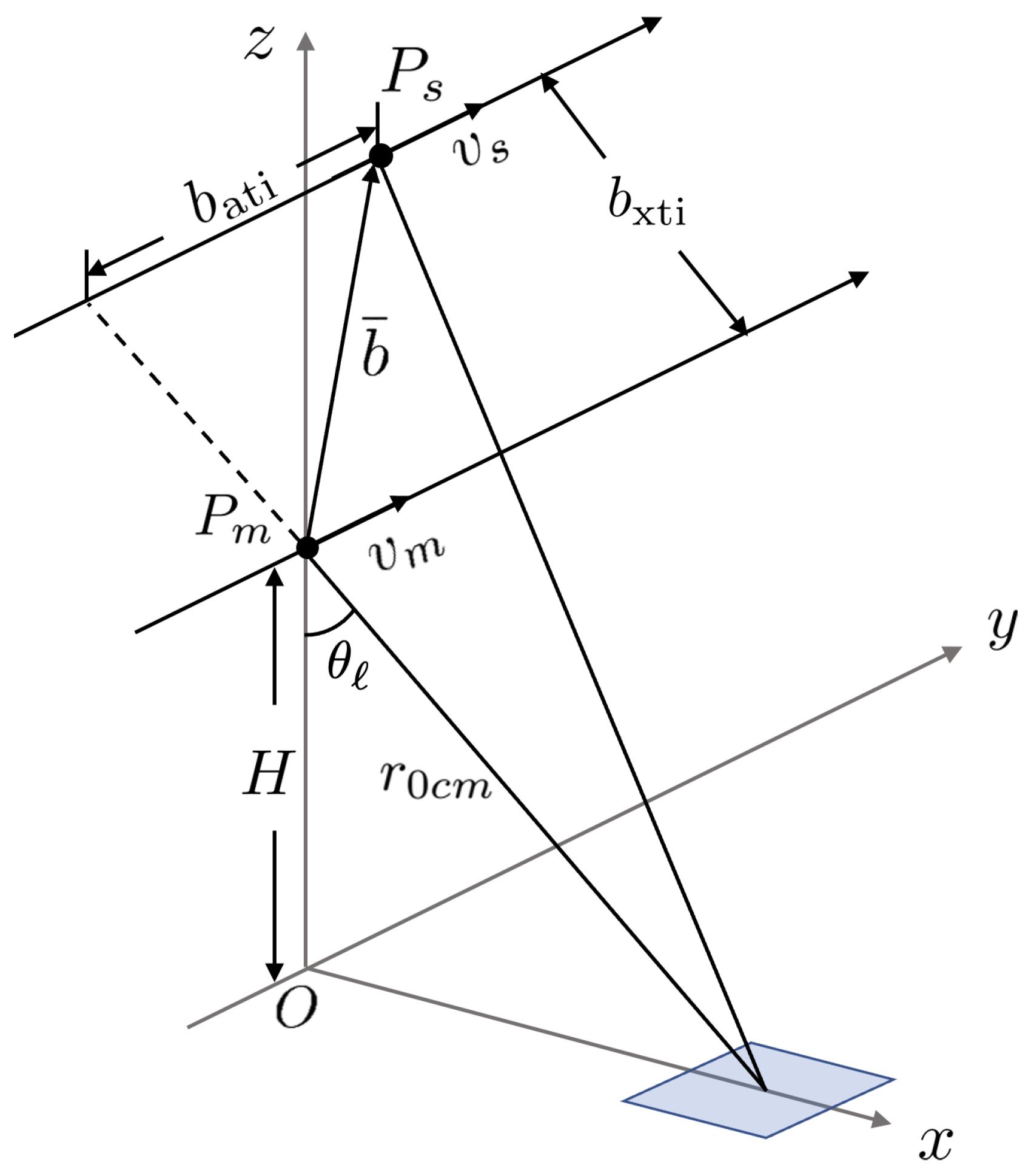
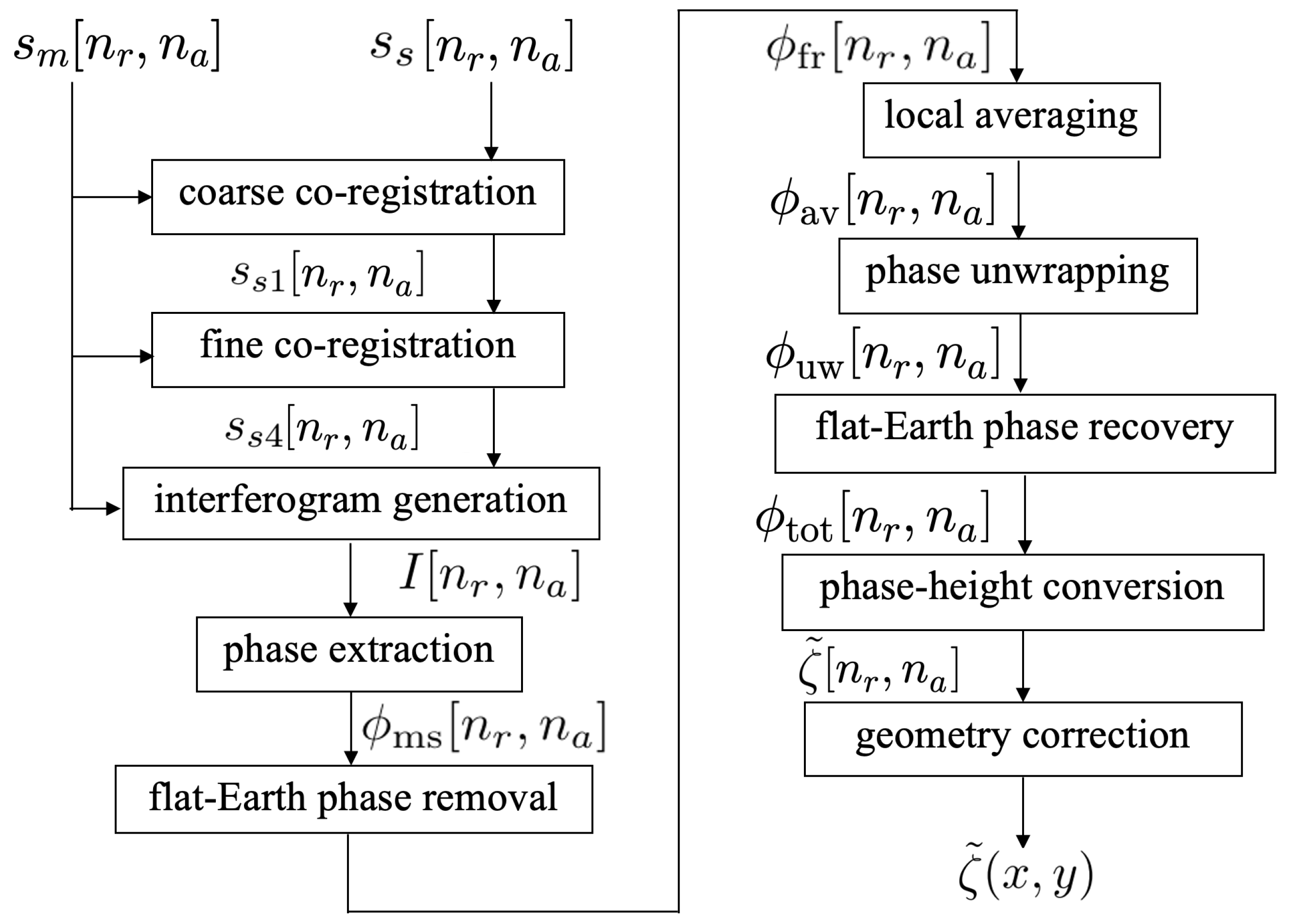
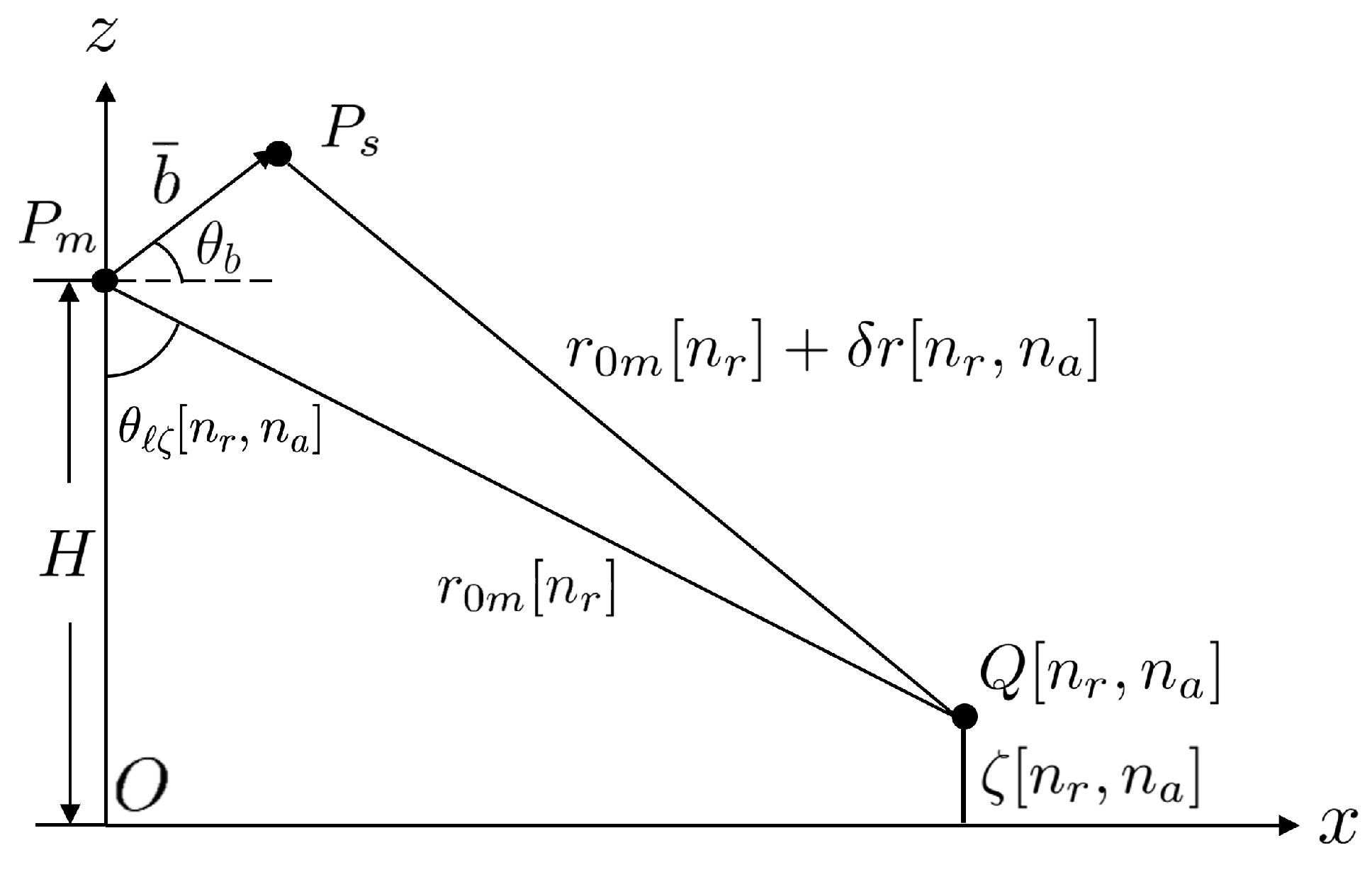
3. XTI-SAR Imaging Approach
3.1. Co-Registration
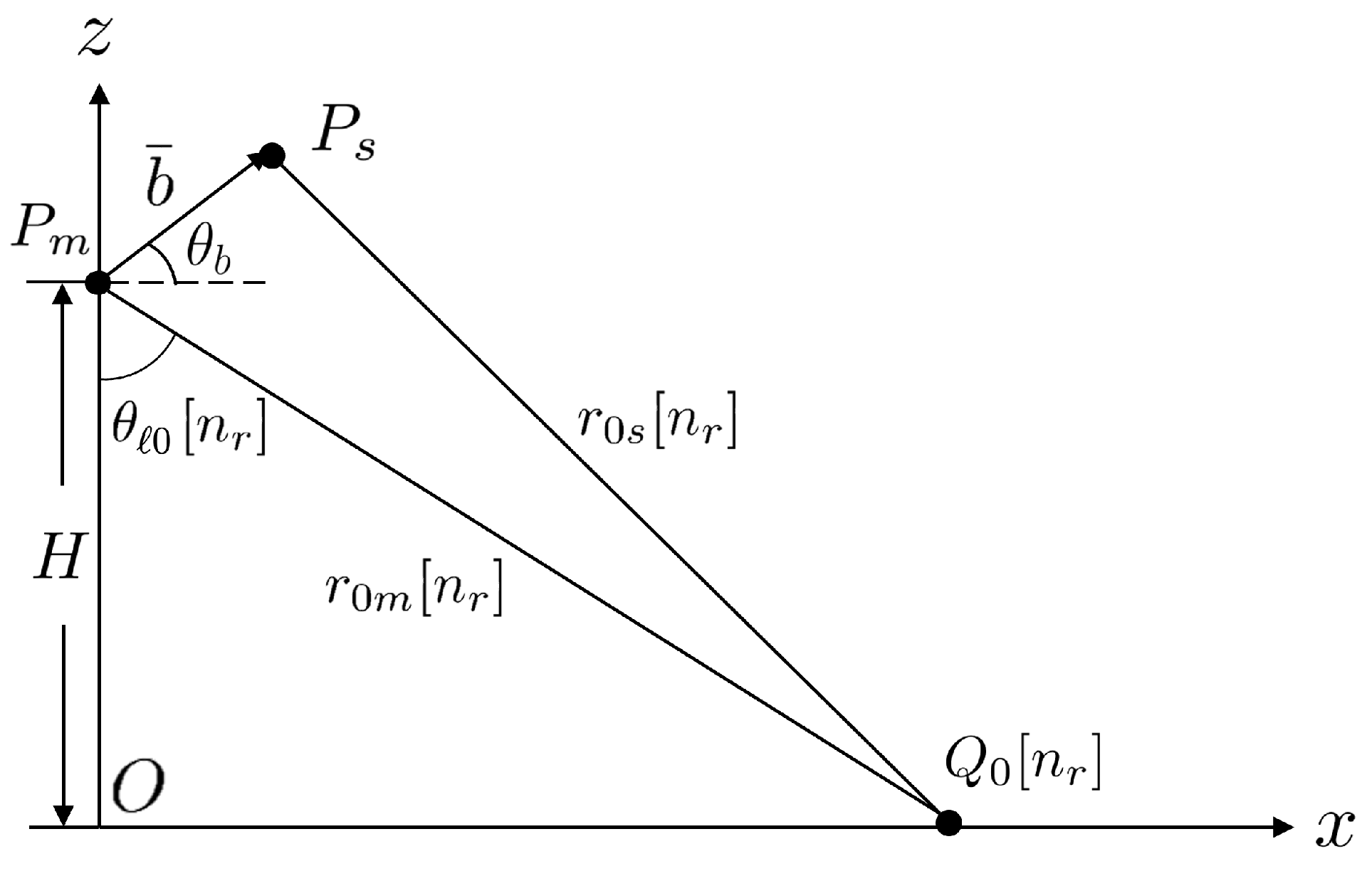
3.2. Removal of Flat-Earth Phase
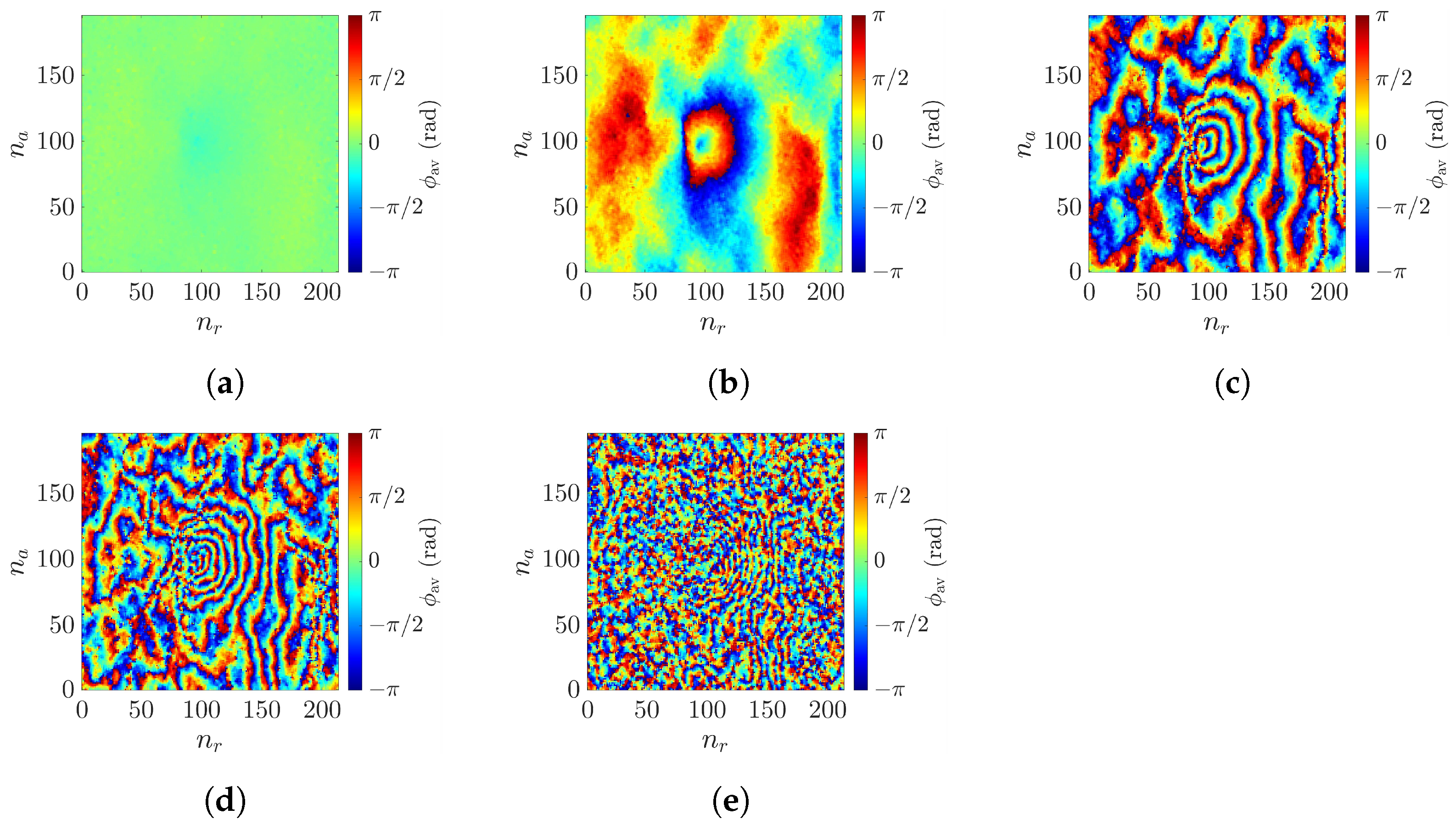
3.3. Phase Unwrapping and Mean Filter
3.4. Surface Height Mapping and Geometric Correction
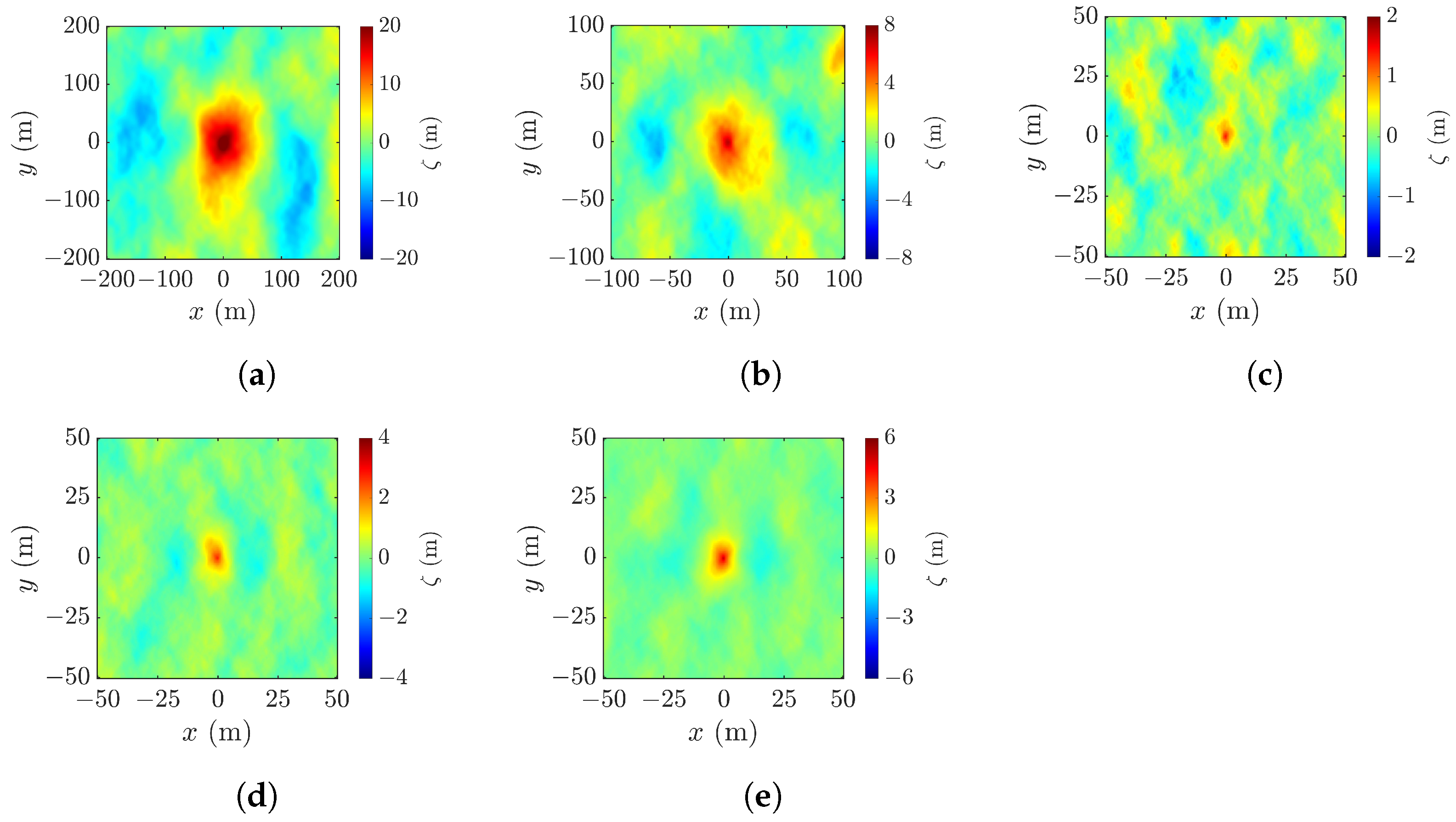
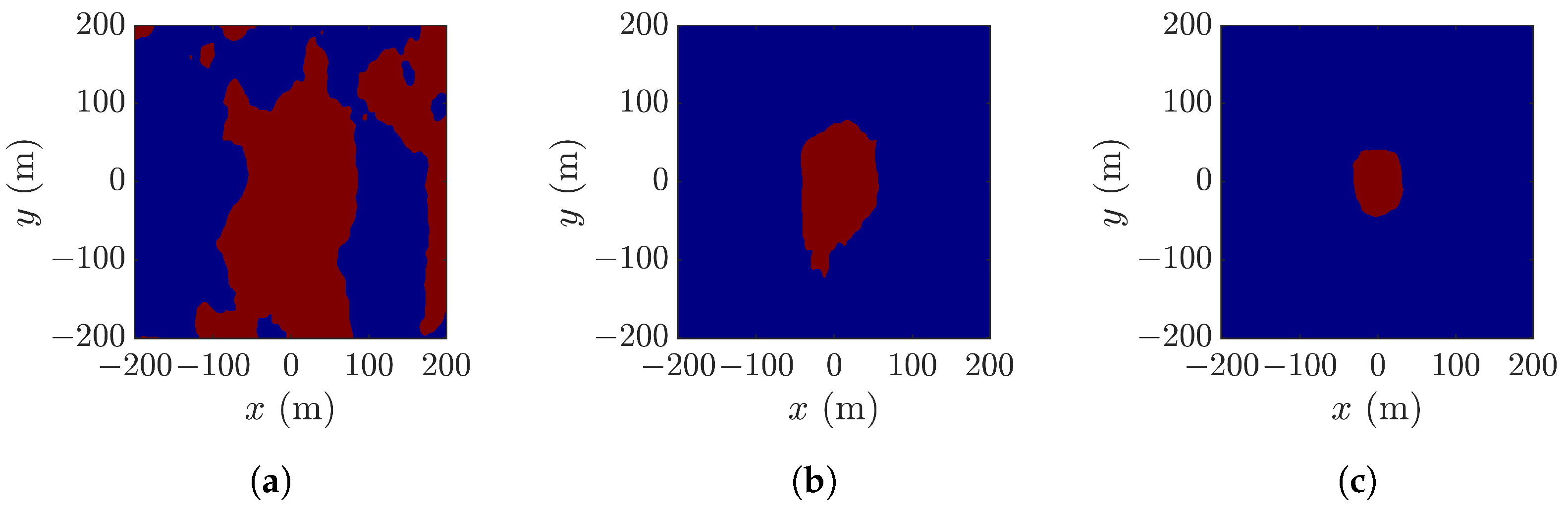
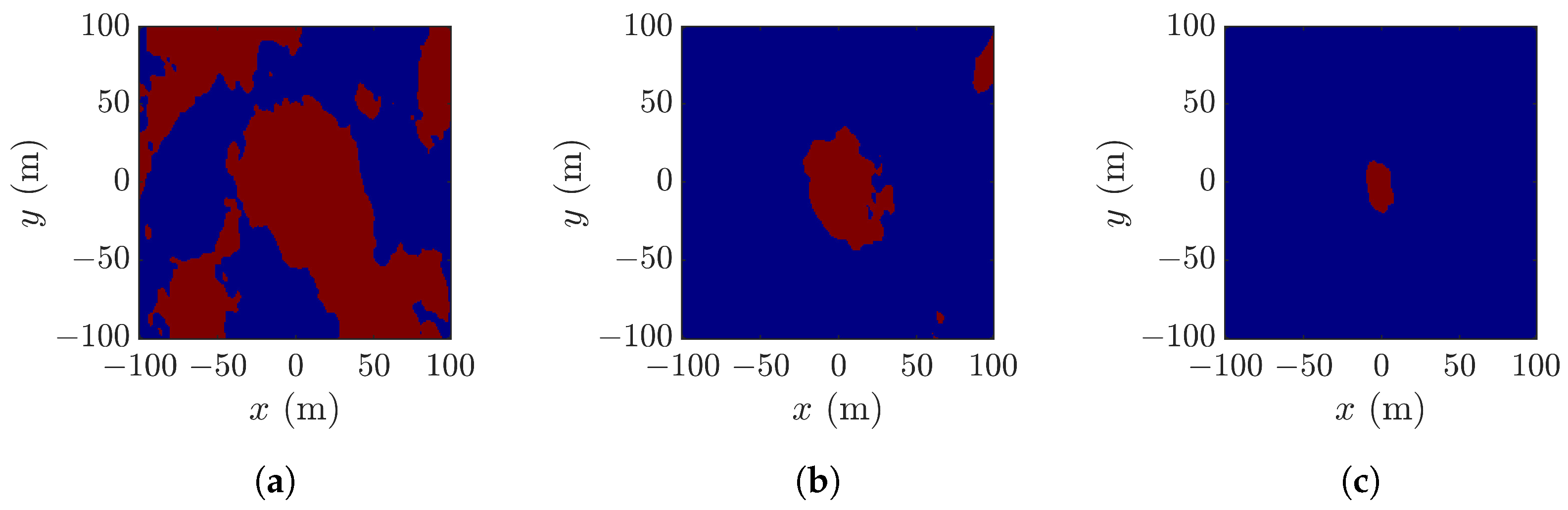
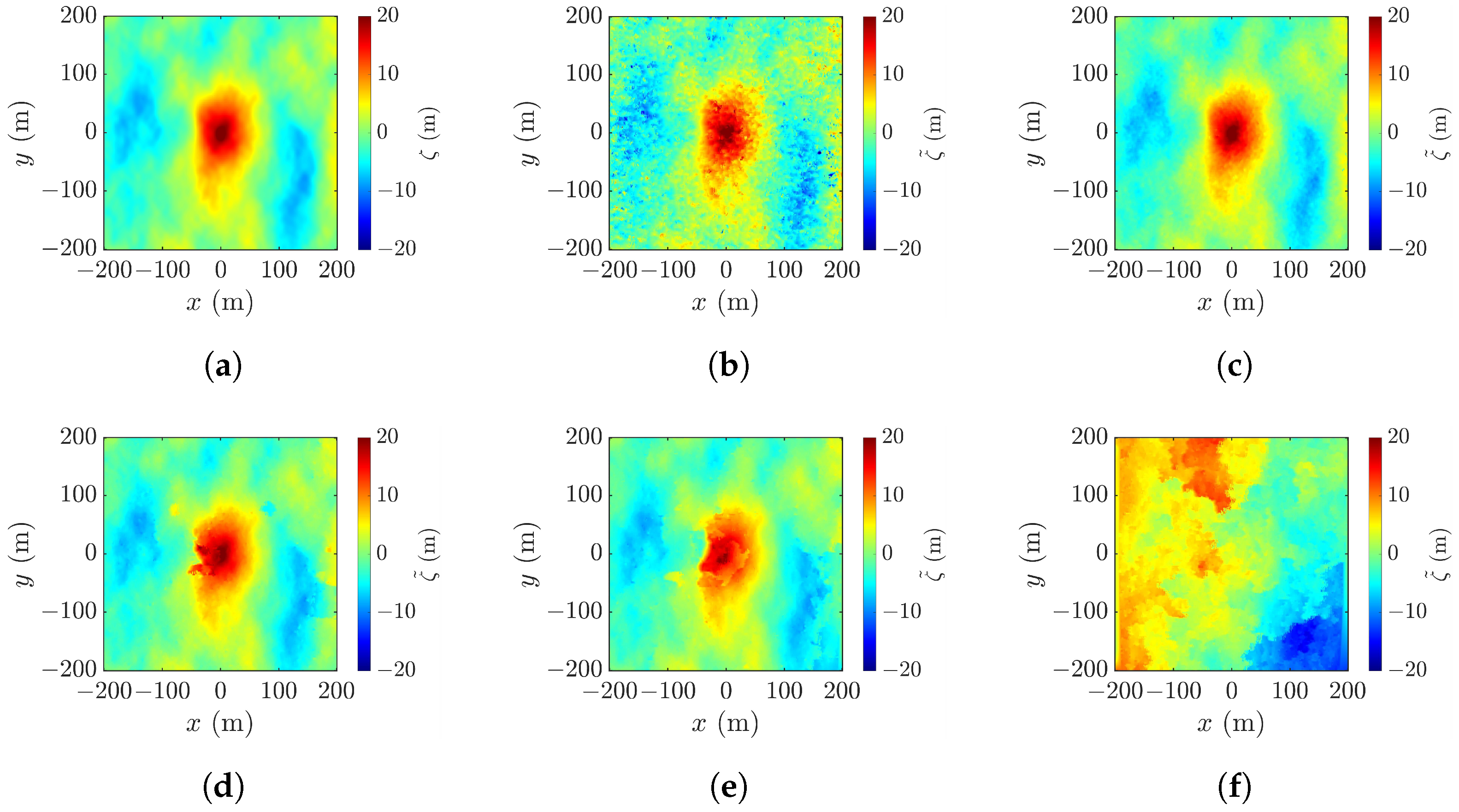
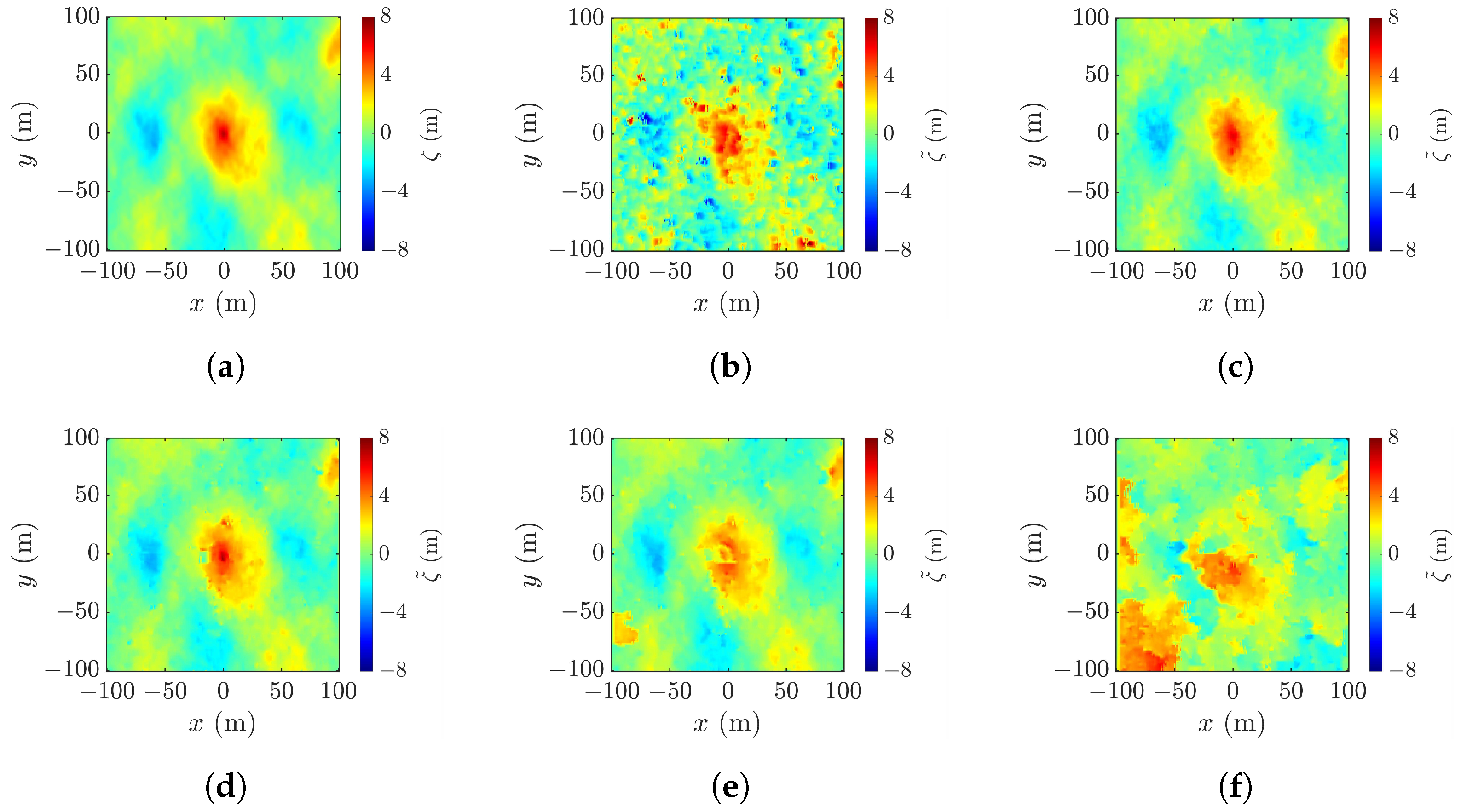
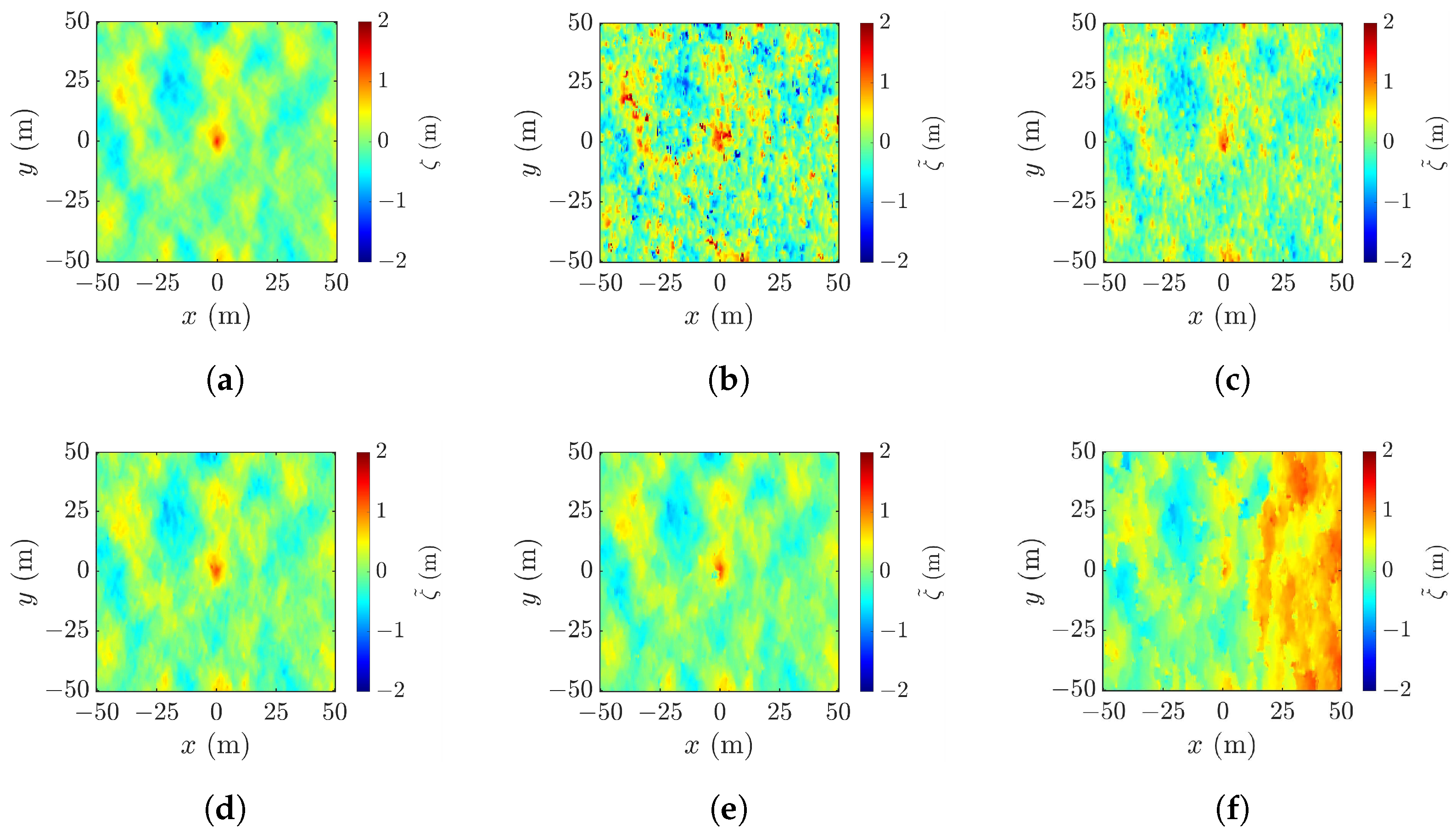
4. Simulations and Discussions
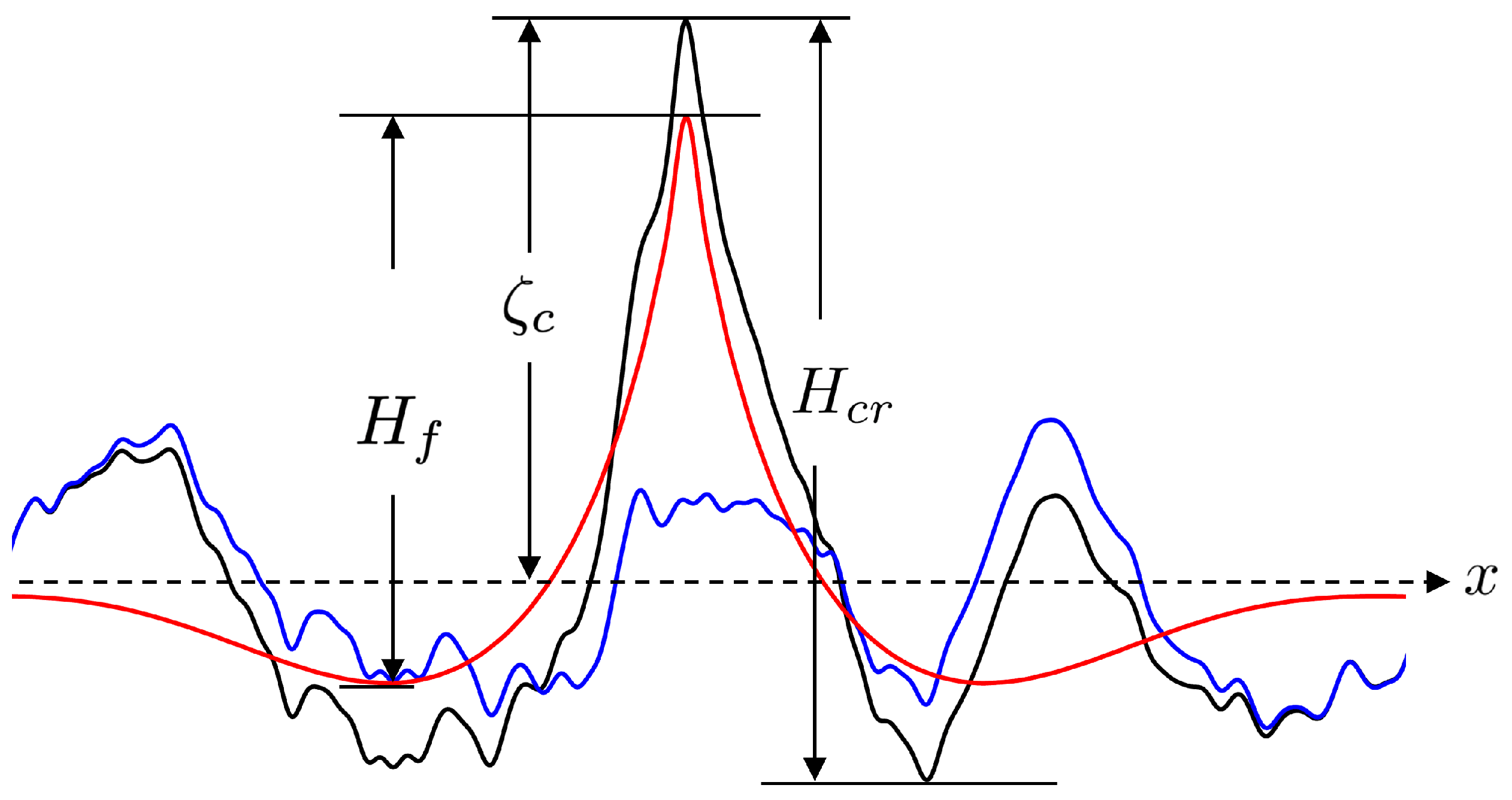
4.1. Radar Parameters for Rogue Wave Reconstruction and Performance Indices
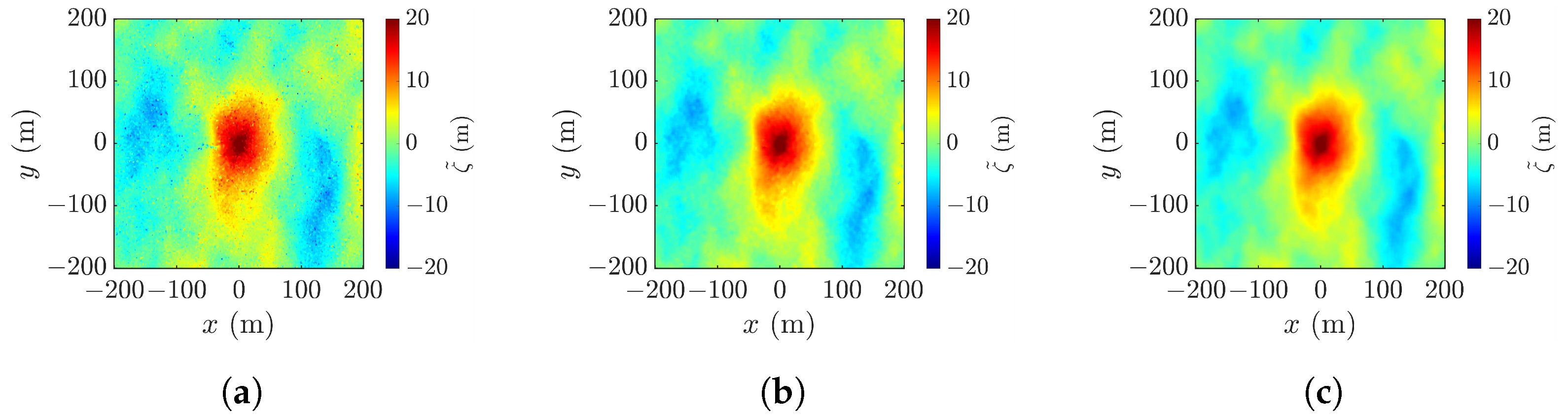
4.2. Effect of Look Angle
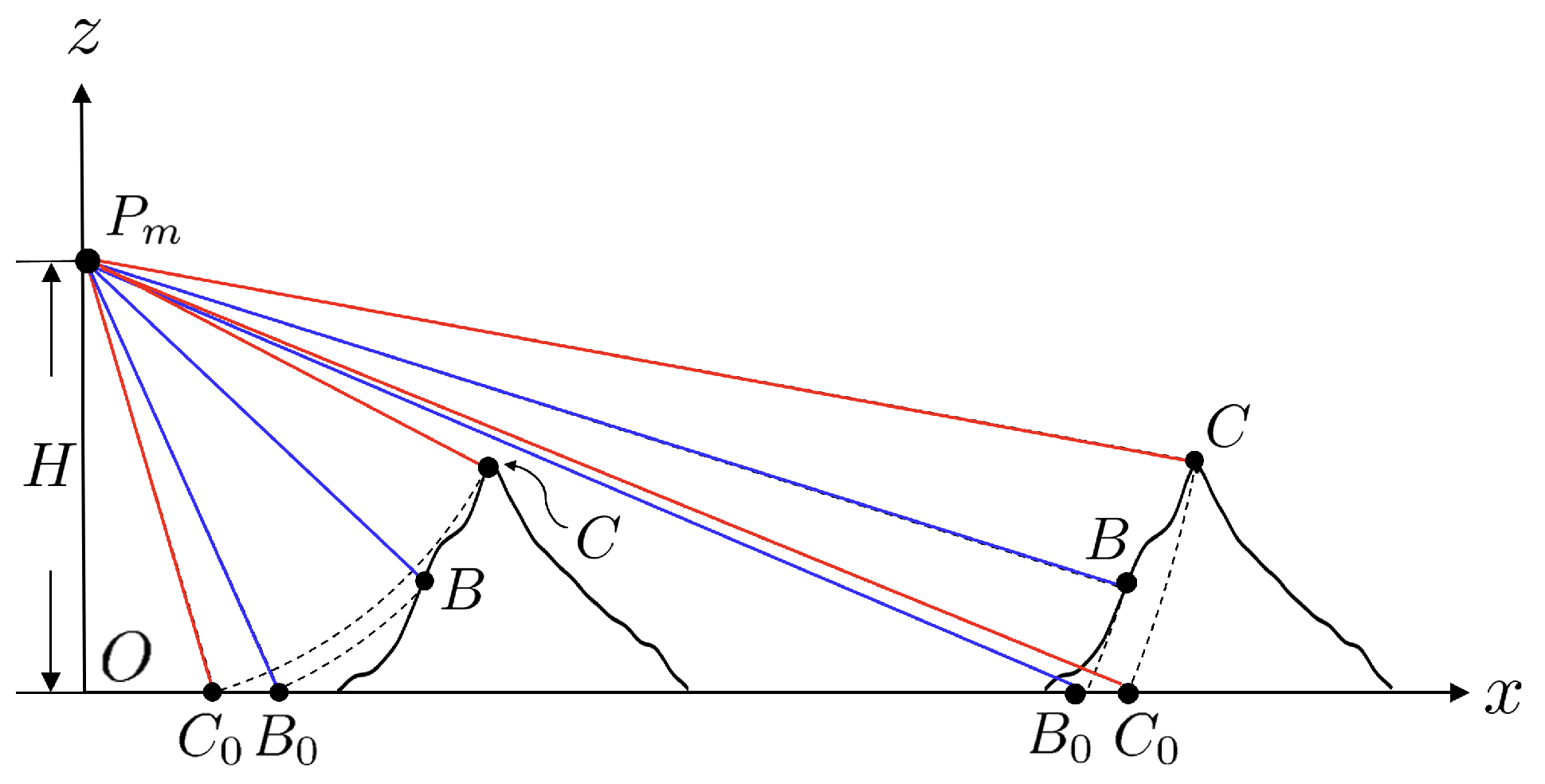
4.3. Layover Effect and Constraint on Look Angle
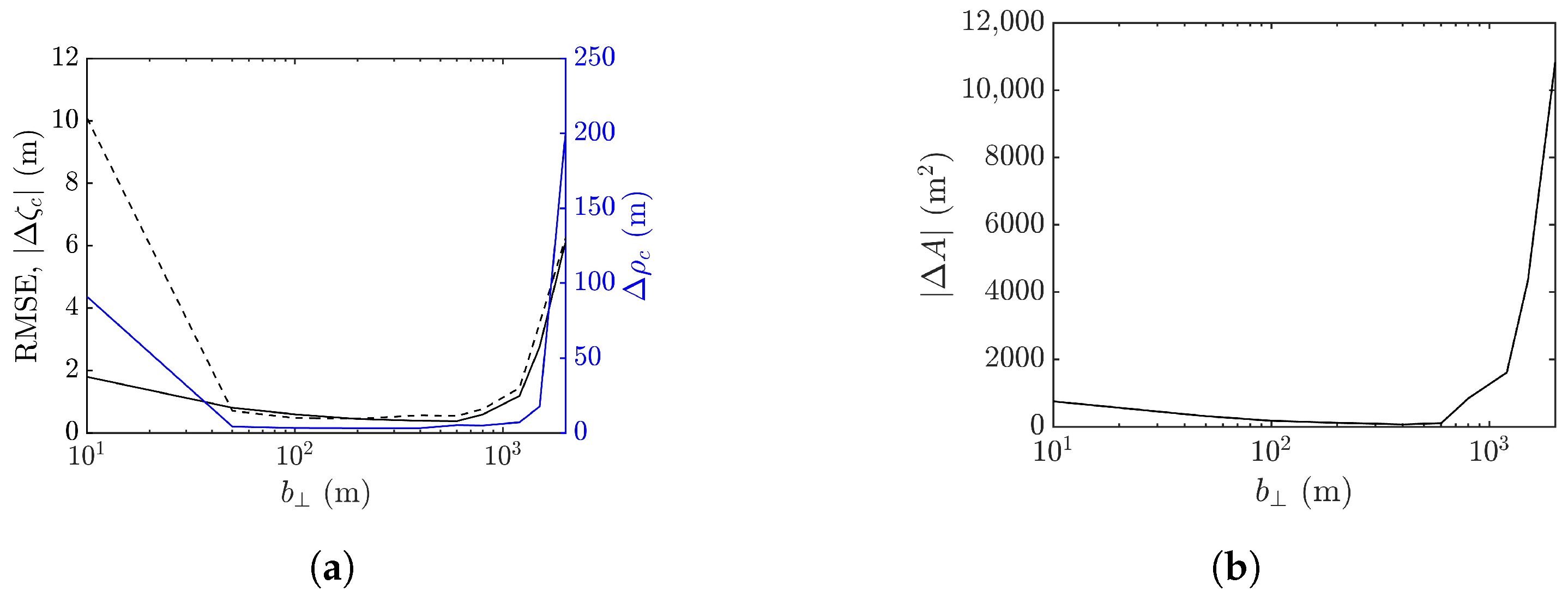
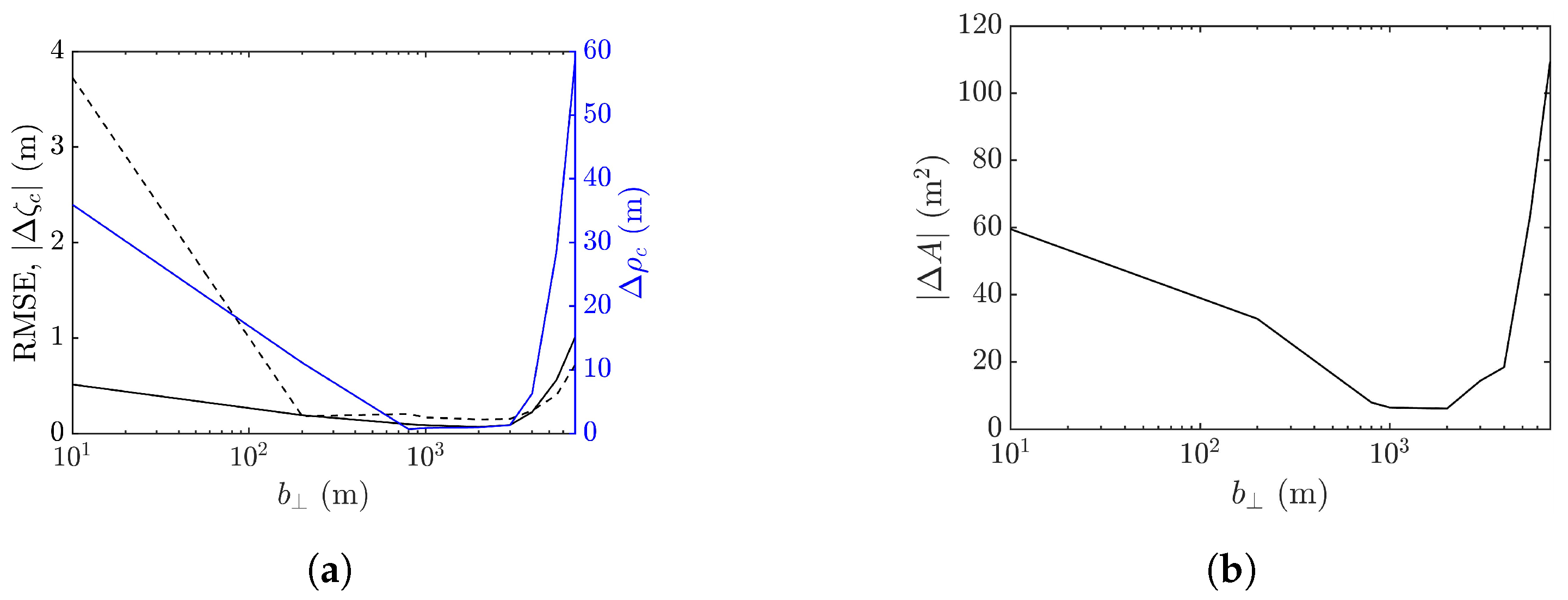
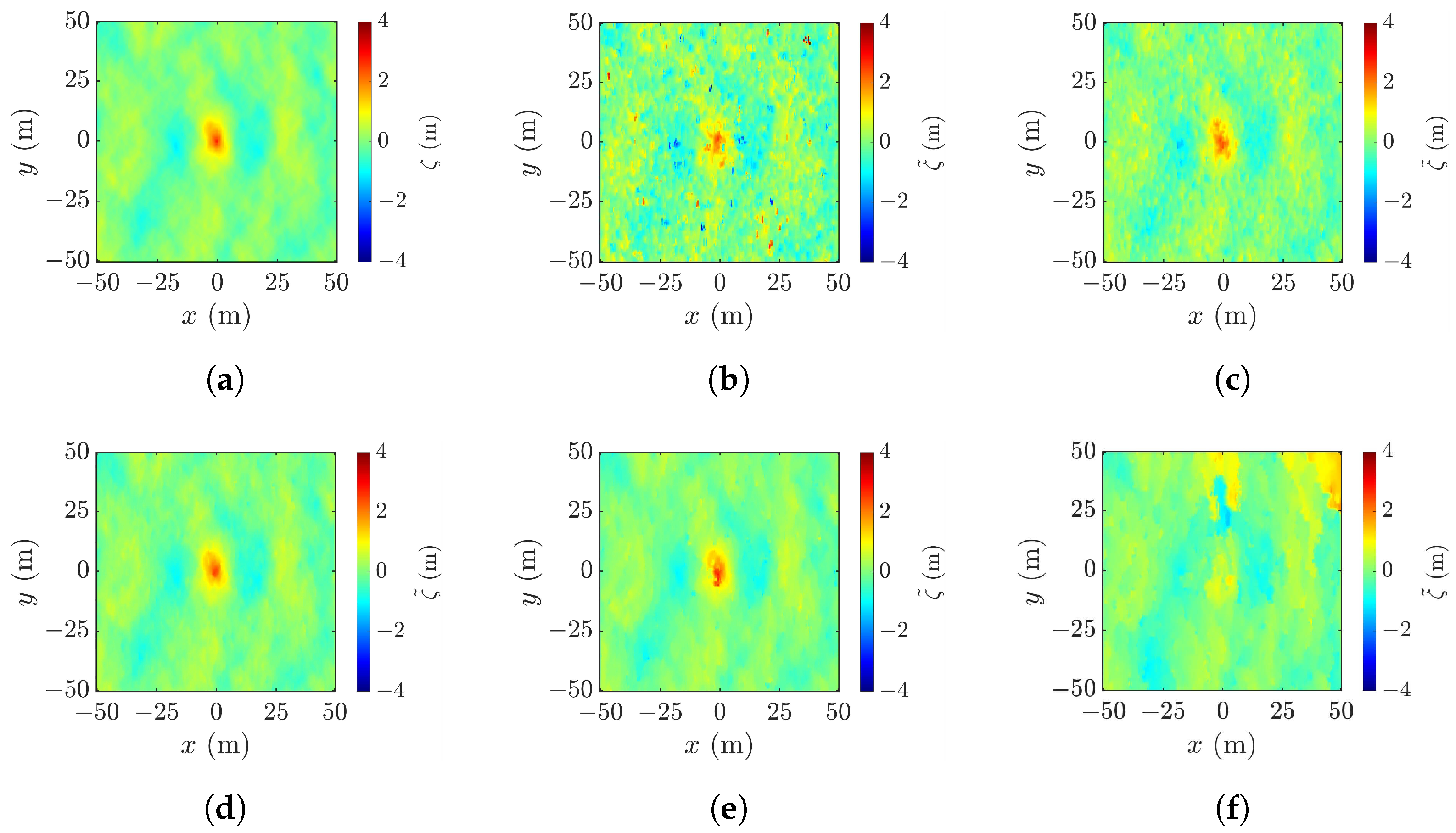
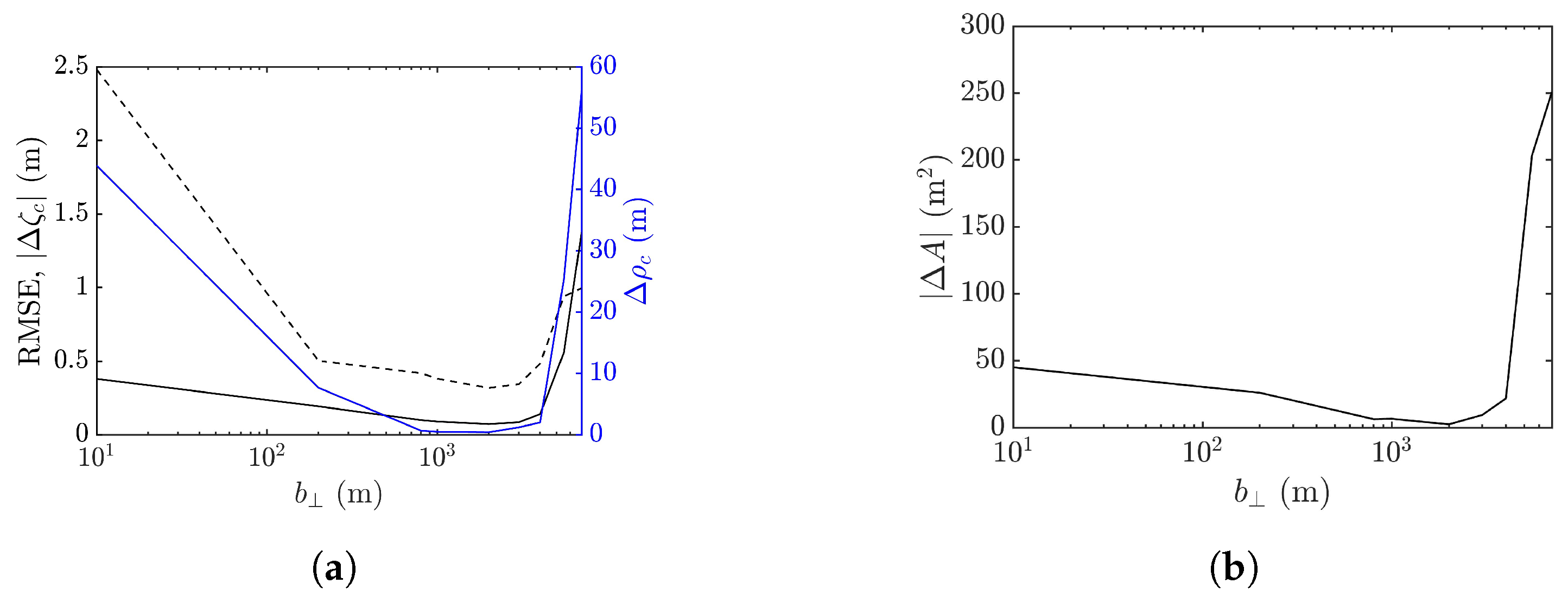
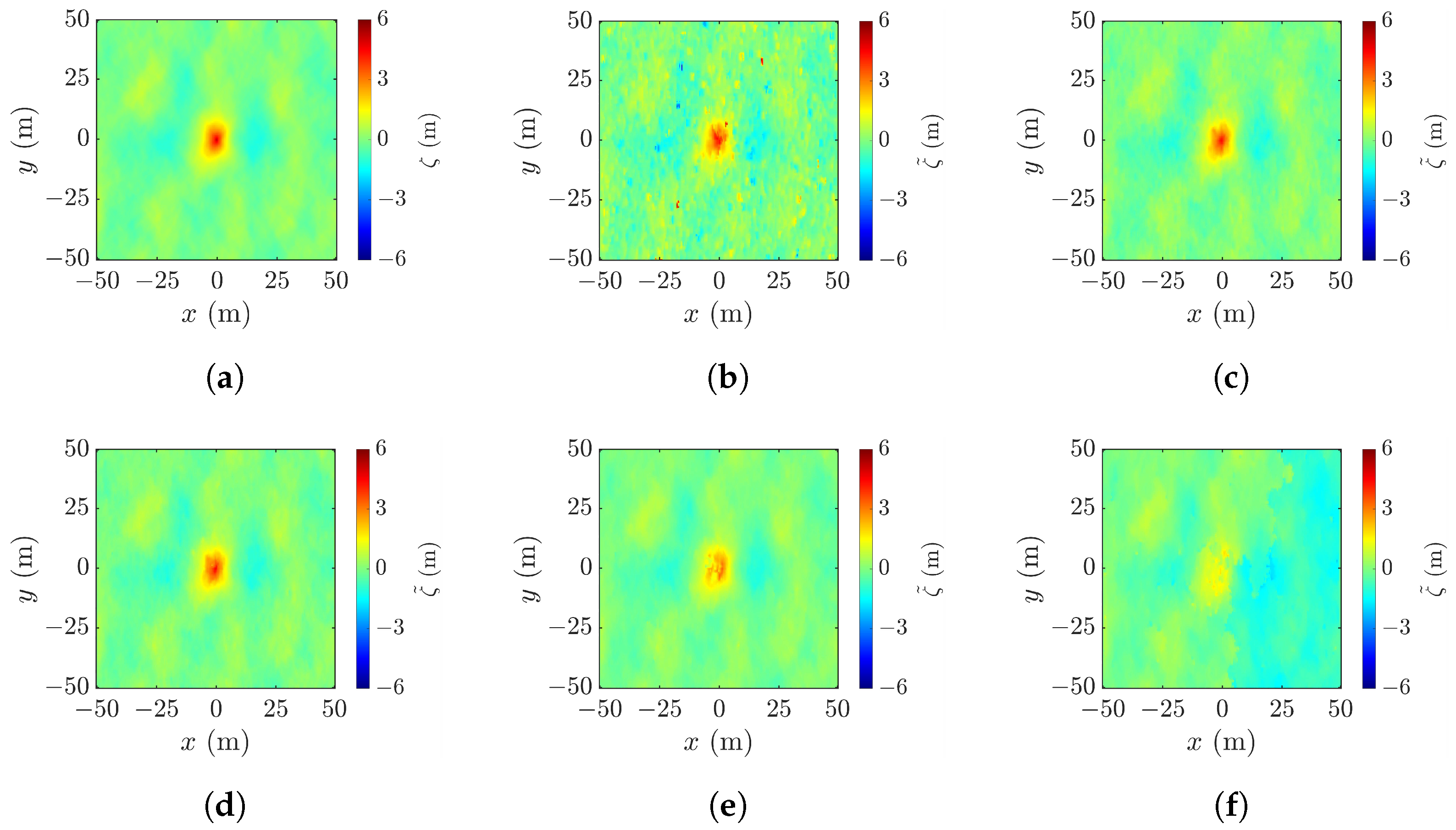
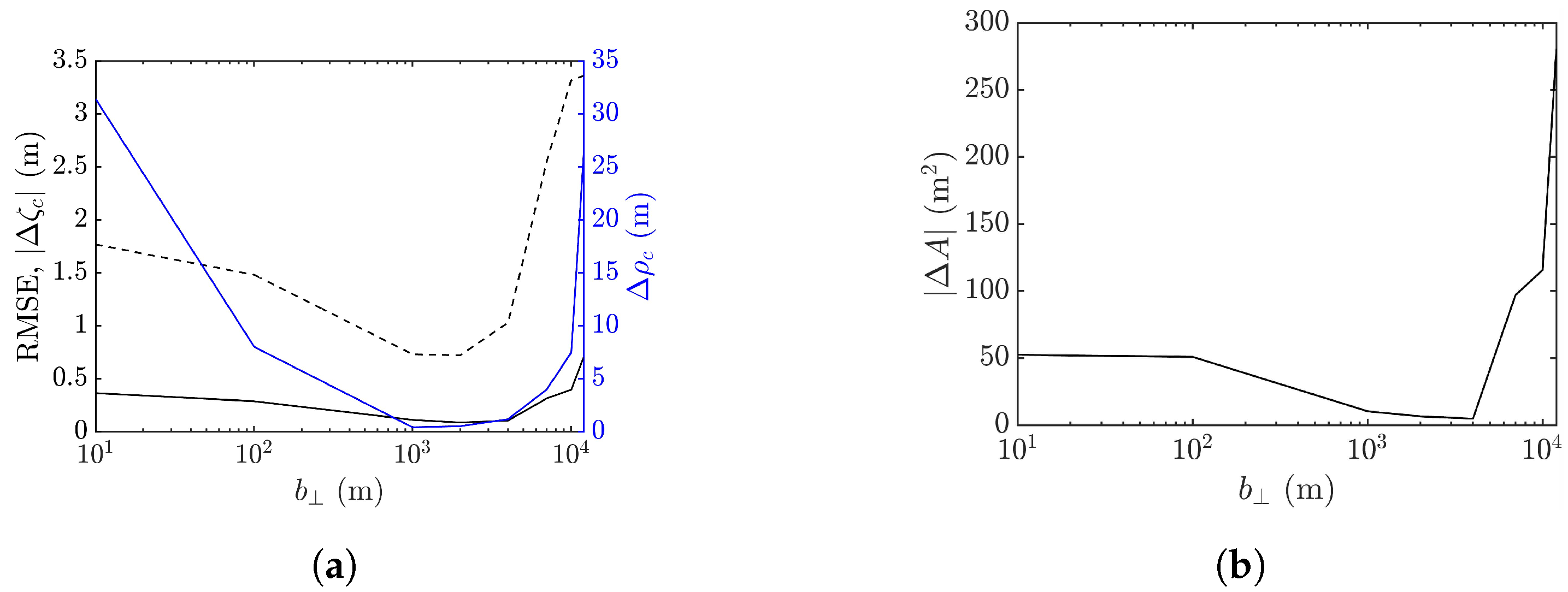
4.4. Effect of Cross-Track Baseline
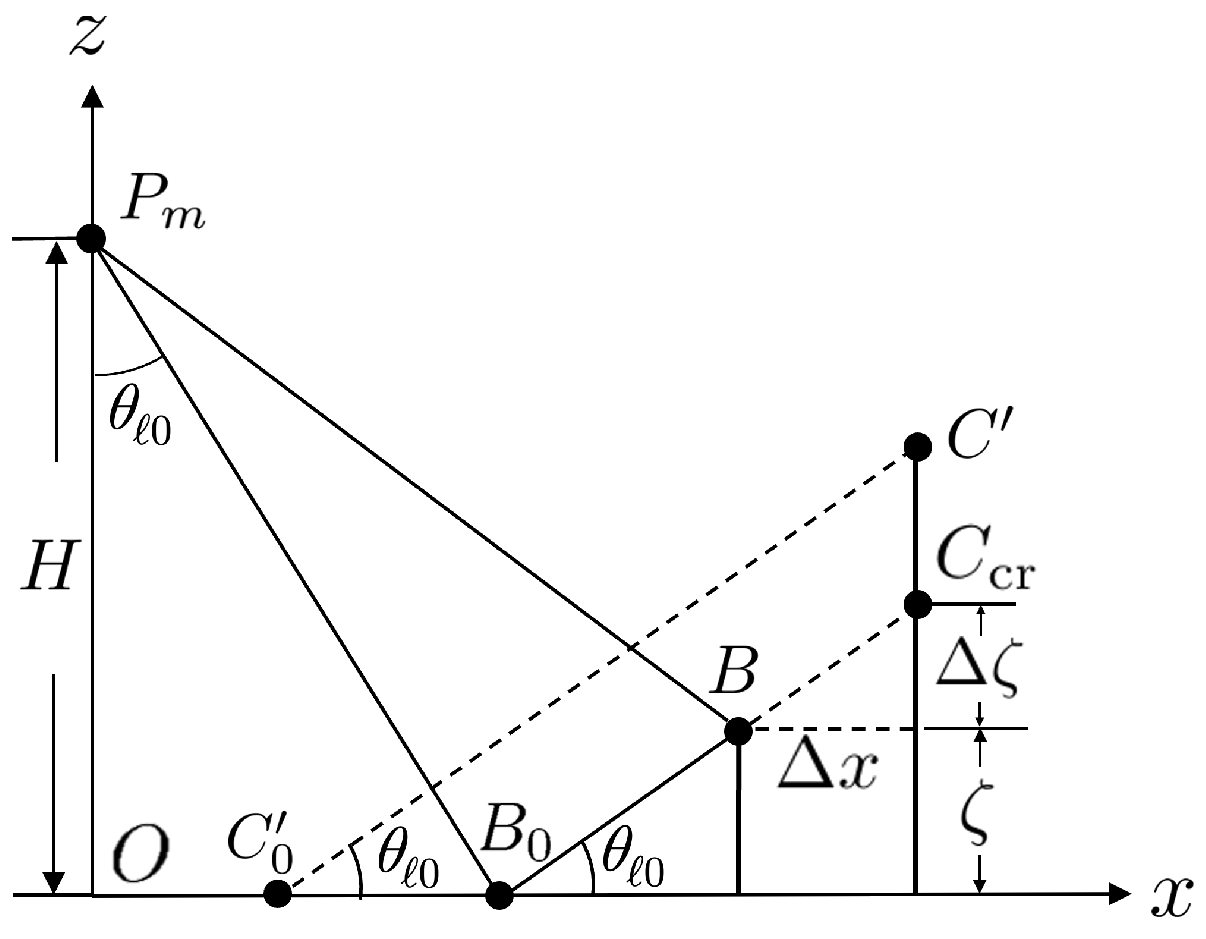
4.5. Geometric Correction
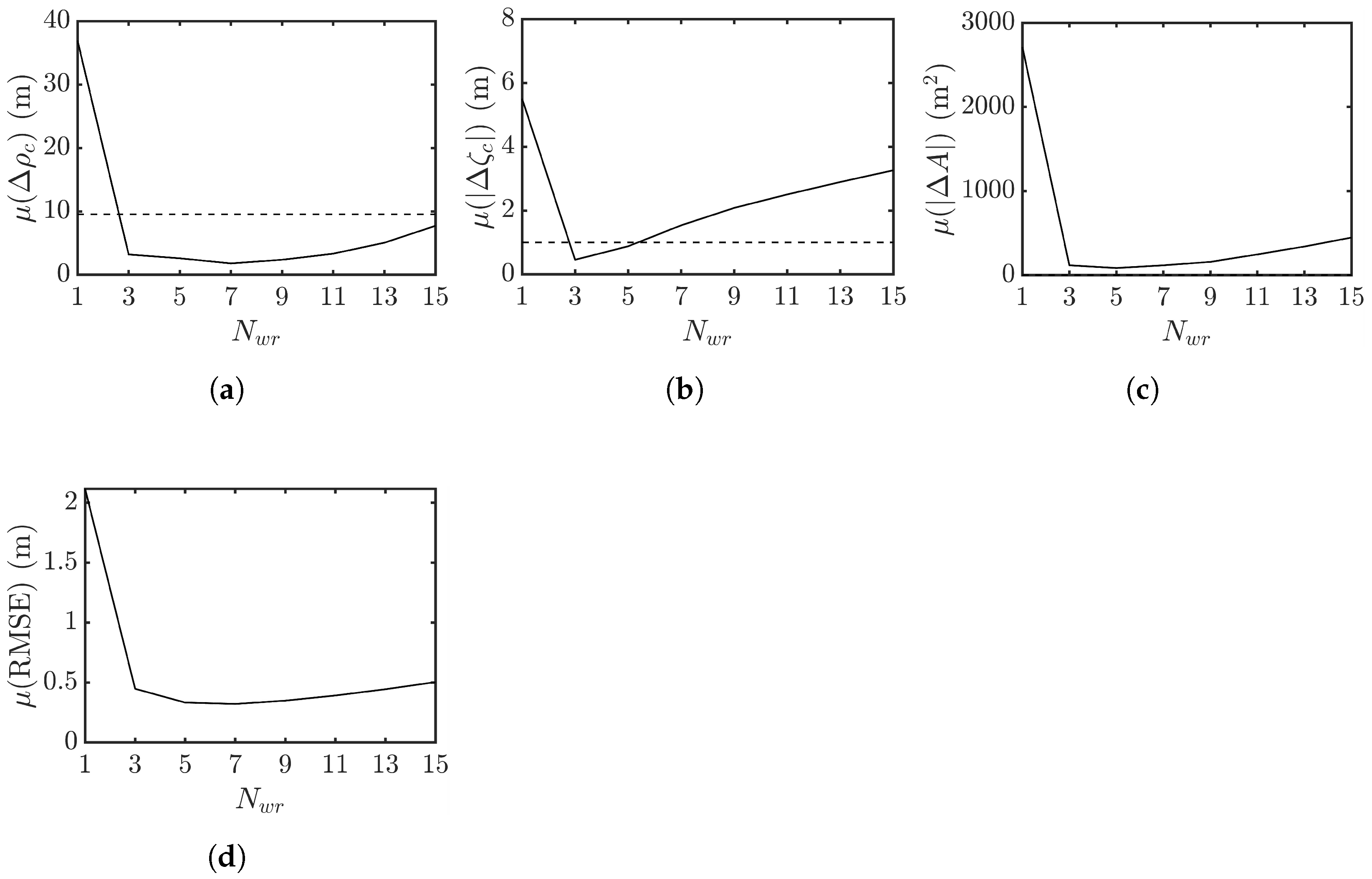
4.6. Effect of Multi-Look Window Size
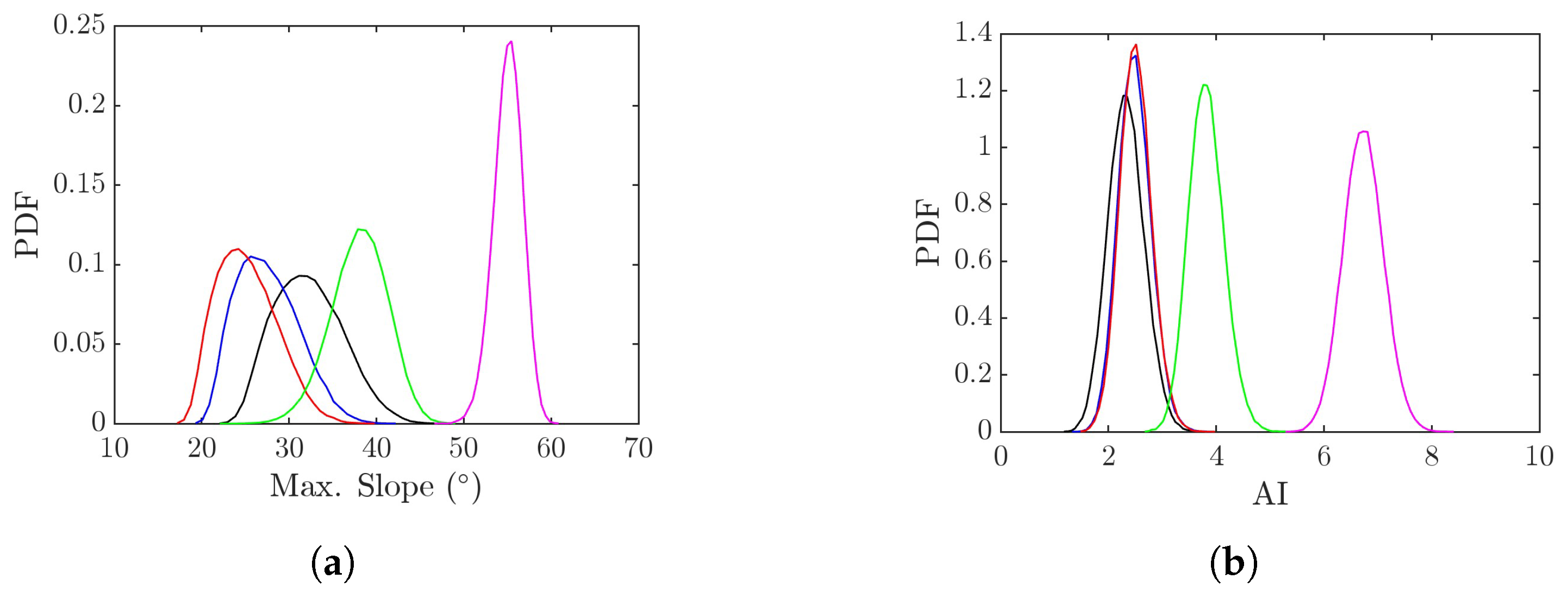
4.7. Effects of Wind Speed and Focusing Wave Ratio
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nikolkina, I.; Didenkulova, I. Rogue waves in 2006–2010. Nat. Hazards Earth Syst. Sci. 2011, 11, 2913–2924. [Google Scholar] [CrossRef]
- Dysthe, K.; Krogstad, H.; Hüller, P. Oceanic rogue waves. Ann. Rev. Fluid Mech. 2008, 40, 287–310. [Google Scholar] [CrossRef]
- Meucci, A.; Young, I.; Hemer, M.; Kirezci, E.; Ranasinghe, R. Projected 21st century changes in extreme wind-wave events. Sci. Adv. 2020, 6, eaaz7295. [Google Scholar] [CrossRef] [PubMed]
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Rosenthal, W.; Lehner, S. Rogue waves: Results of the MaxWave project. J. Offsh. Mech. Arct. Eng. 2008, 130, 021006. [Google Scholar] [CrossRef]
- Haver, S. A possible freak wave event measured at the Draupner jacket January 1 1995. In Proceedings of the Rogue Waves Workshop, Brest, France, 20–22 October 2004; pp. 1–8. [Google Scholar]
- McAllister, M.; Draycott, S.; Adcock, T.; Taylor, P.; van den Bremer, T. Laboratory recreation of the Draupner wave and the role of breaking in crossing seas. J. Fluid Mech. 2019, 860, 767–786. [Google Scholar] [CrossRef]
- Kuang, H.; Xie, T.; Chen, W.; Zou, G. Numerical study on SAR-based rogue wave detection Part one: SAR image simulation. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 24–26 June 2011; pp. 6572–6575. [Google Scholar]
- Kuang, H.; Xie, T.; Chen, W.; Zou, G. Numerical study on SAR-based rogue wave detection Part two: Rogue wave detection. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 24–26 June 2011; pp. 8743–8745. [Google Scholar]
- Han, L.; Wu, G.; Liu, B. Study on numerical simulation and electromagnetic scattering of time-invariant freak waves. Int. J. Ant. Propagat. 2022, 2022, 1951162. [Google Scholar] [CrossRef]
- Janssen, P.; Alpers, W. Why SAR wave mode data of ERS and Envisat are inadequate for giving the probability of occurrence of freak waves. In Proceedings of the SEASAR Workshop, Frascati, Italy, 23–26 January 2006; pp. 1–11. [Google Scholar]
- Vignudelli, S.; Birol, F.; Benveniste, J.; Fu, L.-L.; Picot, N.; Raynal, M.; Roinard, H. Satellite altimetry measurements of sea level in the coastal zone. Surv. Geophys. 2019, 40, 1319–1345. [Google Scholar] [CrossRef]
- Santos-Ferreira, A.; da Silva, J.; Srokosz, M. SAR-Mode altimetry observations of internal solitary waves in the tropical ocean part 1: Case studies. Remote Sens. 2018, 10, 644. [Google Scholar] [CrossRef]
- Rosen, P.; Hensley, S.; Joughin, I.; Li, F.; Madsen, S.; Rodriguez, E.; Goldstein, R. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, Y.; Zhang, L.; Wilson, J.P.; Zhu, R.; Chen, R.; Li, Z. Multibaseline interferometry based on independent component analysis and InSAR combinatorial modeling for high-precision DEM reconstruction. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5205417. [Google Scholar] [CrossRef]
- Liu, Y.; He, Y.; Yang, W.; Zhang, L. Spatio-temporal characteristics and driving mechanism of alpine peatland InSAR surface deformation–A case study of Maduo County, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 4492–4514. [Google Scholar] [CrossRef]
- Moller, D.; Hensley, S.; Sadowy, G.; Fisher, C.; Michel, T.; Zawadzki, M.; Rignot, E. The glacier and land ice surface topography interferometer: An airborne proof-of-concept demonstration of high-precision Ka-band single-pass elevation mapping. IEEE Trans. Geosci. Remote Sens. 2011, 49, 827–842. [Google Scholar] [CrossRef]
- Kong, W.; Liu, B.; Sui, X.; Zhang, R.; Sun, J. Ocean surface topography altimetry by large baseline cross-interferometry from satellite formation. Remote Sens. 2020, 12, 3519. [Google Scholar] [CrossRef]
- D’Amico, S.; Montenbruck, O. Proximity operations of formation-flying spacecraft using an eccentricity/inclination vector separation. J. Guid. Control Dyn. 2006, 29, 554–563. [Google Scholar] [CrossRef]
- Theodosiou, A.; Kleinherenbrink, M.; López-Dekker, P. Wide-swath ocean altimetry using multisatellite single-pass interferometry. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5210721. [Google Scholar] [CrossRef]
- Kong, W.; Chong, J.; Tan, H. Performance analysis of ocean surface topography altimetry by Ku-band near-nadir interferometric SAR. Remote Sens. 2017, 9, 933. [Google Scholar] [CrossRef]
- Fu, L.-L.; Pavelsky, T.; Cretaux, J.-F.; Morrow, R.; Farrar, J.-T.; Vaze, P.; Sengenes, P.; Vinogradova-Shiffer, N.; Sylvestre-Baron, A.; Picot, N.; et al. The Surface Water and Ocean Topography Mission: A breakthrough in radar remote sensing of the ocean and land surface water. Geophys. Res. Lett. 2024, 51, e2023GL107652. [Google Scholar] [CrossRef]
- Zhu, F.; Li, J.; Li, Y.; Xu, J.; Guo, J.; Zhou, J.; Sun, H. Estimating seafloor topography of the South China Sea using SWOT wide-swath altimetry data. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2025, 18, 3569–3580. [Google Scholar] [CrossRef]
- Zhang, B.; Wen, L.; Perrie, W.; Kudryavtsev, V. Sea surface height response to tropical cyclone from satellite altimeter observations and SAR estimates. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4203809. [Google Scholar] [CrossRef]
- Zhao, Y.; Fu, J.; Pang, Z.; Jiang, W.; Zhang, P.; Qi, Z. Validation of inland water surface elevation from SWOT satellite products: A case study in the middle and lower reaches of the Yangtze River. Remote Sens. 2025, 17, 1330. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, C.; Meng, J.; Li, S.; Sun, L. Research on internal solitary wave detection and analysis based on interferometric imaging radar altimeter onboard the Tiangong-2 space laboratory. Remote Sens. 2022, 14, 174. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, Y.; Dong, X.; Shi, X. Performance of Tiangong-2 interferometric imaging radar altimeter on marine gravity recovery over the South China Sea. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4207513. [Google Scholar] [CrossRef]
- Gemmrich, J.; Cicon, L. Generation mechanism and prediction of an observed extreme rogue wave. Sci. Rep. 2022, 12, 1718. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Slunyaev, A.; Mori, N.; Chabchoub, A. Experimental evidence of nonlinear focusing in standing water waves. Phys. Rev. Lett. 2022, 129, 144502. [Google Scholar] [CrossRef]
- Akhmediev, N. Waves that appear from nowhere: Complex rogue wave structures and their elementary particles. Front. Phys. 2021, 8, 612318. [Google Scholar] [CrossRef]
- Akhmediev, N.; Soto-Crespo, J.; Devine, N.; Hoffmann, N. Rogue wave spectra of the Sasa–Satsuma equation. Physica D 2015, 294, 37–42. [Google Scholar] [CrossRef]
- Ankiewicz, A.; Soto-Crespo, J.; Akhmediev, N. Rogue waves and rational solutions of the Hirota equation. Phys. Rev. E 2010, 81, 046602. [Google Scholar] [CrossRef]
- Ankiewicz, A.; Akhmediev, N. Rogue wave-type solutions of the mKdV equation and their relation to known NLSE rogue wave solutions. Nonlinear Dyn. 2018, 91, 1931–1938. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, W.; Wang, B.; Qin, H. The occurrence probability prediction model of 2D and 3D freak waves generated by wave superposition. Ocean Eng. 2023, 270, 113640. [Google Scholar] [CrossRef]
- Wu, G.; Liu, C.; Liang, Y. Computational simulation and modeling of freak waves based on Longuet-Higgins model and its electromagnetic scattering calculation. Complexity 2020, 2020, 2727681. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, N.; Yu, Y. An efficient focusing model for generation of freak waves. Acta Oceanol. Sin. 2011, 30, 19–26. [Google Scholar] [CrossRef]
- Hu, Z.; Tang, W.; Xue, H. A probability-based superposition model of freak wave simulation. Appl. Ocean Res. 2014, 47, 284–290. [Google Scholar] [CrossRef]
- Adcock, T.; Taylor, P.; Yan, S.; Ma, Q.; Janssen, P. Did the Draupner wave occur in a crossing sea? Proc. R. Soc. A 2011, 467, 3004–3021. [Google Scholar] [CrossRef]
- Holthuijsen, L. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Stansberg, C.; Contento, G.; Hong, S.; Irani, M.; Ishida, S.; Mercier, R.; Wang, Y.; Wolfram, J.; Chaplin, J.; Kriebel, D. The specialist committee on waves: Final report and recommendations to the 23rd ITTC. In Proceedings of the International Towing Tank Conference, Venice, Italy, 8–14 September 2002; pp. 505–551. [Google Scholar]
- Longuet-Higgins, M. On the statistical distribution of the heights of sea waves. J. Mar. Res. 1953, 11, 245–266. [Google Scholar]
- Apel, J. Principles of Ocean Physics; International Geophysics Series; Academic Press: Cambridge, MA, USA, 1987; Volume 38. [Google Scholar]
- Richards, M. A beginner’s guide to interferometric SAR concepts and signal processing. IEEE Aerosp. Electron. Syst. Mag. 2006, 21, 5–29. [Google Scholar]
- Zou, W.; Li, Y.; Li, Z.; Dong, X. Improvement of the accuracy of InSAR image co-registration based on tie points—A review. Sensors 2009, 9, 1259–1281. [Google Scholar] [CrossRef]
- Smith, J. Spectral Audio Signal Processing. Available online: https://ccrma.stanford.edu/%7Ejos/sasp/Practical_Zero_Padding.html (accessed on 11 October 2023).
- Arevalillo-Herráez, M.; Villatoro, F.; Gdeisat, M. A robust and simple measure for quality-guided 2D phase unwrapping algorithms. IEEE Trans. Image Proc. 2016, 25, 2601–2609. [Google Scholar] [CrossRef]
- Arevalillo-Herráez, M.; Burton, D.; Lalor, M.; Gdeisat, M. Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path. Appl. Opt. 2002, 41, 7437–7444. [Google Scholar] [CrossRef]
- Ghiglia, D.; Pritt, M. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Cavaleri, L.; Barbariol, F.; Benetazzo, A.; Bertotti, L.; Bidlot, J.-R.; Janssen, P.; Wedi, N. The Draupner wave: A fresh look and the emerging view. J. Geophys. Res. Oceans 2016, 121, 6061–6075. [Google Scholar] [CrossRef]
- van Groesen, E.; Turnip, P.; Kurnia, R. High waves in Draupner seas—Part 1: Numerical simulations and characterization of the seas. J. Ocean Eng. Mar. Energy 2017, 3, 233–245. [Google Scholar] [CrossRef]
- Fjørtoft, R.; Gaudin, J.M.; Pourthié, N.; Lalaurie, J.C.; Mallet, A.; Nouvel, J.F.; Martinot-Lagarde, J.; Oriot, H.; Borderies, P.; Ruiz, C.; et al. KaRIn on SWOT: Characteristics of near-nadir Ka-band interferometric SAR imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2172–2185. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Q.; Hu, J. Generation of complete SAR geometric distortion maps based on DEM and neighbor gradient algorithm. Appl. Sci. 2018, 8, 2206. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Li, T.; Gao, Y.; Chen, Q.; Zhang, X. Modeling the optimal baseline for a spaceborne bistatic SAR system to generate DEMs. ISPRS Int. J. Geo-Inf. 2020, 9, 108. [Google Scholar] [CrossRef]
- Han, X.; Wang, X.; He, Z.; Wu, J. Significant wave height retrieval in tropical cyclone conditions using CYGNSS data. Remote Sens. 2024, 16, 4782. [Google Scholar] [CrossRef]
- Qiao, X.; Huang, W. WaveTransNet: A transformer-based network for global significant wave height retrieval from spaceborne GNSS-R data. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4208011. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Y.; Wang, W. A new approach for ocean surface wind speed retrieval using Sentinel-1 dual-polarized imagery. Remote Sens. 2023, 15, 4267. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
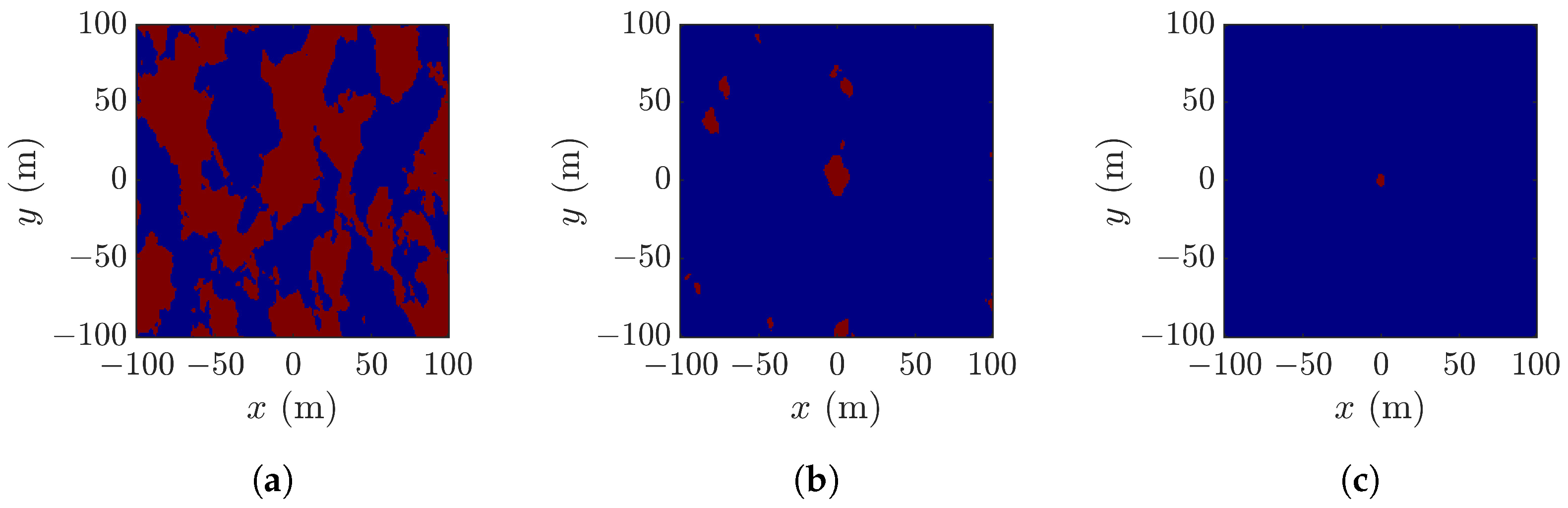






| Parameter | Symbol | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|---|
| wind speed | (m/s) | 23 | 13.7 | 7 | 7 | 7 |
| significant wave height | (m) | 12 | 4 | 1 | 1 | 1 |
| peak angular frequency | (rad/s) | 0.44 | 0.70 | 1.36 | 1.36 | 1.36 |
| enhancement factor | 2.51 | 2.51 | 2.51 | 2.51 | 2.51 | |
| energy scaling factor | 0.0129 | 0.0092 | 0.0081 | 0.0081 | 0.0081 | |
| no. of freq. components | 200 | 200 | 200 | 200 | 200 | |
| no. of angular components | 36 | 36 | 36 | 36 | 36 | |
| focusing wave ratio | 0.01 | 0.01 | 0.01 | 0.03 | 0.1 |
| Parameter | Symbol | Case a | Case b | Case c |
|---|---|---|---|---|
| carrier frequency | (GHz) | 35 | 35 | 35 |
| signal bandwidth | (MHz) | 93.9 | 375.6 | 306.7 |
| radar wavelength | (cm) | 0.86 | 0.86 | 0.86 |
| look angle | (°) | 4/45 | 45 | 60 |
| polarization | ||||
| squint angle | (°) | 0 | 0 | 0 |
| platform altitude | H (km) | 873 | 873 | 873 |
| platform velocity | (m/s) | 7412.4 | 7412.4 | 7412.4 |
| range sampling freq. | (MHz) | 112.7 | 450.7 | 368.0 |
| pulse repetition freq. | (Hz) | 3600 | 6900 | 6900 |
| pulse width | (s) | 3/1.5 | 1.5 | 1.5 |
| range samples | 4096/512 | 2048 | 1024 | |
| azimuth samples | 1024/2048 | 8192 | 8192 | |
| coherent interval | (s) | 0.31 | 0.62 | 0.88 |
| along-track baseline | (m) | 0 | 0 | 0 |
| cross-track baseline | (m) | 200/400 | 2000 | 2000 |
| perp. baseline | (m) | 200/400 | 2000 | 2000 |
| parallel baseline | (m) | 0 | 0 | 0 |
| ground range reso. | (m) | 2 | 0.5 | 0.5 |
| azimuth reso. | (m) | 2 | 1 | 1 |
| oversampling ratio | 16 | 16 | 16 | |
| no. of sub-images | ||||
| multi-look window |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.-C.; Kiang, J.-F. Detection of Elusive Rogue Wave with Cross-Track Interferometric Synthetic Aperture Radar Imaging Approach. Sensors 2025, 25, 2781. https://doi.org/10.3390/s25092781
Wang T-C, Kiang J-F. Detection of Elusive Rogue Wave with Cross-Track Interferometric Synthetic Aperture Radar Imaging Approach. Sensors. 2025; 25(9):2781. https://doi.org/10.3390/s25092781
Chicago/Turabian StyleWang, Tung-Cheng, and Jean-Fu Kiang. 2025. "Detection of Elusive Rogue Wave with Cross-Track Interferometric Synthetic Aperture Radar Imaging Approach" Sensors 25, no. 9: 2781. https://doi.org/10.3390/s25092781
APA StyleWang, T.-C., & Kiang, J.-F. (2025). Detection of Elusive Rogue Wave with Cross-Track Interferometric Synthetic Aperture Radar Imaging Approach. Sensors, 25(9), 2781. https://doi.org/10.3390/s25092781






