Understanding Acceleration-Based Load Metrics: From Concepts to Implementation
Abstract
1. Introduction
2. Analysis of External Load Metrics Based on Acceleration
3. Experimental Implementation
3.1. Data Acquisition, Processing, and Statistical Analysis
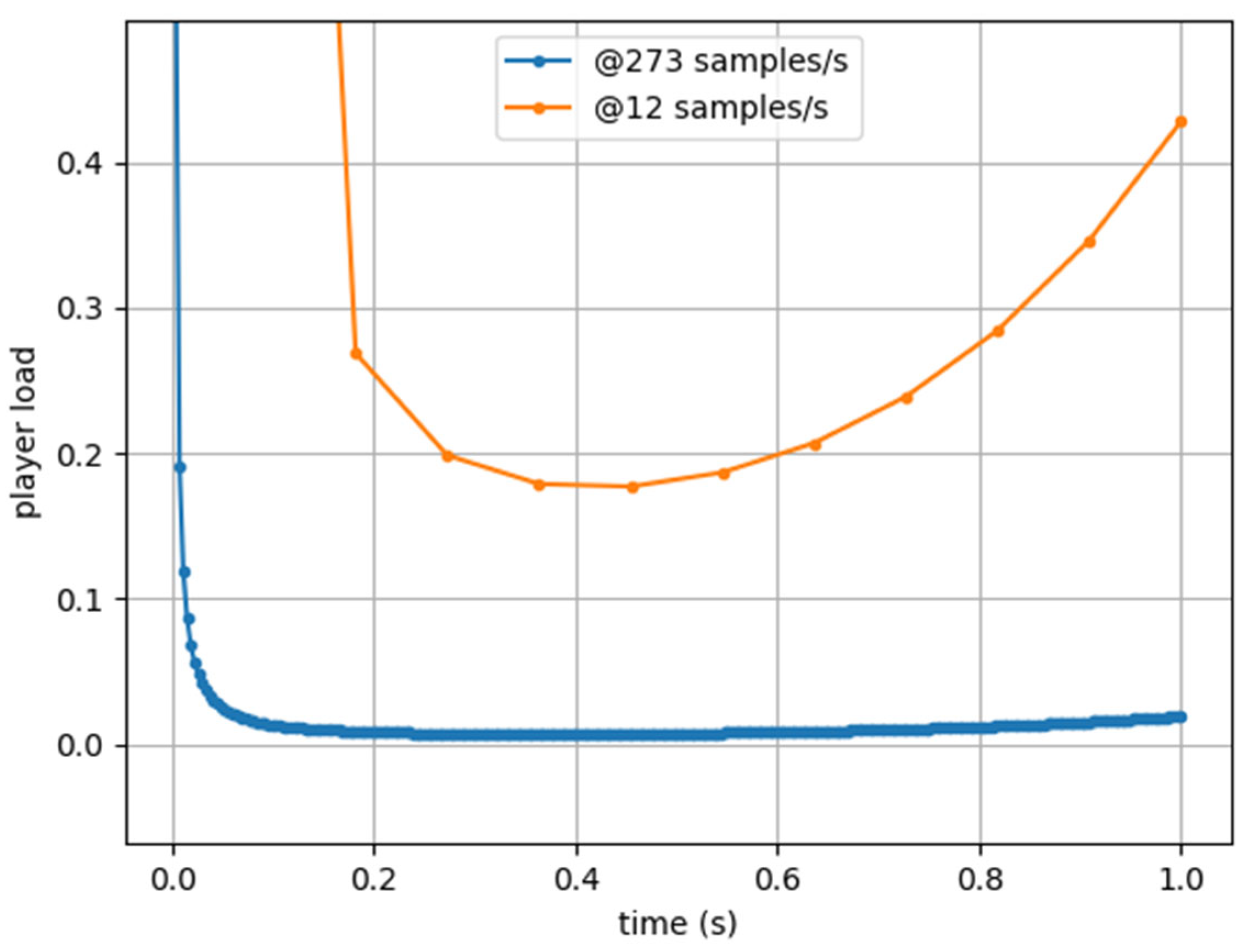
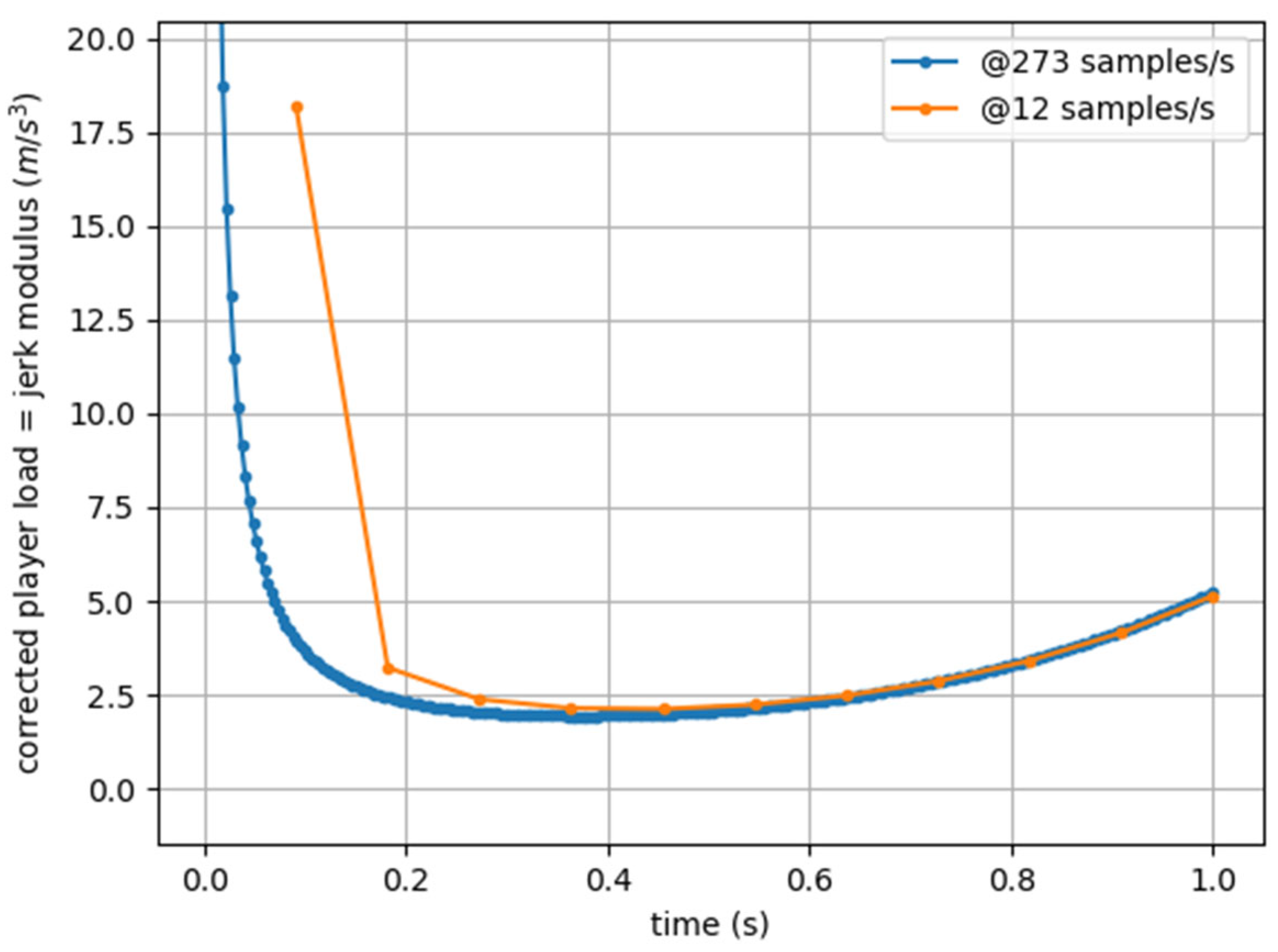
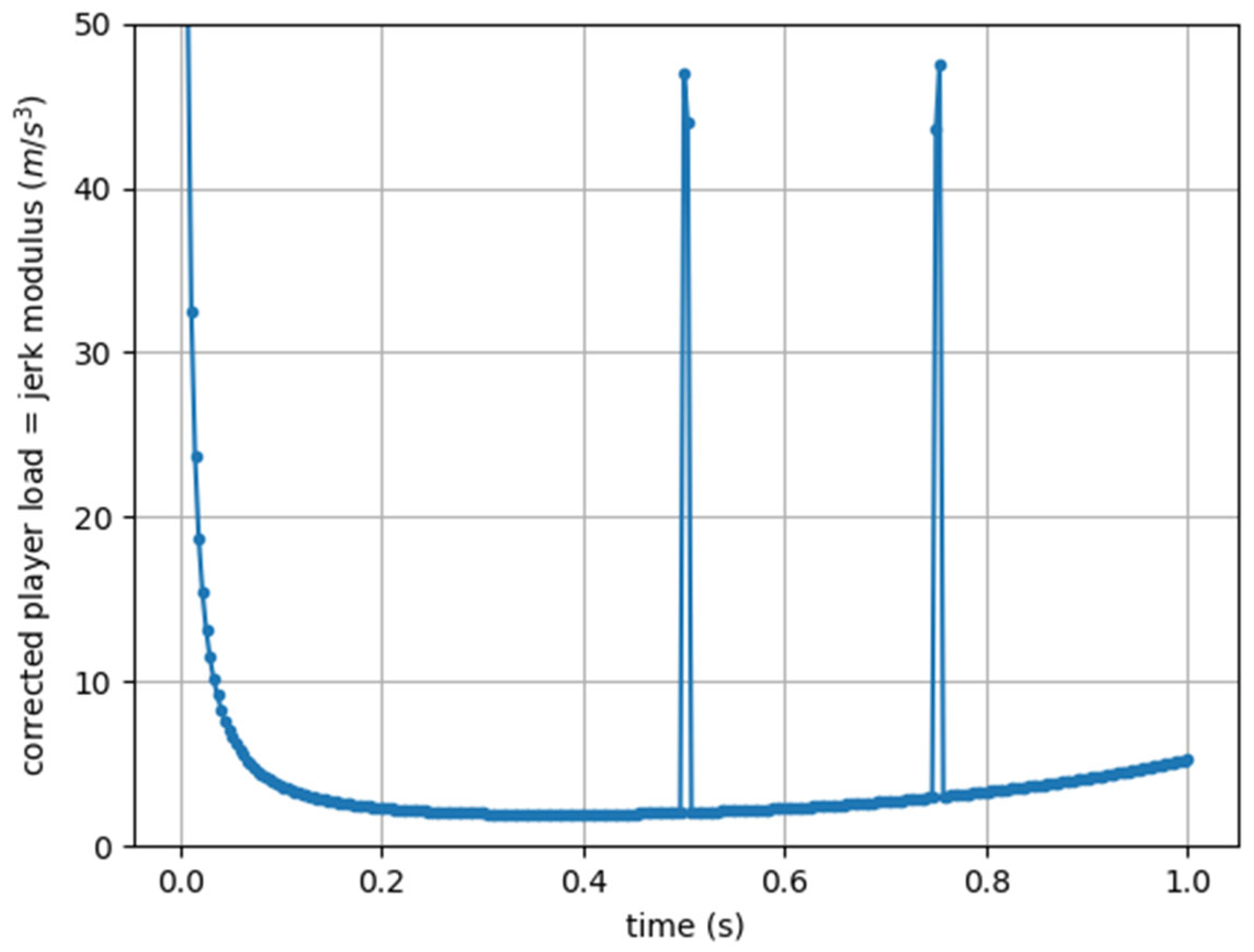
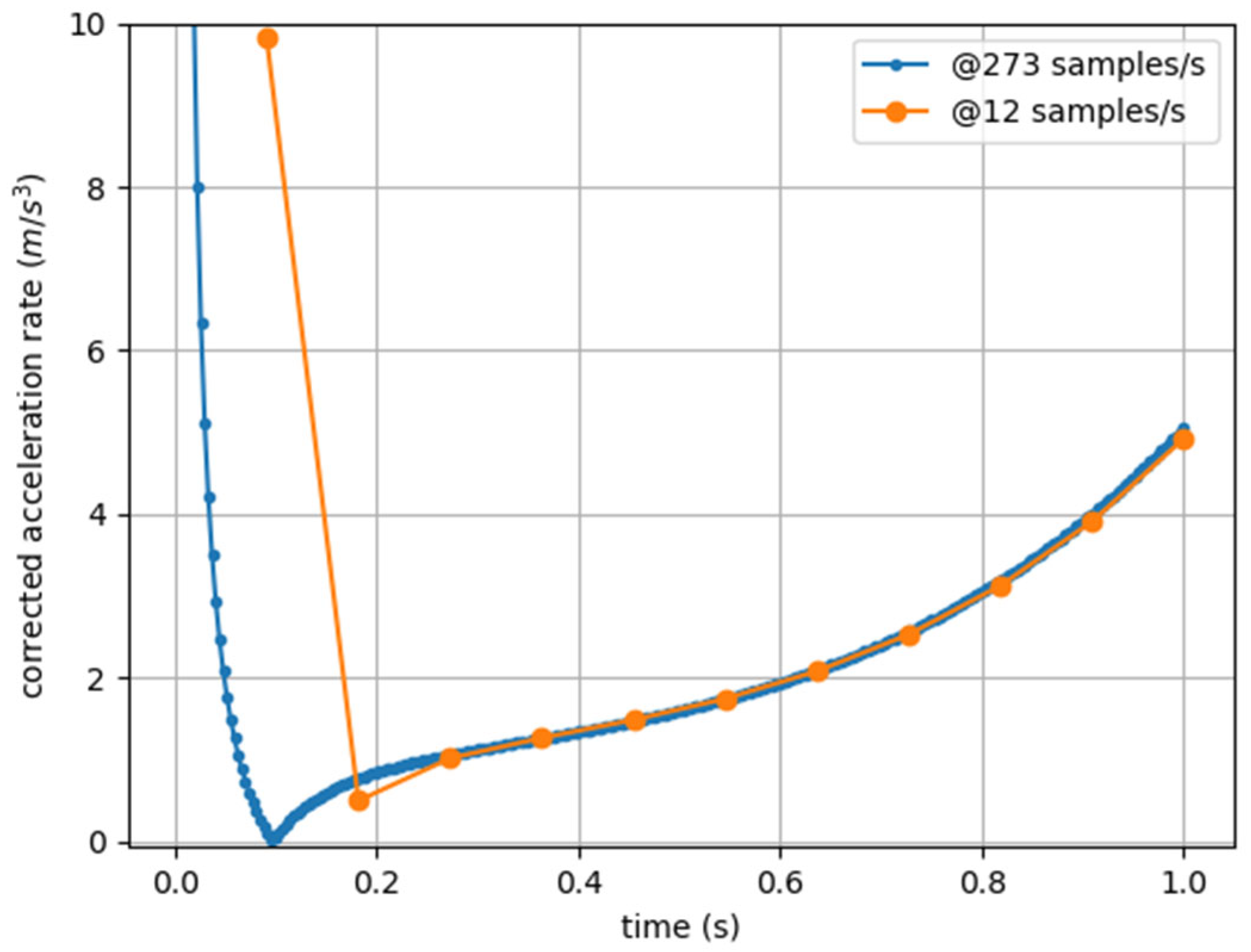
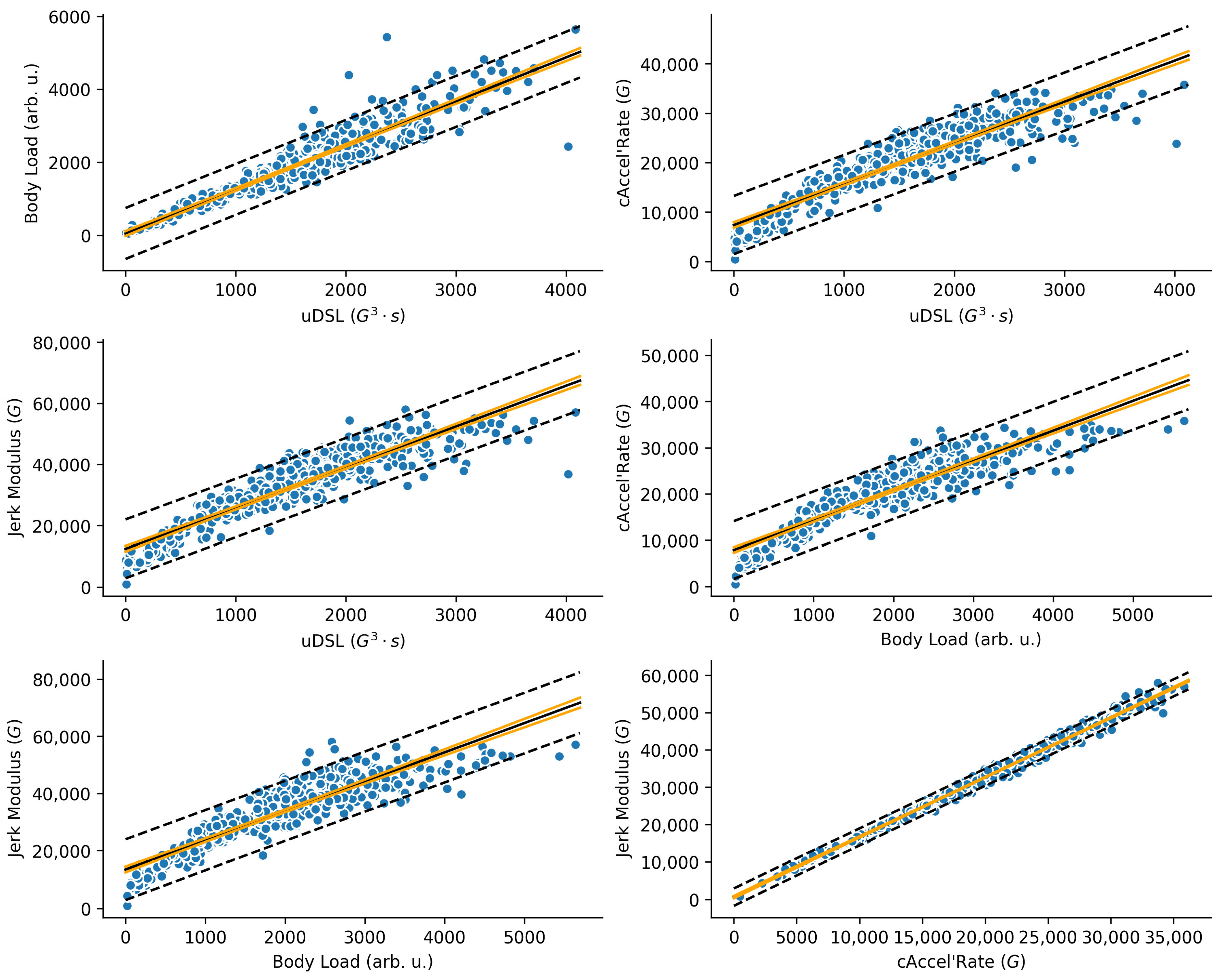
3.2. Experimental Results
4. Discussion
5. Final Considerations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends Supporting the In-Field Use of Wearable Inertial Sensors for Sport Performance Evaluation: A Systematic Review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef]
- Staunton, C.A.; Abt, G.; Weaving, D.; Wundersitz, D.W.T. Misuse of the term ‘load’ in sport and exercise science. J. Sci. Med. Sport 2022, 25, 439–444. [Google Scholar] [CrossRef] [PubMed]
- Vanrenterghem, J.; Nedergaard, N.J.; Robinson, M.A.; Drust, B. Training Load Monitoring in Team Sports: A Novel Framework Separating Physiological and Biomechanical Load-Adaptation Pathways. Sports Med. 2017, 47, 2135–2142. [Google Scholar] [CrossRef]
- Bredt, S.D.T.; Chagas, M.H.; Peixoto, G.H.; Menzel, H.J.; de Andrade, A.G.P. Understanding Player Load: Meanings and Limitations. J. Hum. Kinet. 2020, 71, 5–9. [Google Scholar] [CrossRef] [PubMed]
- Impellizzeri, F.M.; Jeffries, A.C.; Weisman, A.; Coutts, A.J.; McCall, A.; McLaren, S.J.; Kalkhoven, J. The ‘training load’ construct: Why it is appropriate and scientific. J. Sci. Med. Sport 2022, 25, 445–448. [Google Scholar] [CrossRef] [PubMed]
- Trost, S.G.; Mciver, K.L.; Pate, R.R. Conducting accelerometer-based activity assessments in field-based research. Med. Sci. Sports Exerc. 2005, 37, S531–S543. [Google Scholar] [CrossRef]
- Cunniffe, B.; Proctor, W.; Baker, J.S.; Davies, B. An Evaluation of the Physiological Demands of Elite Rugby Union Using Global Positioning System Tracking Software. J. Strength Cond. Res. 2009, 23, 1195–1203. [Google Scholar] [CrossRef]
- Treuth, M.S.; Schmitz, K.; Catellier, D.J.; McMurray, R.G.; Murray, D.M.; Almeida, M.J.; Going, S.; Norman, J.E.; Pate, R. Defining accelerometer thresholds for activity intensities in adolescent girls. Med. Sci. Sports Exerc. 2004, 36, 1259–1266. [Google Scholar]
- Rowlands, A.V.; Stiles, V.H. Accelerometer counts and raw acceleration output in relation to mechanical loading. J. Biomech. 2012, 45, 448–454. [Google Scholar] [CrossRef]
- Delves, R.I.M.; Aughey, R.J.; Ball, K.; Duthie, G.M. The Quantification of Acceleration Events in Elite Team Sport: A Systematic Review. Sports Med.—Open 2021, 7, 45. [Google Scholar] [CrossRef]
- Montgomery, P.G.; Pyne, D.B.; Minahan, C.L. The Physical and Physiological Demands of Basketball Training and Competition. Int. J. Sport Physiol. 2010, 5, 75–86. [Google Scholar] [CrossRef]
- Gomez-Carmona, C.D.; Bastida-Castillo, A.; Ibanez, S.J.; Pino-Ortega, J. Accelerometry as a method for external workload monitoring in invasion team sports. A systematic review. PLoS ONE 2020, 15, e0236643. [Google Scholar] [CrossRef] [PubMed]
- García-Sánchez, C.; Navarro, R.M.; Karcher, C.; de la Rubia, A. Physical Demands during Official Competitions in Elite Handball: A Systematic Review. Int. J. Environ. Res. Public Health 2023, 20, 3353. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Carmona, C.D.; Pino-Ortega, J.; Sánchez-Ureña, B.; Ibáñez, S.J.; Rojas-Valverde, D. Accelerometry-Based External Load Indicators in Sport: Too Many Options, Same Practical Outcome? Int. J. Environ. Res. Public Health 2019, 16, 5101. [Google Scholar] [CrossRef] [PubMed]
- Gaudino, P.; Iaia, F.M.; Strudwick, A.J.; Hawkins, R.D.; Alberti, G.; Atkinson, G.; Gregson, W. Factors influencing perception of effort (session rating of perceived exertion) during elite soccer training. Int. J. Sports Physiol. Perform. 2015, 10, 860–864. [Google Scholar] [CrossRef]
- Hollville, E.; Couturier, A.; Guilhem, G.; Rabita, G. A Novel Accelerometry-Based Metric to Improve Estimation of Whole-Body Mechanical Load. Sensors 2021, 21, 3398. [Google Scholar] [CrossRef]
- Mateus, N.; Abade, E.; Coutinho, D.; Gómez, M.-Á.; Peñas, C.L.; Sampaio, J. Empowering the Sports Scientist with Artificial Intelligence in Training, Performance, and Health Management. Sensors 2025, 25, 139. [Google Scholar] [CrossRef]
- Buchheit, M.; Laursen, P.B. Sports Science 3.0: Integrating Technology and AI with Foundational Knowledge. Sport Perform. Sci. Rep. 2024, 231, 1–6. [Google Scholar]
- Gabbett, T.J.; Oetter, E. From Tissue to System: What Constitutes an Appropriate Response to Loading? Sports Med. 2025, 55, 17–35. [Google Scholar] [CrossRef]
- Hanson, B.; Stall, S.; Cutcher-Gershenfeld, J.; Vrouwenvelder, K.; Wirz, C.; Rao, Y.D.; Peng, G. Garbage in, garbage out: Mitigating risks and maximizing benefits of AI in research. Nature 2023, 623, 28–31. [Google Scholar] [CrossRef]
- Boyd, L.J.; Ball, K.; Aughey, R.J. The Reliability of MinimaxX Accelerometers for Measuring Physical Activity in Australian Football. Int. J. Sport Physiol. 2011, 6, 311–321. [Google Scholar] [CrossRef] [PubMed]
- Beato, M.; De Keijzer, K.L.; Carty, B.; Connor, M. Monitoring Fatigue During Intermittent Exercise With Accelerometer-Derived Metrics. Front. Physiol. 2019, 10, 780. [Google Scholar] [CrossRef]
- Bowen, L.; Gross, A.S.; Gimpel, M.; Li, F.-X. Accumulated workloads and the acute: Chronic workload ratio relate to injury risk in elite youth football players. Br. J. Sports Med. 2017, 51, 452–459. [Google Scholar] [CrossRef]
- Reche-Soto, P.; Cardona-Nieto, D.; Diaz-Suarez, A.; Bastida-Castillo, A.; Gomez-Carmona, C.; Garcia-Rubio, J.; Pino-Ortega, J. Player Load and Metabolic Power Dynamics as Load Quantifiers in Soccer. J. Hum. Kinet. 2019, 69, 259–269. [Google Scholar] [CrossRef]
- Dalen, T.; Jorgen, I.; Gertjan, E.; Havard, H.G.; Ulrik, W. Player Load, Acceleration, and Deceleration during Forty-Five Competitive Matches of Elite Soccer. J. Strength Cond. Res. 2016, 30, 351–359. [Google Scholar] [CrossRef] [PubMed]
- Colby, M.J.; Dawson, B.; Heasman, J.; Rogalski, B.; Gabbett, T.J. Accelerometer and GPS-Derived Running Loads and Injury Risk in Elite Australian Footballers. J. Strength Cond. Res. 2014, 28, 2244–2252. [Google Scholar] [CrossRef]
- WIMU PRO. Hudl 9.87; WIMU: Lincoln, NE, USA, 2022; Available online: https://www.hudl.com/en_gb/products/wimu/wimu-hardware (accessed on 15 February 2025).
- Migueles, J.H.; Cadenas-Sanchez, C.; Ekelund, U.; Delisle Nyström, C.; Mora-Gonzalez, J.; Löf, M.; Labayen, I.; Ruiz, J.R.; Ortega, F.B. Accelerometer Data Collection and Processing Criteria to Assess Physical Activity and Other Outcomes: A Systematic Review and Practical Considerations. Sports Med. 2017, 47, 1821–1845. [Google Scholar] [CrossRef]
- Thomas, S.J.; Zeni, J.A.; Winter, D.A. Winter’s Biomechanics and Motor Control of Human Movement, 5th ed.; Wiley: Hoboken, NJ, USA, 2022. [Google Scholar]
- Bakdash, J.Z.; Marusich, L.R. Repeated Measures Correlation. Front. Psychol. 2017, 8, 456. [Google Scholar] [CrossRef] [PubMed]
- Staunton, C.; Wundersitz, D.; Gordon, B.; Kingsley, M. Discrepancies Exist between Exercise Prescription and Dose in Elite Women’s Basketball Pre-Season. Sports 2020, 8, 70. [Google Scholar] [CrossRef]
- Saal, C.; Baumgart, C.; Wegener, F.; Ackermann, N.; Sölter, F.; Hoppe, M.W. Physical match demands of four LIQUI-MOLY Handball-Bundesliga teams from 2019–2022: Effects of season, team, match outcome, playing position, and halftime. Front. Sports Act. Living 2023, 5, 1183881. [Google Scholar] [CrossRef]
- Aguiar, M.V.D.; Botelho, G.M.A.; Gonçalves, B.S.V.; Sampaio, J.E. Physiological Responses and Activity Profiles of Football Small-Sided Games. J. Strength Cond. Res. 2013, 27, 1287–1294. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Carmona, C.D.; Bastida-Castillo, A.; González-Custodio, A.; Olcina, G.; Pino-Ortega, J. Using an Inertial Device (WIMU PRO) to Quantify Neuromuscular Load in Running: Reliability, Convergent Validity, and Influence of Type of Surface and Device Location. J. Strength Cond. Res. 2020, 34, 365–373. [Google Scholar] [CrossRef] [PubMed]
- Edwards, S.; White, S.; Humphreys, S.; Robergs, R.; O’Dwyer, N. Caution using data from triaxial accelerometers housed in player tracking units during running. J. Sports Sci. 2019, 37, 810–818. [Google Scholar] [CrossRef] [PubMed]

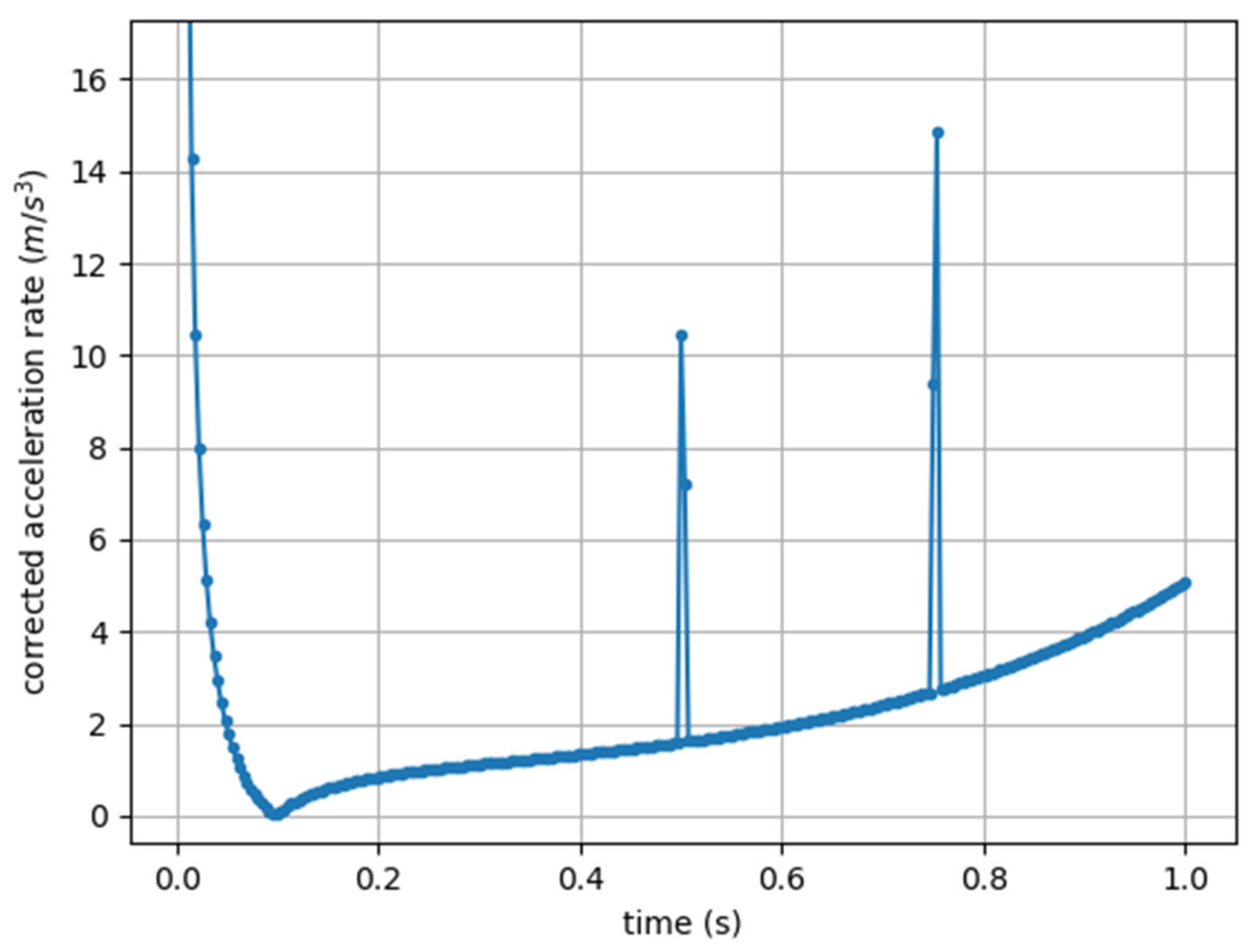
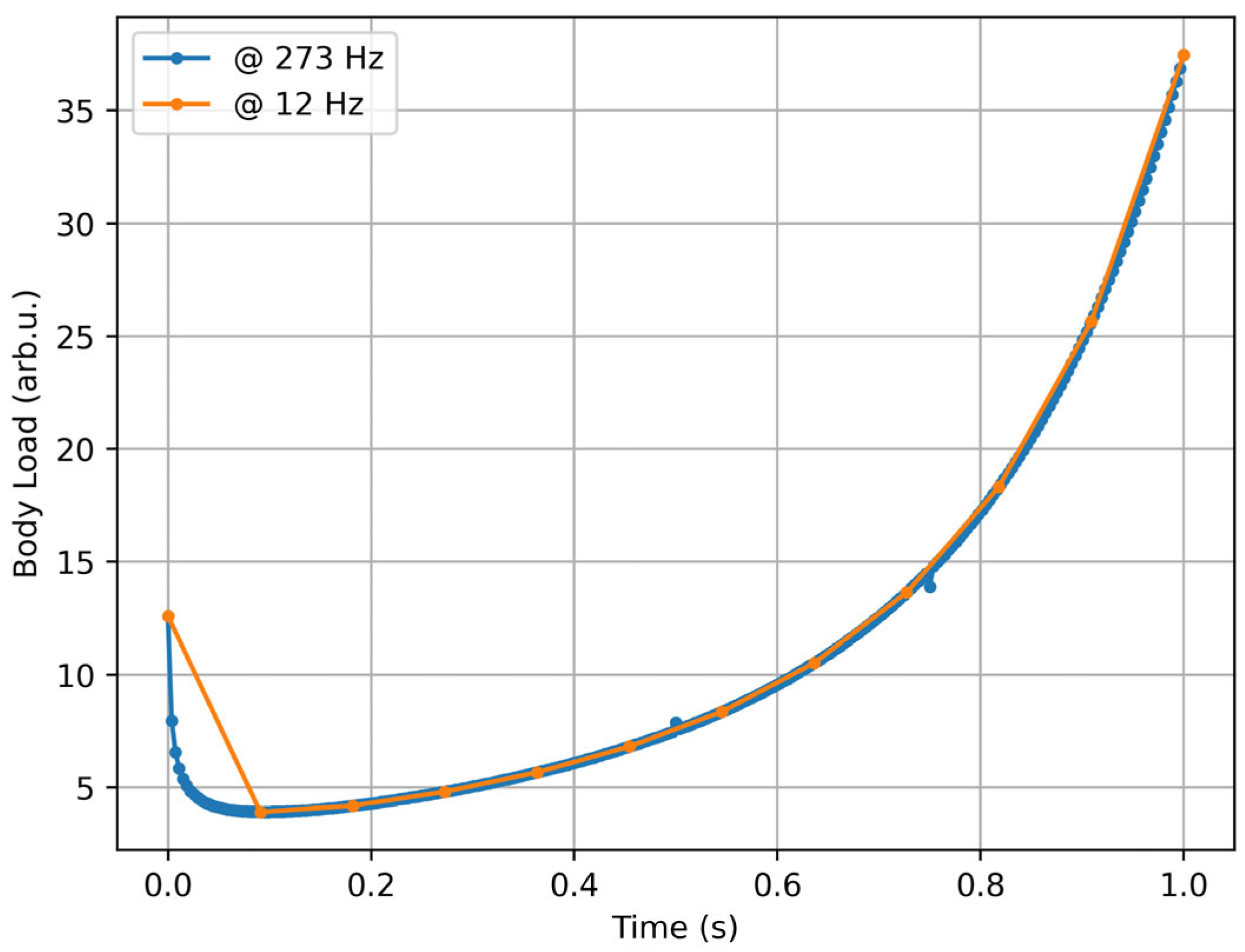


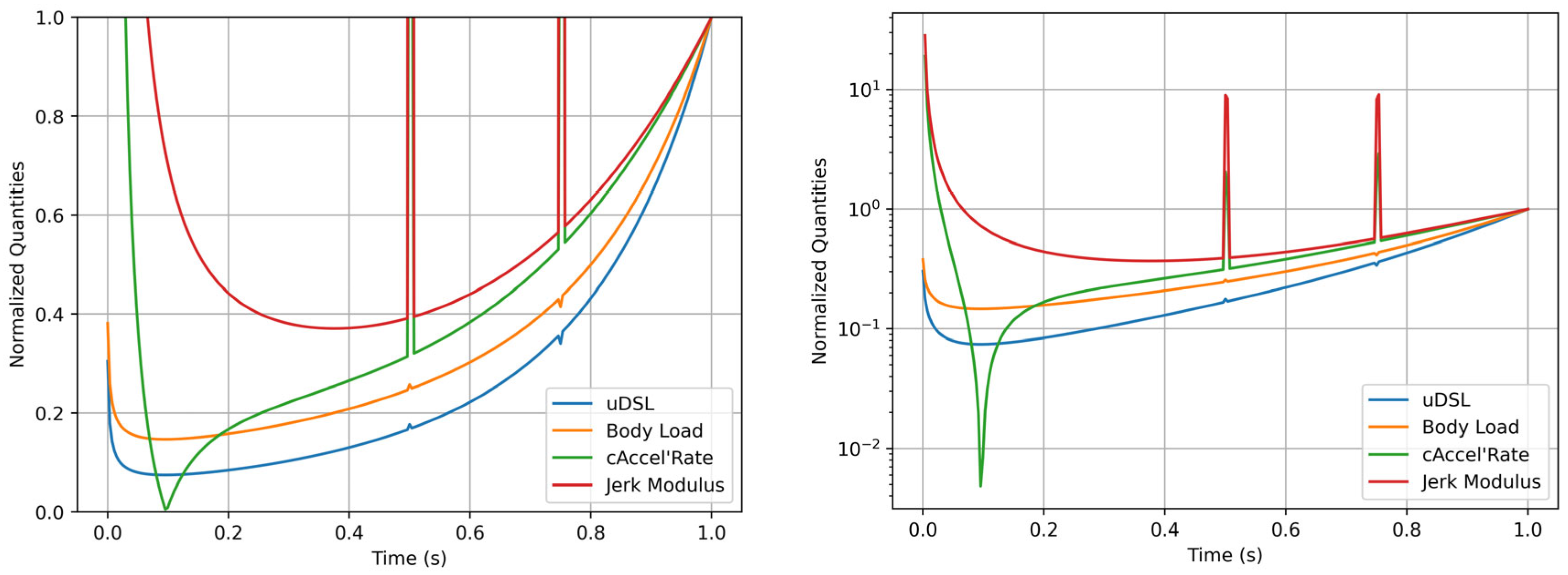
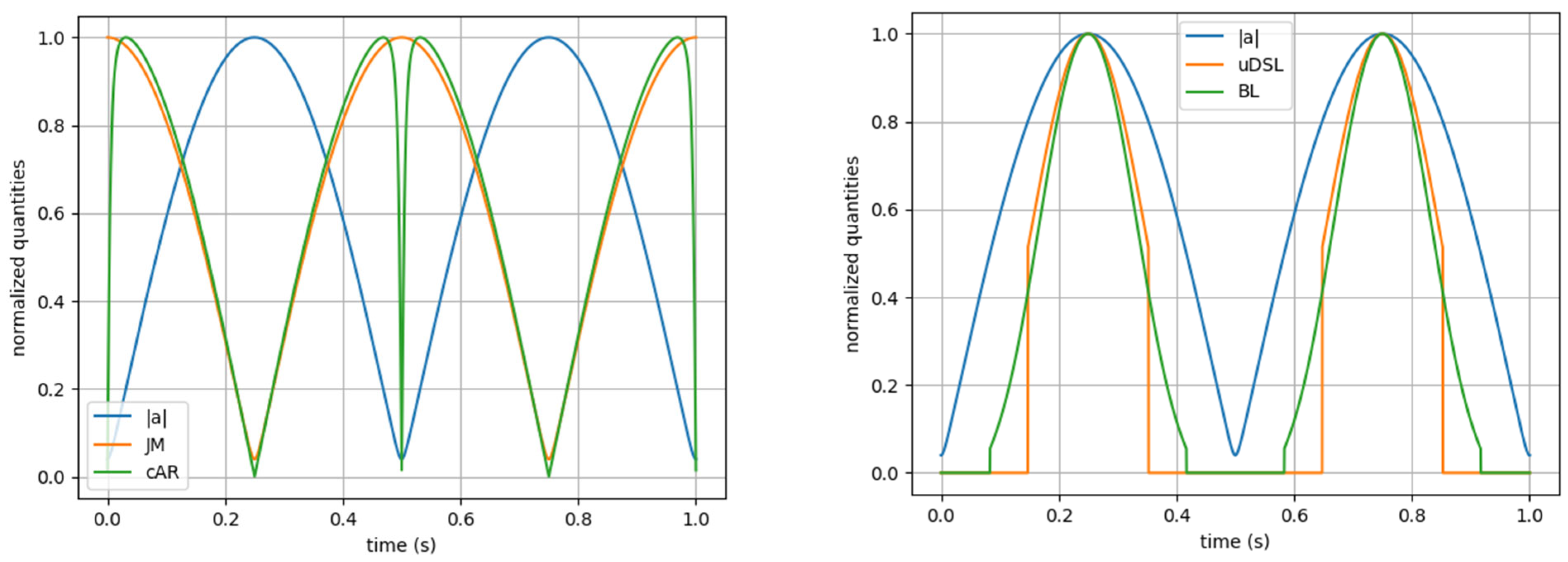

| Metric | Original Formula | Corrected Formula | Concerns |
|---|---|---|---|
| Jerk Modulus |
| ||
| cAccel’Rate |
| ||
| Body Load |
| ||
| uDSL |
|
| Metric | Mean | Min. | 25th Perc. | Median | 75th Perc. | Max. | SD |
|---|---|---|---|---|---|---|---|
| Jerk Modulus (G) | 33,063.1 | 871.5 | 25,828.6 | 34,898.6 | 42,128.7 | 57,973.2 | 12,254.1 |
| cAccel’Rate (G) | 20,267.7 | 488.5 | 15,776.1 | 21,107.4 | 25,805.1 | 35,815.0 | 7627.4 |
| Body Load (arb. u.) | 1921.6 | 16.1 | 1172.4 | 1907.2 | 2631.3 | 5638.0 | 1076.7 |
| uDSL (G3⋅s) | 1549.9 | 5.6 | 930.0 | 1596.1 | 2099.3 | 4084.3 | 844.1 |
| SD) | ||
|---|---|---|
| cAccel’Rate | Jerk Modulus | 0.02 |
| Body Load | 0.07 | |
| uDSL | 0.08 | |
| Jerk Modulus | Body Load | 0.08 |
| uDSL | 0.10 | |
| Body Load | uDSL | 0.08 |
| rrm | CI95% | p-Value | ||
|---|---|---|---|---|
| Jerk Modulus | cAccel’Rate | 1 | [1.00, 1.00] | <0.001 |
| uDSL | 0.95 | [0.94, 0.96] | <0.001 | |
| Body Load | 0.94 | [0.93, 0.95] | <0.001 | |
| cAccel’Rate | uDSL | 0.95 | [0.94, 0.96] | <0.001 |
| Body Load | 0.94 | [0.93, 0.95] | <0.001 | |
| uDSL | Body Load | 0.97 | [0.96, 0.97] | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freitas, J.; Moreira, A.; Carvalho, J.; Conceição, F.; Estriga, L. Understanding Acceleration-Based Load Metrics: From Concepts to Implementation. Sensors 2025, 25, 2764. https://doi.org/10.3390/s25092764
Freitas J, Moreira A, Carvalho J, Conceição F, Estriga L. Understanding Acceleration-Based Load Metrics: From Concepts to Implementation. Sensors. 2025; 25(9):2764. https://doi.org/10.3390/s25092764
Chicago/Turabian StyleFreitas, João, Alexandre Moreira, João Carvalho, Filipe Conceição, and Luisa Estriga. 2025. "Understanding Acceleration-Based Load Metrics: From Concepts to Implementation" Sensors 25, no. 9: 2764. https://doi.org/10.3390/s25092764
APA StyleFreitas, J., Moreira, A., Carvalho, J., Conceição, F., & Estriga, L. (2025). Understanding Acceleration-Based Load Metrics: From Concepts to Implementation. Sensors, 25(9), 2764. https://doi.org/10.3390/s25092764









