MSCSO: A Modified Sand Cat Swarm Algorithm for 3D UAV Path Planning in Complex Environments with Multiple Threats
Abstract
1. Introduction
- (1)
- Development of MSCSO through four strategies. These strategies significantly boost the algorithm’s convergence speed while maintaining accuracy.
- (2)
- The performance of MSCSO is evaluated using 18 classical benchmark functions and compared against seven renowned algorithms to demonstrate its effectiveness.
- (3)
- We further confirm the superiority and robustness of MSCSO in practical applications by employing it in eight diverse UAV path planning scenarios, each varying in complexity.
2. Kinematic Analysis and Cost Function
2.1. Kinematic Constraints
2.1.1. Simplifications in UAV Modeling
- Macro-environmental factors: The Earth’s rotational effects and gravitational acceleration are considered invariant to UAV dynamics.
- Local environmental factors: Atmospheric parameters including humidity, acoustic noise, and wind direction are assumed negligible, with extreme weather conditions (e.g., storms, hurricanes) excluded.
- UAV body simplification: The UAV is modeled as a symmetric rigid body with uniform mass distribution, invariant to temporal or environmental variations.
- Trajectory: Only the translational motion of the center of mass is tracked, with all rotational dynamics referenced to this centroid.
2.1.2. Dynamical Constraints of UAVs
- Maximum operational speed
- 2.
- Maximum acceleration and deceleration
- 3.
- Maximum yaw angle, climb angle, and dive angle
- 4.
- Maximum yaw rate constraint
- 5.
- Minimum path segment length
2.2. Cost Function
2.2.1. Path Length Cost
2.2.2. Collision Risk Cost
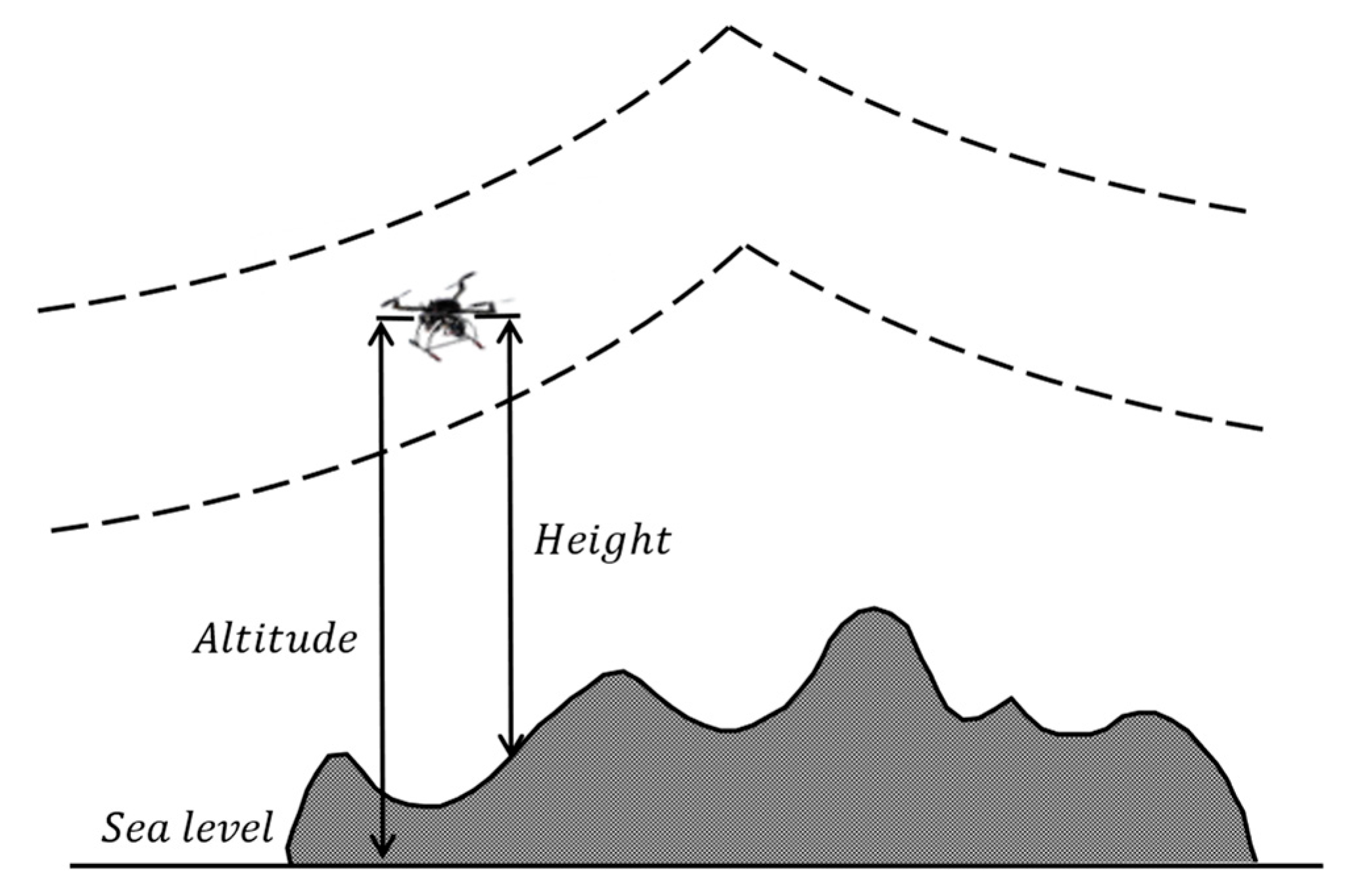
2.2.3. Altitude Deviation Cost
2.2.4. Smoothness Cost
2.2.5. Overall Cost Function
3. SCSO and the Proposed MSCSO Method
3.1. Sand Cat Swarm Optimization
3.1.1. Initialization
3.1.2. SCSO Optimization Process
- Prey Search Phase (Exploration)
- 2.
- Prey Attack Phase (Exploitation)
- 3.
- Phase Switching Control Parameter
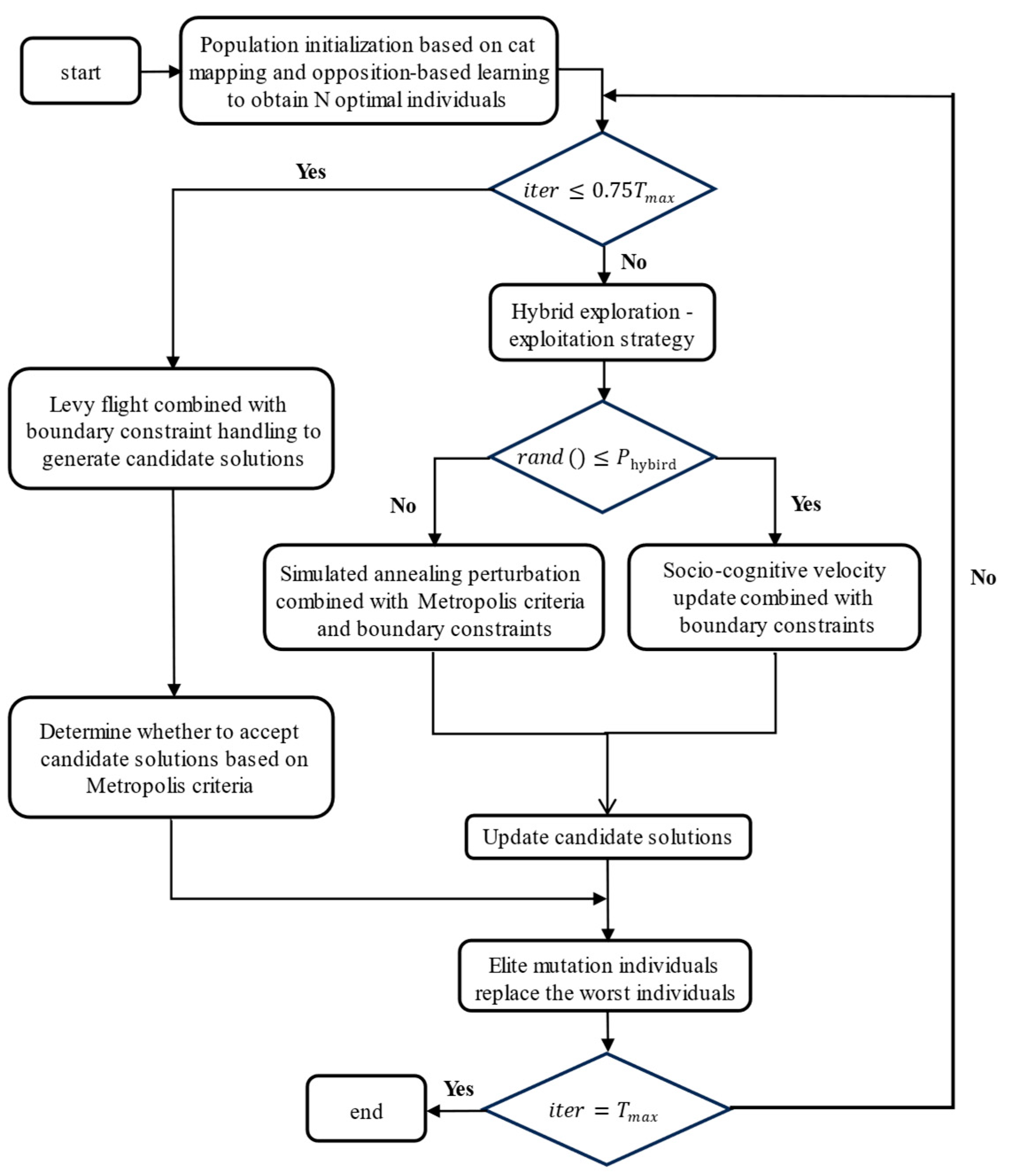
3.2. The Proposed Modified Sand Cat Swarm Optimization
3.2.1. Population Initialization Based on Cat Mapping and Opposition-Based Learning
- 1.
- Cat Mapping
- 2.
- Opposition-Based Learning (OBL) Strategy
- 3.
- Merged Population
3.2.2. Lévy Flight–Metropolis Criterion Hybrid Exploration Mechanism
- 1.
- Lévy Flight Candidate Solution Generation
- 2.
- Metropolis Criterion for Solution Acceptance
3.2.3. Hybrid Exploitation Strategy
- 1.
- Simulated Annealing Perturbation
- 2.
- Social Cognitive Velocity Update Model
- 3.
- Hybrid Probability Adaptation Mechanism
3.2.4. Elite Mutation Strategy
| Algorithm 1: The MSCSO |
| Input: Output:
|
3.2.5. Complexity Analysis
- (1)
- The initialization parameter time is .
- (2)
- Initialization of the population position time , including chaotic mapping and opposition-based learning.
- (3)
- Time required for the global exploration phase , involving Lévy flight and Metropolis criterion.
- (4)
- Time required for the local exploitation phase , including hybrid exploitation strategy updates.
- (5)
- Time required for elite mutation .
- (6)
- The cost time of the calculation function includes the base evaluation time , Lévy flight walk time , and hybrid exploitation strategy evaluation time , totaling .
4. Performance Testing and Analysis of MSCSO
4.1. Experimental Environment and Parameter Configuration
4.1.1. Benchmark Function Setup
4.1.2. Competitive Algorithm Parameter Configuration
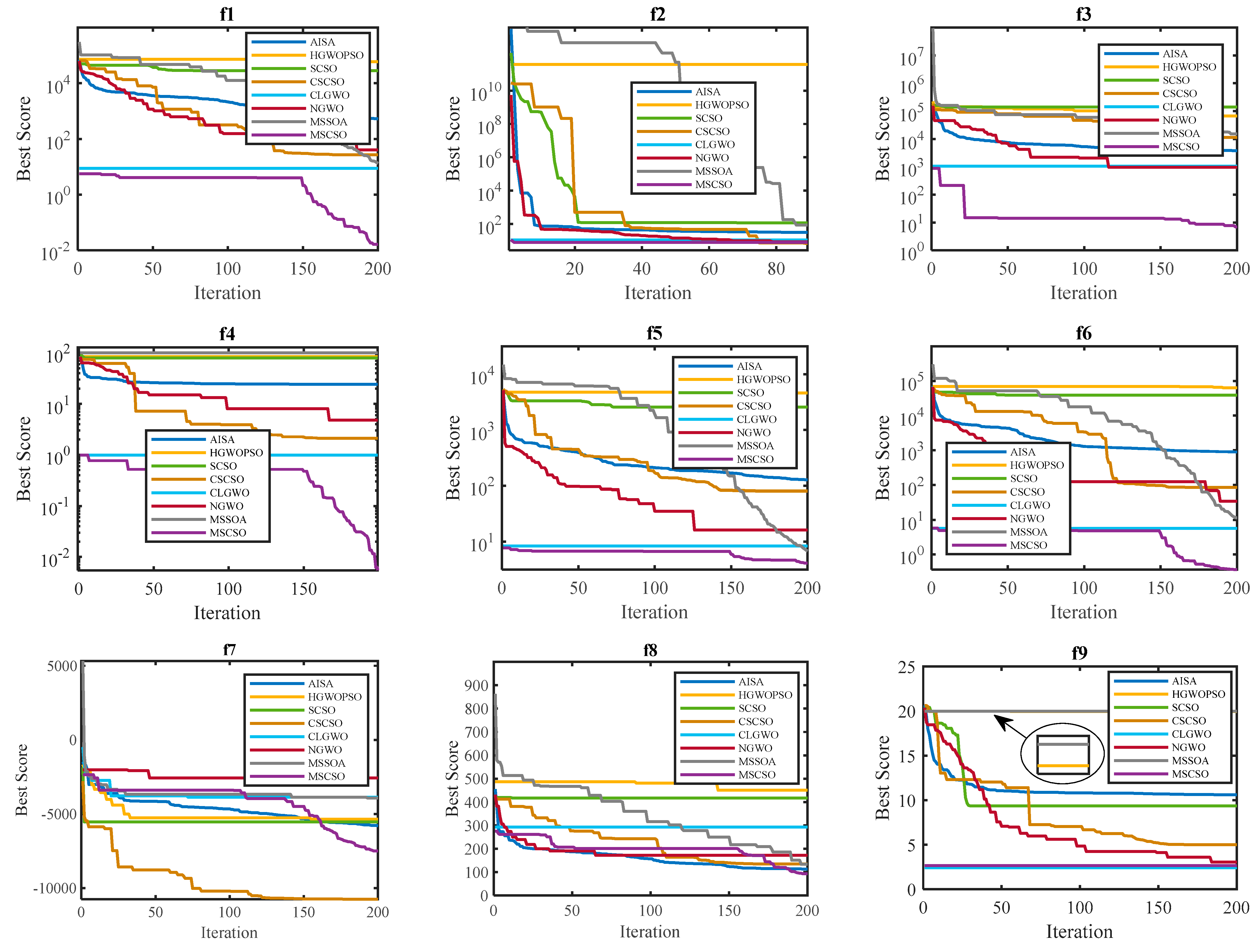
4.1.3. Algorithm Comparison
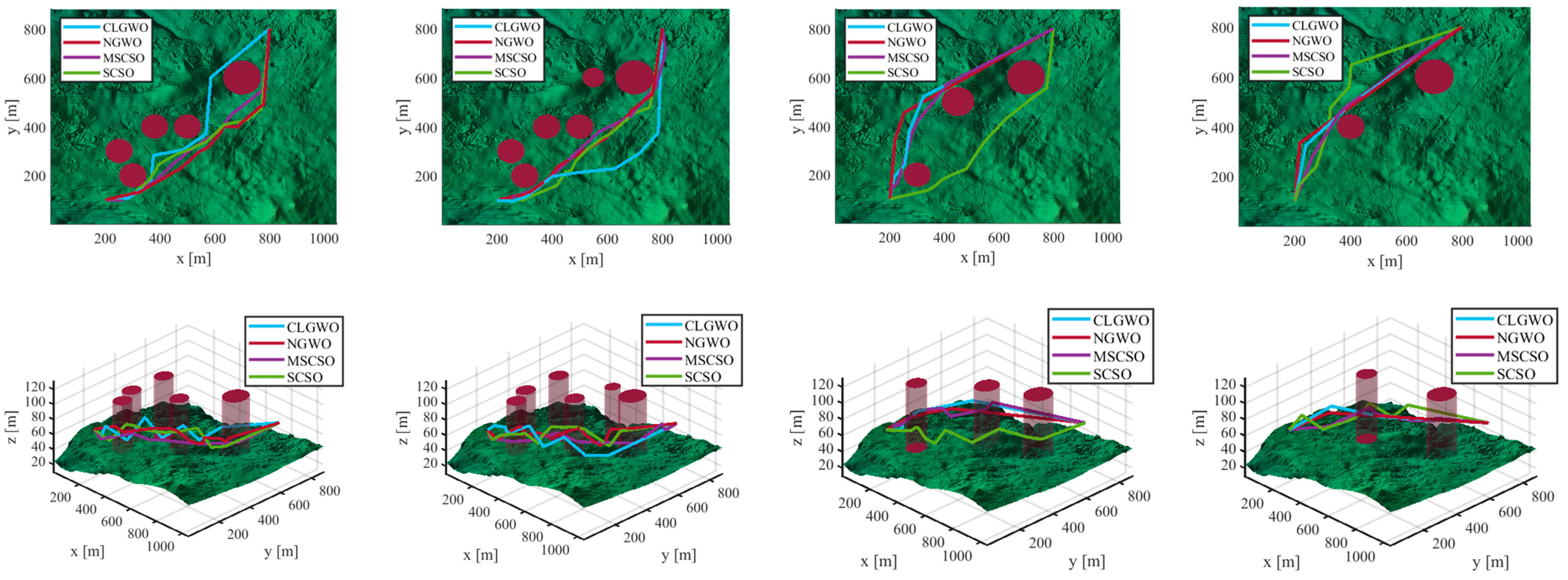
4.2. UAV Path Planning in Complex Environments
5. Conclusions and Future Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, P.; Wen, L.; Du, D.; Bian, X.; Fan, H.; Hu, Q.; Ling, H. Detection and Tracking Meet Drones Challenge. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 7380–7399. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Li, D.; Wang, D.; Ignatius, J.; Cheng, T.; Wang, S. A branch-and-price-and-cut algorithm for the truck-based drone delivery routing problem with time windows. Eur. J. Oper. Res. 2023, 309, 1125–1144. [Google Scholar] [CrossRef]
- Rejeb, A.; Rejeb, K.; Simske, S.J.; Treiblmaier, H. Drones for supply chain management and logistics: A review and research agenda. Int. J. Logist. Res. Appl. 2023, 26, 708–731. [Google Scholar] [CrossRef]
- Moshref-Javadi, M.; Winkenbach, M. Applications and Research avenues for drone-based models in logistics: A classification and review. Expert Syst. Appl. 2021, 177, 114854. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Othman, N.Q.H.; Li, Y.; Alsharif, M.H.; Khan, M.A. Unmanned aerial vehicles (UAVs): Practical aspects, applications, open challenges, security issues, and future trends. Intell. Serv. Robot. 2023, 16, 109–137. [Google Scholar] [CrossRef]
- Jemmali, M.; Kayed, B.M.L.; Boulila, W.; Amdouni, H.; Alharbi, M.T. Optimizing Forest Fire Prevention: Intelligent Scheduling Algorithms for Drone-Based Surveillance System. Procedia Comput. Sci. 2023, 225, 1562–1571. [Google Scholar] [CrossRef]
- Huang, C.; Fei, J.; Deng, W. A novel route planning method of fixed-wing unmanned aerial vehicle based on improved QPSO. IEEE Access 2020, 8, 65071–65084. [Google Scholar] [CrossRef]
- Jones, M.R.; Djahel, S.; Welsh, K. Path-Planning for Unmanned Aerial Vehicles with Environment Complexity Considerations: A Survey. ACM Comput. Surv. 2023, 55, 234. [Google Scholar] [CrossRef]
- Su, H.; Hua, Y. Research on the optimum synchronous network search data extraction based on swarm intelligence algorithm. Future Gener. Comput. Syst. 2021, 125, 151–155. [Google Scholar]
- Chen, G.; Wu, H. Optimization simulation of sports stadium training based on Ant colony algorithm and sensor network. Meas. Sens. 2024, 33, 101100. [Google Scholar] [CrossRef]
- Liu, M.; Wu, J.; Zhang, Q.; Zheng, H. Fault Recovery of Distribution Network with Distributed Generation Based on Pigeon-Inspired Optimization Algorithm. Electronics 2024, 13, 886. [Google Scholar] [CrossRef]
- Mohamed, A.; Reda, M.; Mohammed, J.; Abouhawwash, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl.-Based Syst. 2023, 262, 110248. [Google Scholar]
- Mohanty, J.; Pattanayak, P.; Nandi, A.; Baishnab, K.L.; Gurjar, D.S.; Mandloi, M. MIMO broadcast scheduling using binary spider monkey optimization algorithm. Int. J. Commun. Syst. 2021, 34, e4975. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8129. [Google Scholar] [CrossRef] [PubMed]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Anka, F.; Aghayev, N. Advances in Sand Cat Swarm Optimization: A Comprehensive Study. Arch. Comput. Methods Eng. 2025; early access. [Google Scholar]
- Wang, L.; Sheng, J.; Zhang, Q.; Yang, Z.; Xin, Y.; Song, Y.; Zhang, Q.; Wang, B. A novel sand cat swarm optimization algorithm-based SVM for diagnosis imaging genomics in Alzheimer’s disease. Cereb. Cortex 2024, 34, bhae329. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, L.; Wang, Y.; Wen, Q. Improved sand cat swarm optimization algorithm for enhancing coverage of wireless sensor networks. Measurement 2024, 233, 114649. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J. Short-Term Rockburst Damage Assessment in Burst-Prone Mines: An Explainable XGBOOST Hybrid Model with SCSO Algorithm. Rock Mech. Rock Eng. 2023, 56, 8745–8770. [Google Scholar] [CrossRef]
- Tang, J.; Duan, H.; Lao, S. Swarm intelligence algorithms for multiple unmanned aerial vehicles collaboration: A comprehensive review. Artif. Intell. Rev. 2023, 56, 4295–4327. [Google Scholar] [CrossRef]
- Wang, X.; Gong, Y.; Ji, W.; Zhou, G. Research on natural computing method of multi-spatially cooperative game based on clustering. Appl. Intell. 2023, 53, 4841–4858. [Google Scholar] [CrossRef]
- Jia, H.; Zhang, J.; Rao, H.; Abualigah, L. Improved sandcat swarm optimization algorithm for solving global optimum problems. Artif. Intell. Rev. 2025, 58, 5. [Google Scholar] [CrossRef]
- Li, X.; Qi, Y.; Xing, Q.; Hu, Y. IMSCSO: An Intensified Sand Cat Swarm Optimization With Multi-Strategy for Solving Global and Engineering Optimization Problems. IEEE Access 2023, 11, 122315–122344. [Google Scholar] [CrossRef]
- Adegboye, O.R.; Feda, A.K.; Ojekemi, O.R.; Agyekum, E.B.; Khan, B.; Kamel, S. DGS-SCSO: Enhancing Sand Cat Swarm Optimization with Dynamic Pinhole Imaging and Golden Sine Algorithm for improved numerical optimization performance. Sci. Rep. 2024, 14, 1491. [Google Scholar] [CrossRef]
- Kiani, F.; Nematzadeh, S.; Anka, F.A.; Findikli, M.A. Chaotic Sand Cat Swarm Optimization. Mathematics 2023, 11, 2340. [Google Scholar] [CrossRef]
- Li, Y.; Wang, G. Sand Cat Swarm Optimization Based on Stochastic Variation With Elite Collaboration. IEEE Access 2022, 10, 89989–90003. [Google Scholar] [CrossRef]
- Phung, M.D.; Ha, Q.P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization. Appl. Soft Comput. 2021, 107, 107376. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A modified Artificial Bee Colony (ABC) algorithm for constrained optimization problems. Appl. Soft Comput. J. 2010, 11, 3021–3031. [Google Scholar] [CrossRef]
- Bogar, E.; Beyhan, S. Adolescent Identity Search Algorithm (AISA): A novel metaheuristic approach for solving optimization problems. Appl. Soft Comput. 2020, 95, 106503. [Google Scholar] [CrossRef]
- Ocran, D.; Ikiensikimama, S.S.; Broni-Bediako, E. A compositional function hybridization of PSO and GWO for solving well placement optimisation problem. Pet. Res. 2022, 7, 401–408. [Google Scholar] [CrossRef]
- Hu, G.; Wang, J.; Li, Y.; Yang, M.; Zheng, J. An enhanced hybrid seagull optimization algorithm with its application in engineering optimization. Eng. Comput. 2023, 39, 1653–1696. [Google Scholar] [CrossRef]
- Yi, Z. Research on Resource Scheduling Method of Cloud Computing Based on New Grey Wolf (NGWO) Algorithm. In Proceedings of the 2023 IEEE 5th International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Dali, China, 11–13 October 2023; pp. 856–861. [Google Scholar]
- Lou, L.; Zhang, H. Grey Wolf Optimization algorithm based on Hybrid Multi-strategy. In Proceedings of the 2023 8th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 21–23 April 2023; pp. 1342–1345. [Google Scholar]
- Geoscience Australia. Digital Elevation Model (DEM) of Australia Derived from LiDAR 5 Metre Grid. 2015. Available online: https://researchdata.edu.au/digital-elevation-model-metre-grid/3408984 (accessed on 22 April 2025).
- Qian, Y.; Zheng, J.; Hu, H. Dynamic time-delay perturbation: A strategy for enhancing chaotic system performance and its applications. Nonlinear Dyn. 2025, 113, 4815–4837. [Google Scholar] [CrossRef]







| Type | ID | Description | Range | |
|---|---|---|---|---|
| Unimodal Test Functions | f1 | Sphere Function | [−100, 100] | 0 |
| f2 | Schwefel’s Problem 2.22 | [−10, 10] | 0 | |
| f3 | Schwefel’s Problem 1.2 | [−100, 100] | 0 | |
| f4 | Schwefel’s Problem 2.21 | [−100, 100] | 0 | |
| f5 | Generalized Rosenbrock’s Function | [−30, 30] | 0 | |
| f6 | Step Function | [−100, 100] | 0 | |
| Multimodal Test Functions | f7 | Generalized Schwefel’s Problem 2.26 | [−500, 500] | −12,569.487 |
| f8 | Generalized Rastrigin’s Function | [−5.12, 5.12] | 0 | |
| f9 | Ackley’s Function | [−32, 32] | 0 | |
| f10 | Generalized Griewank’s Function | [−600, 600] | 0 | |
| f11 | Generalized Penalized Function | [−50, 50] | 0 | |
| f12 | Generalized Penalized Functions | [−50, 50] | 0 | |
| Fixed-Dimensional Multimodal Test Functions | f13 | Shekel’s Foxholes Function | [−65.536, 65.536] | ~0.998 |
| f14 | Kowalik’s Function | [−5, 5] | ~0.0003 | |
| f15 | Six-Hump Camel Back Function | [−5, 5] | −1.0316 | |
| f16 | Branin Function | [−5, 0] to [10, 15] | 0.3979 | |
| f17 | Goldstein–Price Function | [−2, 2] | 3 | |
| f18 | Hartman’s Function | [0, 1] | −3.86 |
| ID | Metrics | AISA | HGWOPSO | SCSO | CSCSO | MSCSO | CLGWO | NGWO | MSSOA |
|---|---|---|---|---|---|---|---|---|---|
| f1 | Best | 2.446 × 102 | 4.743 × 104 | 1.120 × 104 | 5.920 × 100 | 2.479 × 10−5 | 5.734 × 100 | 2.066 × 101 | 1.441 × 100 |
| Ave | 7.812 × 102 | 5.986 × 104 | 3.841 × 104 | 1.192 × 102 | 4.424 × 10−1 | 8.381 × 100 | 6.958 × 101 | 7.645 × 100 | |
| Std | 5.489 × 102 | 6.109 × 103 | 1.705 × 104 | 9.231 × 101 | 6.939 × 10−1 | 1.252 × 100 | 3.871 × 101 | 6.019 × 100 | |
| f2 | Best | 9.057 × 100 | 1.748 × 107 | 2.755 × 101 | 7.443 × 10−1 | 1.879 × 10−1 | 9.685 × 100 | 1.539 × 100 | 2.866 × 10−1 |
| Ave | 1.723 × 101 | 5.940 × 1010 | 7.391 × 108 | 4.660 × 100 | 4.039 × 100 | 1.154 × 101 | 2.860 × 100 | 6.318 × 10−1 | |
| Std | 4.819 × 100 | 1.373 × 1011 | 4.048 × 109 | 3.097 × 100 | 7.276 × 10−1 | 7.335 × 10−1 | 6.607 × 10−1 | 2.632 × 10−1 | |
| f3 | Best | 1.445 × 103 | 6.301 × 104 | 2.593 × 104 | 2.138 × 102 | 2.011 × 10−1 | 1.944 × 102 | 1.297 × 102 | 5.539 × 103 |
| Ave | 3.505 × 103 | 7.568 × 104 | 9.875 × 104 | 1.122 × 104 | 1.585 × 100 | 9.366 × 102 | 5.222 × 102 | 1.192 × 104 | |
| Std | 1.242 × 103 | 8.091 × 103 | 3.587 × 104 | 9.796 × 103 | 1.791 × 100 | 2.854 × 102 | 3.272 × 102 | 4.015 × 103 | |
| f4 | Best | 1.492 × 101 | 7.664 × 101 | 3.893 × 101 | 8.477 × 10−1 | 2.966 × 10−2 | 9.833 × 10−1 | 1.889 × 100 | 8.858 × 100 |
| Ave | 2.351 × 101 | 8.680 × 101 | 7.197 × 101 | 4.715 × 100 | 4.675 × 10−1 | 9.869 × 10−1 | 4.684 × 100 | 5.351 × 101 | |
| Std | 4.442 × 100 | 3.409 × 100 | 1.429 × 101 | 3.026 × 100 | 4.316 × 10−3 | 5.280 × 10−3 | 1.301 × 100 | 3.539 × 101 | |
| f5 | Best | 9.964 × 103 | 9.663 × 107 | 4.450 × 105 | 6.374 × 101 | 9.048 × 101 | 4.640 × 102 | 2.126 × 102 | 8.156 × 101 |
| Ave | 1.096 × 105 | 2.039 × 108 | 8.274 × 107 | 3.029 × 103 | 2.122 × 102 | 6.030 × 102 | 1.544 × 103 | 1.019 × 103 | |
| Std | 1.583 × 105 | 5.298 × 107 | 6.811 × 107 | 5.161 × 103 | 5.888 × 101 | 6.863 × 101 | 1.187 × 103 | 1.180 × 103 | |
| f6 | Best | 2.297 × 102 | 4.738 × 104 | 1.304 × 104 | 3.512 × 100 | 1.763 × 10−1 | 5.321 × 100 | 6.779 × 100 | 7.835 × 10−1 |
| Ave | 7.886 × 102 | 6.137 × 104 | 3.843 × 104 | 1.196 × 102 | 5.094 × 10−1 | 5.729 × 100 | 7.224 × 100 | 1.016 × 101 | |
| Std | 4.936 × 102 | 5.881 × 103 | 1.547 × 104 | 1.166 × 102 | 1.595 × 10−1 | 1.657 × 10−1 | 2.446 × 10−1 | 7.219 × 100 | |
| f7 | Best | −6.730 × 103 | −5.748 × 103 | −7.361 × 103 | −1.257 × 104 | −6.848 × 103 | −4.205 × 103 | −4.072 × 103 | −4.430 × 103 |
| Ave | −6.153 × 103 | −5.517 × 103 | −6.302 × 103 | −1.257 × 104 | −6.154 × 103 | −3.803 × 103 | −3.863 × 103 | −4.044 × 103 | |
| Std | 5.214 × 102 | 2.025 × 102 | 9.756 × 102 | 3.013 × 10−1 | 6.726 × 102 | 4.248 × 102 | 2.036 × 102 | 3.437 × 102 | |
| f8 | Best | 9.000 × 101 | 3.936 × 102 | 2.768 × 102 | 1.552 × 100 | 1.116 × 102 | 3.045 × 102 | 4.186 × 101 | 1.533 × 102 |
| Ave | 1.076 × 102 | 4.128 × 102 | 3.234 × 102 | 3.474 × 101 | 1.239 × 102 | 3.155 × 102 | 9.861 × 101 | 1.836 × 102 | |
| Std | 2.035 × 101 | 2.108 × 101 | 7.816 × 101 | 5.392 × 101 | 1.145 × 101 | 9.834 × 100 | 3.873 × 101 | 4.633 × 101 | |
| f9 | Best | 9.924 × 100 | 1.996 × 101 | 5.749 × 100 | 1.333 × 100 | 2.269 × 100 | 2.282 × 100 | 2.055 × 100 | 1.999 × 101 |
| Ave | 1.170 × 101 | 1.997 × 101 | 1.898 × 101 | 3.622 × 100 | 2.692 × 100 | 2.546 × 100 | 2.969 × 100 | 1.999 × 101 | |
| Std | 1.060 × 100 | 4.694 × 10−3 | 3.378 × 100 | 1.330 × 100 | 1.741 × 10−1 | 1.816 × 10−1 | 5.212 × 10−1 | 0.000 × 100 | |
| f10 | Best | 9.298 × 100 | 5.722 × 102 | 1.331 × 102 | 1.119 × 100 | 3.812 × 10−2 | 1.868 × 10−1 | 1.376 × 100 | 1.035 × 100 |
| Ave | 1.144 × 101 | 5.874 × 102 | 2.432 × 102 | 1.513 × 100 | 4.809 × 10−2 | 2.829 × 10−1 | 1.606 × 100 | 1.048 × 100 | |
| Std | 2.429 × 100 | 1.798 × 101 | 1.411 × 102 | 3.751 × 10−1 | 8.675 × 10−3 | 8.678 × 10−2 | 2.034 × 10−1 | 1.494 × 10−2 | |
| f11 | Best | 8.566 × 100 | 1.708 × 108 | 2.438 × 105 | 1.062 × 10−2 | 1.257 × 10−2 | 5.493 × 10−2 | 8.058 × 10−1 | 2.346 × 10−1 |
| Ave | 3.040 × 101 | 4.301 × 108 | 1.983 × 108 | 1.232 × 100 | 2.462 × 10−2 | 1.350 × 10−1 | 1.871 × 100 | 1.910 × 100 | |
| Std | 1.936 × 101 | 1.252 × 108 | 1.815 × 108 | 1.563 × 100 | 9.381 × 10−3 | 3.492 × 10−2 | 5.440 × 10−1 | 1.455 × 100 | |
| f12 | Best | 7.840 × 101 | 5.577 × 108 | 9.697 × 106 | 2.509 × 10−1 | 7.872 × 10−2 | 8.217 × 10−1 | 3.310 × 100 | 1.544 × 100 |
| Ave | 1.291 × 104 | 9.534 × 108 | 4.201 × 108 | 5.589 × 100 | 2.102 × 10−1 | 1.041 × 100 | 5.596 × 100 | 4.911 × 100 | |
| Std | 3.256 × 104 | 1.718 × 108 | 3.803 × 108 | 4.973 × 100 | 1.031 × 10−1 | 1.409 × 10−1 | 1.202 × 100 | 2.438 × 100 | |
| f13 | Best | 9.980 × 10−1 | 1.002 × 100 | 1.992 × 100 | 1.992 × 100 | 9.980 × 10−1 | 9.980 × 10−1 | 2.272 × 100 | 9.980 × 10−1 |
| Ave | 1.329 × 100 | 1.263 × 100 | 1.030 × 101 | 2.651 × 100 | 9.980 × 10−1 | 9.980 × 10−1 | 3.198 × 100 | 9.980 × 10−1 | |
| Std | 5.739 × 10−1 | 4.468 × 10−1 | 9.740 × 100 | 1.141 × 100 | 2.898 × 10−10 | 4.161 × 10−10 | 1.050 × 100 | 4.881 × 10−7 | |
| f14 | Best | 3.075 × 10−4 | 1.037 × 10−3 | 2.255 × 10−3 | 5.752 × 10−4 | 5.834 × 10−4 | 3.835 × 10−4 | 3.100 × 10−4 | 5.258 × 10−4 |
| Ave | 1.519 × 10−3 | 5.927 × 10−3 | 4.266 × 10−2 | 2.658 × 10−3 | 1.253 × 10−3 | 7.871 × 10−4 | 9.605 × 10−4 | 1.433 × 10−3 | |
| Std | 3.987 × 10−3 | 8.126 × 10−3 | 3.951 × 10−2 | 3.935 × 10−3 | 4.392 × 10−4 | 2.149 × 10−4 | 2.770 × 10−3 | 3.579 × 10−3 | |
| f15 | Best | −1.032 × 100 | −1.032 × 100 | −1.032 × 100 | −1.032 × 100 | −1.032 × 100 | −1.032 × 100 | −1.032 × 100 | −1.032 × 100 |
| Ave | −1.032 × 100 | −1.029 × 100 | −7.888 × 10−1 | −1.032 × 100 | −1.032 × 100 | −1.031 × 100 | −1.032 × 100 | −1.032 × 100 | |
| Std | 5.952 × 10−6 | 3.013 × 10−3 | 3.456 × 10−1 | 1.479 × 10−4 | 3.643 × 10−6 | 7.708 × 10−6 | 1.939 × 10−5 | 1.147 × 10−4 | |
| f16 | Best | 3.979 × 10−1 | 3.981 × 10−1 | 3.979 × 10−1 | 3.979 × 10−1 | 3.979 × 10−1 | 3.979 × 10−1 | 3.979 × 10−1 | 3.979 × 10−1 |
| Ave | 3.981 × 10−1 | 4.036 × 10−1 | 1.038 × 100 | 3.979 × 10−1 | 3.979 × 10−1 | 3.980 × 10−1 | 4.004 × 10−1 | 7.076 × 10−1 | |
| Std | 3.067 × 10−7 | 8.358 × 10−3 | 1.233 × 100 | 1.190 × 10−5 | 8.553 × 10−6 | 6.955 × 10−4 | 3.070 × 10−3 | 1.178 × 100 | |
| f17 | Best | 3.000 × 100 | 3.001 × 100 | 3.000 × 100 | 3.000 × 100 | 3.000 × 100 | 3.000 × 100 | 3.000 × 100 | 3.000 × 100 |
| Ave | 3.000 × 100 | 3.029 × 100 | 2.359 × 101 | 3.000 × 100 | 3.000 × 100 | 3.000 × 100 | 3.000 × 100 | 3.000 × 100 | |
| Std | 1.046 × 10−4 | 3.121 × 10−2 | 3.046 × 101 | 2.079 × 10−5 | 4.151 × 10−5 | 6.396 × 10−6 | 2.322 × 10−4 | 1.676 × 10−4 | |
| f18 | Best | −3.863 × 100 | −3.859 × 100 | −3.858 × 100 | −3.863 × 100 | −3.863 × 100 | −3.863 × 100 | −3.862 × 100 | −3.863 × 100 |
| Ave | −3.863 × 100 | −3.854 × 100 | −3.627 × 100 | −3.855 × 100 | −3.863 × 100 | −3.861 × 100 | −3.860 × 100 | −3.859 × 100 | |
| Std | 1.937 × 10−5 | 2.516 × 10−3 | 3.342 × 10−1 | 2.180 × 10−2 | 1.450 × 10−5 | 3.538 × 10−3 | 1.897 × 10−3 | 3.671 × 10−3 |
| Algorithm | Ave | Std | Best | Running Time (s) | |
|---|---|---|---|---|---|
| 2 | CLGWO | 956.93 | 6.07 | 954.25 | 0.10 |
| NGWO | 969.06 | 12.32 | 961.25 | 0.08 | |
| MSCSO | 942.01 | 8.77 | 931.14 | 0.23 | |
| SCSO | 983.53 | 23.67 | 975.49 | 0.09 | |
| 3 | CLGWO | 978.07 | 16.62 | 965.58 | 0.11 |
| NGWO | 1002.11 | 12.89 | 980.15 | 0.10 | |
| MSCSO | 959.91 | 5.23 | 944.05 | 0.27 | |
| SCSO | 1019 | 27.12 | 987.70 | 0.09 | |
| 5 | CLGWO | 1016.89 | 23.88 | 1000.43 | 0.21 |
| NGWO | 1000.15 | 21.01 | 977.31 | 0.15 | |
| MSCSO | 981.10 | 11.57 | 945.77 | 0.38 | |
| SCSO | 1022.32 | 43.07 | 1009.79 | 0.15 | |
| 6 | CLGWO | 1041.31 | 42.44 | 1015.58 | 0.14 |
| NGWO | 1012.97 | 11.00 | 998.70 | 0.13 | |
| MSCSO | 992.86 | 4.21 | 980.83 | 0.39 | |
| SCSO | 1053.55 | 65.66 | 1021.18 | 0.13 |
| Algorithm | Ave | Std | Best | Running Time (s) | |
|---|---|---|---|---|---|
| 2 | CLGWO | 968.83 | 10.44 | 960.14 | 0.16 |
| NGWO | 977.08 | 7.37 | 970.18 | 0.13 | |
| MSCSO | 946.81 | 6.92 | 937.93 | 0.35 | |
| SCSO | 1054.59 | 31.44 | 1024.35 | 0.13 | |
| 3 | CLGWO | 997.07 | 16.34 | 986.15 | 0.17 |
| NGWO | 1014.31 | 10.03 | 1005.26 | 0.15 | |
| MSCSO | 964.10 | 3.76 | 949.85 | 0.41 | |
| SCSO | 1060.46 | 51.22 | 1028.37 | 0.14 | |
| 5 | CLGWO | 1019.95 | 30.79 | 1002.72 | 0.22 |
| NGWO | 1009.95 | 22.17 | 983.77 | 0.19 | |
| MSCSO | 990.69 | 16.69 | 963.94 | 0.51 | |
| SCSO | 1094.27 | 45.33 | 1050.72 | 0.17 | |
| 6 | CLGWO | 1072.71 | 40.01 | 1049.11 | 0.23 |
| NGWO | 1023.23 | 12.11 | 1014.84 | 0.20 | |
| MSCSO | 1000.88 | 5.97 | 965.69 | 0.52 | |
| SCSO | 1103.77 | 30.62 | 1050.51 | 0.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, Z.; Lai, D.; Huang, C.; Zhang, Z.; Deng, Y.; Yang, J. MSCSO: A Modified Sand Cat Swarm Algorithm for 3D UAV Path Planning in Complex Environments with Multiple Threats. Sensors 2025, 25, 2730. https://doi.org/10.3390/s25092730
Zhan Z, Lai D, Huang C, Zhang Z, Deng Y, Yang J. MSCSO: A Modified Sand Cat Swarm Algorithm for 3D UAV Path Planning in Complex Environments with Multiple Threats. Sensors. 2025; 25(9):2730. https://doi.org/10.3390/s25092730
Chicago/Turabian StyleZhan, Zhengsheng, Dangyue Lai, Canjian Huang, Zhixiang Zhang, Yongle Deng, and Jian Yang. 2025. "MSCSO: A Modified Sand Cat Swarm Algorithm for 3D UAV Path Planning in Complex Environments with Multiple Threats" Sensors 25, no. 9: 2730. https://doi.org/10.3390/s25092730
APA StyleZhan, Z., Lai, D., Huang, C., Zhang, Z., Deng, Y., & Yang, J. (2025). MSCSO: A Modified Sand Cat Swarm Algorithm for 3D UAV Path Planning in Complex Environments with Multiple Threats. Sensors, 25(9), 2730. https://doi.org/10.3390/s25092730





