1. Introduction
Alzheimer’s disease (AD) affects millions of people each year, especially those over 65. It is marked by a decline in cognitive functions, including memory loss, difficulties with language, spatial awareness, face recognition, and reasoning [
1]. The exact causes of AD are yet to be clearly understood. Still, there is a correlation with factors such as familiarity, high blood pressure, smoking, excessive alcohol consumption, physical inactivity, social isolation, and depression [
2].
There is no currently available single test capable of definitively diagnosing Alzheimer’s disease or other forms of dementia. Instead, physicians rely on a combination of diagnostic tools, including neurological and behavioral examinations, cognitive and functional tests, genetic testing, brain-imaging techniques such as magnetic resonance imaging (MRI), computed tomography (CT), and positron emission tomography (PET), and analyses of cerebrospinal fluid (CSF) or blood biomarkers. These tools are integrated with the patient’s medical history and other relevant information to ensure the most accurate diagnosis [
3,
4,
5].
With the progress of the disease, at the middle- and late stages, amyloid plaques and neurofibrillary tangles accumulate in the brain, followed by brain atrophy. MRI, PET, and CT can detect these AD biomarkers [
6,
7]. However, these techniques are most effective at the latter stages of the disease. Moreover, they are expensive, require bulky equipment, and may involve ionizing radiation exposure in the case of PET and CT.
Research shows that AD induces physiological changes up to twenty years before symptoms become evident [
8]. The first indicators of AD are elevated concentrations of amyloid-beta
, tau, and p-tau, and the increasing amyloid-beta
ratio in the CSF [
9,
10,
11]. Amyloid-beta and tau proteins form amyloid plaques and neurofibrillary tangles, respectively, which are known to contribute to brain degeneration in AD. Yet, estimating those biomarkers is not trivial. The standard methodology analyzes a CSF sampled through a lumbar puncture extraction, a highly invasive procedure that often causes pain and discomfort. Ongoing research aims to identify these biomarkers in blood and urine and evaluate their reliability as predictive AD indicators. Alternative early diagnostics include microbiota-based methods and genetic tests. Machine learning (ML) can integrate these techniques to improve accuracy. In [
12,
13,
14,
15,
16,
17], ML algorithms have been explored to analyze speech data as a potential diagnostic tool. Overall, there is no established technique for early AD detection, and the interest in non-invasive, low-cost, portable alternatives is open. These would enable access to medical treatment before the disease symptoms become evident—i.e., at a stage of the disease when current treatments are more effective.
In [
18,
19], a correlation has been shown between the concentration of
and
in the CSF and its electromagnetic properties (i.e., dielectric relative permittivity and electrical conductivity). This led us to propose identifying these permittivity alterations due to
and
concentration variations through microwave sensing (MWS) technology and ML algorithms [
20,
21,
22]. Moreover, the chiral properties of
have been numerically investigated, exploring the consequent deflection of incident electromagnetic waves [
23]. MWS is a non-invasive, low-cost method that investigates dielectric properties through interactions with electromagnetic fields [
24]. Raw MWS data can be complex, noisy, and difficult to interpret. Machine learning (ML) enhances MWS capabilities by improving data processing, pattern recognition, and decision-making [
25].
MWS is used in applications where variations in dielectric contrast leave a measurable impact on the system’s scattering response. This principle is leveraged in various fields, including structural damage analysis [
26,
27], food quality assessment [
28,
29], stroke detection [
30,
31,
32], glucose sensing [
33,
34], and breast cancer screening [
35,
36,
37,
38]. Recently, MWS has also been investigated for neurodegenerative disorders, including AD [
39,
40,
41,
42,
43]. In [
39], a wearable device equipped with electromagnetic sensors was designed to non-invasively track brain atrophy and the expansion of the lateral ventricles associated with Alzheimer’s disease, performing numerical and experimental validation. Numerical studies on MWS have been conducted in [
40,
41,
42] to detect different stages of Alzheimer’s disease by analyzing dielectric changes in gray and white matter as well as brain atrophy. In particular, Refs. [
40,
41,
43] utilize machine learning algorithms to classify data samples according to disease severity.
To the best of our knowledge, this is the first experimental demonstration of using ML-based MWS to identify and classify CSF permittivity changes linked to early AD biomarkers. To this end, starting from numerical feasibility studies and preliminary assessment of the approach mechanism [
20,
21,
22], this work recreates realistically different pathological AD severity scenarios with an ad-hoc anthropomorphic multi-tissue head phantom, and a six-antenna-based MWS composed of a multi-port vector network analyzer (VNA) and custom monopoles featuring a simple design. The antennas are designed to operate from 500 MHz to 6.5 GHz, considering adequate sensing penetration, system dynamics, and scattering sensitivity. A multilayer perceptron (MLP) is then optimized to classify CSF conditions across different severity levels using measured scattering parameters. Multiple training, validation, and testing schemes support the reliability of the results. The analysis is carried out using both complex and only amplitude scattering parameters, showing comparable performance, with over 94% accuracy in detection and an f1-score of up to 87% in severity classification.
The structure of this paper is as follows:
Section 2 describes the implemented MWS system.
Section 3 details the experimental validation, including the phantom creation and measurement procedure.
Section 4 provides a comprehensive description of the machine learning algorithm used for classification. The results of the testing procedure on the test set are presented in
Section 5, and finally,
Section 6 summarizes the conclusions of this study.
2. Microwave Sensing System
The implemented MWS system, depicted in
Figure 1, consists of a laptop and an M9804A PXIe six-port VNA (Keysight Technologies, Santa Rosa, CA, USA) [
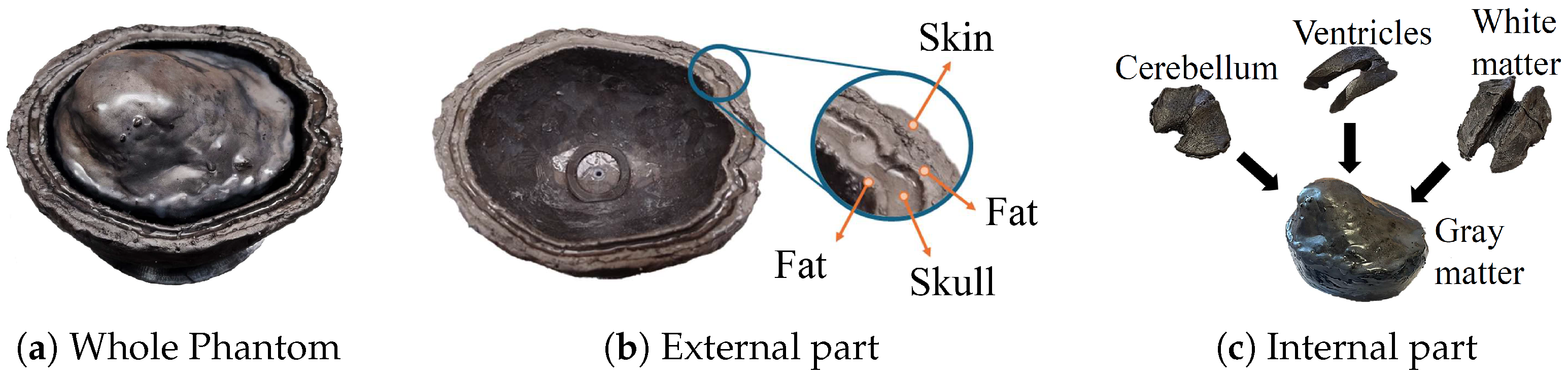
44], connected via low-loss coaxial cables to a custom wideband six-antenna array. The antennas are conformally positioned along the sides of the upper portion of a head phantom. The VNA acquires the scattering parameters through the antenna array and sends the measured data to the laptop for processing. The antennas are placed on the lateral sides of the head phantom rather than the front and back, as the relatively thinner skull in these regions facilitates deeper field penetration.
Various antenna designs have been proposed in the literature for human body monitoring using microwave technologies, e.g., [
45,
46,
47]. In our work, each antenna of the sensing system is a circular monopole antenna printed on Rogers RO4003C substrate (Rogers Corporation, Chandler, AZ, USA) by PCB international (Seattle, WA, USA) with a standard thickness of 1.52 mm, entailing easy manufacturing and compactness. The working frequency band of the antenna is about 500 MHz–6.5 GHz, in agreement with the device requirements. The minimum frequency is dictated by the thickness of the CSF layer, which corresponds to around
where
is the wavelength inside the CSF. The highest frequency is chosen according to the wave penetration within the head. Considering the variability of the human head, the antenna is optimized by placing it on a multilayer block of size
, a simplified scenario that mimics the head’s multi-layer structure and dielectric properties. The block is constituted of six stacked slabs, encompassing skin, fat, skull, fat, CSF, and gray matter, with thicknesses of 3, 5, 8, 3, 6, and 38 mm, respectively, as portrayed by the contour lines in
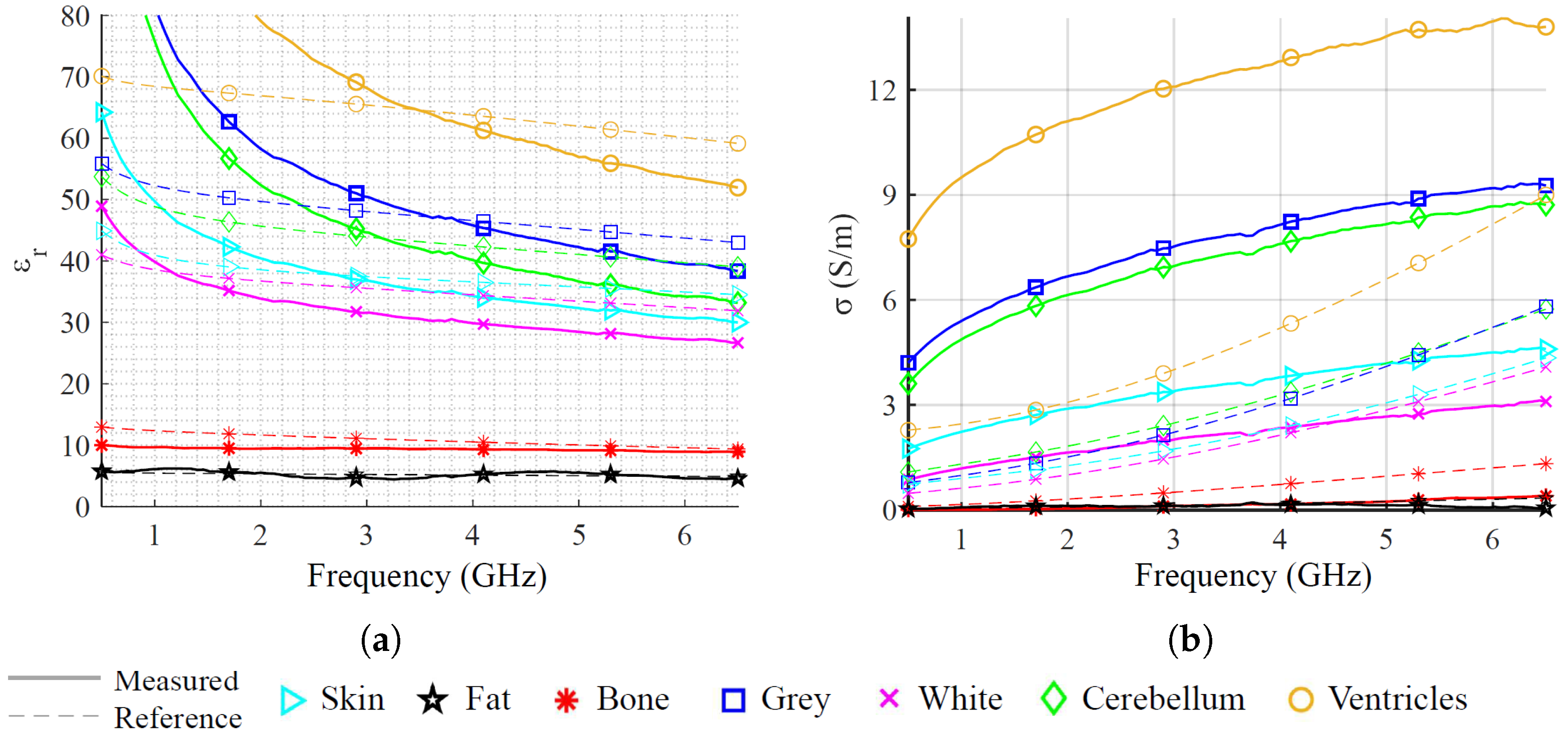
Figure 2, and dielectric characteristics taken from [
48].
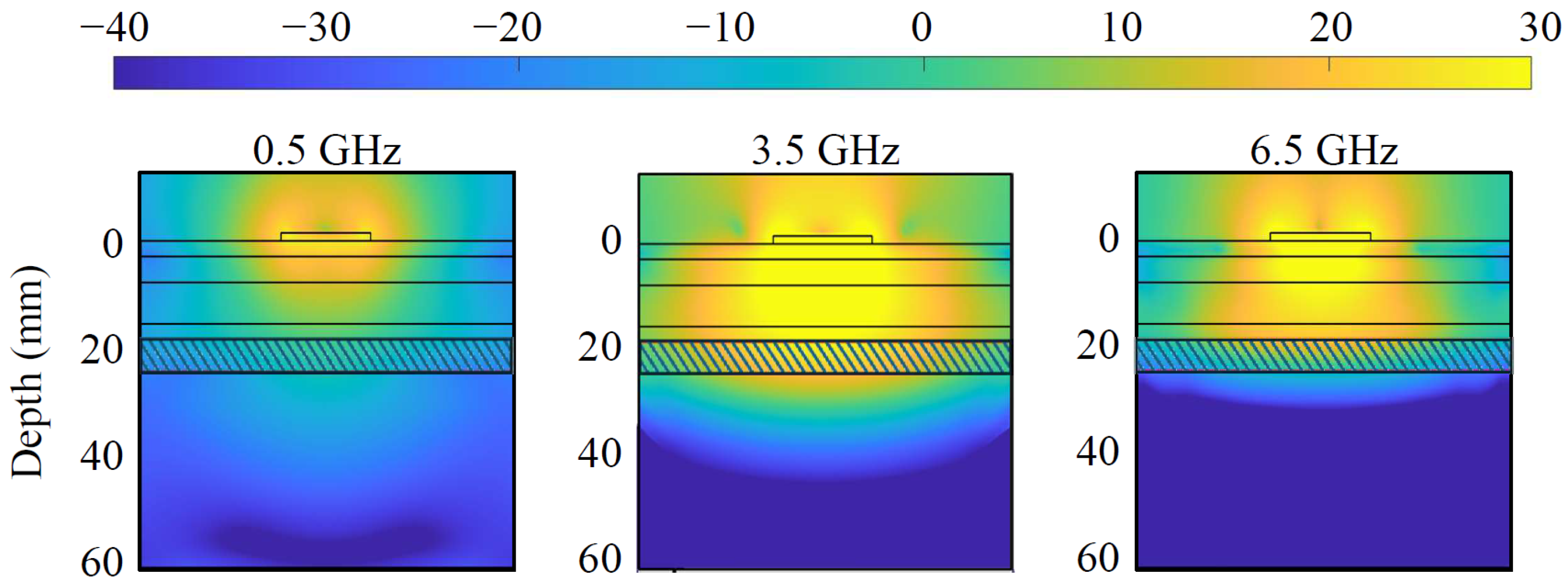
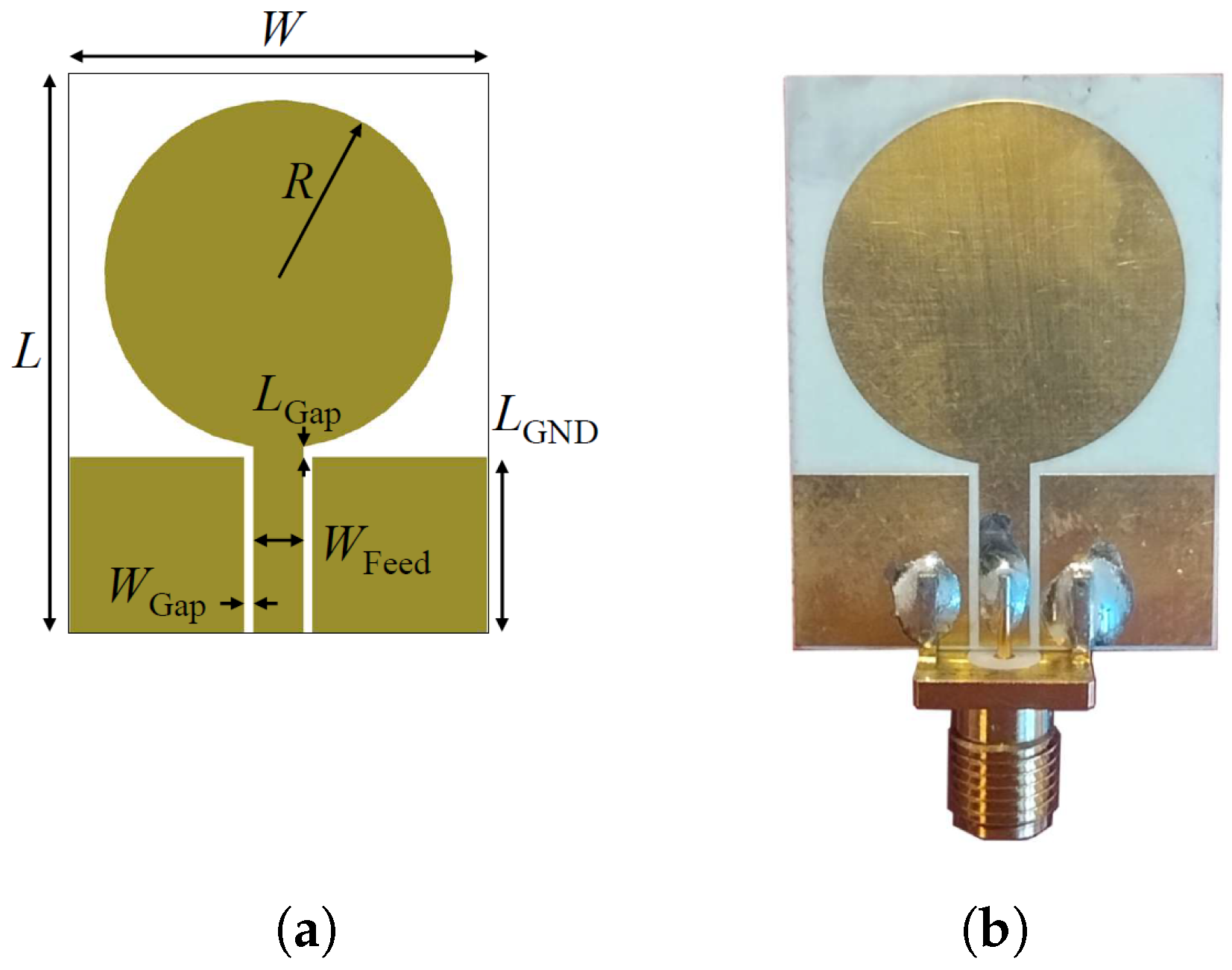
Figure 2 depicts the simulated power density distribution within the multi-tissue block at the lowest, center, and highest frequencies. A lower power density can be observed at the lowest frequency, 500 MHz, due to the non-optimal antenna matching and decreased penetration at the highest, 6.5 GHz, due to higher tissue losses. Nevertheless, the power density distribution reaches an adequate level at CSF in each case, and so does the sensing capability. The antenna optimization uses the circular monopole layout displayed in
Figure 3a as a baseline while varying the radius of the circular section (
R) and the feeding line width (
), maintaining constant the gap (
) between the ground plane and the feeding line and the substrate dimension (
). The objective of the optimization is to minimize the reflection coefficients within the desired frequency band. The realized antenna is shown in
Figure 3b, with its repetitively optimized geometrical parameters reported in
Table 1.
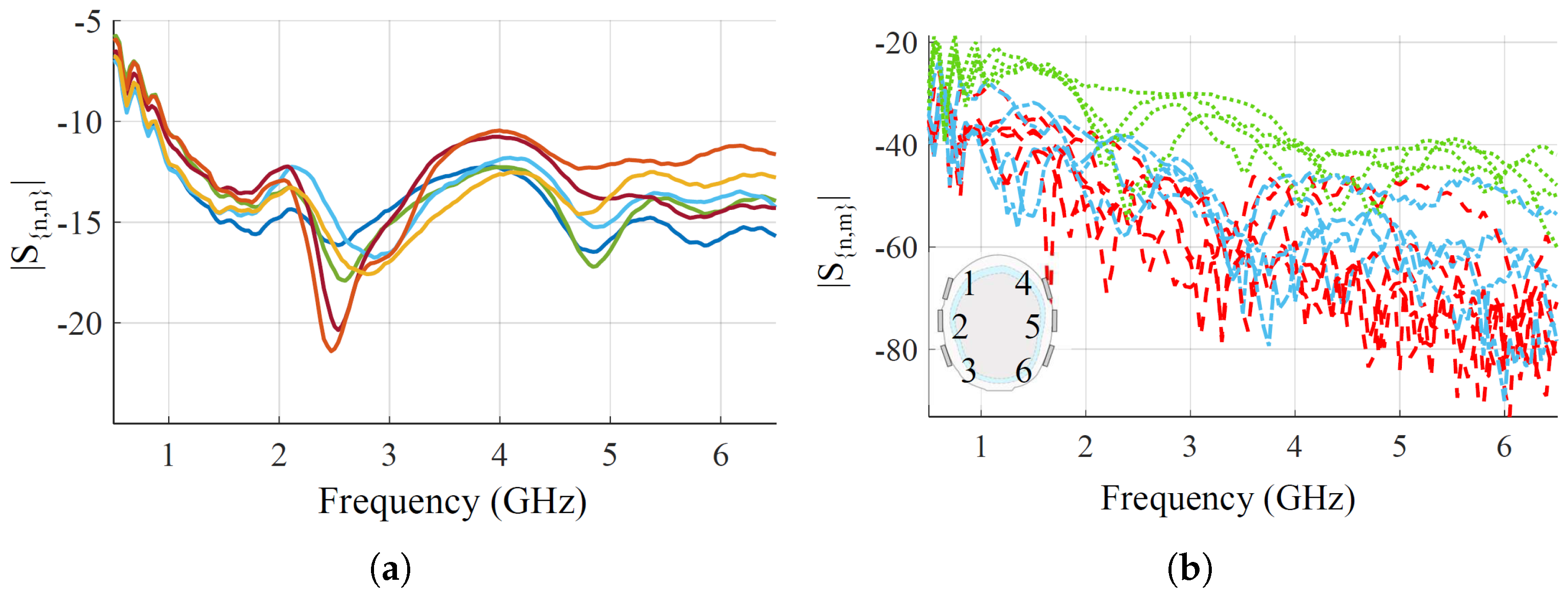
Finally,
Figure 4 shows the measured reflection and transmission coefficients, when placing the optimized antennas on the head phantom. Regarding the reflections, all the antennas have very good matching, lower than
dB, from around 1 GHz up to the end of the chosen bandwidth. At the lower end of the bandwidth, from 500 MHz to 1 GHz, the matching is worse but still lower than
dB. For reflections, there are above around
dB in the whole frequency band for all the antenna pairs, which is within the VNA dynamic range with the chosen setup parameters [
44]. The transmission-reported pairs are grouped into three families based on relative distances for visualization. First, close-by pairs,
,
,
,
; medium-distance pairs,
,
,
,
; and long-distance pairs, the remaining ones.
4. Machine-Learning-Driven Sensing
This work employs the MLP algorithm, a type of Artificial Neural Network (ANN) commonly used for complex medical classification tasks [
54]. For instance, it has been applied in [
55] for brain stroke detection, and in [
56] for the detection and monitoring of heart and liver diseases and for lung cancer. The MLP is based on a number of neurons, as in the human brain, which are linked together with weighted connections, and the output of each neuron is regulated by an activation function. The network consists of at least three layers of neurons: an input layer, a hidden layer, and an output layer [
57]. The supervised method is adopted, where the algorithm is trained on labeled samples to create a surrogate model. In this study, the MLP is used for binary classification (healthy vs pathological) and multi-class classification to differentiate AD severity levels.
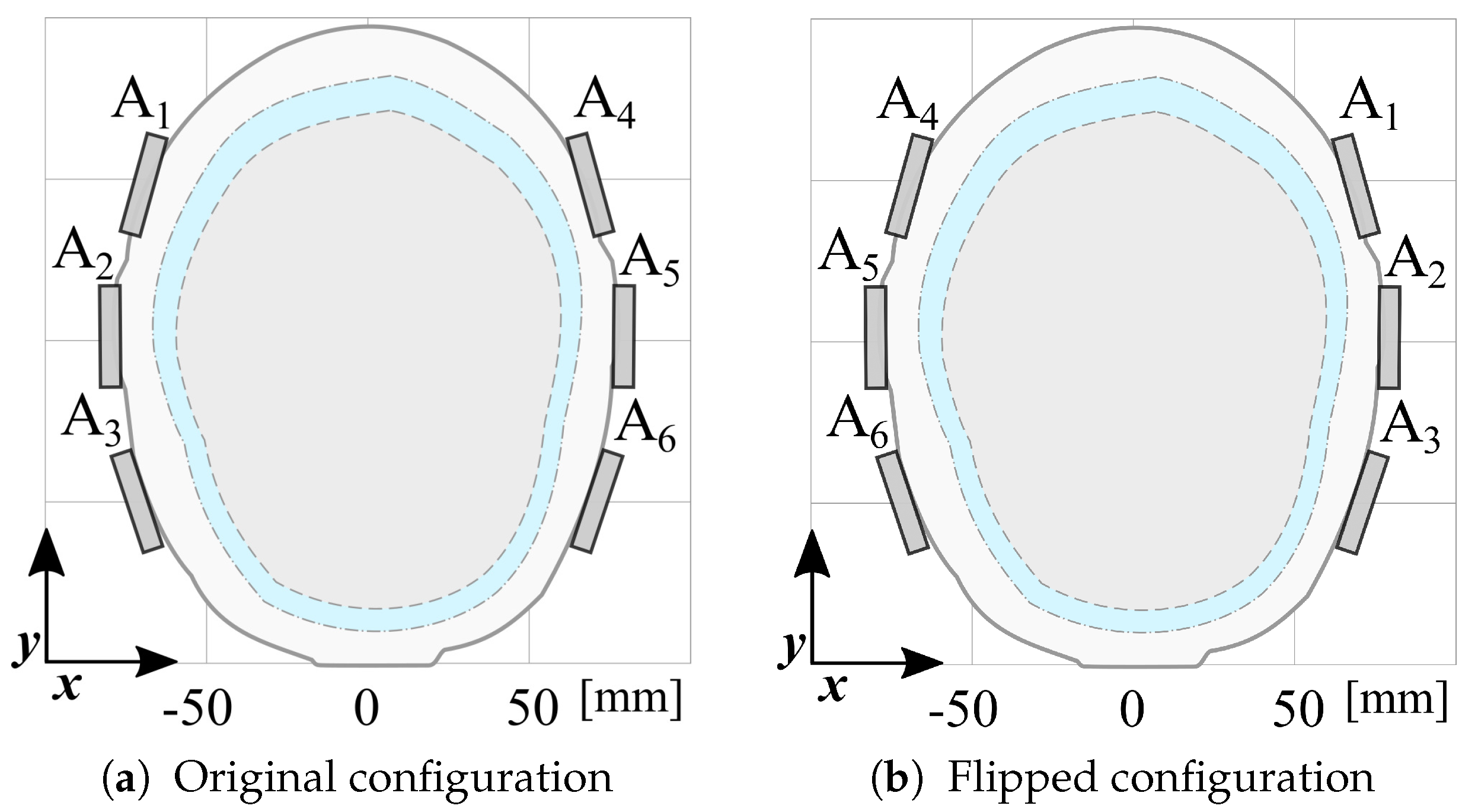
The dataset is augmented by doubling its size, generating virtual scattering matrices by swapping left and right antennas, as illustrated in
Figure 8. This data augmentation process enhances the variability by accounting for the phantom’s asymmetry and is exploited to overcome the limitations of having a single phantom manufactured for this study.
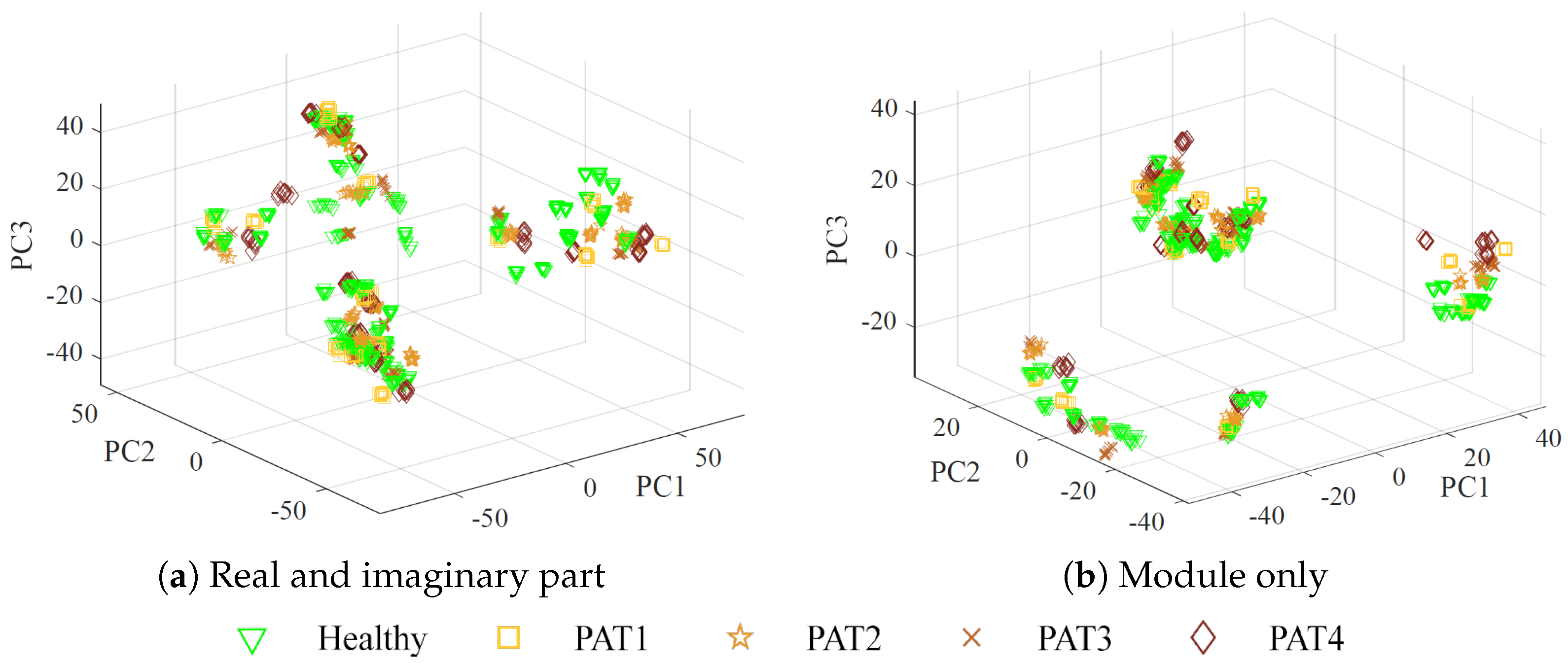
The augmented dataset used as input for the MLP algorithm is structured as a matrix, where each row represents a measurement, and the columns contain the corresponding reshaped complex scattering parameters at different frequencies, for a total of
columns. Two cases are considered: using real and imaginary parts separately (
features), or using only the magnitude (3636 features). Considering magnitude-only information may be of utmost importance in practice, due to the lower cost and greater simplicity of receivers that measure the module only [
55].
The ANN optimization procedure consists of three phases: training, validation, and testing. During training, the model learns patterns and relationships within the dataset by adjusting its parameters to minimize the loss function. The validation tunes hyperparameters and prevents overfitting by evaluating the model’s performance on an independent validation set. Typically, the dataset is divided into training and validation subsets, with a split ratio that ensures sufficient data for learning and model assessment. In this work, the impact on classification performance is evaluated by employing three training–validation split ratios: 60:40, 70:30, and 80:20, using the data from the first two days of measurements. Training and validation sets are generated using two approaches. In data division one (DD1), all the samples are grouped by class. Then, for each class, the samples are randomly split into training and validation sets according to the specified ratios. In data division two (DD2), the 10 measurements within each of the 192 measurement sets are randomly split using the same percentages, ensuring that each measurement set contributes samples to both the training and validation sets; see the scheme in
Figure 9. This helps assess whether performance depends on specific measurement sets while maintaining class balance. Finally, the testing phase evaluates the NN’s generalization capability using unseen data, verifying its effectiveness in real-world scenarios. In this case, data from the third day is used.
The hyperparameters affect the model structure and the learning process. In this work, to select the best set of hyperparameters, the grid-search method is used [
58]. In this method, different values of the hyperparameters are given as input. For each hyperparameter combination, a model is trained using the training set and then evaluated on the validation set. Finally, the combination with the best score is chosen. For binary classification, the score is evaluated using the accuracy, which measures the proportion of correctly predicted samples as:
where TP stands for true positive and TN for true negative, indicating the number of samples correctly predicted as positive and negative, respectively. FP refers to false positive, and FN to false negative, indicating the number of samples wrongly predicted as positive and negative, respectively. Moreover, other commonly used metrics for performance evaluation are precision, recall, and
:
Precision quantifies the proportion of correct positive predictions, while recall measures the proportion of true positive samples correctly identified. The f1-score is the combination of precision and recall via a harmonic mean; it becomes advantageous when the dataset classes are not balanced. It is used as an evaluation score for the multi-class classifier.
During the grid-search optimization process, the considered MLP hyperparameters are: the number of neurons for each layer, the learning rate (the step size towards the minimization of a loss function at each iteration), the training function (the function used to train the algorithm to recognize the input and to produce the correct output), and the loss function. The optimized hyper-parameters for binary classification are reported in
Table 4 and
Table 5 for DD1 and DD2, respectively, considering the different training and validation proportions and the use of the complex scattering parameters or the module only. Specifically, for the training function, CGB and S-CGB correspond to the conjugate gradient method and scaled conjugate gradient method, while for the loss function, MSE and SAE are the mean squared error and the sum absolute error, respectively.
The other hyperparameters are set, for all the considered configurations, as in [
59]: the minimum gradient of the performance function is
, the validation and test ratios for the training data are
, the momentum (a parameter that helps the training acceleration in the relevant direction and dampens oscillations) is
, and the maximum number of validation failures (the worsening of the performances before training stops) is six. Finally, the number of hidden layers is set to two [
20], and the maximum number of epochs to 2000.
6. Conclusions and Perspectives
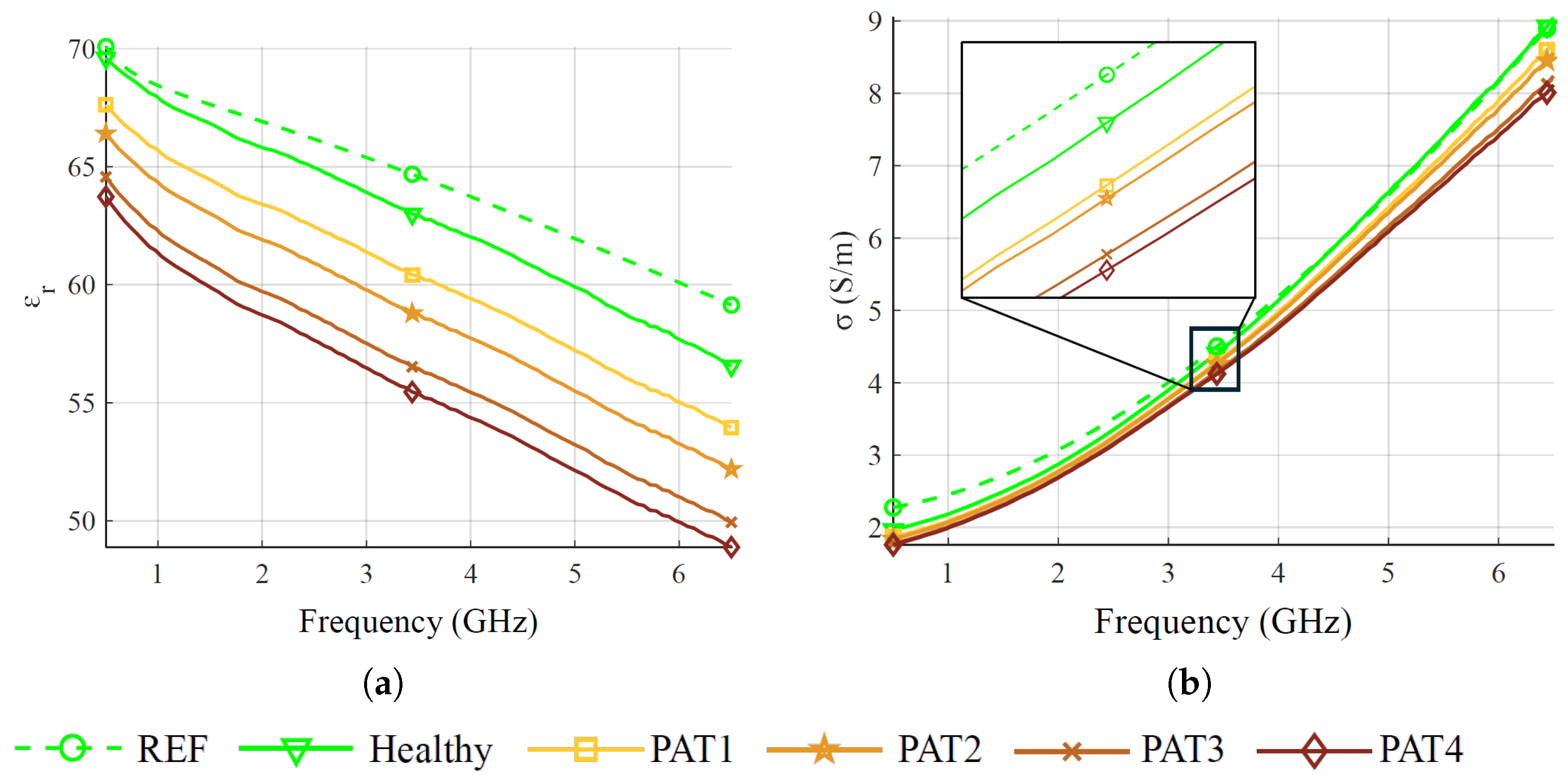
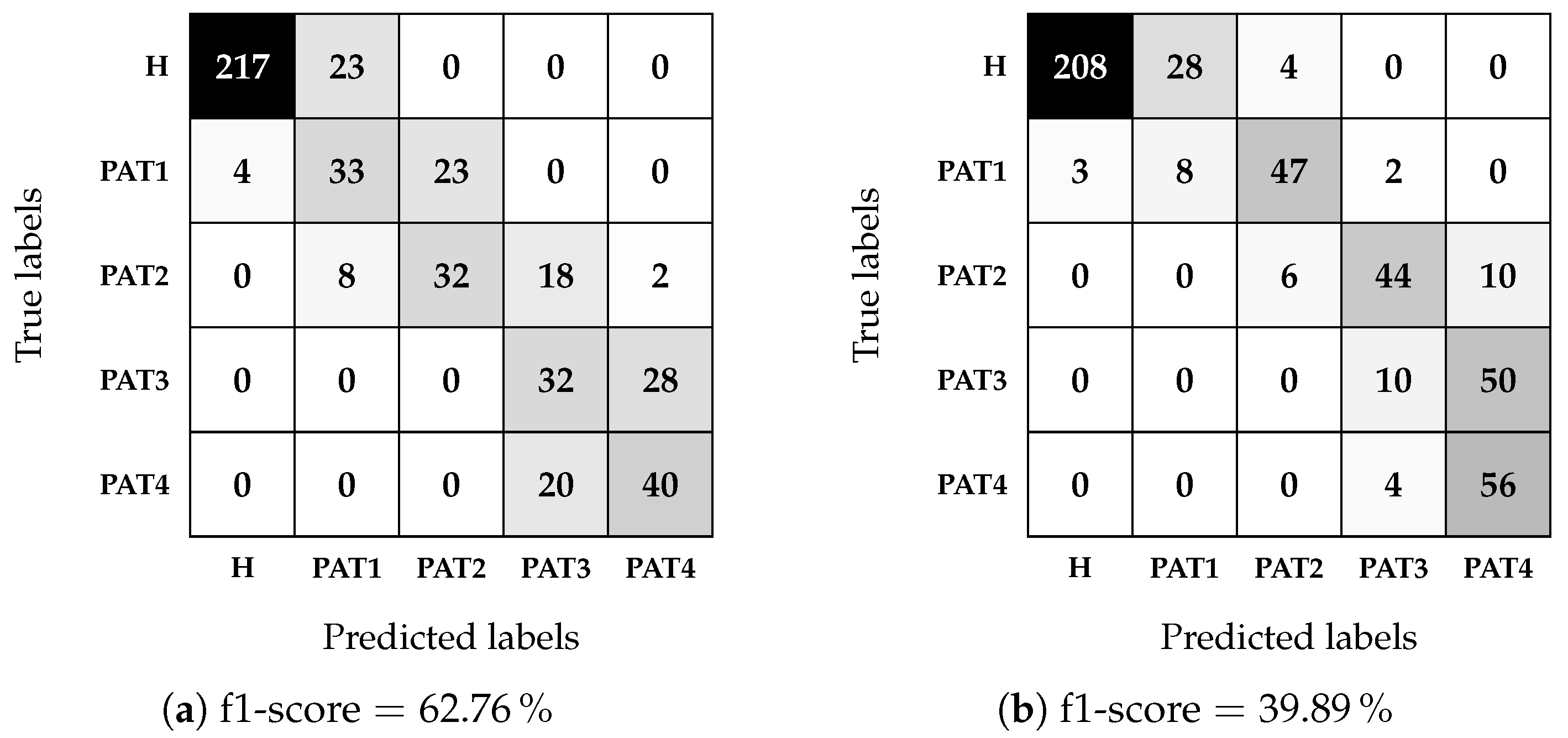
In this work, we described an approach to investigate the feasibility of microwave sensing and machine learning to achieve early AD detection. The physiological basis of this assumption is the reduced permittivity of CSF in AD patients. For this reason, we built a measurement system using a VNA and an array of six custom wide-band antennas designed for this application. To validate the approach, we realized a custom multi-tissue realistic phantom of a human head where the CSF layer can be changed to assume different permittivity values, representing the healthy case or different severity levels of the pathological case. The antennas were placed around the phantom to acquire the scattering parameters in the healthy and AD conditions. A data augmentation technique was used to double the dimension and the variability of the original dataset. Then, the augmented dataset was used to train, validate, and test the MLP classification algorithms. When tested on data belonging to an entirely different day with respect to training and validation, the classifiers achieved an accuracy higher than on binary classification (healthy/pathological), and an f1-score higher than in multi-class classification using two pathological severity levels, confirming the potential impact of this technology on AD early detection.
We acknowledge that real-world scenarios involve additional complexities, and while our proposed method has shown potential, the primary goal of this study is to demonstrate its feasibility. Further research will be necessary to evaluate its effectiveness and generalizability on real patient data. In the future, we plan to conduct controlled in vivo tests to assess the system’s performance in real biological conditions, to combine the designed microwave sensing system with other machine learning algorithms, and to investigate other placements of the antennas to detect the CSF variations.