Research on Space Targets Simulation Modulation Algorithm Combined Global–Local Multi-Spectral Radiation Features
Abstract
1. Introduction
2. Multi-Spectral Modulation Framework with Combined Global–Local Radiation Features
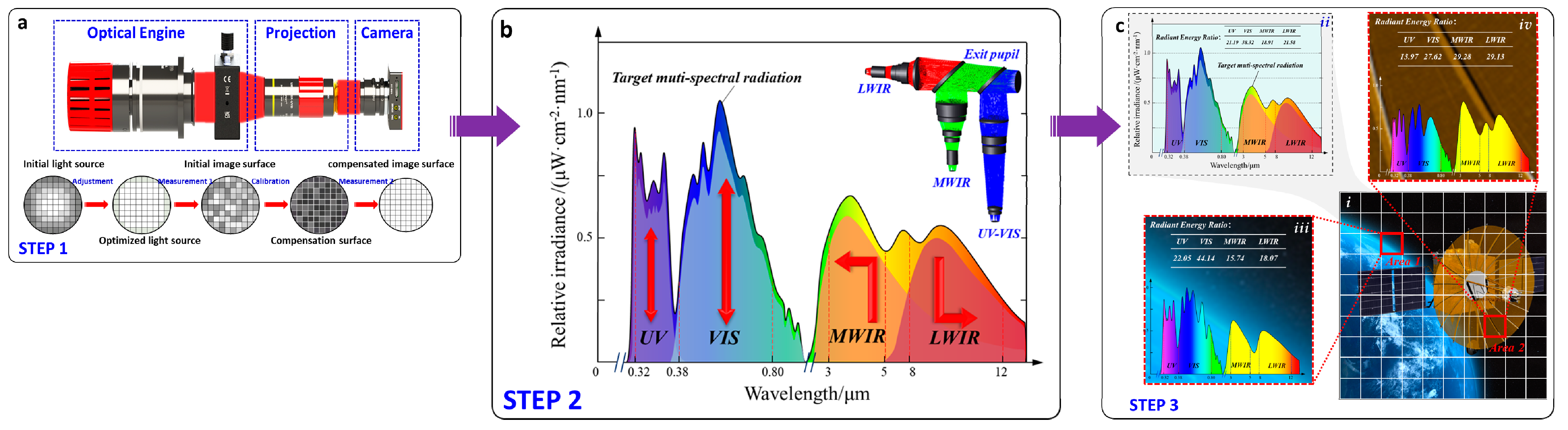
2.1. Overall Architecture of an MIST
2.2. Construction of Multi-Spectral Radiation Features Modulation Link
- (1)
- Optical engine non-uniformity compensation
- (2)
- Global spectral radiant energy modulation
- (3)
- Local radiant grayscale modulation
3. Research on Global–Local Multi-Spectral Radiation Features Modulation Algorithm
3.1. Design of Algorithm Flow
- (1)
- Part I: Optical engine non-uniformity compensation
- (2)
- Part II: Global spectral feature modulation
- (3)
- Part III: Local spectral feature modulation
3.2. Optical Engine Non-Uniformity Compensation
- (1)
- Light source initialization and adjustment
- (2)
- Load area image
- (3)
- Grayscale change
- (4)
- Obtain radiance–grayscale response curve
- (5)
- Complete areas traversal
- (6)
- Obtain the compensation function
3.3. Global Spectral Feature Modulation
- (1)
- Load space target image
- (2)
- Least squares method for solving spectral radiance coefficients
- (3)
- Obtain the spectral radiation ratio error
3.4. Local Spectral Feature Modulation
- (1)
- Input local position coordinates and spectral ratio
- (2)
- Calculate the error difference between the local and global ratios
- (3)
- Local grayscale modulation
- (4)
- Judging whether the ratio error meets the threshold and whether the area traversal is completed
4. Experimentation and Discussion
4.1. Experimental Design
- (1)
- Optical engine non-uniformity compensation experiment
- (2)
- Global spectral radiant energy modulation experiment
- (3)
- Local radiant grayscale modulation experiment
4.2. Experimental Platform Construction
4.3. Experimental Results
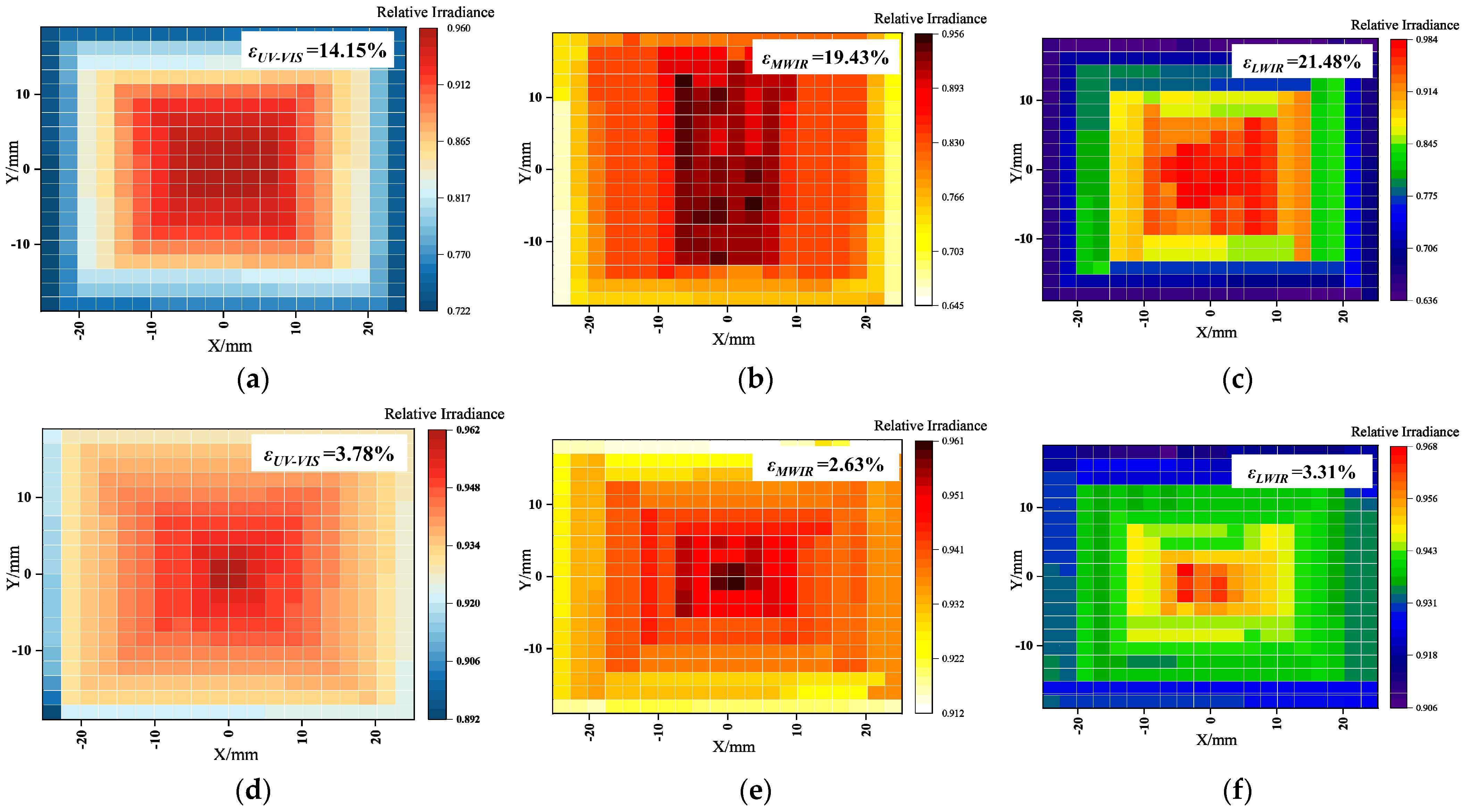
4.3.1. Optical Engine Non-Uniformity Compensation Experiment
4.3.2. Global Spectral Radiant Energy Modulation Experiment
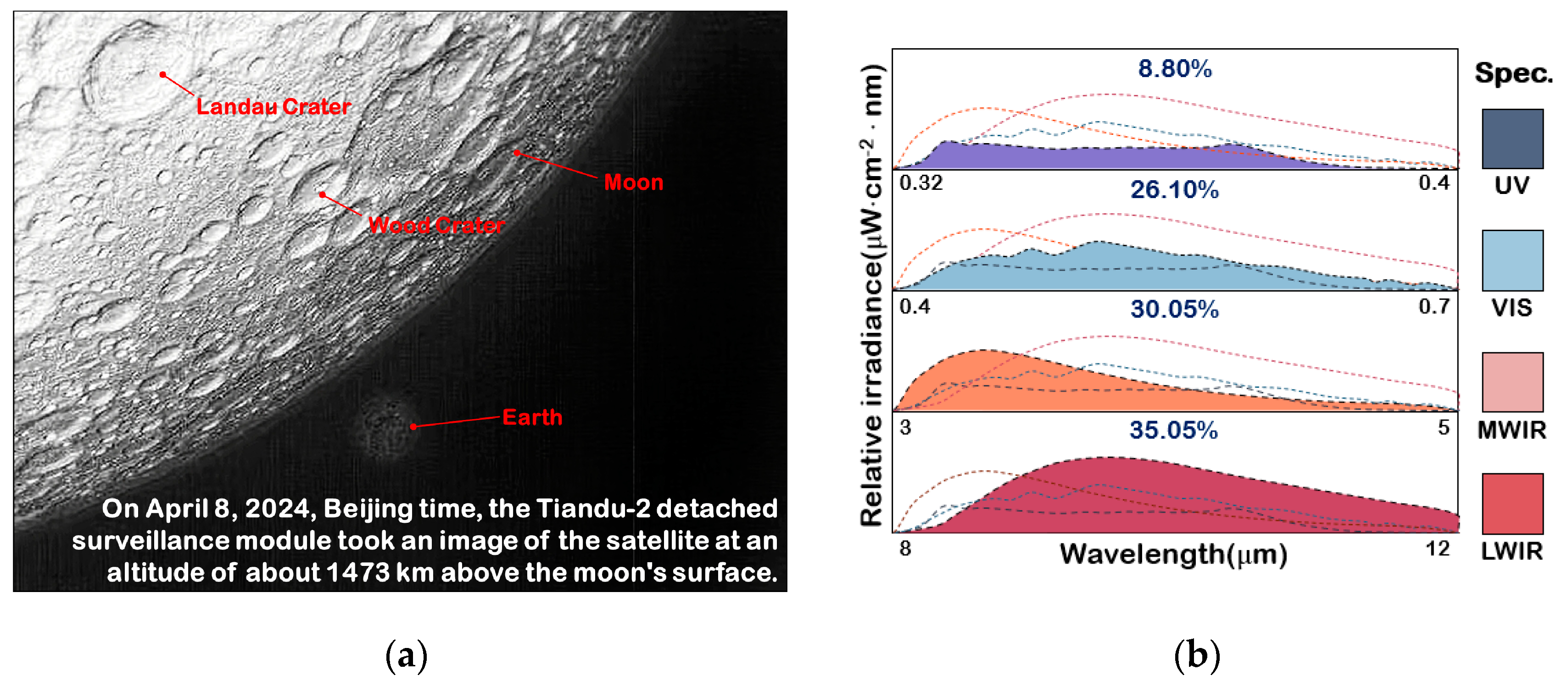
4.3.3. Local Radiant Grayscale Modulation Experiment
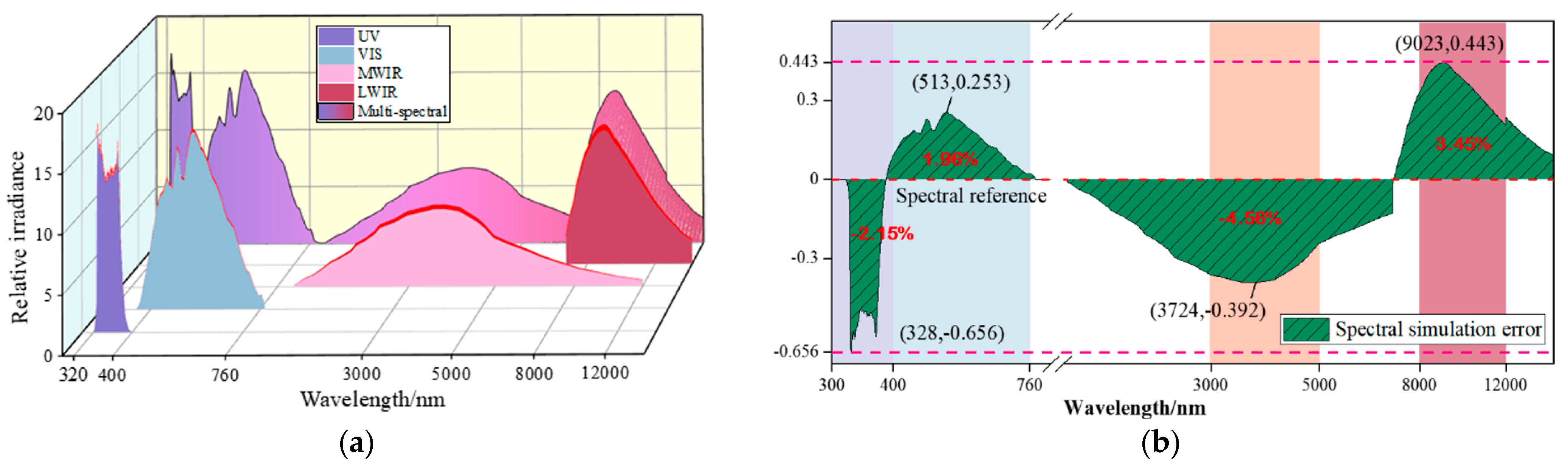
4.4. Discussion and Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bian, L.; Wang, Z.; Zhang, Y.; Li, L.; Zhang, Y.; Yang, C.; Fang, W.; Zhao, J.; Zhu, C.; Meng, Q.; et al. A Broadband Hyperspectral Image Sensor with High Spatio-Temporal Resolution. Nature 2024, 635, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Zheng, Z.; Meng, W.; Chang, S.; Tan, Y.; Chen, L.-J.; Fang, X.; Gu, M.; Chen, J. Harnessing Disordered Photonics via Multi-Task Learning towards Intelligent Four-Dimensional Light Field Sensors. PhotoniX 2023, 4, 26. [Google Scholar] [CrossRef]
- Wu, T.; Guillon, M.; Tessier, G.; Berto, P. Multiplexed Wavefront Sensing with a Thin Diffuser. Optica 2024, 11, 297. [Google Scholar] [CrossRef]
- Cui, Y.; Yao, X.; Chen, X.; Liang, G.; Zhao, S.; Li, L.; Ma, H.; Pan, C.; Wang, B.; Guo, X.; et al. On-Orbit Calibration Techniques for Optical Payloads Onboard Remote-Sensing Satellites. Rev. Sci. Instrum. 2021, 92, 104501. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Fan, L.; Mu, C.; Wang, D. Research on Spacecraft in Orbit Perception Based on Artificial Neural Networks and Digital Twin Technology Using Grating Arrays. Opt. Express 2024, 32, 13065. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Li, Z.; Zhang, S.; Zhao, T.; Shi, R.; Shi, Q. Infrared Scene Projector (IRSP) for Cryogenic Environments Based on a Light-Driven Blackbody Micro Cavity Array (BMCA). Opt. Express 2021, 29, 41428. [Google Scholar] [CrossRef]
- Wu, L.; Wang, J.; Xia, Y.; Li, Y.; Sheng, L. Optimization of Polarization Balance in Beam Splitter Films for Weak Star Simulator. Opt. Express 2024, 32, 25304. [Google Scholar] [CrossRef] [PubMed]
- Jha, S.S.; Kumar, M.; Nidamanuri, R.R. Multi-Platform Optical Remote Sensing Dataset for Target Detection. Data Brief 2020, 33, 106362. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Lei, C.; Yang, Y. A Dynamic Precision Evaluation Method for the Star Sensor in the Stellar-Inertial Navigation System. Sci. Rep. 2017, 7, 4356. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Wang, J.; Sheng, L.; Li, Y.; Xia, Y.; Zhang, S.; Gu, S. Research on Polarization Effect Suppression Method of Weak Starlight Simulation Device. Opt. Express 2024, 32, 39818–39830. [Google Scholar] [CrossRef] [PubMed]
- Dupuis, J.R.; Mansur, D.J.; Vaillancourt, R.; Benedict-Gill, R.; Newbry, S.P. High-Dynamic Range DMD-Based IR Scene Projector. In Proceedings of the SPIE, the International Society for Optical Engineering/Proceedings of SPIE, San Francisco, CA, USA, 2–7 February 2013. [Google Scholar]
- Knežević, D.; Redjimi, A.; Mišković, K.; Vasiljević, D.; Nikolić, Z.; Babić, J. Minimum Resolvable Temperature Difference Model, Simulation, Measurement and Analysis. Opt. Quantum Electron. 2016, 48, 332. [Google Scholar] [CrossRef]
- Ellithey, M.; El-sheikh, H.; Mahmoud, A.; Mokhtar, A.M. Field Performance Evaluation of Aged Thermal Imaging Systems. In Proceedings of the Volume 11906, Infrared, Millimeter-Wave, and Terahertz Technologies VIII, Nantong, China, 10–20 October 2021. [Google Scholar]
- Danielson, T.; Franks, G.; Holmes, N.; LaVeigne, J.; Matis, G.; McHugh, S.; Norton, D.; Vengel, T.; Lannon, J.; Goodwin, S. Achieving Ultra-High Temperatures with a Resistive Emitter Array. In Proceedings of the SPIE, the International Society for Optical Engineering/Proceedings of SPIE, Baltimore, MD, USA, 17–21 April 2016. [Google Scholar]
- Pan, Y.; Xu, X.; Qiao, Y. Design of Two-DMD Based Zoom MW and LW Dual-Band IRSP Using Pixel Fusion. Infrared Phys. Technol. 2018, 91, 90–100. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, G.; Zhang, Y.; Zhang, J.; Sun, G.; Liang, W.; Shi, H.; Du, Z.; Zhao, B.; Ren, T.; et al. Multi-Color Temperature and Magnitude Simulation for Astronomical Spectral Velocity Measurement. IEEE Access 2023, 11, 108104–108116. [Google Scholar] [CrossRef]
- Yun, Z.; Zhang, Y.; Liu, Q.; Ren, T.; Zhao, B.; Xu, D.; Yang, S.; Ren, D.; Yang, J.; Mo, X.; et al. Research on Simulation Method of BP Neural Network PID Control for Stellar Spectrum. Opt. Express 2024, 32, 38879–38895. [Google Scholar] [CrossRef] [PubMed]
- Quan, F.; Liu, S.; Sun, G.; Zhang, J.; Zhang, Y.; Zhao, B.; Zhang, J. A Compensation Method for Full-Field-of-View Energy Nonuniformity in Dark-And-Weak-Target Simulators. Sensors 2024, 24, 4147. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Zhang, Y.; Zhao, B.; Meng, Y.; Ren, D.; Zhang, J.; Sun, G.; Du, Z.; Zhang, G. Simulation Method for Multi-Source Information Fusion Space Target. Opt. Express 2024, 32, 21820. [Google Scholar] [CrossRef] [PubMed]
- Nussbaum, M.; Schafer, E.; Yoon, Z.; Keil, D.; Stoll, E. Spectral Light Curve Simulation for Parameter Estimation from Space Debris. Aerospace 2022, 9, 403. [Google Scholar] [CrossRef]
- Wang, F.; Zhan, H.; Ji, L.; Yang, T.; Meng, Q.; Li, Y.; Li, B.; Zang, Y.; Chen, J.; Huang, Y.; et al. The Elimination of Stressed Induced Light Leakage for In-Plane-Switching LCD. Sci. Rep. 2022, 12. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Liu, Z.; Sun, Y.; Teng, H.; Wang, W.; Bayanheshig; Li, W. Bidirectional Littrow Double Grating Interferometry for Quadruple Optical Interpolation. Opt. Laser Technol. 2024, 175, 110751. [Google Scholar] [CrossRef]
- Zhang, L.; Xiong, L.; Sun, J.; Chen, L.; Xiao, C.; Zhou, W.; Wang, Y.; Liu, W.; Guan, Y.; Chen, T.; et al. System design and validation of Queqiao-2 lunar relay communication satellite. Chin. Space Sci. Technol. 2024, 44, 23–39. [Google Scholar]




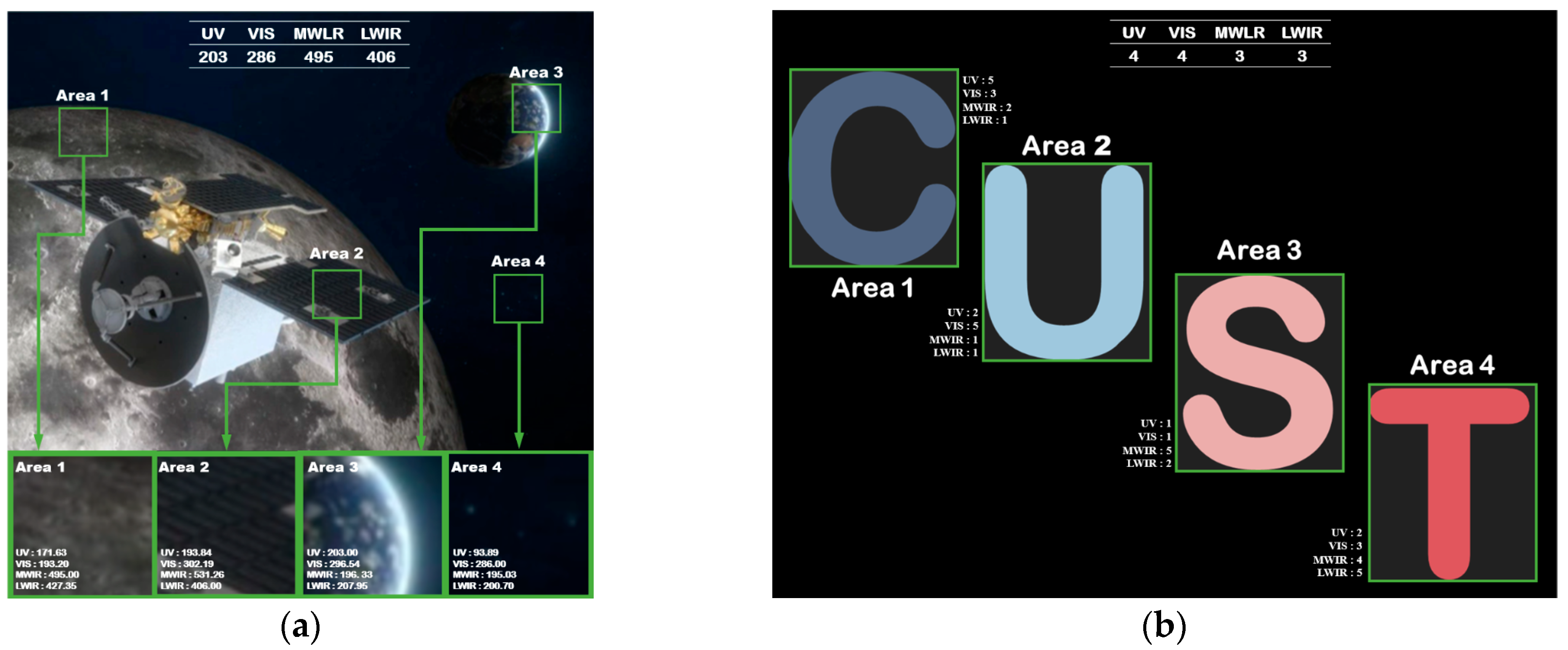
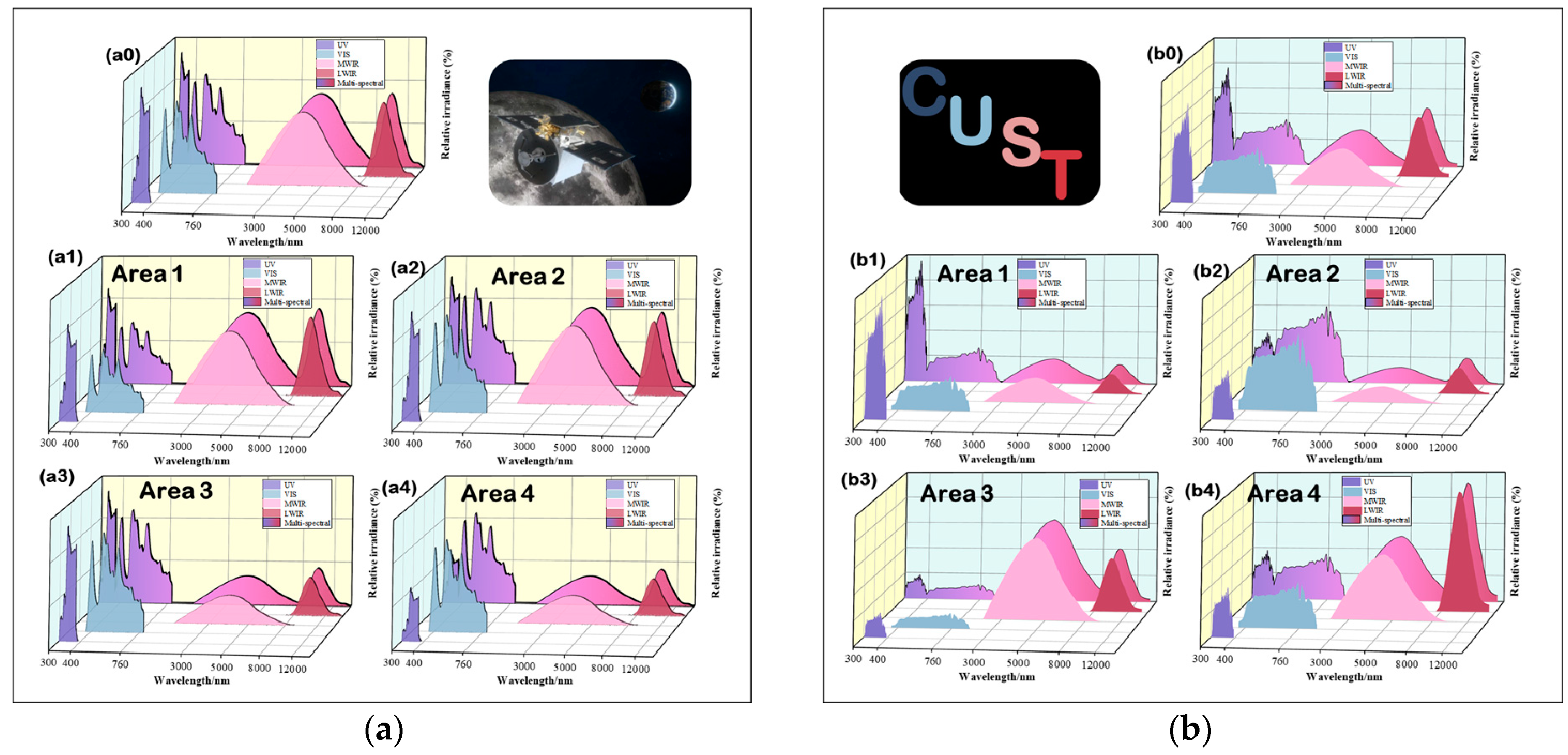
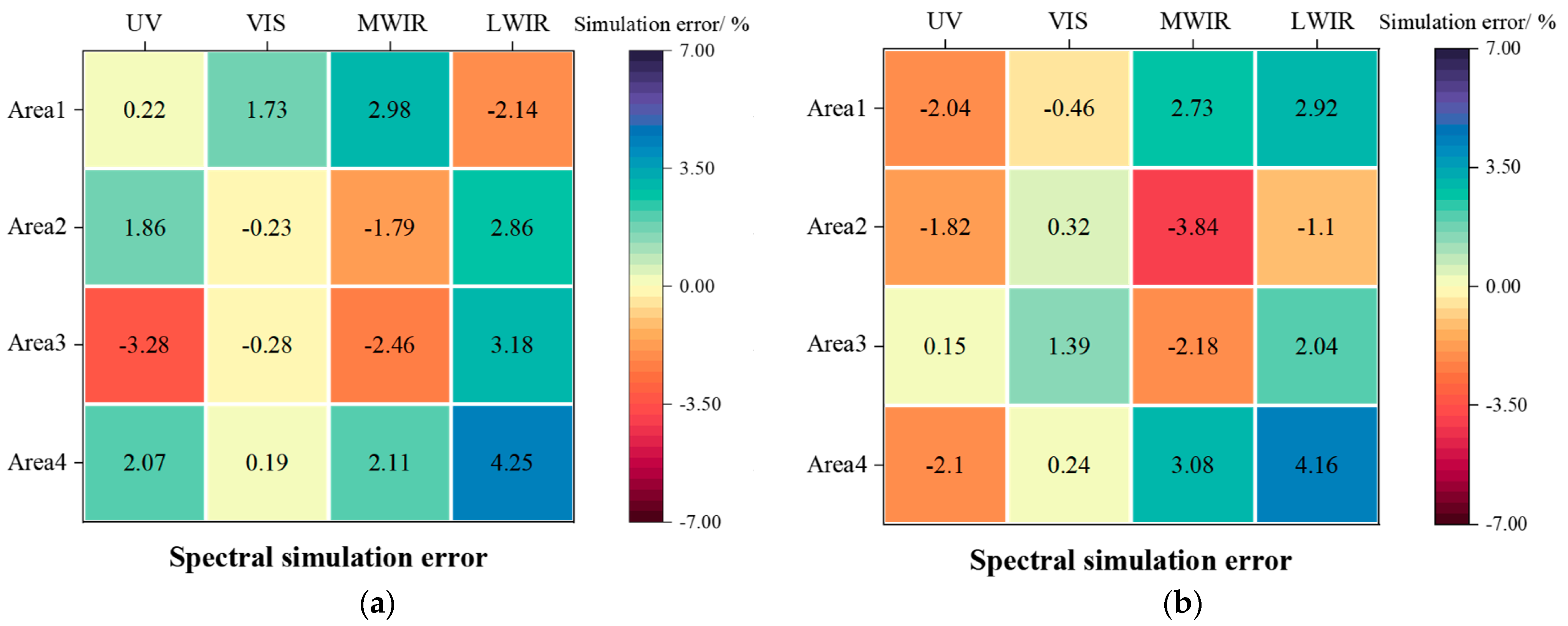
| Serial Number | Experiment Name | Purpose |
|---|---|---|
| 1 | Optical engine non-uniformity compensation experiment | Testing the effectiveness of the algorithm in optical engine non-uniformity compensation for each sub-spectral band. |
| 2 | Global spectral radiant energy modulation experiment | Testing the modulation accuracy of the algorithm on the global radiant energy ratio of each spectral band. |
| 3 | Local radiant grayscale modulation experiment | Testing the accuracy of the algorithm for modulation of localized radiant energy ratios. |
| Spectral Band/μm | Non-Uniformity/% | Optimization Ratio/% |
|---|---|---|
| 0.32–0.76 | Before compensation: 14.15 | 73.32 |
| After compensation: 3.78 | ||
| 3–5 | Before compensation: 19.43 | 86.53 |
| After compensation: 2.62 | ||
| 8–12 | Before compensation: 21.48 | 84.60 |
| After compensation: 3.31 |
| Related Studies | Spectral Range/μm | Target Type | Simulation Accuracy/% | Global/Local Modulation | |
|---|---|---|---|---|---|
| In 2013, OPTRA Inc.’s study [11] | 3–5 and 8–12 | Dynamic surface | / | / | |
| In 2016, Inframet Inc.’s study [12] | 1.1–8 and 0.4–12 | Static surface | / | Global | |
| In 2016, SBIR Inc.’s study [14] | 3–5 and 8–12 | Dynamic surface | / | Global | |
| In 2018, Pan’s study [15] | 3.7–4.8 and 8–12 | Dynamic surface | / | Global | |
| In 2023, Liu’s study [16] | 0.45–1 | Static point | ±4.996% | / | |
| In 2024, Yun’s study [17] | 0.4–0.8 | Static point | ±3.50% | / | |
| This study | Global spectral feature modulation algorithm | 0.32–0.76 and 3–5 and 8–12 | Dynamic surface | ±4.56% | Combined global–local |
| Local spectral feature modulation algorithm | Dynamic surface | ±4.25% | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yang, S.; Wei, Z.; Zhang, J.; Zhao, B.; Ren, D.; Sun, J.; Wang, L.; Ren, T.; Yang, D.; et al. Research on Space Targets Simulation Modulation Algorithm Combined Global–Local Multi-Spectral Radiation Features. Sensors 2025, 25, 2702. https://doi.org/10.3390/s25092702
Zhang Y, Yang S, Wei Z, Zhang J, Zhao B, Ren D, Sun J, Wang L, Ren T, Yang D, et al. Research on Space Targets Simulation Modulation Algorithm Combined Global–Local Multi-Spectral Radiation Features. Sensors. 2025; 25(9):2702. https://doi.org/10.3390/s25092702
Chicago/Turabian StyleZhang, Yu, Songzhou Yang, Zhipeng Wei, Jian Zhang, Bin Zhao, Dianwu Ren, Jingrui Sun, Lu Wang, Taiyang Ren, Dongpeng Yang, and et al. 2025. "Research on Space Targets Simulation Modulation Algorithm Combined Global–Local Multi-Spectral Radiation Features" Sensors 25, no. 9: 2702. https://doi.org/10.3390/s25092702
APA StyleZhang, Y., Yang, S., Wei, Z., Zhang, J., Zhao, B., Ren, D., Sun, J., Wang, L., Ren, T., Yang, D., & Zhang, G. (2025). Research on Space Targets Simulation Modulation Algorithm Combined Global–Local Multi-Spectral Radiation Features. Sensors, 25(9), 2702. https://doi.org/10.3390/s25092702






