Extending Sensing Range by Physics Constraints in Multiband-Multiline Absorption Spectroscopy for Flame Measurement
Abstract
1. Introduction
2. Methods
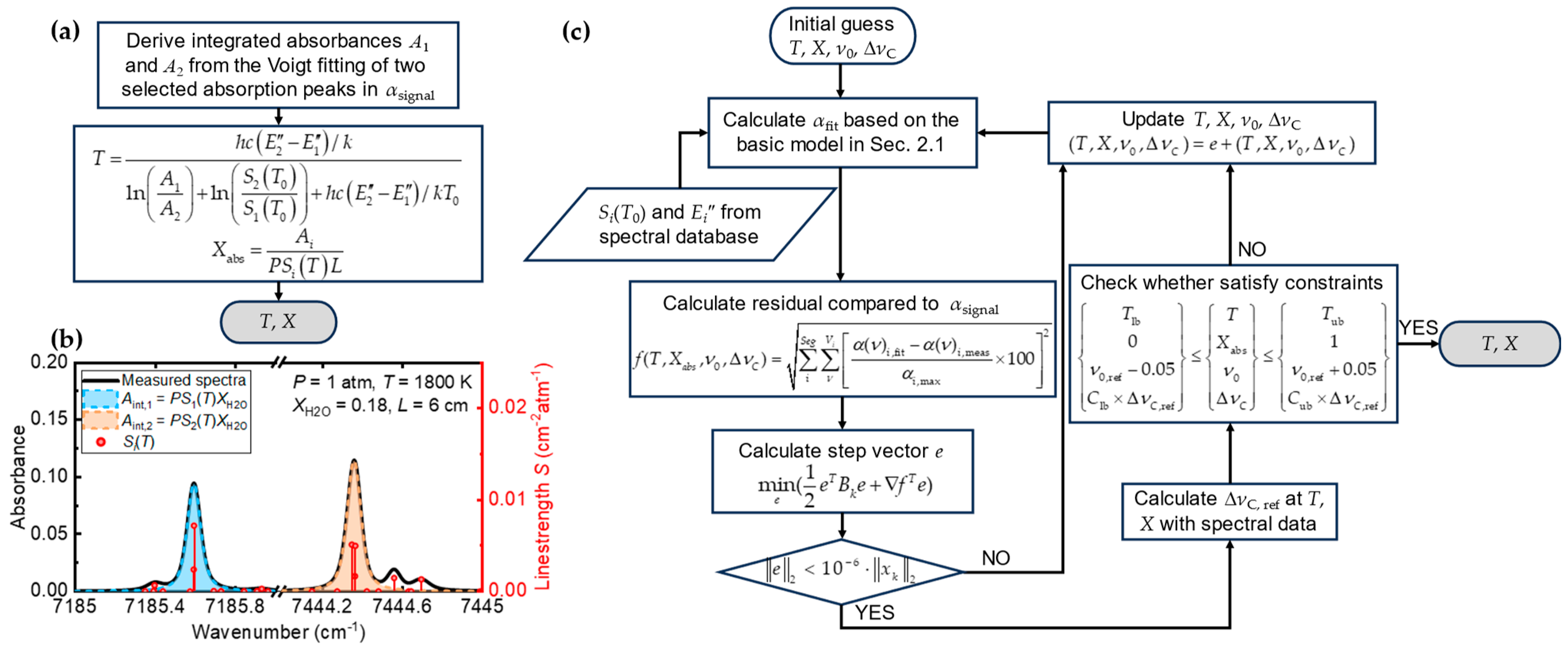
2.1. Laser Absorption Spectroscopy
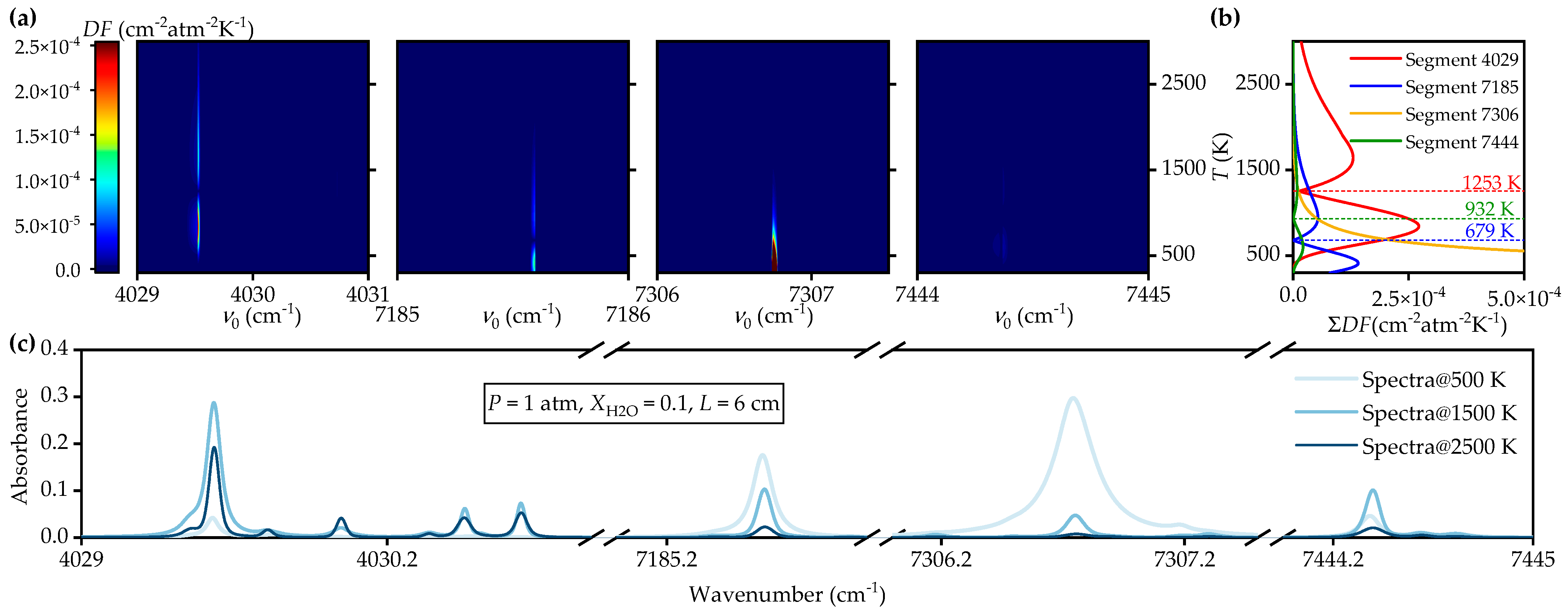
2.2. Line Selection Criterion
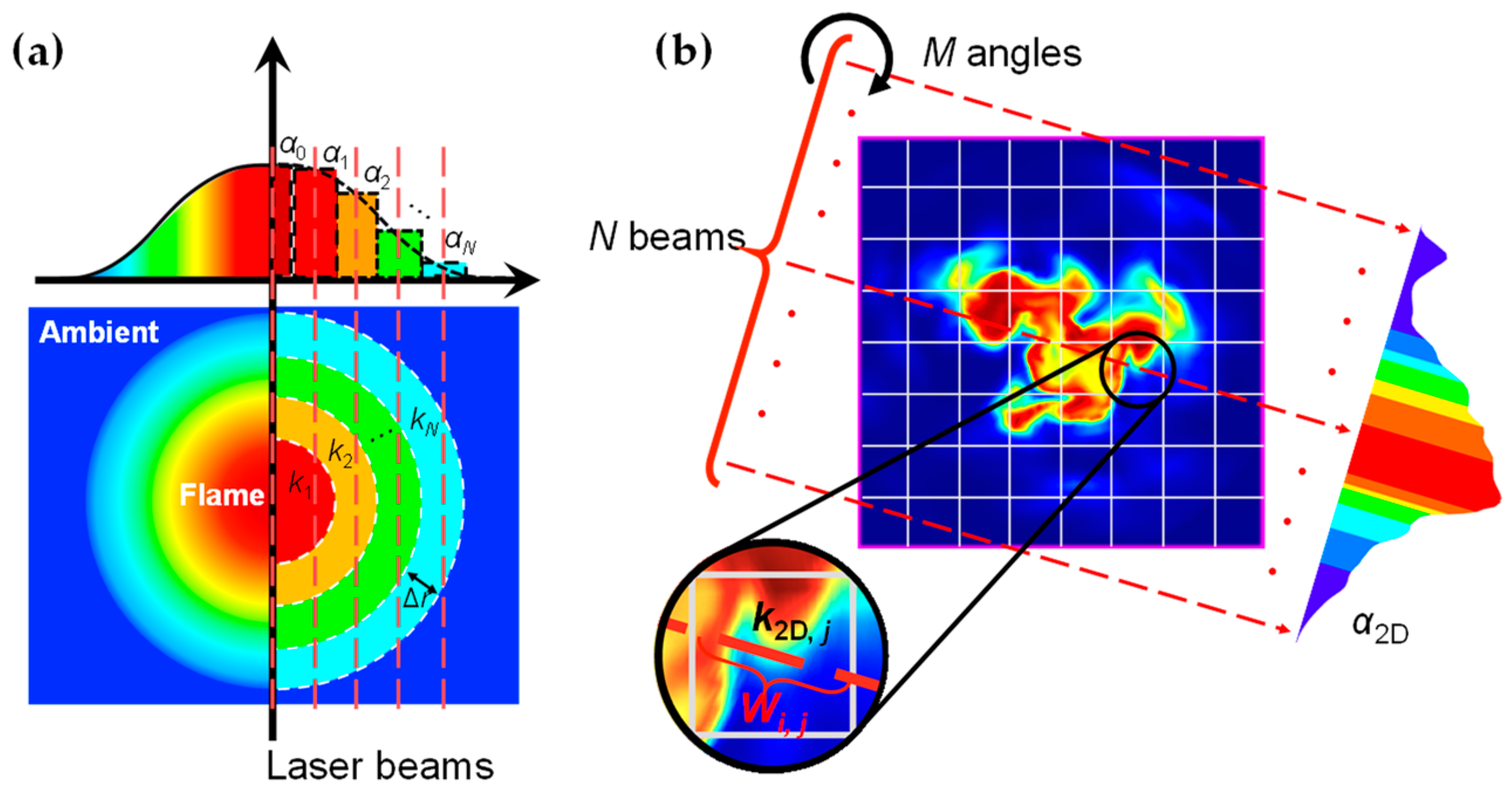
2.3. Tomography
3. Results and Analysis
3.1. Selection and Validation of Spectral Lines in Uniform Thermal Field
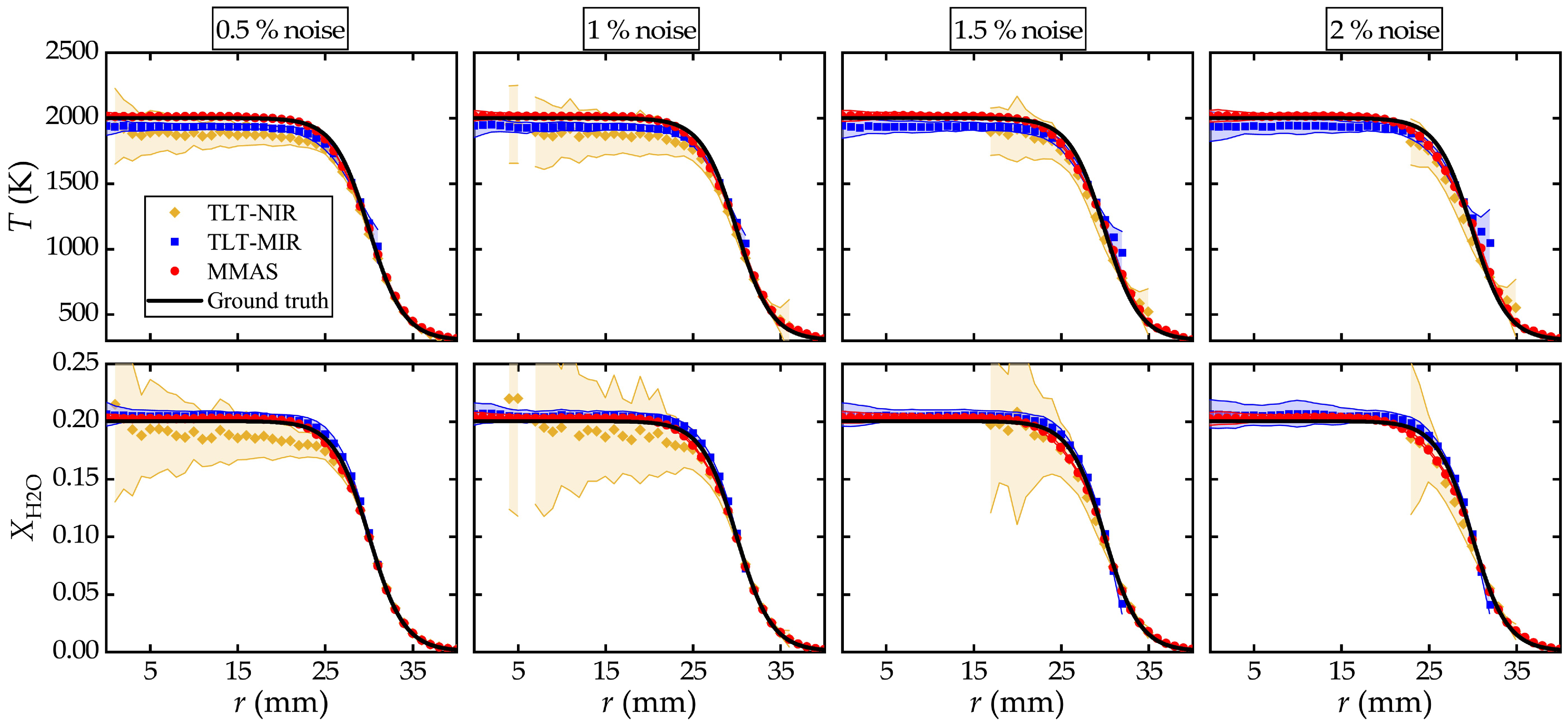
3.2. Axisymmetric Flame
3.3. Two-Dimensional Combustion Field
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hanson, R.K. Applications of Quantitative Laser Sensors to Kinetics, Propulsion and Practical Energy Systems. Proc. Combust. Inst. 2011, 33, 1–40. [Google Scholar] [CrossRef]
- Farooq, A.; Alquaity, A.B.S.; Raza, M.; Nasir, E.F.; Yao, S.; Ren, W. Laser Sensors for Energy Systems and Process Industries: Perspectives and Directions. Prog. Energy Combust. Sci. 2022, 91, 100997. [Google Scholar] [CrossRef]
- Cai, W.; Kaminski, C.F. Tomographic Absorption Spectroscopy for the Study of Gas Dynamics and Reactive Flows. Prog. Energy Combust. Sci. 2017, 59, 1–31. [Google Scholar] [CrossRef]
- Schroeder, P.J.; Wright, R.J.; Coburn, S.; Sodergren, B.; Cossel, K.C.; Droste, S.; Truong, G.W.; Baumann, E.; Giorgetta, F.R.; Coddington, I.; et al. Dual Frequency Comb Laser Absorption Spectroscopy in a 16 MW Gas Turbine Exhaust. Proc. Combust. Inst. 2017, 36, 4565–4573. [Google Scholar] [CrossRef]
- Ma, L.; Li, X.; Sanders, S.T.; Caswell, A.W.; Roy, S.; Plemmons, D.H.; Gord, J.R. 50-kHz-Rate 2D Imaging of Temperature and H2O Concentration at the Exhaust Plane of a J85 Engine Using Hyperspectral Tomography. Opt. Express 2013, 21, 1152–1162. [Google Scholar] [CrossRef] [PubMed]
- Upadhyay, A.; Lengden, M.; Enemali, G.; Stewart, G.; Johnstone, W.; Wilson, D.; Humphries, G.; Benoy, T.; Black, J.; Chighine, A.; et al. Tomographic Imaging of Carbon Dioxide in the Exhaust Plume of Large Commercial Aero-Engines. Appl. Opt. 2022, 61, 8540. [Google Scholar] [CrossRef]
- Cheong, K.-P.; Ma, L.; Wang, Z.; Ren, W. Influence of Line Pair Selection on Flame Tomography Using Infrared Absorption Spectroscopy. Appl. Spectrosc. 2019, 73, 529–539. [Google Scholar] [CrossRef]
- Hanson, R.K.; Spearrin, R.M.; Goldenstein, C.S. Spectroscopy and Optical Diagnostics for Gases; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-23251-5. [Google Scholar]
- Picqué, N.; Hänsch, T.W. Frequency Comb Spectroscopy. Nat. Photonics 2019, 13, 146–157. [Google Scholar] [CrossRef]
- Wei, C.; Pineda, D.I.; Goldenstein, C.S.; Spearrin, R.M. Tomographic Laser Absorption Imaging of Combustion Species and Temperature in the Mid-Wave Infrared. Opt. Express 2018, 26, 20944–20951. [Google Scholar] [CrossRef]
- Cui, B.; Ma, L.; Sun, B.; Li, Q.; Wang, Y. Mid-Infrared Absorption Spectroscopy for in-Situ and Spatially Resolved Measurements of Nitric Oxide in Premixed Ammonia-Methane Co-Fired Flames. Opt. Express 2025, 33, 3262. [Google Scholar] [CrossRef]
- Pineda, D.I.; Urban, J.L.; Mitchell Spearrin, R. Interband Cascade Laser Absorption of Hydrogen Chloride for High-Temperature Thermochemical Analysis of Fire-Resistant Polymer Reactivity. Appl. Opt. 2020, 59, 2141. [Google Scholar] [CrossRef]
- Karpf, A.; Rao, G.N. Real-Time Trace Gas Sensor Using a Multimode Diode Laser and Multiple-Line Integrated Cavity Enhanced Absorption Spectroscopy. Appl. Opt. 2015, 54, 6085. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.H.; Lau, L.Y.; Ren, W. Non-Uniform Temperature and Species Concentration Measurements in a Laminar Flame Using Multi-Band Infrared Absorption Spectroscopy. Appl. Phys. B 2017, 123, 83. [Google Scholar] [CrossRef]
- Ma, L.; Cheong, K.-P.; Duan, K.; Yuan, C.; Ren, W. Hybrid Constraint Multi-Line Absorption Spectroscopy for Non-Uniform Thermochemical Measurements in Axisymmetric Laminar and Jet Flames. Opt. Lasers Eng. 2022, 154, 107014. [Google Scholar] [CrossRef]
- Wei, C.; Perakis, N.; Pineda, D.I.; Egolfopoulos, F.N.; Ihme, M.; Spearrin, R.M. Turbulence-Induced Bias in Time-Averaged Laser Absorption Tomography of Correlated Concentration and Temperature Fields with a First-Order Correction. Combust. Flame 2022, 242, 112210. [Google Scholar] [CrossRef]
- Sentko, M.M.; Schulz, S.; Stelzner, B.; Anderlohr, C.; Vicari, M.; Trimis, D. Determination of Temperature and Water-Concentration in Fuel-Rich Oxy-Fuel Methane Flames Applying TDLAS. Combust. Flame 2020, 214, 336–345. [Google Scholar] [CrossRef]
- Minesi, N.Q.; Richmond, M.O.; Jelloian, C.C.; Kuenning, N.M.; Nair, A.P.; Spearrin, R.M. Multi-Line Boltzmann Regression for near-Electronvolt Temperature and CO Sensing via MHz-Rate Infrared Laser Absorption Spectroscopy. Appl. Phys. B 2022, 128, 214. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hargreaves, R.J.; Hashemi, R.; Karlovets, E.V.; Skinner, F.M.; Conway, E.K.; Hill, C.; Kochanov, R.V.; Tan, Y.; et al. The HITRAN2020 Molecular Spectroscopic Database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Rothman, L.S.; Gordon, I.E.; Barber, R.J.; Dothe, H.; Gamache, R.R.; Goldman, A.; Perevalov, V.I.; Tashkun, S.A.; Tennyson, J. HITEMP, the High-Temperature Molecular Spectroscopic Database. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 2139–2150. [Google Scholar] [CrossRef]
- Cubillas, A.M.; Silva-Lopez, M.; Lazaro, J.M.; Conde, O.M.; Petrovich, M.N.; Lopez-Higuera, J.M. Methane Detection at 1670-Nm Band Using a Hollow-Core Photonic Bandgap Fiber and a Multiline Algorithm. Opt. Express 2007, 15, 17570. [Google Scholar] [CrossRef]
- Wang, W.F.; Yang, B.; Liu, H.F.; Ren, L.F.; He, D.; Zhao, X.C.; Li, J. A Multiline Fitting Method for Measuring Ethylene Concentration Based on WMS-2f/1f. Sci. Rep. 2023, 13, 15302. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, G.; Huang, Y.; Wang, Y.; Qi, F. Two-Dimensional Temperature and Carbon Dioxide Concentration Profiles in Atmospheric Laminar Diffusion Flames Measured by Mid-Infrared Direct Absorption Spectroscopy at 4.2 Μm. Appl. Phys. B Lasers Opt. 2018, 124, 61. [Google Scholar] [CrossRef]
- Cheong, K.-P.; Ma, L.; Duan, K.; Ren, W. A Numerical Study of Multiline-Multiband Tomographic Absorption Spectroscopy for Axisymmetric Flames. In Proceedings of the Global Intelligent Industry Conference 2020, Guangzhou, China, 20–21 November 2020; Wang, L., Ed.; SPIE: Bellingham, WA, USA, 2021; p. 117801J. [Google Scholar]
- Goldenstein, C.S.; Spearrin, R.M.; Jeffries, J.B.; Hanson, R.K. Infrared Laser-Absorption Sensing for Combustion Gases. Prog. Energy Combust. Sci. 2017, 60, 132–176. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Strand, C.L.; Hanson, R.K. Two-Temperature Collisional-Radiative Modeling of Partially Ionized O2–Ar Mixtures over 8000–10,000 K Behind Reflected Shock Waves. J. Phys. Chem. A 2020, 124, 3687–3697. [Google Scholar] [CrossRef]
- Goldenstein, C.S.; Schultz, I.A.; Jeffries, J.B.; Hanson, R.K. Two-Color Absorption Spectroscopy Strategy for Measuring the Column Density and Path Average Temperature of the Absorbing Species in Nonuniform Gases. Appl. Opt. 2013, 52, 7950. [Google Scholar] [CrossRef]
- Li, H.; Farooq, A.; Jeffries, J.B.; Hanson, R.K. Diode Laser Measurements of Temperature-Dependent Collisional-Narrowing and Broadening Parameters of Ar-Perturbed H2O Transitions at 1391.7 and 1397.8 nm. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 132–143. [Google Scholar] [CrossRef]
- McLean, A.B.; Mitchell, C.E.J.; Swanston, D.M. Implementation of an Efficient Analytical Approximation to the Voigt Function for Photoemission Lineshape Analysis. J. Electron. Spectrosc. Relat. Phenom. 1994, 69, 125–132. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Series in Operations Research; Springer: New York, NY, USA, 2006; ISBN 978-0-387-30303-1. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Dasch, C.J. One-Dimensional Tomography: A Comparison of Abel, Onion-Peeling, and Filtered Backprojection Methods. Appl. Opt. 1992, 31, 1146. [Google Scholar] [CrossRef]
- Hansen, P.C.; O’Leary, D.P. The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Åkesson, E.O.; Daun, K.J. Parameter Selection Methods for Axisymmetric Flame Tomography through Tikhonov Regularization. Appl. Opt. 2008, 47, 407. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P.C.; Jørgensen, J.S. AIR Tools II: Algebraic Iterative Reconstruction Methods, Improved Implementation. Numer. Algorithms 2018, 79, 107–137. [Google Scholar] [CrossRef]
- Zhao, W.; Xu, L.; Huang, A.; Gao, X.; Luo, X.; Zhang, H.; Chang, H.; Cao, Z. A WMS Based TDLAS Tomographic System for Distribution Retrievals of Both Gas Concentration and Temperature in Dynamic Flames. IEEE Sens. J. 2020, 20, 4179–4188. [Google Scholar] [CrossRef]
- Van Aarle, W.; Palenstijn, W.J.; De Beenhouwer, J.; Altantzis, T.; Bals, S.; Batenburg, K.J.; Sijbers, J. The ASTRA Toolbox: A Platform for Advanced Algorithm Development in Electron Tomography. Ultramicroscopy 2015, 157, 35–47. [Google Scholar] [CrossRef]
- Van Aarle, W.; Palenstijn, W.J.; Cant, J.; Janssens, E.; Bleichrodt, F.; Dabravolski, A.; De Beenhouwer, J.; Joost Batenburg, K.; Sijbers, J. Fast and Flexible X-Ray Tomography Using the ASTRA Toolbox. Opt. Express 2016, 24, 25129. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Farooq, A.; Hanson, R.K. H2O Temperature Sensor for Low-Pressure Flames Using Tunable Diode Laser Absorption near 2.9 μm. Meas. Sci. Technol. 2011, 22, 125301. [Google Scholar] [CrossRef]
- Farooq, A.; Jeffries, J.B.; Hanson, R.K. In Situ Combustion Measurements of H2O and Temperature near 2.5 μm Using Tunable Diode Laser Absorption. Meas. Sci. Technol. 2008, 19, 075604. [Google Scholar] [CrossRef]
- Wang, F.; Wu, Q.; Huang, Q.; Zhang, H.; Yan, J.; Cen, K. Simultaneous Measurement of 2-Dimensional H2O Concentration and Temperature Distribution in Premixed Methane/Air Flame Using TDLAS-Based Tomography Technology. Opt. Commun. 2015, 346, 53–63. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, Z.; Li, Z.; Guo, Q.; Dong, F. A Study of Two Dimensional Tomography Reconstruction of Temperature and Gas Concentration in a Combustion Field Using TDLAS. Appl. Sci. 2017, 7, 990. [Google Scholar] [CrossRef]
- Liu, C.; Xu, L.; Li, F.; Cao, Z.; Tsekenis, S.A.; McCann, H. Resolution-Doubled One-Dimensional Wavelength Modulation Spectroscopy Tomography for Flame Flatness Validation of a Flat-Flame Burner. Appl. Phys. B Lasers Opt. 2015, 120, 407–416. [Google Scholar] [CrossRef]
- Liu, C.; Cao, Z.; Lin, Y.; Xu, L.; McCann, H. Online Cross-Sectional Monitoring of a Swirling Flame Using TDLAS Tomography. IEEE Trans. Instrum. Meas. 2018, 67, 1338–1348. [Google Scholar] [CrossRef]
- Shi, D.; Cheong, K.-P.; Jiao, T.; Wu, J.; Song, Y.; Liu, Y.; Ren, W. Time-Averaged Tomographic Absorption Spectroscopy for H2O Diffusion in Turbulent Jet Flow at Room Temperature. Int. J. Hydrogen Energy 2023, 52, 133–146. [Google Scholar] [CrossRef]
- Cheong, K.-P.; Shi, D.; Liu, S.; Wu, J.; Duan, K.; Song, Y.; Ren, W. Tomographic Absorption Spectroscopy for H2O Transport in a Laminar Jet with Inverse Concentration Gradient. Sensors 2022, 22, 5939. [Google Scholar] [CrossRef] [PubMed]
- Shi, D.; Jiao, T.; Cheong, K.-P.; Chen, W.; Liu, Y.; Song, Y.; Liu, Y.; Ren, W. Volumetric Imaging of H2O Transportation in Laminar Jets Issuing from Polygonal Nozzles by Masked and Regularized Tomographic Absorption Spectroscopy. Opt. Express 2024, 32, 48421. [Google Scholar] [CrossRef]
- Wang, G.; Mi, J. What Differences Does Large Eddy Simulation Find among Traditional, High-Temperature, and Moderate or Intense Low Oxygen Dilution Combustion Processes of a CH4/H2 Jet Flame in Hot Oxidizer Coflow? Energy Fuels 2018, 32, 5544–5558. [Google Scholar] [CrossRef]
- Wei, C.; Schwarm, K.K.; Pineda, D.I.; Spearrin, R.M. Volumetric Laser Absorption Imaging of Temperature, CO and CO2 in Laminar Flames Using 3D Masked Tikhonov Regularization. Combust. Flame 2021, 224, 239–247. [Google Scholar] [CrossRef]
- Nicolas, F.; Todoroff, V.; Plyer, A.; Le Besnerais, G.; Donjat, D.; Micheli, F.; Champagnat, F.; Cornic, P.; Le Sant, Y. A Direct Approach for Instantaneous 3D Density Field Reconstruction from Background-Oriented Schlieren (BOS) Measurements. Exp. Fluids 2016, 57, 13. [Google Scholar] [CrossRef]




| Line Pair | Wavenumber (cm−1) | S@296K (cm−2 atm−1) | E″ (cm−1) | ΔE″ (cm−1) |
|---|---|---|---|---|
| MIR | 4029.524 | 1.11 × 10−4 | 2660.95 | 2228.534 |
| 4030.729 | 2.59 × 10−9 | 4889.488 | ||
| NIR | 7185.574 | 1.99 × 10−2 | 1045.058 | 750.973 |
| 7444.364 | 1.08 × 10−3 | 1796.031 |
| Candidate Spectral Segments in Wavenumber (cm−1) | |
|---|---|
| MIR | 3459.65–3460.7 [39], 3981.75–3982.95 [40], 4029.0–4031.0 [7], 7153.4–7154.6 [41] |
| NIR | 7164.5–7166.5 [42], 7185.0–7186.0 [7,43,44], 7306–7307.5 [45,46,47], 7444.0–7445.0 [7,43,44] |
| Segment | 4029 | 7185 | ||
|---|---|---|---|---|
| Line center (cm−1) | 4028.178363 4028.25667 4028.733351 4029.428428 4029.523702 4029.524128 | 4029.732972 4029.779592 4030.022402 4030.091518 4030.36021 4030.492872 | 4030.51014 4030.568963 4030.728405 4030.729398 4030.734884 4031.402871 | 7185.394189 7185.400573 7185.442365 7185.596113 7185.596433 7185.936277 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, T.; Kou, S.; Ma, L.; Cheong, K.-P.; Ren, W. Extending Sensing Range by Physics Constraints in Multiband-Multiline Absorption Spectroscopy for Flame Measurement. Sensors 2025, 25, 2317. https://doi.org/10.3390/s25072317
Jiao T, Kou S, Ma L, Cheong K-P, Ren W. Extending Sensing Range by Physics Constraints in Multiband-Multiline Absorption Spectroscopy for Flame Measurement. Sensors. 2025; 25(7):2317. https://doi.org/10.3390/s25072317
Chicago/Turabian StyleJiao, Tengfei, Sheng Kou, Liuhao Ma, Kin-Pang Cheong, and Wei Ren. 2025. "Extending Sensing Range by Physics Constraints in Multiband-Multiline Absorption Spectroscopy for Flame Measurement" Sensors 25, no. 7: 2317. https://doi.org/10.3390/s25072317
APA StyleJiao, T., Kou, S., Ma, L., Cheong, K.-P., & Ren, W. (2025). Extending Sensing Range by Physics Constraints in Multiband-Multiline Absorption Spectroscopy for Flame Measurement. Sensors, 25(7), 2317. https://doi.org/10.3390/s25072317








