Concrete Damage Identification and Localization for Structural Health Monitoring Based on Piezoelectric Sensors
Abstract
1. Introduction
2. Materials and Methods
2.1. Stress Wave Propagation Theory
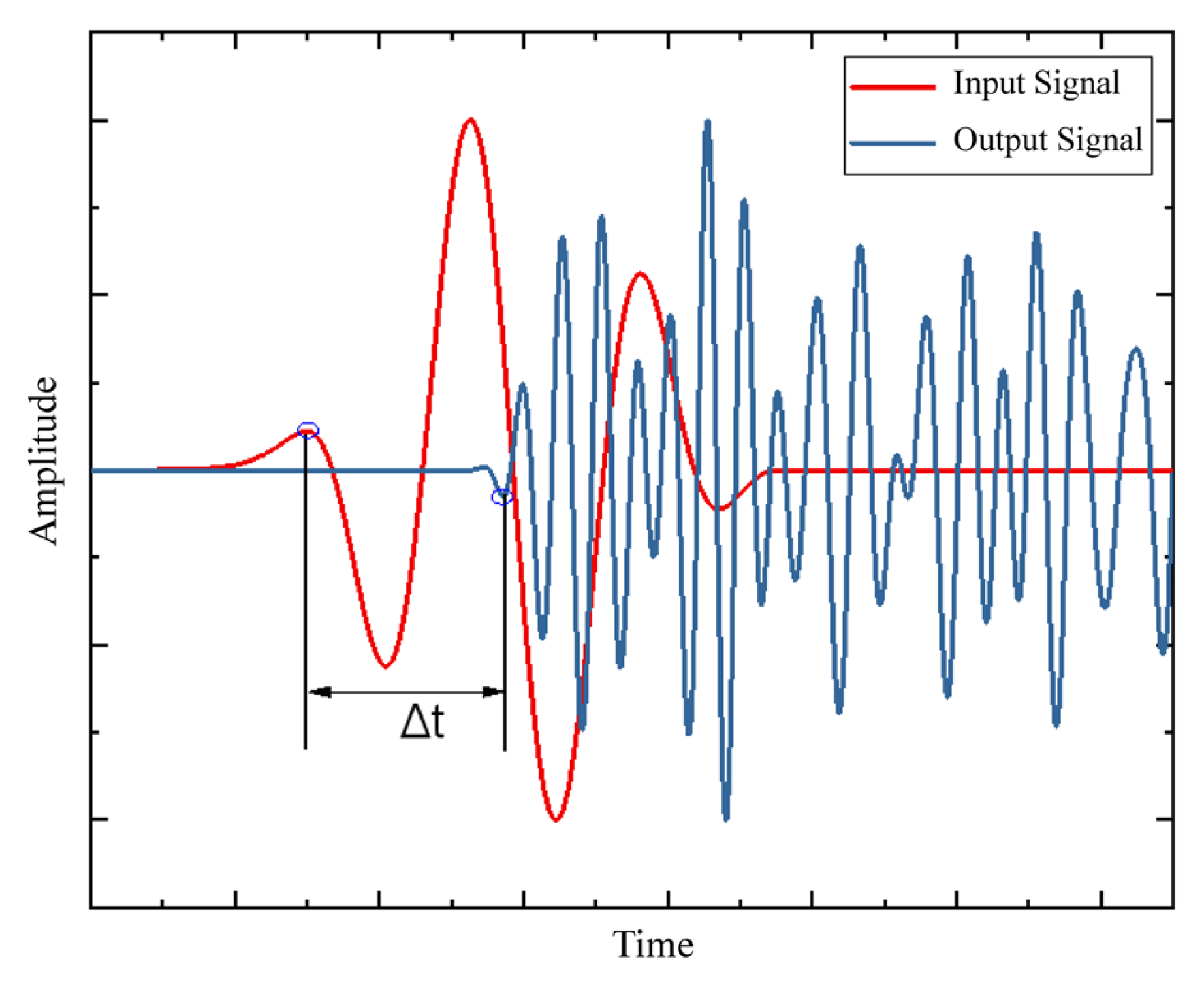
2.2. Wave Speed
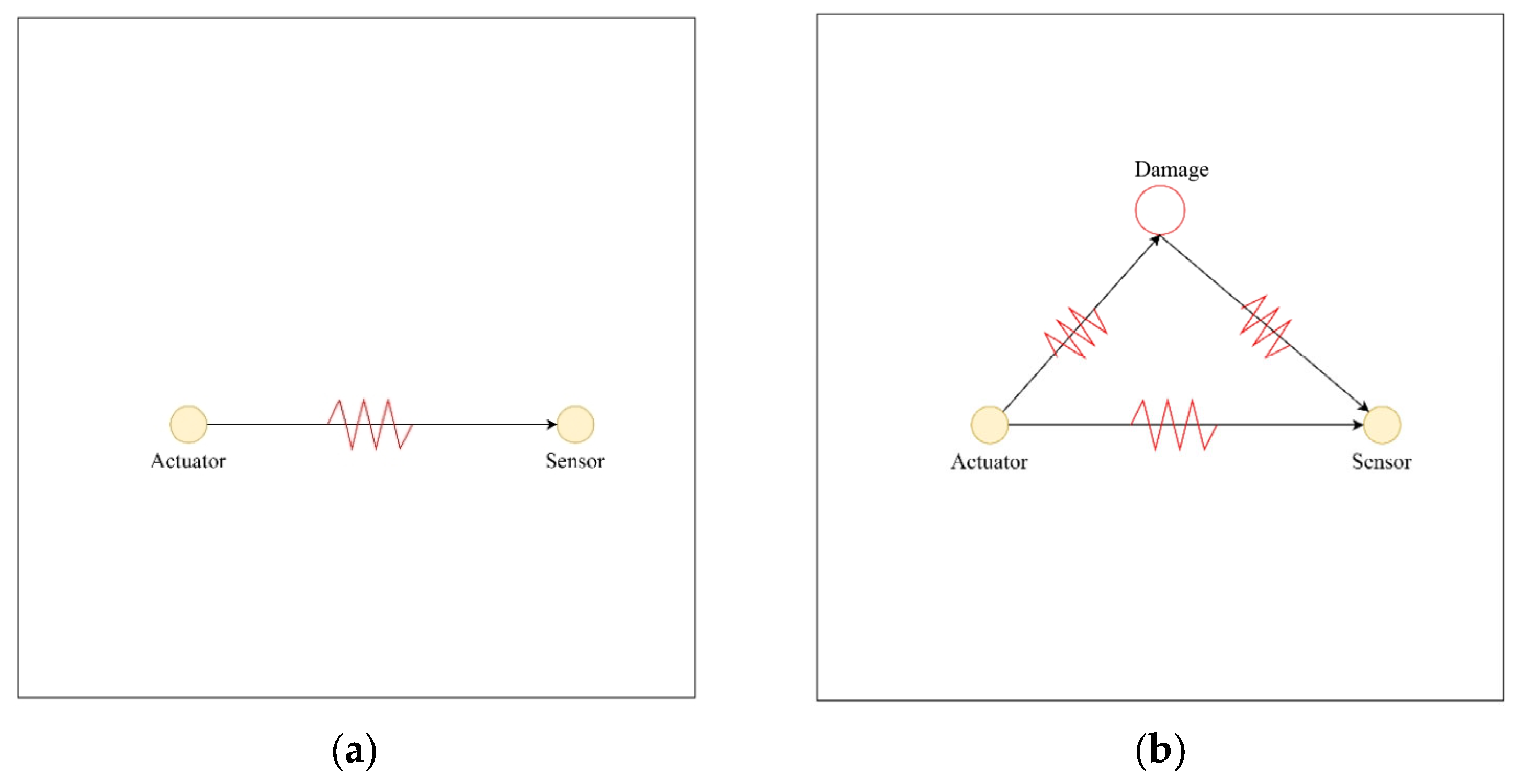
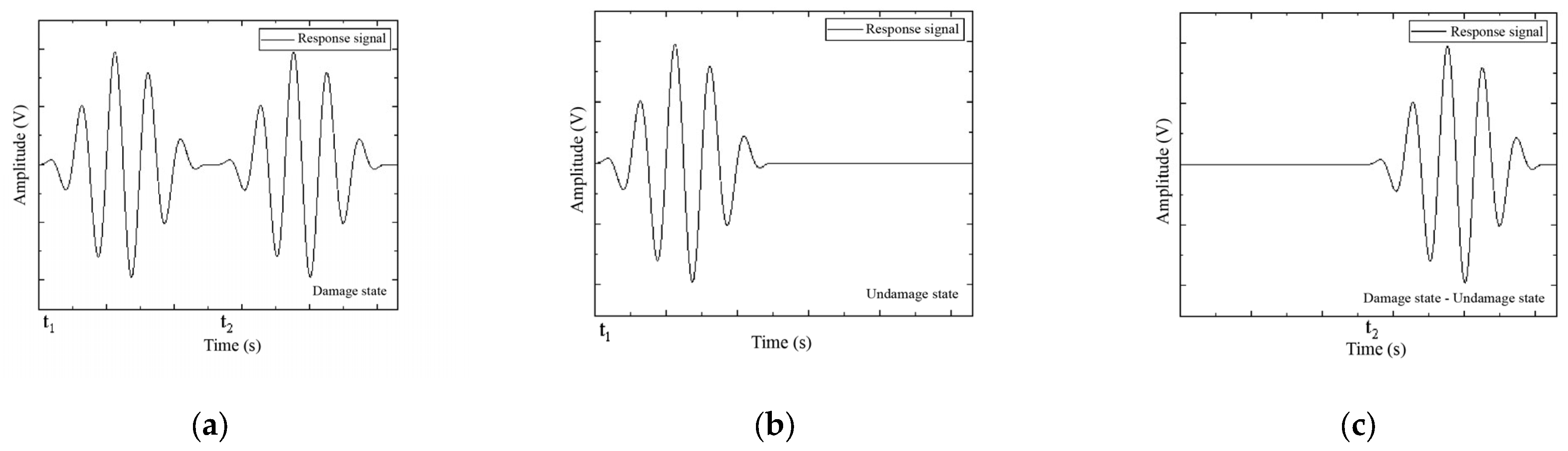
2.3. Damage Scattering Signals
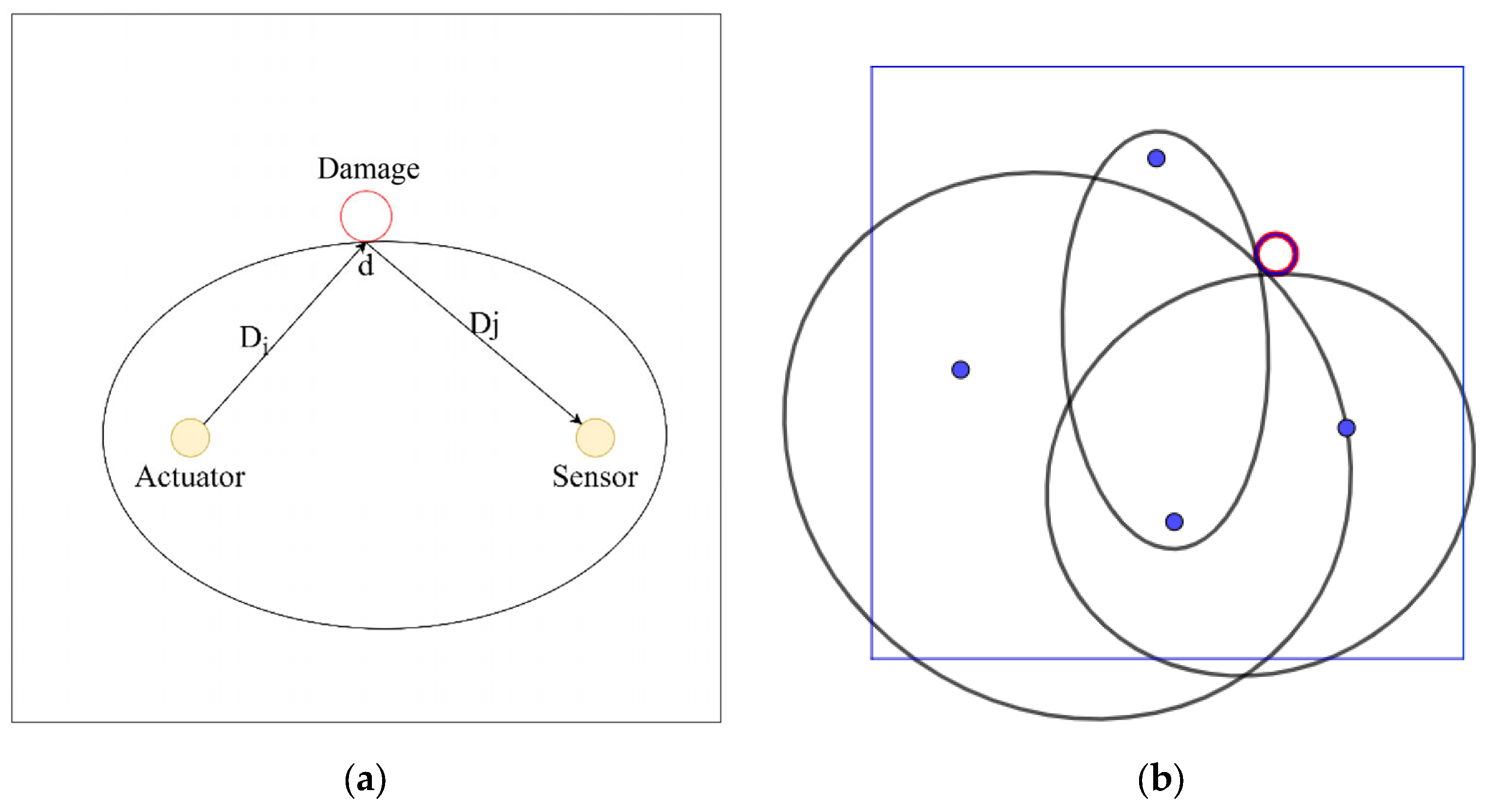
2.4. Concrete Damage Localization Method
3. Experiments and Results
3.1. Experimental Specimens
3.2. Experimental Setup
3.3. Data Processing and Results Analysis
3.3.1. Wave Speed Calculation
3.3.2. Damage Scattering Signal
3.3.3. Damage Identification and Localization
3.3.4. Uncertainty Analysis
4. Numerical Simulation
4.1. Numerical Model
4.1.1. Specimen
4.1.2. Material Parameters
4.1.3. Boundary
4.1.4. Mesh Division
4.1.5. Data Acquisition
4.2. Data Processing and Results Analysis
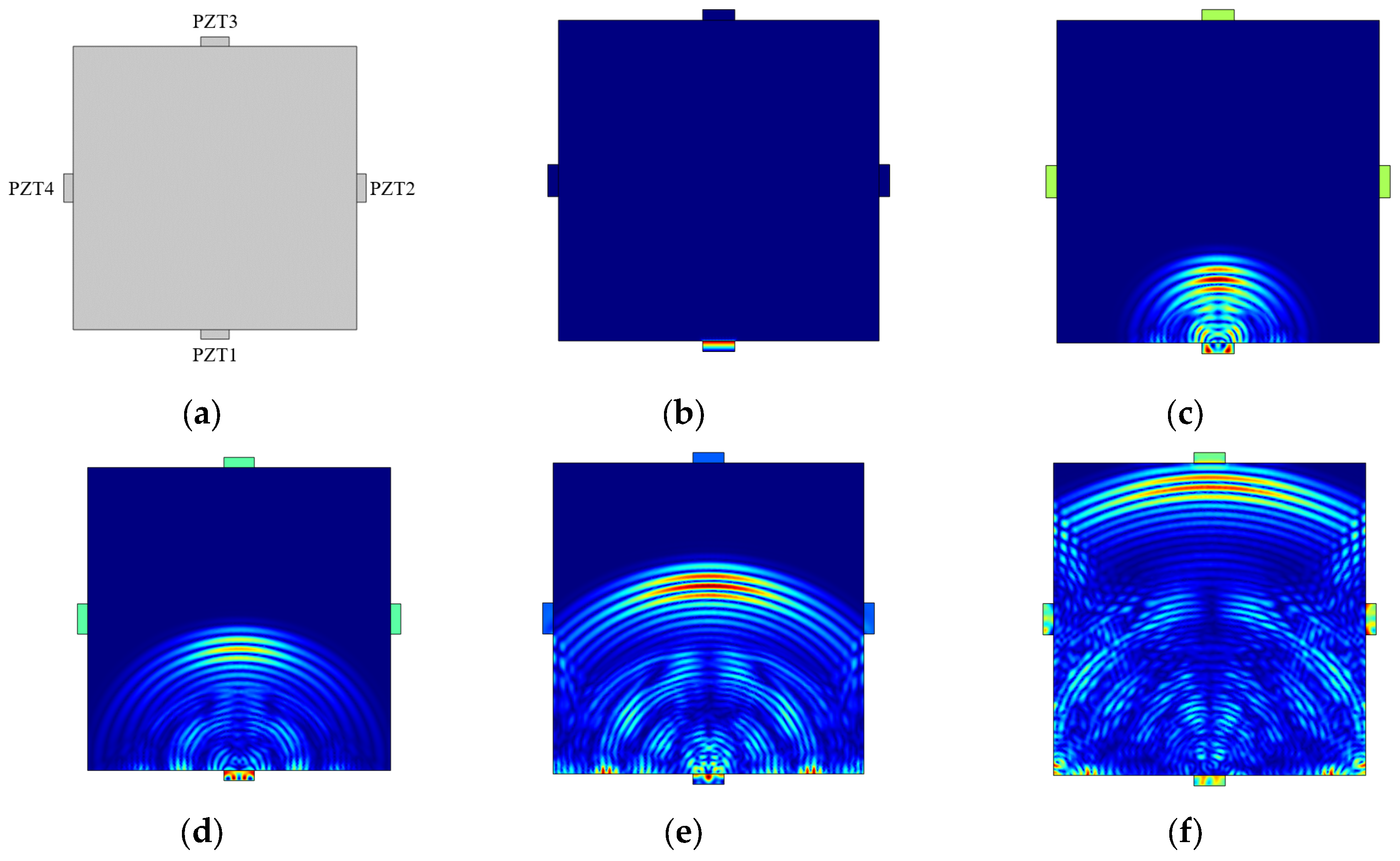
4.2.1. Stress Wave Propagation Process
4.2.2. Stress Wave Speed Analysis
4.2.3. Damage Scattering Signal Analysis
4.2.4. Localization Results
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SHM | structural health monitoring |
| NDT | non-destructive testing |
| SA | smart aggregates |
References
- Ammann, O.H.; Von Kármán, T.; Woodruff, G.B. The Failure of the Tacoma Narrows Bridge; Federal Works Agency: Washington, DC, USA, 1941. [Google Scholar]
- Calvi, G.M.; Moratti, M.; O’Reilly, G.J.; Scattarreggia, N.; Monteiro, R.; Malomo, D.; Calvi, P.M.; Pinho, R. Once upon a Time in Italy: The Tale of the Morandi Bridge. Struct. Eng. Int. 2018, 29, 198–217. [Google Scholar] [CrossRef]
- Chen, J.; Yu, Z.; Jin, H. Nondestructive testing and evaluation techniques of defects in fiber-reinforced polymer composites: A review. Front. Mater. 2022, 9, 986645. [Google Scholar] [CrossRef]
- Dwivedi, S.K.; Vishwakarma, M.; Soni, A. Advances and researches on non destructive testing: A review. Mater. Today Proc. 2018, 5, 3690–3698. [Google Scholar] [CrossRef]
- Helal, J.; Sofi, M.; Mendis, P. Non-destructive testing of concrete: A review of methods. Electron. J. Struct. Eng. 2015, 14, 97–105. [Google Scholar] [CrossRef]
- Ortiz, J.D.; Dolati, S.S.K.; Malla, P.; Mehrabi, A.; Nanni, A. Nondestructive testing (NDT) for damage detection in concrete elements with externally bonded fiber-reinforced polymer. Buildings 2024, 14, 246. [Google Scholar] [CrossRef]
- Matzkanin, G.A. Selecting a nondestructive testing method: Visual inspection. Ammtiac Q. 2006, 1, 7–10. [Google Scholar]
- Blitz, J.; Simpson, G. Ultrasonic Methods of Non-Destructive Testing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995; Volume 2. [Google Scholar]
- Hanke, R.; Fuchs, T.; Uhlmann, N. X-ray based methods for non-destructive testing and material characterization. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2008, 591, 14–18. [Google Scholar] [CrossRef]
- Gelman, L.; Kırlangıç, A.S. Novel vibration structural health monitoring technology for deep foundation piles by non-stationary higher order frequency response function. Struct. Control Health Monit. 2020, 27, e2526. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef]
- Sohn, H.; Farrar, C.R.; Hemez, F.M.; Shunk, D.D.; Stinemates, D.W.; Nadler, B.R.; Czarnecki, J.J. A Review of Structural Health Monitoring Literature: 1996–2001; Los Alamos National Laboratory: Los Alamos, NM, USA, 2003; Volume 20, pp. 34–45. [Google Scholar]
- Hanif, A.; Alam, T.; Islam, M.T.; Albadran, S.; Alsaif, H.; Alshammari, A.S.; Alzamil, A. Compact Complementary Highly Sensitive Microwave Planer Sensor for Reliable Material Dielectric Characterization. IEEE Sens. J. 2024, 25, 4749–4756. [Google Scholar] [CrossRef]
- Allain, B.; Delmonte, N.; Silvestri, L.; Marconi, S.; Alaimo, G.; Auricchio, F.; Bozzi, M. Exploiting the Coupling Variation of 3-D-Printed Cavity Filters for Complex Dielectric Permittivity Sensing. IEEE Microw. Wirel. Technol. Lett. 2024, 34, 717–720. [Google Scholar] [CrossRef]
- Wang, S.; Wan, C.; Chung, K.L.; Zheng, Y. Investigation of Compact Near-Equidistant Multimode Resonator Integrating Skyrmionic Metamaterial with SIW Cavity and Its Application in Dielectric Material Detection. IEEE Trans. Microw. Theory Tech. 2024. [Google Scholar] [CrossRef]
- Ai, D.; Zhu, H.; Luo, H. Sensitivity of embedded active PZT sensor for concrete structural impact damage detection. Constr. Build. Mater. 2016, 111, 348–357. [Google Scholar] [CrossRef]
- Divsholi, B.S.; Yang, Y. Application of PZT sensors for detection of damage severity and location in concrete. In Smart Structures, Devices, and Systems IV; SPIE: Bellingham, WA, USA, 2008; Volume 7268, pp. 254–261. [Google Scholar] [CrossRef]
- Zhou, L.; Zheng, Y.; Huo, L.; Ye, Y.; Chen, D.; Ma, H.; Song, G. Monitoring of bending stiffness of BFRP reinforced concrete beams using piezoceramic transducer enabled active sensing. Smart Mater. Struct. 2020, 29, 105012. [Google Scholar] [CrossRef]
- Zeng, L.; Parvasi, S.M.; Kong, Q.; Huo, L.; Li, M.; Song, G. Bond slip detection of concrete-encased composite structure using shear wave based active sensing approach. Smart Mater. Struct. 2015, 24, 125026. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, G.; Li, H.; Huo, L.; Song, G. A novel time reversal sub-group imaging method with noise suppression for damage detection of plate-like structures. Struct. Control Health Monit. 2018, 25, e2111. [Google Scholar] [CrossRef]
- Sapidis, G.M.; Naoum, M.C.; Papadopoulos, N.A.; Golias, E.; Karayannis, C.G.; Chalioris, C.E. A Novel Approach to Monitoring the Performance of Carbon-Fiber-Reinforced Polymer Retrofitting in Reinforced Concrete Beam–Column Joints. Appl. Sci. 2024, 14, 9173. [Google Scholar] [CrossRef]
- Ospitia, N.; Korda, E.; Kalteremidou, K.-A.; Lefever, G.; Tsangouri, E.; Aggelis, D.G. Recent developments in acoustic emission for better performance of structural materials. Dev. Built Environ. 2023, 13, 100106. [Google Scholar] [CrossRef]
- Gao, W.; Huo, L.; Li, H.; Song, G. An embedded tubular PZT transducer based damage imaging method for two-dimensional concrete structures. IEEE Access 2018, 6, 30100–30109. [Google Scholar] [CrossRef]
- Memmolo, V.; Ricci, F.; Maio, L.; Boffa, N.D.; Monaco, E. Model assisted probability of detection for a guided waves based SHM technique. In Health Monitoring of Structural and Biological Systems; SPIE: Bellingham, WA, USA, 2016; Volume 9805, pp. 38–49. [Google Scholar] [CrossRef]
- Qiao, L.; Esmaeily, A. An overview of signal-based damage detection methods. Appl. Mech. Mater. 2011, 94, 834–851. [Google Scholar] [CrossRef]
- Sofi, A.; Regita, J.J.; Rane, B.; Lau, H.H. Structural health monitoring using wireless smart sensor network–An overview. Mech. Syst. Signal Process. 2022, 163, 108113. [Google Scholar] [CrossRef]
- Pavlopoulou, S.; Staszewski, W.J.; Soutis, C. Evaluation of instantaneous characteristics of guided ultrasonic waves for structural quality and health monitoring. Struct. Control Health Monit. 2013, 20, 937–955. [Google Scholar] [CrossRef]
- Zhu, S.; Kang, J.; Wang, Y.; Zhou, F. Effect of CO2 on coal P-wave velocity under triaxial stress. Int. J. Min. Sci. Technol. 2022, 32, 17–26. [Google Scholar] [CrossRef]
- Chacón-Hernández, F. The shear wave splitting technique as a methodology to retrieve temporary variations of induced stress. J. Volcanol. Geotherm. Res. 2024, 446, 108009. [Google Scholar] [CrossRef]
- Sun, T.P.; Álvarez-Novoa, F.; Andrade, K.; Gutiérrez, P.; Gordillo, L.; Cheng, X. Stress distribution and surface shock wave of drop impact. Nat. Commun. 2022, 13, 1703. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, T.J.; Johnson, P.A.; Guyer, R.A. Interaction Dynamics of Elastic Waves with a Complex Nonlinear Scatterer through the Use of a Time Reversal Mirror. Phys. Rev. Lett. 2007, 98, 104301. [Google Scholar] [CrossRef]
- Shi, R.; Sun, X. Numerical simulation of elastic stress wave refraction at air-solid interfaces. J. Beijing Inst. Technol. 2020, 29, 209–221. [Google Scholar] [CrossRef]
- Cheng, Y.; Song, Z.; Chang, X.; Wang, T. Energy evolution principles of shock-wave in sandstone under unloading stress. KSCE J. Civ. Eng. 2020, 24, 2912–2922. [Google Scholar] [CrossRef]
- Wang, Y. Anisotropic decay and global well-posedness of viscous surface waves without surface tension. Adv. Math. 2020, 374, 107330. [Google Scholar] [CrossRef]
- Zhu, W.; Zhao, L.; Yang, Z.; Cao, H.; Wang, Y.; Chen, W.; Shan, R. Stress Relaxing Simulation on Digital Rock: Characterize Attenuation Due To Wave-Induced Fluid Flow and Scattering. J. Geophys. Res. Solid Earth 2023, 128, e2022JB024850. [Google Scholar] [CrossRef]
- Treiber, M.P. Characterization of Cement-Based Multiphase Materials Using Ultrasonic Wave Attenuation. Master’s Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2008. Available online: https://core.ac.uk/reader/4719780 (accessed on 1 June 2023).
- Wang, Y.; Li, X.; Li, J.; Wang, Q.; Xu, B.; Deng, J. Debonding damage detection of the CFRP-concrete interface based on piezoelectric ceramics by the wave-based method. Constr. Build. Mater. 2019, 210, 514–524. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L.; Wu, X.; Zhang, K.; Skibniewski, M.J. Structural health monitoring and assessment using wavelet packet energy spectrum. Saf. Sci. 2019, 120, 652–665. [Google Scholar] [CrossRef]
- Bulut, A.; Singh, A.K.; Shin, P.; Fountain, T.; Jasso, H.; Yan, L.; Elgamal, A. Real-time nondestructive structural health monitoring using support vector machines and wavelets. In Advanced Sensor Technologies for Nondestructive Evaluation and Structural Health Monitoring; SPIE: Bellingham, WA, USA, 2005; Volume 5770, pp. 180–189. [Google Scholar]


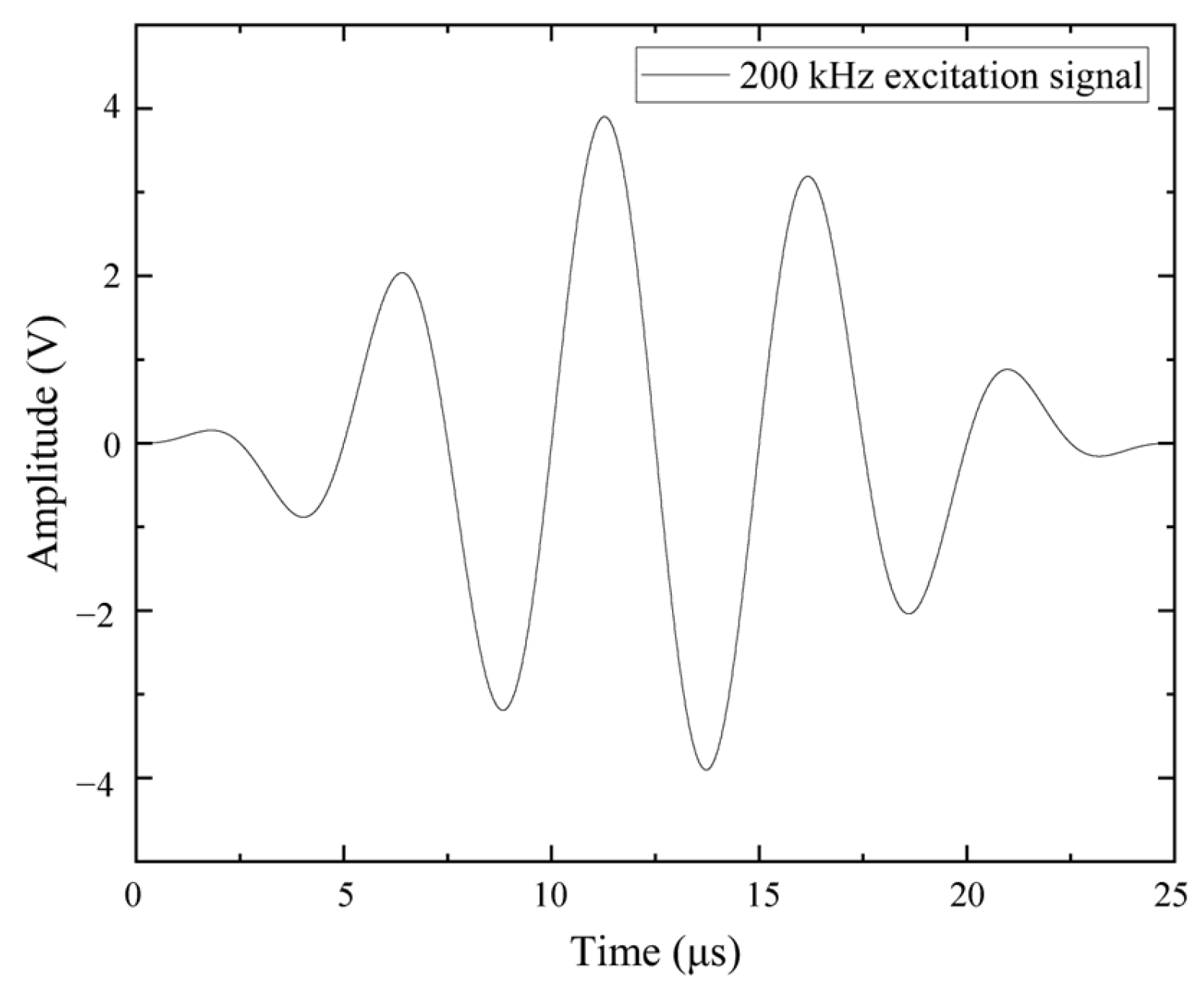
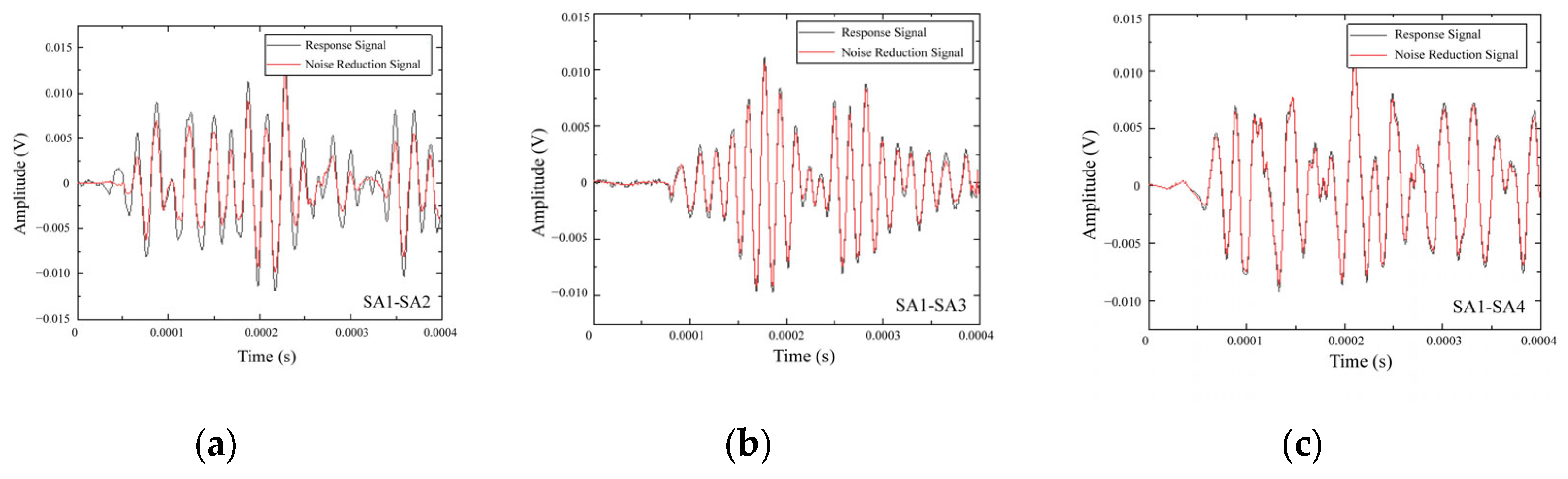
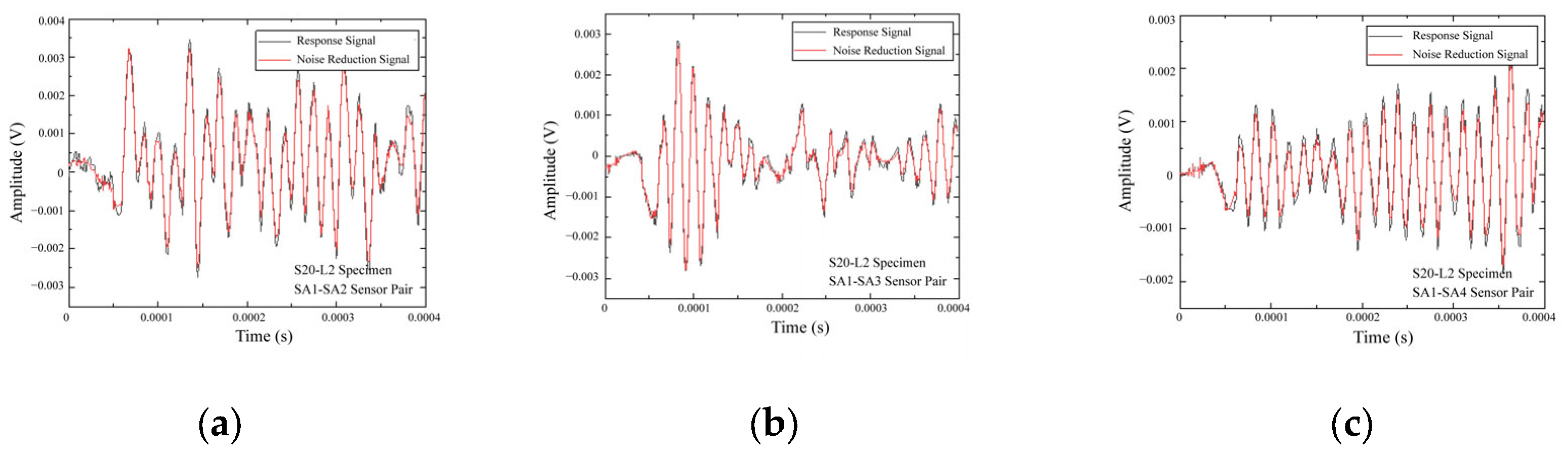
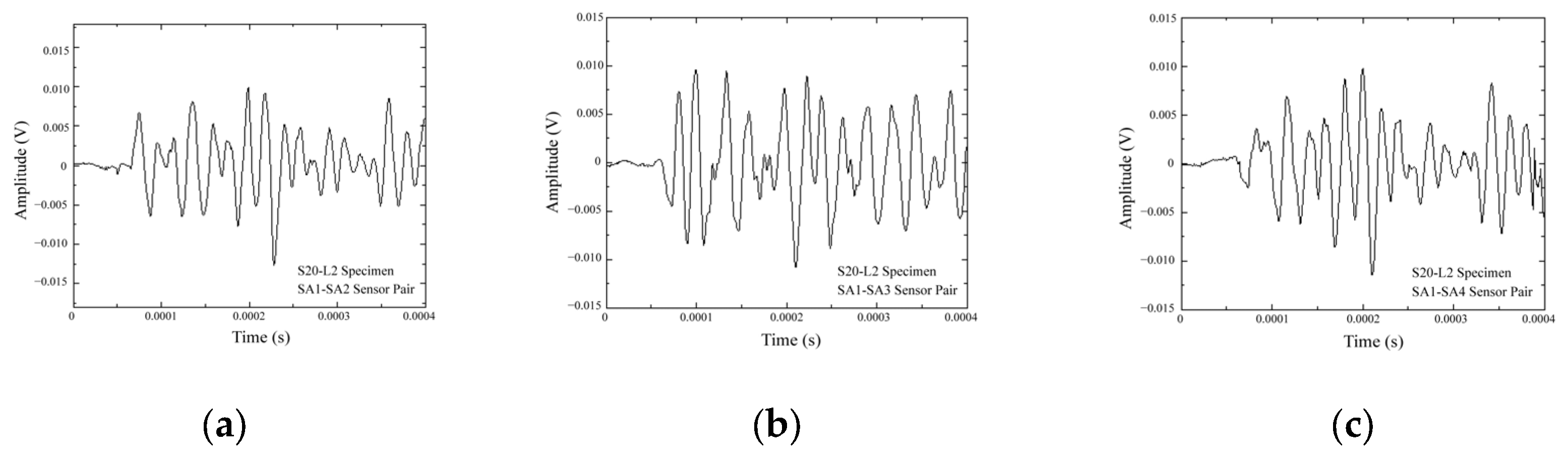




| Specimen Number | Length (mm) | Width (mm) | Damage Diameter (mm) | Damage Position (mm, mm) |
|---|---|---|---|---|
| S0 | 300 | 300 | / | / |
| S20-L1 | 300 | 300 | 20 | (150, 150) |
| S20-L2 | 300 | 300 | 20 | (205, 205) |
| S20-L3 | 300 | 300 | 20 | (205, 150) |
| S30-L1 | 300 | 300 | 30 | (150, 150) |
| S30-L2 | 300 | 300 | 30 | (205, 205) |
| S30-L3 | 300 | 300 | 30 | (205, 150) |
| Sensor Pair | Distance (mm) | Δt (μs) | Speed (m/s) | Average Speed (m/s) |
|---|---|---|---|---|
| SA1-SA2 | 212 | 54.2 | 3911 | 3847 |
| SA1-SA3 | 300 | 79.2 | 3788 | |
| SA1-SA4 | 212 | 55.2 | 3841 |
| Specimen | Sensor Pair | First Wave Arrival Time (μs) |
|---|---|---|
| S20-L1 | SA1-SA2 | 75 |
| SA1-SA4 | 73 | |
| SA2-SA3 | 74 | |
| S20-L2 | SA1-SA2 | 79 |
| SA1-SA3 | 82 | |
| SA1-SA4 | 106 | |
| S20-L3 | SA1-SA2 | 65 |
| SA1-SA3 | 85 | |
| SA1-SA4 | 91 | |
| S30-L1 | SA1-SA2 | 75 |
| SA1-SA4 | 74 | |
| SA2-SA3 | 74 | |
| S30-L2 | SA1-SA2 | 77 |
| SA1-SA3 | 83 | |
| SA1-SA4 | 103 | |
| S30-L3 | SA1-SA2 | 64 |
| SA1-SA3 | 83 | |
| SA1-SA4 | 90 |
| Specimen Number | Real Damage Location (mm, mm) | Estimated Damage Location (mm, mm) | Real Damage Radius (mm) | Estimated Damage Radius (mm) |
|---|---|---|---|---|
| S20-L1 | (150, 150) | (145.7, 152.0) | 10.0 | 18.0 |
| S20-L2 | (205, 205) | (208.0, 217.0) | 10.0 | 24.5 |
| S20-L3 | (205, 150) | (203.0, 141.6) | 10.0 | 5.8 |
| S30-L1 | (150, 150) | (151.7, 150.1) | 15.0 | 15.0 |
| S30-L2 | (205, 205) | (201.7, 191.2) | 15.0 | 10.5 |
| S30-L3 | (205, 150) | (203.6, 144.0) | 15.0 | 11.0 |
| Material | Young’s Modulus (GPa) | Density (kg/m3) | Poisson’s Ratio | Damping Ratio |
|---|---|---|---|---|
| Concrete | 30 | 2500 | 0.25 | 0.05 |
| Material | Density, ρ (kg/m3) | Relative Permittivity Matrix | Elastic Matrix (Pa) | Coupling Matrix |
|---|---|---|---|---|
| PZT | 7500 | (Values not specified are assumed to be 0) | (Values not specified are assumed to be 0) |
| Sensor Pair | Distance Between Sensor Pairs (mm) | Δt (μs) | Speed (m/s) | Average Speed (m/s) |
|---|---|---|---|---|
| PZT1-PZT2 | 212 | 55.31 | 3833 | 3803 |
| PZT1-PZT3 | 300 | 80.11 | 3744 | |
| PZT1-PZT4 | 212 | 55.31 | 3833 |
| Specimen | Sensor Pair | First Wave Arrival Time (μs) |
|---|---|---|
| S20-L1 | PZT1-PZT2 | 78.1 |
| PZT1-PZT4 | 78.2 | |
| PZT2-PZT3 | 78.7 | |
| S20-L2 | PZT1-PZT2 | 81.9 |
| PZT1-PZT3 | 83.6 | |
| PZT1-PZT4 | 108.1 | |
| S20-L3 | PZT1-PZT2 | 67.3 |
| PZT1-PZT3 | 82.2 | |
| PZT1-PZT4 | 91.6 | |
| S30-L1 | PZT1-PZT2 | 76.2 |
| PZT1-PZT4 | 75.0 | |
| PZT2-PZT3 | 76.5 | |
| S30-L2 | PZT1-PZT2 | 83.0 |
| PZT1-PZT3 | 81.9 | |
| PZT1-PZT4 | 105.3 | |
| S30-L3 | PZT1-PZT2 | 68.2 |
| PZT1-PZT3 | 81.9 | |
| PZT1-PZT4 | 91.9 |
| Specimen Number | Real Damage Location (mm, mm) | Estimated Damage Location (mm, mm) | Real Damage Radius (mm) | Estimated Damage Radius (mm) |
|---|---|---|---|---|
| S20-L1 | (150, 150) | (149.9, 148.9) | 10.0 | 6.9 |
| S20-L2 | (205, 205) | (205.1, 208.8) | 10.0 | 12.9 |
| S20-L3 | (205, 150) | (200.1, 161.5) | 10.0 | 16.9 |
| S30-L1 | (150, 150) | (148.0, 149.1) | 15.0 | 13.7 |
| S30-L2 | (205, 205) | (198.7, 218.4) | 15.0 | 23.3 |
| S30-L3 | (205, 150) | (200.7, 156.5) | 15.0 | 15.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Di, B.; Zheng, Y.; Ma, H.; Huang, X.; Wu, H.; Zhang, J. Concrete Damage Identification and Localization for Structural Health Monitoring Based on Piezoelectric Sensors. Sensors 2025, 25, 2532. https://doi.org/10.3390/s25082532
Li H, Di B, Zheng Y, Ma H, Huang X, Wu H, Zhang J. Concrete Damage Identification and Localization for Structural Health Monitoring Based on Piezoelectric Sensors. Sensors. 2025; 25(8):2532. https://doi.org/10.3390/s25082532
Chicago/Turabian StyleLi, Hongjie, Bo Di, Yu Zheng, Hongwei Ma, Xiaomiao Huang, Hekun Wu, and Jize Zhang. 2025. "Concrete Damage Identification and Localization for Structural Health Monitoring Based on Piezoelectric Sensors" Sensors 25, no. 8: 2532. https://doi.org/10.3390/s25082532
APA StyleLi, H., Di, B., Zheng, Y., Ma, H., Huang, X., Wu, H., & Zhang, J. (2025). Concrete Damage Identification and Localization for Structural Health Monitoring Based on Piezoelectric Sensors. Sensors, 25(8), 2532. https://doi.org/10.3390/s25082532








