Enhanced Wind Power Forecasting Using a Hybrid Multi-Strategy Coati Optimization Algorithm and Backpropagation Neural Network
Abstract
1. Introduction
- Numerical Weather Prediction (NWP) [5] models form the backbone of wind power forecasting. By employing physical equations and meteorological data, these models simulate atmospheric dynamics to estimate the power output at wind farms. While NWP models are recognized for their accuracy and reliability, their performance can be affected by uncertainties in initial conditions and high computational demands. Nevertheless, ongoing advancements in technology continue to enhance their spatial resolution and predictive accuracy, thereby strengthening their role in wind power forecasting.
- Statistical models, such as ARMA and ARIMA [6], utilize historical data to detect autocorrelation and moving average properties. These models are particularly effective for datasets with clear periodic or trend-based patterns. However, their reliance on linear assumptions limits their ability to capture complex nonlinear relationships, reducing their applicability in more intricate scenarios [7].
- Machine learning models have gained significant attention for their ability to handle complex, nonlinear datasets [8]. Techniques such as Artificial Neural Networks (ANNs), Support Vector Machines (SVMs), and Extreme Learning Machines (ELMs) are widely used. Among these, backpropagation (BP) neural networks are especially notable. Using a backpropagation algorithm, these networks iteratively optimize weights and biases through gradient descent to minimize error, making them well suited for time-series forecasting. BP networks excel at capturing intricate input–output relationships without requiring predefined equations, enhancing their utility in wind power prediction.
- Ensemble forecasting approaches have emerged as an effective strategy to improve prediction accuracy by combining the strengths of multiple models. For example, hybrid models like ARIMA-LSTM integrate ARIMA’s strength in linear trend analysis with LSTM’s capability to capture nonlinear time-series patterns. Similarly, optimization-based enhancements, such as the PSO-BP model [9], employ Particle Swarm Optimization (PSO) to fine-tune the parameters of BP networks, significantly reducing forecasting errors. These hybrid and ensemble methods are particularly advantageous in regions with limited or lower-quality data, offering robust solutions for diverse forecasting challenges [10].
2. The SZCOA-BP Neural Network Prediction Model
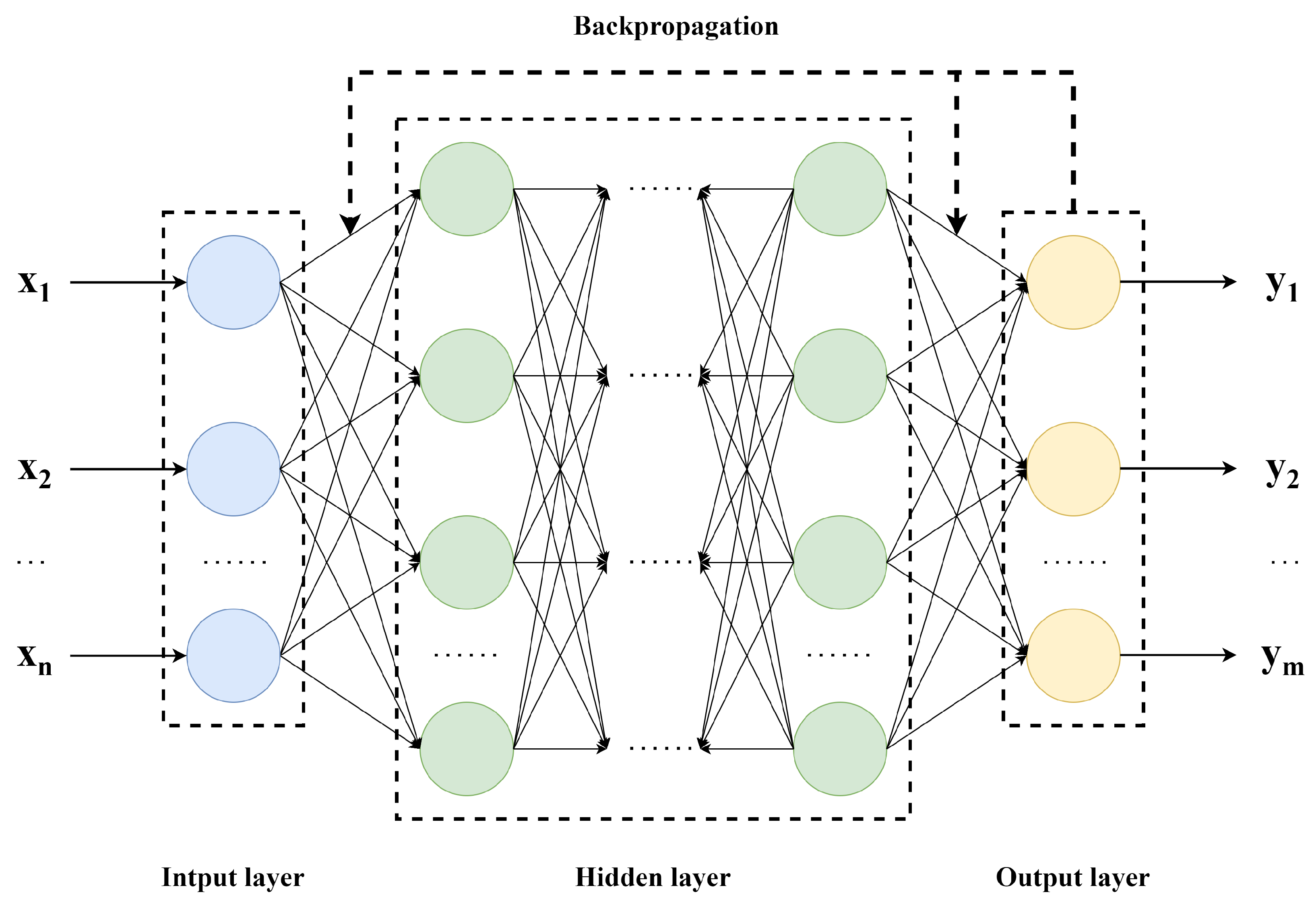
2.1. BP Neural Network Model
2.2. Coati Optimization Algorithm (COA)
2.2.1. Initialization Phase
2.2.2. Exploration Phase: Hunting and Attacking Strategy
2.2.3. Exploitation Phase: Escaping Predator Strategy
2.3. The Multi-Strategy Coati Optimization Algorithm (SZCOA)
2.3.1. Population Position Update Strategy
- Iteration-Related Variable:where t is the current iteration count, and T represents the maximum number of iterations. k decreases as the number of iterations increases, thereby promoting exploration in the initial iterations while encouraging exploitation as the algorithm converges. This dynamic adjustment enhances the algorithm’s ability to navigate complex optimization landscapes and effectively improves the process of converging to the optimal solution.
- Random Variables:
- : A random number in the range .
- : Computed as follows:where is a random variable in that follows a normal distribution.is a uniformly distributed random number within .
- : Determined by
The flexible use of these random variables enhances the algorithm’s dynamism, enabling it to adjust its search strategy based on the characteristics of the optimization landscape. This adaptability is crucial for avoiding local optima and ensuring robust global search capabilities. - Condition Variables:
- Z: Derived from a combination of and k:where is a uniformly distributed random number within .
- M: Defined as a binary variable where
2.3.2. Olfactory Tracing Strategy
- represents the fitness value of the i-th individual at time t, corresponding to the optimization objective.
- is a small constant used to avoid division by zero.
2.3.3. Soft Frost Searching Strategy
2.3.4. Computational Complexity and Cost Analysis
- Computational Complexity:The overall computational complexity of the SZCOA is × . This complexity is comparable to that of many classical optimization algorithms and is primarily influenced by the processes of initial population generation, fitness evaluations, and parameter updates during the main iteration loops. While we recognize that the time complexity remains stable, the introduction of enhanced optimization strategies has significantly improved the algorithm’s convergence performance, allowing it to identify superior solutions in a reduced timeframe.
- Computational Cost Evaluation:Although the implementation of the soft frost search strategy leads to a higher number of fitness evaluations, resulting in a slight increase in computational time, this increase is balanced by a marked enhancement in algorithm performance. Our results demonstrate that, even with this elevated evaluation frequency, the SZCOA consistently achieves better solution quality within the same number of iterations compared to traditional algorithms—particularly in complex optimization scenarios, where it exhibits superior convergence paths.
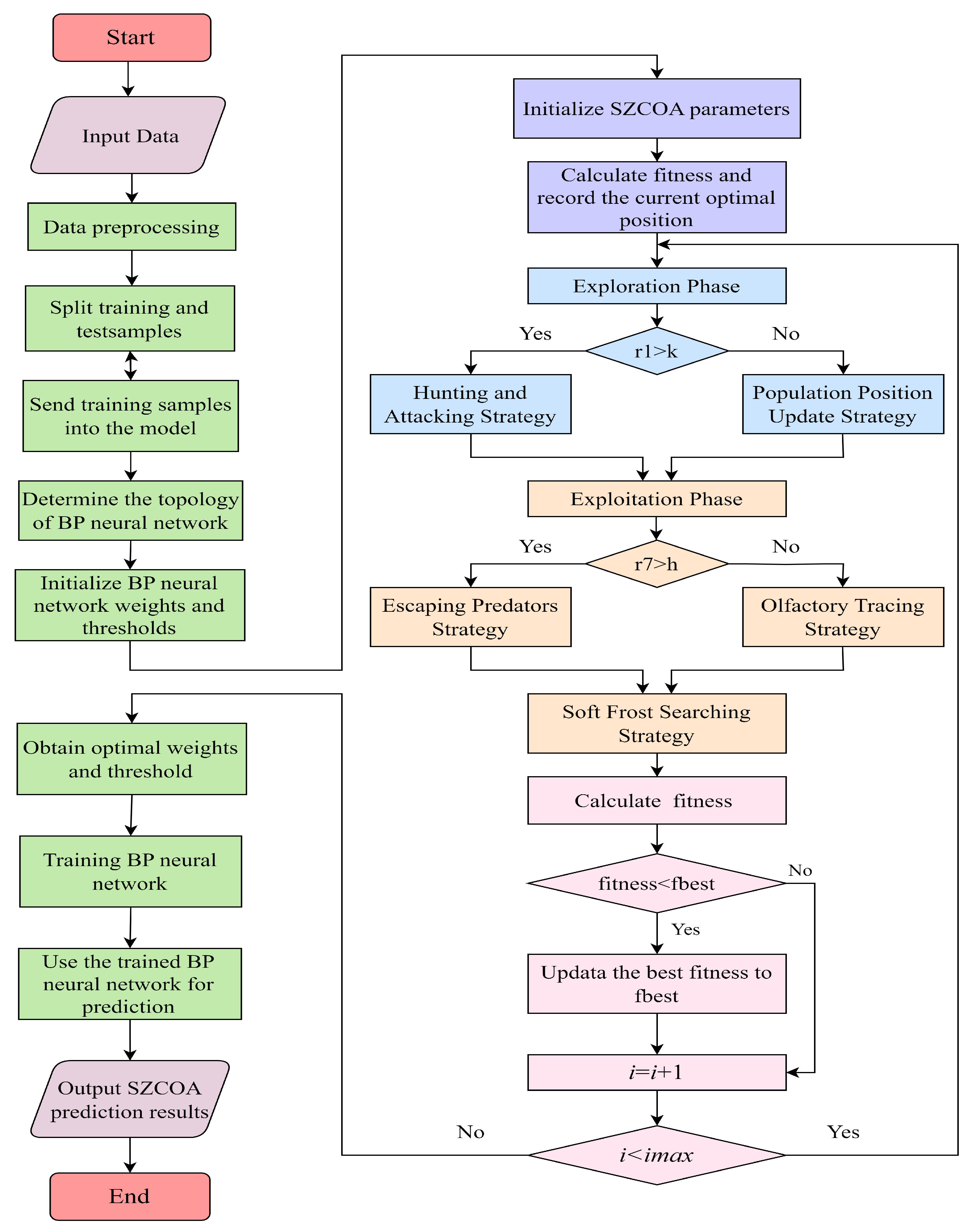
2.4. SZCOA-BP Model
3. Numerical Experiments and Comparative Analysis
3.1. Experiments and Results of the Algorithm in CEC2017 Test
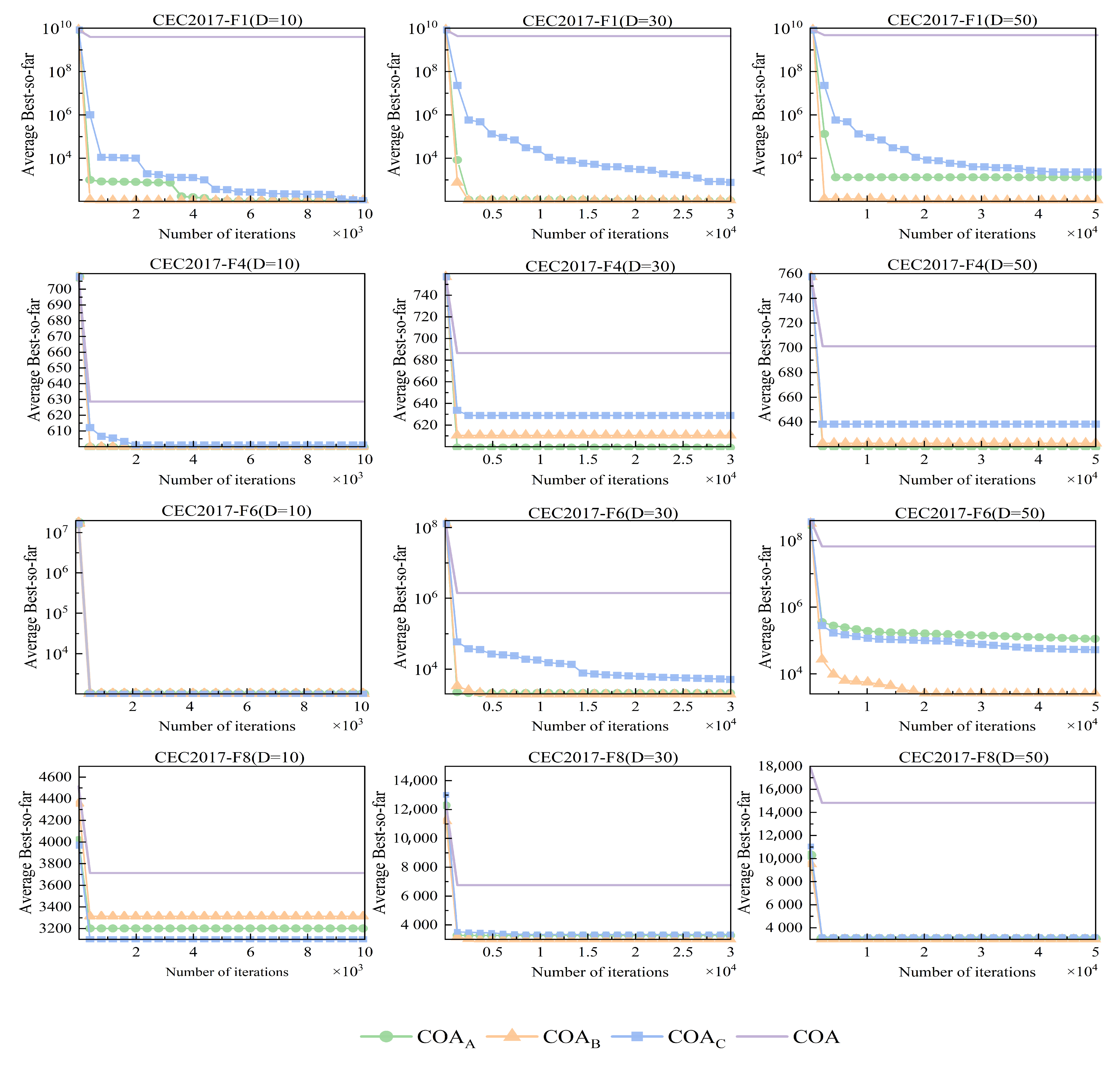
3.1.1. Verification of the Effectiveness of Improvement Strategy
3.1.2. Comparison and Analysis of the SZCOA Algorithm with Others
3.2. Prediction of Wind Power
3.2.1. Data Processing
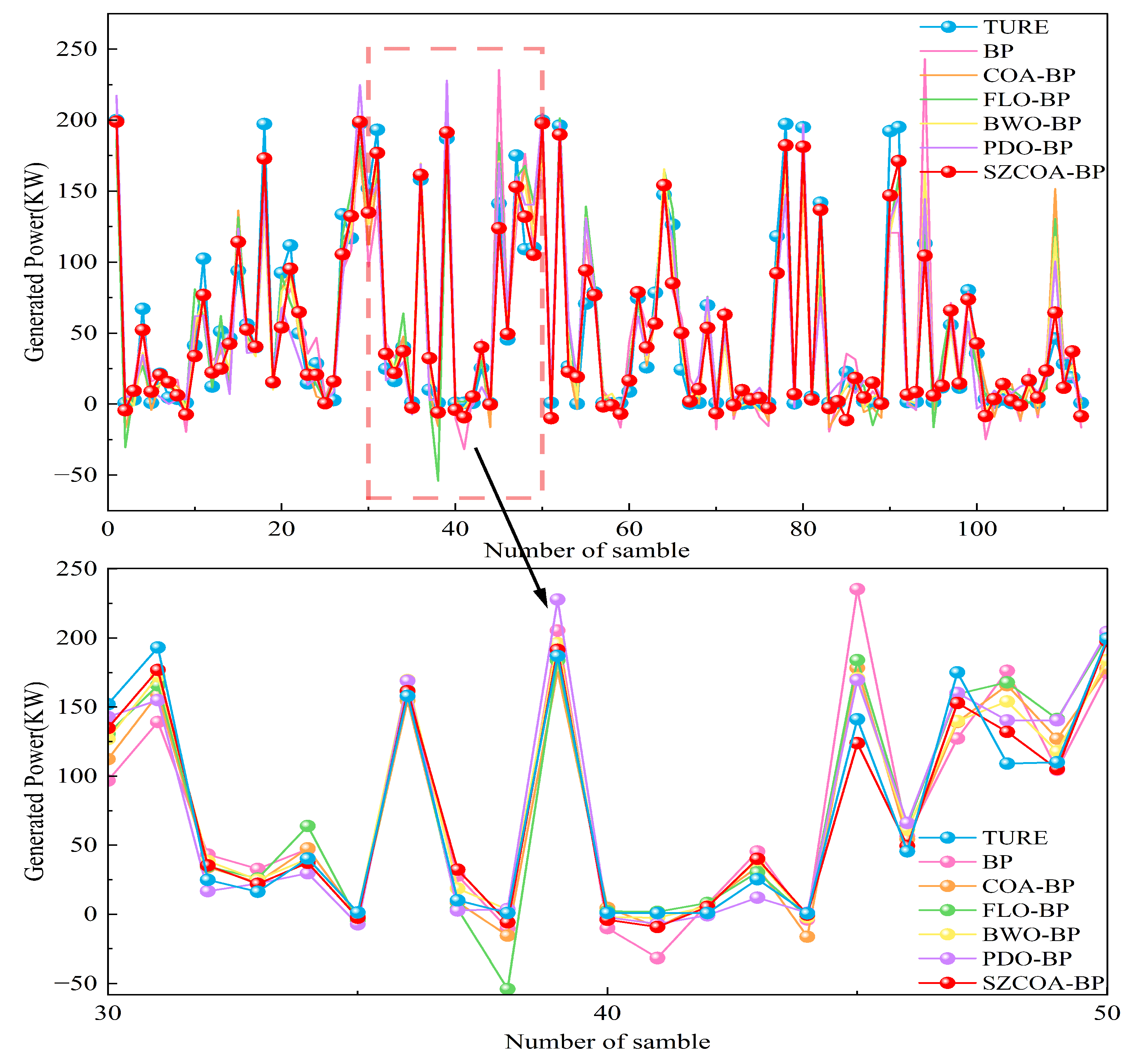
3.2.2. Comparison Results with Other Benchmark Models
3.2.3. Statistical Validation
- Statistical Validation ImplementationWe systematically validated the performance of the SZCOA-BP model through independent statistical tests. This was achieved using t-tests to assess performance differences between the SZCOA-BP model and several benchmark models: standard BP, COA-BP, BWO-BP, FLO-BP, and PDO-BP.
- t-Test AnalysisUtilizing the SciPy library in Python 3.9, we organized and analyzed the R² data through t-tests. The results of these comparisons are presented in Table 6.
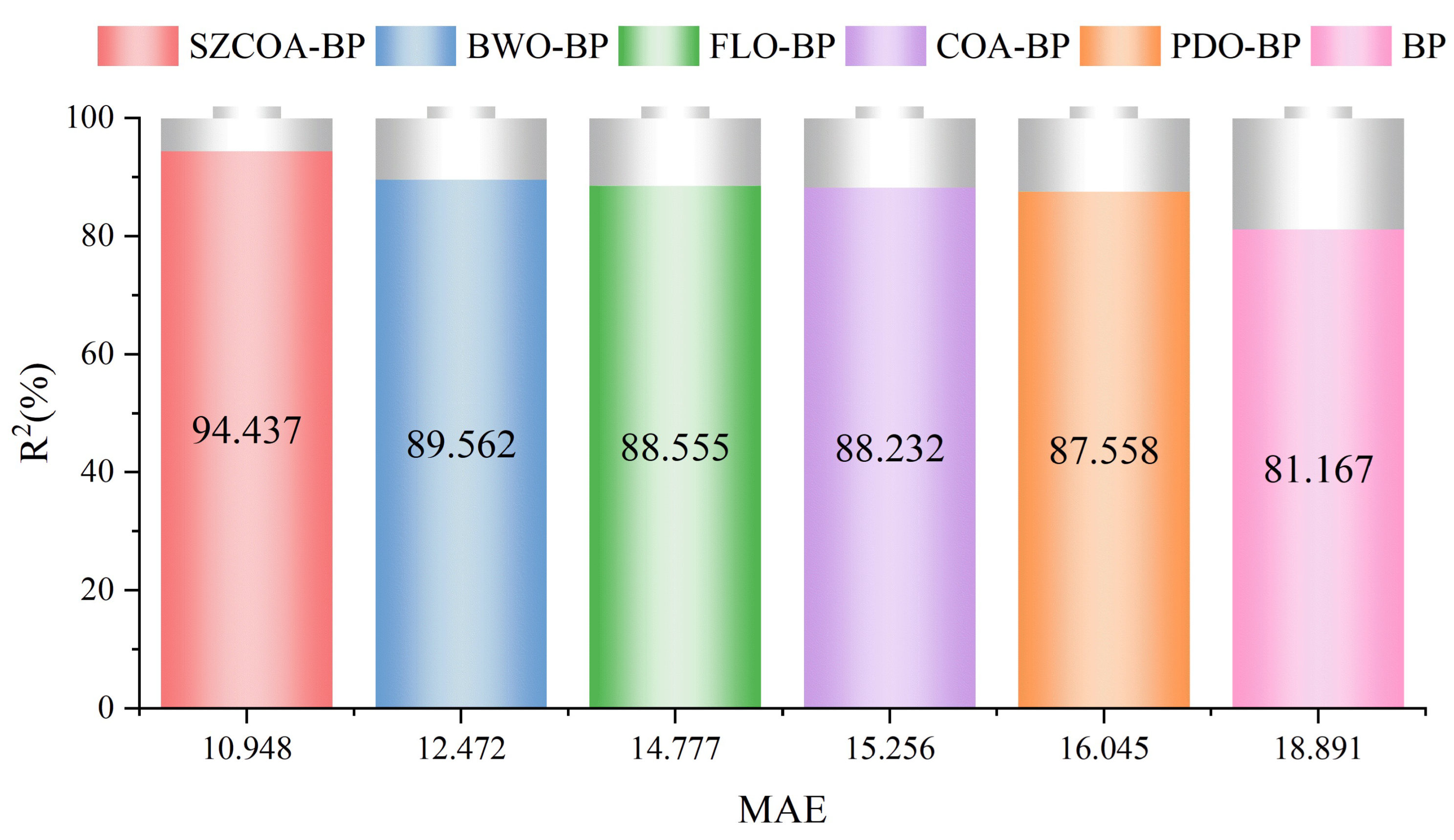
- Summary of ResultsThe statistical analysis demonstrated that all p-values obtained were below the significance threshold of 0.05, indicating a statistically significant performance advantage of the SZCOA-BP model over the other models assessed. For instance, a p-value of 0.0003 in the comparison with the standard BP model indicates substantial improvement in wind energy forecasting. The R² value of the SZCOA-BP model (94.437) significantly exceeds that of the standard BP model (81.167), reinforcing its practical effectiveness.
3.2.4. Cause Analysis
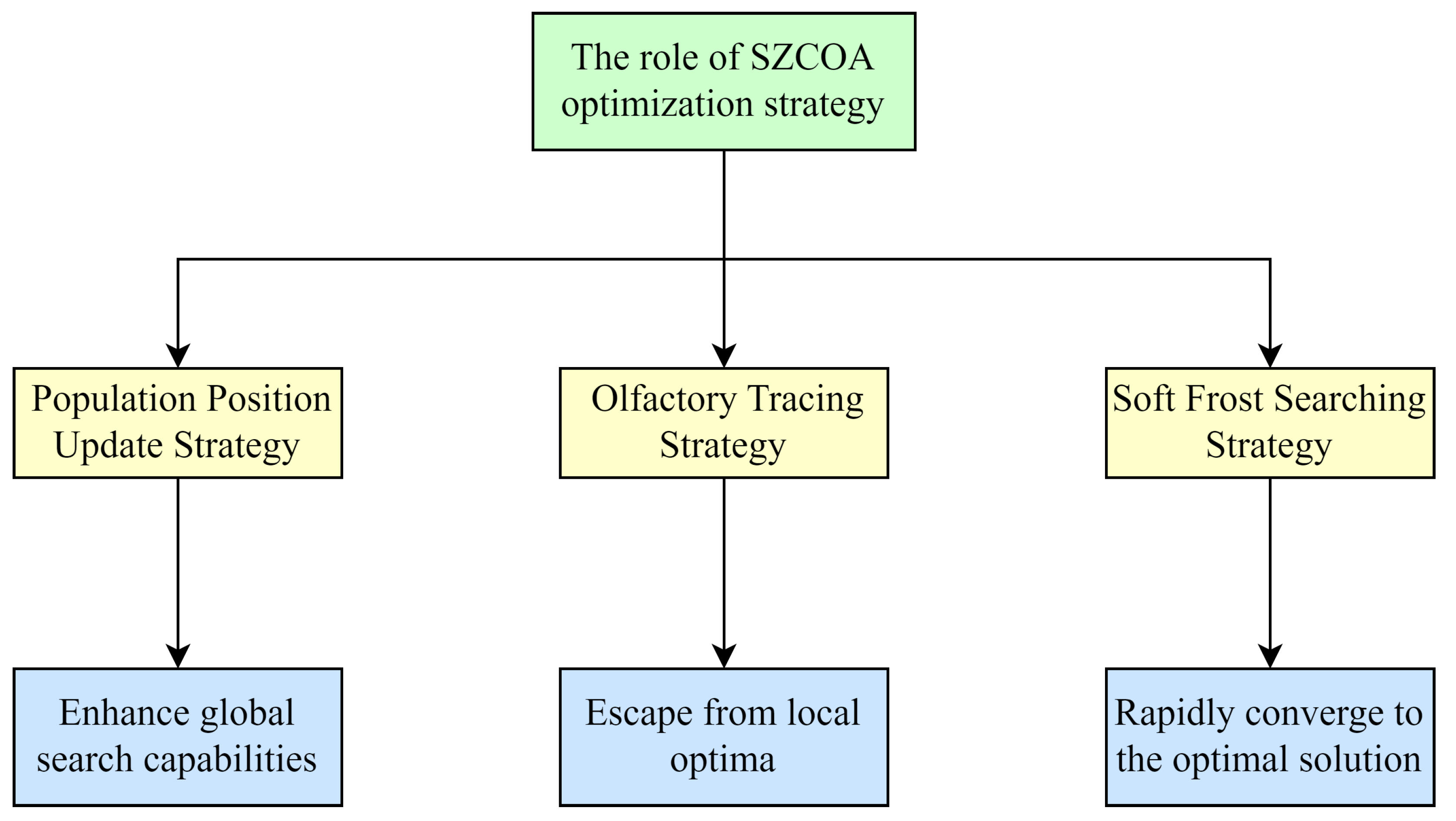
- Improvement of Population Position Update StrategyThis strategy draws inspiration from the Wild Horse Optimization algorithm (WHO) and aims to enhance the algorithm’s global search capability. By dynamically updating the positions of raccoons, the algorithm can explore a broader search space, avoiding premature convergence due to local searches. In traditional optimization algorithms, populations may quickly concentrate on a local optimum, preventing the discovery of better solutions. The SZCOA introduces randomness and a flexible updating mechanism, allowing the population to move over a larger range, thereby increasing the chances of finding the global optimum.
- Enhanced Ability to Escape Local OptimaInspired by the keen sense of smell of raccoons, this strategy enables the algorithm to promptly perceive changes in the surrounding environment when faced with complex multimodal problems. By simulating the raccoon’s response to predator scents, the algorithm can effectively adjust its search near local optima. In multimodal optimization problems, algorithms often become trapped in local optima. The scent-tracking strategy introduces an environmental perception mechanism, allowing the raccoon to quickly adjust its search direction upon sensing potential threats, thereby effectively escaping local optima and increasing the probability of finding the global optimum.
- Optimization of Individual Update MechanismThis strategy simulates the growth characteristics of frost particles, utilizing their strong randomness and coverage to enable the algorithm to quickly cover the entire search space. This approach allows the algorithm not only to rapidly identify potential high-quality solutions but also to maintain high precision during the search process. The introduction of the soft frost search strategy enables the algorithm to explore different areas more effectively during the search, avoiding inefficiencies caused by local searches. Additionally, as the number of iterations increases, the algorithm can gradually converge to better solutions, enhancing the overall search accuracy.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Batrancea, L.M.; Rathnaswamy, M.M.; Rus, M.-I.; Tulai, H. Determinants of economic growth for the last half of century: A panel data analysis on 50 countries. J. Knowl. Econ. 2022, 13, 1–25. [Google Scholar] [CrossRef]
- Lu, P.; Ye, L.; Zhao, Y.; Dai, B.; Pei, M.; Tang, Y. Review of meta-heuristic algorithms for wind power prediction: Methodologies, applications and challenges. Appl. Energy 2021, 301, 117446. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Ma, K. Wind energy systems. Proc. IEEE 2017, 105, 2116–2131. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J.; Chen, B.; Yan, H. Pseudo-Twin Neural Network of Full Multi-Layer Perceptron for Ultra-Short-Term Wind Power Forecasting. Electronics 2025, 14, 887. [Google Scholar] [CrossRef]
- Wu, S.-H.; Wu, Y.-K. Probabilistic wind power forecasts considering different NWP models. In Proceedings of the 2020 International Symposium on Computer, Consumer and Control (IS3C), Taichung City, Taiwan, 13–16 November 2020; pp. 428–431. [Google Scholar] [CrossRef]
- Zaman, U.; Teimourzadeh, H.; Sangani, E.H.; Liang, X.; Chung, C.Y. Wind speed forecasting using ARMA and neural network models. In Proceedings of the 2021 IEEE Electrical Power and Energy Conference (EPEC), Toronto, ON, Canada, 22–31 October 2021; pp. 243–248. [Google Scholar] [CrossRef]
- Li, B.; Shen, H.; Guo, R.; Wang, Y.; Li, C.; Yang, H. Optimization of metering asset scheduling in storage warehouses based on digital twin. J. South-Cent. Univ. Natl. (Nat. Sci. Ed.) 2022, 41, 720–727. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, C.; Song, Y. Chance constrained extreme learning machine for nonparametric prediction intervals of wind power generation. IEEE Trans. Power Syst. 2020, 35, 3869–3884. [Google Scholar] [CrossRef]
- Li, G.; Xu, Z.; Zhou, Y. Wind power prediction based on PSO-BP neural network. In Proceedings of the 2024 6th International Conference on Energy Systems and Electrical Power (ICESEP), Wuhan, China, 21–23 June 2024; pp. 34–37. [Google Scholar] [CrossRef]
- Yang, H.; Wang, J.; Shen, H.; Zhang, S.; Feng, L.; Xiao, J. Text detection method based on Attention-DBNet algorithm. J. South-Cent. Univ. Natl. (Nat. Sci. Ed.) 2024, 43, 674–682. [Google Scholar] [CrossRef]
- Jiang, F.; Zhu, Q.; Tian, T. An ensemble interval prediction model with change point detection and interval perturbation-based adjustment strategy: A case study of air quality. Expert Syst. Appl. 2023, 222, 119823. [Google Scholar] [CrossRef]
- Zhu, Q.; Jiang, F.; Li, C. Time-varying interval prediction and decision-making for short-term wind power using convolutional gated recurrent unit and multi-objective elephant clan optimization. Energy 2023, 271, 127006. [Google Scholar] [CrossRef]
- Lu, X.; Chen, S.; Nielsen, C.P.; Zhang, C.; Li, J.; Xu, H.; Wu, Y.; Wang, S.; Song, F.; Wei, C.; et al. Combined solar power and storage as cost-competitive and grid-compatible supply for China’s future carbon-neutral electricity system. Proc. Natl. Acad. Sci. USA 2021, 118, e2103471118. [Google Scholar] [CrossRef]
- Wang, W.; Cui, X.; Qi, Y.; Xue, K.; Liang, R.; Bai, C. Prediction Model of Coal Gas Permeability Based on Improved DBO Optimized BP Neural Network. Sensors 2024, 24, 2873. [Google Scholar] [CrossRef] [PubMed]
- El Ghouate, N.; Bencherqui, A.; Mansouri, H.; El Maloufy, A.; Tahiri, M.A.; Karmouni, H.; Sayyouri, M.; Askar, S.S.; Abouhawwash, M. Improving the Kepler optimization algorithm with chaotic maps: Comprehensive performance evaluation and engineering applications. Artif. Intell. Rev. 2024, 57, 313. [Google Scholar] [CrossRef]
- Jiang, F.; Zhu, Q.; Yang, J.; Chen, G.; Tian, T. Clustering-based interval prediction of electric load using multi-objective pathfinder algorithm and Elman neural network. Appl. Soft Comput. 2022, 129, 109602. [Google Scholar] [CrossRef]
- Cao, W.; Wang, G.; Liang, X.; Hu, Z. A STAM-LSTM model for wind power prediction with feature selection. Energy 2024, 296, 131030. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Li, C.; Guo, R.; Yang, Y.; Yang, H. Research on the optimization of storage location allocation in opposing warehouses based on improved neighborhood search algorithm. J. South-Cent. Univ. Natl. (Nat. Sci. Ed.) 2023, 42, 551–557. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E. Learning internal representations by backpropagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati optimization algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Jia, H.; Wen, Q.; Wu, D.; Wang, Z.; Wang, Y.; Wen, C.; Abualigah, L. Modified beluga whale optimization with multi-strategies for solving engineering problems. J. Comput. Des. Eng. 2023, 10, 2065–2093. [Google Scholar] [CrossRef]
- Jia, H.; Shi, S.; Wu, D.; Rao, H.; Zhang, J.; Abualigah, L. Improve coati optimization algorithm for solving constrained engineering optimization problems. J. Comput. Des. Eng. 2023, 10, 2223–2250. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2022, 38 (Suppl. S4), 3025–3056. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested porcupine optimizer: A new nature-inspired metaheuristic. Knowl.-Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A physics-based optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Ren, C.; An, N.; Wang, J.; Li, L.; Hu, B.; Shang, D. Optimal parameters selection for BP neural network based on particle swarm optimization: A case study of wind speed forecasting. Knowl.-Based Syst. 2014, 56, 226–239. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization; Technical Report; National University of Defense Technology: Changsha, China; Kyungpook National University: Daegu, Republic of Korea; Nanyang Technological University: Singapore, 2017. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.E. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X.; Qiu, L.; Zhang, H. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M.; Trojovský, P. Zebra optimization algorithm: A new bio-inspired optimization algorithm for solving optimization problems. IEEE Access 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]





| No. | Functions | Dim | Best Value |
|---|---|---|---|
| F1 | Shifted and Rotated Bent Cigar Function | 10/30/50 | 100 |
| F2 | Shifted and Rotated Zakharov Function | 10/30/50 | 300 |
| F3 | Shifted and Rotated Rosenbrock’s Function | 10/30/50 | 400 |
| F4 | Shifted and Rotated Expanded Scaffer’s F6 Function | 10/30/50 | 600 |
| F5 | Hybrid Function 1 () | 10/30/50 | 1100 |
| F6 | Hybrid Function 4 () | 10/30/50 | 1400 |
| F7 | Composition Function 2 () | 10/30/50 | 2200 |
| F8 | Composition Function 6 () | 10/30/50 | 2800 |
| Function | Dim | Indicator | ||||
|---|---|---|---|---|---|---|
| F1 | 10 | Best | ||||
| Average | ||||||
| STD | ||||||
| 30 | Best | |||||
| Average | ||||||
| STD | ||||||
| 50 | Best | |||||
| Average | ||||||
| STD | ||||||
| F2 | 10 | Best | ||||
| Average | ||||||
| STD | ||||||
| 30 | Best | |||||
| Average | ||||||
| STD | ||||||
| 50 | Best | |||||
| Average | ||||||
| STD | ||||||
| F3 | 10 | Best | ||||
| Average | ||||||
| STD | ||||||
| 30 | Best | |||||
| Average | ||||||
| STD | ||||||
| 50 | Best | |||||
| Average | ||||||
| STD | ||||||
| F4 | 10 | Best | ||||
| Average | ||||||
| STD | ||||||
| 30 | Best | |||||
| Average | ||||||
| STD | ||||||
| 50 | Best | |||||
| Average | ||||||
| STD | ||||||
| F5 | 10 | Best | ||||
| Average | ||||||
| STD | ||||||
| 30 | Best | |||||
| Average | ||||||
| STD | ||||||
| 50 | Best | |||||
| Average | ||||||
| STD | ||||||
| F6 | 10 | Best | ||||
| Average | ||||||
| STD | ||||||
| 30 | Best | |||||
| Average | ||||||
| STD | ||||||
| 50 | Best | |||||
| Average | ||||||
| STD | ||||||
| F7 | 10 | Best | ||||
| Average | ||||||
| STD | ||||||
| 30 | Best | |||||
| Average | ||||||
| STD | ||||||
| 50 | Best | |||||
| Average | ||||||
| STD | ||||||
| F8 | 10 | Best | ||||
| Average | ||||||
| STD | ||||||
| 30 | Best | |||||
| Average | ||||||
| STD | ||||||
| 50 | Best | |||||
| Average | ||||||
| STD |
| Function | Dim | Indicator | SZCOA | ICOA | DBO | ZOA | BWO | PSO | BKA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 10 | Best | |||||||
| Average | |||||||||
| STD | |||||||||
| 30 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| 50 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| F2 | 10 | Best | |||||||
| Average | |||||||||
| STD | |||||||||
| 30 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| 50 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| F3 | 10 | Best | |||||||
| Average | |||||||||
| STD | |||||||||
| 30 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| 50 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| F4 | 10 | Best | |||||||
| Average | |||||||||
| STD | |||||||||
| 30 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| 50 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| F5 | 10 | Best | |||||||
| Average | |||||||||
| STD | |||||||||
| 30 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| 50 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| F6 | 10 | Best | |||||||
| Average | |||||||||
| STD | |||||||||
| 30 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| 50 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| F7 | 10 | Best | |||||||
| Average | |||||||||
| STD | |||||||||
| 30 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| 50 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| F8 | 10 | Best | |||||||
| Average | |||||||||
| STD | |||||||||
| 30 | Best | ||||||||
| Average | |||||||||
| STD | |||||||||
| 50 | Best | ||||||||
| Average | |||||||||
| STD |
| No. | 10-m Wind Speed of the Wind Measurement Tower/m·s−1 | ⋯ | 10-m Wind Direction of the Wind Measurement Tower/° | ⋯ | Temperature /°C | Air Pressure /hPa |
|---|---|---|---|---|---|---|
| 1 | 2.803 | 214.542 | 13.155 | 874.684 | ||
| 2 | 3.132 | 209.531 | 13.117 | 874.684 | ||
| 3 | 1.359 | 219.760 | 13.085 | 874.005 | ||
| ⋮ | ⋮ | ⋯ | ⋮ | ⋯ | ⋮ | ⋮ |
| 497 | 4.940 | 252.930 | 14.476 | 871.126 | ||
| 498 | 4.662 | 237.509 | 14.521 | 870.690 | ||
| 499 | 3.515 | 254.262 | 14.591 | 870.219 | ||
| ⋮ | ⋮ | ⋯ | ⋮ | ⋯ | ⋮ | ⋮ |
| 911 | 8.877 | 59.365 | 13.230 | 869.825 | ||
| 912 | 7.479 | 76.038 | 13.184 | 869.994 |
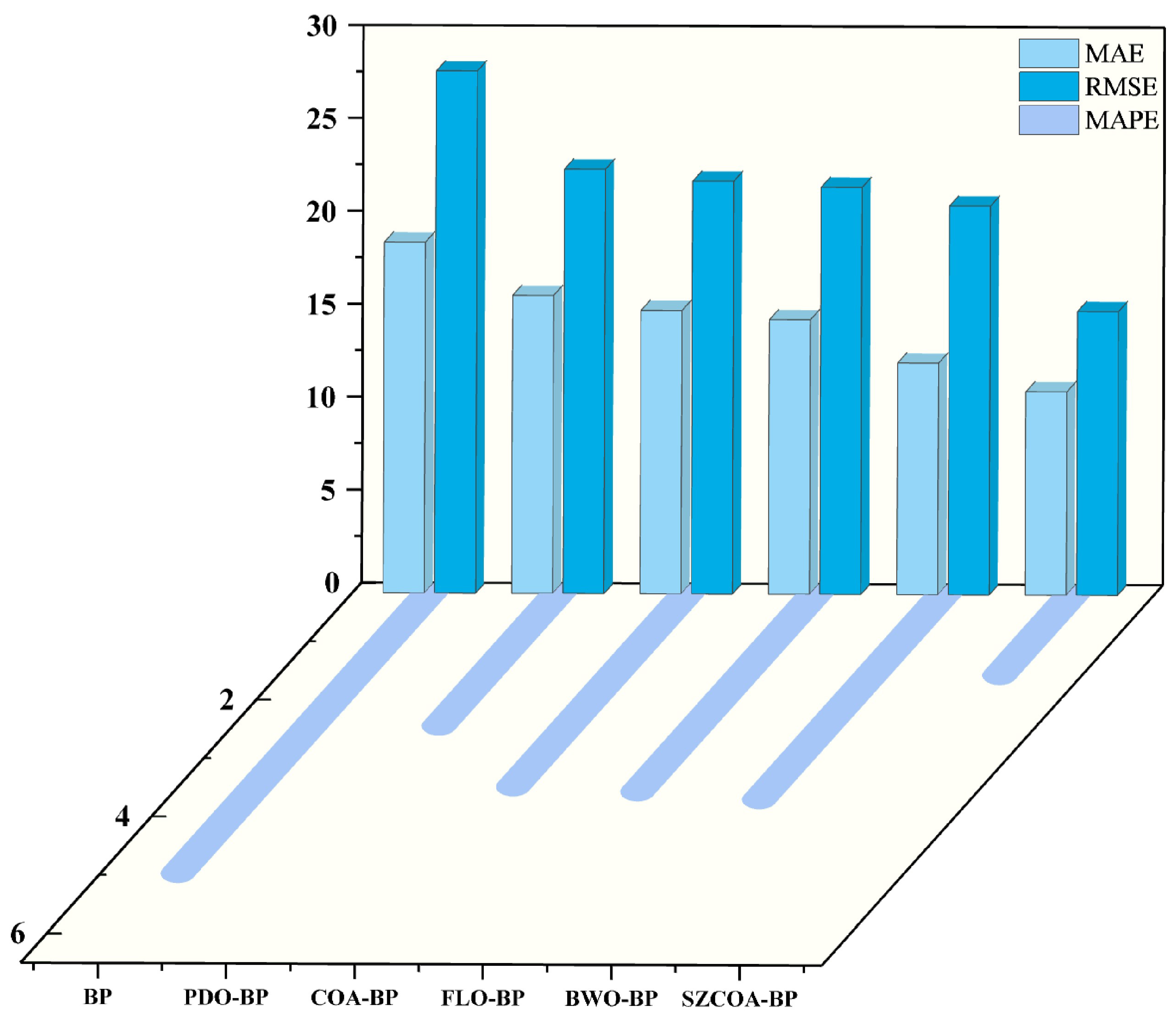
| Model | MAE | MAPE | MSE | RMSE | T (min) | |
|---|---|---|---|---|---|---|
| BP | 18.891 | 4.9717 | 790.23 | 28.111 | 0.81167 | 2 |
| COA-BP | 15.256 | 3.4731 | 493.78 | 22.221 | 0.88232 | 5 |
| FLO-BP | 14.777 | 3.5506 | 480.21 | 21.914 | 0.88555 | 8 |
| BWO-BP | 12.472 | 3.6762 | 437.98 | 20.928 | 0.89562 | 10.5 |
| PDO-BP | 16.045 | 2.4381 | 522.05 | 22.848 | 0.87558 | 11 |
| SZCOA-BP | 10.948 | 1.542 | 233.43 | 15.278 | 0.94437 | 6 |
| Model | t-Statistic | p-Value |
|---|---|---|
| Standard BP | 6.484 | 0.0003 |
| COA-BP | 3.064 | 0.012 |
| BWO-BP | 3.418 | 0.003 |
| FLO-BP | 2.981 | 0.005 |
| PDO-BP | 2.355 | 0.008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Shu, Z.; Li, Z. Enhanced Wind Power Forecasting Using a Hybrid Multi-Strategy Coati Optimization Algorithm and Backpropagation Neural Network. Sensors 2025, 25, 2438. https://doi.org/10.3390/s25082438
Yang H, Shu Z, Li Z. Enhanced Wind Power Forecasting Using a Hybrid Multi-Strategy Coati Optimization Algorithm and Backpropagation Neural Network. Sensors. 2025; 25(8):2438. https://doi.org/10.3390/s25082438
Chicago/Turabian StyleYang, Hua, Zhan Shu, and Zhonger Li. 2025. "Enhanced Wind Power Forecasting Using a Hybrid Multi-Strategy Coati Optimization Algorithm and Backpropagation Neural Network" Sensors 25, no. 8: 2438. https://doi.org/10.3390/s25082438
APA StyleYang, H., Shu, Z., & Li, Z. (2025). Enhanced Wind Power Forecasting Using a Hybrid Multi-Strategy Coati Optimization Algorithm and Backpropagation Neural Network. Sensors, 25(8), 2438. https://doi.org/10.3390/s25082438





