FMCW Radar-Aided Navigation for Unmanned Aircraft Approach and Landing in AAM Scenarios: System Requirements and Processing Pipeline
Abstract
1. Introduction
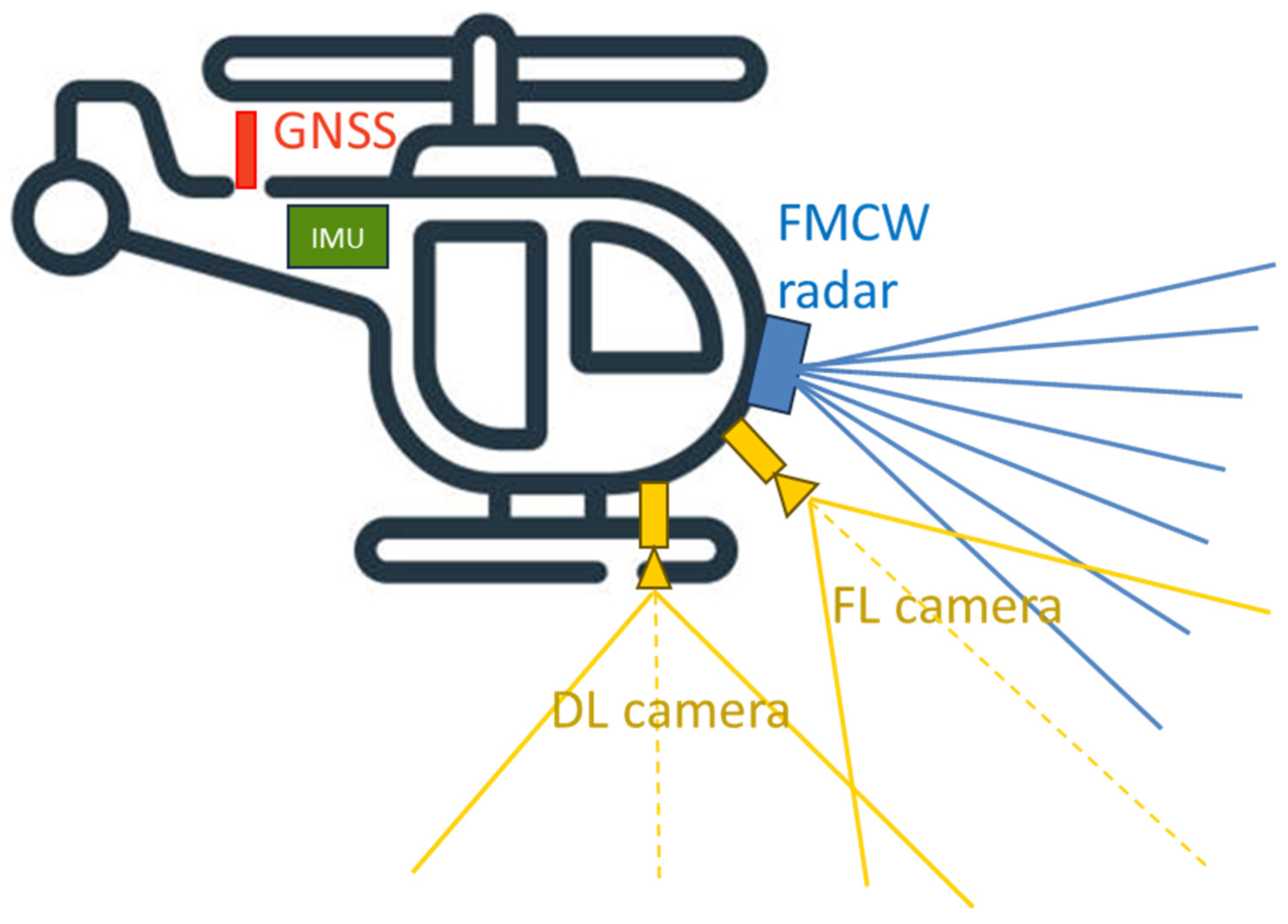
- A GNSS receiver, which is the main source of aircraft positioning information at long range from the landing area and is integrated with different onboard sensors to avoid the aforementioned limitations that might occur in the final phases of UAM operations at low altitudes;
- An Inertial Measurement Unit (IMU) to propagate the aircraft navigation state, providing high-frequency data and robustness to rapid platform movements;
- Two onboard cameras (namely Forward-Looking, FL, and Down-Looking, DL), which are optimized to provide accurate relative aircraft navigation information in the whole final phase of the approach trajectory;
- An FMCW radar, with the aim to enable vertiport detection at higher ranges (compared to vision-aided navigation) and provide relative navigation information even under reduced visibility conditions.
1.1. State of the Art
1.2. Paper Contributions
- The analysis of airborne radar system requirements in relation to operational constraints, including the approach trajectory and infrastructure defined by EASA regulations for vertiport design;
- The preliminary design of an FMCW radar, compliant with the identified requirements, and the definition of an ad hoc radar signal processing pipeline to extract navigation information from collected data. This includes a strategy to identify and match targets of interest located within the vertiport area;
- The definition of the multi-sensor navigation architecture, including the integration of matched radar target coordinates into the navigation filter architecture in a tightly coupled manner. This integration supports different operational modes based on the sensors contributing to the correction step of the navigation filter;
- The development and adoption of a high-fidelity simulation environment to simulate data collected by onboard exteroceptive sensors and validate the complete navigation architecture. The adoption of a physics-based simulator enables detailed modelling of radar interactions with the environment, incorporating realistic representations of object properties, noise patterns, and artifacts such as multipath reflections and clutter. These simulations realistically assess the contribution of radar data to the proposed navigation architecture, including scenarios with reduced visibility (e.g., intense fog), where camera activation occurs later compared to nominal visibility conditions.
- Analyzing radar system requirements with consideration of their impact on the autonomous AAM vehicle in terms of SWaP characteristics;
- Providing a detailed design of the radar system, ensuring compliance with the minimum identified requirements, followed by its simulation. This process effectively verifies the contribution of critical parameters, such as radar azimuth resolution, which were not analyzed in previous works;
- Incorporating statistical simulations within the high-fidelity simulation environment, enabling an evaluation of the navigation performance across different test cases. This approach assesses the designed radar’s contribution to the multi-sensor architecture relative to the specifically assumed required performance.
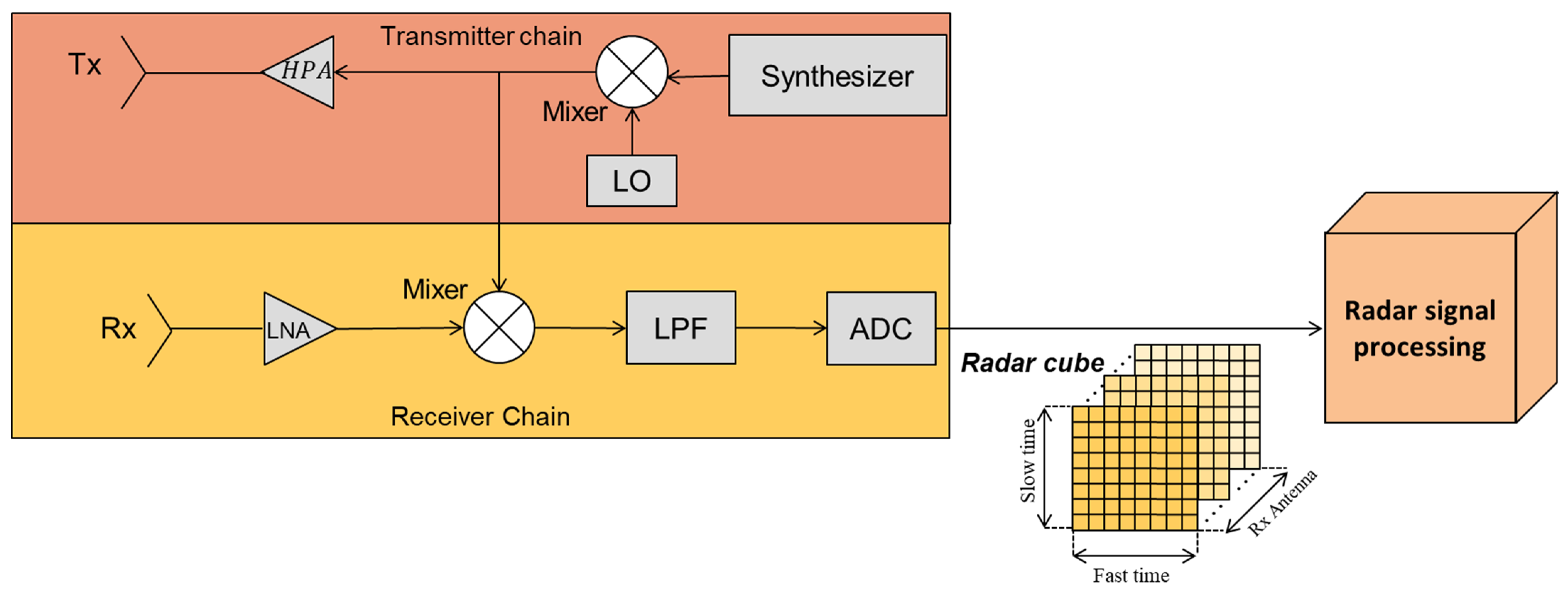
2. FMCW Radar System
2.1. Operational Constraints in AAM Scenarios
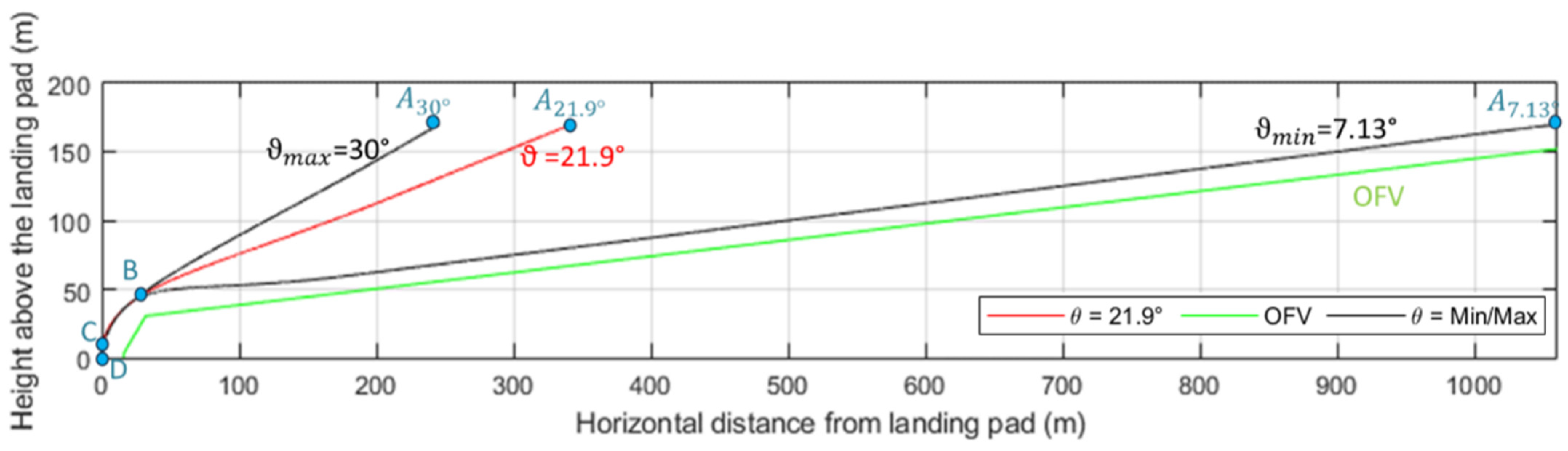
- A first descent at constant slope (ϑ) starting from the cruise altitude. The EASA regulations extend the OFV up to 152 m above the vertiport; thus, this work assumes a cruise altitude ( of 170 m to account for potential vertical positioning errors of the VTOL aircraft. The slope value is determined by the aerodynamic and power constraints of the landing vehicle, ranging from a minimum of 7.13° (per EASA guidelines) to a maximum of 30° [51]. For this study, an intermediate value of slope among these limits (i.e., ϑ = 21.9°) is assumed. This trajectory phase is defined by points A-B in Figure 1, illustrating the OFV and trajectory variations as a function of slope.
- A second and steeper descent aligning the vehicle horizontally with the center of the landing pad. The endpoint of this segment (Point C in Figure 1) is located 3 m above the landing area, horizontally centered over the pad.
- A vertical descent for the final 3 m of approach. This phase concludes with the aircraft reaching Point D, located at the center of the landing pad (i.e., the ideal touchdown point).
- A North-East-Down (NED) reference frame centered in the landing pattern, which serves as the local reference frame. The VTOL aircraft trajectory, as well as the coordinates of the radar targets and visual key points, are defined relative to this reference frame;
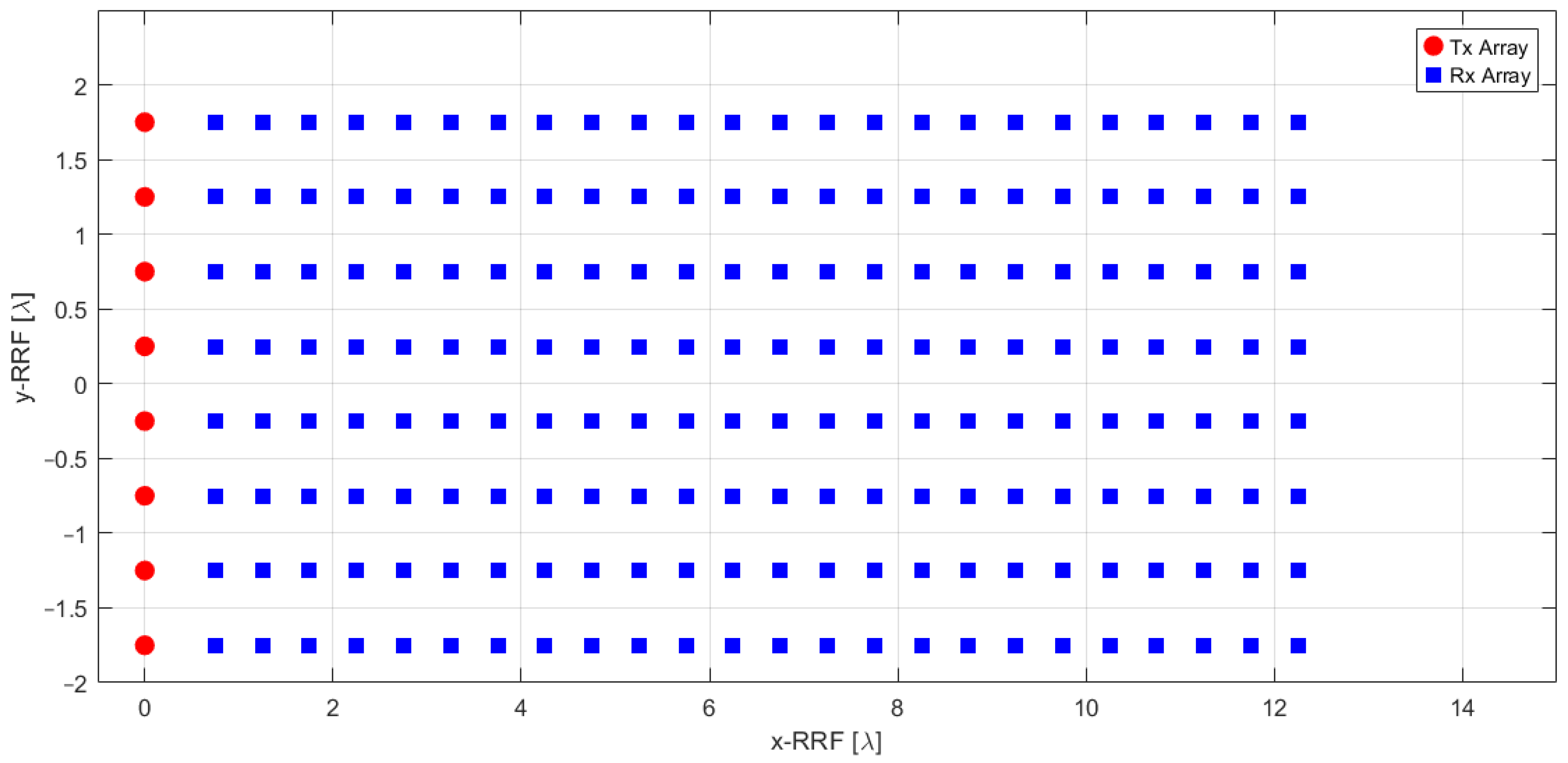
- A Radar Reference Frame (RRF) with its origin located in correspondence of the onboard FMCW radar. The RRF has its x–y plane aligned with the phased radar antenna elements, while the z-axis is the radar boresight direction. The position of specific targets in this reference frame can also be expressed in polar coordinates, defined by range, azimuth (Az), and elevation (El). Azimuth is the horizontal angle between the radar boresight (z-axis) and the target, measured in the x–z plane, positive in clockwise direction where Az = 0° means the target is directly along the boresight. Elevation is the vertical angle between the z-axis and the target, measured in the y–z plane, with positive angles above the x–z plane and negative angles below it. The antenna elements of the designed phased array and the collected radar data are expressed relative to this reference frame.
2.2. Minimum Radar System Requirements
2.2.1. Radar Resolution Requirements
2.2.2. Radar Frequency Band Analysis
2.2.3. Radar Antenna
2.2.4. Transmitted Power Computation
2.3. Preliminary Radar System Design
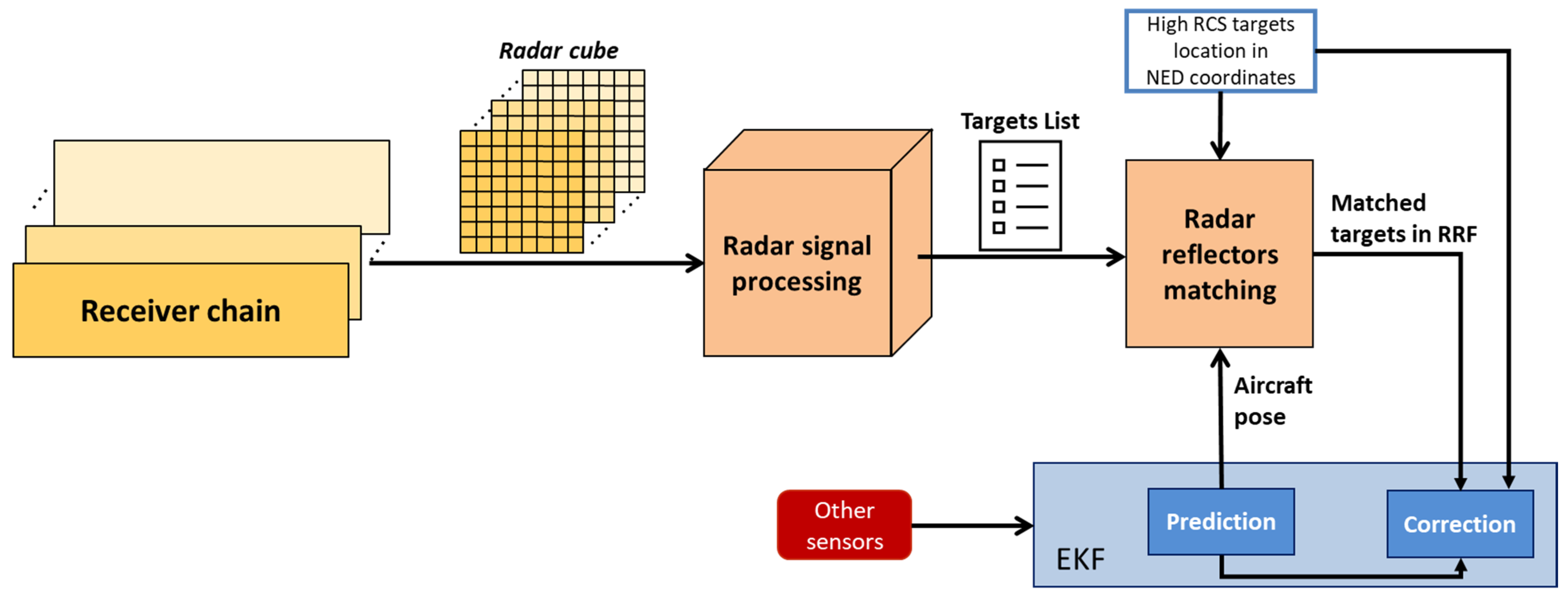
3. Radar Data Processing and Fusion Architecture
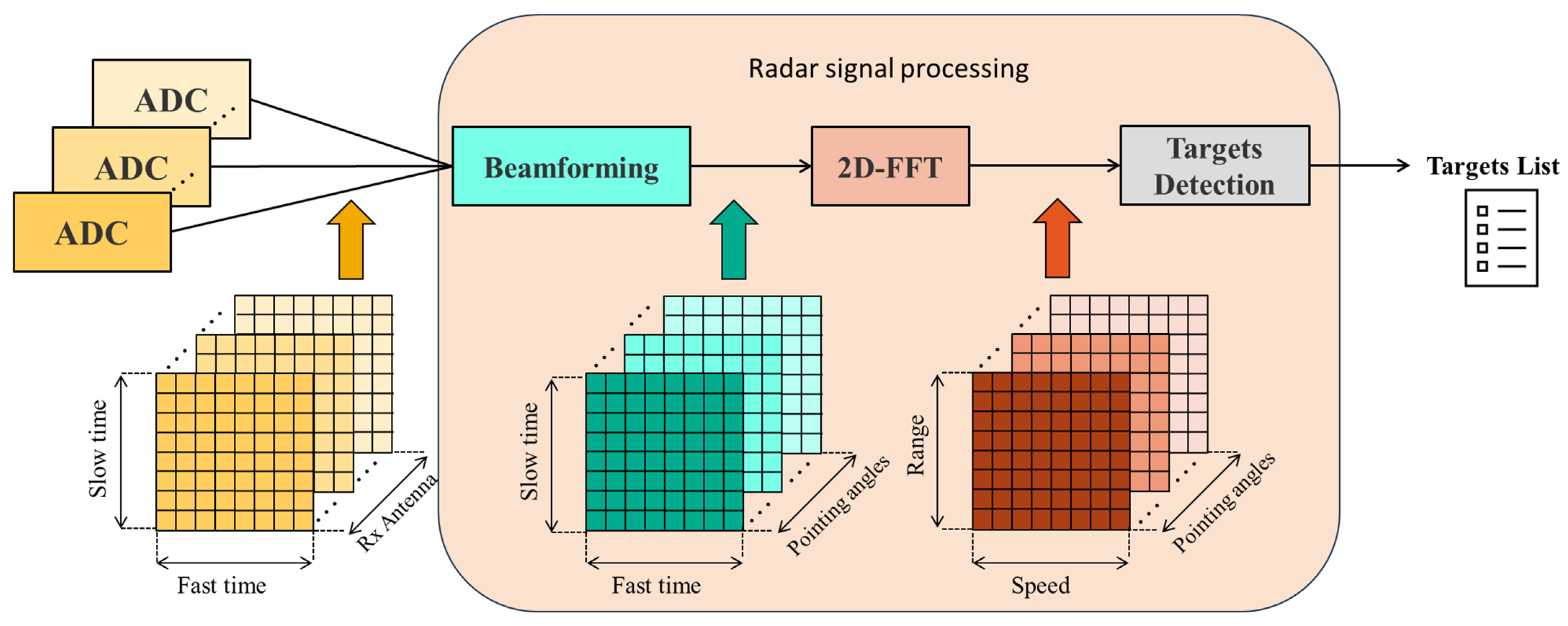
3.1. Radar Signal Processing and Targets Detection
- RRF polar coordinates (Az, El, Range);
- Radial velocity;
- Signal peak power;
- Background noise level.
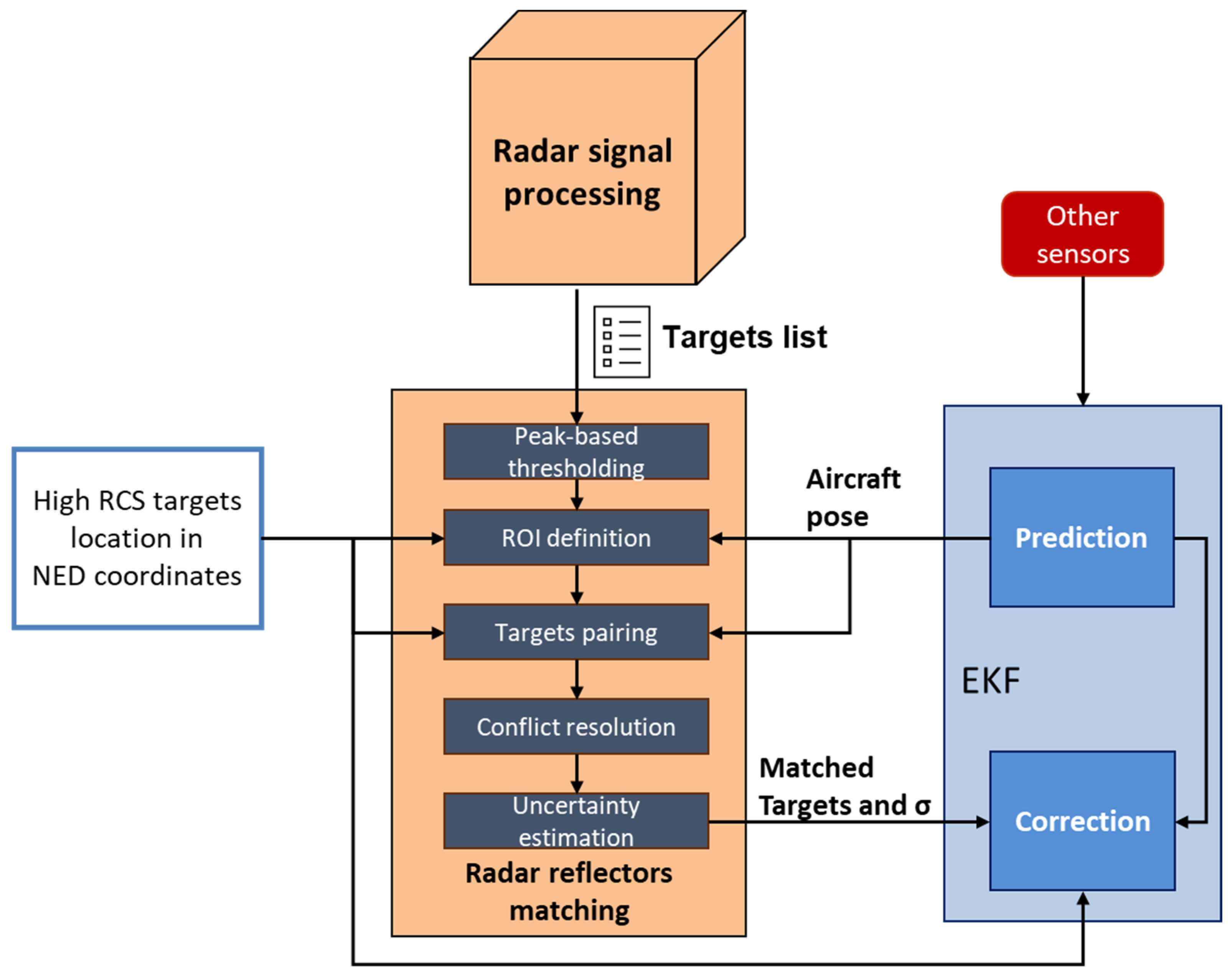
3.2. Radar Reflector Matching
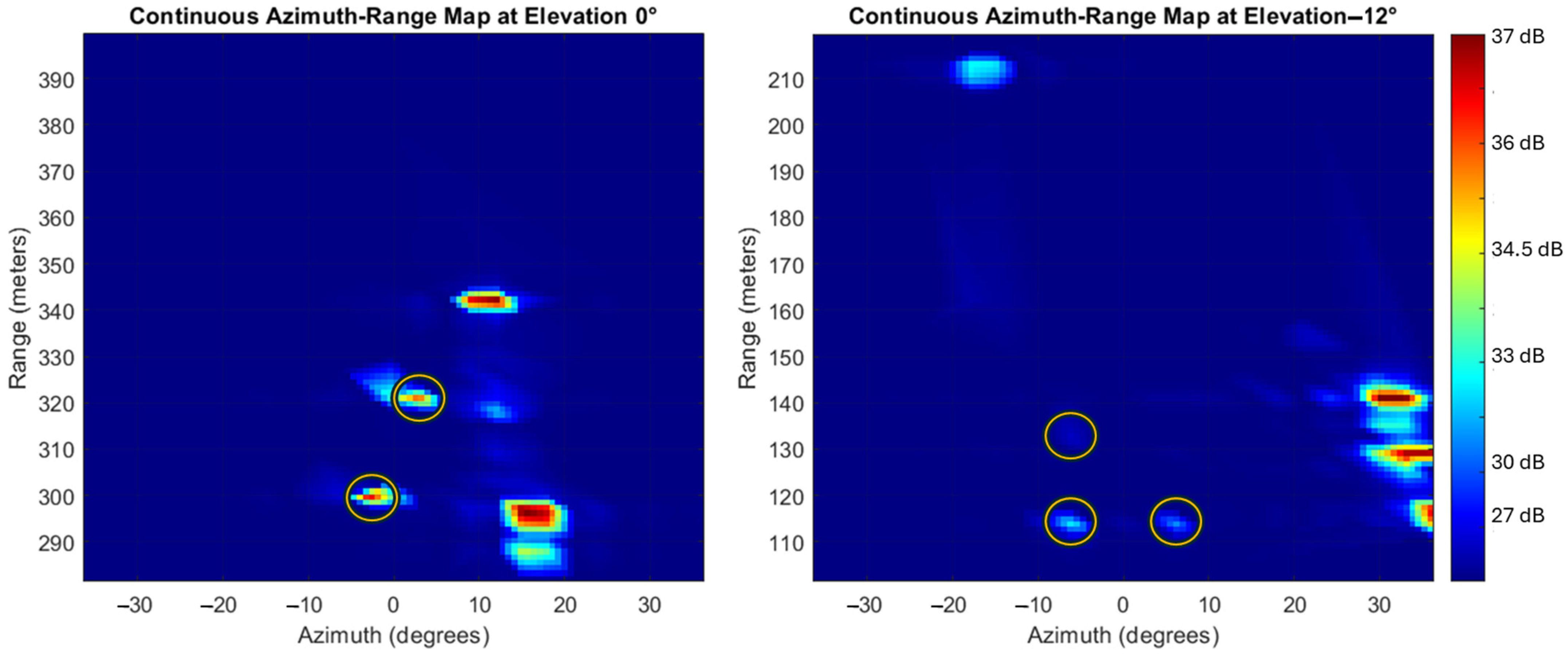
- Peak-based thresholding. A threshold based on the targets’ signal peak power filters out target returns with lower intensities than the ones expected for the targets of interest. The threshold can be selected through a calibration process by observing target returns at the relevant ranges. This threshold is here set to a value marginally below (e.g., −1 dB) the expected return power of the farthest detected target but may adapt with range as sufficient data becomes available to characterize targets’ returns.
- Region of Interest (ROI) Definition. The known coordinates of the radar reflectors in the NED reference frame are used to define an ROI that is expected to include the target detections. The ROI is initially defined in NED by projecting the reflector locations and then expanded based on the navigation uncertainty. Specifically, the a priori state covariance is used to determine confidence bounds, such as a 95% interval, by extending the ROI along each axis in North-East-Down coordinates. Once the expanded ROI is established in NED, its vertices are transformed into the RRF. The list of detected radar targets, which is expressed in RRF, is then filtered by retaining only those within the transformed ROI. This ensures that the target selection process accounts for navigation uncertainty, preventing the exclusion of valid detections due to estimation errors. The navigation state covariance, used for ROI expansion, is propagated in the prediction step of the EKF using Van Loan’s method [62] and updated in the correction step through the measurement covariance matrix and Kalman gain [63].
- Targets Pairing. The remaining targets, including reflections from both the targets of interest and nearby objects/clutter, are matched to the reprojected radar reflector coordinates in the RRF. Each radar return is associated with the closest radar reflector by minimizing the distance to the four reprojected coordinates. The spacing of 24 m between the reflectors (i.e., ) ensures reliable matching, even in the presence of navigation state errors.
- Conflict Resolution. When multiple returns are paired to the same reflector, only the strongest return is retained, based on the assumption that the high RCS targets installed in the landing area generate the highest intensity returns compared to nearby objects.
- Uncertainty Estimation. Detection uncertainties are calculated using the formulas [61]:
3.3. Radar-Aided Extended Kalman Filter
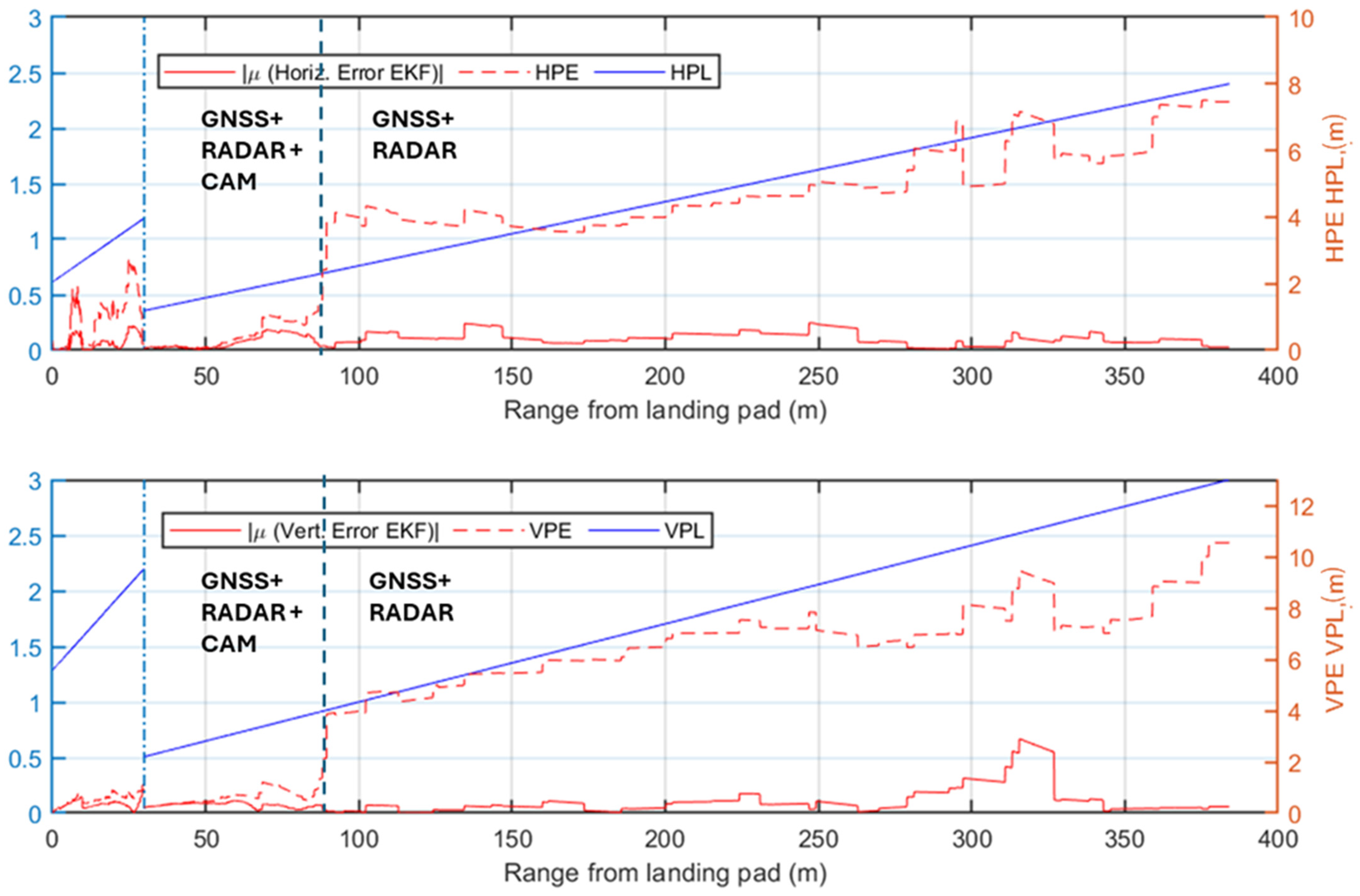
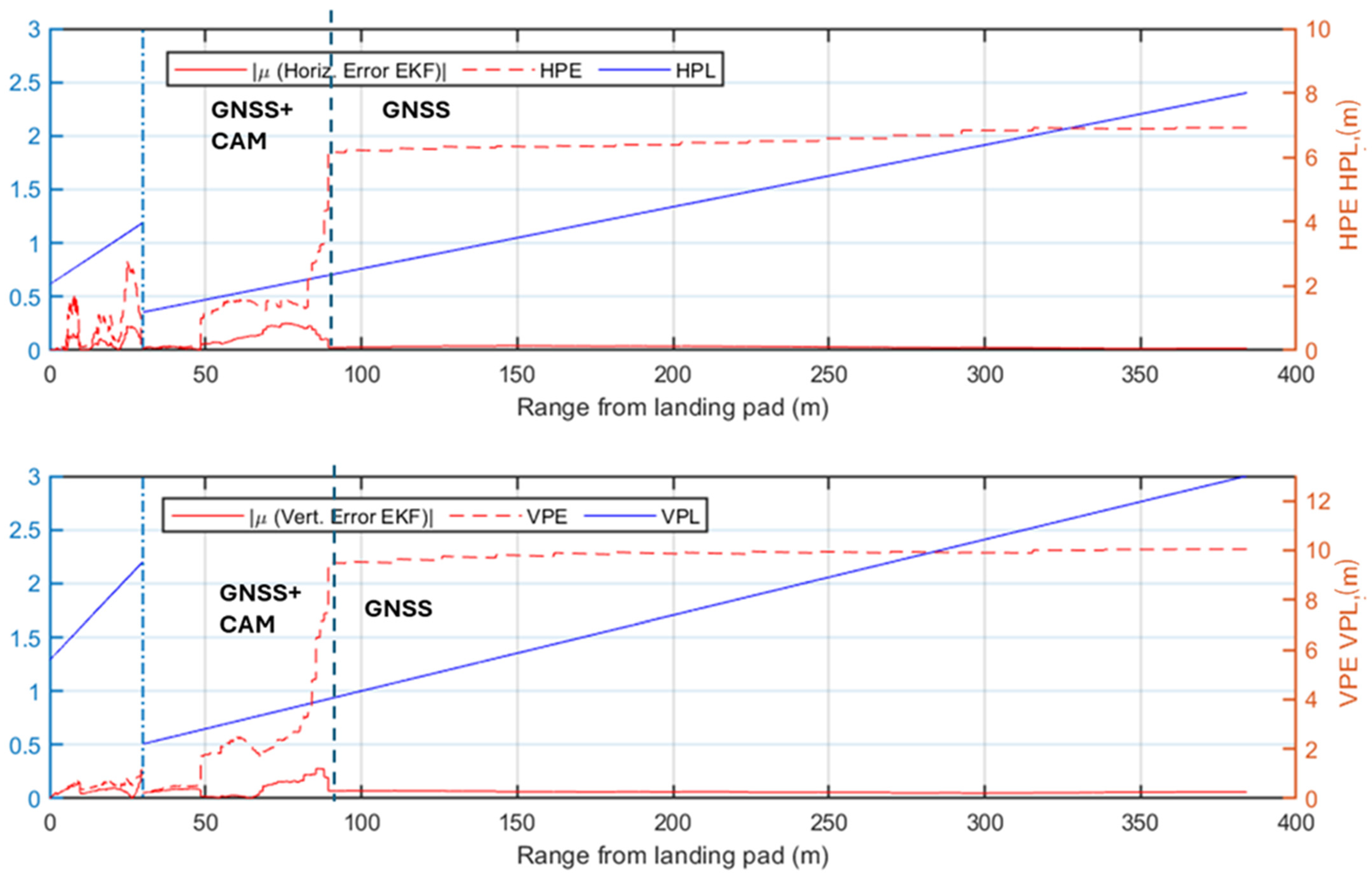
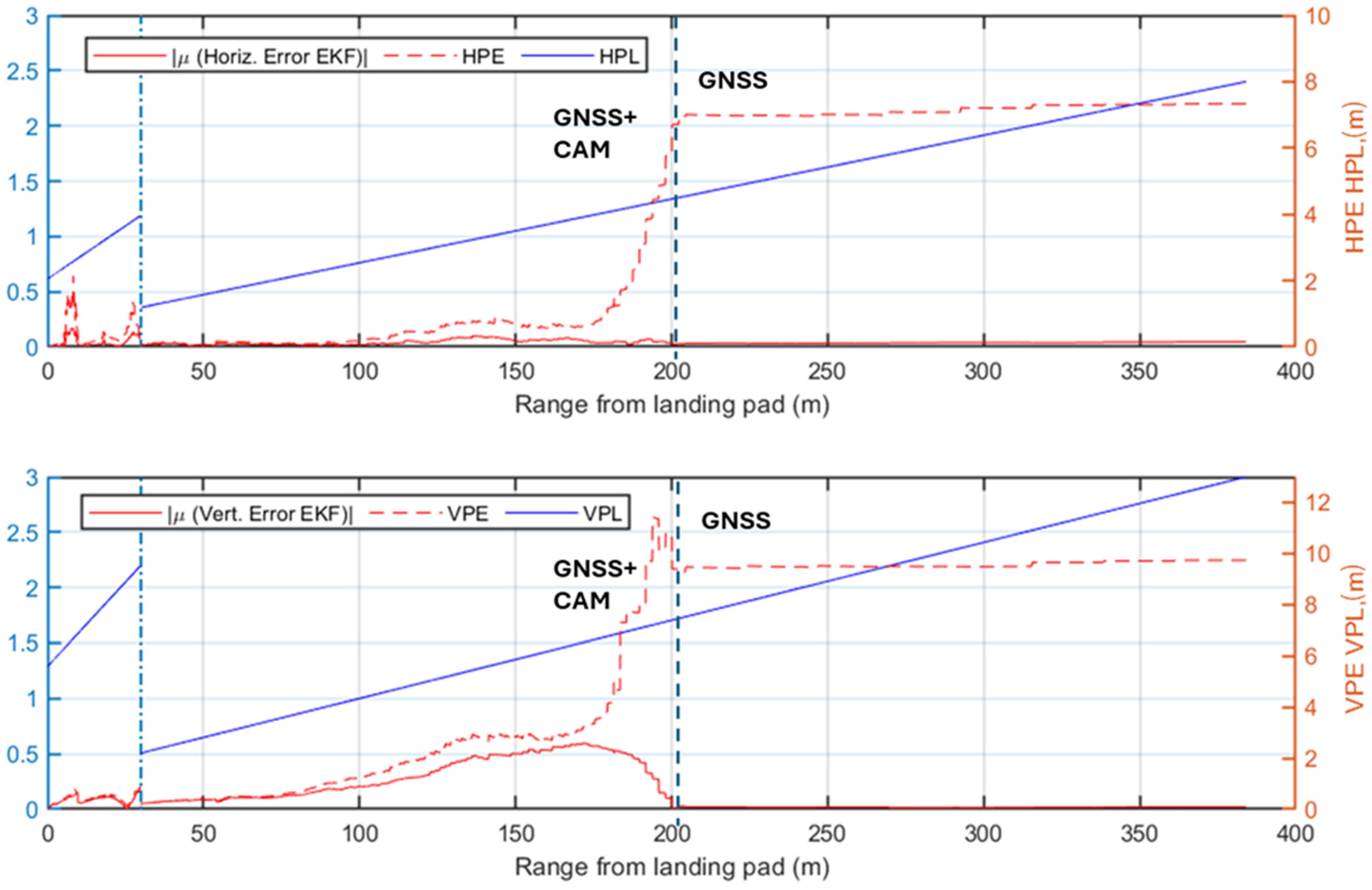
- Long-Range Phase. This corresponds to the time interval at which the estimated range from the landing pad is larger than . In this phase, only GNSS measurements are utilized for the correction step of the EKF. Since this range exceeds the radar detection capability, it lies outside the scope of the present study and is not considered part of the final approach procedure. The lower limit of this phase is determined by the radar maximum effective detection range.
- Radar-Aided Phase. This corresponds to the time interval at which the estimated range is between and . This phase relies on radar data as a key augmentation of the GNSS-IMU fusion to ensure precise navigation during the transition towards the landing site.
- Full multi-sensor Phase. This corresponds to the time interval at which the estimated range is smaller than . At closer distances, visual measurements are also integrated into the EKF correction step. Vision-based pose estimation becomes reliable at approximately 200 m under nominal visibility conditions. Sensors’ contributions are dynamically weighted based on their estimated uncertainties, and a covariance-based gating mechanism excludes erroneous data, such as GNSS multipath errors or misidentified image features. This multi-sensor fusion ensures robust navigation, maintaining accuracy even in the event of a sensor failure. Vision-aided measurements provide the precision required for the final stages of approach, enabling the unmanned/autonomous VTOL aircraft to complete its landing procedure safely.
4. Simulation Environment and Results
4.1. Simulation Environment and Test Cases
- GNSS positioning and raw IMU data are generated with the MATLAB® R2024b (Natick, Apple Hill Campus, Massachusetts, United States) Navigation Toolbox;
- Camera frames are produced by linking the MATLAB® R2024b UAV Toolbox to Unreal Engine 4 (UE4, Cary, 620 Crossroads Blvd, United States), which renders a customized urban environment, including the landing pattern depicted in Figure 2. The Exponential Height Fog actor within UE allows for the simulation of varied visibility conditions;
- For raw radar data, the high-fidelity physics-based tools Ansys (Canonsburg, Pennsylvania, United States) AVxcelerate Sensor Labs™ 2024 R1 and Ansys Asset Preparation™ 2024 R1 are used. Sensor Labs™ models the radar system, including its waveform generator, antenna arrays, analog signal conditioning, and ADC sampling. Asset Preparation™ is employed to create the radar environment, specifying the dielectric properties (and hence reflectivity) of various elements in the scenario. Together, these tools ensure the generation of realistic radar data reflecting the interaction of radar signals with the environment.
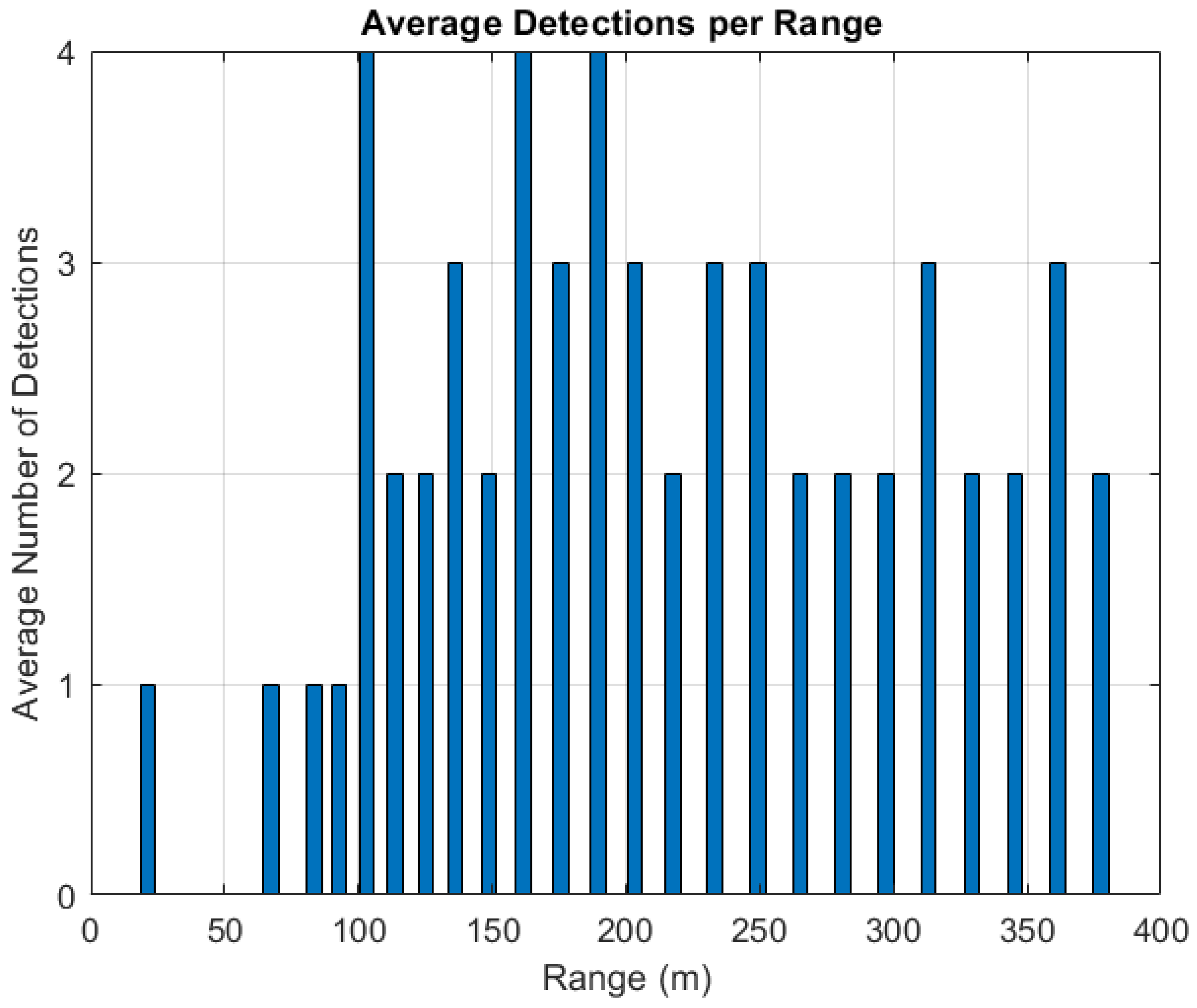
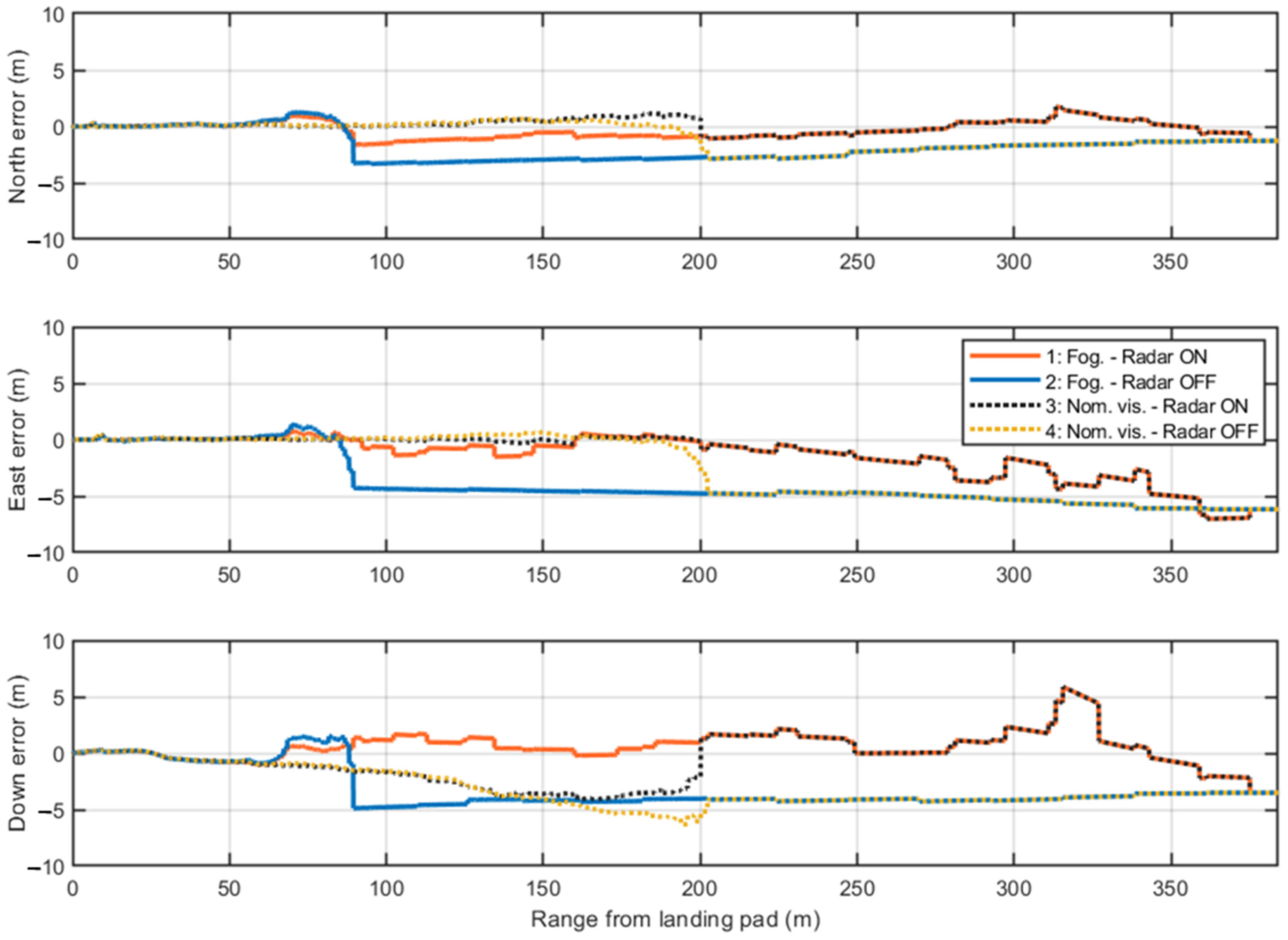
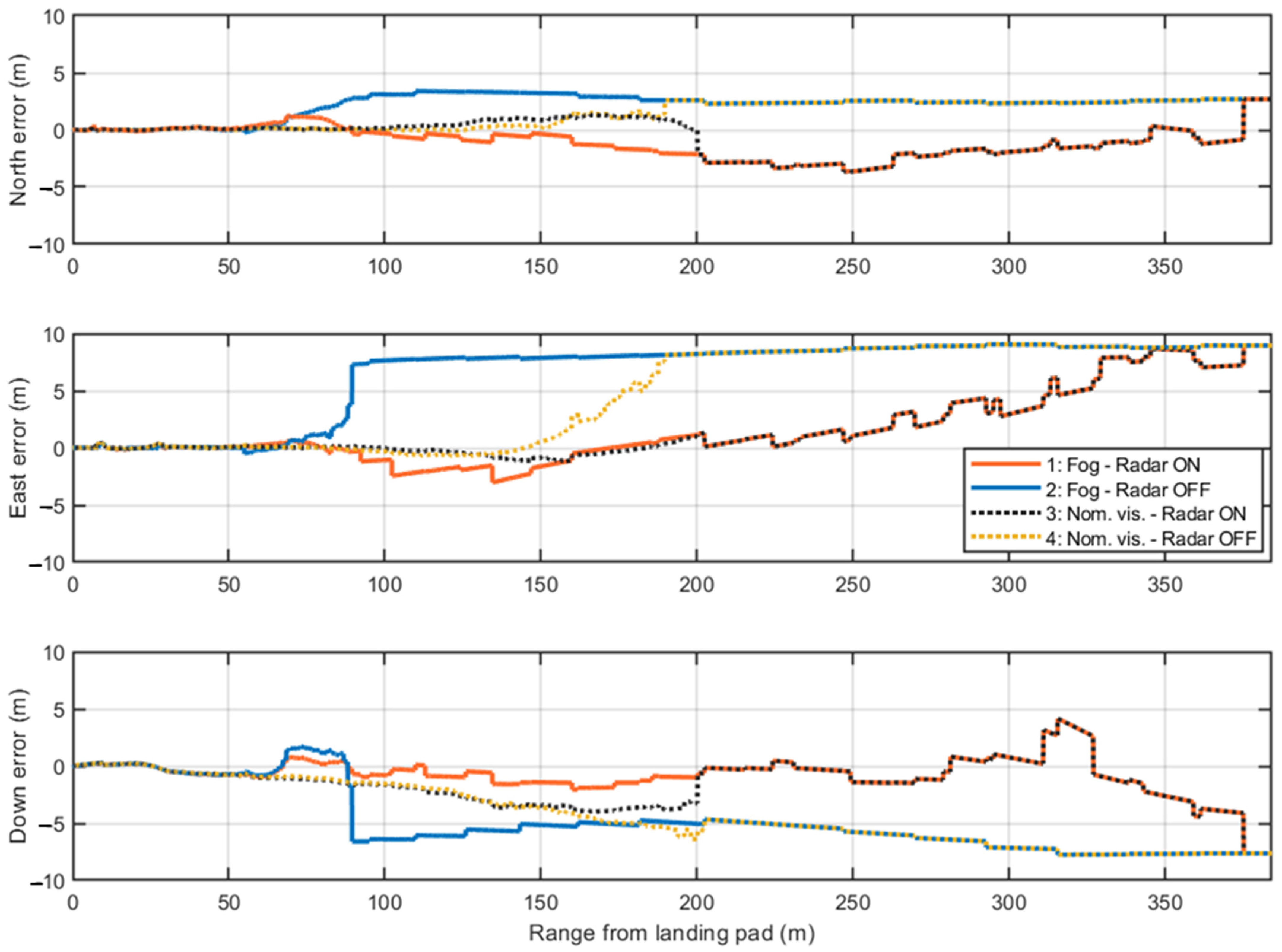
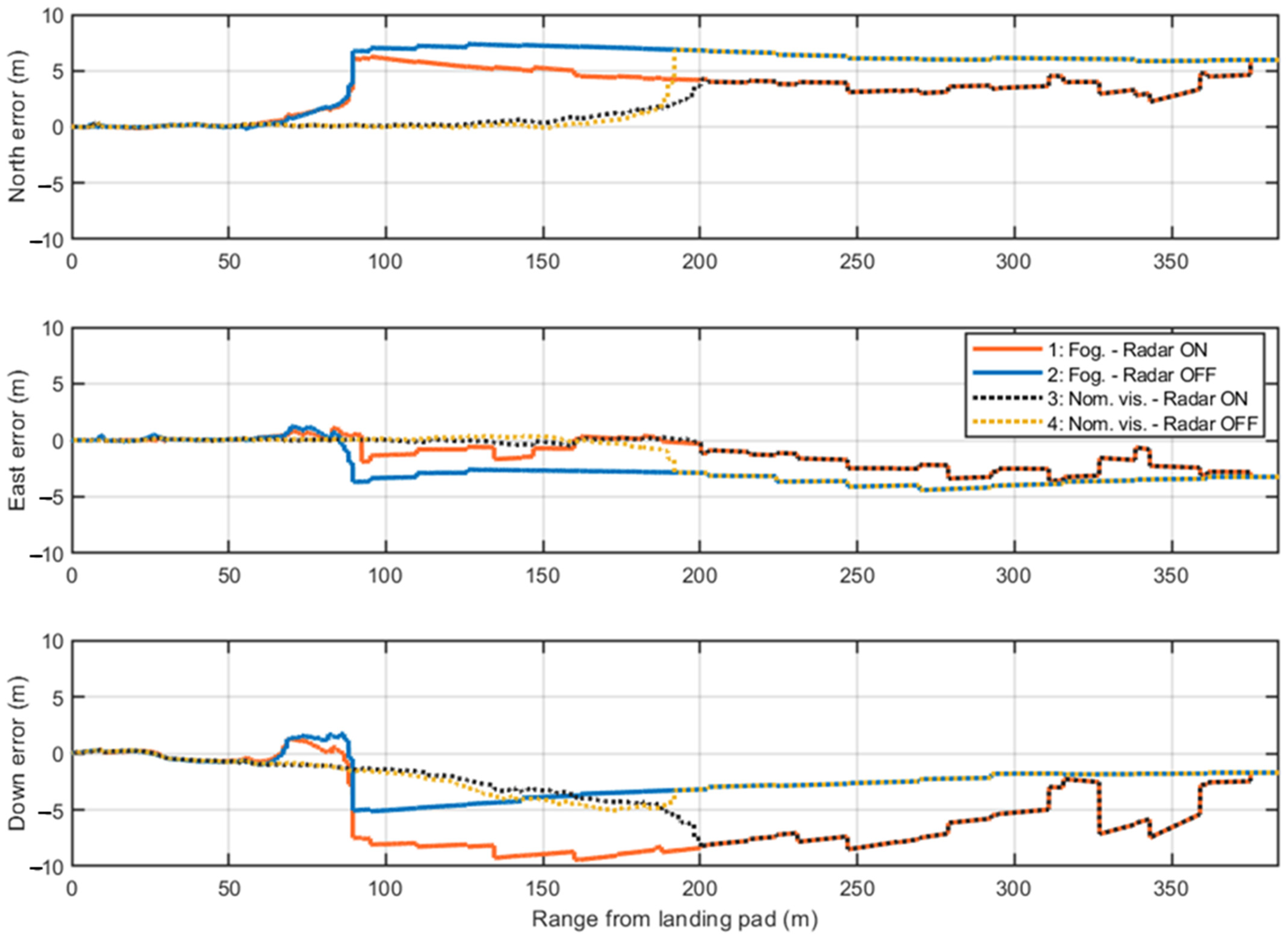
4.2. Simulation Results
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Civil Aviation Organization ICAO Accident Statistics. Available online: https://www.icao.int/safety/iStars/Pages/Accident-Statistics.aspx (accessed on 8 November 2024).
- European Union Aviation Safety Agency. Annual Safety Review 2024. 2024. Available online: https://www.easa.europa.eu/en/document-library/general-publications/annual-safety-review-2024 (accessed on 10 January 2025).
- Ippolito, C.; Hashemi, K.; Kawamura, E.; Gorospe, G.; Holforty, W.; Kannan, K.; Stepanyan, V.; Lombaerts, T.; Brown, N.; Jaffe, A. Concepts for Distributed Sensing and Collaborative Airspace Autonomy in Advanced Urban Air Mobility. In Proceedings of the AIAA SciTech Forum and Exposition, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Stefanescu, E.R.; Chekh, V.; Shastry, A.; Biresaw, T. Advanced Air Mobility (AAM) Aircraft Precision Landing Design for Instrument Meteorological Conditions (IMC) Operations. In Proceedings of the AIAA AVIATION Forum, Las Vegas, NV, USA, 29 July–2 August 2024. [Google Scholar]
- Kawamura, E.; Dolph, C.; Kannan, K.; Lombaerts, T.; Ippolito, C.A. Simulated Vision-Based Approach and Landing System for Advanced Air Mobility. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Bijjahalli, S.; Sabatini, R.; Gardi, A. GNSS Performance Modelling and Augmentation for Urban Air Mobility. Sensors 2019, 19, 4209. [Google Scholar] [CrossRef] [PubMed]
- Causa, F.; Fasano, G. Multiple UAVs Trajectory Generation and Waypoint Assignment in Urban Environment Based on DOP Maps. Aerosp. Sci. Technol. 2021, 110, 106507. [Google Scholar] [CrossRef]
- Federal Aviation Administration. AC 90-106B—Enhanced Flight Vision System Operations. 2022. Available online: https://www.faa.gov/regulations_policies/advisory_circulars/index.cfm/go/document.information/documentID/1040987 (accessed on 30 October 2024).
- Federal Aviation Administration. AC 20-167A—Airworthiness Approval of Enhanced Vision System, Synthetic Vision System, Combined Vision System, and Enhanced Flight Vision System Equipment. 2016. Available online: https://www.faa.gov/regulations_policies/advisory_circulars/index.cfm/go/document.information/documentid/1030367 (accessed on 30 October 2024).
- European Union Aviation Safety Agency. Acceptable Means of Compliance (AMC) and Guidance Material (GM) to Annex IV Commercial Air Transport Operations [Part-CAT]. 2017. Available online: https://www.easa.europa.eu/sites/default/files/dfu/Consolidated%20unofficial%20AMC-GM_Annex%20IV%20Part-CAT%20March%202017.pdf (accessed on 30 October 2024).
- Internation Civil Aviation Organization Annex 6 to the Convention on International Civil Aviation—Operation of Aircraft. 2018. Available online: https://www.icao.int/safety/CAPSCA/PublishingImages/Pages/ICAO-SARPs-(Annexes-and-PANS)/Annex%206.pdf (accessed on 30 October 2024).
- Collins Aerospace Collins Aerospace—Vision Systems. Available online: https://www.collinsaerospace.com/what-we-do/industries/business-aviation/flight-deck/vision-systems (accessed on 8 November 2024).
- Brailovsky, A.; Bode, J.; Cariani, P.; Cross, J.; Gleason, J.; Khodos, V.; Macias, G.; Merrill, R.; Randall, C.; Rudy, D. REVS: A Radar-Based Enhanced Vision System for Degraded Visual Environments. In Proceedings of the Degraded Visual Environments: Enhanced, Synthetic, and External Vision Solutions, Baltimore, MD, USA, 7–8 May 2014; Güell, J.J., Sanders-Reed, J., Eds.; SPIE: Pune, India, 2014; Volume 9087, p. 908708. [Google Scholar]
- Kerr, J. Enhanced Detection of LED Runway/Approach Lights for EVS. In Proceedings of the SPIE—The International Society for Optical Engineering, Orlando, FL, USA, 16–20 March 2008. [Google Scholar] [CrossRef]
- Doehler, H.-U.; Korn, B.R. Autonomous Infrared-Based Guidance System for Approach and Landing. In Proceedings of the Enhanced and Synthetic Vision, Orlando, FL, USA, 12–13 April 2004; Verly, J.G., Ed.; Society of Photo Optical: Bellingham, WA, USA, 2004; Volume 5424, pp. 140–147. [Google Scholar]
- Korn, B.R. Enhanced and Synthetic Vision System for Autonomous All Weather Approach and Landing. In Proceedings of the Enhanced and Synthetic Vision, Rohnert Park, CA, USA, 7–10 May 2007; Verly, J.G., Guell, J.J., Eds.; SPIE: Pune, India, 2007; Volume 6559, p. 65590A. [Google Scholar]
- Zimmermann, M.; Gestwa, M.; König, C.; Wolfram, J.; Klasen, S.; Lederle, A. First Results of LiDAR-Aided Helicopter Approaches during NATO DVE-Mitigation Trials. CEAS Aeronaut. J. 2019, 10, 859–874. [Google Scholar] [CrossRef]
- Ernst, J.M.; Schmerwitz, S.; Lueken, T.; Ebrecht, L. Designing a Virtual Cockpit for Helicopter Offshore Operations. In Proceedings of the Proceeding SPIE, Orlando, FL, USA, 5 May 2017; Volume 10197, p. 101970Z. [Google Scholar]
- Ernst, J.M.; Ebrecht, L.; Korn, B. Virtual Cockpit Instruments—How Head-Worn Displays Can Enhance the Obstacle Awareness of Helicopter Pilots. IEEE Aerosp. Electron. Syst. Mag. 2021, 36, 18–34. [Google Scholar] [CrossRef]
- Ernst, J.M.; Peinecke, N.; Ebrecht, L.; Schmerwitz, S.; Doehler, H.-U. Virtual Cockpit: An Immersive Head-Worn Display as Human–Machine Interface for Helicopter Operations. Opt. Eng. 2019, 58, 1–15. [Google Scholar] [CrossRef]
- Szoboszlay, Z.; Fujizawa, B.; Ltc, C.; Ott; Savage, J.; Goodrich, S.; Mckinley, R.; Soukup, J. 3D-LZ Flight Test of 2013: Landing an EH-60L Helicopter in a Brownout Degraded Visual Environment. In Proceedings of the American Helicopter Society Annual Forum, Montreal, QC, Canada, 20–22 May 2014. [Google Scholar]
- Miller, J.D.; Godfroy-Cooper, M.; Szoboszlay, Z.P. Degraded Visual Environment Mitigation (DVE-M) Program, Bumper RADAR Obstacle Cueing Flight Trials 2020. In Proceedings of the Vertical Flight Society 77th Annual Forum, Virtual, 10–14 May 2021. [Google Scholar]
- Dogaru, T. Polar Format Algorithm for 3-D Imaging with Forward-Looking Synthetic Aperture Radar. 2020. Available online: https://apps.dtic.mil/sti/trecms/pdf/AD1111206.pdf (accessed on 10 October 2024).
- Dogaru, T. Synthetic Aperture Radar for Helicopter Landing in Degraded Visual Environments. 2018. Available online: https://apps.dtic.mil/sti/tr/pdf/AD1064582.pdf (accessed on 10 October 2024).
- Kenyon, C.S. Exploration of Ground Obstacle Visibility in a Degraded Visibility Environment by an Airborne Landing Radar. 2021. Available online: https://apps.dtic.mil/sti/trecms/pdf/AD1131839.pdf (accessed on 10 October 2024).
- Michalczyk, J.; Jung, R.; Weiss, S. Tightly-Coupled EKF-Based Radar-Inertial Odometry. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 12336–12343. [Google Scholar]
- Almalioglu, Y.; Turan, M.; Lu, C.X.; Trigoni, N.; Markham, A. Milli-RIO: Ego-Motion Estimation With Low-Cost Millimetre-Wave Radar. IEEE Sens. J. 2021, 21, 3314–3323. [Google Scholar] [CrossRef]
- Doer, C.; Atman, J.; Trnmmer, G.F. GNSS Aided Radar Inertial Odometry for UAS Flights in Challenging Conditions. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–10. [Google Scholar]
- Wu, S.; Decker, S.; Chang, P.; Camus, T.; Eledath, J. Collision Sensing by Stereo Vision and Radar Sensor Fusion. IEEE Trans. Intell. Transp. Syst. 2009, 10, 606–614. [Google Scholar] [CrossRef]
- Pavlenko, T.; Schütz, M.; Vossiek, M.; Walter, T.; Montenegro, S. Wireless Local Positioning System for Controlled UAV Landing in GNSS-Denied Environment. In Proceedings of the 2019 IEEE 5th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Torino, Italy, 19–21 June 2019; pp. 171–175. [Google Scholar]
- Dobrev, Y.; Dobrev, Y.; Gulden, P.; Lipka, M.; Pavlenko, T.; Moormann, D.; Vossiek, M. Radar-Based High-Accuracy 3D Localization of UAVs for Landing in GNSS-Denied Environments. In Proceedings of the 2018 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility, ICMIM, Munich, Germany, 16–18 April 2018; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2018. [Google Scholar]
- Doer, C.; Koenig, R.; Trommer, G.F.; Stumpf, E. Radar Based Autonomous Precision Takeoff and Landing System for VTOLs in GNSS Denied Environments. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 922–931. [Google Scholar]
- Yasentsev, D.; Shevgunov, T.; Efimov, E.; Tatarskiy, B. Using Ground-Based Passive Reflectors for Improving UAV Landing. Drones 2021, 5, 137. [Google Scholar] [CrossRef]
- Hübner, F.; Wolkow, S.; Dekiert, A.; Angermann, M.; Bestmann, U. Assessment of Optical Markers for On-Board Autonomous Localization of EVTOLs during Landing. In Proceedings of the 2020 9th International Conference on Research in Air Transportation, Virtual, 15 September 2020. [Google Scholar]
- Hübner, F.; Haupt, R.; Bestmann, U.; Hecker, P. Navigation Augmentation for Landing on Vertipads Utilizing Optical Detection of Standard ICAO Circular Markings. In Proceedings of the 37th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2024), Baltimore, MD, USA, 16–20 September 2024; pp. 2031–2045. [Google Scholar]
- Lee, J.; Choi, S.Y.; Bretl, T. The Use of Multi-Scale Fiducial Markers To Aid Takeoff and Landing Navigation by Rotorcraft. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Kawamura, E.; Kannan, K.; Lombaerts, T.; Ippolito, C.A. Vision-Based Precision Approach and Landing for Advanced Air Mobility. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; American Institute of Aeronautics and Astronautics: Reston, VA, USA. [Google Scholar]
- Kannan, K.; Baculi, J.E.; Lombaerts, T.; Kawamura, E.; Gorospe, G.E.; Holforty, W.; Ippolito, C.A.; Stepanyan, V.; Dolph, C.; Brown, N. A Simulation Architecture for Air Traffic Over Urban Environments Supporting Autonomy Research in Advanced Air Mobility. In Proceedings of the AIAA SciTech 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; p. 895. [Google Scholar]
- Oberkampf, D.; DeMenthon, D.F.; Davis, L.S. Iterative Pose Estimation Using Coplanar Feature Points. Comput. Vis. Image Underst. 1996, 63, 495–511. [Google Scholar] [CrossRef]
- Kawamura, E.; Dolph, C.; Kannan, K.; Brown, N.; Lombaerts, T.; Ippolito, C.A. VSLAM and Vision-Based Approach and Landing for Advanced Air Mobility. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; AIAA SciTech Forum. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2023. [Google Scholar]
- Brown, N.; Kawamura, E.; Bard, L.; Jaffe, A.J.; Ringelberg, W.; Kannan, K.; Ippolito, C.A. Visual & Inertial Datasets for an EVTOL Aircraft Approach and Landing Scenario. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; AIAA SciTech Forum. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2024. [Google Scholar]
- Akagi, D.; McLain, T.; Joshua, M. Robust IR-Based Pose Estimation for Precision VTOL Aircraft Landing in Urban Environments. In Proceedings of the 2024 International Conference on Unmanned Aircraft Systems (ICUAS), Crete, Greece, 4–7 June 2024. [Google Scholar]
- Dekiert, A.; Hübner, F.; Scholz, L.; Bestmann, U. Nonlinear Temperature Mapping for Infrared-Based Landing Site Detection. In Proceedings of the 2022 IEEE/AIAA 41st Digital Avionics Systems Conference (DASC), Portsmouth, VA, USA, 18–22 September 2022; pp. 1–7. [Google Scholar]
- European Union Aviation Safety Agency. Vertiports—Prototype Technical Specifications for the Design of VFR Vertiports for Operation with Manned VTOL-Capable Aircraft Certified in the Enhanced Category (PTS-VPT-DSN). 2022. Available online: https://www.easa.europa.eu/en/downloads/136259/en (accessed on 27 March 2022).
- National Aeronautics and Space Administration. UAM Vision Concept of Operations (ConOps) UAM Maturity Level (UML) 4. 2021. Available online: https://ntrs.nasa.gov/api/citations/20205011091/downloads/UAM%20Vision%20Concept%20of%20Operations%20UML-4%20v1.0.pdf (accessed on 10 January 2022).
- Miccio, E.; Veneruso, P.; Fasano, G.; Tiana, C.; Opromolla, R.; Gentile, G. AI-Powered Vision-Aided Navigation and Ground Obstacles Detection for UAM Approach and Landing. In Proceedings of the 2023 AIAA/IEE Digital Avionics Systems Conference, Barcelona, Spain, 1–5 October 2023; pp. 1–10. [Google Scholar]
- Veneruso, P.; Opromolla, R.; Tiana, C.; Gentile, G.; Fasano, G. Sensing Requirements and Vision-Aided Navigation Algorithms for Vertical Landing in Good and Low Visibility UAM Scenarios. Remote Sens. 2022, 14, 3764. [Google Scholar] [CrossRef]
- Miccio, E.; Veneruso, P.; Opromolla, R.; Fasano, G.; Gentile, G.; Tiana, C. Vision-Aided Sensing Pipeline with AI-Based Vertiport Detection for Precision Navigation in UAM Approach and Landing Scenarios. In Aerospace Science and Technology—Submitted on 12/2024; Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5059951 (accessed on 19 February 2025).
- Veneruso, P.; Miccio, E.; Causa, F.; Opromolla, R.; Fasano, G.; Gentile, G.; Tiana, C. Radar-Visual Navigation for All-Weather Approach and Landing to Vertiports. In Proceedings of the 2023 AIAA/IEE Digital Avionics Systems Conference, Barcelona, Spain, 1–5 October 2023; pp. 1–10. [Google Scholar]
- Veneruso, P.; Miccio, E.; Opromolla, R.; Fasano, G.; Manica, L.; Gentile, G.; Tiana, C. Assessing Radar-Aided Navigation for UAM Approach and Landing Through High-Fidelity Simulations and Flight Testing. In Proceedings of the 2024 AIAA DATC/IEEE 43rd Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 29 September–3 October 2024; pp. 1–9. [Google Scholar]
- Webber D NASA Advanced Air Mobility (AAM) National Campaign (NC) [Powerpoint]. Available online: https://aam-cms.marqui.tech/uploads/aam-portal-cms/originals/d96309f2-7258-40d3-a74a-368a3a684b74.pdf (accessed on 20 February 2024).
- EVTOL Aircraft Directory. Available online: https://evtol.news/aircraft (accessed on 31 March 2022).
- Curry, G.R. Radar System Performance Modeling, 2nd ed.; Artech: Kerala, India, 2004. [Google Scholar]
- ITU-R M.2204; Characteristics and Spectrum Considerations for Sense and Avoid Systems Use on Unmanned Aircraft Systems (UAS).
- Federal Communications Commission. Table of Frequency Allocations Chart. 2015. Available online: https://transition.fcc.gov/oet/spectrum/table/fcctable.pdf (accessed on 10 September 2024).
- Goldsmith, A. Wireless Communication, 1st ed.; Cambridge University: Cambridge, UK, 2005. [Google Scholar]
- ITU, R.I.-R.P. 676-12; Attenuation by Atmospheric Gases and Related Effects, (ITU-R P.676). 2020. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.676-12-201908-S!!PDF-E.pdf (accessed on 10 September 2024).
- ITU, I.-R.P. 838-3; Specific Attenuation Model for Rain for Use in Prediction Model, (ITU-R P.838-3). 2005. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.838-3-200503-I!!PDF-E.pdf (accessed on 10 September 2024).
- Elliott, R.S. Beamwidth and Directivity of Large Scanning Arrays; Last of Two Parts; The Microwave Journal: Norwood, MA, USA, 1964; pp. 74–82. [Google Scholar]
- Balanis, C.A. Antenna Theory—Analysis and Design, 3rd ed.; Wiley-Interscience, John Wiley & Sons.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Mark, A.; Richards. Fundamental of Radar Signal Processing, 2nd ed.; McGraw Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Van Loan, C. Computing Integrals Involving the Matrix Exponential. IEEE Trans. Autom. Contr. 1978, 23, 395–404. [Google Scholar] [CrossRef]
- Groves, P. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, 2nd ed.; Artech: Morristown, NJ, USA, 2013. [Google Scholar]
- Ward, J. Space-Time Adaptive Processing for Airborne Radar. 1994. Available online: https://digital-library.theiet.org/doi/abs/10.1049/ic%3A19980240 (accessed on 10 September 2024).
- Burger, W. Space-Time Adaptive Processing: Algorithms. In NATO—RTO-EN-SET-086; 2006; Available online: https://www.sto.nato.int/publications/STO%20Educational%20Notes/RTO-EN-SET-086/EN-SET-086-07.pdf (accessed on 10 September 2024).
- García Crespillo, O.; Zhu, C.; Simonetti, M.; Gerbeth, D.; Lee, Y.-H.; Hao, W. Vertiport Navigation Requirements and Multisensor Architecture Considerations for Urban Air Mobility. CEAS Aeronaut. J. 2024. [Google Scholar] [CrossRef]
- EUSPA—European Union Agency for the Space Programme. Report on Aviation and Drones. 2023. Available online: https://www.euspa.europa.eu/sites/default/files/report_on_aviation_and_drones_user_needs_and_requirements.pdf (accessed on 10 September 2024).







| Band | Frequency Range [GHz] | Center Frequency fc [GHz] | Wavelength λ [cm] |
|---|---|---|---|
| Ku | 13.25–13.40 | 13.325 | 2.25 |
| K | 24.45–24.65 | 24.55 | 1.23 |
| Ka | 32.30–33.40 | 32.85 | 0.91 |
| W | 92.00–95.50 | 93.75 | 0.32 |
| Band | fc [GHz] | |||
|---|---|---|---|---|
| 100 [m] | 200 [m] | 400 [m] | ||
| Ku | 13.325 | 94.94 | 100.96 | 106.98 |
| K | 24.45 | 100.25 | 106.27 | 112.29 |
| Ka | 32.85 | 102.78 | 108.80 | 114.82 |
| W | 93.75 | 111.89 | 117.91 | 123.93 |
| Band | fc [GHz] | γatm [dB/km] |
|---|---|---|
| Ku | 13.325 | 0.0218 |
| K | 24.55 | 0.1606 |
| Ka | 32.85 | 0.0955 |
| W | 93.75 | 0.4134 |
| Band | fc [GHz] | |||
|---|---|---|---|---|
| 2 [mm/h] | 4 [mm/h] | 6 [mm/h] | ||
| Ku | 13.325 | 0.1632 | 0.3314 | 0.5024 |
| K | 24.45 | 0.6119 | 0.1377 | 1.6367 |
| Ka | 32.85 | 1.0788 | 1.9096 | 2.6686 |
| W | 93.75 | 3.4630 | 5.3174 | 6.8356 |
| Band | Center Frequency fc [Ghz] | Wavelength λ [cm] | Antenna Size [cm2] |
|---|---|---|---|
| Ku | 13.325 | 2.25 | 9 × 27 |
| K | 24.55 | 1.23 | 4.9 × 14 |
| Ka | 32.85 | 0.91 | 3.7 × 11 |
| W | 93.75 | 0.32 | 1.3 × 3.9 |
| Band | λ [cm] | |
|---|---|---|
| Ku | 2.25 | 0.3760 |
| K | 1.23 | 0.6928 |
| Ka | 0.91 | 0.9270 |
| W | 0.32 | 2.6456 |
| Sensor | Parameter | Value |
|---|---|---|
| IMU | Accelerometer Velocity Random Walk (VRW) | 0.6 m/s/sqrt (h) |
| Accelerometer Bias Instability (ABI) | 0.50 mg | |
| Gyroscope Angular Random Walk (ARW) | 0.05 deg/sqrt (h) | |
| Gyroscope Bias Instability (BI) | 0.6 deg/h | |
| Sample Frequency | 200 Hz | |
| GNSS receiver | GNSS Position Standard Deviation | 2.5 m Horizontal 5 m Vertical |
| Sample Frequency | 1 Hz | |
| FMCW radar | Center frequency | Ka-band, 32.85 GHz |
| Tx Array | 1 × 8 antennas | |
| Rx Array | 24 × 8 antennas | |
| Range resolution, ΔR | 3 m | |
| 4°, 12° | ||
| Mounting Angle α | 20° | |
| Elevation Scan Rate | 10 Hz | |
| Image Size [pixels] | [1920, 1200] | |
| Principal Point [pixels] | [960, 600] | |
| FL camera | Focal Length [pixels] | [1365, 1365] |
| Mounting Angle α | 45° | |
| FOV (Az, El) | [81°, 50°] | |
| Frame Rate | 10 Hz | |
| Image Size [pixels] | [2048, 2048] | |
| Principal Point [pixels] | [1024, 1024] | |
| DL camera | Focal Length [pixels] | [1181, 1181] |
| Mounting Angle α | 90° | |
| FOV (Az, El) | [99°, 99°] | |
| Frame Rate | 10 Hz |
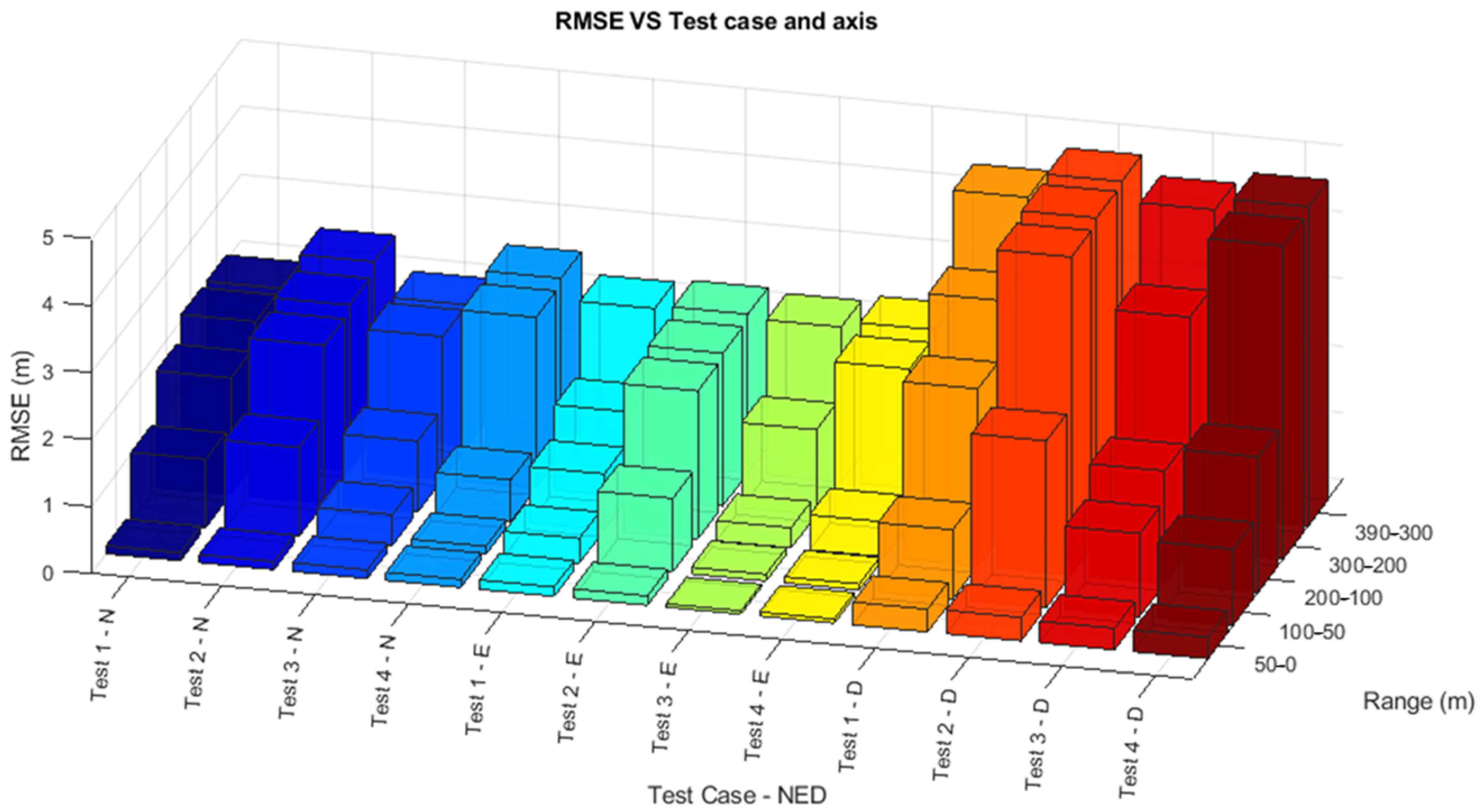
| Test Case | EKF—RMSE [m] | |||||
|---|---|---|---|---|---|---|
| 390 m < R < 300 m | 200 m < R < 300 m | 100 m < R < 200 m | 50 m < R < 100 m | 0 m < R < 50 m | ||
| 1. | N | 2.09 | 2.09 | 1.74 | 1.02 | 0.12 |
| Fog, | E | 2.32 | 1.27 | 0.84 | 0.37 | 0.14 |
| Radar ON | D | 4.51 | 3.46 | 2.64 | 1.03 | 0.34 |
| 2. | N | 2.62 | 2.47 | 2.36 | 1.33 | 0.12 |
| Fog, | E | 2.37 | 2.28 | 2.21 | 1.10 | 0.14 |
| Radar OFF | D | 4.88 | 4.83 | 4.74 | 2.49 | 0.35 |
| 3. | N | 2.11 | 2.13 | 1.06 | 0.46 | 0.13 |
| Nominal visibility, | E | 2.31 | 1.27 | 0.30 | 0.10 | 0.05 |
| Radar ON | D | 4.59 | 3.48 | 1.68 | 1.24 | 0.32 |
| 4. | N | 2.64 | 2.55 | 0.62 | 0.12 | 0.12 |
| Nominal visibility, | E | 2.40 | 2.31 | 0.52 | 0.09 | 0.06 |
| Radar OFF | D | 4.77 | 4.68 | 2.02 | 1.14 | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veneruso, P.; Manica, L.; Miccio, E.; Opromolla, R.; Tiana, C.; Gentile, G.; Fasano, G. FMCW Radar-Aided Navigation for Unmanned Aircraft Approach and Landing in AAM Scenarios: System Requirements and Processing Pipeline. Sensors 2025, 25, 2429. https://doi.org/10.3390/s25082429
Veneruso P, Manica L, Miccio E, Opromolla R, Tiana C, Gentile G, Fasano G. FMCW Radar-Aided Navigation for Unmanned Aircraft Approach and Landing in AAM Scenarios: System Requirements and Processing Pipeline. Sensors. 2025; 25(8):2429. https://doi.org/10.3390/s25082429
Chicago/Turabian StyleVeneruso, Paolo, Luca Manica, Enrico Miccio, Roberto Opromolla, Carlo Tiana, Giacomo Gentile, and Giancarmine Fasano. 2025. "FMCW Radar-Aided Navigation for Unmanned Aircraft Approach and Landing in AAM Scenarios: System Requirements and Processing Pipeline" Sensors 25, no. 8: 2429. https://doi.org/10.3390/s25082429
APA StyleVeneruso, P., Manica, L., Miccio, E., Opromolla, R., Tiana, C., Gentile, G., & Fasano, G. (2025). FMCW Radar-Aided Navigation for Unmanned Aircraft Approach and Landing in AAM Scenarios: System Requirements and Processing Pipeline. Sensors, 25(8), 2429. https://doi.org/10.3390/s25082429










