Task-Independent Cognitive Workload Discrimination Based on EEG with Stacked Graph Attention Convolutional Networks
Abstract
:1. Introduction
2. Related Works
2.1. Functional Brain Network
2.2. Classification Model Based on Cognitive Workload
3. Materials
3.1. Subjects
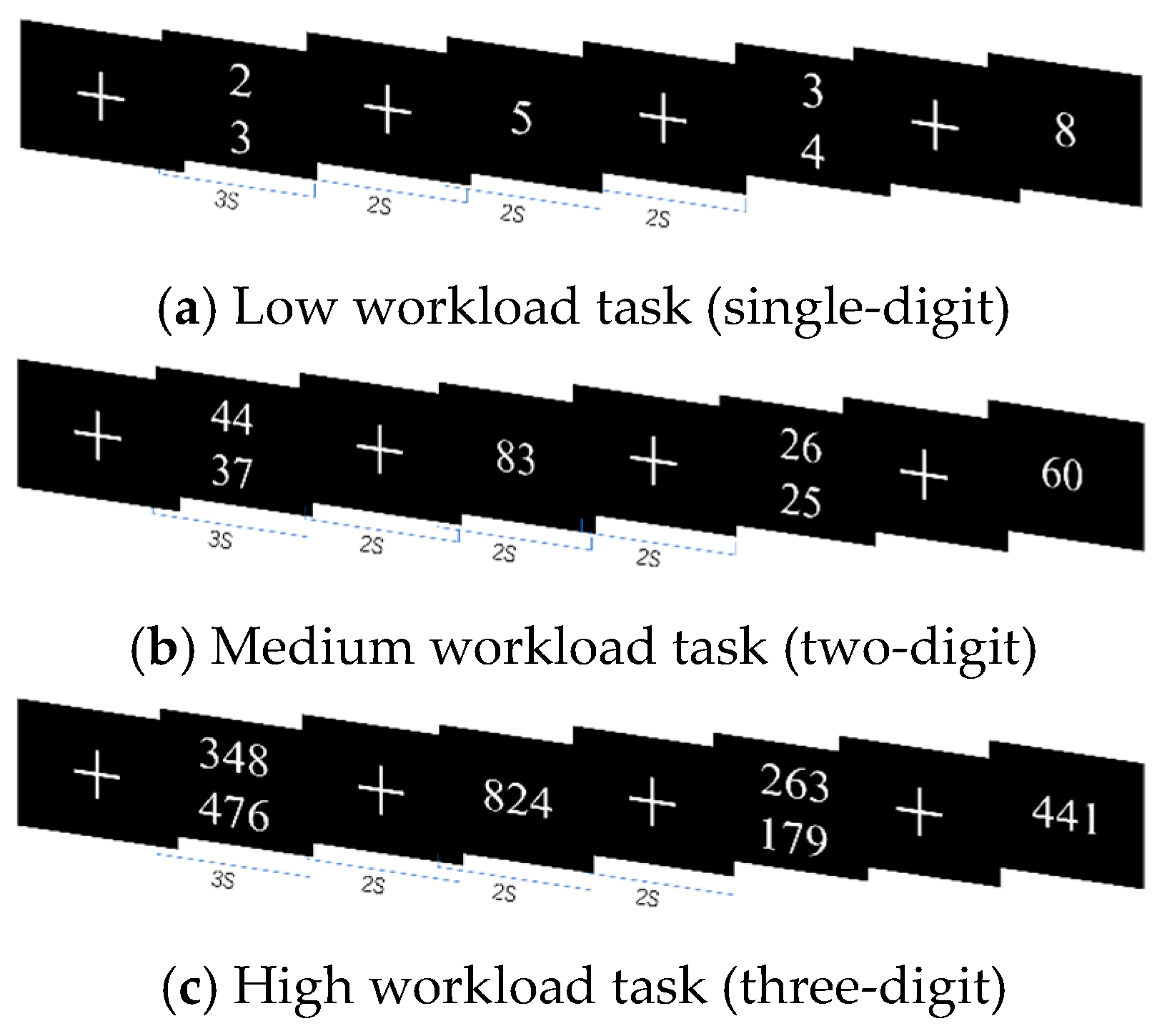
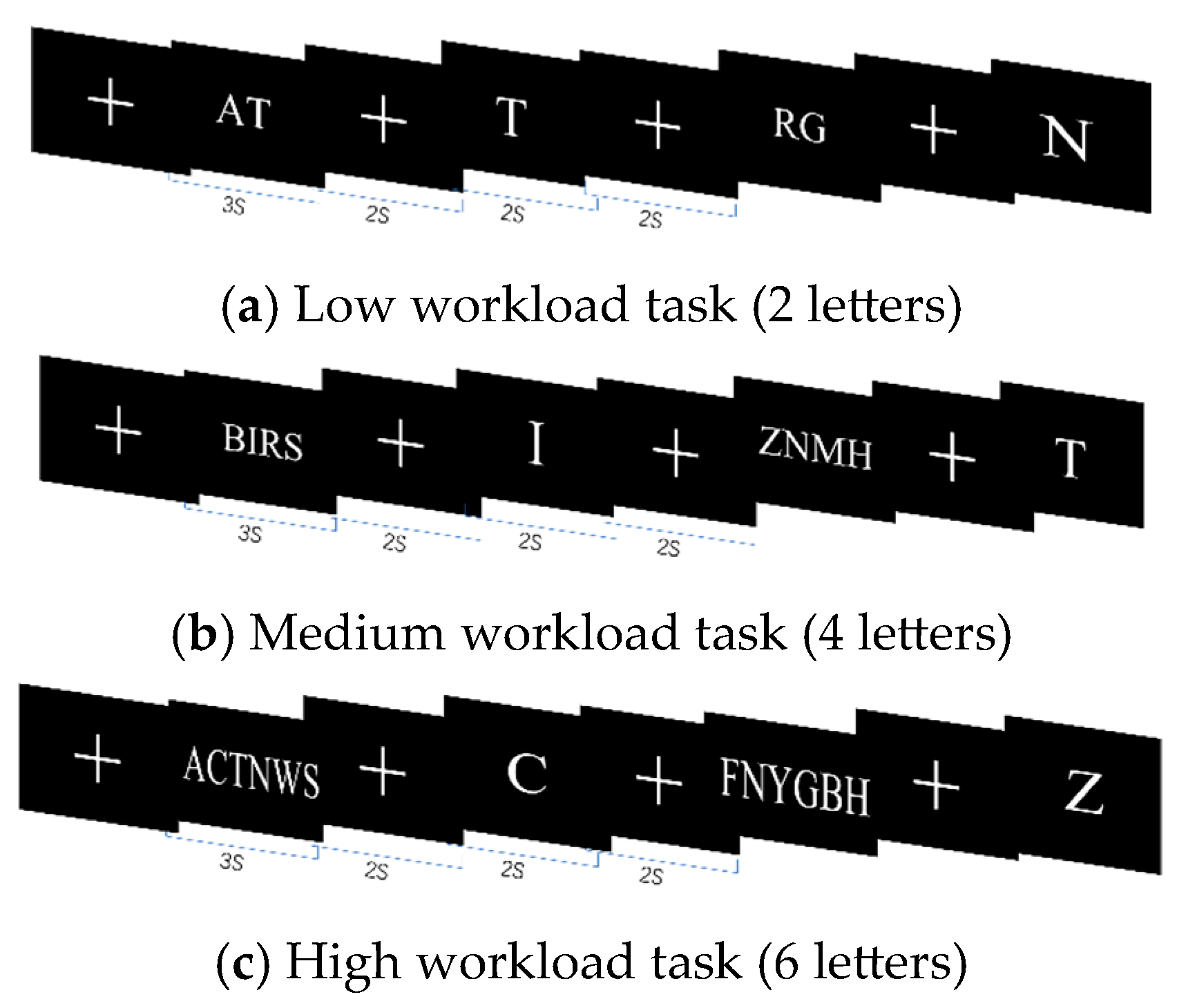
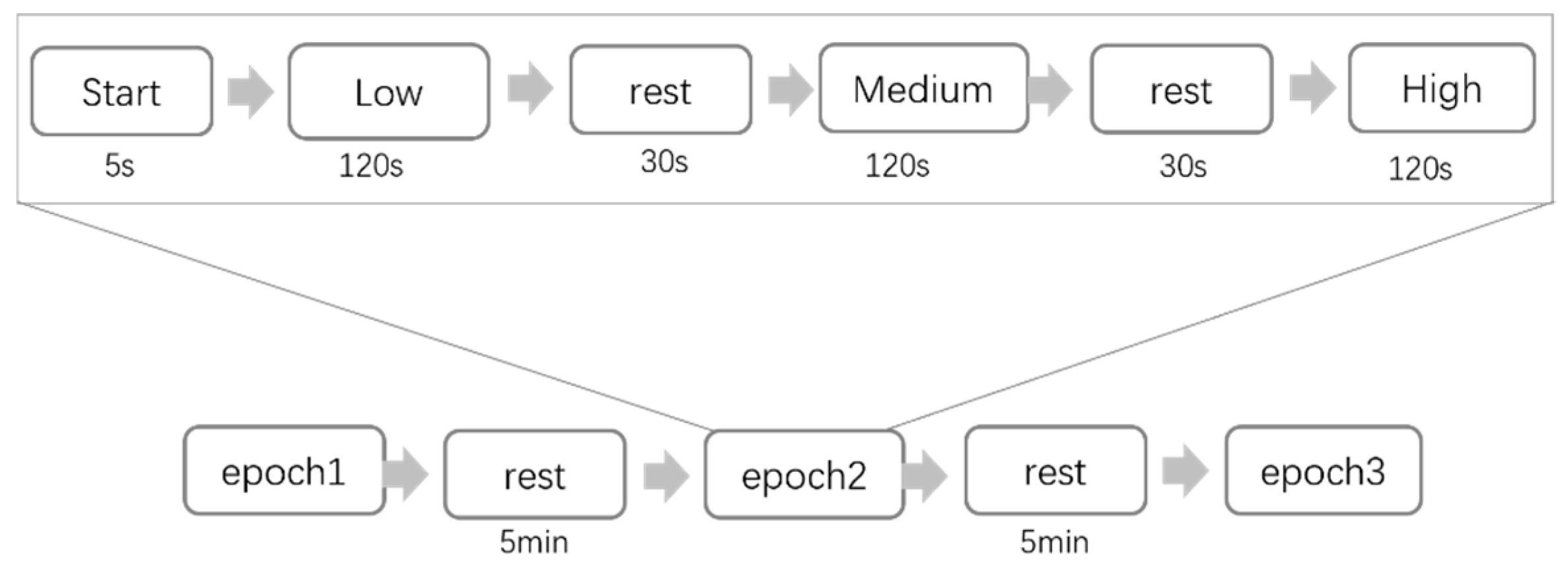
3.2. Experimental Setup
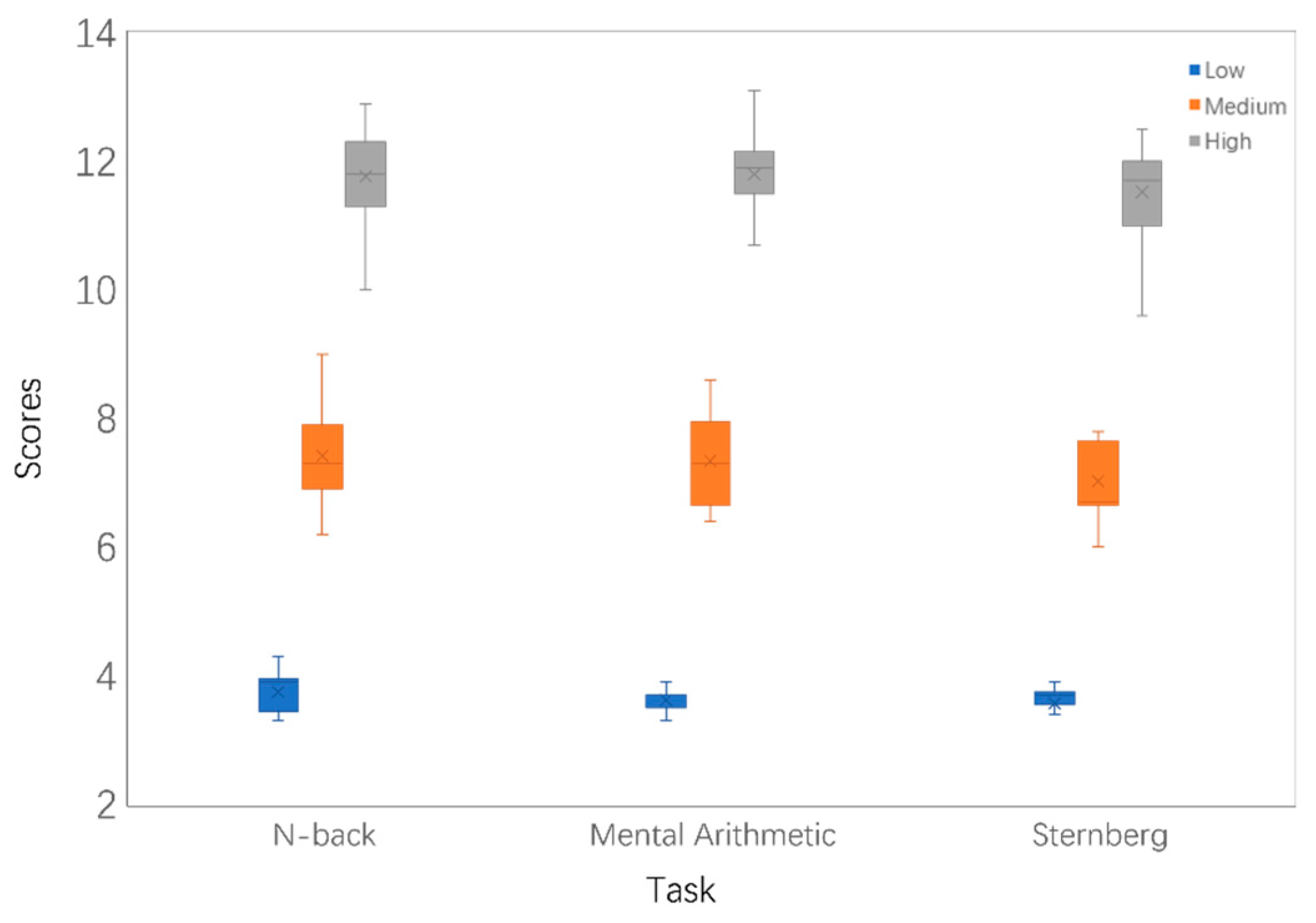
3.3. Feasibility Analysis via the NASA-TLX Workload Scale
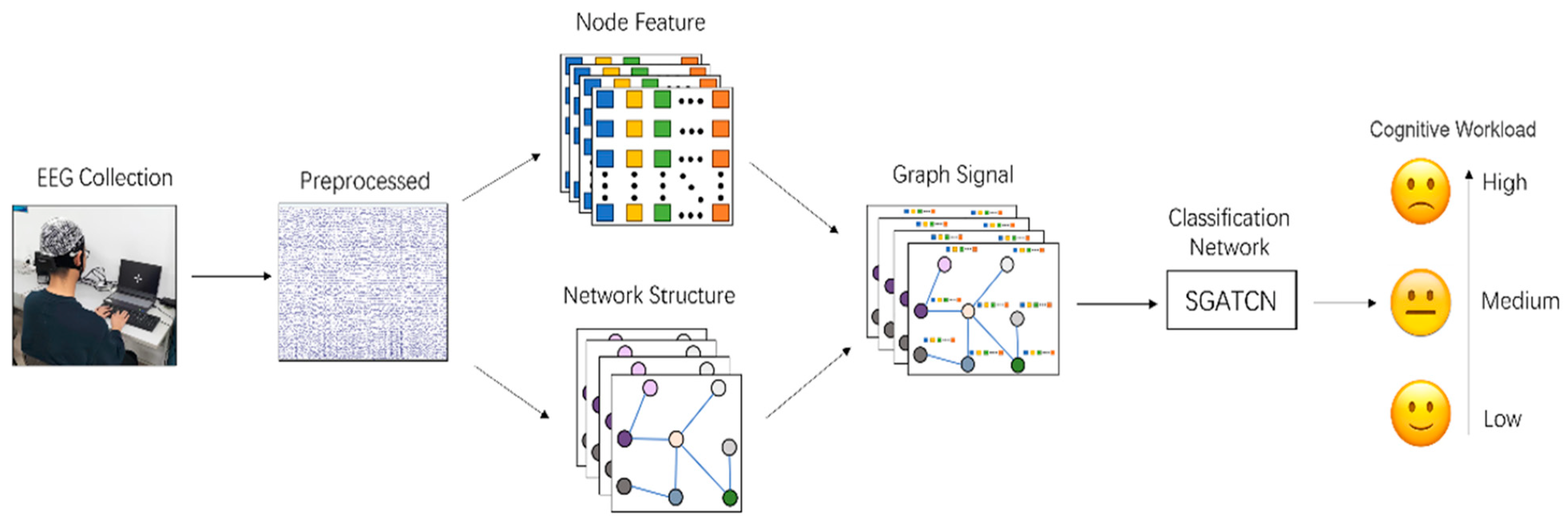
4. Methods
4.1. EEG Preprocessing
4.2. Node Information Extraction
4.3. Functional Brain Network Construction
4.4. Network Topology Parameters
4.5. Stacked Graph Attention Convolutional Networks (SGATCN)
5. Experimental Results
5.1. Task-Independent Cognitive Workload Recognition via Subject-Independent Mapping
5.2. Task-Independent Cognitive Workload Recognition via Subject-Dependent Mapping
6. Discussion
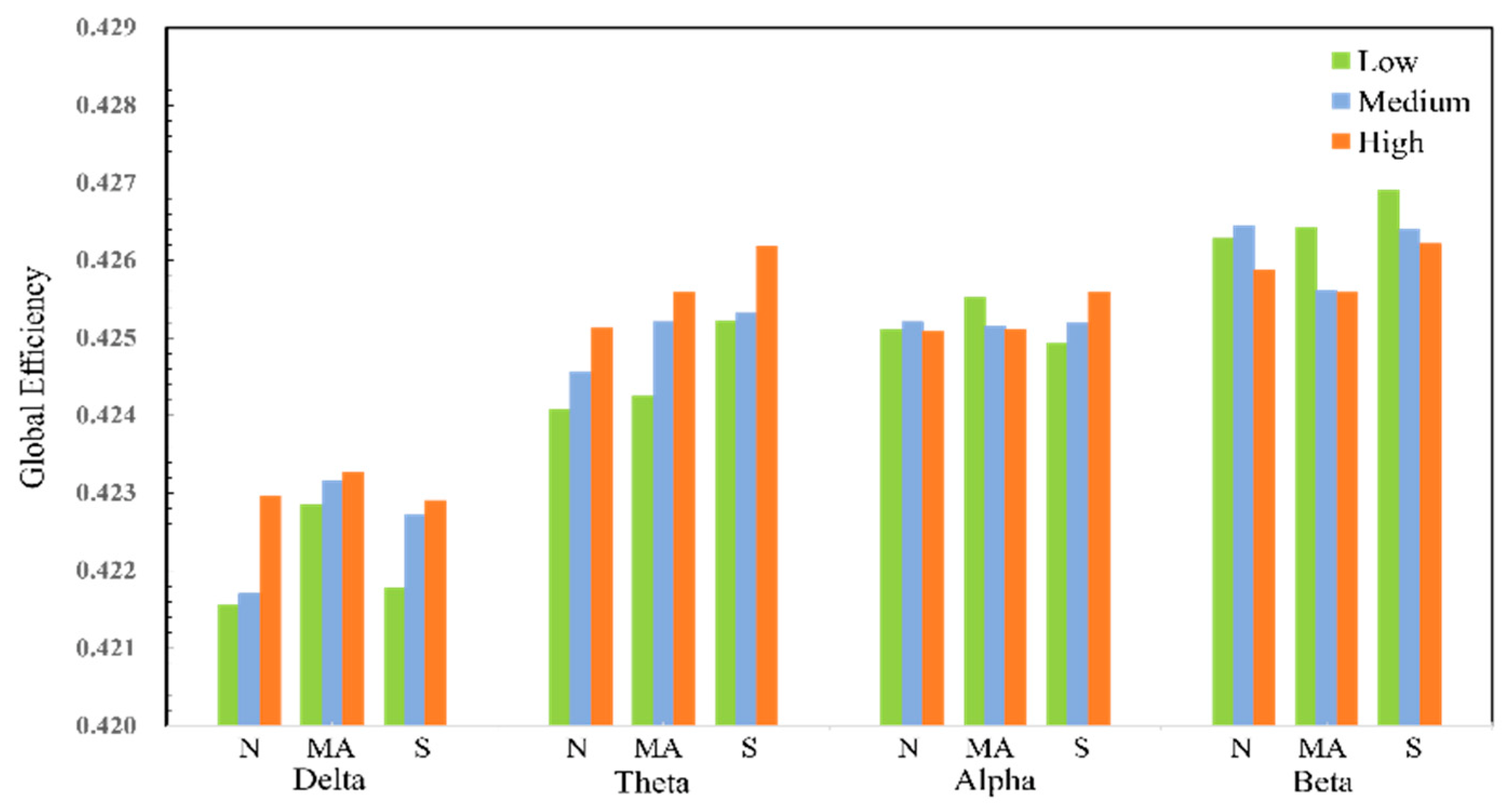
6.1. Network Global Parameter Analysis
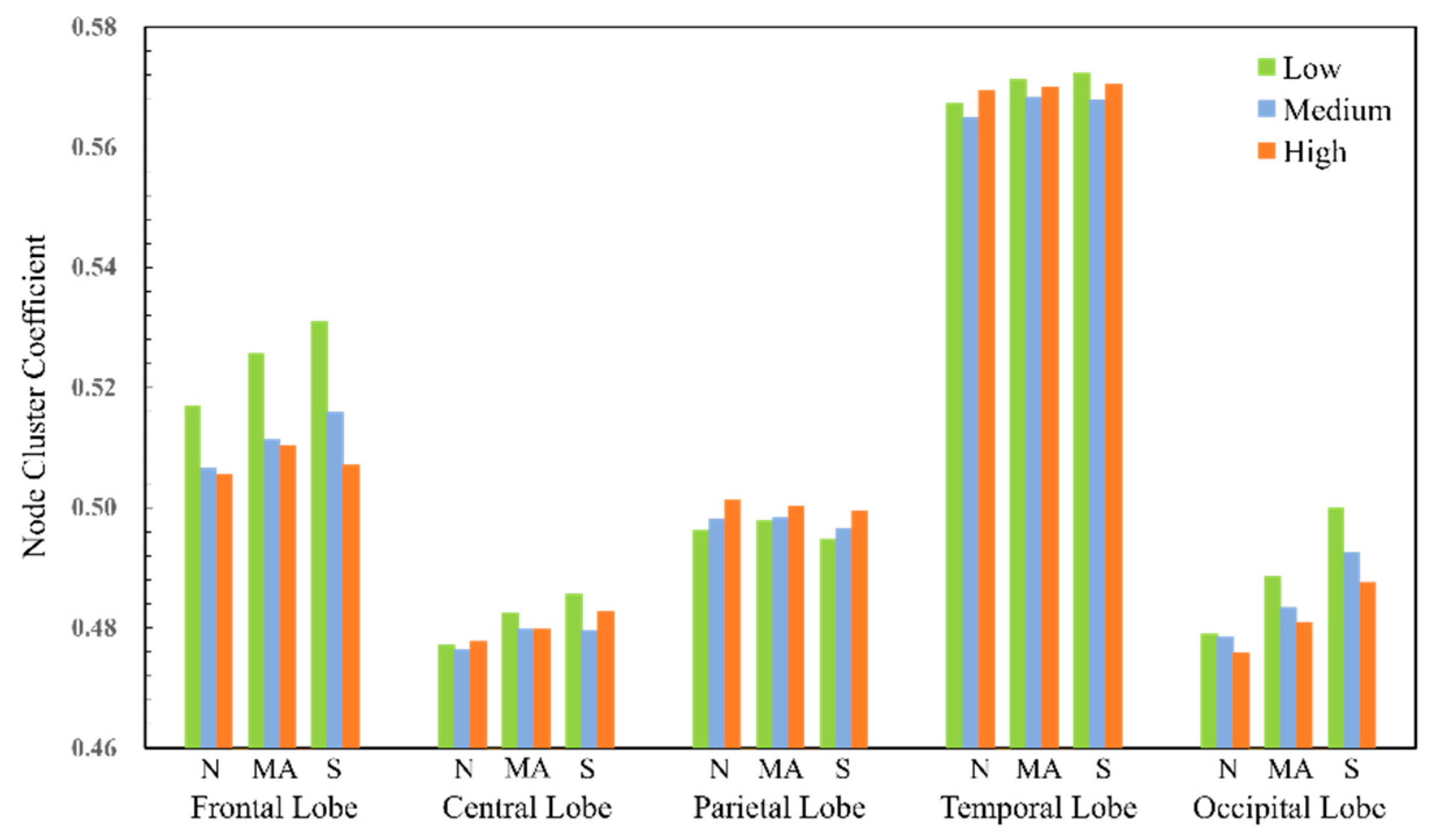
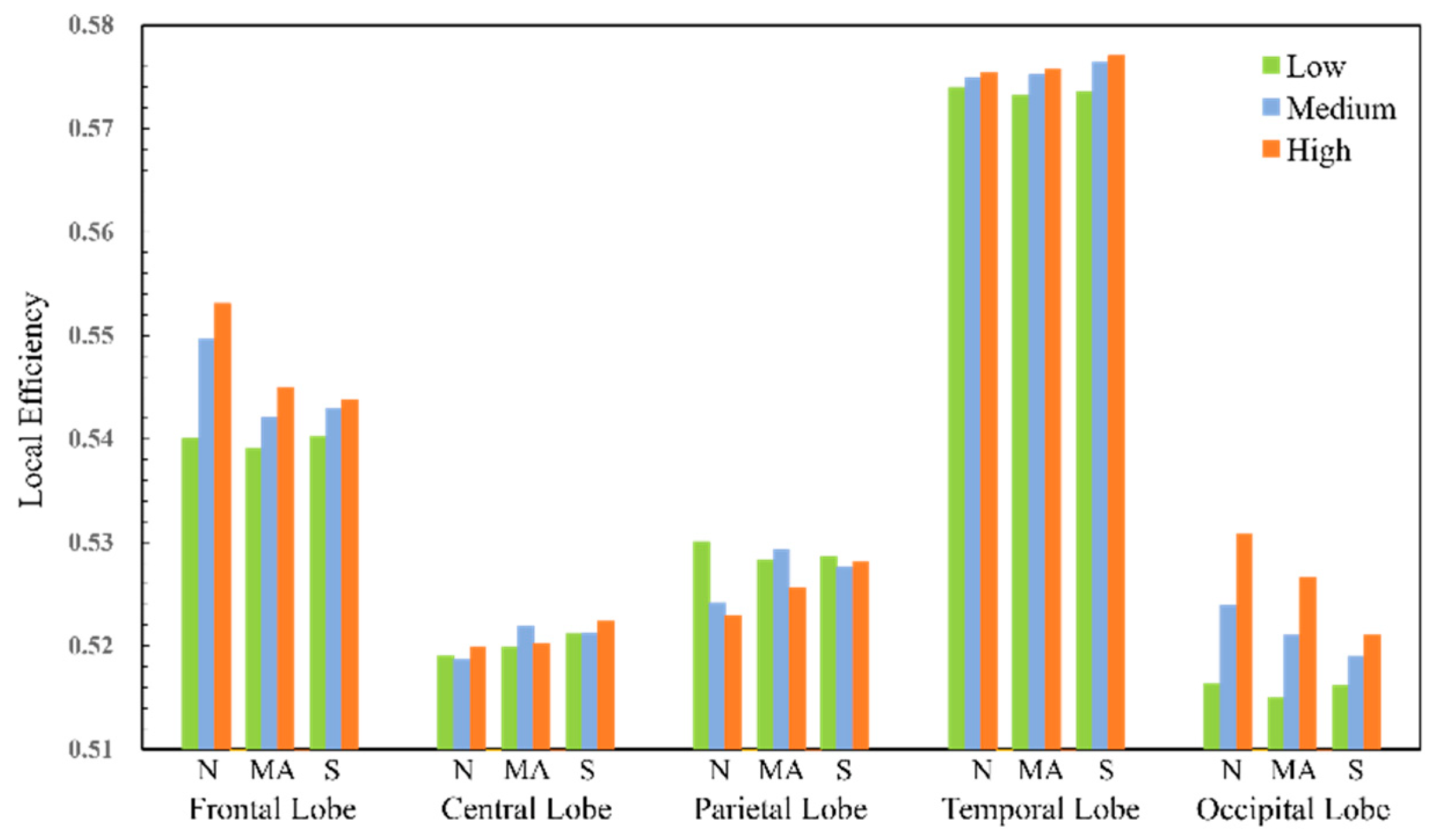
6.2. Network Local Parameter Analysis
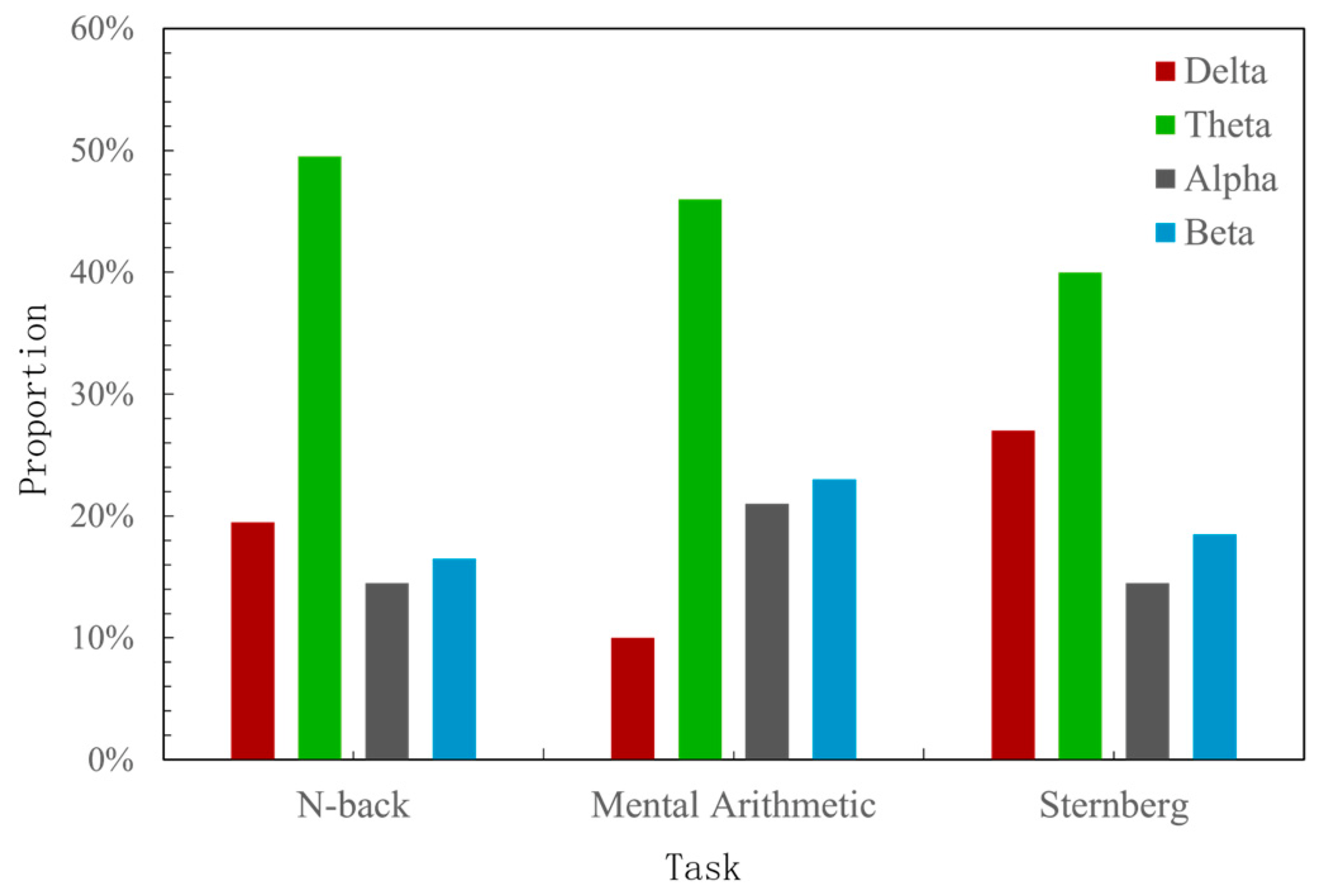
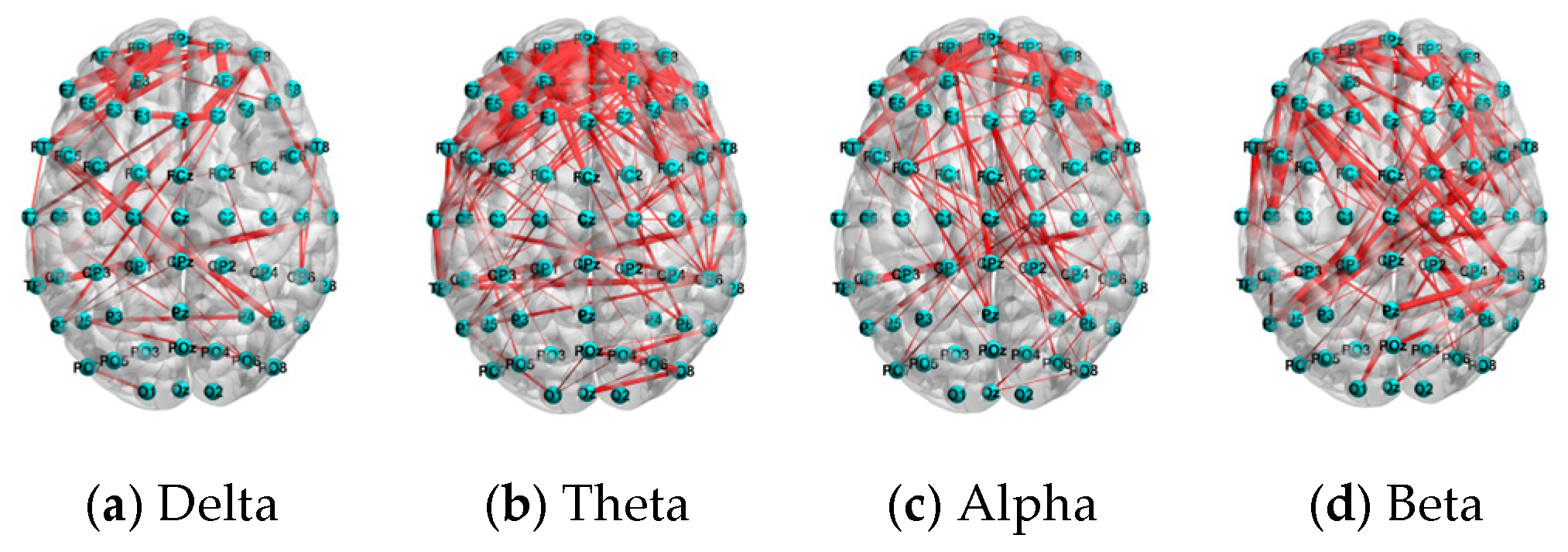
6.3. Performance Comparison by Different Frequency Bands
6.4. Cross-Task Classification Performance Based on COG-BCI Public Dataset via Subject-Dependent Mapping
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sweller, J. Cognitive Load During Problem Solving: Effects on Learning. Cogn. Sci. 1988, 12, 257–285. [Google Scholar] [CrossRef]
- Skulmowski, A. Guidelines for Choosing Cognitive Load Measures in Perceptually Rich Environments. Mind Brain Educ. 2023, 17, 20–28. [Google Scholar] [CrossRef]
- Bagheri, M.; Power, S.D. EEG-based detection of mental workload level and stress: The effect of variation in each state on classification of the other. J. Neural Eng. 2020, 17, 056015. [Google Scholar] [CrossRef]
- Midha, S.; Maior, H.A.; Wilson, M.L.; Sharples, S. Measuring mental workload variations in office work tasks using fNIRS. Int. J. Hum.-Comput. Stud. 2021, 147, 102580. [Google Scholar] [CrossRef]
- Cardone, D.; Perpetuini, D.; Filippini, C.; Mancini, L.; Nocco, S.; Tritto, M.; Rinella, S.; Giacobbe, A.; Fallica, G.; Ricci, F.; et al. Classification of Drivers’ Mental Workload Levels: Comparison of Machine Learning Methods Based on ECG and Infrared Thermal Signals. Sensors 2022, 22, 7300. [Google Scholar] [CrossRef] [PubMed]
- Alrashdan, A.; Ghaleb, A.M.; Alswailem, N.; Alswailem, N.; Almaziad, A.; Al Saud, D. The sensitivity of Galvanic Skin Response and Heart Rate for assessing mental workload in Saudi Arabia. In Proceedings of the IIE Annual Conference, Seattle, WA, USA, 21–24 May 2022; Proceedings. Institute of Industrial and Systems Engineers (IISE): Peachtree Corners, GA, USA, 2022; pp. 1–6. [Google Scholar]
- Ladekar, M.Y.; Gupta, S.S.; Joshi, Y.V.; Manthalkar, R.R. EEG based visual cognitive workload analysis using multirate IIR filters. Biomed. Signal Process. Control 2021, 68, 102819. [Google Scholar] [CrossRef]
- Yang, S.; Yin, Z.; Wang, Y.; Zhang, W.; Wang, Y.; Zhang, J. Assessing cognitive mental workload via EEG signals and an ensemble deep learning classifier based on denoising autoencoders. Comput. Biol. Med. 2019, 109, 159–170. [Google Scholar] [CrossRef]
- Gao, Z.; Dang, W.; Wang, X.; Hong, X.; Hou, L.; Ma, K.; Perc, M. Complex networks and deep learning for EEG signal analysis. Cogn. Neurodyn. 2021, 15, 369–388. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, O.; Hong, Z. ARFN: An attention-based recurrent fuzzy network for EEG mental workload assessment. IEEE Trans. Instrum. Meas. 2024, 73, 1–14. [Google Scholar] [CrossRef]
- Kwak, Y.; Song, W.J.; Min, B.K.; Kim, S.E. 3D CNN based Multilevel Feature Fusion for Workload Estimation. In Proceedings of the 2020 8th International Winter Conference on Brain-Computer Interface (BCI), Gangwon, Republic of Korea, 26–28 February 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar]
- Ramaswamy, A.; Bal, A.; Das, A.; Gubbi, J.; Muralidharan, K.; Ramakrishnan, R.K.; Pal, A. Single feature spatio-temporal architecture for EEG Based cognitive load assessment. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Virtual, 1–5 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 3717–3720. [Google Scholar]
- Suárez, L.E.; Markello, R.D.; Betzel, R.F.; Misic, B. Linking structure and function in macroscale brain networks. Trends Cogn. Sci. 2020, 24, 302–315. [Google Scholar] [CrossRef]
- Naseri, N.; Parastesh, F.; Ghassemi, F.; Jafari, M.; Perc, M.; Završnik, J. Synchronization levels in EEG connectivity during cognitive workloads while driving. Nonlinear Dyn. 2025, 113, 7243–7258. [Google Scholar] [CrossRef]
- Guan, K.; Zhang, Z.; Chai, X.; Tian, Z.; Liu, T.; Niu, H. EEG based dynamic functional connectivity analysis in mental workload tasks with different types of information. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 632–642. [Google Scholar] [CrossRef] [PubMed]
- Ji, Z.; Tang, J.; Wang, Q.; Xie, X.; Liu, J.; Yin, Z. Cross-task cognitive workload recognition using a dynamic residual network with attention mechanism based on neurophysiological signals. Comput. Methods Programs Biomed. 2023, 230, 107352. [Google Scholar] [CrossRef] [PubMed]
- Dimitrakopoulos, G.N.; Kakkos, I.; Anastasiou, A.; Bezerianos, A.; Sun, Y.; Matsopoulos, G.K. Cognitive Reorganization Due to Mental Workload: A Functional Connectivity Analysis Based on Working Memory Paradigms. Appl. Sci. 2023, 13, 2129. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, Z.; Niu, Y.; Wang, P.; Wen, X.; Wu, X. Cross-task cognitive workload recognition based on EEG and domain adaptation. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 50–60. [Google Scholar] [CrossRef]
- Gupta, A.; Siddhad, G.; Pandey, V.; Roy, P.P.; Kim, B.G. Subject-specific cognitive workload classification using EEG-based functional connectivity and deep learning. Sensors 2021, 21, 6710. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Z.; Qu, H.; Liu, C.; Pang, L. A Mental Workload Classification Method Based on GCN Modified by Squeeze-and-Excitation Residual. Mathematics 2023, 11, 1189. [Google Scholar] [CrossRef]
- Alam, R.; Zhao, H.; Goodwin, A.; Kavehei, O.; McEwan, A. Differences in power spectral densities and phase quantities due to processing of eeg signals. Sensors 2020, 20, 6285. [Google Scholar] [CrossRef]
- Erdelić, T.; Carić, T. A survey on the electric vehicle routing problem: Variants and solution approaches. J. Adv. Transp. 2019, 2019, 5075671. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 2010, 52, 1059–1069. [Google Scholar] [CrossRef]
- Liu, X.; Li, T.; Tang, C.; Xu, T.; Chen, P.; Bezerianos, A.; Wang, H. Emotion recognition and dynamic functional connectivity analysis based on EEG. IEEE Access 2019, 7, 143293–143302. [Google Scholar] [CrossRef]
- Demuru, M.; La Cava, S.M.; Pani, S.M.; Fraschini, M. A comparison between power spectral density and network metrics: An EEG study. Biomed. Signal Process. Control 2020, 57, 101760. [Google Scholar] [CrossRef]
- Kılıç, B.; Aydın, S. Classification of contrasting discrete emotional states indicated by EEG based graph theoretical network measures. Neuroinformatics 2022, 20, 863–877. [Google Scholar] [CrossRef] [PubMed]
- Veličković, P. Everything is connected: Graph neural networks. Curr. Opin. Struct. Biol. 2023, 79, 102538. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: A comprehensive review. Comput. Soc. Netw. 2019, 6, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Cheema, B.S.; Samima, S.; Sarma, M.; Samanta, D. Mental workload estimation from EEG signals using machine learning algorithms. In Proceedings of the Engineering Psychology and Cognitive Ergonomics: 15th International Conference, EPCE 2018, Held as Part of HCI International 2018, Las Vegas, NV, USA, 15–20 July 2018; Proceedings 15. Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 265–284. [Google Scholar]
- Pandey, V.; Choudhary, D.K.; Verma, V.; Sharma, G.; Singh, R.; Chandra, S. Mental workload estimation using EEG. In Proceedings of the 2020 Fifth International Conference on Research in Computational Intelligence and Communication Networks (ICRCICN), Bangalore, India, 26–27 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 83–86. [Google Scholar]
- Khan, M.A.; Asadi, H.; Hoang, T.; Lim, C.P. Measuring Cognitive Load: Leveraging fNIRS and Machine Learning for Classification of Workload Levels. In Proceedings of the International Conference on Neural Information Processing, Changsha, China, 20–23 November 2023; Springer Nature: Singapore, 2023; pp. 313–325. [Google Scholar]
- Raufi, B.; Longo, L. An Evaluation of the EEG alpha-to-theta and theta-to-alpha band Ratios as Indexes of Mental Workload. Front. Neuroinform. 2022, 16, 44. [Google Scholar] [CrossRef]
- Baldwin, C.L.; Penaranda, B.N. Adaptive Training Using an Artificial Neural Network and EEG Metrics for Within- and Cross-Task Workload Classification. Neuroimage 2012, 59, 48–56. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, X.; Zhang, W.; Chen, J. Learning Spatial–Spectral–Temporal EEG Features with Recurrent 3D Convolutional Neural Networks for Cross-Task Mental Workload Assessment. IEEE Trans. Neural Syst. Rehabil. Eng. (TNSRE) 2019, 27, 31–42. [Google Scholar] [CrossRef]
- Dimitrakopoulos, G.N.; Kakkos, I.; Dai, Z.; Lim, J.; Desouza, J.J.; Bezerianos, A.; Sun, Y. Task-Independent Mental Workload Classification Based Upon Common Multiband EEG Cortical Connectivity. IEEE Trans. Neural Syst. Rehabil. Eng. (TNSRE) 2017, 25, 1940–1949. [Google Scholar] [CrossRef]
- Ke, Y.; Qi, H.; Zhang, L.; Chen, S.; Jiao, X.; Zhou, P.; Zhao, X.; Wan, B.; Ming, D. Towards an Effective Cross-task Mental Workload Recognition Model Using Electroencephalography Based on Feature Selection and Support Vector Machine Regression. Int. J. Psychophysiol. 2015, 98, 157–166. [Google Scholar] [CrossRef]
- Guan, K.; Zhang, Z.; Liu, T.; Niu, H. Cross-Task Mental Workload Recognition Based on EEG Tensor Representation and Transfer Learning. IEEE Trans. Neural Syst. Rehabil. Eng. (TNSRE) 2023, 31, 2632–2639. [Google Scholar] [CrossRef] [PubMed]







| Classifier | Parameter | |
|---|---|---|
| 1 | SGATCN | Epoch = 800, Learning rate: 0.001, batch_size = 30 |
| 2 | GAT | Epoch = 500, Learning rate: 0.005, batch_size = 50 |
| 3 | GCN | Epoch = 500, Learning rate: 0.01, batch_size = 50 |
| 4 | SVM | C = 0.5 |
| 5 | RF | n_estimators = 20, max_depth = 10 |
| 6 | KNN | K = 15 |
| 7 | LR | C = 0.5, max_iter = 1000 |
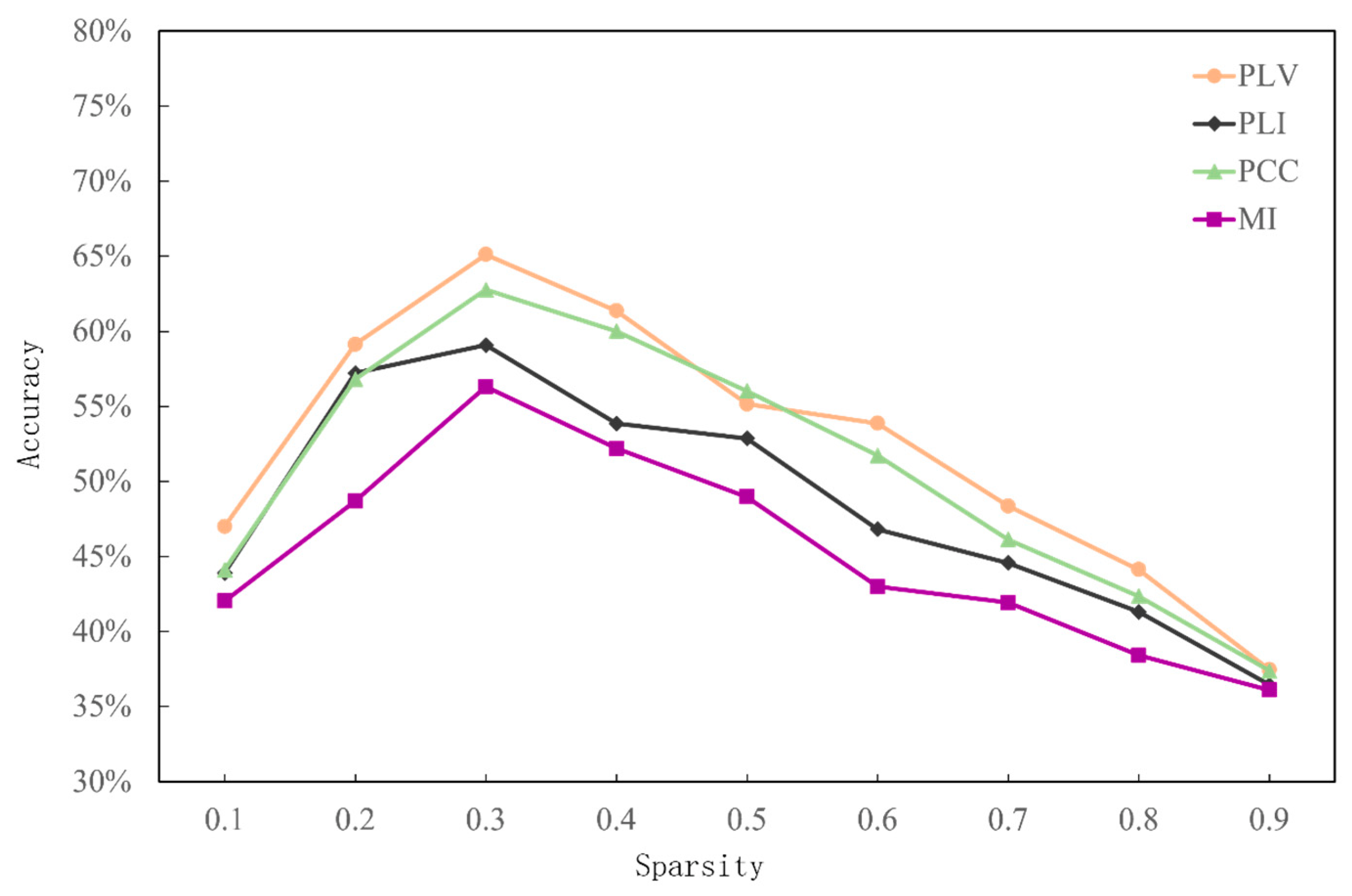
| Sparsity | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| PLV | N | 47.52 | 60.23 | 66.12 | 62.33 | 56.63 | 54.98 | 49.25 | 45.12 | 39.21 |
| MA | 46.59 | 59.35 | 64.88 | 61.22 | 55.67 | 54.43 | 47.51 | 43.15 | 36.05 | |
| S | 46.92 | 57.86 | 64.35 | 60.54 | 53.21 | 52.21 | 48.35 | 44.12 | 37.15 | |
| PLI | N | 44.53 | 57.98 | 59.62 | 54.31 | 53.71 | 46.83 | 45.01 | 41.68 | 36.9 |
| MA | 43.64 | 57.44 | 58.84 | 54.11 | 52.72 | 47.53 | 44.52 | 41.96 | 36.68 | |
| S | 43.32 | 56.82 | 62.12 | 60.13 | 55.72 | 51.44 | 45.09 | 41.86 | 36.77 | |
| PCC | N | 44.71 | 57.42 | 63.34 | 60.72 | 56.46 | 51.98 | 46.55 | 43.06 | 37.96 |
| MA | 44.32 | 56.18 | 62.86 | 59.18 | 55.87 | 51.76 | 46.77 | 42.15 | 37.42 | |
| S | 43.55 | 56.23 | 58.76 | 53.12 | 52.17 | 46.07 | 44.18 | 40.28 | 35.74 | |
| MI | N | 43.08 | 49.39 | 56.79 | 53.01 | 49.52 | 42.18 | 42.6 | 39.81 | 36.81 |
| MA | 41.86 | 48.56 | 56.31 | 52.36 | 48.73 | 43.16 | 42.12 | 37.56 | 35.56 | |
| S | 41.17 | 48.1 | 55.83 | 51.22 | 48.66 | 43.62 | 41.08 | 37.91 | 35.91 | |
| Classifier | Accuracy | Precision | F1 Scores | |
|---|---|---|---|---|
| 1 | SGATCN | 65.11 | 65.07 | 65.28 |
| 2 | GCN | 56.46 | 56.31 | 55.36 |
| 3 | GAT | 57.44 | 56.94 | 56.89 |
| 4 | SVM | 52.12 | 51.74 | 51.08 |
| 5 | RF | 48.85 | 49.82 | 47.73 |
| 6 | KNN | 45.89 | 46.26 | 45.45 |
| 7 | LR | 47.61 | 46.92 | 46.47 |
| Network Global Parameters | Task | Delta | Theta | Alpha | Beta |
|---|---|---|---|---|---|
| Small-world properties | N | 12.11 (<0.001) | 20.727 (<0.001) | 1.699 (0.182) | 1.534 (<0.001) |
| MA | 6.31 (0.001) | 9.994 (<0.001) | 3.277 (0.037) | 2.355 (0.094) | |
| S | 4.28 (0.013) | 8.477 (<0.001) | 13.29 (<0.001) | 7.078 (<0.001) | |
| Global efficiency | N | 11.354 (<0.001) | 20.216 (<0.001) | 0.782 (0.481) | 0.985 (0.373) |
| MA | 2.951 (0.06) | 38.731 (<0.001) | 3.468 (0.031) | 6.854 (<0.001) | |
| S | 7.161 (<0.001) | 14.596 (<0.001) | 7.781 (<0.001) | 8.851 (<0.001) |
| Feature | Task | Delta | Theta | Alpha | Beta |
|---|---|---|---|---|---|
| Node clustering coefficient | N | 45.76% | 57.63% | 32.20% | 38.98% |
| MA | 40.68% | 54.24% | 18.64% | 35.59% | |
| S | 28.81% | 62.71% | 40.68% | 42.31% | |
| local efficiency | N | 42.37% | 64.41% | 27.12% | 37.29% |
| MA | 32.20% | 42.98% | 16.95% | 27.12% | |
| S | 23.73% | 57.63% | 27.12% | 35.59% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, C.; Zhao, X.; Song, Y.; Liu, Y. Task-Independent Cognitive Workload Discrimination Based on EEG with Stacked Graph Attention Convolutional Networks. Sensors 2025, 25, 2390. https://doi.org/10.3390/s25082390
Wei C, Zhao X, Song Y, Liu Y. Task-Independent Cognitive Workload Discrimination Based on EEG with Stacked Graph Attention Convolutional Networks. Sensors. 2025; 25(8):2390. https://doi.org/10.3390/s25082390
Chicago/Turabian StyleWei, Chenyu, Xuewen Zhao, Yu Song, and Yi Liu. 2025. "Task-Independent Cognitive Workload Discrimination Based on EEG with Stacked Graph Attention Convolutional Networks" Sensors 25, no. 8: 2390. https://doi.org/10.3390/s25082390
APA StyleWei, C., Zhao, X., Song, Y., & Liu, Y. (2025). Task-Independent Cognitive Workload Discrimination Based on EEG with Stacked Graph Attention Convolutional Networks. Sensors, 25(8), 2390. https://doi.org/10.3390/s25082390







