Uncertainty Analysis of Fiber Optic Shape Sensing Under Core Failure
Abstract
1. Introduction
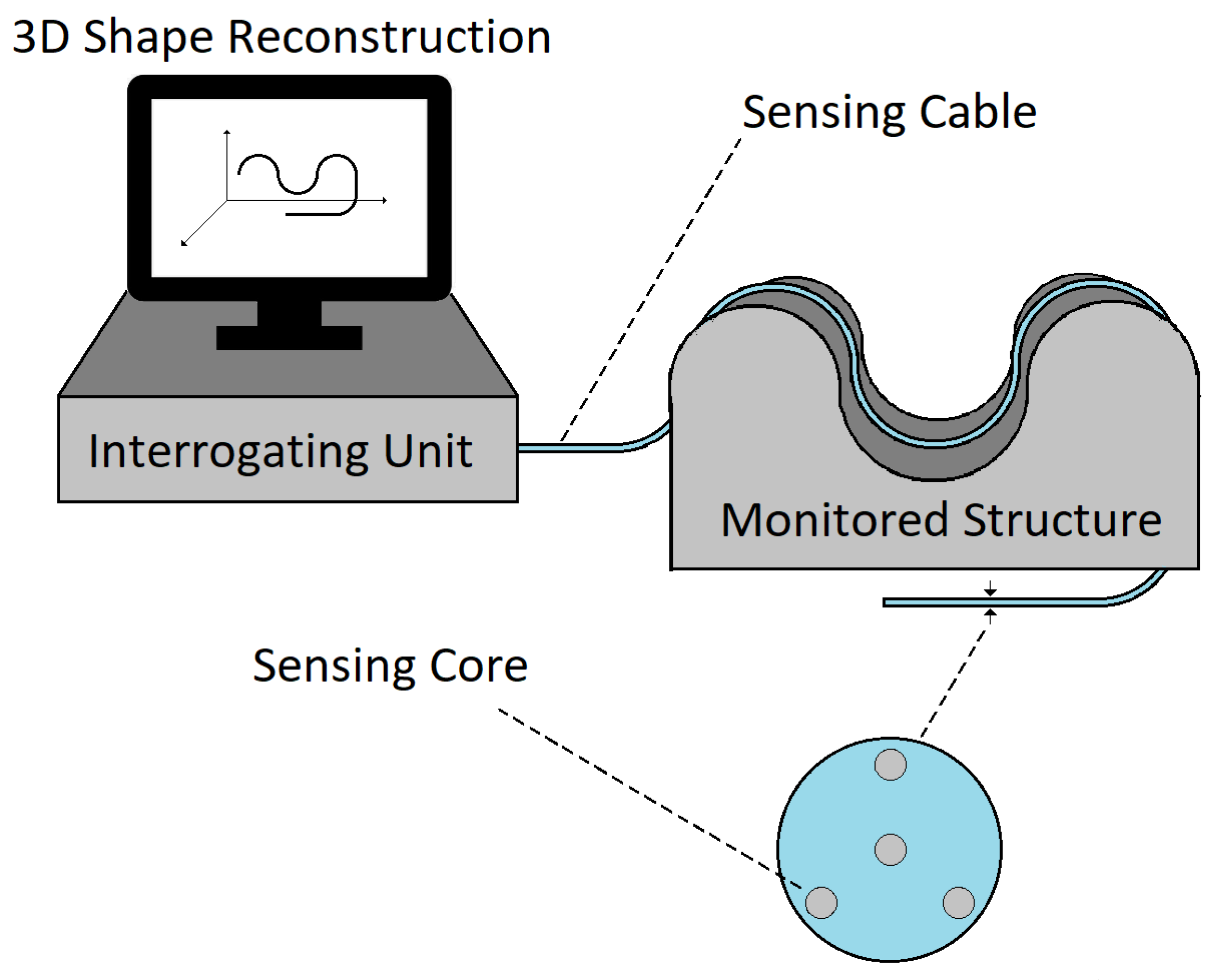
2. Materials and Methods
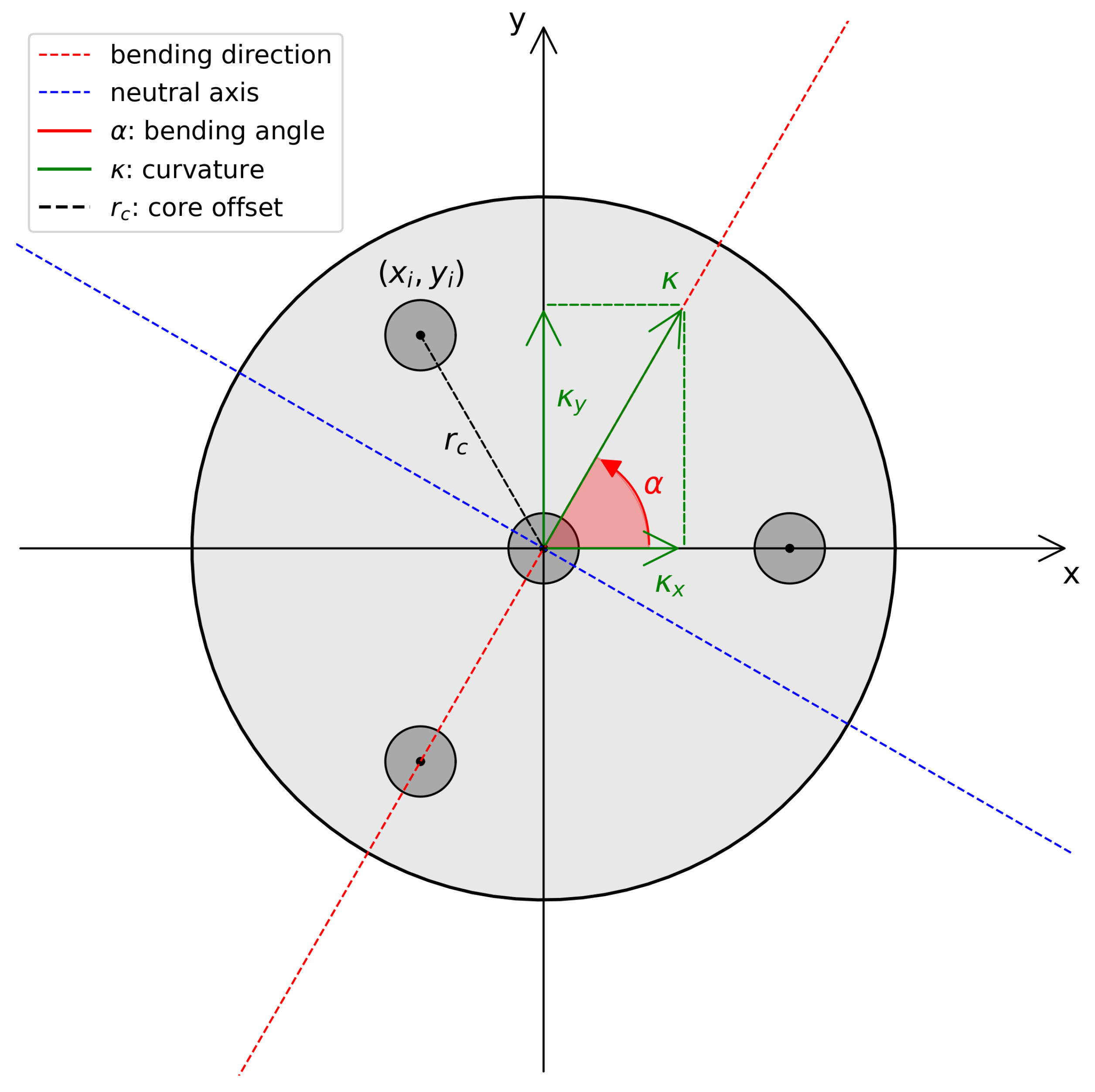
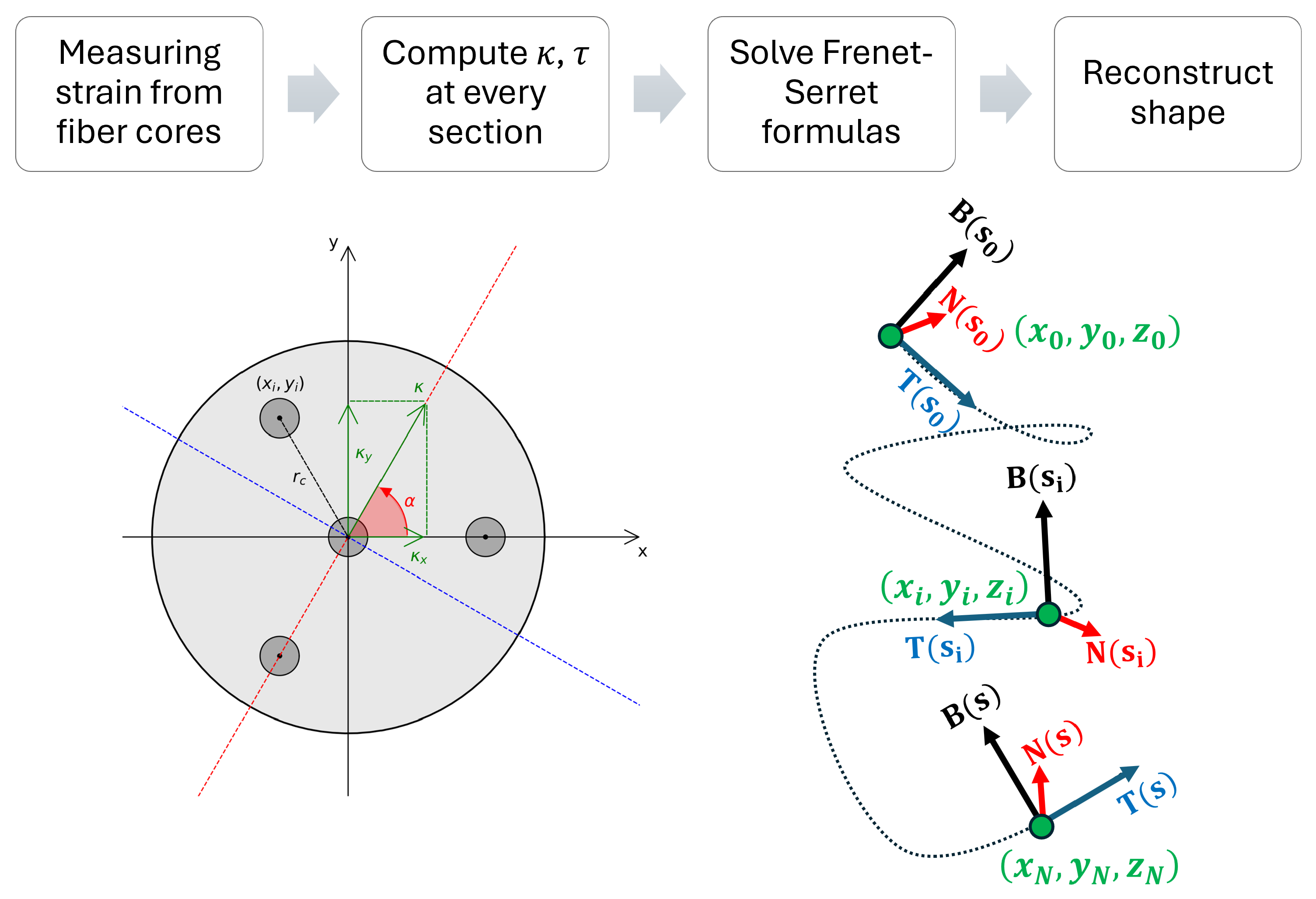
2.1. Shape Sensing Theory
2.2. Core Failure Compensation
2.3. Design of Simulations
2.3.1. Single-Sensing-Point Simulations
2.3.2. Full 3D Reconstruction Simulations
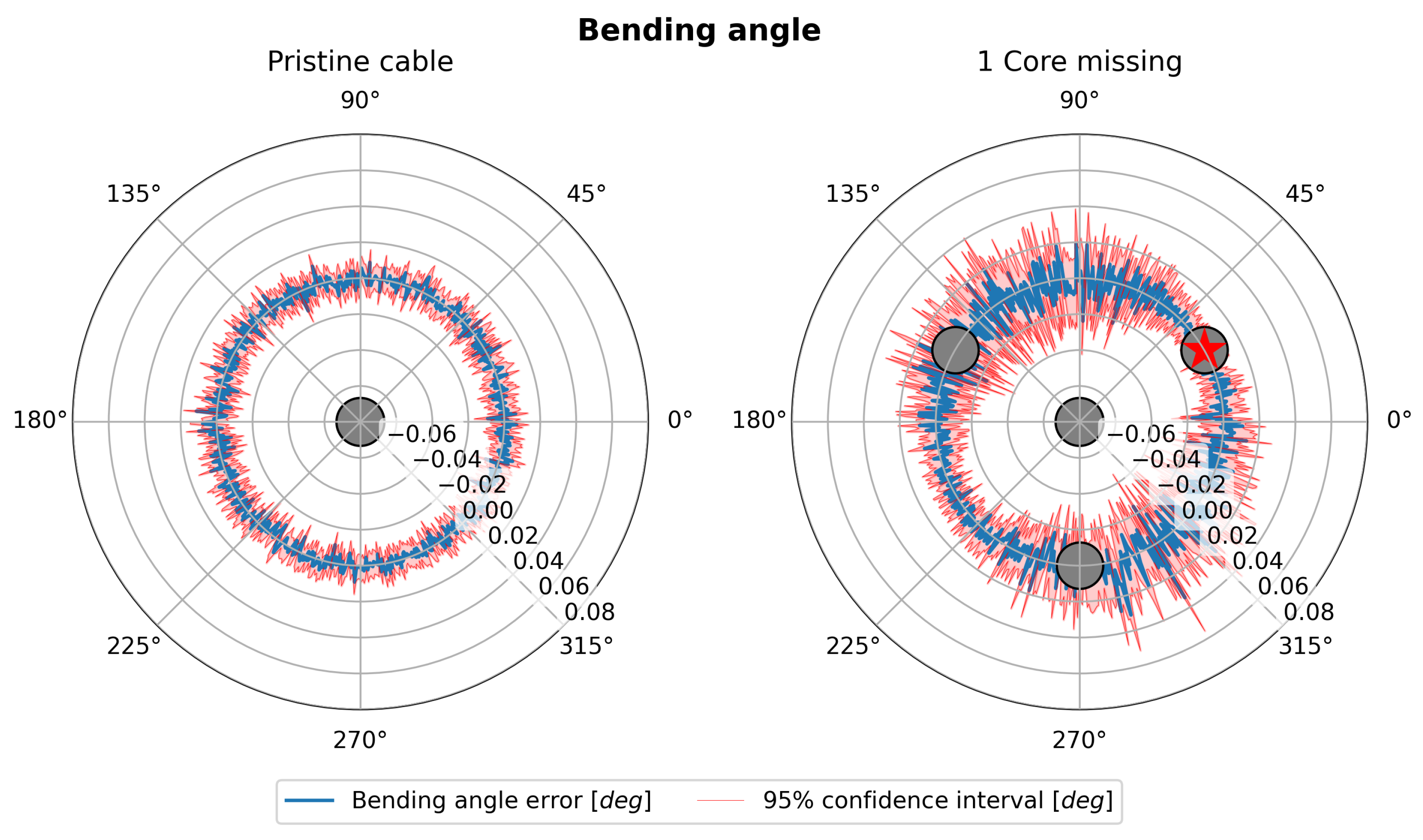
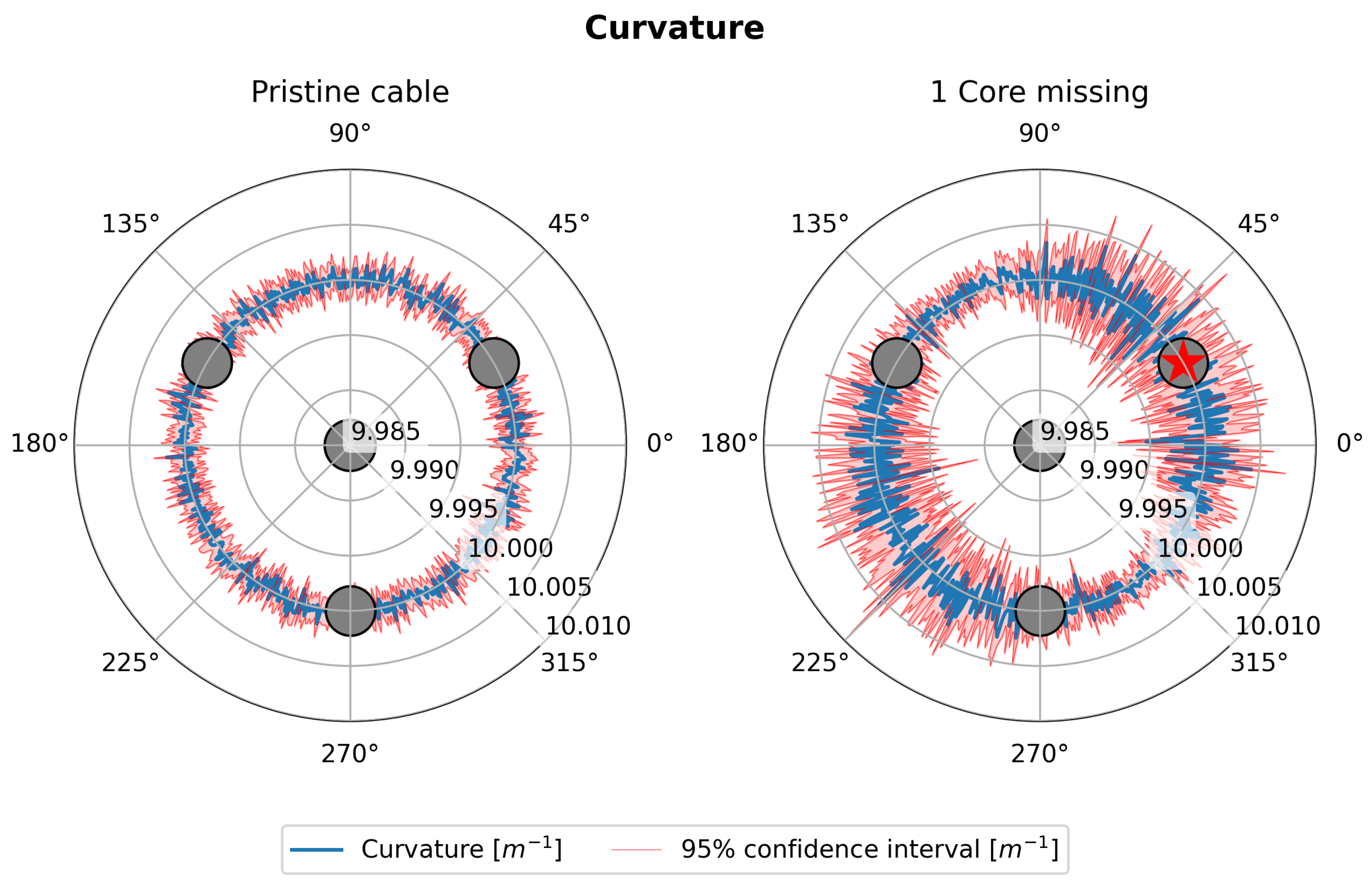
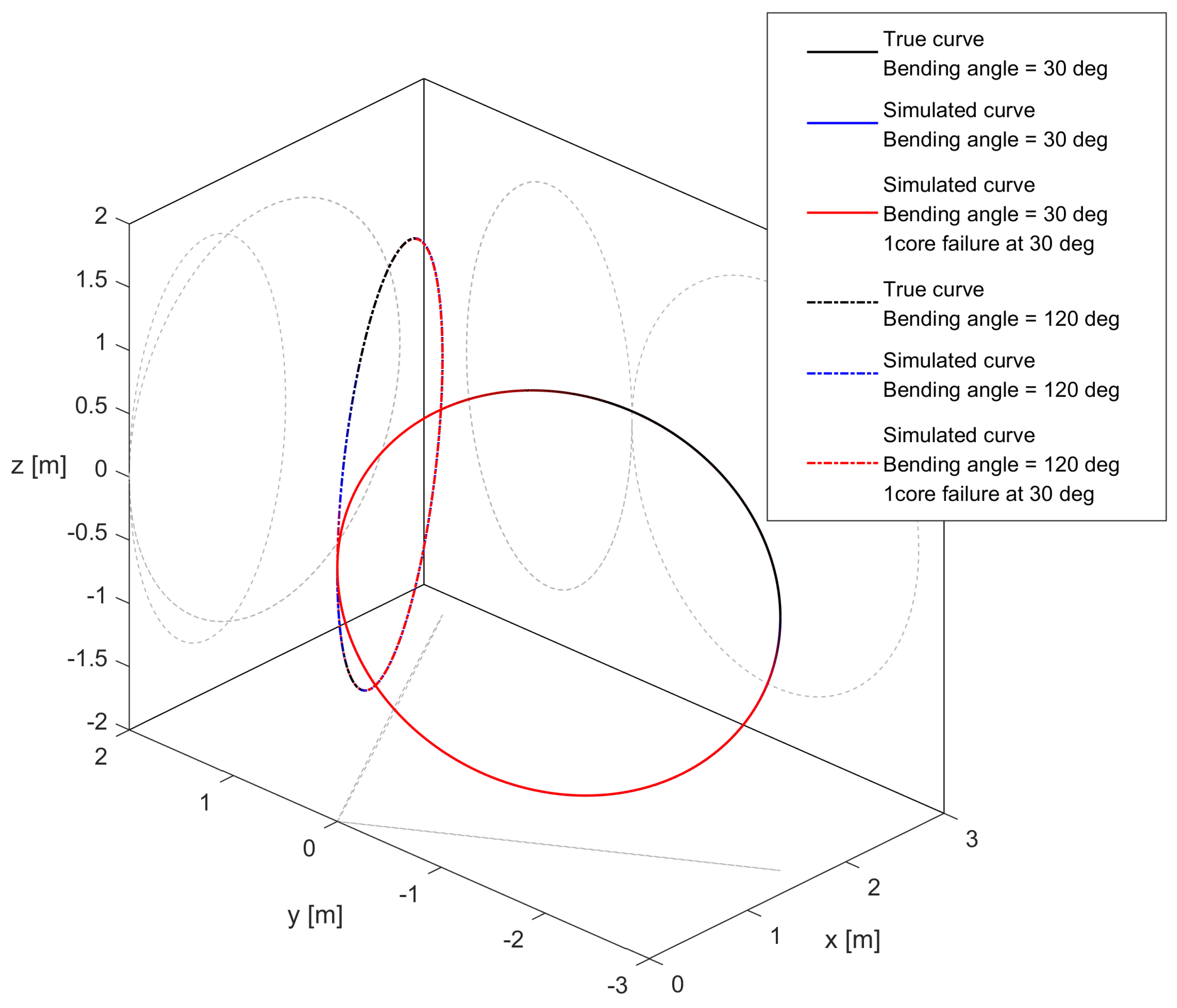
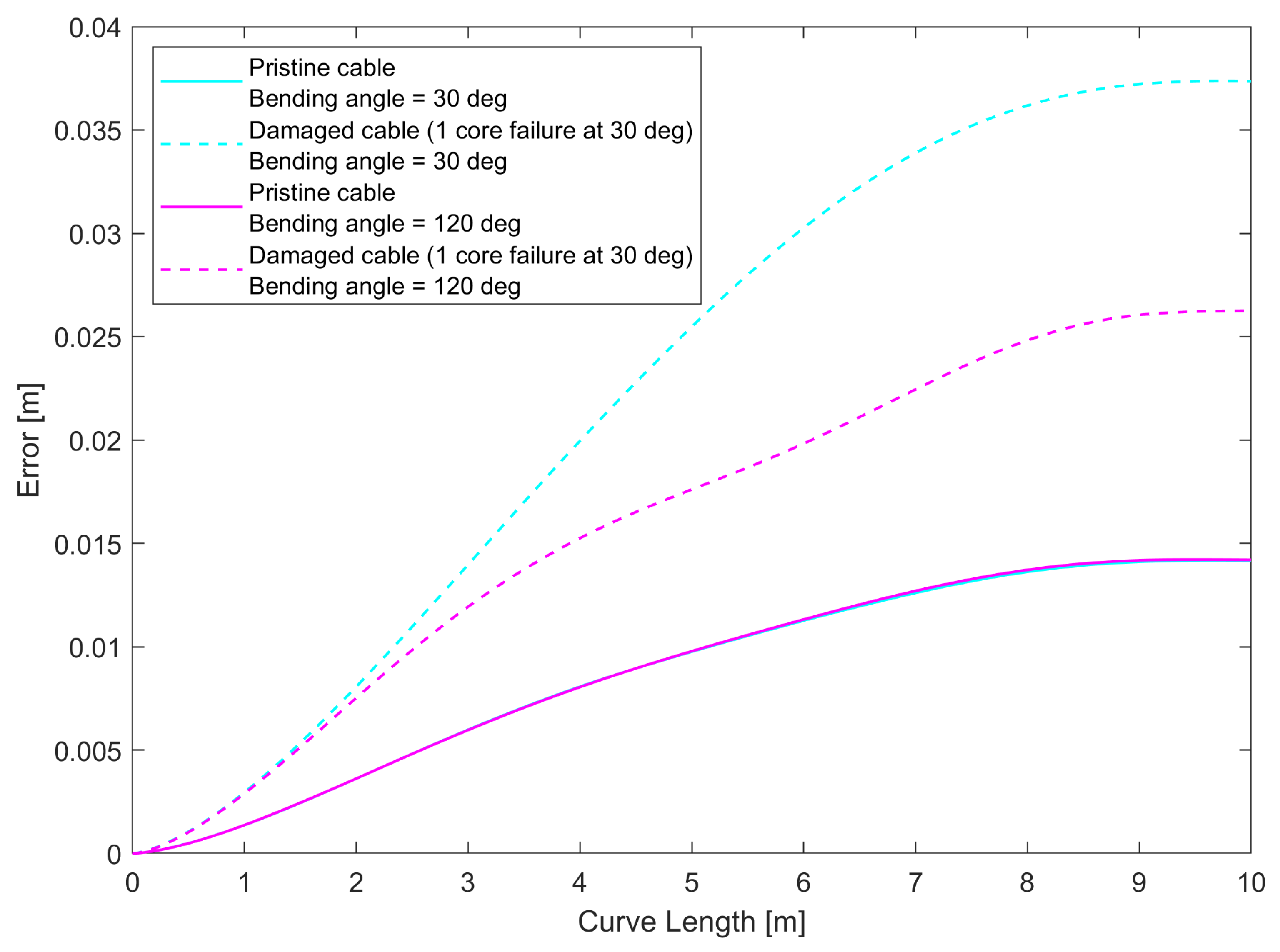
2.3.3. Core Failure Effect on Measurement Symmetry
3. Results
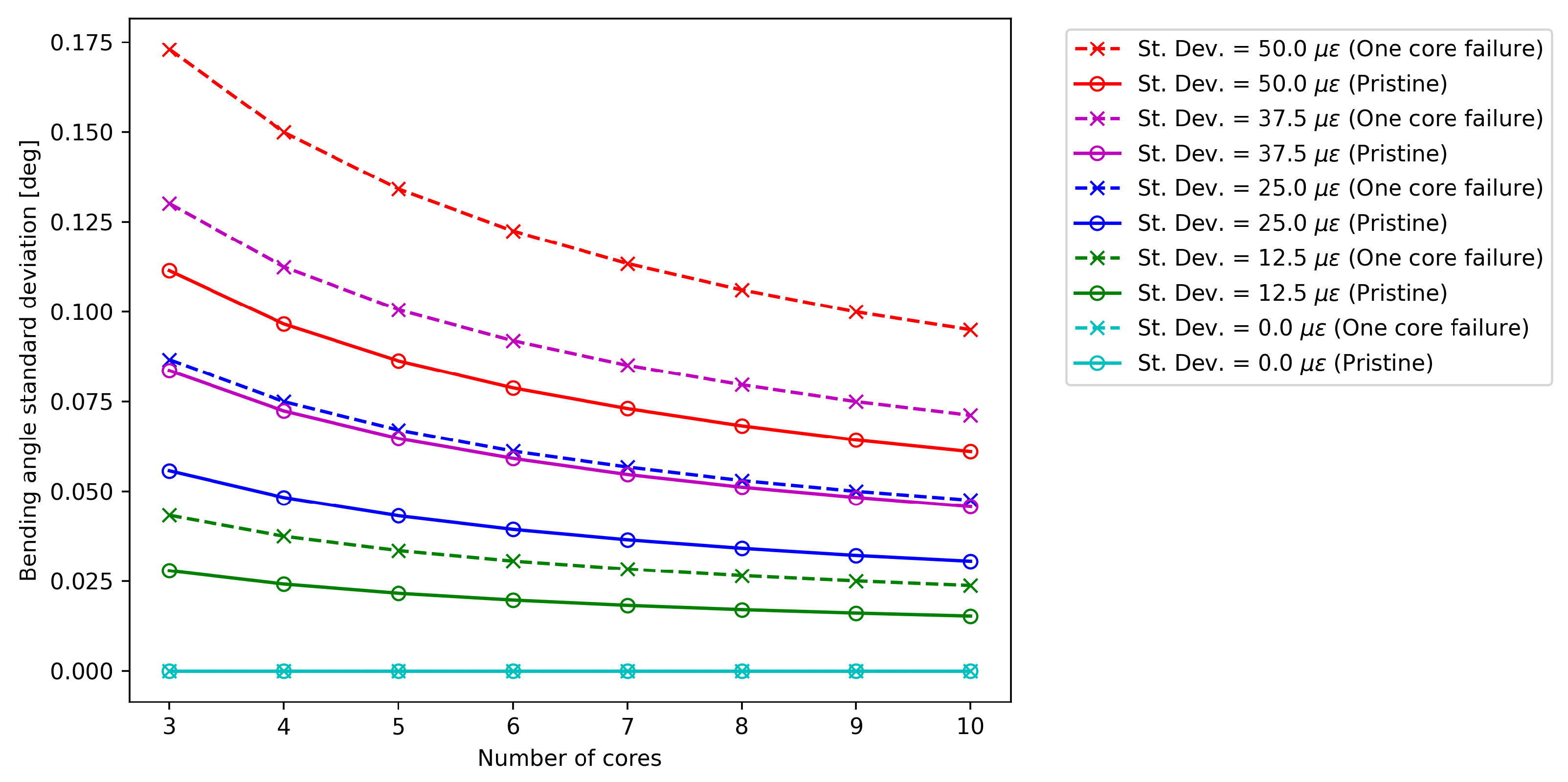
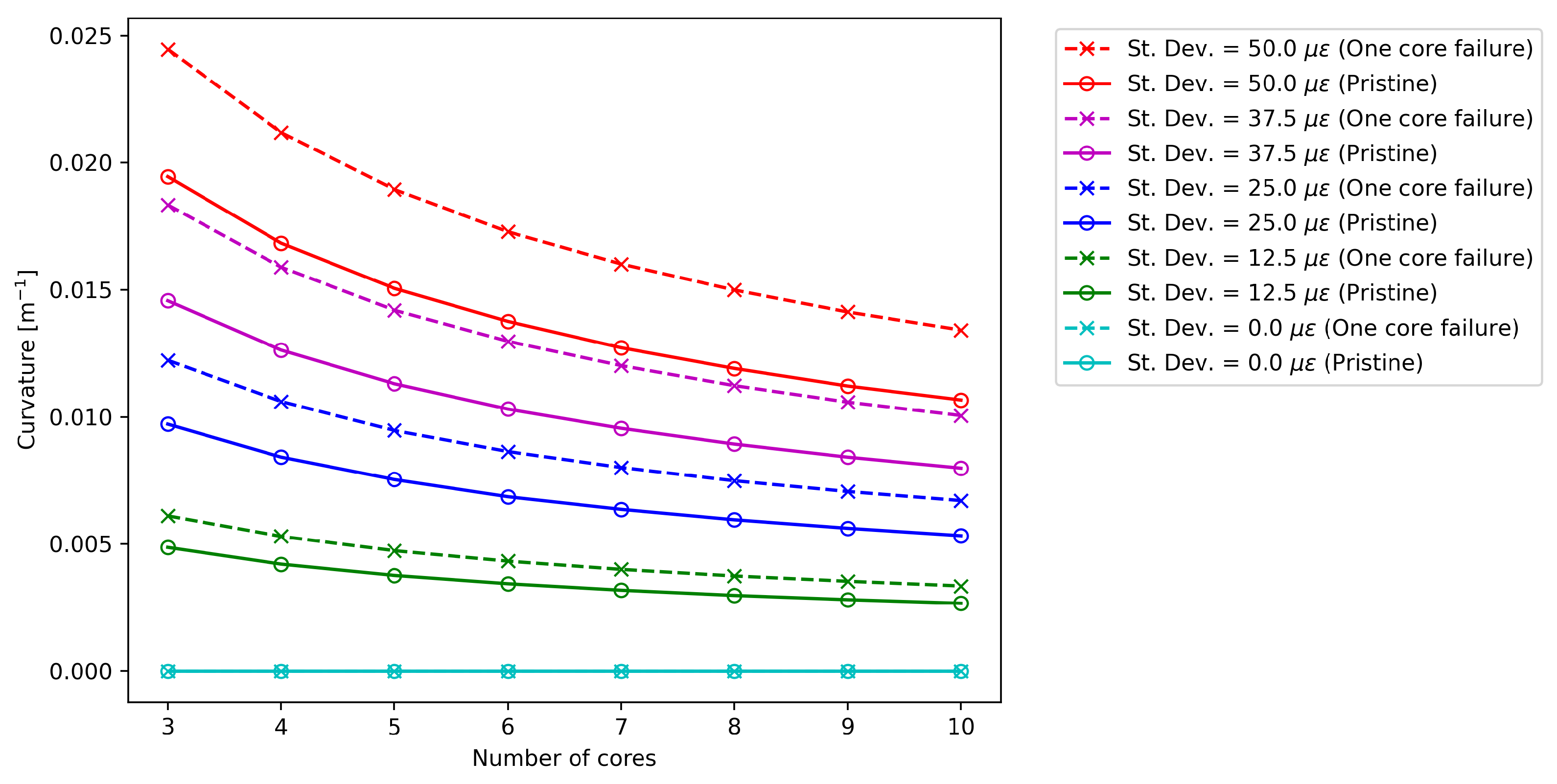
3.1. Core Failure Analysis on a Single Cross-Section
3.2. Polar Analysis
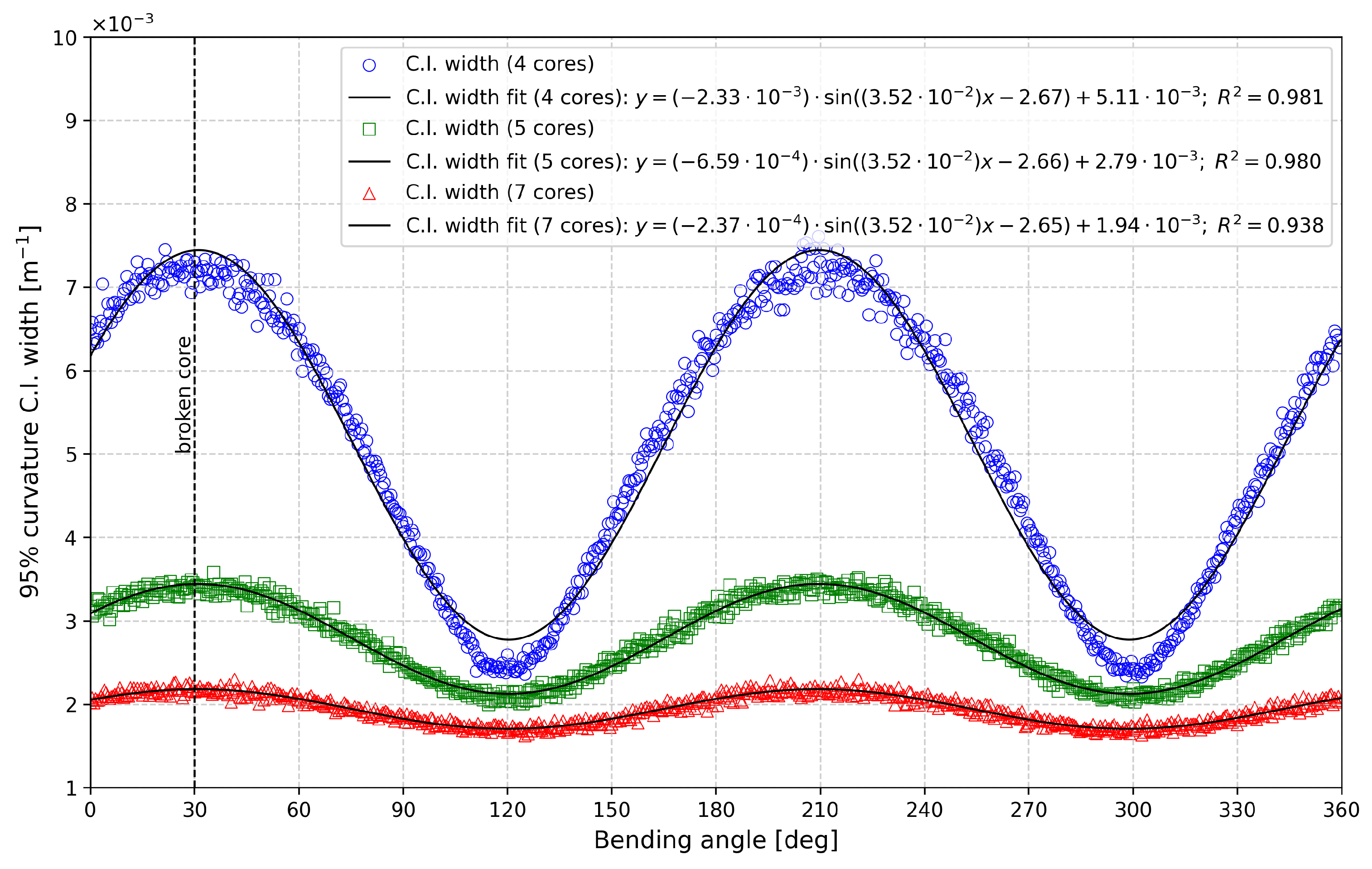
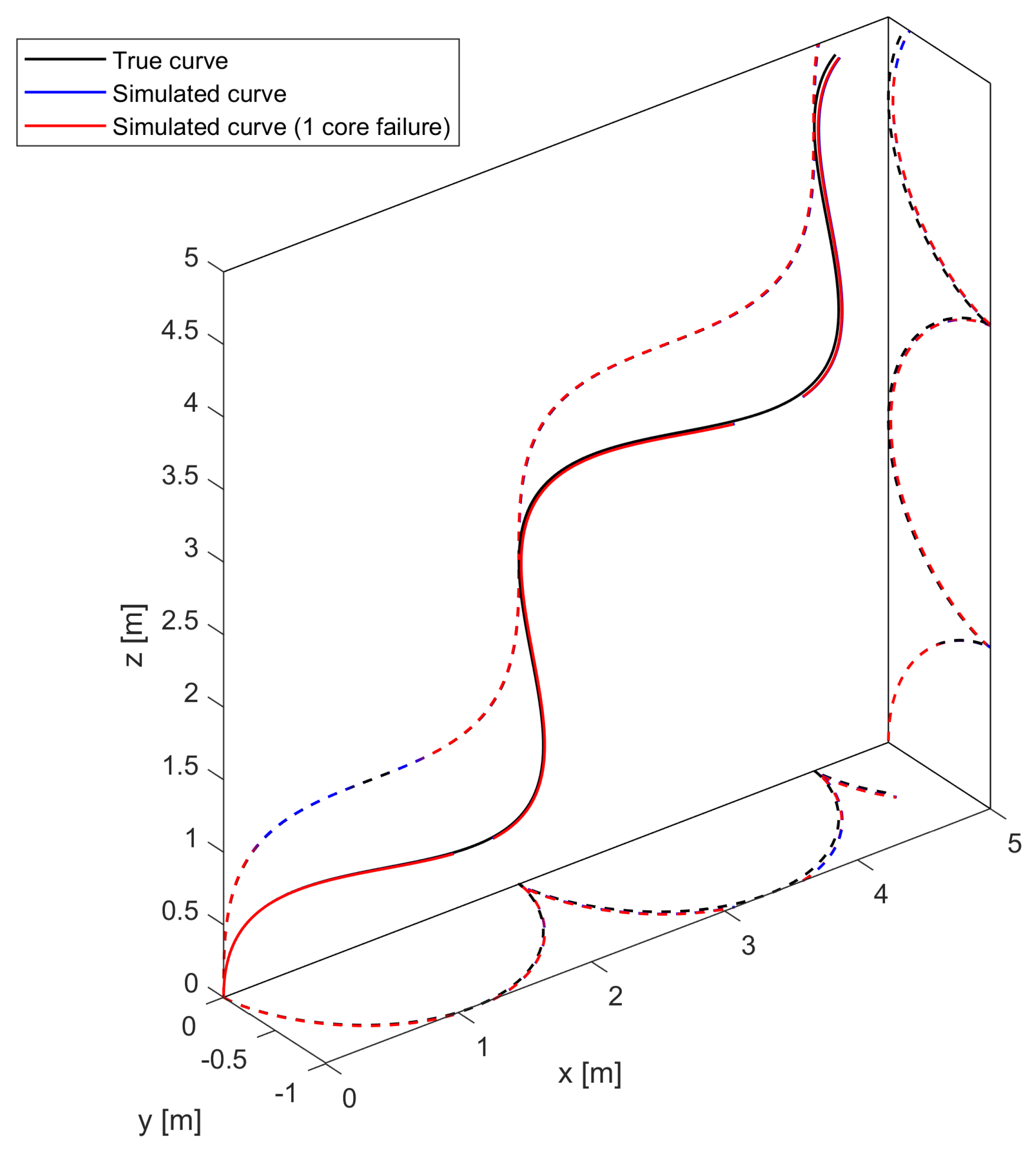
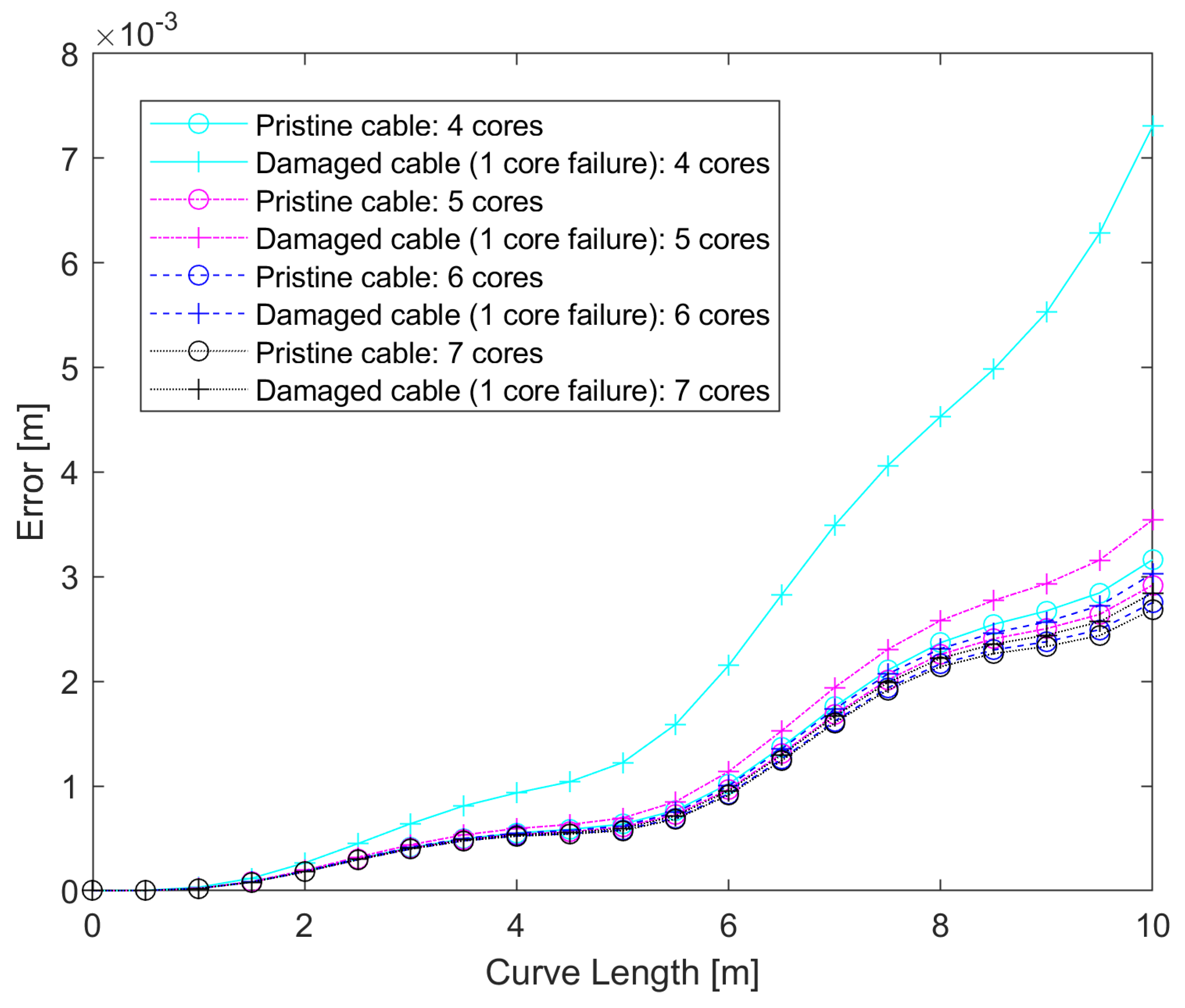
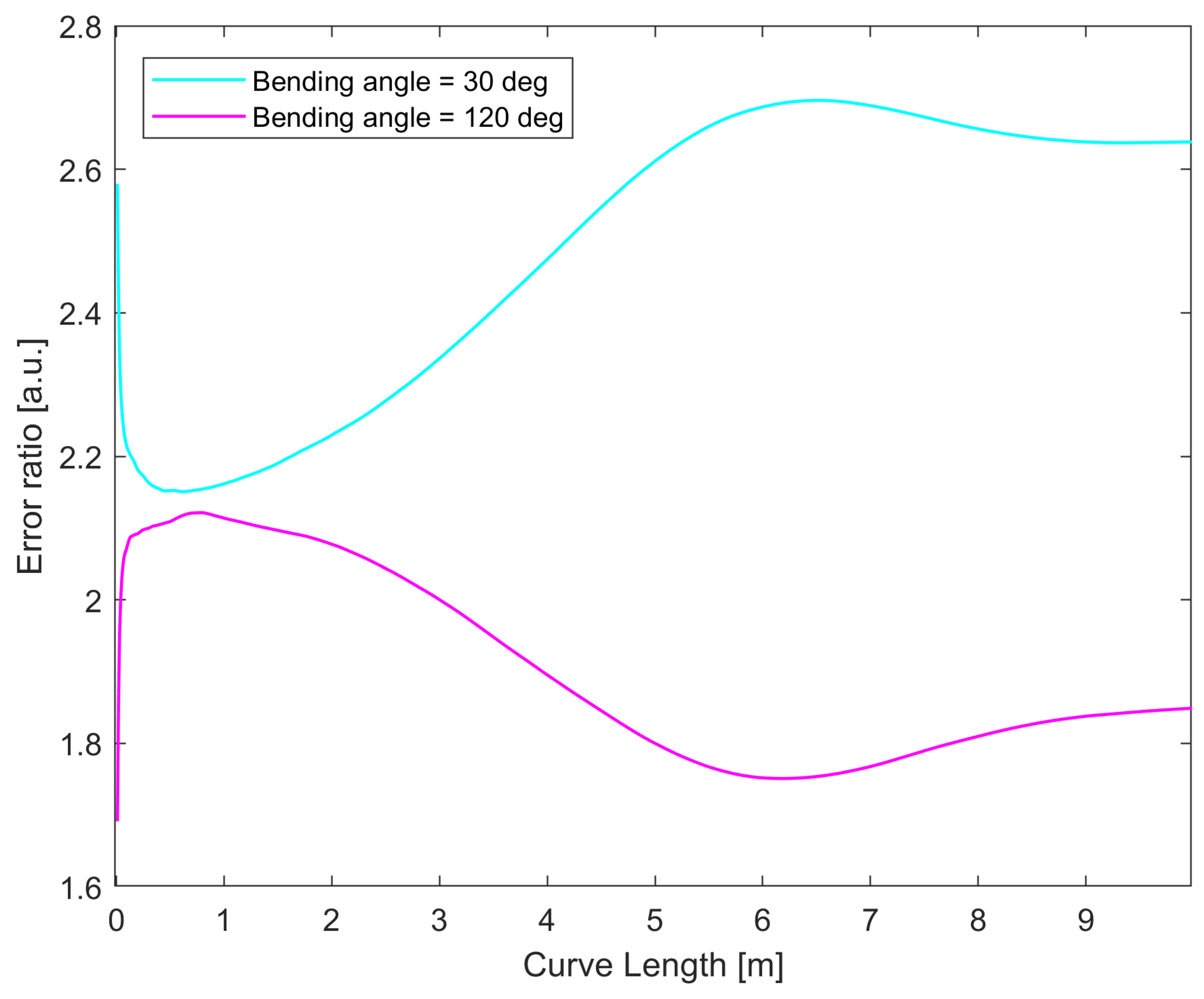
3.3. Effect of Core Failure on Curve Reconstruction
4. Conclusions
- The asymmetry introduced by the loss of a sensing core causes the uncertainty in both curvature and bending angle to depend on the orientation of the curvature vector, with their maximum and minimum values occurring at opposite angles.
- The effect of this asymmetry on measurement uncertainty is reduced by an increased number of sensing cores, with the highest improvement seen when going from four to five cores.
- The accuracy of 3D reconstruction for shapes that mostly lie on a plane will depend on the plane’s orientation with respect to the missing core.
- If it is established that the possibility of core breakage is likely (for instance, if the insertion or removal of cables is difficult and potentially damaging), then a suitable sensing cable configuration can be chosen to allow shape sensing with an acceptable accuracy even if one of the sensing cores is lost. While, in general, adding more sensing cores will provide better results, each additional core corresponds to an increased length of fiber that has to be monitored, with consequent costs, either in terms of measurement range, measurement bandwidth, or measurement channels, depending on the type of optical fiber sensor employed. The results in this paper suggest that a sensing cable with four peripheral and one central core provides the best compromise in terms of retained accuracy with the minimum number of cores. In the case where higher accuracy is required, additional sensing cores can be added, and we estimated the improvement for multiple configurations.
- When core breakage occurs, an industrial user might have the need to decide whether the cable can still be used or it has to be replaced. While replacement would be the optimal solution for maintaining sensing performance, it might be a difficult process depending on the application. Since in industrial environments, the goal of a sensor is usually to determine a specific set of events with a certain degree of reliability (that is, a minimum probability of detection), it would be worthwhile to determine whether a damaged cable is still viable for the required specifications. In this context, the results presented in this paper show a way to determine how the accuracy of the cable can change in the presence of core breakage and specific aspects that should be taken into consideration, such as the orientation of the broken cable with respect to the bending angles that are detected, which might also have an impact on measurement accuracy, especially if the shape that is being detected mostly lies on a specific plane, which can be expected to occur in some applications (e.g., shape sensing for railway monitoring). All of these factors that we highlighted in this work could have a significant impact on the decision-making process for deciding whether the sensing cable has to be replaced or can keep being employed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| C.I. | Confidence Intervals |
| FBG | Fiber Bragg Grating |
| OFSs | Optical Fiber Sensors |
| SHM | Structural Health Monitoring |
| SLAM-DAST | Smart LightwAve Multi-modal Distributed Acoustic Strain and Temperature sensor |
| SSE | Sum of Squared Errors |
References
- Di Sante, R. Fibre optic sensors for structural health monitoring of aircraft composite structures: Recent advances and applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef]
- Falcetelli, F.; Cristiani, D.; Yue, N.; Sbarufatti, C.; Troiani, E.; Di Sante, R.; Zarouchas, D. Qualification of distributed optical fiber sensors using probability of detection curves for delamination in composite laminates. Struct. Health Monit. 2022, 22, 2972–2986. [Google Scholar] [CrossRef]
- Falcetelli, F.; Yue, N.; Rossi, L.; Bolognini, G.; Bastianini, F.; Zarouchas, D.; Di Sante, R.D. A Model-Assisted Probability of Detection Framework for Optical Fiber Sensors. Sensors 2023, 23, 4813. [Google Scholar] [CrossRef] [PubMed]
- Amanzadeh, M.; Aminossadati, S.M.; Kizil, M.S.; Rakić, A.D. Recent developments in fibre optic shape sensing. Measurement 2018, 128, 119–137. [Google Scholar] [CrossRef]
- Moore, J.P.; Rogge, M.D. Shape sensing using multi-core fiber optic cable and parametric curve solutions. Opt. Express 2012, 20, 2967. [Google Scholar] [CrossRef]
- Parent, F.; Loranger, S.; Mandal, K.K.; Iezzi, V.L.; Lapointe, J.; Boisvert, J.S.; Baiad, M.D.; Kadoury, S.; Kashyap, R. Enhancement of accuracy in shape sensing of surgical needles using optical frequency domain reflectometry in optical fibers. Biomed. Opt. Express 2017, 8, 2210. [Google Scholar] [CrossRef]
- Shi, C.; Luo, X.; Qi, P.; Li, T.; Song, S.; Najdovski, Z.; Fukuda, T.; Ren, H. Shape Sensing Techniques for Continuum Robots in Minimally Invasive Surgery: A Survey. IEEE Trans. Biomed. Eng. 2017, 64, 1665–1678. [Google Scholar] [CrossRef]
- Khan, F.; Roesthuis, R.J.; Misra, S. Force sensing in continuum manipulators using fiber Bragg grating sensors. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 2531–2536. [Google Scholar] [CrossRef]
- Lu, Y.; Lu, B.; Li, B.; Guo, H.; Liu, Y.H. Robust Three-Dimensional Shape Sensing for Flexible Endoscopic Surgery Using Multi-Core FBG Sensors. IEEE Robot. Autom. Lett. 2021, 6, 4835–4842. [Google Scholar] [CrossRef]
- Henken, K.R.; Dankelman, J.; van den Dobbelsteen, J.J.; Cheng, L.K.; van der Heiden, M.S. Error Analysis of FBG-Based Shape Sensors for Medical Needle Tracking. IEEE/ASME Trans. Mechatronics 2014, 19, 1523–1531. [Google Scholar] [CrossRef]
- Floris, I.; Sales, S.; Calderón, P.A.; Adam, J.M. Measurement uncertainty of multicore optical fiber sensors used to sense curvature and bending direction. Measurement 2019, 132, 35–46. [Google Scholar] [CrossRef]
- Floris, I.; Calderón, P.A.; Sales, S.; Adam, J.M. Effects of core position uncertainty on optical shape sensor accuracy. Measurement 2019, 139, 21–33. [Google Scholar] [CrossRef]
- Megens, M.; Leistikow, M.D.; Van Dusschoten, A.; Van Der Mark, M.B.; Horikx, J.J.L.; Van Putten, E.G.; Hooft, G.W.T. Shape accuracy of fiber optic sensing for medical devices characterized in bench experiments. Med. Phys. 2021, 48, 3936–3947. [Google Scholar] [CrossRef] [PubMed]
- Falcetelli, F.; Rossi, L.; Bastianini, F.; Bolognini, G.; Di Sante, R. Optical Fibers Shape Sensing Accuracy under Different Uncertainty Sources: A Monte Carlo Experiment. In Proceedings of the 2023 Photonics & Electromagnetics Research Symposium (PIERS), Prague, Czech Republic, 3–6 July 2023; pp. 1546–1552. [Google Scholar] [CrossRef]
- Paloschi, D.; Bronnikov, K.A.; Korganbayev, S.; Wolf, A.A.; Dostovalov, A.; Saccomandi, P. 3D Shape Sensing With Multicore Optical Fibers: Transformation Matrices Versus Frenet-Serret Equations for Real-Time Application. IEEE Sens. J. 2021, 21, 4599–4609. [Google Scholar] [CrossRef]
- Todd, M.D.; Stull, C.J.; Dickerson, M. A Local Material Basis Solution Approach to Reconstructing the Three-Dimensional Displacement of Rod-Like Structures From Strain Measurements. J. Appl. Mech. 2013, 80, 041028. [Google Scholar] [CrossRef]
- Chadha, M.; Todd, M.D. A Generalized Approach for Reconstructing the Three-Dimensional Shape of Slender Structures Including the Effects of Curvature, Shear, Torsion, and Elongation. J. Appl. Mech. 2017, 84, 041003. [Google Scholar] [CrossRef]
- Cui, J.; Zhao, S.; Yang, C.; Tan, J. Parallel Transport Frame for Fiber Shape Sensing. IEEE Photonics J. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Antunes, P.; Domingues, F.; Granada, M.; André, P. Mechanical Properties of Optical Fibers; INTECH Open Access Publisher: London, UK, 2012; pp. 537–550. [Google Scholar] [CrossRef]
- Danzer, R.; Supancic, P.; Pascual, J.; Lube, T. Fracture statistics of ceramics – Weibull statistics and deviations from Weibull statistics. Eng. Fract. Mech. 2007, 74, 2919–2932. [Google Scholar] [CrossRef]
- Falcetelli, F.; Rossi, L.; Di Sante, R.; Bolognini, G. Strain Transfer in Surface-Bonded Optical Fiber Sensors. Sensors 2020, 20, 3100. [Google Scholar] [CrossRef]
- Chadha, M.; Hu, Z.; Farrar, C.R.; Todd, M.D. Risk and Value Informed Structural Health Monitoring System Design for Miter Gates. In Proceedings of the 11th European Workshop on Structural Health Monitoring, EWSHM 2024, Potsdam, Germany, 10–13 June 2024. [Google Scholar] [CrossRef]
- Floris, I.; Adam, J.M.; Calderón, P.A.; Sales, S. Fiber Optic Shape Sensors: A comprehensive review. Opt. Lasers Eng. 2021, 139, 106508. [Google Scholar] [CrossRef]
- Wu, Y.; Pei, L.; Jin, W.; Jiang, Y.; Yang, Y.; Shen, Y.; Jian, S. Highly sensitive curvature sensor based on asymmetrical twin core fiber and multimode fiber. Opt. Laser Technol. 2017, 92, 74–79. [Google Scholar] [CrossRef]
- Falcetelli, F.; Rossi, L.; Bastianini, F.; Bolognini, G.; Di Sante, R. Fiber Optic Shape Sensing Robustness Against Cores Failure. In Proceedings of the 2024 Photonics & Electromagnetics Research Symposium (PIERS), Chengdu, China, 21–25 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, H.l.; Zhu, Z.w.; Zheng, Y.; Liu, B.; Xiao, F. Experimental study on an FBG strain sensor. Opt. Fiber Technol. 2018, 40, 144–151. [Google Scholar] [CrossRef]
- Waltermann, C.; Koch, J.; Angelmahr, M.; Burgmeier, J.; Thiel, M.; Schade, W. Fiber-optical 3d shape sensing. In Planar Waveguides and other Confined Geometries: Theory, Technology, Production, and Novel Applications; Marowsky, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 227–250. [Google Scholar] [CrossRef]
- Kissinger, T.; Chehura, E.; Staines, S.E.; James, S.W.; Tatam, R.P. Dynamic fiber-optic shape sensing using fiber segment interferometry. J. Light. Technol. 2017, 36, 917–925. [Google Scholar] [CrossRef]
- Orfanidis, S.J. Applied Optimum Signal Processing; Routledge: England, UK, 2018. [Google Scholar]

| Parameter | Symbols | Values | Units |
|---|---|---|---|
| Core offset | [mm] | ||
| Measurement noise standard deviation | |||
| Target curvature | [m−1] | ||
| Longitudinal strain | |||
| Number of tested directions | 720 | ||
| Monte Carlo iterations | N | 103 |
| N. | Error | Error | Error Ratio | Error Ratio Reduction |
|---|---|---|---|---|
| Cores | Pristine Cable | One Core Failure Cable | (Last Point) | (One Core Increment) |
| 4 | 3.2 mm | 7.3 mm | 2.28 | - |
| 5 | 2.9 mm | 3.5 mm | 1.21 | 46.9% |
| 6 | 2.8 mm | 3.0 mm | 1.07 | 11.6% |
| 7 | 2.7 mm | 2.8 mm | 1.04 | 2.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falcetelli, F.; Rossi, L.; Di Sante, R.; Bolognini, G. Uncertainty Analysis of Fiber Optic Shape Sensing Under Core Failure. Sensors 2025, 25, 2353. https://doi.org/10.3390/s25082353
Falcetelli F, Rossi L, Di Sante R, Bolognini G. Uncertainty Analysis of Fiber Optic Shape Sensing Under Core Failure. Sensors. 2025; 25(8):2353. https://doi.org/10.3390/s25082353
Chicago/Turabian StyleFalcetelli, Francesco, Leonardo Rossi, Raffaella Di Sante, and Gabriele Bolognini. 2025. "Uncertainty Analysis of Fiber Optic Shape Sensing Under Core Failure" Sensors 25, no. 8: 2353. https://doi.org/10.3390/s25082353
APA StyleFalcetelli, F., Rossi, L., Di Sante, R., & Bolognini, G. (2025). Uncertainty Analysis of Fiber Optic Shape Sensing Under Core Failure. Sensors, 25(8), 2353. https://doi.org/10.3390/s25082353









