Adapting Young Adults’ In-Shoe Motion Sensor Gait Models for Knee Evaluation in Older Adults: A Study on Osteoarthritis and Healthy Knees
Abstract
1. Introduction
1.1. Background
1.2. Main Contribution of This Study
2. Materials and Methods
2.1. Participant
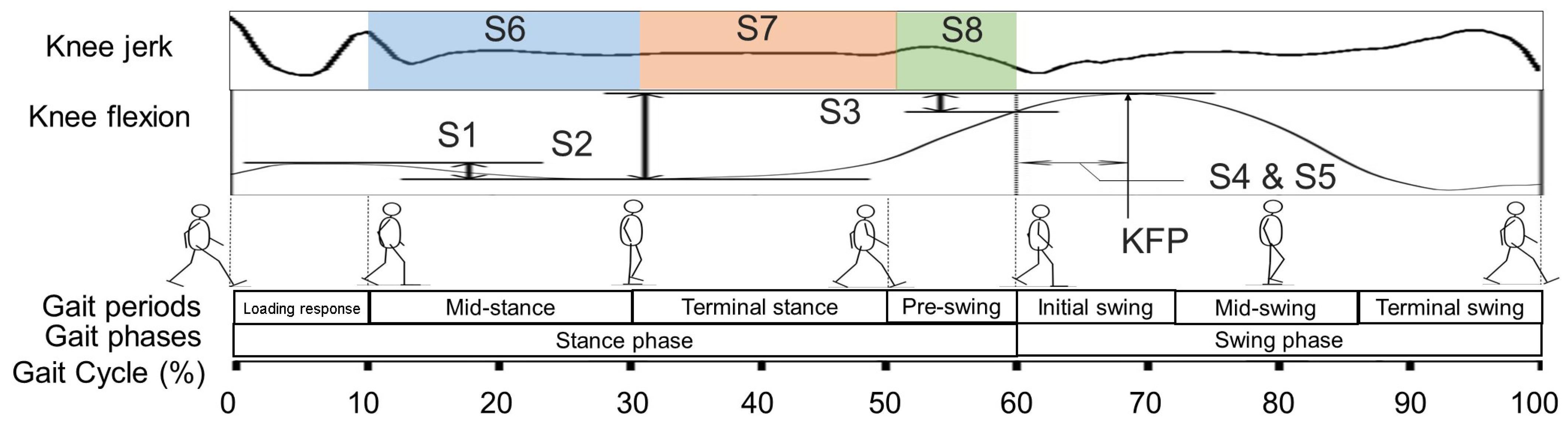
2.2. Target Knee Indicators
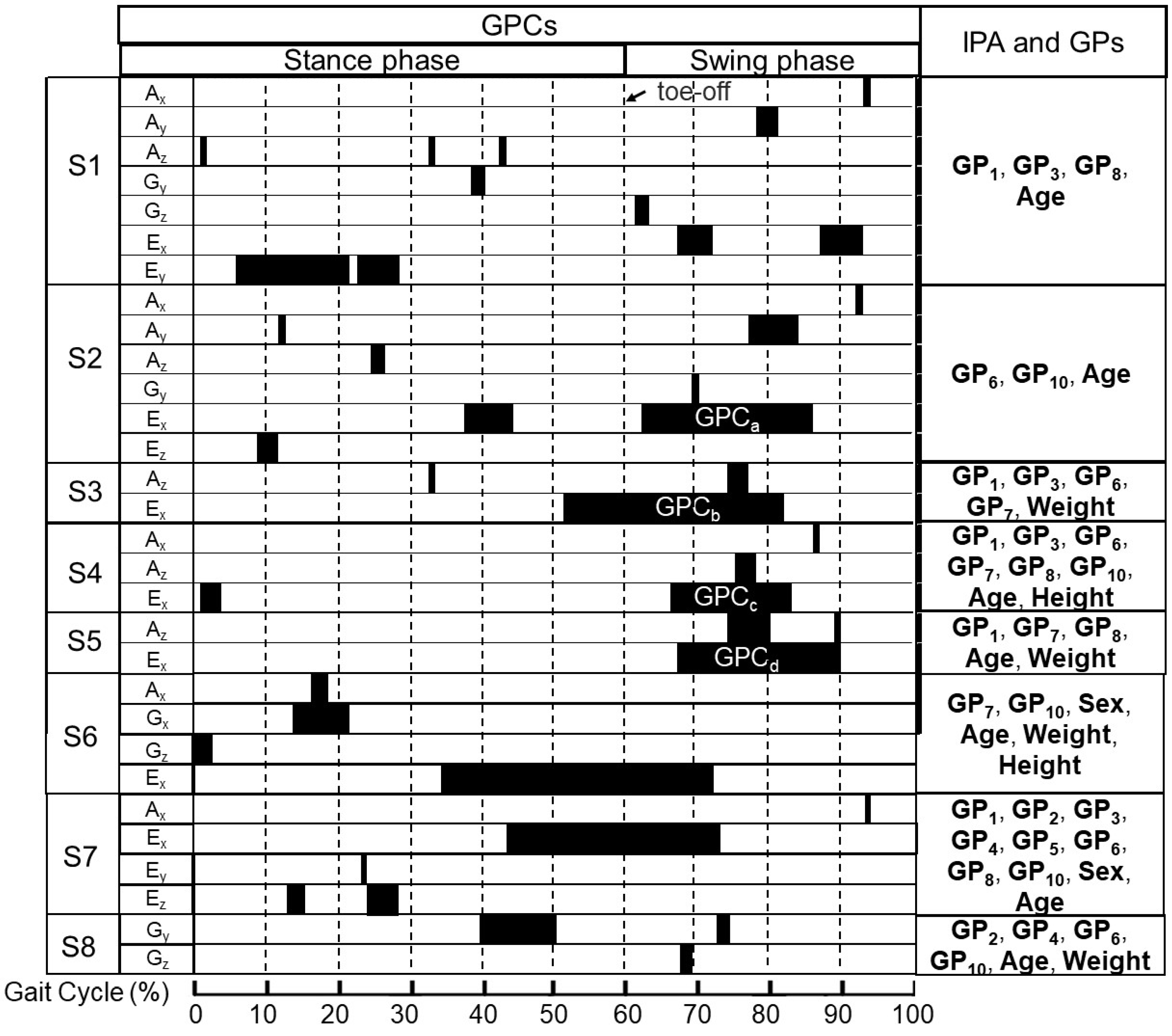
2.3. The Details for Preliminarily Determined Predictors
2.4. Experiments
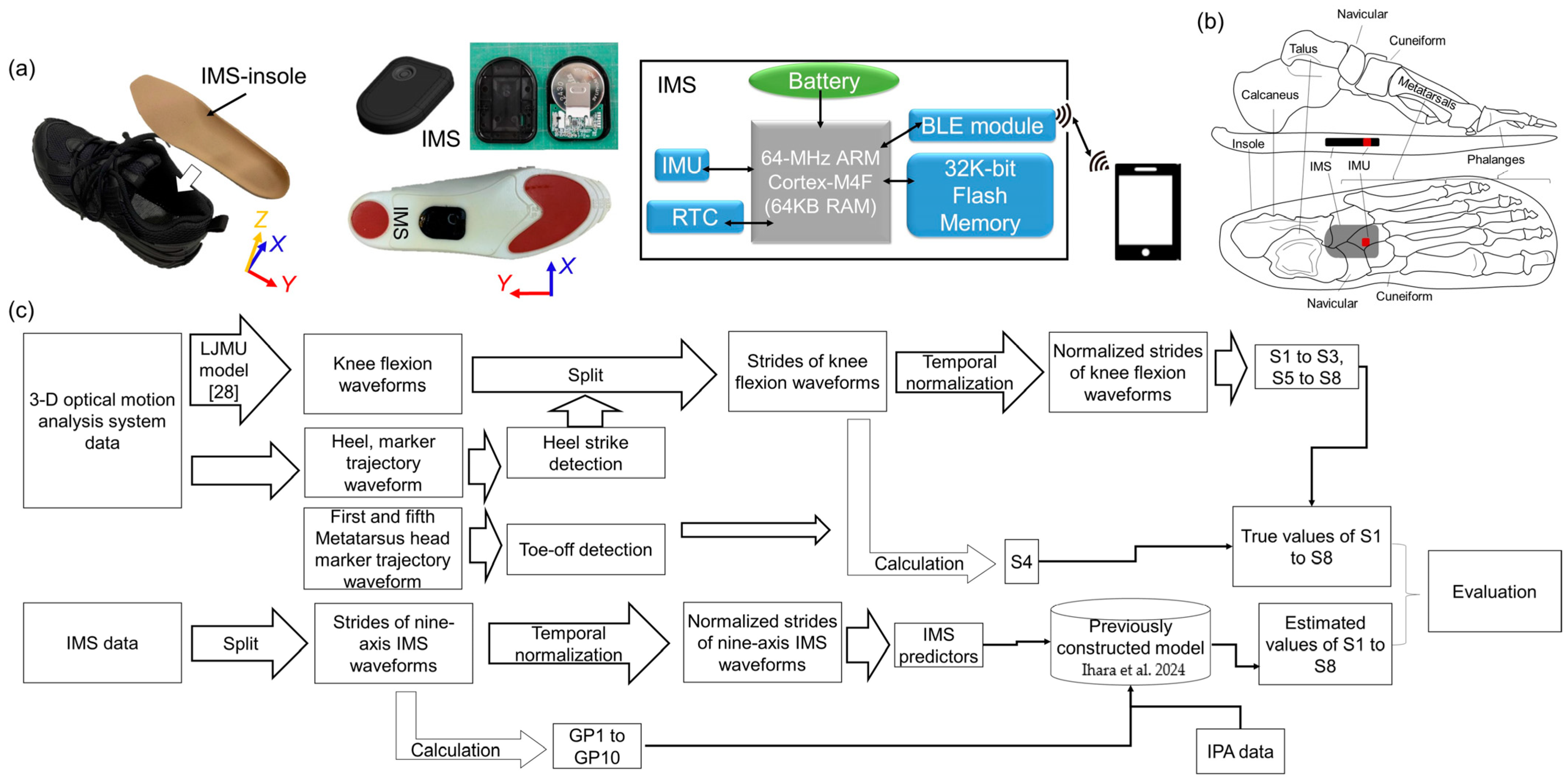
2.4.1. Data Collection
2.4.2. Signal Processing
2.4.3. Result Analyses
3. Results
3.1. Gait Parameters in Different Groups
3.2. Quantitative Evaluation of the Constructed Model
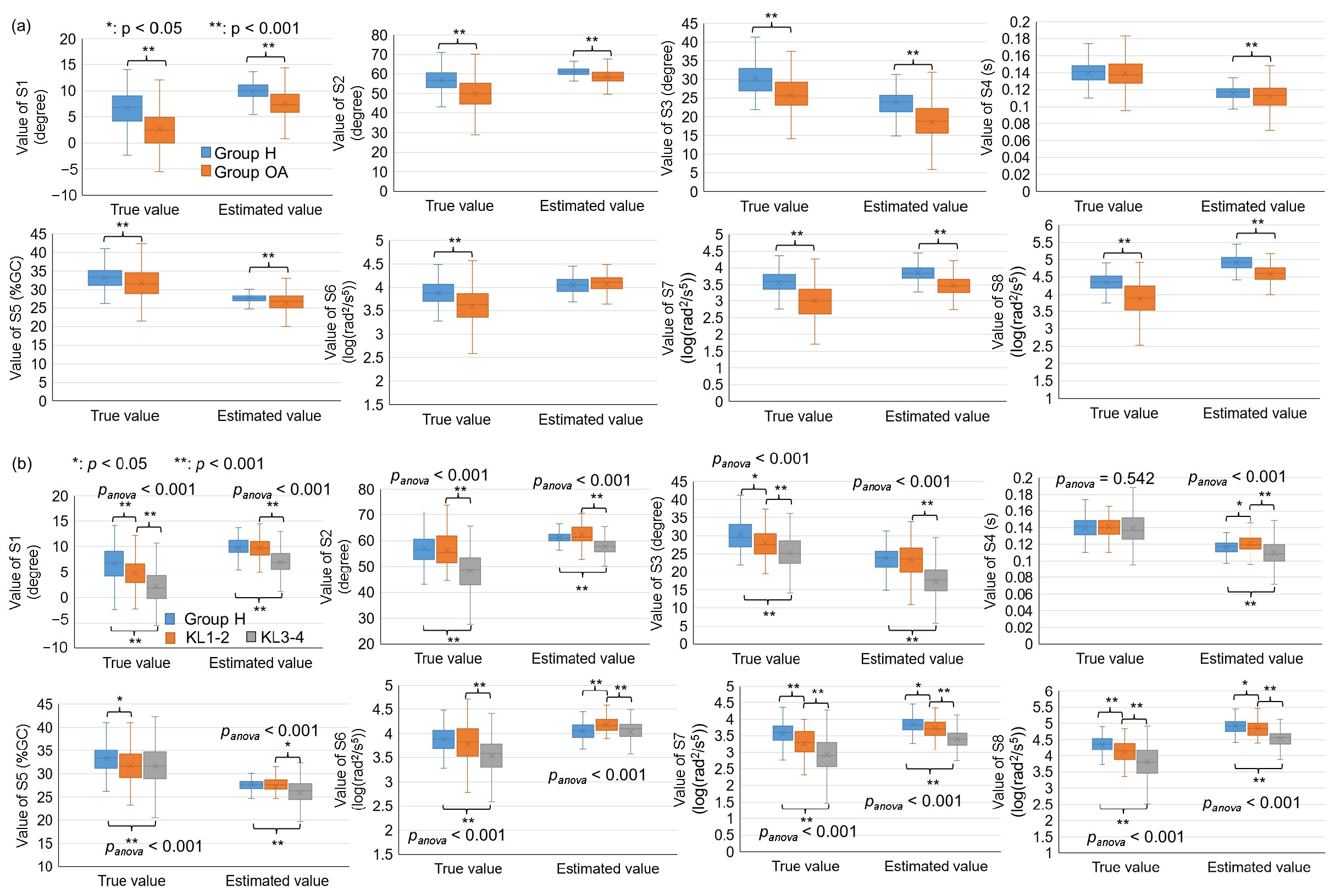
3.3. Comparison of Different Groups
3.4. Connection Between Knee Motion Parameters and Foot Rotation in Sagittal Plane
4. Discussion
4.1. Connection Between Knee and Other Foot Motion Parameters
4.2. Limitation of This Technology
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Corrêa Dias, R.; Domingues Dias, J.M.; Ramos, L.R. Impact of an exercise and walking protocol on quality of life for elderly people with OA of the knee. Physiother. Res. Int. 2003, 8, 121–130. [Google Scholar] [CrossRef]
- Farr, J., II; Miller, L.E.; Block, J.E. Quality of life in patients with knee osteoarthritis: A commentary on nonsurgical and surgical treatments. Open Orthop. J. 2013, 7, 619–623. [Google Scholar] [CrossRef]
- Toda, H.; Maruyama, T.; Fujita, K.; Yamauchi, Y.; Tada, M. Self-Reported Walking Difficulty Associated with Stiff-Knee Gait in Japanese Patients with Knee Osteoarthritis: A Preliminary Cross-Sectional Study. Healthcare 2021, 9, 1308. [Google Scholar] [CrossRef]
- Eskofier, B.M.; Lee, S.I.; Baron, M.; Simon, A.; Martindale, C.F.; Gaßner, H.; Klucken, J. An overview of smart shoes in the internet of health things: Gait and mobility assessment in health promotion and disease monitoring. Appl. Sci. 2017, 7, 986. [Google Scholar] [CrossRef]
- Fukushi, K.; Huang, C.; Wang, Z.; Kajitani, H.; Nihey, F.; Nakahara, K. On-Line Algorithms of Stride-Parameter Estimation for in-Shoe Motion-Sensor System. IEEE Sens. J. 2022, 22, 9636–9648. [Google Scholar] [CrossRef]
- Huang, C.; Nihey, F.; Fukushi, K.; Kajitani, H.; Nozaki, Y.; Ihara, K.; Nakahara, K. Feature Selection, Construction, and Validation of a Lightweight Model for Foot Function Assessment During Gait With In-Shoe Motion Sensors. IEEE Sens. J. 2023, 23, 8839–8855. [Google Scholar] [CrossRef]
- Huang, C.; Nihey, F.; Ihara, K.; Fukushi, K.; Kajitani, H.; Nozaki, Y.; Nakahara, K. Healthcare Application of In-Shoe Motion Sensor for Older Adults: Frailty Assessment Using Foot Motion during Gait. Sensors 2023, 23, 5446. [Google Scholar] [CrossRef]
- Huang, C.; Nihey, F.; Fukushi, K.; Kajitani, H.; Nozaki, Y.; Wang, Z.; Ihara, K.; Nakahara, K. Assessment method of balance ability of older adults using an in-shoe motion sensor. In Proceedings of the 2022 IEEE Biomedical Circuits and Systems Conference (BioCAS), Taipei, Taiwan, 13–15 October 2022; pp. 448–452. [Google Scholar] [CrossRef]
- Huang, C.; Nihey, F.; Fukushi, K.; Kajitani, H.; Nozaki, Y.; Nakahara, K. Constructing and testing a lightweight model of converting single stride of in-shoe motion sensor-measured foot motion to TUG-represented mobility. IEEE Sens. Lett. 2023, 7, 1–4. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, C.; Ihara, K.; Nihey, F.; Fukushi, K.; Kajitani, H.; Nozaki, Y.; Nakahara, K. Estimating range of pelvic motion during gait by using in-shoe motion sensors. In Proceedings of the 2023 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Kuala Lumpur, Malaysia, 22–25 May 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Yaguchi, H.; Honda, K.; Sekiguchi, Y.; Huang, C.; Fukushi, K.; Wang, Z.; Nakahara, K.; Kamimura, M.; Aki, T.; Ogura, K.; et al. Differences in kinematic parameters during gait between the patients with knee osteoarthritis and healthy controls using an insole with a single inertial measurement unit: A case-control study. Clin. Biomech. 2024, 112, 106191. [Google Scholar] [CrossRef]
- Raza, A.; Sekiguchi, Y.; Yaguchi, H.; Honda, K.; Fukushi, K.; Huang, C.; Ihara, K.; Nozaki, Y.; Nakahara, K.; Izumi, S.I.; et al. Gait classification of knee osteoarthritis patients using shoe-embedded internal measurement units sensor. Clin. Biomech. 2024, 117, 106285. [Google Scholar] [CrossRef]
- Jagadamma, K.C.; Owen, E.; Coutts, F.J.; Herman, J.; Yirrell, J.; Mercer, T.H.; Van Der Linden, M.L. The effects of tuning an ankle-foot orthosis footwear combination on kinematics and kinetics of the knee joint of an adult with hemiplegia. Prosthet. Orthot. Int. 2010, 34, 270–276. [Google Scholar] [PubMed]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Andriacchi, T.P.; Mündermann, A.; Smith, R.L.; Alexander, E.J.; Dyrby, C.O.; Koo, S. A framework for the in vivo pathomechanics of osteoarthritis at the knee. Ann. Biomed. Eng. 2004, 32, 447–457. [Google Scholar] [CrossRef] [PubMed]
- Englund, M. The role of biomechanics in the initiation and progression of OA of the knee. Best Pract. Res. Clin. Rheumatol. 2010, 24, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Kean, C.O.; Bennell, K.L.; Wrigley, T.V.; Hinman, R.S. Modified walking shoes for knee osteoarthritis: Mechanisms for reductions in the knee adduction moment. J. Biomech. 2013, 46, 2060–2066. [Google Scholar] [CrossRef]
- Hausdorff, J.M. Gait variability: Methods, modeling and meaning. J. Neuroeng. Rehabil. 2005, 2, 19. [Google Scholar] [CrossRef]
- Ihara, K.; Huang, C.; Nihey, F.; Kajitani, H.; Nakahara, K. Estimating Indicators for Assessing Knee Motion Impairment During Gait Using In-Shoe Motion Sensors: A Feasibility Study. Sensors 2024, 24, 7615. [Google Scholar] [CrossRef]
- Bytyqi, D.; Shabani, B.; Lustig, S.; Cheze, L.; Karahoda Gjurgjeala, N.; Neyret, P. Gait knee kinematic alterations in medial osteoarthritis: Three-dimensional assessment. Int. Orthop. 2014, 38, 1191–1198. [Google Scholar] [CrossRef]
- Goldberg, S.R.; Anderson, F.C.; Pandy, M.G.; Delp, S.L. Muscles that influence knee flexion velocity in double support: Implications for stiff-knee gait. J. Biomech. 2004, 37, 1189–1196. [Google Scholar] [CrossRef]
- Ounpuu, S.; Muik, E.; Davis, R.B., III; Gage, J.R.; DeLuca, P.A. Rectus femoris surgery in children with cerebral palsy. Part I: The effect of rectus femoris transfer location on knee motion. J. Pediatr. Orthop. 1993, 13, 325–330. [Google Scholar]
- Goldberg, S.R.; Ounpuu, S.; Delp, S.L. The importance of swing-phase initial conditions in stiff-knee gait. J. Biomech. 2003, 36, 1111–1116. [Google Scholar] [CrossRef]
- Sutherland, D.H.; Santi, M.; Abel, M.F. Treatment of stiff-knee gait in cerebral palsy: A comparison by gait analysis of distal rectus femoris transfer versus proximal rectus release. J. Pediatr. Orthop. 1990, 10, 433–441. Available online: https://www.ncbi.nlm.nih.gov/pubmed/2358477 (accessed on 10 October 2023). [PubMed]
- Gage, J.R.; Perry, J.; Hicks, R.R.; Koop, S.; Werntz, J.R. Rectus femoris transfer to improve knee function of children with cerebral palsy. Dev. Med. Child Neurol. 1987, 29, 159–166. [Google Scholar] [CrossRef] [PubMed]
- Fukaya, T.; Mutsuzaki, H.; Wadano, Y. Smoothness Using Angular Jerk Cost of the Knee Joint Movement after a Reduction in Walking Speed. J. Mech. Med. Biol. 2013, 13, 1350037. [Google Scholar] [CrossRef]
- Kellgren, J.H.; Lawrence, J.S. Radiological assessment of osteo-arthrosis. Ann. Rheum. Dis. 1957, 16, 494–502. [Google Scholar] [CrossRef]
- Malfait, B.; Sankey, S.; Firhad Raja Azidin, R.M.; Deschamps, K.; Vanrenterghem, J.; Robinson, M.A.; Staes, F.; Verschueren, S. How reliable are lower limb kinematics and kinetics during a drop vertical jump? Med. Sci. Sports Exerc. 2014, 46, 678–685. [Google Scholar] [CrossRef]
- Cicchetti, D.V. Guidelines, criteria, and rules of thumb for evaluating normed and standardized assessment instruments in psychology. Psychol. Assess. 1994, 6, 284. [Google Scholar] [CrossRef]
- Cohen, J. A power primer. Psychol. Bull. 1992, 112, 155–159. [Google Scholar] [CrossRef]
- Dixon, S.J.; Hinman, R.S.; Creaby, M.W.; Kemp, G.; Crossley, K.M. Knee joint stiffness during walking in knee osteoarthritis. Arthritis Care Res. 2010, 62, 38–44. [Google Scholar] [CrossRef]
- Ezaki, S.; Kadone, H.; Kubota, S.; Abe, T.; Shimizu, Y.; Tan, C.K.; Miura, K.; Hada, Y.; Sankai, Y.; Koda, M.; et al. Analysis of Gait Motion Changes by Intervention Using Robot Suit Hybrid Assistive Limb (HAL) in Myelopathy Patients After Decompression Surgery for Ossification of Posterior Longitudinal Ligament. Front. Neurorobot. 2021, 15, 650118. [Google Scholar] [CrossRef]
- Deasy, M.; Leahy, E.; Semciw, A.I. Hip Strength Deficits in People With Symptomatic Knee Osteoarthritis: A Systematic Review With Meta-analysis. J. Orthop. Sports Phys. Ther. 2016, 46, 629–639. [Google Scholar] [CrossRef]
- Fukuoka, T.; Irie, S.; Watanabe, Y.; Kutsuna, T.; Abe, A. The relationship between spatiotemporal gait parameters and cognitive function in healthy adults: Protocol for a cross-sectional study. Pilot Feasibility Stud. 2022, 8, 154. [Google Scholar] [CrossRef] [PubMed]
- Teufl, W.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G. Validity, Test-Retest Reliability and Long-Term Stability of Magnetometer Free Inertial Sensor Based 3D Joint Kinematics. Sensors 2018, 18, 1980. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Deng, W. Deep visual domain adaptation: A survey. Neurocomputing 2018, 312, 135–153. [Google Scholar] [CrossRef]

| Mean ± SD | |||
|---|---|---|---|
| Participants for Training [19] | Group H | Group OA | |
| Number (M/F) | 66 (35/31) | 20 (12/8) | 44 (11/33) |
| Number (KL1–2/KL3–4) | – | – | 10/34 |
| Age (years) | 44.5 ± 15.9 | 69.0 ± 8.0 * | 70.8 ± 9.4 * |
| Height (cm) | 164.5 ± 9.3 | 161.0 ± 7.9 * | 155.6 ± 9.7 * |
| Weight (kg) | 61.4 ± 14.1 | 56.4 ± 11.0 | 63.0 ± 13.4 |
| Gait Parameters | Description |
|---|---|
| GP1 (m) | Stride length |
| GP2 (m/s) | Gait speed |
| GP3 (°) | Maximum SGA in dorsiflexion direction |
| GP4 (°) | Maximum SGA in plantarflexion direction |
| GP5 (cm) | Maximum circumduction during swing phase |
| GP6 (cm) | Maximum foot height during swing phase |
| GP7 (°) | Toe in/out angle in the transverse plane |
| GP8 (%GC) | Proportion of stance phase |
| GP9 (%GC) | Proportion of stance phase |
| GP10 (s) | Stride time |
| Mean ± SD | ||
|---|---|---|
| Group H | Group OA | |
| Data number (KL1-2/KL3-4) | 204 | 385 (79/306) |
| GP1 (m) | 1.32 ± 0.14 | 1.06 ± 0.22 * |
| GP2 (m/s) | 1.24 ± 0.17 | 0.88 ± 0.22 * |
| GP3 (°) | 27.13 ± 5.27 | 21.51 ± 7.09 * |
| GP4 (°) | 64.34 ± 6.81 | 56.40 ± 10.70 * |
| GP5 (cm) | 2.27 ± 0.91 | 2.37 ± 1.58 |
| GP6 (cm) | 13.72 ± 1.60 | 11.14 ± 2.57 * |
| GP7 (°) | 11.27 ± 8.26 | 8.72 ± 8.39 * |
| GP8 (%GC) | 63.04 ± 1.68 | 66.10 ± 3.10 * |
| GP9 (%GC) | 36.96 ± 1.68 | 33.90 ± 3.10 * |
| GP10 (s) | 1.08 ± 0.09 | 1.23 ± 0.13 * |
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | |
|---|---|---|---|---|---|---|---|---|
| ICC | 0.225 | 0.305 | 0.395 | 0.214 | 0.169 | 0.230 | 0.437 | 0.253 |
| r | 0.399 | 0.670 | 0.689 | 0.603 | 0.380 | 0.474 | 0.689 | 0.691 |
| Mt | 8.31 | 59.19 | 27.14 | 0.128 | 30.49 | 3.97 | 3.71 | 4.63 |
| SDt | 3.17 | 5.10 | 5.26 | 0.016 | 3.59 | 0.24 | 0.34 | 0.37 |
| Me | 5.09 | 54.37 | 22.18 | 0.125 | 28.97 | 3.83 | 3.23 | 4.24 |
| SDe | 4.16 | 7.70 | 6.71 | 0.022 | 4.76 | 0.41 | 0.50 | 0.54 |
| Md | 4.24 | 7.08 | −6.93 | −0.024 | −5.45 | 2.55 | 1.21 | 0.41 |
| SDd | 3.93 | 6.40 | 4.52 | 0.010 | 3.93 | 4.61 | 0.44 | 0.36 |
| V | 1.24 | 1.25 | 0.86 | 0.65 | 1.09 | 1.51 | 1.20 | 0.97 |
| tKFP | tSt | |
|---|---|---|
| Group H | −0.250 | −0.249 |
| Group OA | −0.345 | −0.366 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Fukushi, K.; Yaguchi, H.; Honda, K.; Sekiguchi, Y.; Wang, Z.; Nozaki, Y.; Nakahara, K.; Ebihara, S.; Izumi, S.-I. Adapting Young Adults’ In-Shoe Motion Sensor Gait Models for Knee Evaluation in Older Adults: A Study on Osteoarthritis and Healthy Knees. Sensors 2025, 25, 2167. https://doi.org/10.3390/s25072167
Huang C, Fukushi K, Yaguchi H, Honda K, Sekiguchi Y, Wang Z, Nozaki Y, Nakahara K, Ebihara S, Izumi S-I. Adapting Young Adults’ In-Shoe Motion Sensor Gait Models for Knee Evaluation in Older Adults: A Study on Osteoarthritis and Healthy Knees. Sensors. 2025; 25(7):2167. https://doi.org/10.3390/s25072167
Chicago/Turabian StyleHuang, Chenhui, Kenichiro Fukushi, Haruki Yaguchi, Keita Honda, Yusuke Sekiguchi, Zhenwei Wang, Yoshitaka Nozaki, Kentaro Nakahara, Satoru Ebihara, and Shin-Ichi Izumi. 2025. "Adapting Young Adults’ In-Shoe Motion Sensor Gait Models for Knee Evaluation in Older Adults: A Study on Osteoarthritis and Healthy Knees" Sensors 25, no. 7: 2167. https://doi.org/10.3390/s25072167
APA StyleHuang, C., Fukushi, K., Yaguchi, H., Honda, K., Sekiguchi, Y., Wang, Z., Nozaki, Y., Nakahara, K., Ebihara, S., & Izumi, S.-I. (2025). Adapting Young Adults’ In-Shoe Motion Sensor Gait Models for Knee Evaluation in Older Adults: A Study on Osteoarthritis and Healthy Knees. Sensors, 25(7), 2167. https://doi.org/10.3390/s25072167






