Performance Analysis of Data Augmentation Approaches for Improving Wrist-Based Fall Detection System
Abstract
1. Introduction
2. Related Work
2.1. Data Transformation
2.2. Synthetic Minority Over-Sampling Technique (SMOTE)
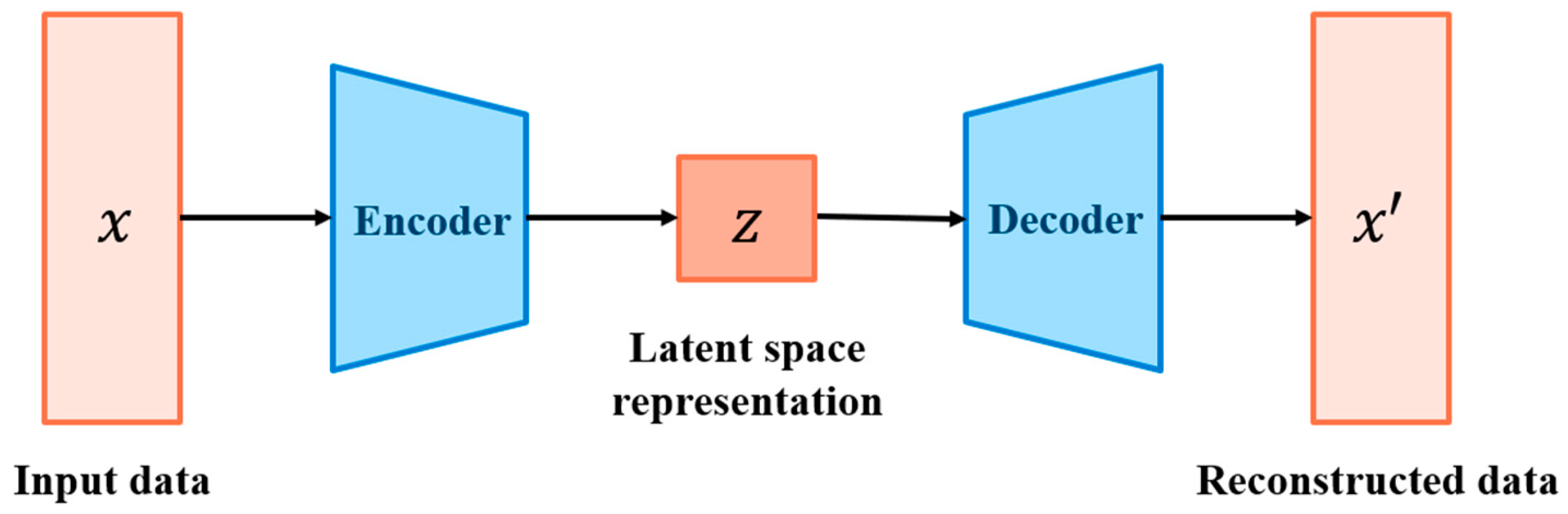
2.3. Autoencoder (AE)
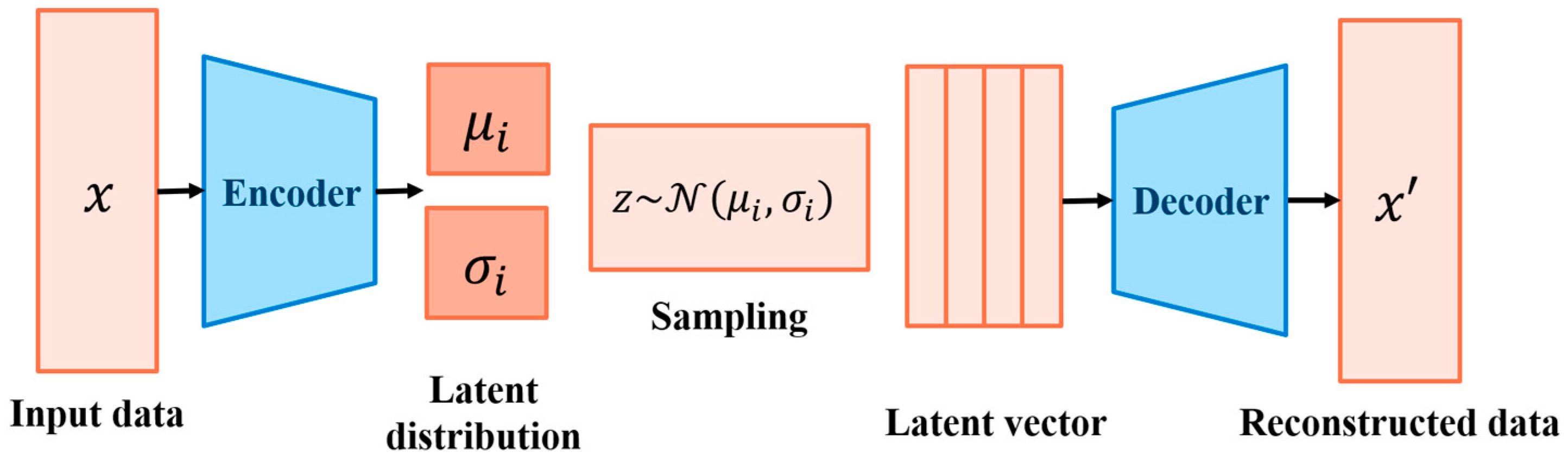
2.4. Variational Autoencoder (VAE)
2.5. Denoising Diffusion Probabilistic Model (DDPM)
3. Materials and Methods
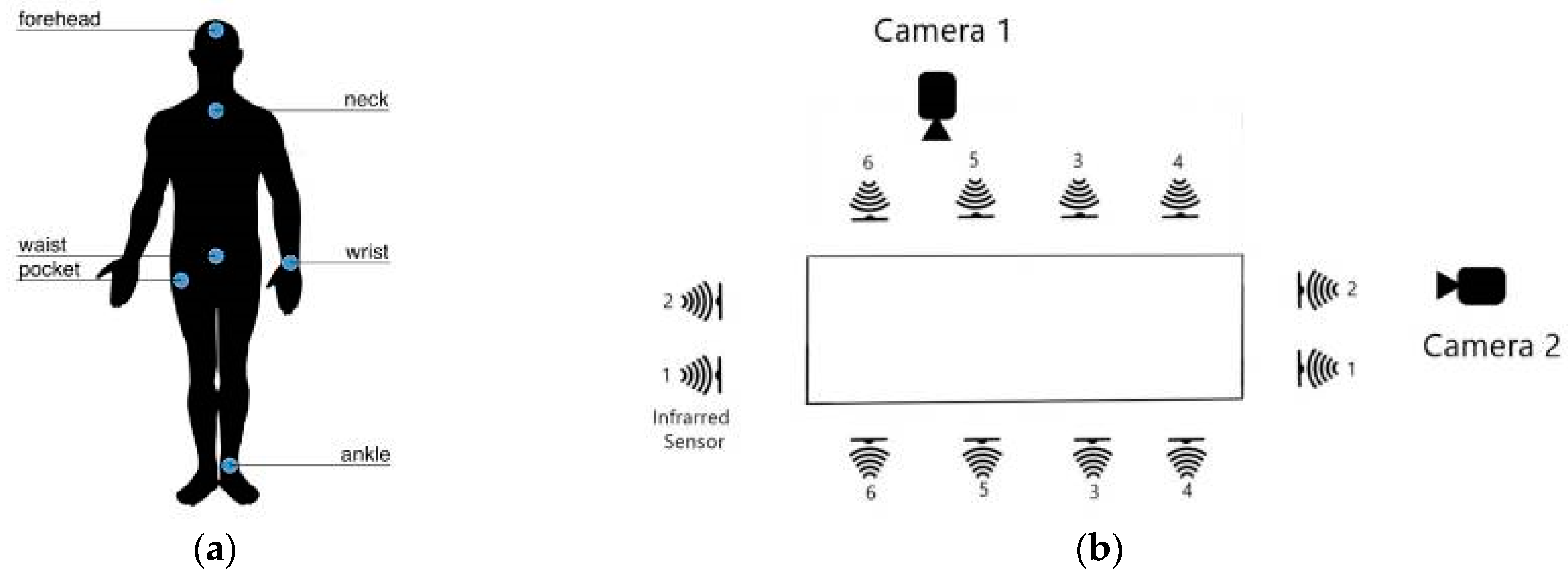
3.1. Dataset
3.2. Data Preprocessing
3.3. Implementation and Configuration
3.4. Evaluation Methodology
3.4.1. Fall Detection Performance
3.4.2. Divergence Comparison
4. Results and Discussions
4.1. Impact of Data Augmentation on Fall Detection Performance
4.2. Quality Assessment of Synthetic Data
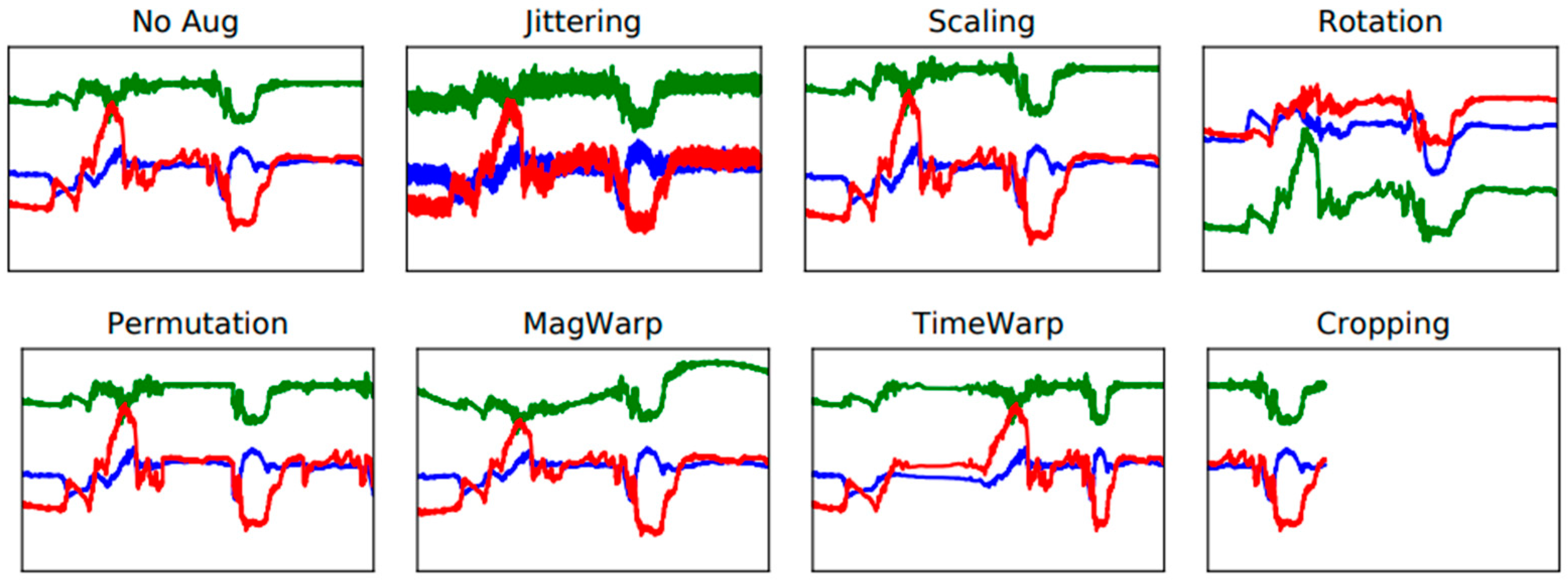
4.2.1. Visualization of Sensor Signals
4.2.2. Train on Synthetic Test on Real Score
4.2.3. Divergence Comparison on Synthetic Data
4.3. Computational Cost of the Data Augmentation Methods
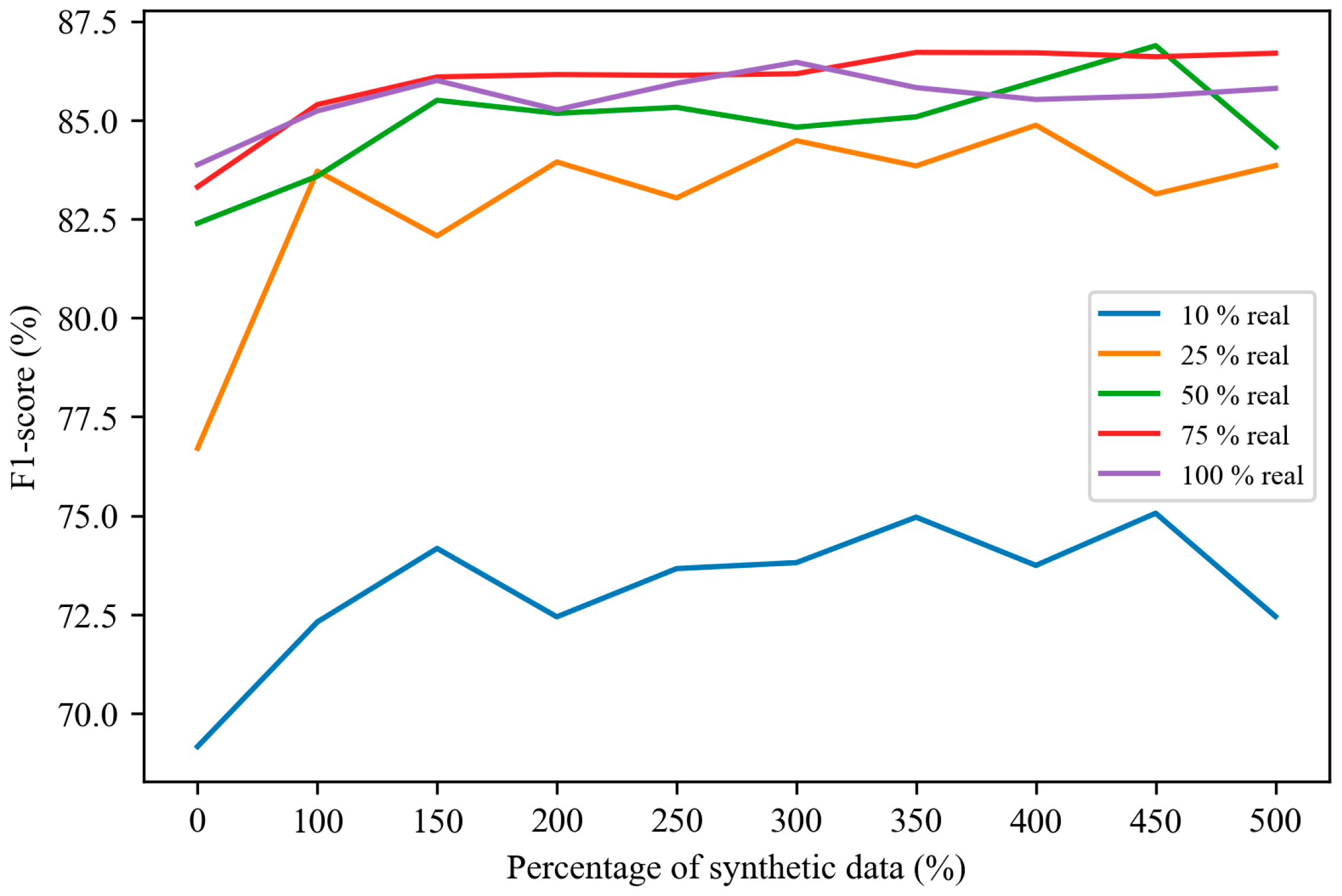
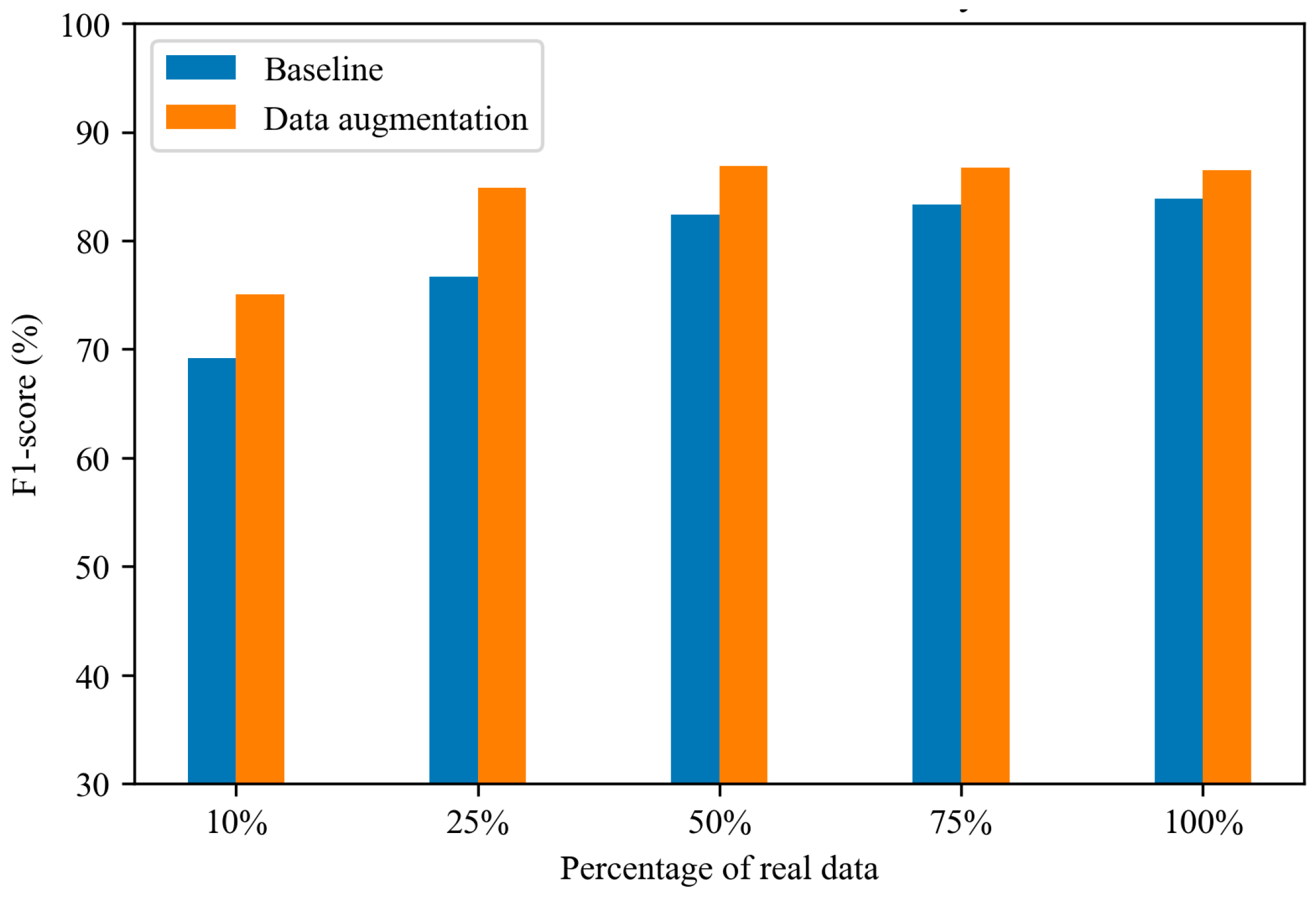
4.4. The Influence of Real-to-Synthetic Data Ratio on Fall Detection Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cutler, D.M.; Poterba, J.M.; Sheiner, L.M.; Summers, L.H.; Akerlof, G.A. An aging society: Opportunity or challenge? Brook. Pap. Econ. Act. 1990, 1990, 1–73. [Google Scholar] [CrossRef]
- Moye, J.; Marson, D.C.; Edelstein, B. Assessment of capacity in an aging society. Am. Psychol. 2013, 68, 158. [Google Scholar] [CrossRef] [PubMed]
- Harper, S. Economic and social implications of aging societies. Science 2014, 346, 587–591. [Google Scholar]
- Kaye, A.D.; Baluch, A.; Scott, J.T. Pain management in the elderly population: A review. Ochsner J. 2010, 10, 179–187. [Google Scholar] [PubMed]
- United States Census Bureau Census Bureau releases new estimates on America’s families and Living Arrangements. Census. Gov. Retr. August 2021, 30, 2022.
- Bergen, G.; Stevens, M.R.; Kakara, R.; Burns, E.R. Understanding modifiable and unmodifiable older adult fall risk factors to create effective prevention strategies. Am. J. Lifestyle Med. 2021, 15, 580–589. [Google Scholar]
- Lee, H.; Lim, J.H. Living alone, environmental hazards, and falls among US older adults. Innov. Aging 2023, 7, igad055. [Google Scholar] [CrossRef]
- Terroso, M.; Rosa, N.; Torres Marques, A.; Simoes, R. Physical consequences of falls in the elderly: A literature review from 1995 to 2010. Eur. Rev. Aging Phys. Act. 2014, 11, 51–59. [Google Scholar] [CrossRef]
- Donald, I.P.; Bulpitt, C.J. The prognosis of falls in elderly people living at home. Age Ageing 1999, 28, 121–125. [Google Scholar]
- Shumway-Cook, A.; Ciol, M.A.; Gruber, W.; Robinson, C. Incidence of and risk factors for falls following hip fracture in community-dwelling older adults. Phys. Ther. 2005, 85, 648–655. [Google Scholar] [CrossRef]
- Florence, C.S.; Bergen, G.; Atherly, A.; Burns, E.; Stevens, J.; Drake, C. Medical costs of fatal and nonfatal falls in older adults. J. Am. Geriatr. Soc. 2018, 66, 693–698. [Google Scholar] [CrossRef]
- Martini, D.; Pettigrew, N.; Wilhelm, J.; Parrington, L.; King, L. Wearable Sensors for Vestibular Rehabilitation: A Pilot Study. J. Physiother. Res 2021, 5, 31. [Google Scholar]
- Guo, Z.; Zhang, Z.; An, K.; He, T.; Sun, Z.; Pu, X.; Lee, C. A Wearable Multidimensional Motion Sensor for AI-Enhanced VR Sports. Research 2023, 6, 0154. [Google Scholar] [CrossRef]
- Seel, T.; Raisch, J.; Schauer, T. IMU-based joint angle measurement for gait analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef]
- Chen, J.; Kwong, K.; Chang, D.; Luk, J.; Bajcsy, R. Wearable sensors for reliable fall detection. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006; pp. 3551–3554. [Google Scholar]
- Hussain, F.; Hussain, F.; Ehatisham-ul-Haq, M.; Azam, M.A. Activity-aware fall detection and recognition based on wearable sensors. IEEE Sens. J. 2019, 19, 4528–4536. [Google Scholar] [CrossRef]
- Sucerquia, A.; López, J.D.; Vargas-Bonilla, J.F. SisFall: A fall and movement dataset. Sensors 2017, 17, 198. [Google Scholar] [CrossRef] [PubMed]
- Chai, X.; Wu, R.; Pike, M.; Jin, H.; Chung, W.-Y.; Lee, B.-G. Smart wearables with sensor fusion for fall detection in firefighting. Sensors 2021, 21, 6770. [Google Scholar] [CrossRef]
- Kangas, M.; Konttila, A.; Lindgren, P.; Winblad, I.; Jämsä, T. Comparison of low-complexity fall detection algorithms for body attached accelerometers. Gait Posture 2008, 28, 285–291. [Google Scholar] [CrossRef]
- Kangas, M.; Konttila, A.; Winblad, I.; Jamsa, T. Determination of simple thresholds for accelerometry-based parameters for fall detection. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 1367–1370. [Google Scholar]
- Bourke, A.K.; O’brien, J.; Lyons, G.M. Evaluation of a threshold-based tri-axial accelerometer fall detection algorithm. Gait Posture 2007, 26, 194–199. [Google Scholar] [CrossRef]
- Rucco, R.; Sorriso, A.; Liparoti, M.; Ferraioli, G.; Sorrentino, P.; Ambrosanio, M.; Baselice, F. Type and location of wearable sensors for monitoring falls during static and dynamic tasks in healthy elderly: A review. Sensors 2018, 18, 1613. [Google Scholar] [CrossRef]
- Pannurat, N.; Thiemjarus, S.; Nantajeewarawat, E. Automatic fall monitoring: A review. Sensors 2014, 14, 12900–12936. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Tan, K.K.; Lee, T.H.; Koh, G.C.H. Power-efficient interrupt-driven algorithms for fall detection and classification of activities of daily living. IEEE Sens. J. 2014, 15, 1377–1387. [Google Scholar]
- Noury, N.; Rumeau, P.; Bourke, A.K.; ÓLaighin, G.; Lundy, J. A proposal for the classification and evaluation of fall detectors. Irbm 2008, 29, 340–349. [Google Scholar] [CrossRef]
- De Quadros, T.; Lazzaretti, A.E.; Schneider, F.K. A movement decomposition and machine learning-based fall detection system using wrist wearable device. IEEE Sens. J. 2018, 18, 5082–5089. [Google Scholar]
- Mauldin, T.R.; Canby, M.E.; Metsis, V.; Ngu, A.H.; Rivera, C.C. SmartFall: A smartwatch-based fall detection system using deep learning. Sensors 2018, 18, 3363. [Google Scholar] [CrossRef]
- Kraft, D.; Srinivasan, K.; Bieber, G. Deep learning based fall detection algorithms for embedded systems, smartwatches, and IoT devices using accelerometers. Technologies 2020, 8, 72. [Google Scholar] [CrossRef]
- Martínez-Villaseñor, L.; Ponce, H.; Brieva, J.; Moya-Albor, E.; Núñez-Martínez, J.; Peñafort-Asturiano, C. UP-fall detection dataset: A multimodal approach. Sensors 2019, 19, 1988. [Google Scholar] [CrossRef]
- Um, T.T.; Pfister, F.M.; Pichler, D.; Endo, S.; Lang, M.; Hirche, S.; Fietzek, U.; Kulić, D. Data augmentation of wearable sensor data for parkinson’s disease monitoring using convolutional neural networks. In Proceedings of the 19th ACM International Conference on Multimodal Interaction, Glasgow, UK, 13–17 November 2017; pp. 216–220. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar]
- Zhai, J.; Zhang, S.; Chen, J.; He, Q. Autoencoder and its various variants. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 415–419. [Google Scholar]
- Kingma, D.P. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18, 2015. pp. 234–241. [Google Scholar]
- Zhang, K.; Li, Y.; Liang, J.; Cao, J.; Zhang, Y.; Tang, H.; Fan, D.-P.; Timofte, R.; Gool, L.V. Practical blind image denoising via Swin-Conv-UNet and data synthesis. Mach. Intell. Res. 2023, 20, 822–836. [Google Scholar]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 205–218. [Google Scholar]
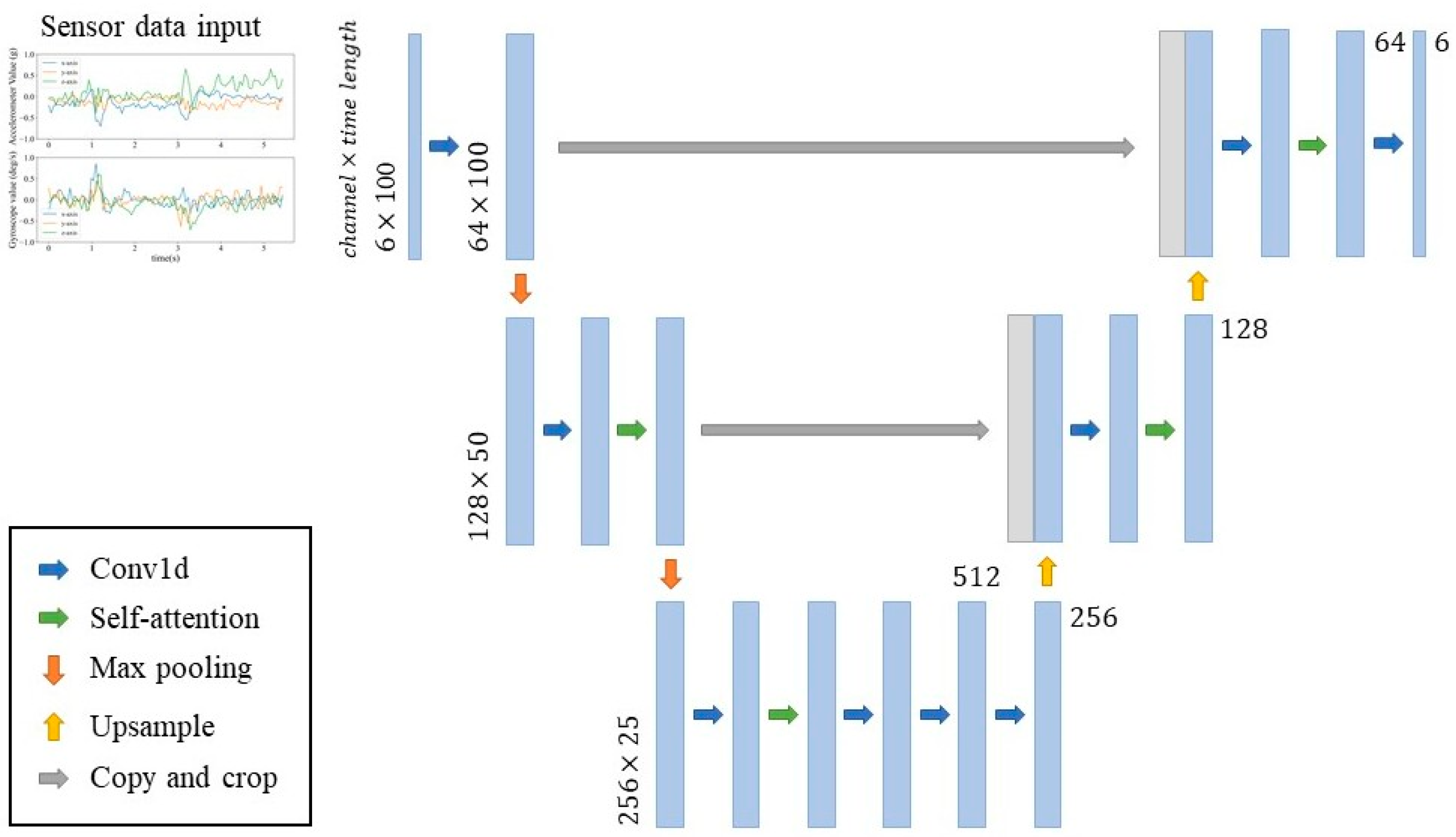
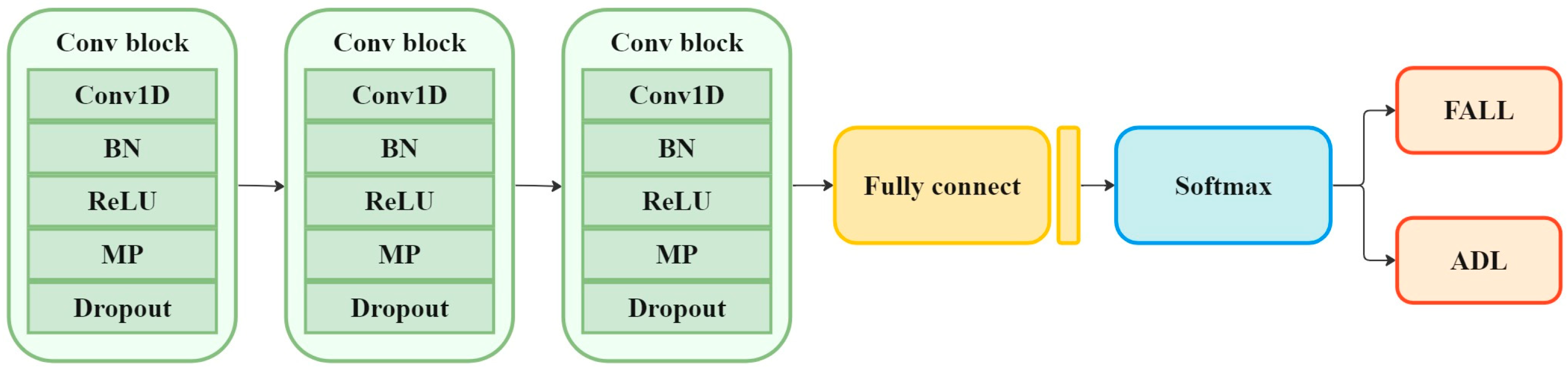
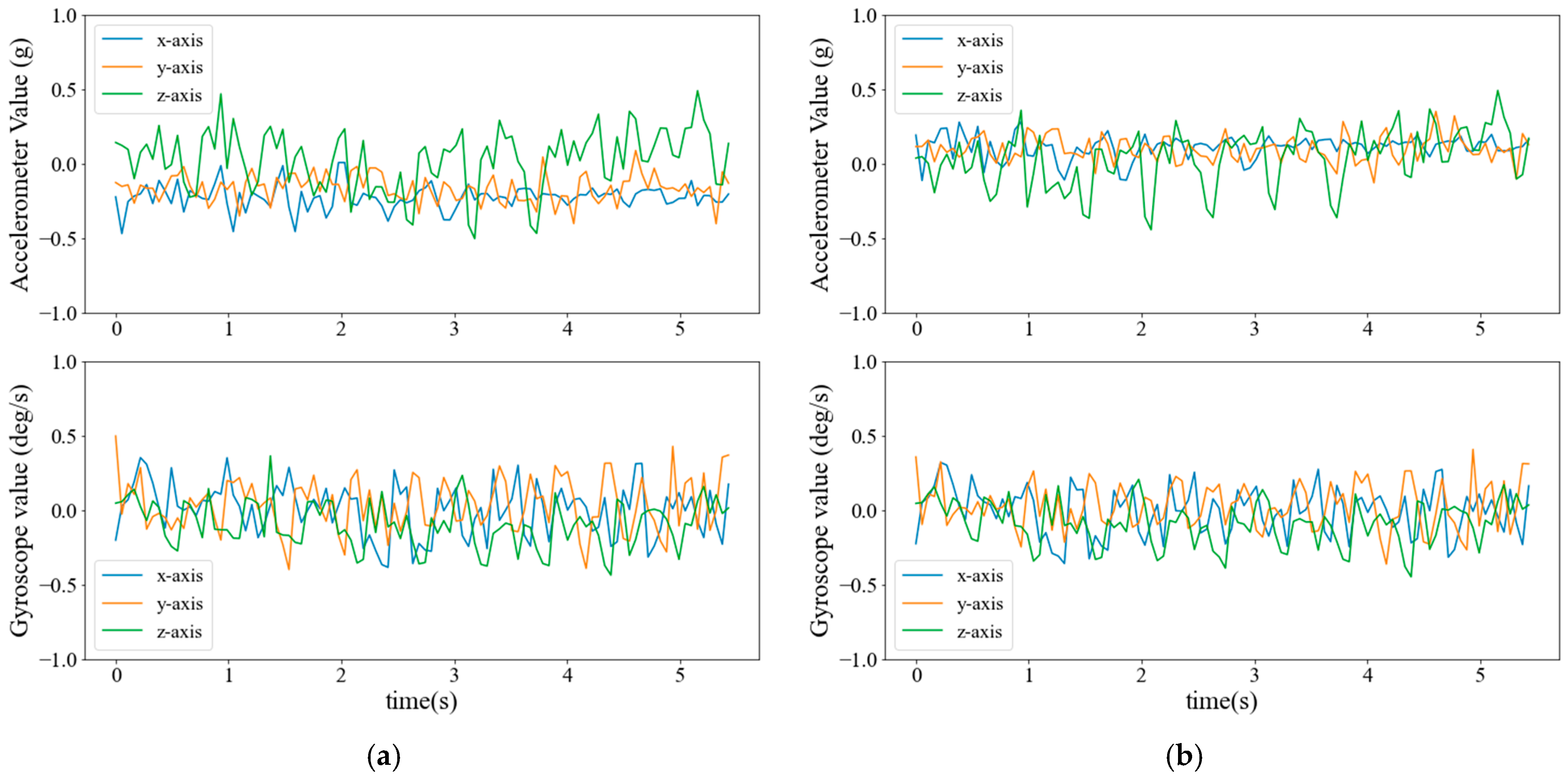

| Module | Layer | Output_Size |
|---|---|---|
| Encoder | Conv1D (64, 3) MaxPool1D (2) Conv1D (128, 3) MaxPool1D (2) Conv1D (256, 3) MaxPool1D (2) | (64, 98) (64, 49) (128, 47) (128, 23) (256, 21) (256, 10) |
| Decoder | Upsample (28) Transposed Conv1D (128, 3) Upsample (61) Transposed Conv1D (64, 3) Upsample (126) Transposed Conv1D (6, 3) | (256, 21) (128, 23) (128, 47) (64, 49) (64, 98) (6, 100) |
| Hyperparameter | Searchspace |
|---|---|
| Learning rate | |
| Epochs | |
| Conv1D layers | |
| Conv1D (number of output channels) | |
| Conv1D (kernel size) |
| Module | Layer | Output_Size |
|---|---|---|
| Encoder | Conv1D (64, 5) Conv1D (64, 5) Conv1D (64, 3) Conv1D (64, 3) MaxPool1D (2) | (64, 100) (64, 100) (64, 100) (64, 100) (64, 50) |
| Bottleneck | Linear (128) | (64, 128) |
| Decoder | Linear (50) Upsample (100) Conv1D (64, 3) Conv1D (64, 3) Conv1D (64, 5) Conv1D (6, 5) | (64, 50) (64, 100) (64, 100) (64, 100) (64, 100) (6, 100) |
| Hyperparameter | Searchspace |
|---|---|
| Learning rate | |
| Epochs | |
| Conv1D layers | |
| Conv1D (number of output channels) | |
| Conv1D (kernel size) |
| Hyperparameter | Searchspace |
|---|---|
| Learning rate | |
| Diffusion timesteps | |
| Epochs | |
| Down and up-sampling layers |
| Model | Hyperparameter | Value |
|---|---|---|
| Autoencoder | Learning rate | 3 × 10−4 |
| Epochs | 100 | |
| Conv1D layers | 3 | |
| Conv1D (number of output channels) | 64, 128, and 256, respectively, in three layers | |
| Conv1D (kernel size) | 3 | |
| VAE | Learning rate | 5 × 10−4 |
| Epochs | 100 | |
| Conv1D layers | 4 | |
| Conv1D (number of output channels) | 64 | |
| Conv1D (kernel size) | 3 and 5, respectively, in four layers | |
| Diffusion model | Learning rate | 3 × 10−4 |
| Diffusion timesteps | 1000 | |
| Epochs | 300 | |
| Down and up-sampling layers | 2 |
| Model | 100% Real | 25% Real | ||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1 | Accuracy | Precision | Recall | F1 | |
| BL | 92.94 | 91.64 | 78.59 | 83.87 | 88.08 | 75.26 | 79.97 | 76.70 |
| DTF | 92.93 | 90.88 | 79.66 | 84.14 | 90.73 | 80.30 | 83.83 | 81.45 |
| SMOTE | 92.89 | 89.09 | 81.08 | 84.44 | 90.39 | 77.35 | 86.42 | 81.44 |
| AE | 92.85 | 91.03 | 78.91 | 83.68 | 91.54 | 82.12 | 83.43 | 82.42 |
| VAE | 93.24 | 91.03 | 80.64 | 84.62 | 91.29 | 83.14 | 82.59 | 81.84 |
| DM | 93.30 | 85.79 | 87.05 | 86.00 | 91.75 | 82.17 | 86.07 | 83.28 |
| Model | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|
| DTF | 99.64 | 98.92 | 99.64 | 99.28 |
| SMOTE | 96.69 | 89.39 | 98.41 | 93.67 |
| AE | 53.13 | 53.48 | 51.52 | 52.44 |
| VAE | 59.30 | 57.60 | 75.38 | 64.95 |
| DM | 91.30 | 75.51 | 96.45 | 84.67 |
| Model | Fall/ADL | Real/Synthetic | ||||
|---|---|---|---|---|---|---|
| Inner | Outer | Ratio | Inner | Outer | Ratio | |
| DTF | 0.0023 | 0.00003 | 0.0130 | 5.50319 | 0.04927 | 0.00895 |
| SMOTE | 0.0019 | 0.00006 | 0.0308 | 5.55463 | 0.04824 | 0.00868 |
| AE | 0.0018 | 0.00001 | 0.0056 | 5.70100 | 0.03291 | 0.00577 |
| VAE | 0.0003 | 0.000002 | 0.0062 | 5.43478 | 0.03999 | 0.00736 |
| DM | 0.0022 | 0.00009 | 0.0404 | 5.45769 | 0.02520 | 0.00462 |
| Model | Computation Time (s) | Parameter (Byte) |
|---|---|---|
| DTF | 195.91 | - |
| SMOTE | 111.30 | - |
| AE | 250.81 | 207,128 |
| VAE | 283.76 | 462,144 |
| DM | 1165.32 | 21,115,928 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, Y.-C.; Lin, C.-Y.; Liu, C.-P.; Chan, C.-T. Performance Analysis of Data Augmentation Approaches for Improving Wrist-Based Fall Detection System. Sensors 2025, 25, 2168. https://doi.org/10.3390/s25072168
Tu Y-C, Lin C-Y, Liu C-P, Chan C-T. Performance Analysis of Data Augmentation Approaches for Improving Wrist-Based Fall Detection System. Sensors. 2025; 25(7):2168. https://doi.org/10.3390/s25072168
Chicago/Turabian StyleTu, Yu-Chen, Che-Yu Lin, Chien-Pin Liu, and Chia-Tai Chan. 2025. "Performance Analysis of Data Augmentation Approaches for Improving Wrist-Based Fall Detection System" Sensors 25, no. 7: 2168. https://doi.org/10.3390/s25072168
APA StyleTu, Y.-C., Lin, C.-Y., Liu, C.-P., & Chan, C.-T. (2025). Performance Analysis of Data Augmentation Approaches for Improving Wrist-Based Fall Detection System. Sensors, 25(7), 2168. https://doi.org/10.3390/s25072168






