MicrocrackAttentionNext: Advancing Microcrack Detection in Wave Field Analysis Using Deep Neural Networks Through Feature Visualization
Abstract
1. Introduction
- Introducing MicrocrackAttentionNext—an improvement over [16]—and introduction of Adaptive Feature Utilization Block for efficient feature utilization.
- Analysis of the impact of activation functions on the performance of MicrocrackAttentionNext through Manifold Discovery and Analysis in the context of microcrack detection.
2. Related Works
3. Method
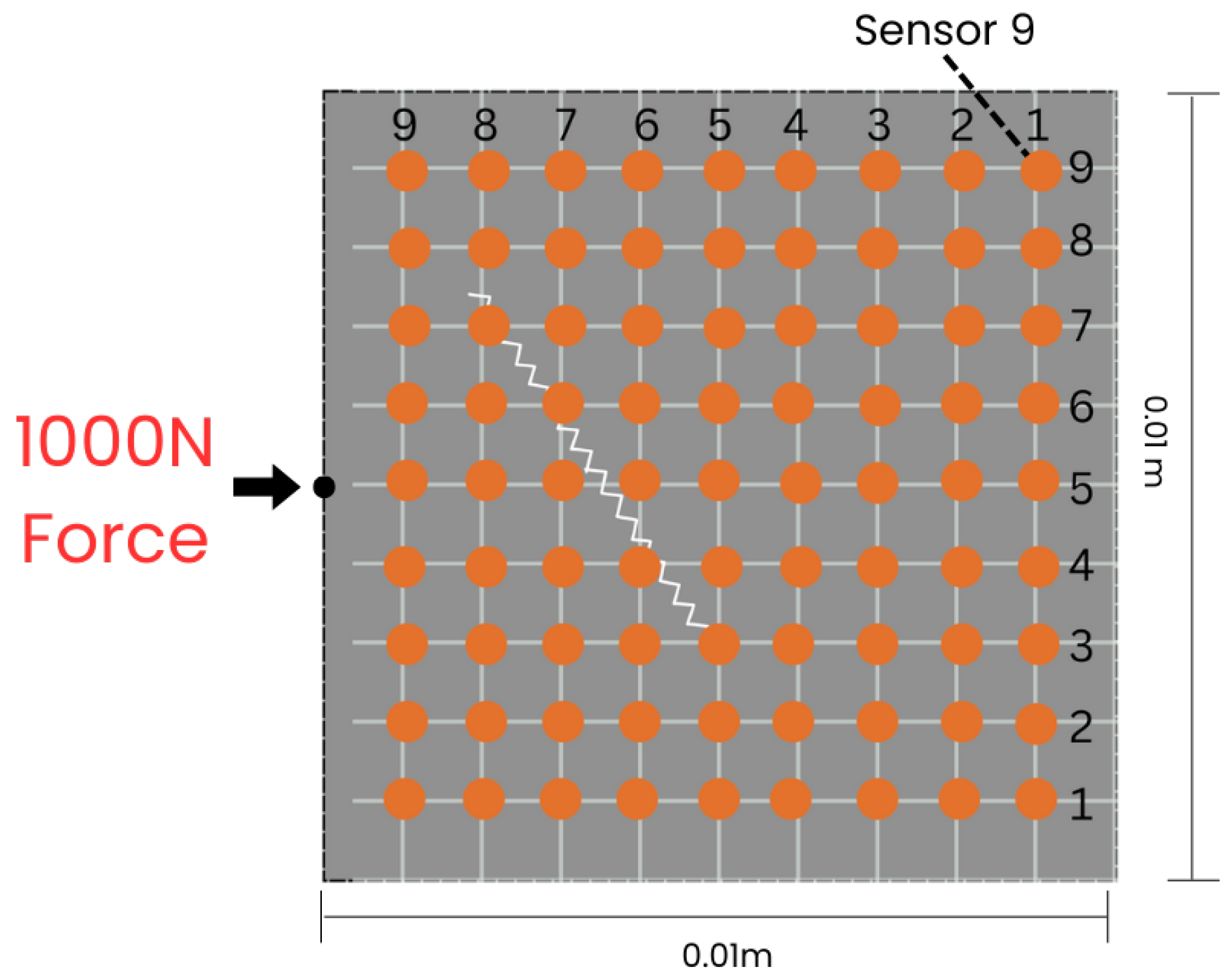
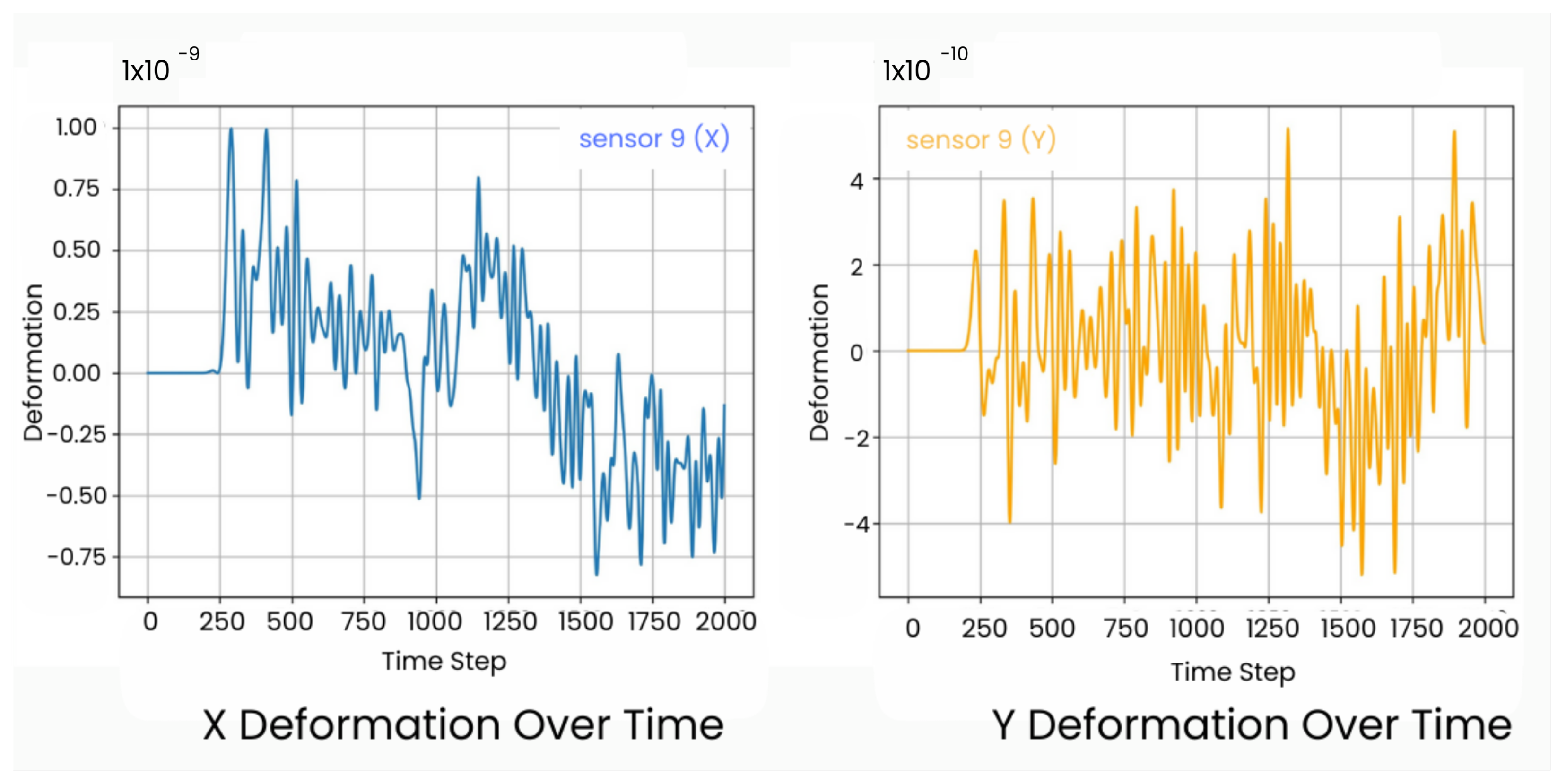
3.1. Wave Field Data
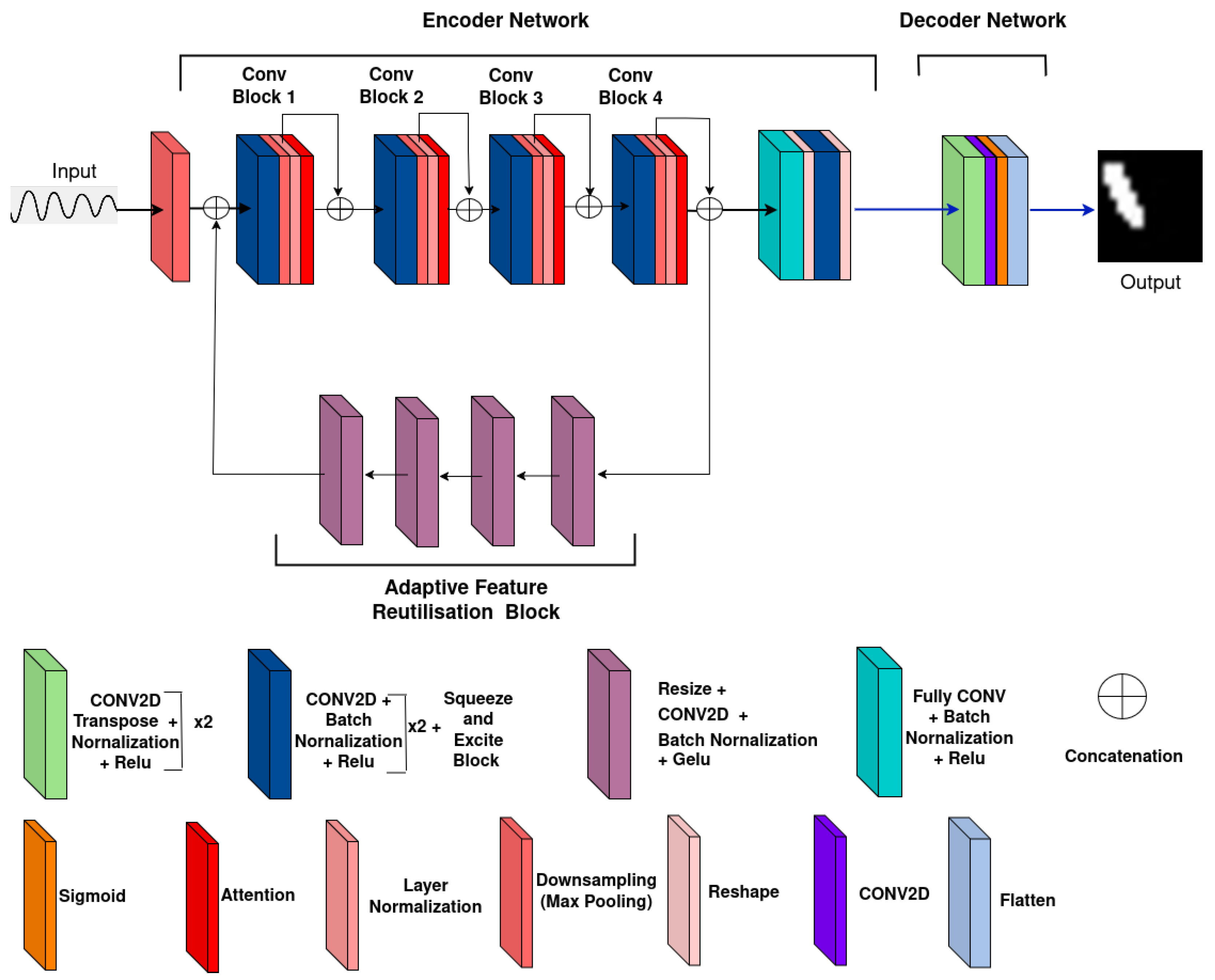
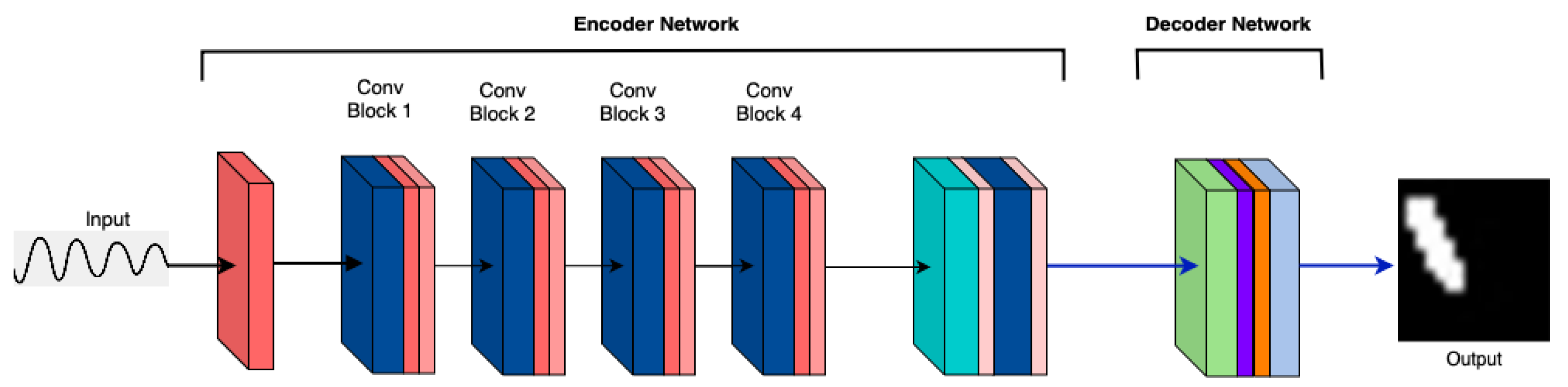
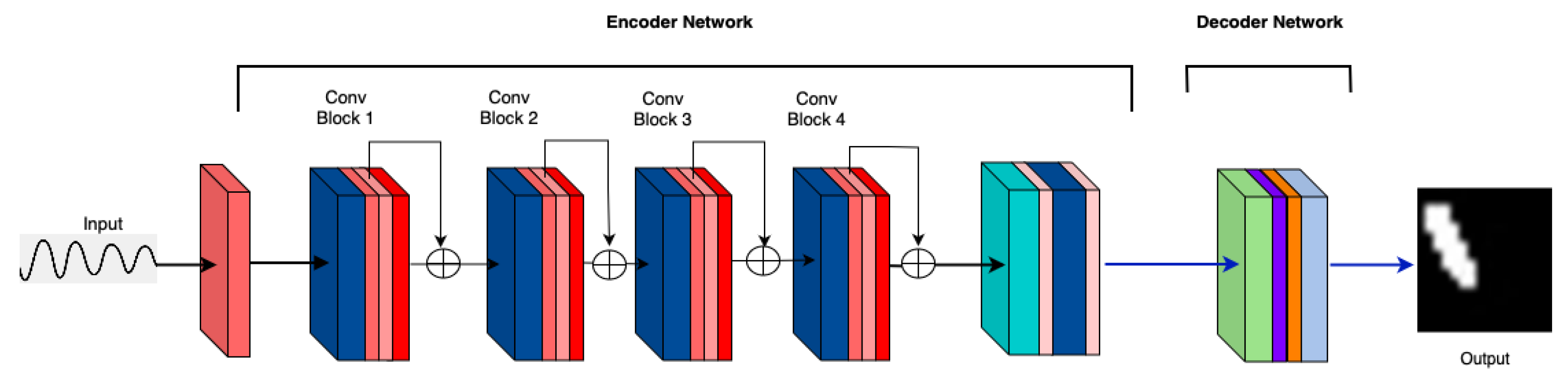
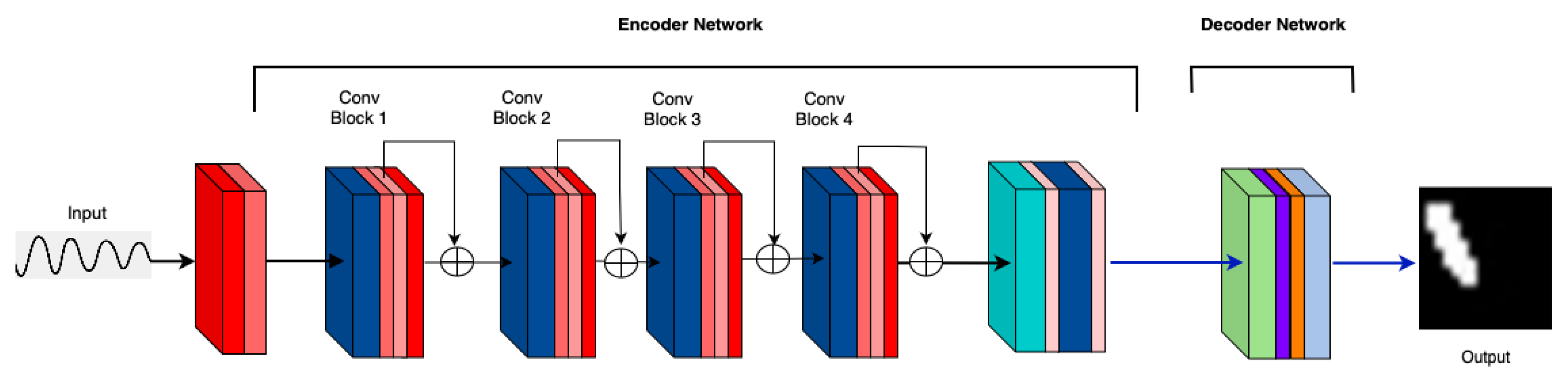
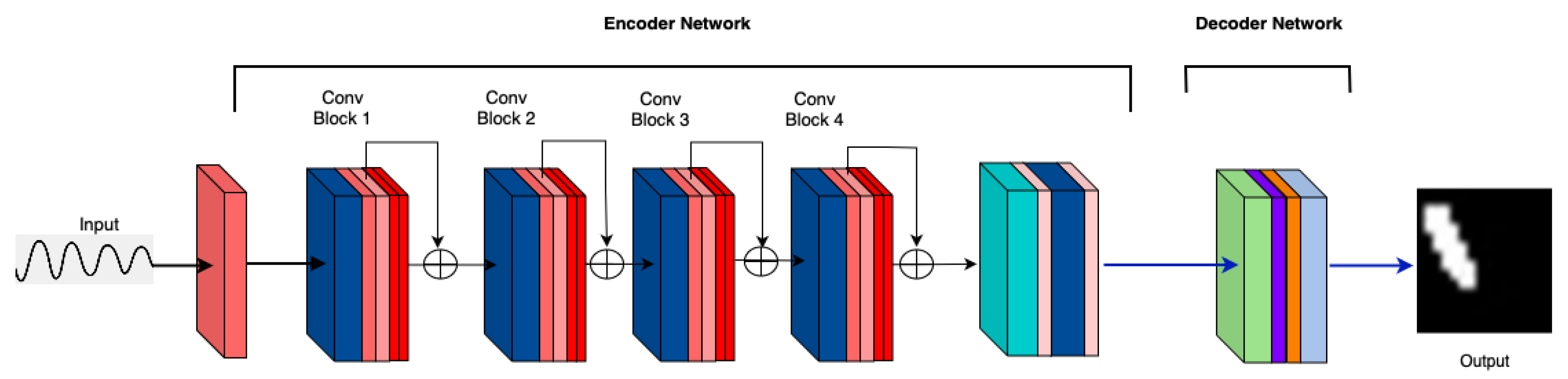
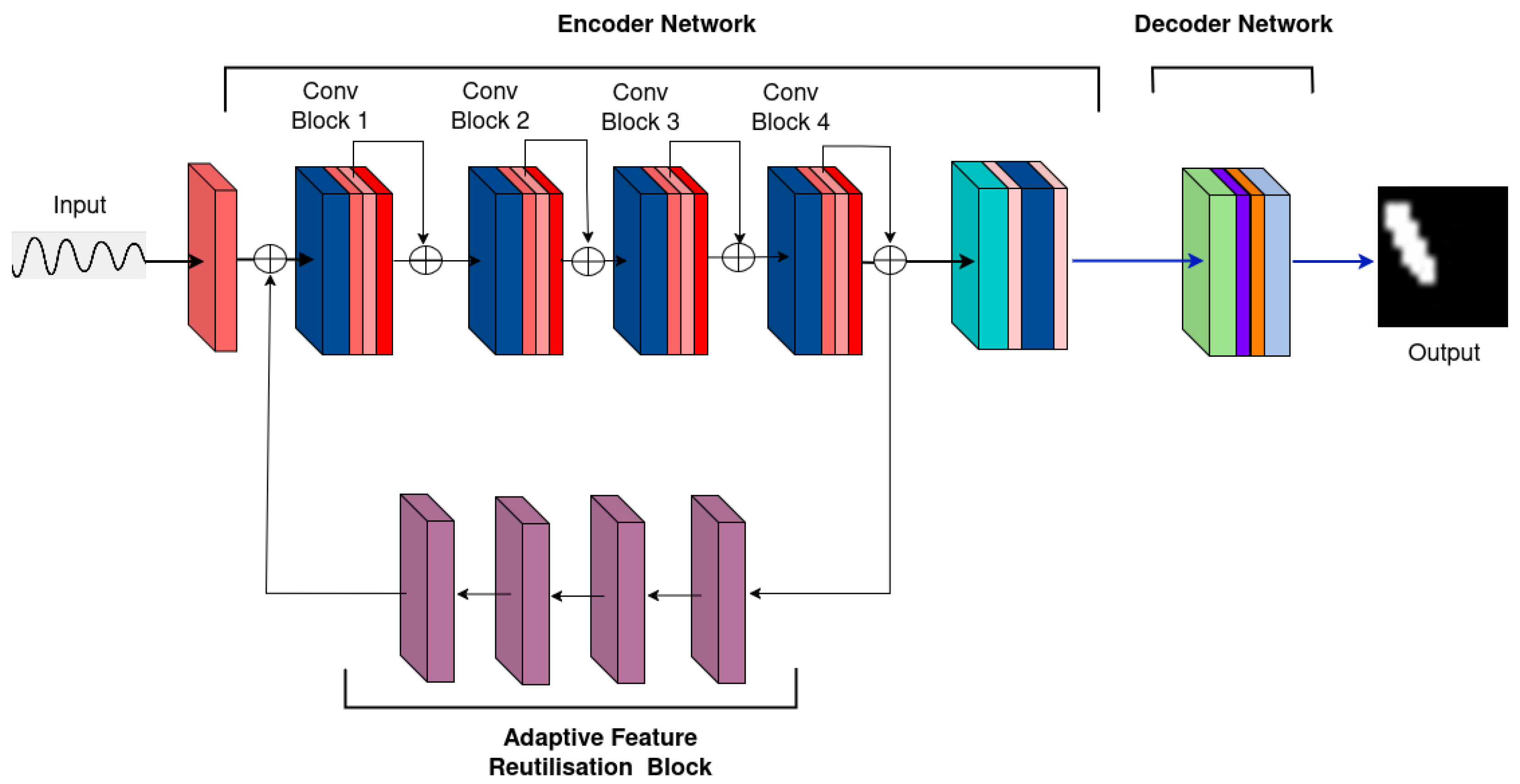
3.2. MicrocrackAttentionNext Model Architecture
4. Experiments
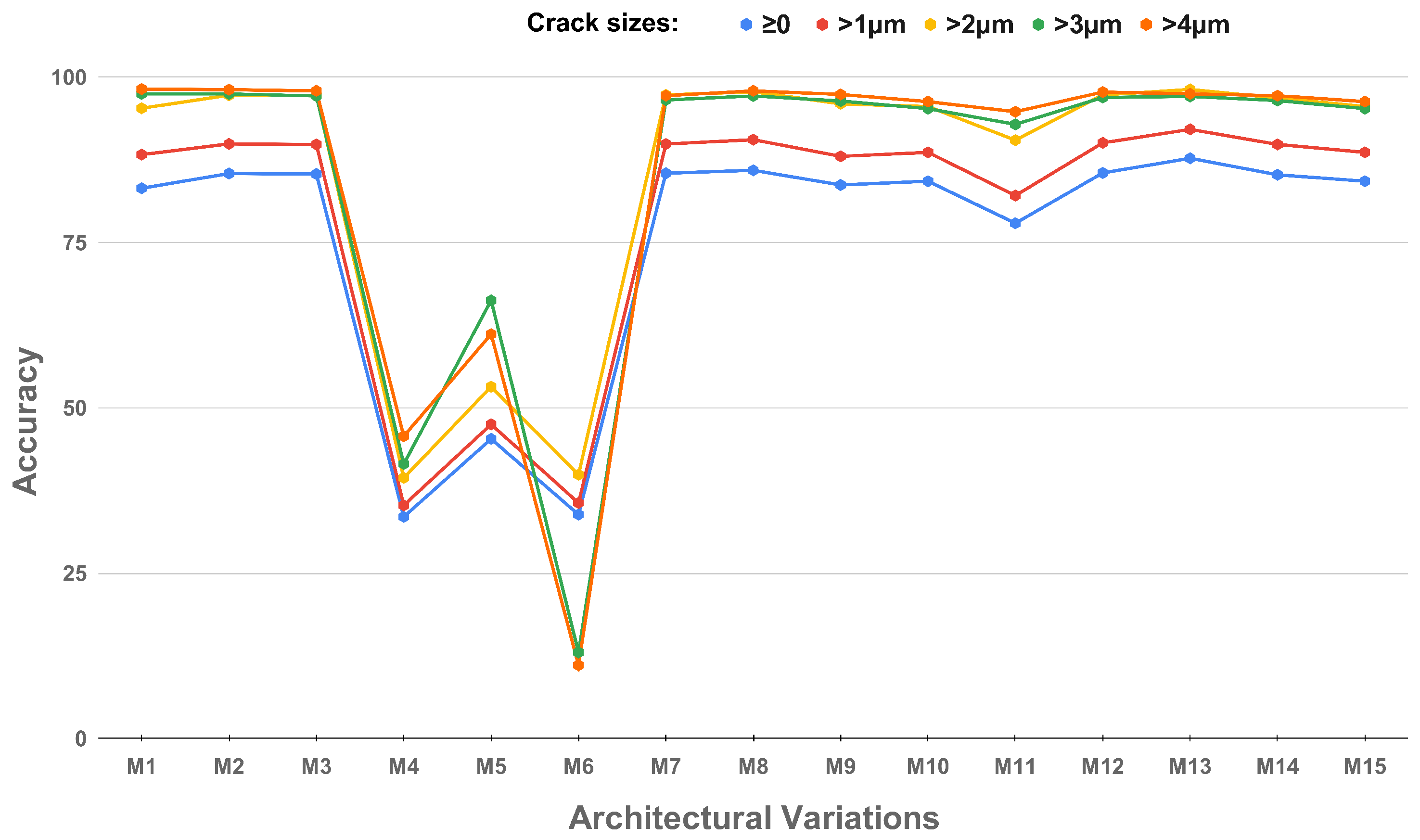
4.1. Architectural Choices
4.1.1. Attention Mechanism Placement
4.1.2. Pooling Variants
4.1.3. Consecutive Attention Layers in the Encoder
4.2. Training Procedure
4.2.1. Activation Functions
4.2.2. Loss Functions
- 1.
- Dice Loss [41]:Dice loss is based on the Dice coefficient and is commonly used for segmentation tasks. It measures the overlap between the predicted and true labels, focusing on improving performance for imbalanced datasets.where X and Y are the predicted and true sets, respectively.
- 2.
- Focal Loss [41]:Focal loss is designed to address class imbalance by down-weighting the loss assigned to well-classified examples, making the model focus more on hard-to-classify instances.where is the predicted probability, is a weighting factor, and is a focusing parameter.
- 3.
- Weighted Dice Loss [42]:Weighted Dice loss is a variation of Dice loss that assigns different weights to different classes, enhancing performance on datasets with imbalanced class distributions by penalizing certain classes more.where is the weight assigned to class i, and , are the predicted and true values for class i.
- 4.
- Combined Weighted Dice Loss [43]:This is a hybrid loss that combines weighted Dice loss and CrossEntropy loss, allowing the model to balance overall performance while addressing class imbalances by tuning the contribution of each component.where CWDL is combined weighted Dice loss, WDL is weighted Dice loss, and is a weighting factor to balance the two loss components.
4.3. Evaluation Metrics
5. Results and Discussion
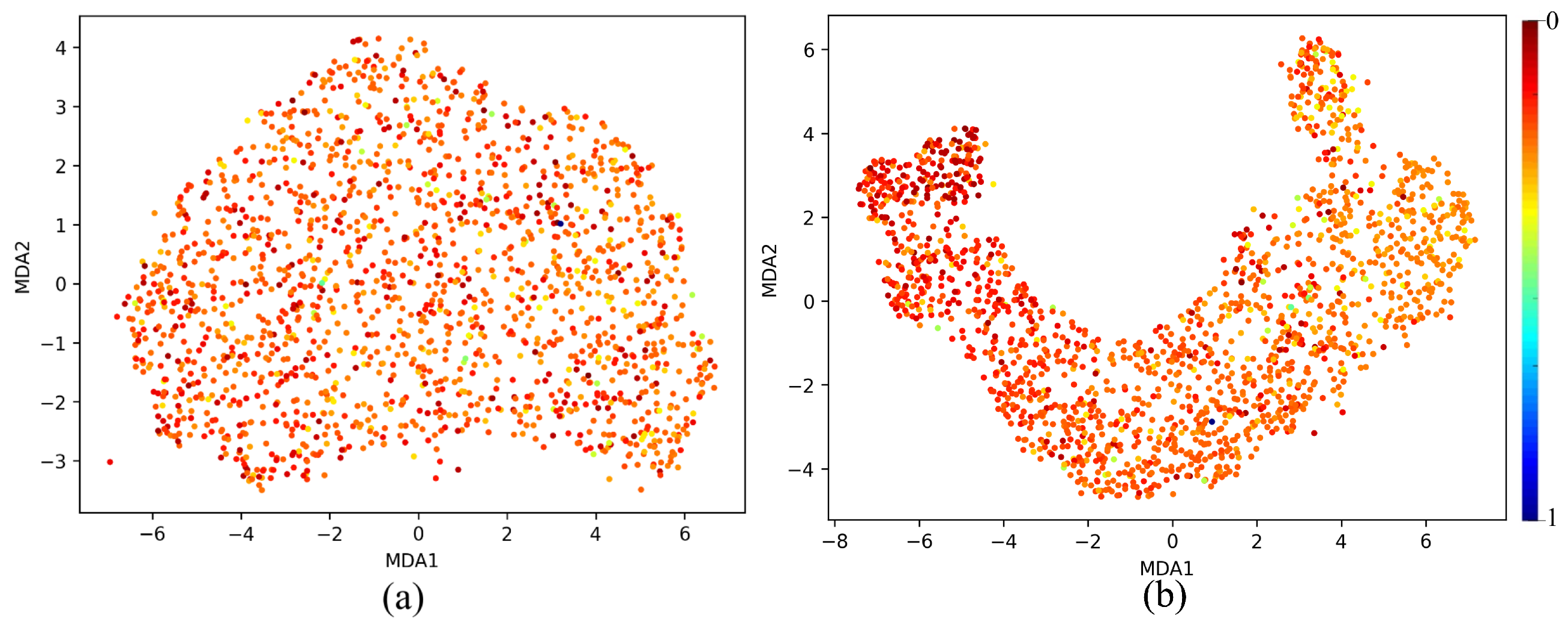
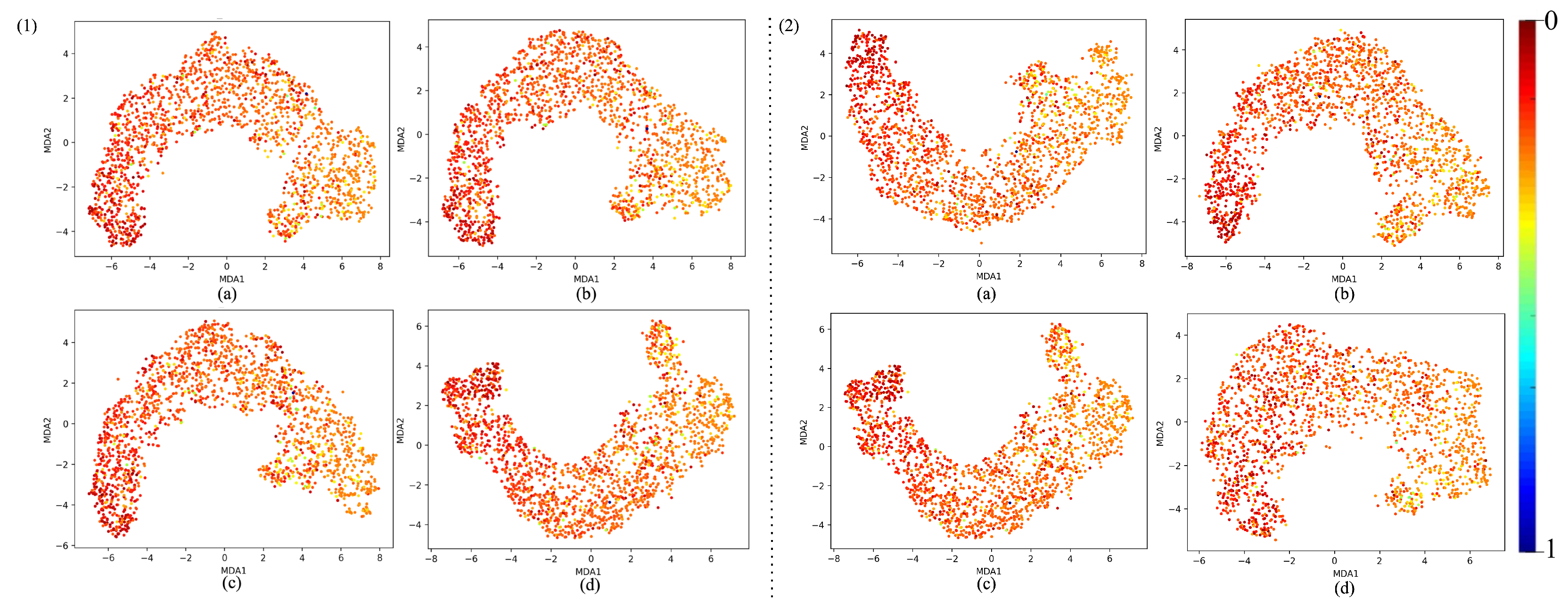
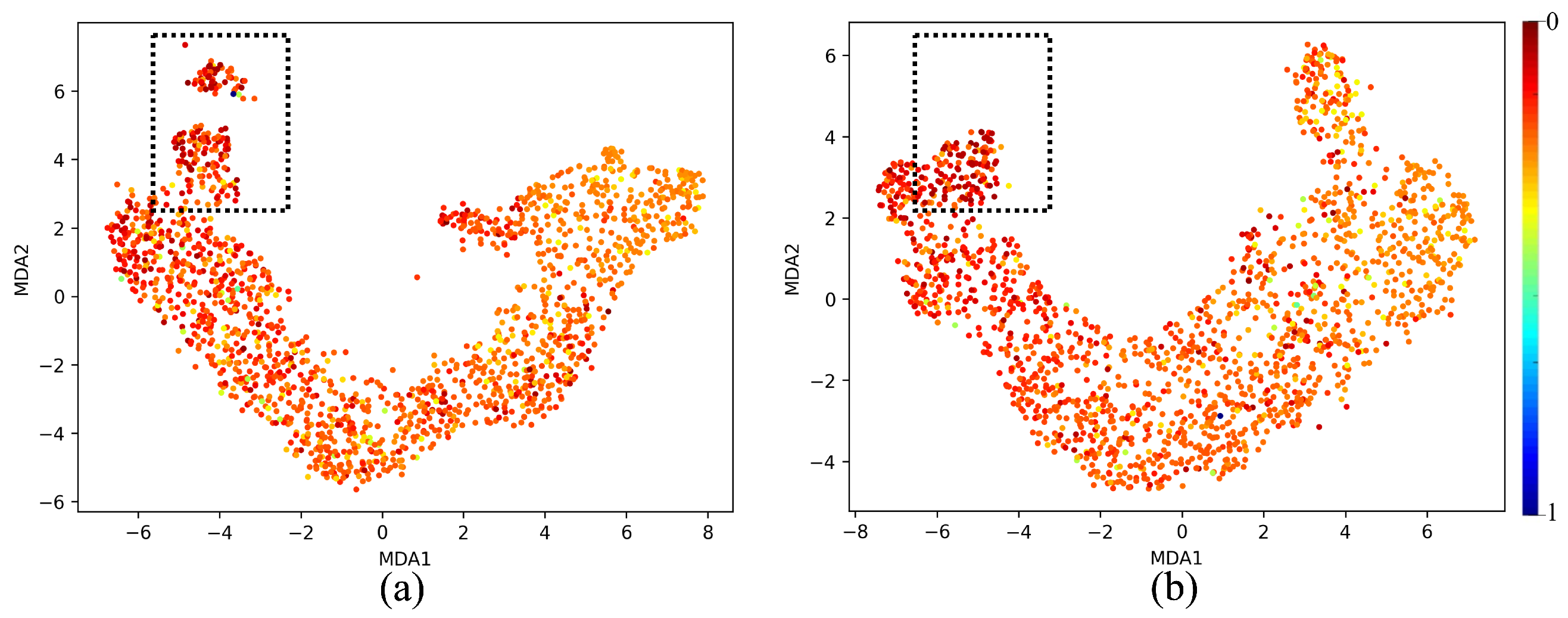
5.1. MDA Analysis
- Feature Separation and Continuity: The MDA visualization shows a curved shape, indicating that the features extracted from the neural network follow a smooth continuum along the manifold. This suggests that the neural network is capturing meaningful information.
- Color Gradient: A spectrum of gradients is shown, implying that the model has learned to separate different features.
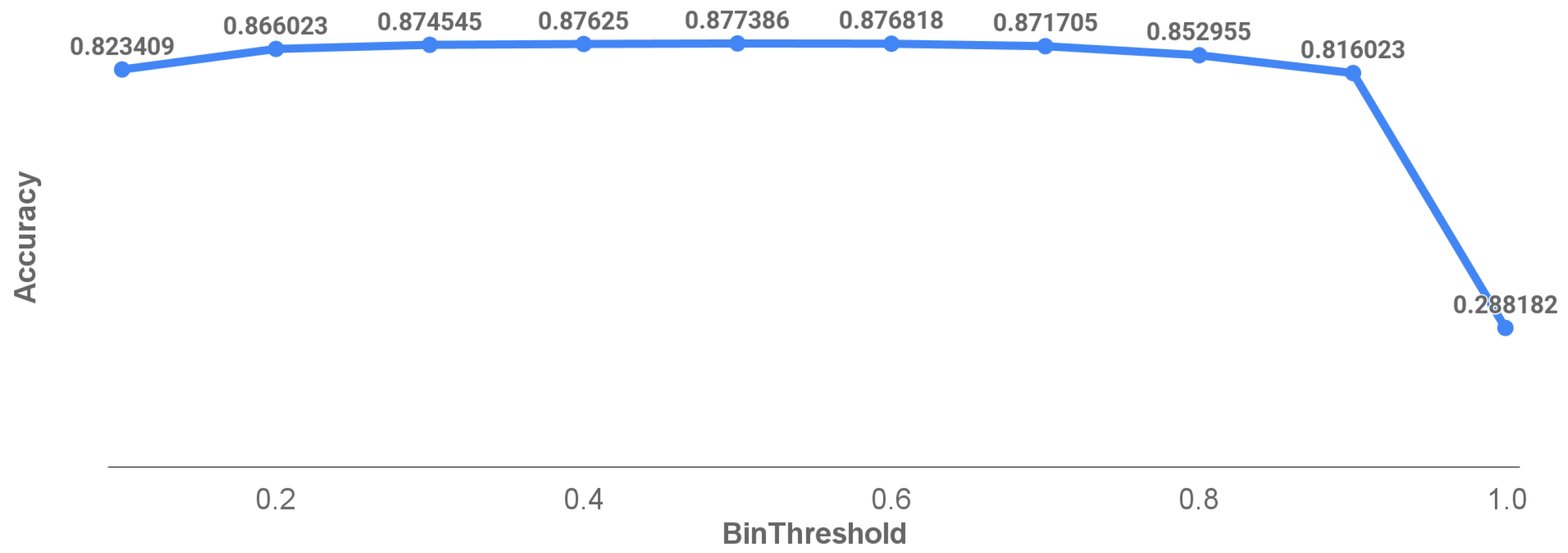
5.2. Thresholding Analysis in Prediction Accuracy
5.3. Comparison with Similar Works
6. Conclusions and Future Work
6.1. Conclusions
6.2. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AE | Acoustic Emission |
| CNN | Convolutional Neural Network |
| CWDL | Combined Weighted Dice Loss |
| DL | Dice Loss |
| DSC | Dice Similarity Coefficient |
| DNN | Deep Neural Network |
| FL | Focal Loss |
| GELU | Gaussian Error Linear Unit |
| IoU | Intersection over Union |
| LEM | Lattice Element Method |
| MDA | Manifold Discovery and Analysis |
| MDPI | Multidisciplinary Digital Publishing Institute |
| NDT | Non-Destructive Testing |
| ReLU | Rectified Linear Unit |
| SAW | Surface Acoustic Wave |
| SE | Squeeze-and-Excitation |
| SELU | Scaled Exponential Linear Unit |
| TConv | Transposed Convolution |
| TOFD | Time-of-Flight Diffraction |
| WDL | Weighted Dice Loss |
References
- Malekloo, A.; Ozer, E.; AlHamaydeh, M.; Girolami, M. Machine learning and structural health monitoring overview with emerging technology and high-dimensional data source highlights. Struct. Health Monit. 2022, 21, 1906–1955. [Google Scholar] [CrossRef]
- Golewski, G.L. The Phenomenon of Cracking in Cement Concretes and Reinforced Concrete Structures: The Mechanism of Cracks Formation, Causes of Their Initiation, Types and Places of Occurrence, and Methods of Detection—A Review. Buildings 2023, 13, 765. [Google Scholar] [CrossRef]
- Chen, B.; Yang, J.; Zhang, D.; Liu, W.; Li, J.; Zhang, M. The Method and Experiment of Micro-Crack Identification Using OFDR Strain Measurement Technology. Photonics 2024, 11, 755. [Google Scholar] [CrossRef]
- Yuan, B.; Ying, Y.; Morgese, M.; Ansari, F. Theoretical and Experimental Studies of Micro-Surface Crack Detections Based on BOTDA. Sensors 2022, 22, 3529. [Google Scholar] [CrossRef]
- Retheesh, R.; Samuel, B.; Radhakrishnan, P.; Mujeeb, A. Detection and analysis of micro cracks in low modulus materials with thermal loading using laser speckle interferometry. Russ. J. Nondestruct. Test. 2017, 53, 236–242. [Google Scholar] [CrossRef]
- Choi, Y.; Park, H.W.; Mi, Y.; Song, S. Crack Detection and Analysis of Concrete Structures Based on Neural Network and Clustering. Sensors 2024, 24, 1725. [Google Scholar] [CrossRef]
- Animashaun, D.; Hussain, M. Automated Micro-Crack Detection within Photovoltaic Manufacturing Facility via Ground Modelling for a Regularized Convolutional Network. Sensors 2023, 23, 6235. [Google Scholar] [CrossRef]
- Andleeb, I.; Hussain, B.Z.; Joncas, J.; Barchi, S.; Roy-Beaudry, M.; Parent, S.; Grimard, G.; Labelle, H.; Duong, L. Automatic Evaluation of Bone Age Using Hand Radiographs and Pancorporal Radiographs in Adolescent Idiopathic Scoliosis. Diagnostics 2025, 15, 452. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Moorthy, J.; Gandhi, U.D. A Survey on Medical Image Segmentation Based on Deep Learning Techniques. Big Data Cogn. Comput. 2022, 6, 117. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2020, arXiv:1802.03426. [Google Scholar]
- Islam, M.T.; Zhou, Z.; Ren, H.; Khuzani, M.B.; Kapp, D.; Zou, J.; Tian, L.; Liao, J.C.; Xing, L. Revealing hidden patterns in deep neural network feature space continuum via manifold learning. Nat. Commun. 2023, 14, 8506. [Google Scholar] [CrossRef]
- Moreh, F.; Lyu, H.; Rizvi, Z.H.; Wuttke, F. Deep neural networks for crack detection inside structures. Sci. Rep. 2024, 14, 4439. [Google Scholar] [CrossRef]
- Punnose, S.; Balasubramanian, T.; Pardikar, R.; Palaniappan, M.; Subbaratnam, R. Time-of-flight diffraction (TOFD) technique for accurate sizing of surface-breaking cracks. Insight 2003, 45, 426–430. [Google Scholar] [CrossRef]
- Kou, X.; Pei, C.; Chen, Z. Fully noncontact inspection of closed surface crack with nonlinear laser ultrasonic testing method. Ultrasonics 2021, 114, 106426. [Google Scholar] [CrossRef]
- Su, C.; Wang, W. Concrete Cracks Detection Using Convolutional NeuralNetwork Based on Transfer Learning. Math. Probl. Eng. 2020, 2020, 7240129. [Google Scholar] [CrossRef]
- Chen, F.C.; Jahanshahi, M. NB-CNN: Deep Learning-based Crack Detection Using Convolutional Neural Network and Naïve Bayes Data Fusion. IEEE Trans. Ind. Electron. 2018, 65, 4392–4400. [Google Scholar] [CrossRef]
- Hamishebahar, Y.; Guan, H.; So, S.; Jo, J. A Comprehensive Review of Deep Learning-Based Crack Detection Approaches. Appl. Sci. 2022, 12, 1374. [Google Scholar] [CrossRef]
- Tran, V.L.; Vo, T.C.; Nguyen, T.Q. One-dimensional convolutional neural network for damage detection of structures using time series data. Asian J. Civ. Eng. 2024, 25, 827–860. [Google Scholar] [CrossRef]
- Jiang, C.; Zhou, Q.; Lei, J.; Wang, X. A Two-Stage Structural Damage Detection Method Based on 1D-CNN and SVM. Appl. Sci. 2022, 12, 10394. [Google Scholar] [CrossRef]
- Barbosh, M.; Ge, L.; Sadhu, A. Automated crack identification in structures using acoustic waveforms and deep learning. J. Infrastruct. Preserv. Resil. 2024, 5, 10. [Google Scholar] [CrossRef]
- Li, X.; Xu, X.; He, X.; Wei, X.; Yang, H. Intelligent Crack Detection Method Based on GM-ResNet. Sensors 2023, 23, 8369. [Google Scholar] [CrossRef]
- Moreh, F.; Hasan, Y.; Rizvi, Z.H.; Wuttke, F.; Tomforde, S. MCMN Deep Learning Model for Precise Microcrack Detection in Various Materials. In Proceedings of the 2024 International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 18–20 December 2024; pp. 1928–1933. [Google Scholar] [CrossRef]
- Moreh, F.; Hasan, Y.; Rizvi, Z.H.; Wuttke, F.; Tomforde, S. Wave-Based Neural Network with Attention Mechanism for Damage Localization in Materials. In Proceedings of the 2024 International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 18–20 December 2024; pp. 122–129. [Google Scholar] [CrossRef]
- Wuttke, F.; Lyu, H.; Sattari, A.S.; Rizvi, Z.H. Wave based damage detection in solid structures using spatially asymmetric encoder–decoder network. Sci. Rep. 2021, 11, 20968. [Google Scholar] [CrossRef]
- Raghu, M.; Unterthiner, T.; Kornblith, S.; Zhang, C.; Dosovitskiy, A. Do Vision Transformers See Like Convolutional Neural Networks? arXiv 2022, arXiv:2108.08810. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Yuan, S. SECNN: Squeeze-and-Excitation Convolutional Neural Network for Sentence Classification. arXiv 2023, arXiv:2312.06088. [Google Scholar] [CrossRef]
- Hong, S.B.; Kim, Y.H.; Nam, S.H.; Park, K.R. S3D: Squeeze and Excitation 3D Convolutional Neural Networks for a Fall Detection System. Mathematics 2022, 10, 328. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. arXiv 2019, arXiv:1709.01507. [Google Scholar]
- Lea, C.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal Convolutional Networks: A Unified Approach to Action Segmentation. arXiv 2016, arXiv:1608.08242. [Google Scholar]
- Zhang, Y.; Ding, X.; Yue, X. Scaling Up Your Kernels: Large Kernel Design in ConvNets towards Universal Representations. arXiv 2024, arXiv:2410.08049. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June2010; pp. 807–814. [Google Scholar]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-Normalizing Neural Networks. arXiv 2017, arXiv:1706.02515. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2023, arXiv:1606.08415. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). arXiv 2016, arXiv:1511.07289. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. arXiv 2018, arXiv:1708.02002. [Google Scholar]
- Yeung, M.; Sala, E.; Schönlieb, C.B.; Rundo, L. Unified Focal loss: Generalising Dice and cross entropy-based losses to handle class imbalanced medical image segmentation. arXiv 2021, arXiv:2102.04525. [Google Scholar] [CrossRef]
- Jadon, S. A survey of loss functions for semantic segmentation. In Proceedings of the 2020 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Via del Mar, Chile, 27–29 October 2020. [Google Scholar] [CrossRef]



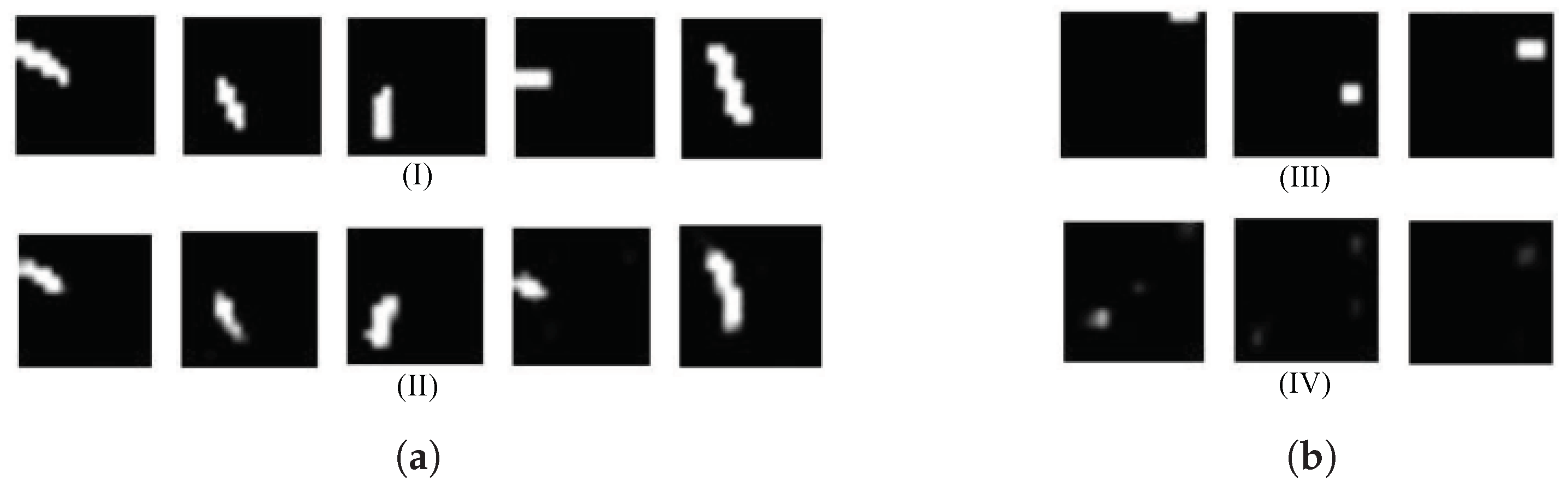
| Literature | Accuracy | IoU | DSC | Precision | Recall |
|---|---|---|---|---|---|
| 1D-DenseNet-TConv (200 epochs) | 0.8368 | 0.7601 | 0.8637 | 0.8753 | 0.8523 |
| MicroCracksAttNet (50 epochs) | 0.8601 | 0.7666 | 0.8684 | 0.8811 | 0.8888 |
| MicroCracksMetaNet (50 epochs) | 0.867 | 0.8082 | 0.8943 | 0.9066 | 0.8911 |
| Proposed MicrocrackAttentionNect (50 epochs) | 0.8777 | 0.8521 | 0.9145 | 0.8601 | 0.8518 |
| Activation Function | Loss Function | μm | μm | μm | μm | μm |
|---|---|---|---|---|---|---|
| GeLU | FL | 0.8275 | 0.8612 | 0.9354 | 0.9501 | 0.9541 |
| DL | 0.8633 | 0.9012 | 0.9585 | 0.9701 | 0.9802 | |
| WDL | 0.8381 | 0.8798 | 0.9415 | 0.9670 | 0.9793 | |
| CWDL | 0.8774 | 0.9211 | 0.9814 | 0.9808 | 0.9848 | |
| ReLU | FL | 0.8252 | 0.8632 | 0.9456 | 0.9701 | 0.9802 |
| DL | 0.8553 | 0.8902 | 0.9646 | 0.9770 | 0.9829 | |
| WDL | 0.8213 | 0.8687 | 0.9293 | 0.9524 | 0.9703 | |
| CWDL | 0.8678 | 0.9134 | 0.9673 | 0.9808 | 0.9866 | |
| ELU | FL | 0.8313 | 0.8797 | 0.9558 | 0.9839 | 0.9911 |
| DL | 0.8502 | 0.9011 | 0.9673 | 0.9831 | 0.9884 | |
| WDL | 0.8563 | 0.9034 | 0.9605 | 0.9739 | 0.9829 | |
| CWDL | 0.8515 | 0.9041 | 0.9673 | 0.9847 | 0.9920 | |
| SeLU | FL | 0.8206 | 0.8671 | 0.9503 | 0.9793 | 0.9902 |
| DL | 0.8412 | 0.8993 | 0.9707 | 0.9870 | 0.9893 | |
| WDL | 0.8201 | 0.8664 | 0.9307 | 0.9555 | 0.9712 | |
| CWDL | 0.8443 | 0.8910 | 0.9625 | 0.9854 | 0.9929 |
| Attributes | MicroCracksAttNet | MicroCracksMetaNet | 1D-DenseNet-TConv | MicrocrackAttentionNext |
|---|---|---|---|---|
| Layers | 58 | 72 | 444 | 94 |
| Epochs | 50 | 50 | 200 | 50 |
| Total params | 1,129,209 | 1,131,690 | 1,393,429 | 1,280,299 |
| Trainable params | 1,127,321 | 1,129,722 | 1,376,137 | 1,277,355 |
| Non-trainable params | 1888 | 1968 | 17,292 | 2944 |
| Time taken by first Epoch | 26.45 s | 42.35 s | 89.14 s | 36.98 s |
| Total training time | 906.33 s | 2117.50 s | 15,560.56 s | 1849.54 s |
| Model | Crack Sizes μm | |||
|---|---|---|---|---|
| 0–3 μm | 3–6 μm | 6–9 μm | 9–14 μm | |
| MicrocrackAttentionNext (50 epochs) | 0.5214 | 0.9787 | 0.9879 | 0.9917 |
| MicroCracksMetaNet (50 epochs) | 0.4513 | 0.9549 | 0.9753 | 0.9862 |
| MicroCracksAttNet (50 epochs) | 0.4420 | 0.9587 | 0.9778 | 0.9862 |
| 1D-DenseNet-TConv (50 epochs) | 0.3719 | 0.9268 | 0.9778 | 0.9835 |
| 1D-DenseNet-TConv (200 epochs) | 0.4682 | 0.9793 | 0.9852 | 0.9972 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreh, F.; Hasan, Y.; Hussain, B.Z.; Ammar, M.; Wuttke, F.; Tomforde, S. MicrocrackAttentionNext: Advancing Microcrack Detection in Wave Field Analysis Using Deep Neural Networks Through Feature Visualization. Sensors 2025, 25, 2107. https://doi.org/10.3390/s25072107
Moreh F, Hasan Y, Hussain BZ, Ammar M, Wuttke F, Tomforde S. MicrocrackAttentionNext: Advancing Microcrack Detection in Wave Field Analysis Using Deep Neural Networks Through Feature Visualization. Sensors. 2025; 25(7):2107. https://doi.org/10.3390/s25072107
Chicago/Turabian StyleMoreh, Fatahlla, Yusuf Hasan, Bilal Zahid Hussain, Mohammad Ammar, Frank Wuttke, and Sven Tomforde. 2025. "MicrocrackAttentionNext: Advancing Microcrack Detection in Wave Field Analysis Using Deep Neural Networks Through Feature Visualization" Sensors 25, no. 7: 2107. https://doi.org/10.3390/s25072107
APA StyleMoreh, F., Hasan, Y., Hussain, B. Z., Ammar, M., Wuttke, F., & Tomforde, S. (2025). MicrocrackAttentionNext: Advancing Microcrack Detection in Wave Field Analysis Using Deep Neural Networks Through Feature Visualization. Sensors, 25(7), 2107. https://doi.org/10.3390/s25072107








