Polarization-Modulated Optical Homodyne for Time-of-Flight Imaging with Standard CMOS Sensors
Abstract
1. Introduction
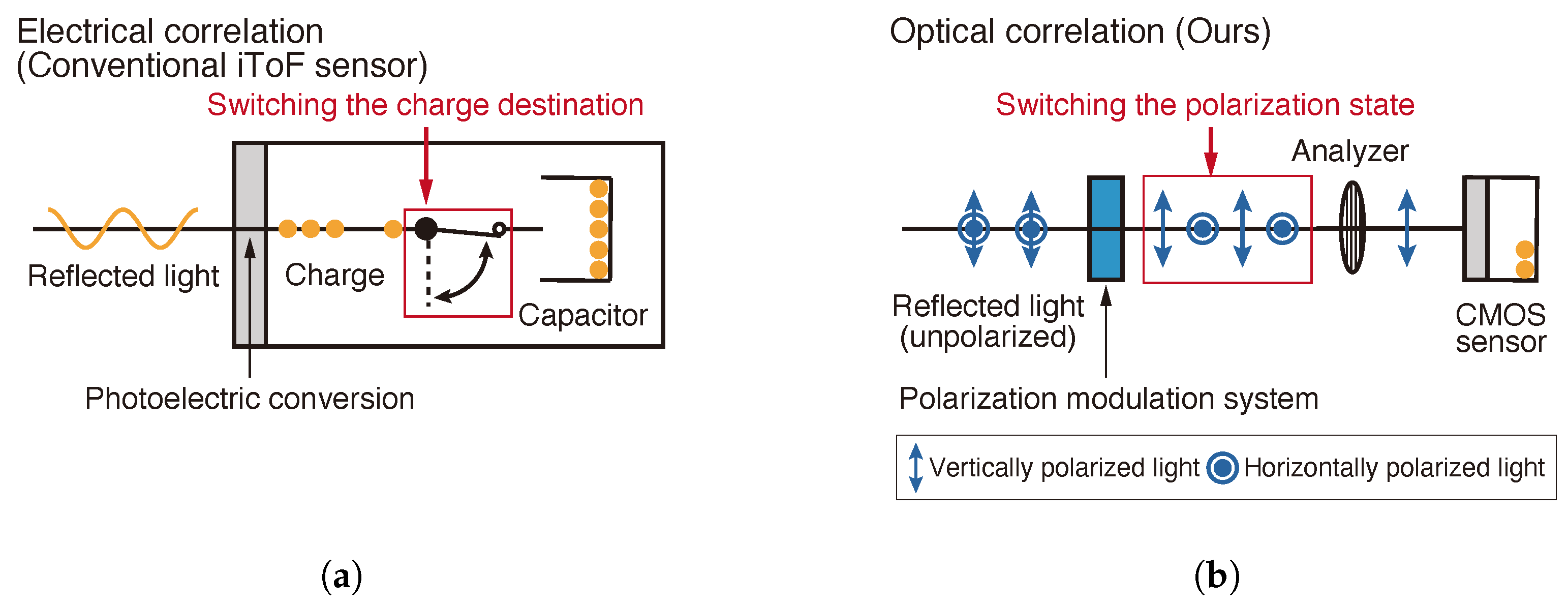
2. Polarization-Modulated Optical Homodyne
2.1. Principle of Polarization Modulation
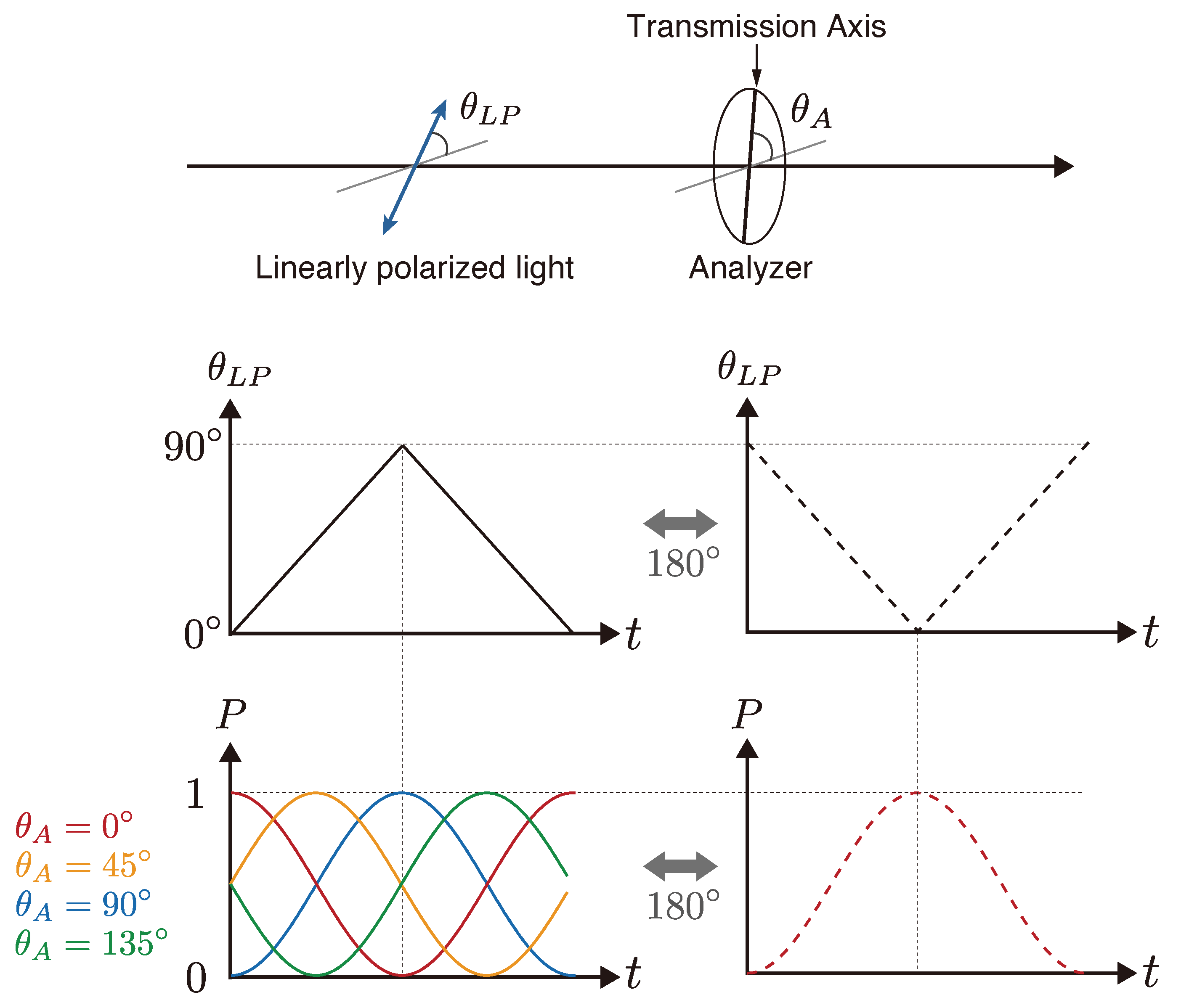
2.2. Optical Transmission Through Polarization Modulation
2.3. iToF Depth Measurement Using Polarization-Modulated Optical Homodyne
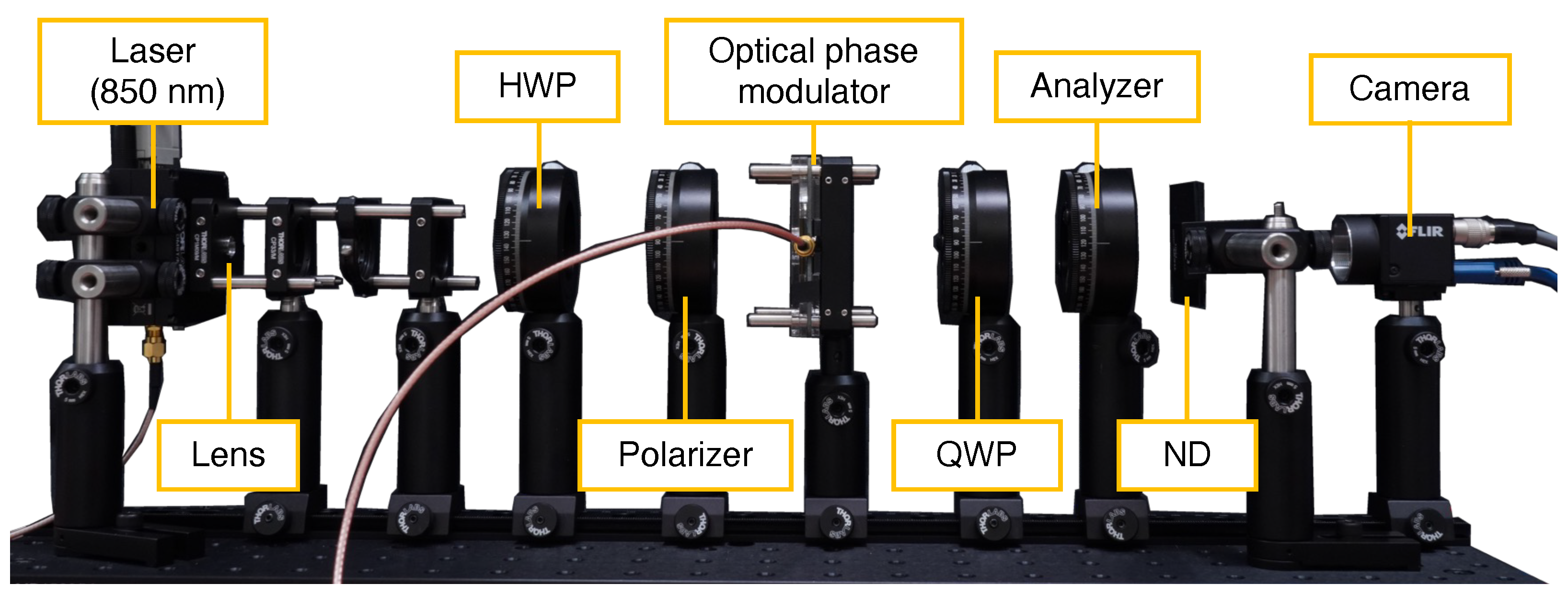
3. Implementation
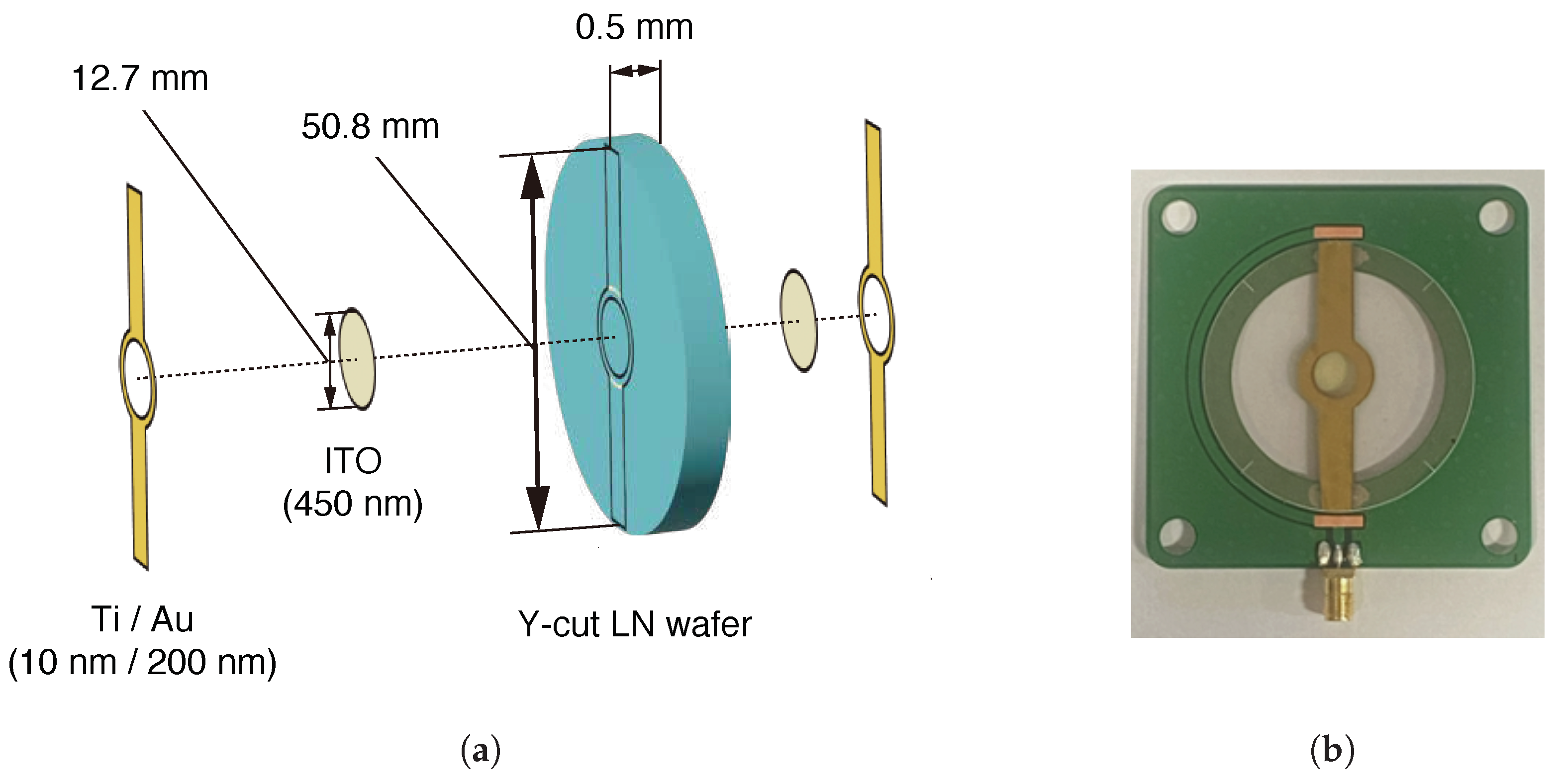
3.1. Fabrication of Optical Phase Modulator
3.2. Modulation Frequency
3.3. The Angle of Analyzer
4. Validation
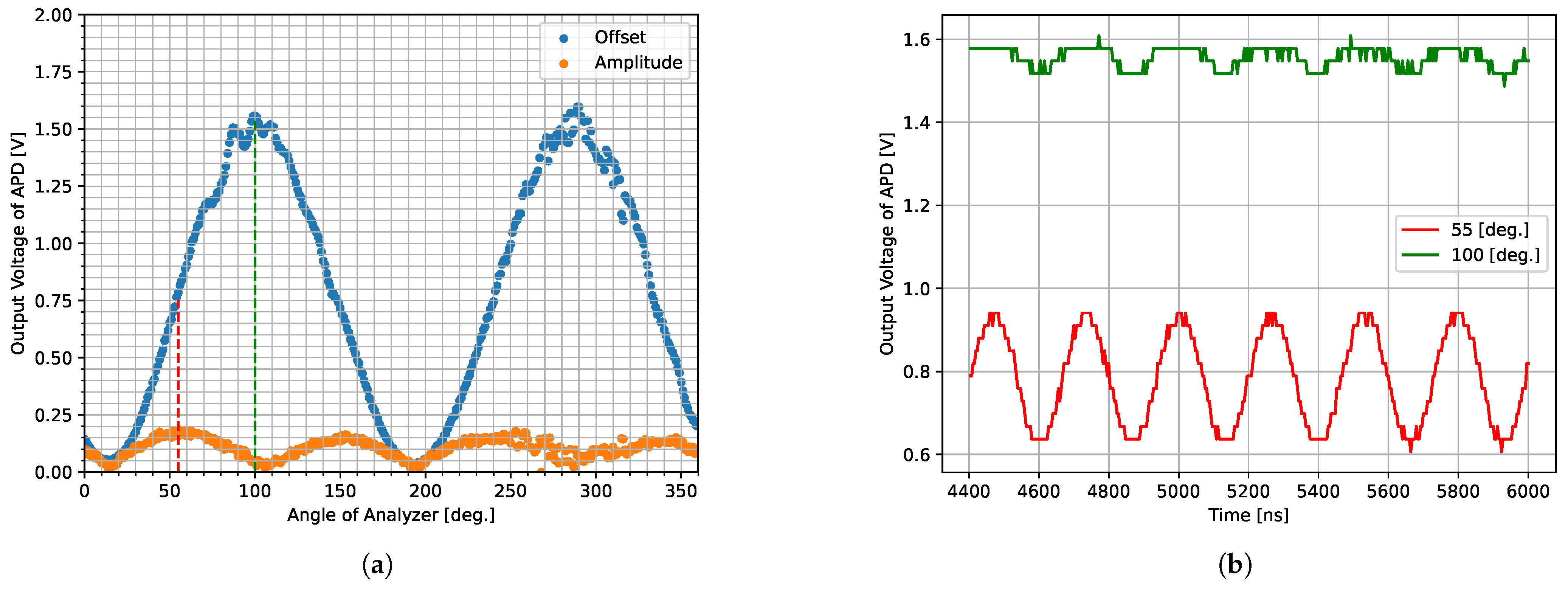
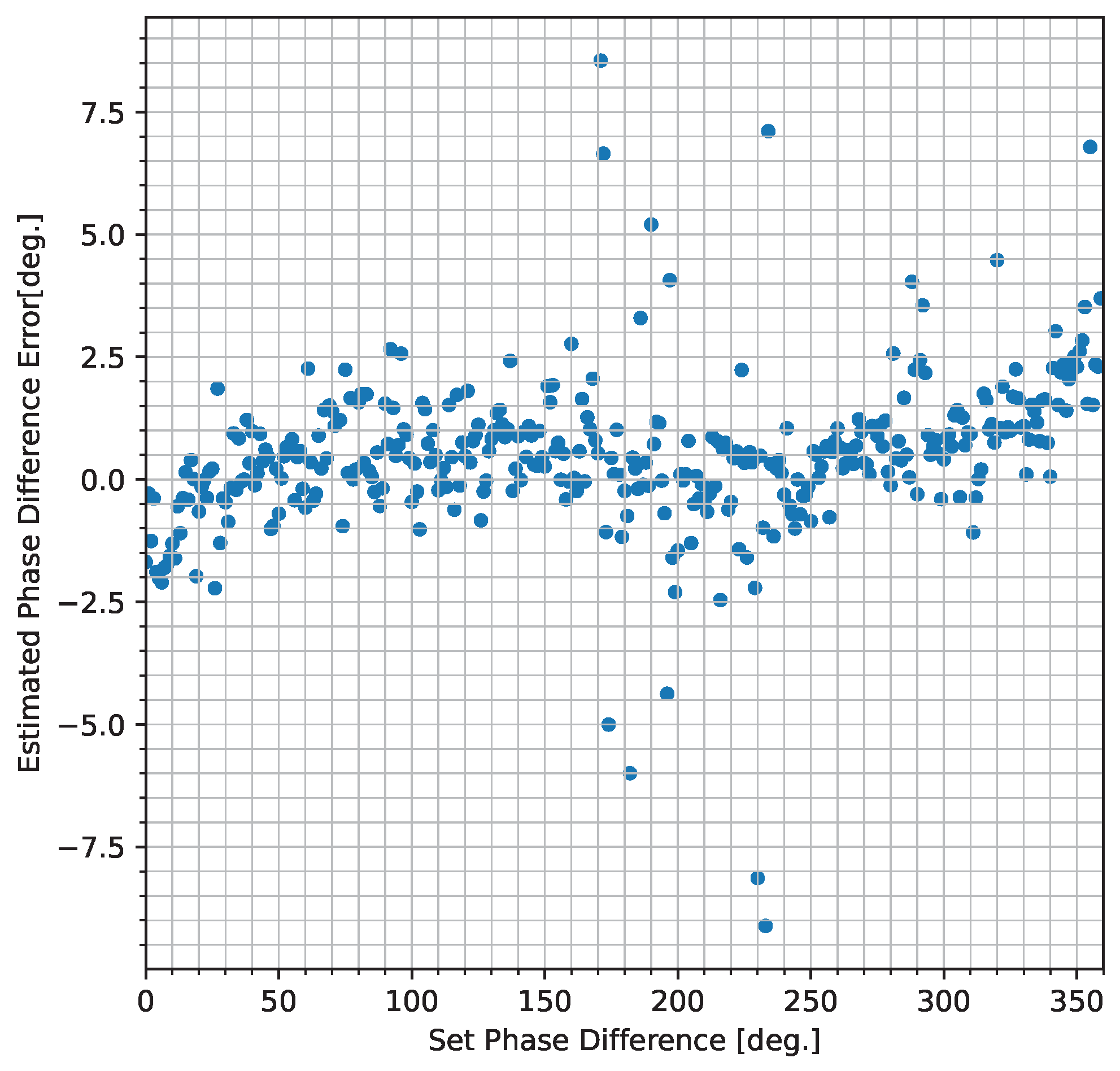
4.1. Phase Difference Measurement Using an APD
4.2. Phase Difference Measurement Using a CMOS Image Sensor
5. Evaluation
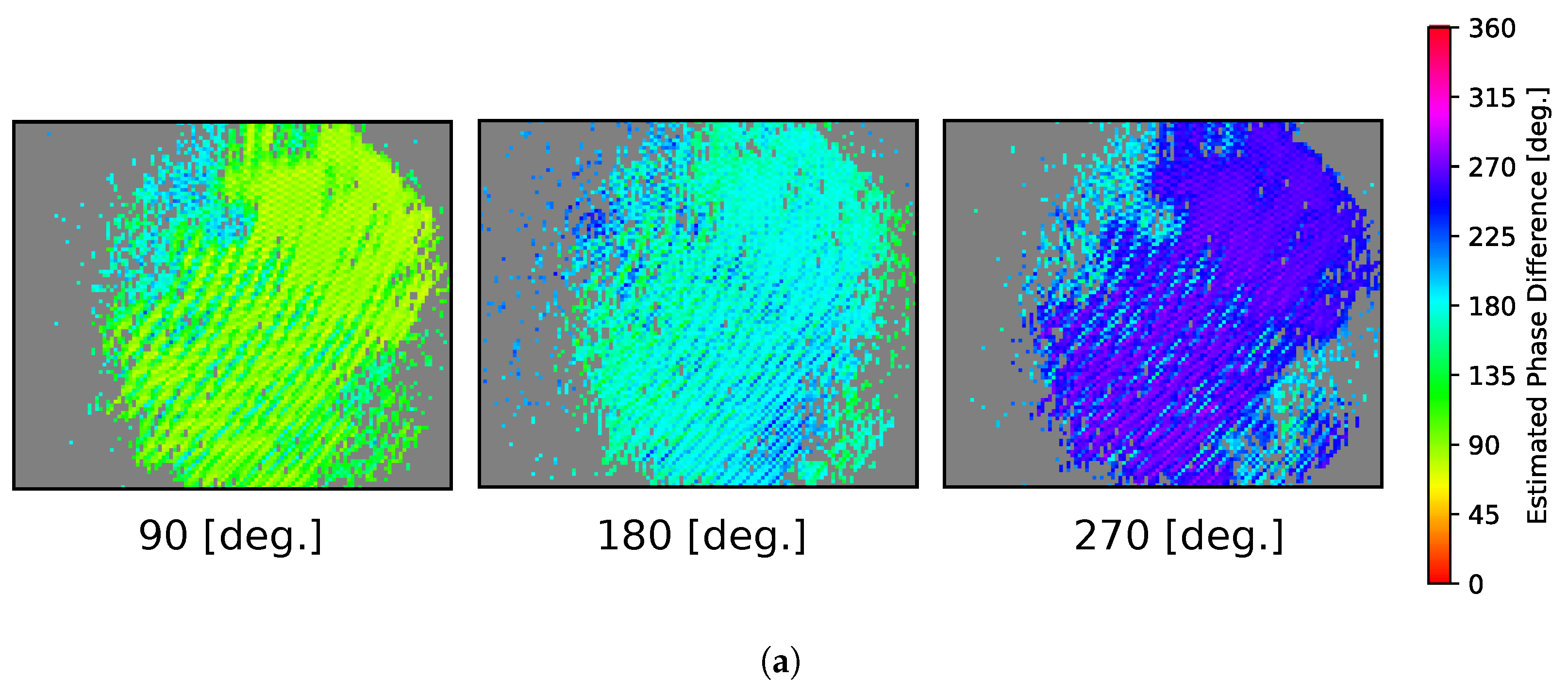
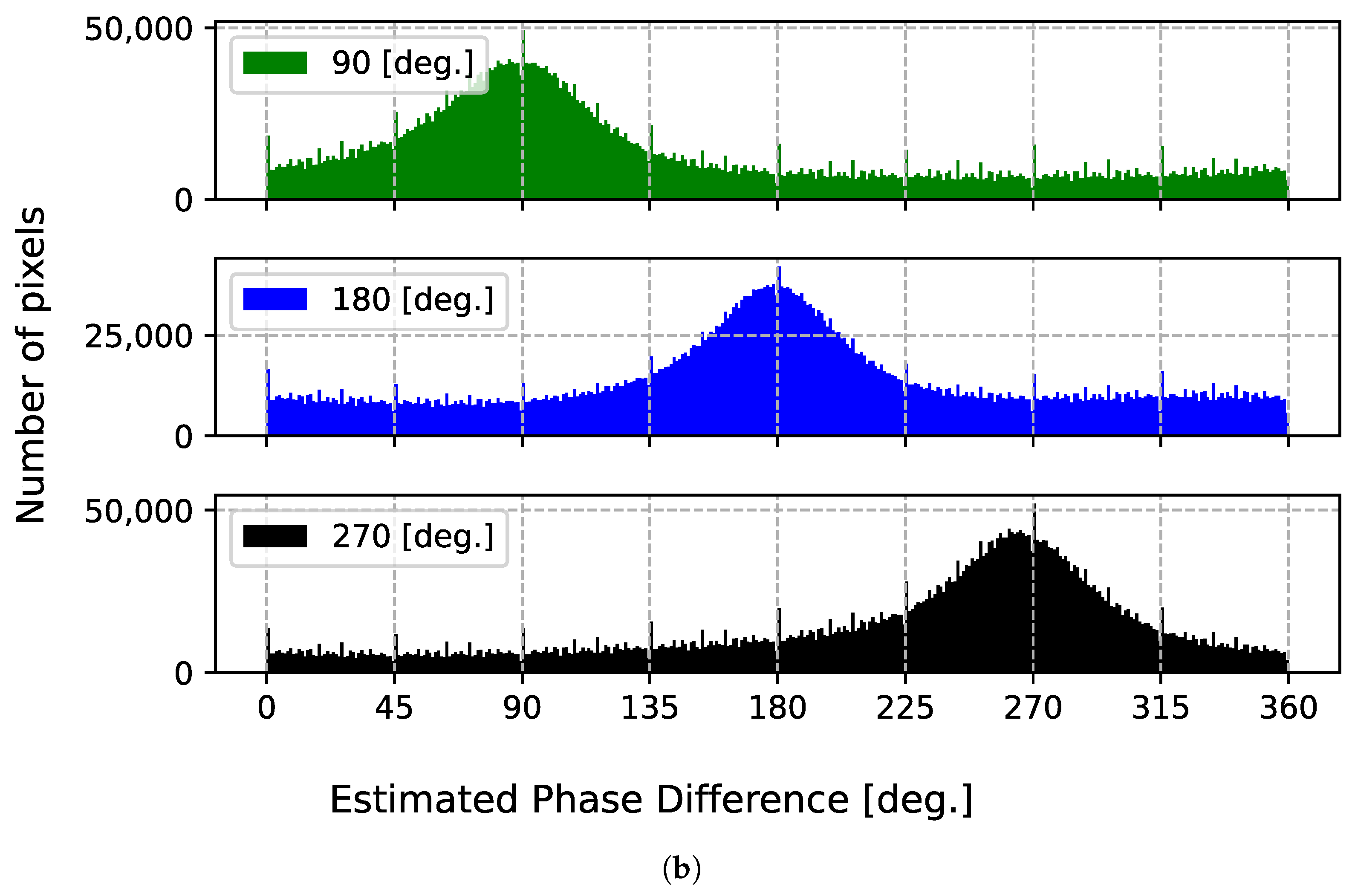
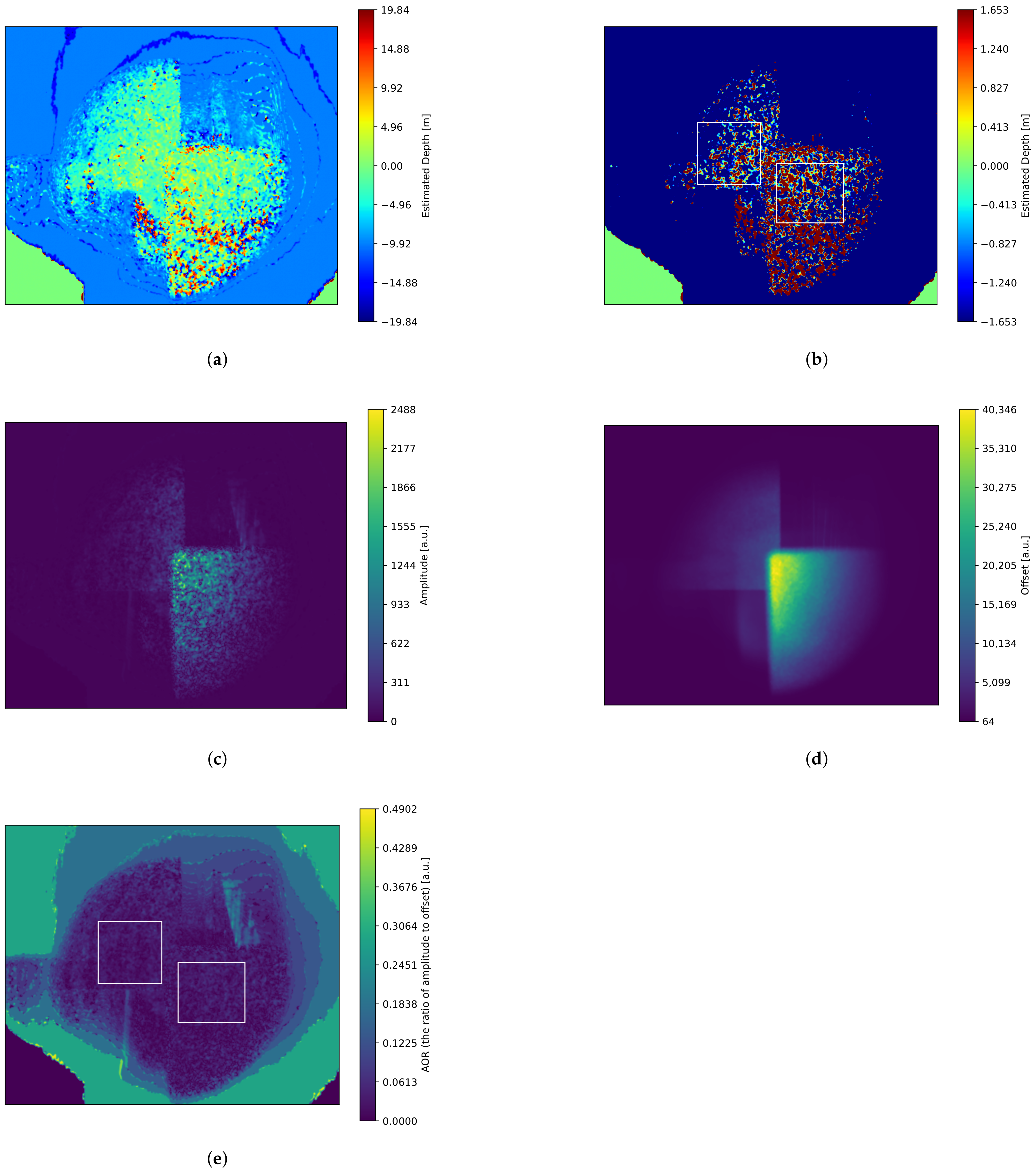
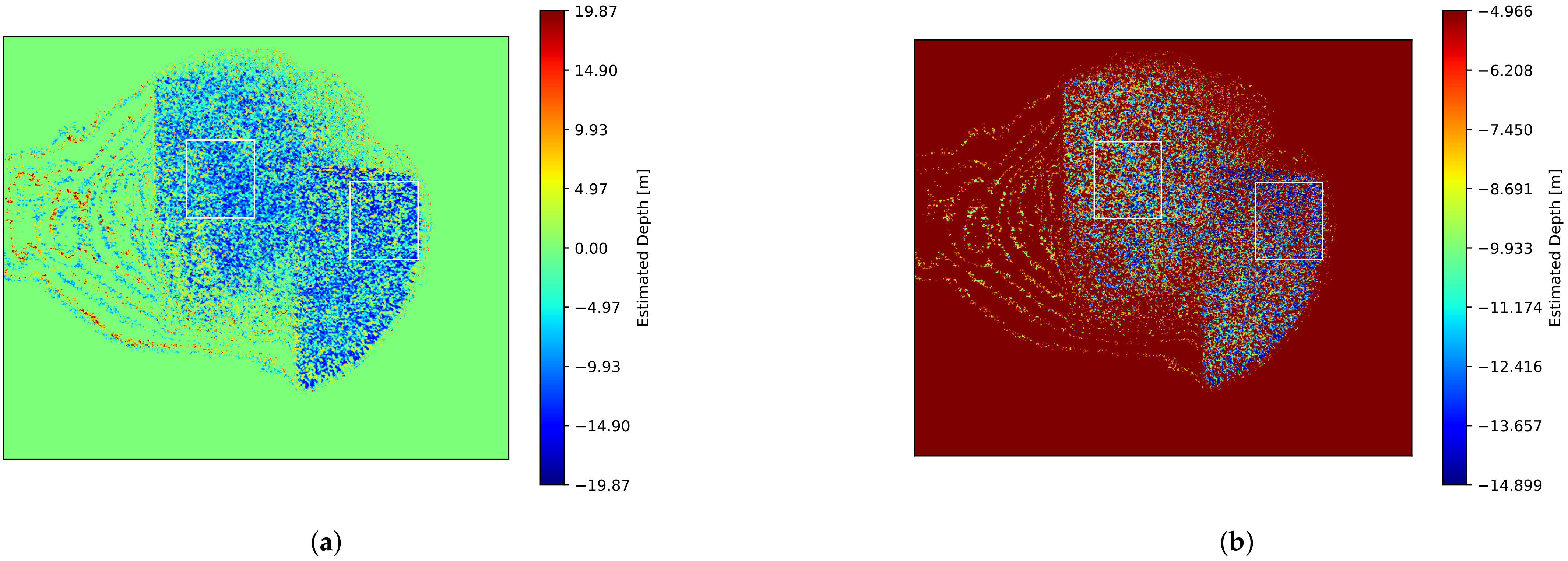
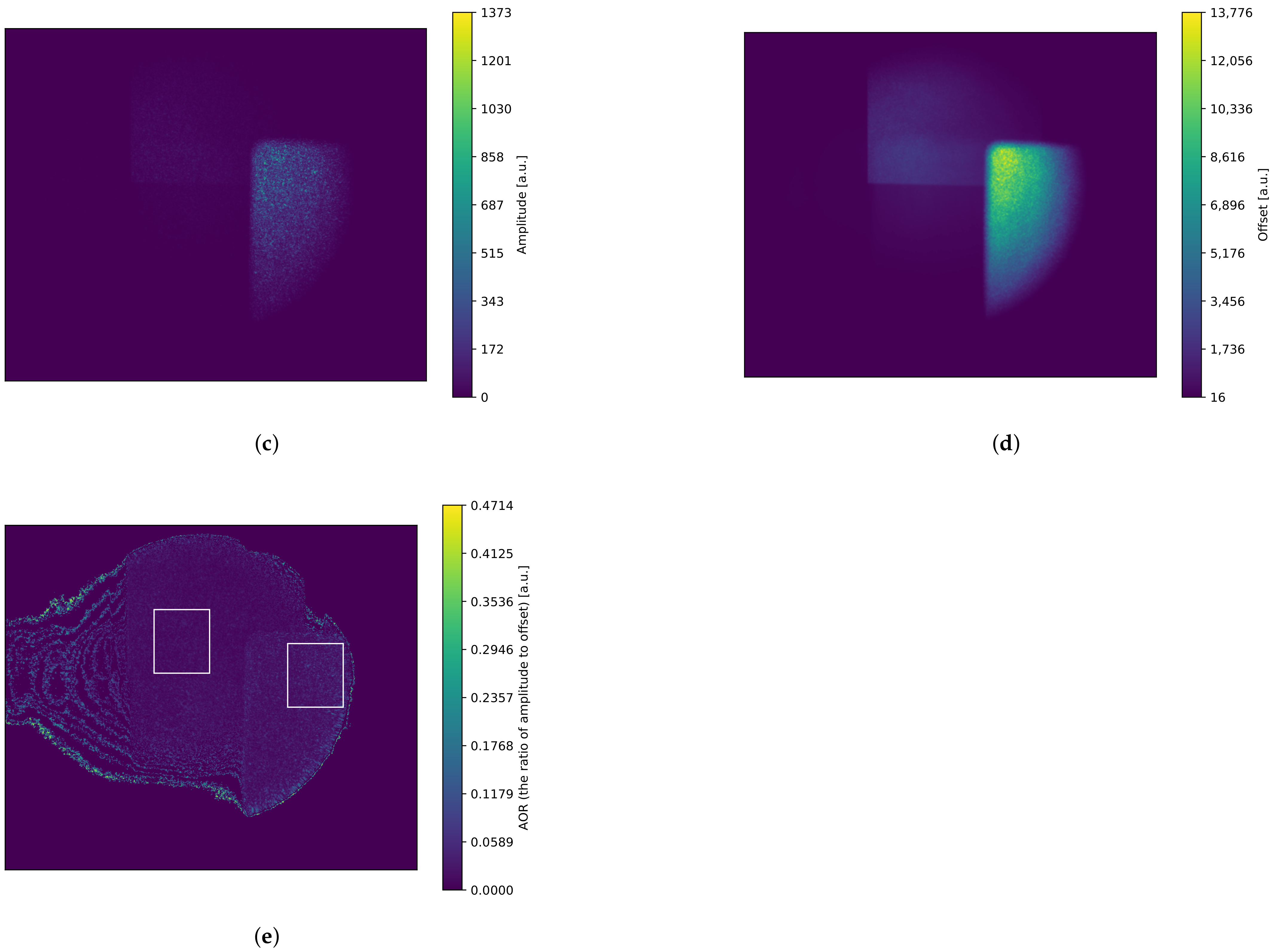
5.1. Depth Imaging with a CMOS Image Sensor
5.2. Depth Imaging with a Polarization Image Sensor
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Foix, S.; Alenya, G.; Torras, C. Lock-in Time-of-Flight (ToF) Cameras: A Survey. IEEE Sens. J. 2011, 11, 1917–1926. [Google Scholar] [CrossRef]
- Yasutomi, K.; Kawahito, S. Lock-in pixel based time-of-flight range imagers: An overview. IEICE Trans. Electron. 2022, 105, 301–315. [Google Scholar] [CrossRef]
- Gupta, M.; Nayar, S.K.; Hullin, M.B.; Martin, J. Phasor imaging: A generalization of correlation-based time-of-flight imaging. ACM Trans. Graph. (ToG) 2015, 34, 1–18. [Google Scholar] [CrossRef]
- Li, F.; Chen, H.; Pediredla, A.; Yeh, C.; He, K.; Veeraraghavan, A.; Cossairt, O. CS-ToF: High-resolution compressive time-of-flight imaging. Opt. Express 2017, 25, 31096–31110. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Song, P.; Wang, X.; Zheng, Z.; Bai, Y.; Geng, H. Fast lightweight framework for time-of-flight super-resolution based on block compressed sensing. Opt. Express 2022, 30, 15096–15112. [Google Scholar] [CrossRef] [PubMed]
- Kawachi, H.; Nakamura, T.; Iwata, K.; Makihara, Y.; Yagi, Y. Snapshot super-resolution indirect time-of-flight camera using a grating-based subpixel encoder and depth-regularizing compressive reconstruction. Opt. Contin. 2023, 2, 1368–1383. [Google Scholar] [CrossRef]
- Li, F.; Willomitzer, F.; Rangarajan, P.; Gupta, M.; Velten, A.; Cossairt, O. SH-ToF: Micro resolution time-of-flight imaging with superheterodyne interferometry. In Proceedings of the 2018 IEEE International Conference on Computational Photography (ICCP), Pittsburgh, PA, USA, 4–6 May 2018; pp. 1–10. [Google Scholar] [CrossRef]
- Li, F.; Willomitzer, F.; Balaji, M.M.; Rangarajan, P.; Cossairt, O. Exploiting wavelength diversity for high resolution time-of-flight 3D imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 2193–2205. [Google Scholar] [CrossRef] [PubMed]
- Ballester, M.; Wang, H.; Li, J.; Cossairt, O.; Willomitzer, F. Single-shot synthetic wavelength imaging: Sub-mm precision ToF sensing with conventional CMOS sensors. Opt. Lasers Eng. 2024, 178, 108165. [Google Scholar] [CrossRef]
- Dorrington, A.A.; Cree, M.J.; Payne, A.D.; Conroy, R.M.; Carnegie, D.A. Achieving sub-millimetre precision with a solid-state full-field heterodyning range imaging camera. Meas. Sci. Technol. 2007, 18, 2809. [Google Scholar] [CrossRef]
- Godbaz, J.P.; Cree, M.J.; Dorrington, A.A. Extending AMCW Lidar Depth-of-Field Using a Coded Aperture. In Computer Vision—ACCV 2010, Proceedings of the 10th Asian Conference on Computer Vision, Queenstown, New Zealand, 8–12 November 2010; Kimmel, R., Klette, R., Sugimoto, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 397–409. [Google Scholar]
- Baek, S.H.; Walsh, N.; Chugunov, I.; Shi, Z.; Heide, F. Centimeter-wave free-space neural time-of-flight imaging. ACM Trans. Graph. 2023, 42, 1–18. [Google Scholar] [CrossRef]
- Miller, M.; Xia, H.; Beshara, M.; Menzel, S.; Ebeling, K.J.; Michalzik, R. Large-area transmission modulators for 3D time-of-flight imaging. In Proceedings of the Unconventional Optical Imaging II, Online, 6–10 April 2020; Fournier, C., Georges, M.P., Popescu, G., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2020; Volume 11351, p. 113511F. [Google Scholar] [CrossRef]
- Miller, M.; Savic, A.; Sassiya, B.; Menzel, S.; Ebeling, K.J.; Michalzik, R. Indirect time-of-flight 3D imaging using large-area transmission modulators. In Proceedings of the Digital Optical Technologies 2021, Online, 21–26 June 2021; Kress, B.C., Peroz, C., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2021; Volume 11788, p. 117880G. [Google Scholar] [CrossRef]
- Abdelhamid, H. Indirect Time-of-Flight 3D Imaging Using Fast Segmented Large-Area Electroabsorption Modulators. Master’s Thesis, Ulm University, Ulm, Germany, 2022. [Google Scholar]
- Miller, M.; Sassiya, B.; Menzel, S.; Ebeling, K.J.; Michalzik, R. 3D indirect time-of-flight imaging employing transmission electroabsorption modulators. In Proceedings of the Unconventional Optical Imaging III, Strasbourg, France, 3 April–23 May 2022; Georges, M.P., Popescu, G., Verrier, N., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2022; Volume 12136, p. 121360Y. [Google Scholar] [CrossRef]
- Atalar, O.; Laer, R.V.; Sarabalis, C.J.; Safavi-Naeini, A.H.; Arbabian, A. Time-of-flight imaging based on resonant photoelastic modulation. Appl. Opt. 2019, 58, 2235–2247. [Google Scholar] [CrossRef] [PubMed]
- Atalar, O.; Yee, S.; Safavi-Naeini, A.H.; Arbabian, A. Y-Z cut lithium niobate longitudinal piezoelectric resonant photoelastic modulator. Opt. Express 2022, 30, 47103–47114. [Google Scholar] [CrossRef] [PubMed]
- Atalar, O.; Van Laer, R.; Safavi-Naeini, A.H.; Arbabian, A. Longitudinal piezoelectric resonant photoelastic modulator for efficient intensity modulation at megahertz frequencies. Nat. Commun. 2022, 13, 1526. [Google Scholar] [CrossRef] [PubMed]
- Atalar, O.; Arbabian, A. Optically isotropic longitudinal piezoelectric resonant photoelastic modulator for wide angle polarization modulation at megahertz frequencies. J. Opt. Soc. Am. A 2023, 40, 2249–2258. [Google Scholar] [CrossRef] [PubMed]
- Atalar, O.; Arbabian, A. Polarization-insensitive wide-angle resonant acousto-optic phase modulator. Opt. Lett. 2024, 49, 2141–2144. [Google Scholar] [CrossRef] [PubMed]
- Atalar, O.; Arbabian, A. Birefringence-free photoelastic modulator with centimeter-square aperture operating at 2.7 MHz with sub-watt drive power. Opt. Lett. 2024, 49, 5051–5054. [Google Scholar] [CrossRef] [PubMed]
- Atalar, O. Resonant Photoelastic Modulation for Time-of-Flight Imaging with Standard Image Sensors. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2022. Available online: https://purl.stanford.edu/kh488xz0210 (accessed on 31 December 2024).
- Lange, R.; Seitz, P. Solid-state time-of-flight range camera. IEEE J. Quantum Electron. 2001, 37, 390–397. [Google Scholar] [CrossRef]




| Method | Correlation | Phase Detection | Number of Pixels | Number of Measurements | Depth Resolution |
|---|---|---|---|---|---|
| Conventional iToF | Electrical | Homodyne | Low | 2 to 4 | Middle |
| SR [4,5,6] | Electrical | Homodyne | Middle | 2 [6], Multiple | Middle |
| SWI [7,8,9] | Optical | Heterodyne | High | 1 [9], Multiple | High |
| HOS-II [10,11] | Optical | Heterodyne | High | Multiple | Middle |
| HOS-EOM [12] | Optical | Homodyne | Single (scanning) | (2 frequencies) | High |
| HOS-EAM [13,14,15,16] | Optical | Heterodyne | High | 4 | Middle |
| HOS-PEM [17,18,19,20,21,22] | Optical | Heterodyne | High | Multiple | Low |
| HOS-PEM (Ours) | Optical | Homodyne | High | 4, 1 (Pol-Cam) | Low |
| Set Phase Difference | Mean Absolute Error (MAE) | Standard Deviation |
|---|---|---|
| 0° ( 0 ) | 0.66° ( ) | 1.1° ( ) |
| 90° ( ) | 0.84° ( ) | 1.0° ( ) |
| Four Phase Shift | Optical Phase Modulator Signal Phase | Analyzer Angle |
|---|---|---|
| 0° | 0° | 0° |
| 90° | 180° | 135° |
| 180° | 180° | 0° |
| 270° | 0° | 135° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebisu, A.; Aoto, T.; Takatani, T. Polarization-Modulated Optical Homodyne for Time-of-Flight Imaging with Standard CMOS Sensors. Sensors 2025, 25, 1886. https://doi.org/10.3390/s25061886
Ebisu A, Aoto T, Takatani T. Polarization-Modulated Optical Homodyne for Time-of-Flight Imaging with Standard CMOS Sensors. Sensors. 2025; 25(6):1886. https://doi.org/10.3390/s25061886
Chicago/Turabian StyleEbisu, Ayaka, Takahito Aoto, and Tsuyoshi Takatani. 2025. "Polarization-Modulated Optical Homodyne for Time-of-Flight Imaging with Standard CMOS Sensors" Sensors 25, no. 6: 1886. https://doi.org/10.3390/s25061886
APA StyleEbisu, A., Aoto, T., & Takatani, T. (2025). Polarization-Modulated Optical Homodyne for Time-of-Flight Imaging with Standard CMOS Sensors. Sensors, 25(6), 1886. https://doi.org/10.3390/s25061886






