1. Introduction
The main pump motor is one of the key equipment in pressurized water reactor nuclear power plants and the only rotating mechanical equipment in the reactor coolant system [
1]. As an important component of the main pump motor, the failure of the shielding sleeve may lead to a series of serious performance problems and safety hazards. According to statistics, the number of failures of the shielding sleeve accounts for about 35% of the total failures of the main pump. The bulging failure of the shielding sleeve may cause mechanical friction between the rotor and the stator, resulting in mechanical wear and damage of the motor components. The rupture or wear of the shielding sleeve may lead to coolant leakage, reducing the cooling efficiency of the motor. As a result, the heat of the reactor core cannot be discharged, causing major accidents such as core meltdown and radioactive leakage, which pose a serious threat to the safety of equipment and personnel. Early detection of the shielding sleeve failure can avoid the occurrence of major accidents [
2,
3]. Therefore, researching the fault diagnosis technology for the failure of the main pump motor shielding sleeve helps to improve the operational reliability of the main pump motor.
As a complex mechanical device, the main pump motor often suffers from the following faults: air gap eccentricity, stator faults [
4], bearing faults [
5,
6,
7], rotor faults [
8,
9], and shielding sleeve faults. At present, the diagnostic methods for air gap eccentricity, stator faults, bearing faults, and rotor faults are relatively mature, but there is a lack of diagnostic methods for the failure of the shielding sleeve. Research on the shielding sleeve mainly focuses on the design level [
10]. Machine learning algorithms are widely used in the field of main pump motor fault diagnosis. He et al. obtained vibration data of the canned motor pump in fault states through simulation tests, then extracted the characteristic quantities of the vibration data, and finally completed the fault diagnosis of the canned motor pump using the Random Forest algorithm [
11]. Sunal et al. compared different fault diagnosis methods for canned motor pumps based on machine learning and analyzed the advantages of using the motor current signature analysis method for fault diagnosis as well as the limitations in obtaining fault diagnosis data [
12]. Ma et al. used the time–frequency domain features of the acceleration sensor as characteristic parameters and completed the online fault diagnosis of the centrifugal pump in the nuclear power plant using the wavelet packet decomposition and Random Forest methods [
13]. However, since machine learning requires manual feature selection, it limits the accuracy of feature extraction and makes it difficult to handle fault situations with high uncertainty [
4].
Convolutional neural networks have the ability to learn autonomously and perform parallel processing, and they show unique advantages in dealing with non-linear and high-uncertainty problems. Therefore, they have been widely used in the field of fault diagnosis [
14,
15]. Traditional convolutional neural networks often use single-scale convolution kernels. However, compared to single-scale convolution kernels, multi-scale convolution kernels have stronger adaptive feature extraction capabilities, resulting in better generalization and accuracy [
16,
17]. Wang et al. proposed a convolutional neural network with feature alignment, which achieved multi-scale feature extraction of vibration signals, thus realizing the fault diagnosis of turbines [
16]. Chen et al. proposed a multi-scale neural network with feature alignment, which achieved the fault diagnosis of bearings under different working conditions [
17]. With the development of deep learning methods, multi-source data fusion methods have emerged to solve the problems of poor robustness of single data sources, the inability to distinguish similar fault modes, and sensitivity to noise and interference. The main fusion methods include data fusion [
18,
19] and feature fusion [
20,
21,
22]. Xie et al. applied a multi-signal-to-RGB-image conversion method based on principal component analysis to fuse multi-signal data into three-channel red–green–blue (RGB) images. Then, they used a CNN with a residual network to achieve the fault diagnosis of mechanical equipment [
18]. Ma et al. fused various sensor data, such as vibration, temperature, and current, and used the MSK-CNN model to automatically extract and analyze features, which improved the accuracy and robustness of synchronous motor fault diagnosis [
19]. Fan et al. proposed a multi-scale feature fusion method based on a residual network. By fusing feature information at different scales and leveraging the deep learning ability of the residual network, they improved the accuracy of fault feature extraction and the reliability of fault identification [
20]. The above-mentioned multi-source data fusion methods often only consider either data fusion or feature fusion without comprehensively considering the multi-scale features of data and their collaborative effects in the fusion process.
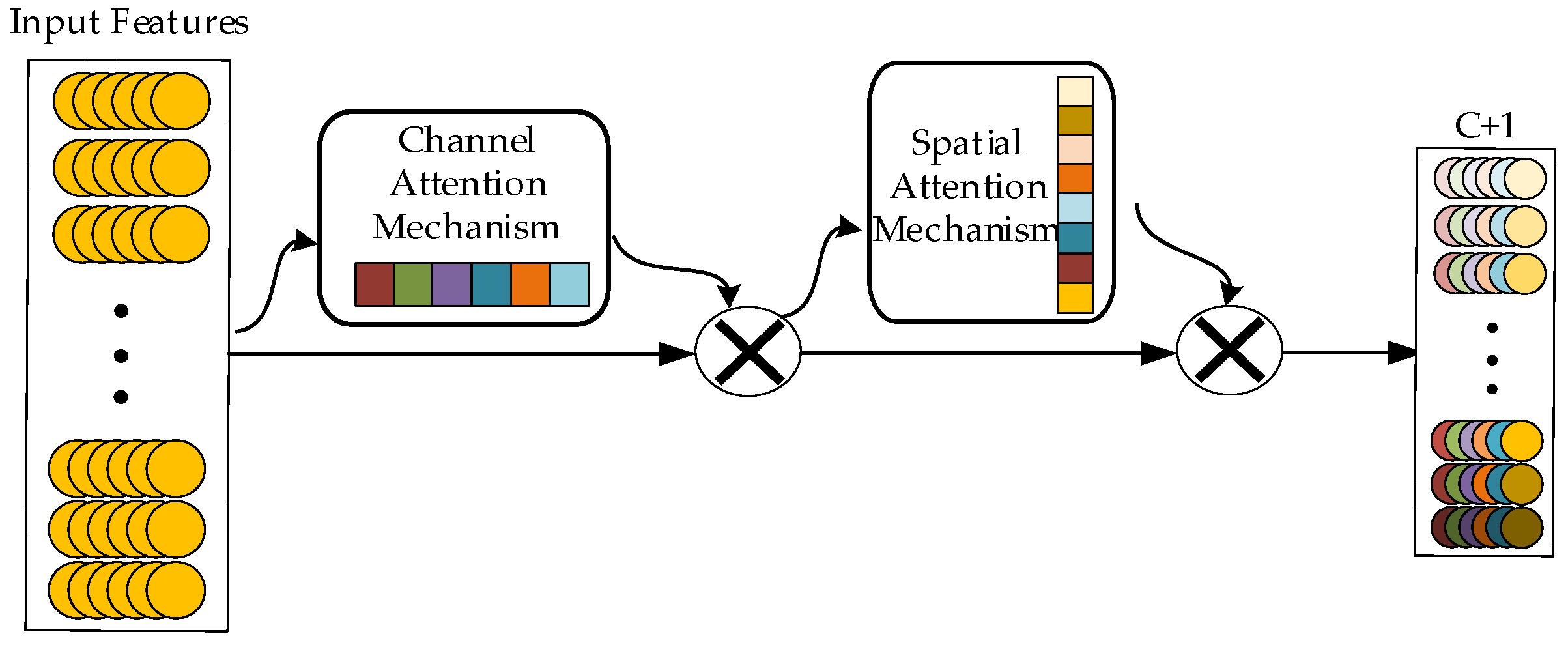
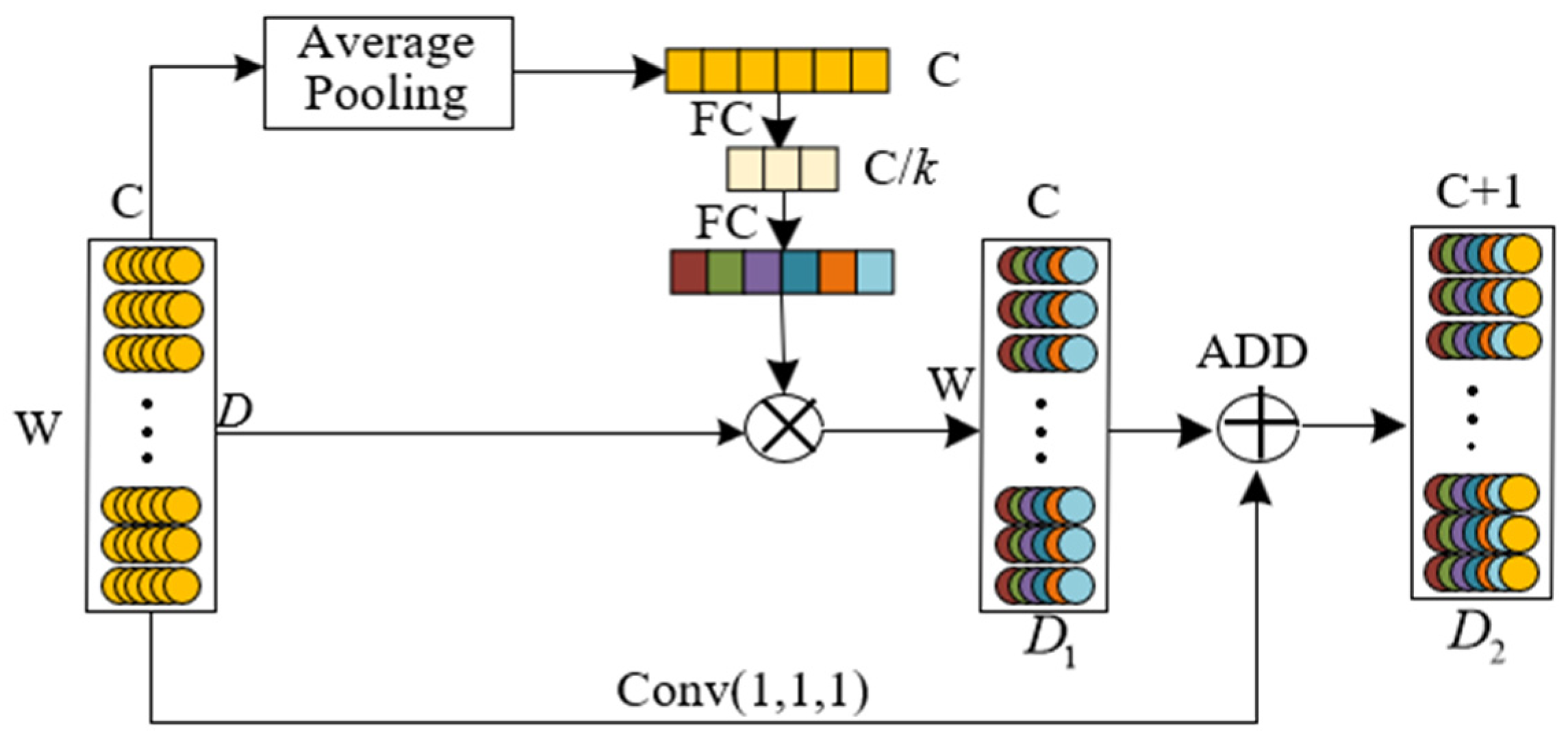
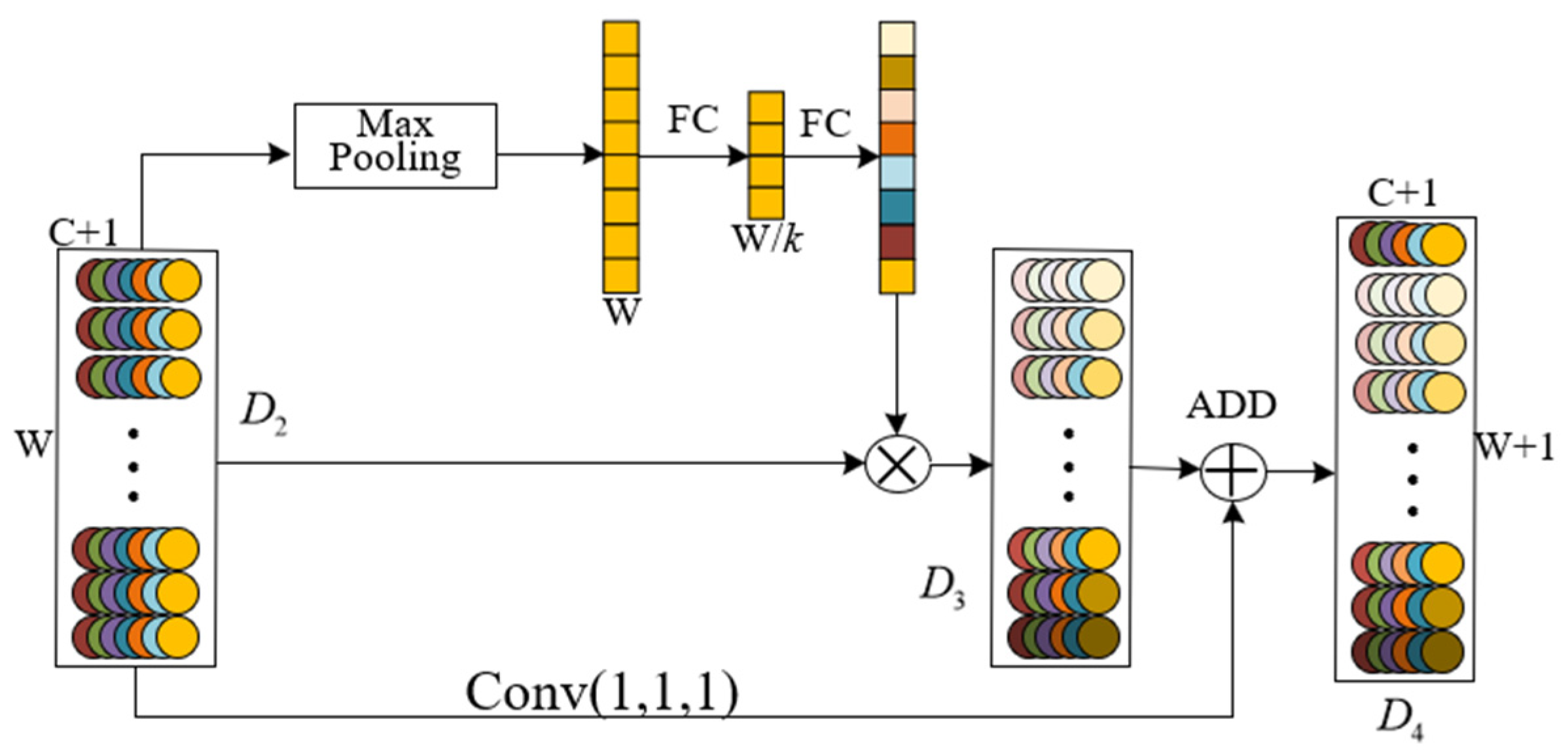
The internal structure of the shielding sleeve is compact, making it difficult to install additional sensors to obtain the characteristic data of the shielding sleeve. Therefore, only the performance curves (voltage, current, torque, and speed) of the main pump motor can be used as the diagnostic input data. The failure of the shielding sleeve has an insignificant impact on a single performance curve. Deeper multi-scale feature extraction of data and multi-source data fusion are required to more comprehensively reflect the failure of the shielding sleeve. Therefore, this paper proposes a multi-source data fusion fault diagnosis method for the main pump motor shielding sleeve under limited measurements. First, a multi-scale convolutional neural network based on the attention mechanism (AM-MSCNN) model is constructed. The multi-scale features of the input signal are extracted through convolution kernels of different scales, and the spatial attention mechanism and channel attention mechanism are used to weight and connect the importance of features at each scale, enhancing the feature extraction and fusion capabilities of the model. Then, on the basis of the AM-MSCNN, a convolutional neural network structure based on the attention mechanism and multi-scale multi-source data fusion (AM-MSMDF-CNN) is designed to achieve multi-source fusion of the data from current, voltage, torque, and speed sensors. Finally, the proposed method was verified using the datasets of shield sleeve failures from finite element simulations and small-scale prototype tests and was compared to other common fault diagnosis methods.
3. Convolutional Neural Network Based on Attention Mechanism and Multi-Scale Multi-Source Data Fusion
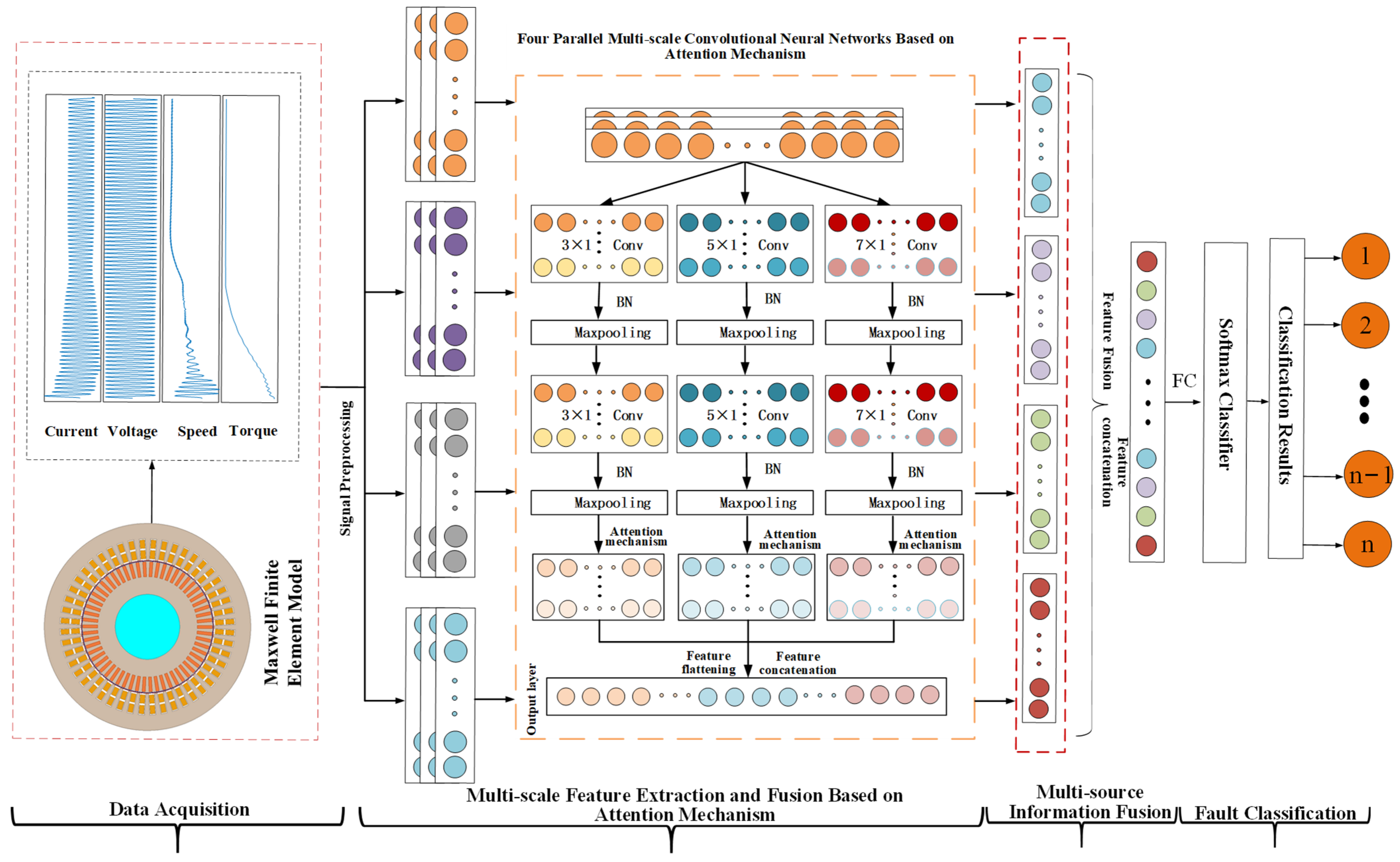
As illustrated in
Figure 5, this paper proposes the AM-MSMDF-CNN fault diagnosis process. Initially, a finite element model of the main pump motor shield failure is established using Ansys 2022 R1/Maxwell, and a series of datasets for the main pump motor shield failure are simulated by setting different operating conditions, various failure modes, and different degrees of failure. Subsequently, the preprocessed data are input into the AM-MSCNN for multi-scale feature extraction, batch normalization, max pooling, attention mechanism weighting, and multi-scale multi-feature fusion. The concatenation function is utilized to complete the feature stitching, further fusing the characteristics of torque, speed, voltage, and current. Finally, the BP algorithm and cross-entropy loss function are employed to diagnose and classify the fused features, thereby accomplishing the fault diagnosis.
3.1. Input Data Selection
The input signals have a significant impact on motor fault diagnosis, and research in this field extensively relies on electrical and mechanical signals. The sources of datasets can be divided into two categories: actual/experimental machines [
23,
24,
25,
26] and machine simulation software generation [
27,
28]. Actual/experimental machines can provide real and accurate fault signals, but they require substantial cost and time investment; machine simulation software offers the advantages of low cost and high flexibility, but the data are less realistic and precise. In addition to building datasets independently, some researchers also opt to use open-source datasets [
29,
30]. Since it is challenging to simulate various failure scenarios of the main pump motor shield sleeve in real-world conditions and the cost of simulation is too high, it is also difficult to collect data under different operating conditions of failures. To address this issue, the advantages and disadvantages of simulated and actual generated datasets were comprehensively compared [
28], as shown in
Table 1, the symbols “√” and “×” in
Table 1 represent meeting and not meeting the corresponding conditions respectively. By comprehensively considering the characteristics of the actual and simulated datasets, this paper selects the simulated dataset of a large-scale motor and the experimental data of a small-scale equivalent motor as the diagnostic objects.
Additionally, the selection of input signals was based on the following characteristics: a. the ease of data acquisition; b. the relevance to shield sleeve failure; c. the advantages of multi-source heterogeneous data; and d. consistency with other studies.
Based on the above four points, the input signals for shield sleeve failure were determined to be current, voltage, torque, and speed. Current and voltage can be collected using conventional electrical measurement equipment, while torque and speed can be monitored through sensors or existing control systems. Shield sleeve failure may cause changes in the electrical and mechanical performance of the motor, thereby affecting parameters such as current, voltage, torque, and speed. In the existing literature, parameters such as current, voltage, torque, and speed are commonly used in motor fault diagnosis research, providing a certain reference value and comparability.
3.2. Modeling of the Main Pump Motor Considering the Failure of the Shielding Sleeve
In order to obtain the simulated dataset after the failure of the main pump motor shielding sleeve, a finite element model of the main pump motor considering the shielding sleeve failure was established. Based on the actual rated parameters of the main pump motor, other parameters of the main pump motor were designed, as shown in
Table 2.
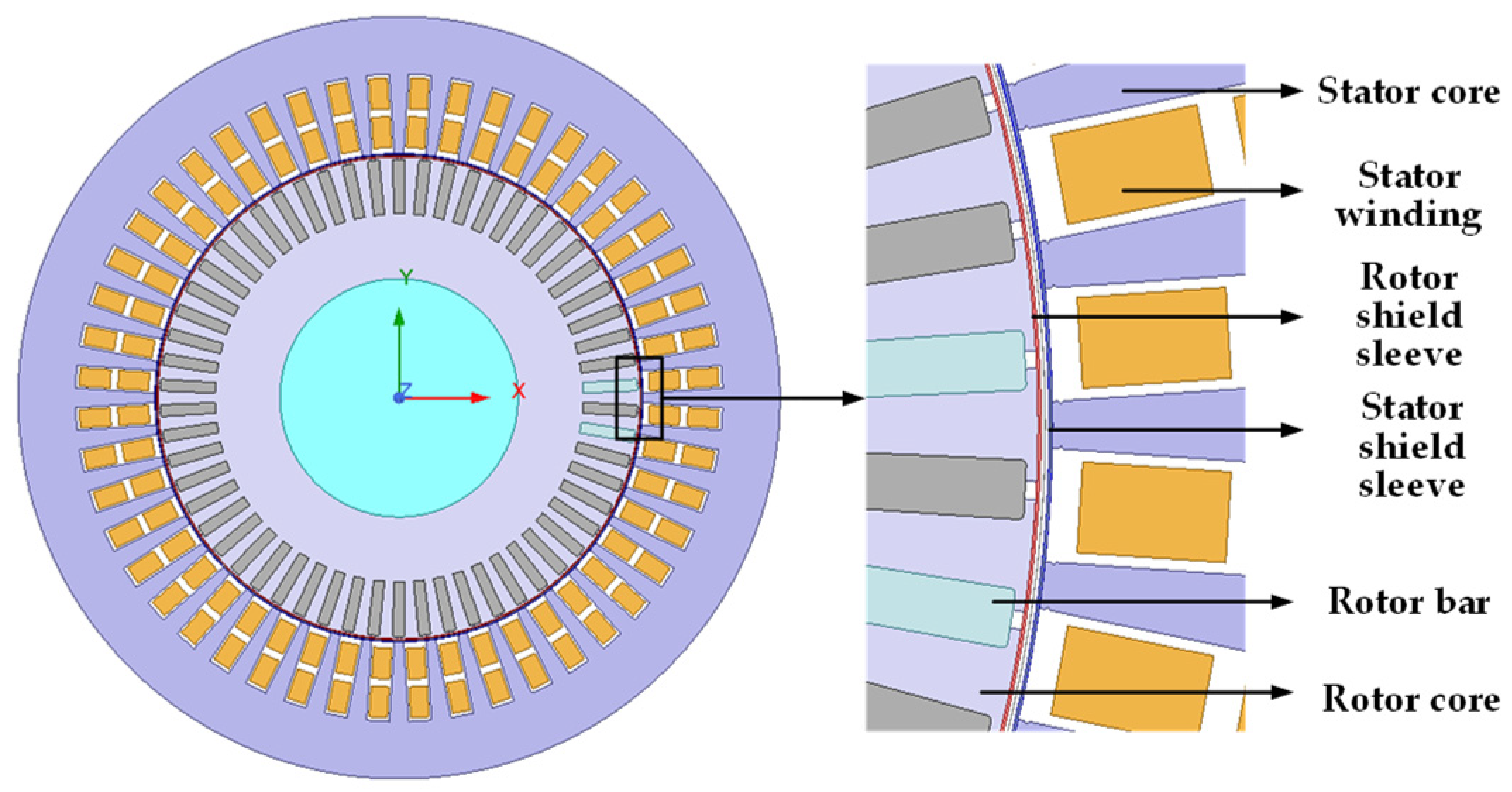
After determining the parameters of the main pump motor, a finite element model of the main pump motor was established using Ansys 2022 R1/Maxwell software, as shown in
Figure 6. The motor used in this paper is a 785 kW/130 kW squirrel-cage shielded induction motor, and the speed control method employed is a 4/8 pole changing speed control.
In order to better simulate different fault states of the main pump motor shield can, a parametric method is used to model the motor and the shield can; for ease of control, scripts are employed to manage the variation of variables, thereby collecting the required dataset.
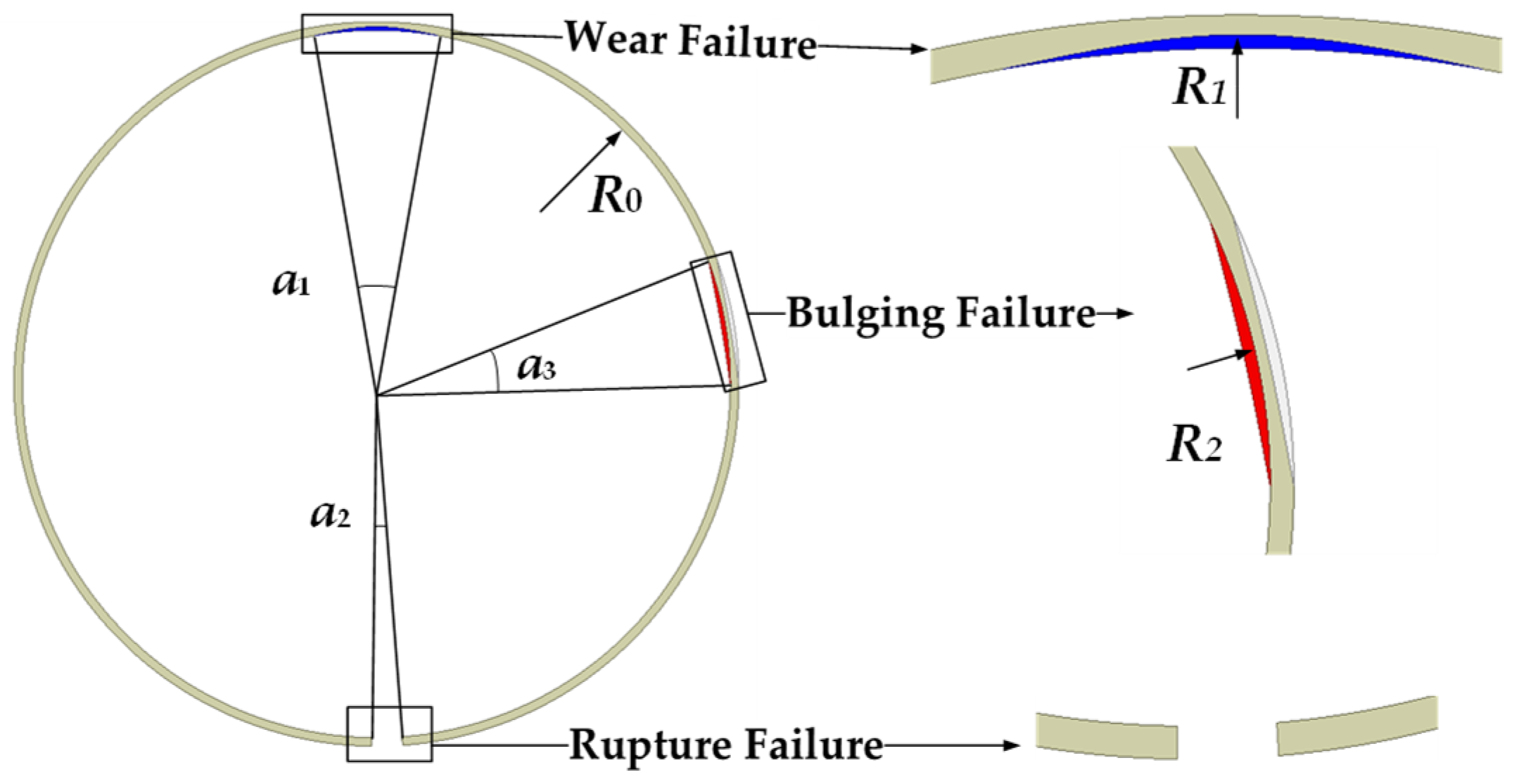
Figure 7 shows the parametric model of the shielding sleeve failure, where
a1,
a2, and
a3 respectively represent the circumferential angle ranges of wear, bulging, and rupture of the shield can and Δ
R1 =
R1 −
R0 and Δ
R2 =
R2 −
R0 respectively represent the changes in the maximum displacement points compared to the normal state during wear and bulging.
The boundary condition of the motor’s finite element model uses a vector boundary. The vector magnetic potential at the outer diameter of the motor stator is set to 0. The excitation source constraint adopts a voltage constraint. The motion constraint takes into account the transient process of the motor’s motion to simulate the motor’s starting process.
3.3. Shielding Sleeve Failure Data Collection and Preprocessing
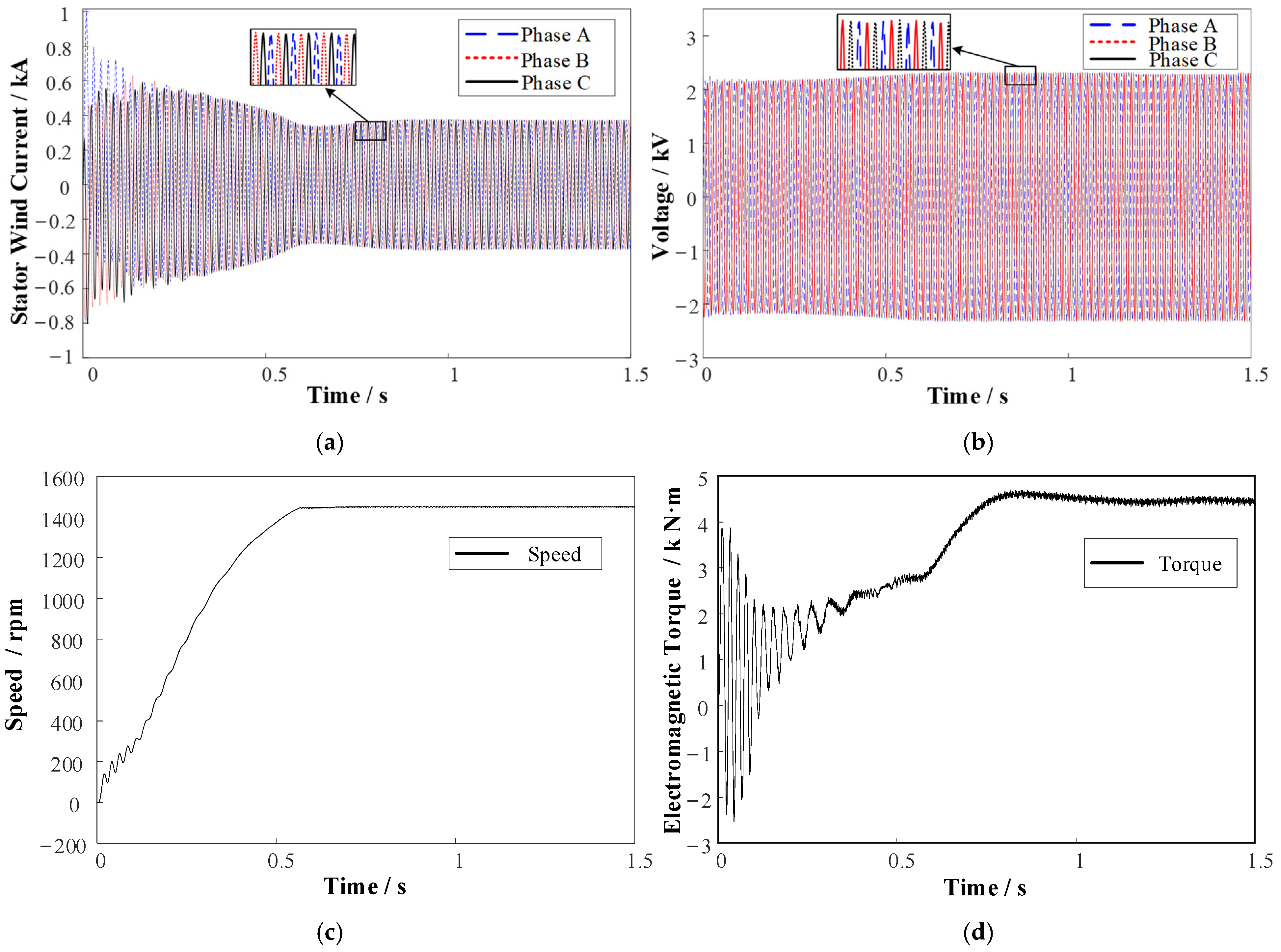
In the previous section, a main pump motor model considering the failure of the shielding sleeve was established. This model was used to simulate normal operating conditions and three different fault conditions of the shielding sleeve (bulging, wear, and rupture). Additionally, simulations were conducted under two different operating conditions and two different levels of fault severity, where smaller numbers represent lighter fault conditions and larger numbers represent more severe fault conditions, thus dividing the failure dataset into 14 distinct classes, as shown in
Table 3. The Maxwell model was able to collect four types of simulation data (current, voltage, torque, and speed), generating eight output signals for the aforementioned 14 classes. For each of these data types, the motor’s operation under a 4-pole condition was simulated for the first 1.5 s with a time step of 0.75 milliseconds and under an 8-pole condition for the first 2 s with a time step of 1 millisecond. Therefore, each sample is represented by one-dimensional data, which consists of 2001 × 8 points and all data were saved into CSV files. Each sample was then individually separated from the CSV files and labeled, as shown in
Table 3. Each time-domain signal (
Va,
Vb,
Vc,
Ia,
Ib,
Ic,
T, and
Sp) was normalized by dividing by their rated values and finally used as input for the CNN for training and testing purposes.
Considering the inconsistency in different failure modes of the shielding sleeve, the failure variables of the parameterized shielding sleeve model from the previous section were controlled. In the case of bulging failure, it is necessary to ensure that the bulge does not come into contact with the rotor to avoid collisions. Therefore, the range of the bulge thickness Δ
R2 was set to 0.1–1.4 mm as the air gap thickness was 1.5 mm, preventing the bulge thickness from exceeding the length of the air gap. For wear failure, the thickness of the shielding sleeve must be considered; so, the range of wear thickness Δ
R1 was set to 0.1–0.4 mm given that the shielding sleeve thickness was 0.5 mm. The ranges for
a1,
a2, and
a3 were set to 1–50°. Each type of data was simulated using a wide range of values, resulting in a relatively extensive dataset. As shown in
Figure 8, a sample of the dataset was obtained through Maxwell simulation.
3.4. Multi-Source Data Fusion Method
The multi-source data fusion process is divided into two stages, and an attention mechanism module is also introduced during the fusion process. In the first stage, after multi-scale feature extraction based on the attention mechanism, features of different scales are first flattened into one-dimensional vectors and then fused together through feature concatenation. The second stage of fusion involves the feature fusion of four channels (current, voltage, speed, and torque). In this process, the conc function is used to directly concatenate features from different data sources, thereby achieving the fusion of data from different channels, as shown in Equation (8).
where
Fi represents the feature extraction results of the multi-scale convolutional neural network based on the attention mechanism for different channels.
3.5. Fault Classification
Similar to traditional fully connected networks, the AM-MSMDF-CNN modifies the parameters of each layer through the BP algorithm and a strategy of minimizing cross-entropy loss. Additionally, the Adam optimizer, which features adaptive learning rates and bias correction, is employed to facilitate parameter updates during the training process. This approach enables rapid convergence of the training process, as illustrated in Equations (9)–(13):
where
L represents the loss value;
n is the size of the input sample;
p is the true label;
q is the actual classification result output by Softmax;
t is the number of training iterations;
mt and
vt denote the first and second moment estimates, respectively;
mt′ and
vt′ represent the bias-corrected estimates;
ε is a very small constant to prevent division by zero error;
θt represents the model’s training parameters; and
β1 and
β2 are the decay rates for the momentum and the squared gradient, respectively.