1. Introduction
Anomaly detection, which is one of the main data mining problems, consists of finding points or objects that do not align with the expected pattern, as related to the other points/objects in a dataset. In database research, anomalies, or exceptional patterns, are also referred to as outliers. In the literature, there is no rigid definition of what constitutes an outlier. Determining whether or not a given unusual observation is an outlier is often an intuitive process that depends strictly on the application domain. In general, an outlier can be defined as a data point (data vector) that differs significantly from the rest of the data in a dataset, or an anomalous observation that diverges from the expected pattern, which may be discovered while studying a particular phenomenon. The problem of outlier detection has been studied in the context of several domains. Not only does it provide the ability to gain new knowledge about a dataset, but it can also be used to aid the performance of machine learning, decision making, or expert systems.
Intelligent data analysis with outlier detection is currently a very rapidly developing area of research based on artificial intelligence and machine learning.
The concept of artificial intelligence was initially aimed at automating the standard human thought process. However, symbolic artificial intelligence based on defining a large number of knowledge processing rules has been extended with machine learning methods. The performance of machine learning models is driven by the exposure to large amounts of data, which allow them to learn and improve through experience—an attempt to mimic the human thought processes and behaviors employed when solving practical engineering problems.
Learning, in this context, can be described as automated search for better representations of some input data. In other words, a machine learning model aims to automatically find ways to transform data into such representations that can facilitate the performance of a particular task.
Machine learning algorithms most often use a predefined set of operations called a hypothesis space or feedback signal. There are several types of machine learning algorithms, including the following: supervised, unsupervised, reinforcement, and deep learning. It is the latter that provides the foundation for the present study. Deep learning is a subset of machine learning that employs artificial neural networks with many input, output, and hidden layers. Each layer converts the input into information that can be used by subsequent layers to perform a predictive task.
Anomaly detection problems can be solved using both supervised and unsupervised methods. An example of an unsupervised learning technique is the density-based spatial clustering of applications with noise (DBSCAN). This algorithm searches for the so-called base points and breakpoints within cluster data, treating everything outside of them as noise or unique patterns. Two other commonly used outlier detection methods are the local outlier factor (LOF) and the connectivity-based outlier factor (COF). LOF uses the nearest neighbors to detect outliers. Each data item is assigned a score indicating the degree of its deviation from its nearest neighbors. The higher the score, the higher the likelihood of the item being an outlier. The supervised anomaly detection algorithms include the One-Class SVM and the Isolation Forest. It should be noted that outlier detection encompasses a broad spectrum of techniques, making use of algorithms from different fields of computing, like intelligent classification algorithms, data grouping, decision rules, neural networks, and genetic algorithms, to name a few.
In this paper, we consider a special type of data, namely data streams. The collection, processing and rapid analysis of such data requires the application of novel methods or the modification of the existing ones. The first formal concepts and definitions of data streams in the literature appeared after 2000. In [
1], the concept was formalized and data stream models were described in detail. An important point of reference in this field is the work of S. Muthukrishnan [
2], which is one of the first comprehensive reviews of algorithms and techniques used for analyzing data streams. In this work, a data stream was defined as follows:
“A data stream is a sequence of data items that arrive online, are potentially unbounded in size, and must be processed under limited memory and time constraints.”
In this article, the following definition is adopted.
Definition 1. A data stream can be formally defined as an ordered sequence of data arriving continuously, potentially infinitely, in real time. Let S denote the data stream, then, the following holds:
is the timestamp (arrival time or generation time) for the i-th element.
is the value of the i-th element (it can be a feature vector or a single value).
T is the time domain, and is the data space.
Outlier detection in data streams may be performed using statistical methods, such as sliding thresholds, the Grubbs method or (), k-sigma, statistical hypothesis testing, Holt-Winters exponential smoothing, ARIMA, etc.
In the works of [
3,
4], the ARIMA method is recognized as an effective anomaly detection algorithm for time data, characterized by the so-called seasonality. Outliers are detected based on regular daily or weekly patterns. Unfortunately, there is a big problem with the dynamic determination of the seasonality period. However, Szmit et al. [
5] claim that setting simple thresholds and exponential smoothing makes it possible to detect spatial anomalies. Unfortunately, the performance of statistical methods for outlier detection in data streams is not satisfactory, as these methods are sensitive to window size changes, as well as threshold changes. Data stream analysis has been performed using incremental algorithms based on hierarchical algorithms [
6], or the k-means algorithm [
7]. Supervised learning methods have been applied, like modified Bayesian networks, for example, as proposed in [
8,
9]. In addition to statistical and stochastic methods, the potential of machine learning techniques for the analysis of data streams has also been examined. Anomaly detection in data streams using deep learning methods is a relatively new area of study. Thus, there is a limited amount of literature strictly related to this topic.
The purpose of this paper is to examine the effectiveness of outlier detection using deep learning methods, with a particular emphasis on the LSTM-CNN hybrid method proposed by the authors. Webscope S5 data streams downloaded from Yahoo! were considered. To check the accuracy of outlier detection, the results of the new hybrid LSTM-CNN method were compared with those of the LSTM and LSTM autoencoder networks. The article’s contributions are as follows:
The discussion of the concept of drift is carried out.
Two methods for determining the anomaly detection threshold are explained, and relevant model features that enable the detection of outliers in data streams are defined.
A LSTM-CNN model for outlier detection is proposed.
The effectiveness of the proposed LSTM-CNN approach for detecting outliers in data streams is evaluated.
In particular, a comparison of the proposed LSTM-CNN system to the already known LSTM and LSTM AE models is exhaustively performed.
The paper is organized as follows:
Section 2 discusses the problem of anomaly detection in data streams.
Section 3 describes and discusses the neural networks that provide the foundation for this investigation. It begins by explaining the basic concept of RNN and its extensions—the standard LSTM model and LSTM autoencoder. This is followed by a characterization of Convolutional Neural Networks (CNNs).
Section 4 presents the essential part of the research. It begins by explaining the operation of the LSTM autoencoder as an outlier detector in data streams based on error reconstruction. Then, it moves on to describe in greater detail the LSTM-CNN method proposed by the authors.
Section 5 is concerned with the stream datasets and methodology used for this study.
Section 6 presents a discussion of the results. Finally, the conclusion gives a brief summary of the findings.
2. Problem Statemets
2.1. Anomalies in Data Streams
Any ordered set of items can be considered a data stream. The analysis of such data allows one to characterize the stream or to extract the information contained in it. The order of items under consideration is determined explicitly, by the timestamp, or implicitly, by the entrance time.
In the simplest standard form of description, the data are ordered by their sequence determined by the moment , while the number of moments can be finite or infinite. To provide high-quality results, the analysis of stream data requires access to a large dataset and continuous data inflow. This not only ensures consistency and reliability of results but also allows one to identify seasonality and trends.
Roughly speaking, an outlier in a data stream is an item which differs significantly from the other items in the stream. Determining the character and significance of the anomaly is a separate problem. Outliers can be divided into the following three main types: point, contextual, and collective. However, for the analysis of data streams, a division into additive and innovative outliers is more often used. Each type can be characterized as follows:
A point outlier is an object located at a significant distance from the other objects.
An outlier is regarded as contextual when its occurrence depends on changes in context, such as time, weather changes, supply, demand, and others, depending on the area under consideration.
A collective outlier occurs when a particular sequence or dataset deviates significantly from the dominant cardinality of the set. Individual objects in a collective outlier do not have to manifest themselves as point or context outliers simultaneously. It is believed that this type of outlier is relatively difficult to define precisely and detect.
An additive outlier is recognized by observing the size of the error in finite time T, which can be caused by a simple human error, or a system error—in the case of data coming from a device. The noise in an incoming signal can also be regarded as an anomalous feature.
The concept of an additive outlier was introduced by Barnet and Lewis in [
10]. It is a measurement error in time
T,
, caused by external factors, e.g., machine failure or human error.
An innovative outlier is usually caused by a sudden change in a process or system. These types of outliers also include change points that evidence a change in an underlying trend.
It should be emphasized that additive outliers are treated as noise. The present study concentrates on finding sudden changes in the signal that may indicate the emergence of a new trend. Thus, it deals with innovative outliers, which can also be treated as contextual outliers.
Most of the current research concerning outlier detection in data streams emphasizes the use of the Long Short-Term Memory (LSTM) model and its variants. LSTM is preferred over the classic Recurrent Neural Network (RNN), since the latter suffers from the vanishing gradient problem. The use of recurrent neural networks for time-series analysis was proposed in [
11,
12,
13]. Zhou et al. [
14] proposed missing data reconstruction based on the LSTM network for Landsat time-series images. In [
15], the authors proposed a new approach for efficient anomaly detection based on utilization of Markov and LSTM-based networks for real-time sensor data.
In [
16], the performance of the LSTM autoencoder, among other methods, has been examined. The paper provides a detailed description of the model’s architecture and parameters applied. The results are evaluated using the universal F1-score. Moreover, the authors offer access to the database containing labeled outliers, which may advantageous for related research. A similar concept, also rated with the F1-score, is presented in [
17]. A hybrid model combining deep learning and a support vector machine (SVM) for anomaly detection was also proposed in [
18]. In [
19], unsupervised hybrid anomaly detection approaches were developed. The anomaly detection was checked by hybrid models created with the combination of the Long Short-Term Memory (LSTM)-Autoencoder, the Local Outlier Factor (LOF), and the Mahalanobis distance. The LSTM-based deep stacked sequence-to-sequence autoencoder learns deep discriminative features from the time-series data by reconstructing the input data. These features are entered into the SVM and then recognized.
In [
20], the LSTM autoencoder is recommended as an effective outlier detection method. The LSTM autoencoder was proposed in [
21] as a model specialized for time-series data. This model learns the patterns of normal data and detects other data as outliers, utilizing the vibration signals from wind generators. In [
22], the authors demonstrate the use of both a LSTM and LSTM autoencoder for solving forecasting and anomaly detection problems. A comparative study of the selected methods used for outlier detection in data streams can be found in [
23]. In paper [
24], the authors proposed a long short-term memory autoencoder (LSTM-AE)-based reconstruction error detector, which designs the LSTM layer in the shape of an autoencoder, to build a reconstruction error-based outlier detection model and extract latent features. In the paper by Mushtaq, et al. [
25], an interesting hybrid framework is proposed. It combines a deep auto-encoder (AE) with both long short-term memory (LSTM) and bidirectional long short-term memory (Bi-LSTM) architectures. This framework is designed for intrusion detection systems. It works by first extracting optimal features using the auto-encoder and then employing LSTMs for the classification of samples into normal and anomaly categories. In [
26], it has been shown that deep learning models can, under certain circumstances, outperform traditional statistical methods at forecasting. The authors proposed three deep learning architectures, namely, cascaded neural networks, reservoir computing, and long short-term memory recurrent neural networks. On the other hand, in [
27], the authors proposed an anomaly detection framework for spacecraft multivariate time-series data based on temporal convolution networks (TCNs). In paper [
28], a novel BI-LSTM-CNN technique for detecting malevolent traffic in smart devices was proposed. The authors combined deep learning techniques, specifically convolutional neural networks (CNN), with long short-term memory (LSTM) for the purpose of detecting and categorizing malevolent Internet traffic. In [
29], the authors developed an improved training algorithm tailored for anomaly detection in unlabeled sequential data, such as time series. Their approach posits that the outputs of a meticulously designed system are derived from an unknown probability distribution, denoted as U, under normal conditions. They introduce a probability criterion grounded in the classical central limit theorem, enabling the real-time assessment of the likelihood that a given data point originates from U. This facilitates the on-the-fly labeling of the data. Real data are then fed into a deep Long Short-Term Memory (LSTM) autoencoder for training, identifying anomalies when the reconstruction error surpasses a predefined threshold. Anomaly detection has been investigated using hybrid models combining Long Short-Term Memory (LSTM) networks and Convolutional Neural Networks (CNNs). In [
30], an intrusion detection model, named the CNN-LSTM, with an Attention Model (CLAM) was proposed for in-vehicle networks, particularly the Controller Area Network (CAN). The CLAM model employed one-dimensional convolutional layers (Conv1D) to effectively extract abstract features from the signal values. Similarly, in [
31], a hybrid Intrusion Detection System (IDS) was developed by integrating Convolutional Neural Networks (CNNs) with Long Short-Term Memory (LSTM) networks. This model incorporated two regularization techniques—L2 regularization (L2 Reg.) and dropout—to mitigate the issue of overfitting. See also works [
32,
33]. The neural network methods used in this investigation were broadly described in [
34,
35,
36,
37,
38].
2.2. The General Problem Statement
This paper seeks to address the problem of contextual anomaly detection in data streams, which is considered an important step in the development of dedicated models using a machine learning approach. A repeated occurrence of outliers or an increase in the number of anomalies in predictive models can indicate changes in the definition of the classes predicted by the model over time, the so-called concept drift. Thus, the detection of outliers in training datasets is recommended to ensure the high quality of these data.
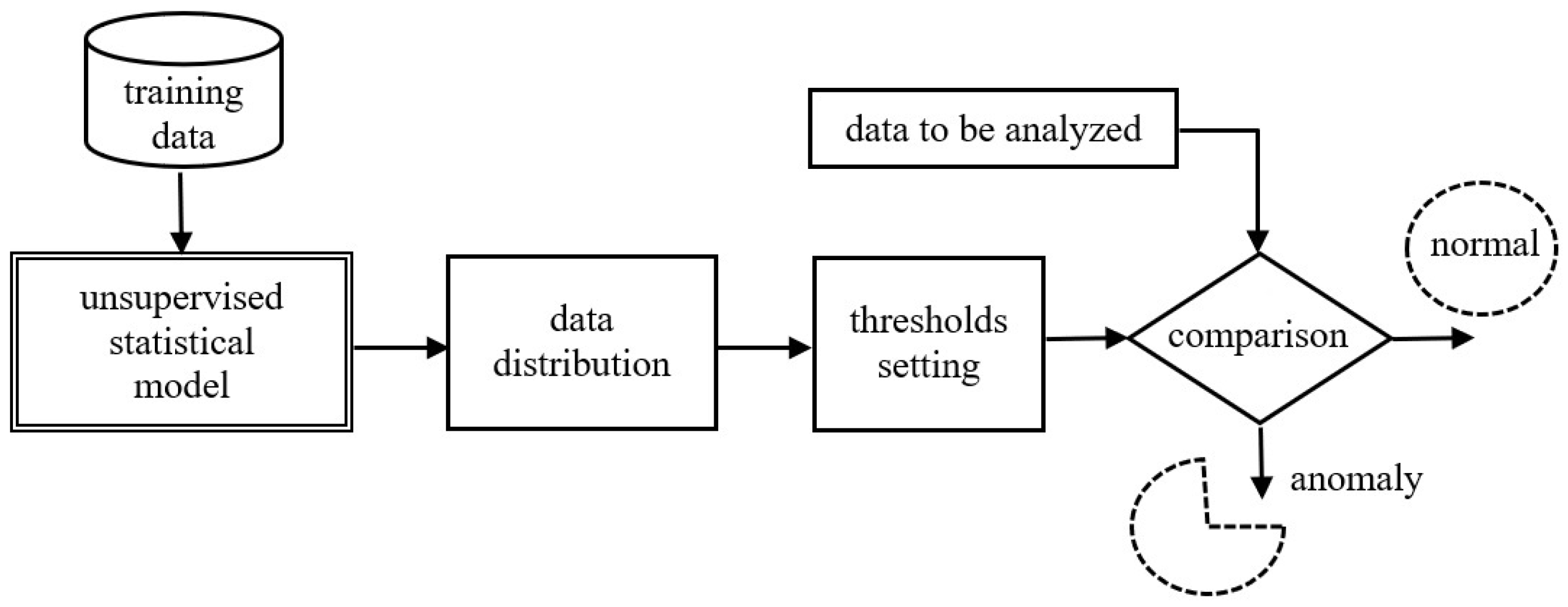
An important aspect is the dimensionality of the problem. For multivariate datasets with all the characteristics of time series, methods dedicated to multidimensional time series can be used. One can also use models that do not take into account the temporal characteristics of the data but attempt to find point outliers in the multidimensional space. There are two main categories of outlier detection techniques as follows: supervised and unsupervised. The present study applies a supervised learning approach, as shown in
Figure 1.
As illustrated below, after transferring the training data to the proposed model, the data prediction process takes place. Based on the prediction, the detection threshold is determined, above which a data point is labeled as an outlier.
There are two methods of determining the anomaly detection threshold, as follows:
Detection by distance and data density. This method considers an outlier as a point. Using density-based methods, data are grouped into clusters using the distance between all cluster points in order to establish a clustering boundary. If values outside the cluster boundaries are detected, they are referred to as outliers. These methods do not apply to outlier detection in data streams.
Detection by prediction. This method applies statistical models to predict the behavior of a dataset in the future. It is possible to predict the probable distribution of data and to highlight points that do not meet the assumed distribution requirements. The model is then capable of identifying all types of anomalies, in particular, collective outliers.
When creating an outlier detection model for data streams, it is important to pay attention to the following elements (model features):
No changes are made to the time series concerning its time intervals.
No interference with the stream length. When conducting outlier detection tests, it is necessary to pay attention to the desired properties of the anomaly detector.
Analysis and predictions must be done online, so the algorithm must identify the state as normal or as an outlier before obtaining the next state .
Learning to identify successive states must be done continuously, without having to store the entire stream.
The model should operate in an automated, unsupervised manner, without modifying the parameters of the algorithm during its operation.
The model should automatically adjust to stream changes (its dynamics, drift).
The model should detect anomalies as quickly as possible and minimize errors.
In the following sections, we examine the performance of the proposed novel hybrid neural network architecture (see
Section 4.2) as compared to the other two approaches presented in
Section 3.2 and
Section 4.1.
4. Outliers Detection Based on Deep Learning Models
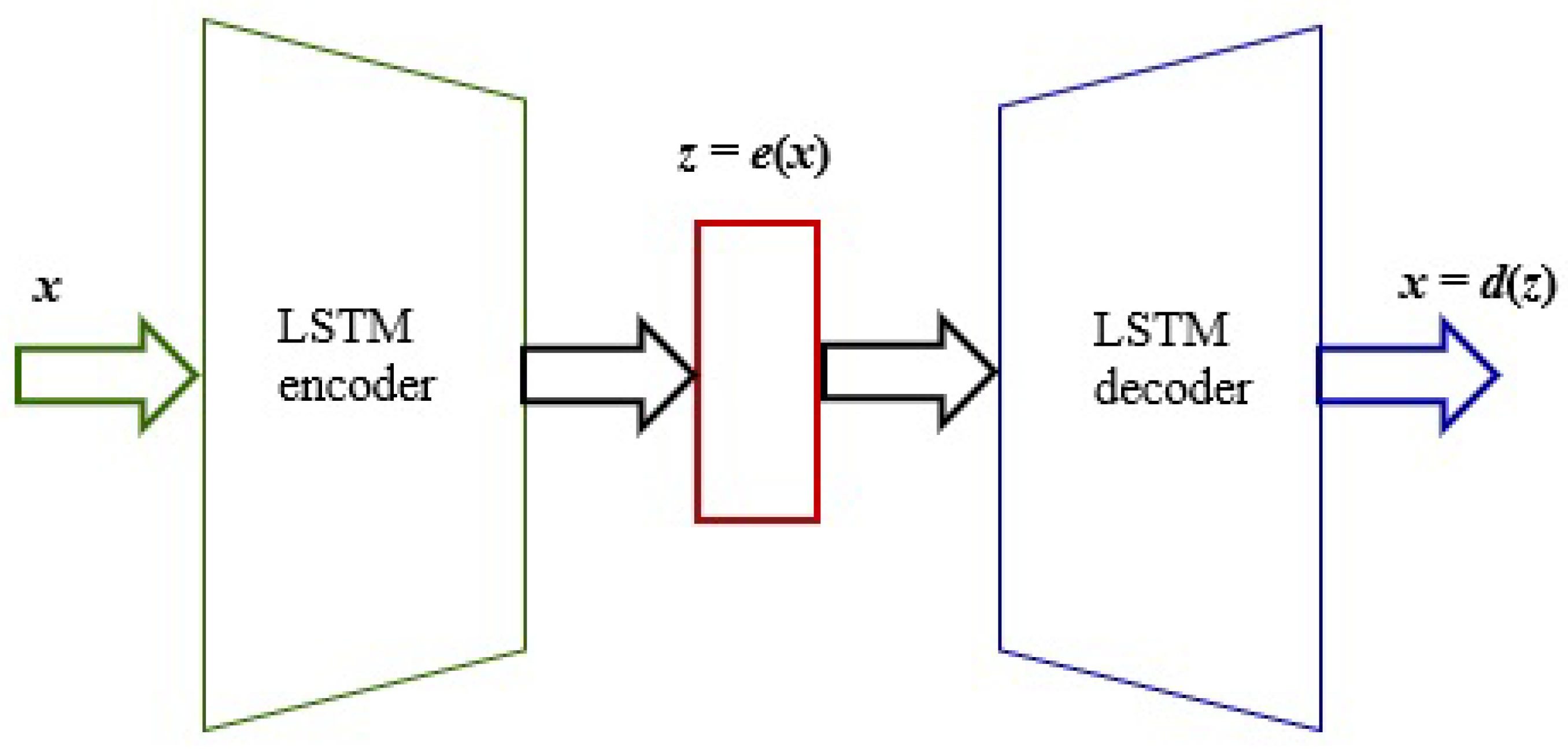
4.1. LSTM Autoencoder as an Anomaly Detector in Data Streams Based on Error Reconstruction
According to [
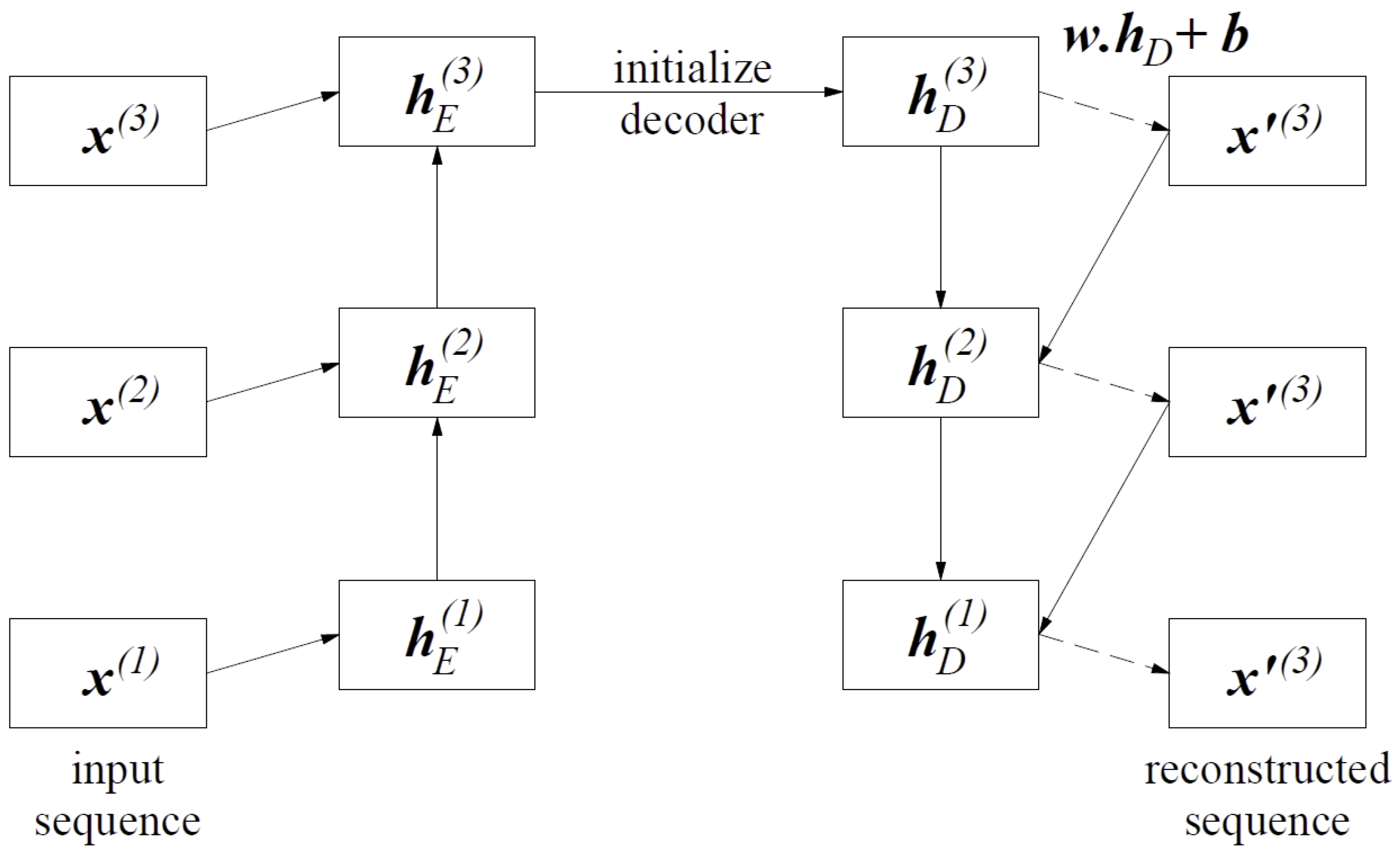
20], the network training process is performed in order to reconstruct the time-series data. The encoding part of the LSTM network learns a sequence of vector data, while the decoding part uses this input to reconstruct the current hidden state and the value predicted at the previous time step. The relations between the input sequence and the reconstructed sequence are shown in
Figure 6.
Given x, is the hidden state of the encoder at time for , where . C is the number of units in the LSTM hidden layer of the encoder, the final encoder status serves as the initial state for the decoder. The prediction takes place on the top layer of the LSTM decoder. During the training process, the decoder takes as the input to obtain state , where the prediction occurs, corresponding to . During the prediction, the value is input to the decoder to obtain and make a prediction .
Figure 6 shows examples of the iterations for three time steps
over the LSTM autoencoder network. The decoder recreates the model for the sequence of step time
. The value of
at time
and the hidden state
on encoder side w time
are used to obtain the hidden state
of the encoder in time
. The hidden state decoder, i.e.,
, at the end of the input sequence serves as the initial state
in the decoder part. To calculate
, a linear layer with a matrix of weights
w of dimensions
and bias
is used at the top of the decoder.
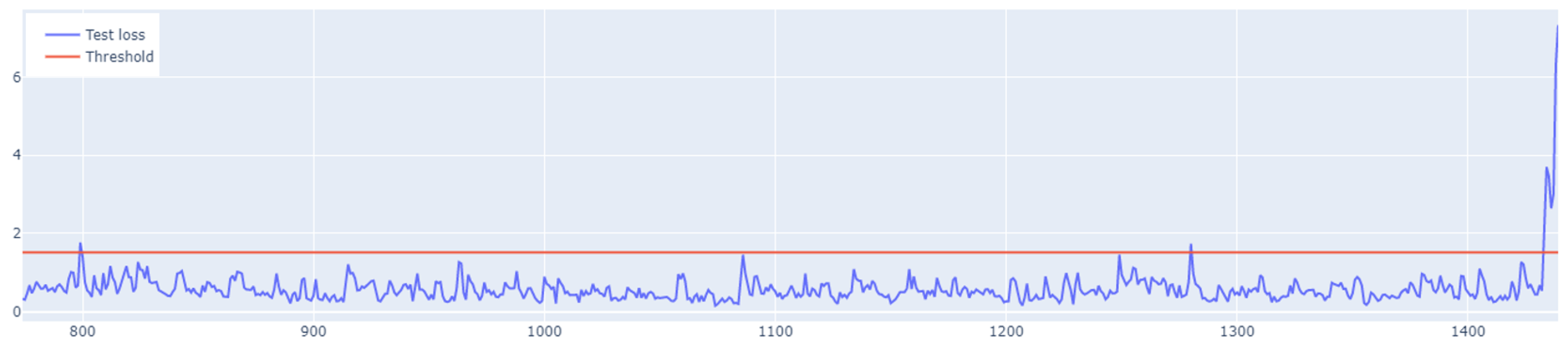
The LSTM autoencoder anomaly detection algorithm involves setting a detection threshold value. If a given value in the dataset exceeds the established threshold, the algorithm treats it as an exception. The mean absolute error of the
, i.e., the sum, is responsible for the detection of absolute errors divided by the sample size. The
error is defined by Equation (
12), where
n is the sample size,
is the real value, and
is the prediction value.
The value of the anomaly is determined after calculating the
for both the training and the test set. The anomaly is detected when the test set’s
error is greater than the maximum
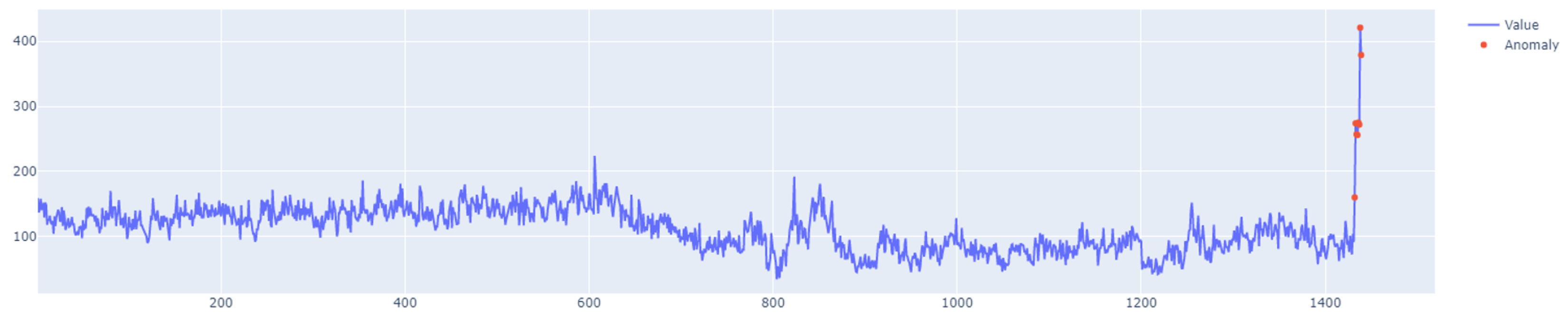
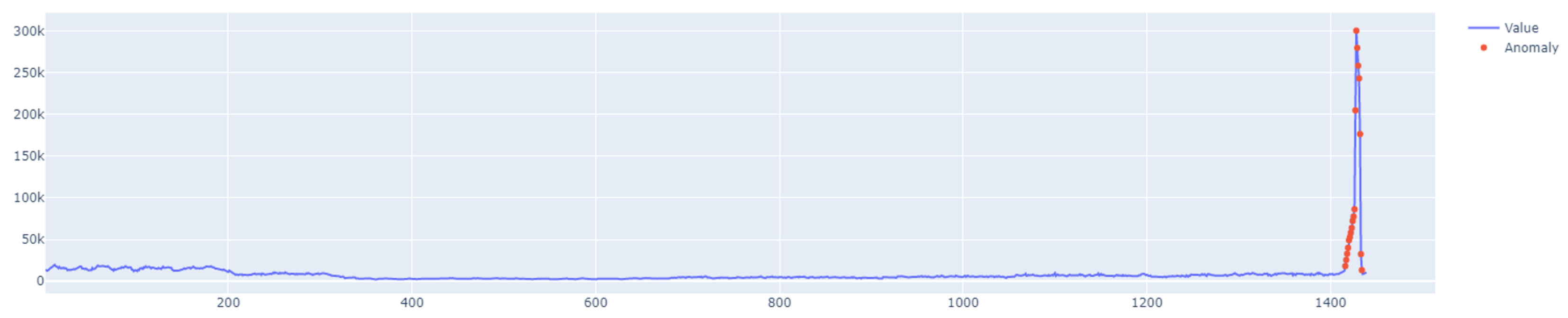
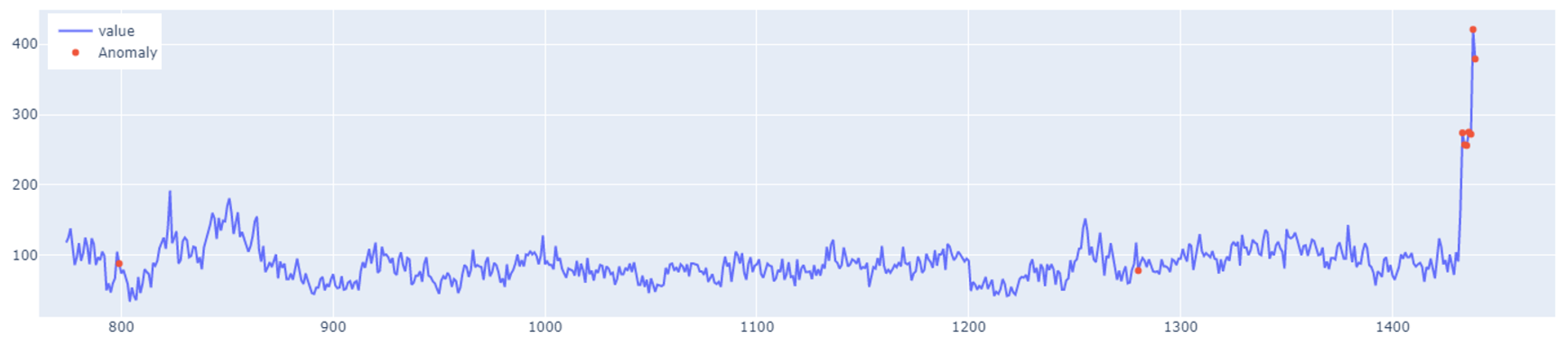
error of the training set. An example of how the LSTM autoencoder algorithm works is shown in
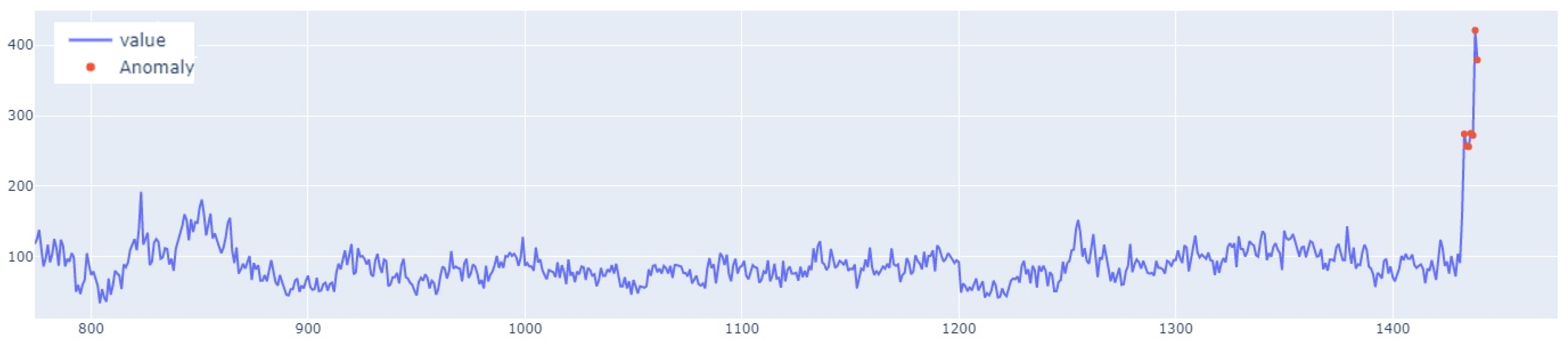
Figure 7. Outliers detected using this method have been highlighted in
Figure 8.
4.2. A Novel LSTM-CNN Hybrid Model
In this paper, supervised learning is used because it directly leverages labeled data. This method effectively captures both the sequential dependencies handled by the LSTM and the spatial features extracted by the CNN. Unsupervised methods focus on discovering latent structures in the data (e.g., clustering, dimensionality reduction) and do not require labeled outputs. While such methods can be useful for pretraining or an exploratory analysis, they lack the capability to directly predict specific labels or outcomes, which is the main goal of the LSTM-CNN hybrid in this study.
Reinforcement Learning (RL) relies on feedback in the form of rewards and penalties, which are derived from interactions with the environment, while RL is powerful in decision-making tasks or control problems, it is computationally expensive and less suitable for static datasets where reward signals are not naturally available. The hybrid LSTM-CNN architecture is optimized for supervised tasks with well-defined input–output relationships rather than iterative environment-based learning. Approaches like Semi-Supervised and Self-Supervised Learning are beneficial in scenarios where labeled data are limited, as they leverage unlabeled data to improve performance. In this study, the availability of labeled data ensures that the supervised learning paradigm can fully exploit the architecture’s capabilities without requiring additional pretraining or assumptions about the data distribution. The preference for supervised learning in this context stems from the structured nature of the problem and the hybrid model’s strengths. However, this approach has limitations, such as dependence on labeled data, susceptibility to label noise, and potential overfitting to specific datasets. Alternative approaches, such as semi-supervised learning, could complement supervised methods in future work by reducing the reliance on labeled data or improving generalization. Supervised learning is the optimal choice for the hybrid LSTM-CNN method due to its ability to directly optimize the model for accurate predictions using labeled data. The method is tailored to extract sequential and spatial features effectively, which aligns naturally with the supervised paradigm. While alternative approaches have merits, their application would either introduce unnecessary complexity or fail to address the specific goals of this study as effectively as supervised learning.
The third architecture proposed and used in this work is a combination of two sequentially connected neural blocks—the Long Short-Term Memory (LSTM) and the Convolutional Neural Network (CNN). The hybrid LSTM-CNN method is inherently designed for tasks where the relationship between input data (e.g., time-series signals, sequential patterns, or spatial features) and the desired output (e.g., classifications, predictions, or labels) are well defined and can be explicitly modeled. Supervised learning is preferred because it directly leverages labeled data to optimize this mapping, ensuring the method effectively captures both the sequential dependencies handled by LSTM and the spatial features extracted by CNN.
The LSTM is recognized as the most effective method for time series. However, after reviewing the literature and other available neural network methods, we decided to look into ways of extending current models to improve their performance. Hence, the idea of combining the LSTM architecture with CNN.
It should be emphasized that the proposed LSTM-CNN hybrid model is analyzed in the context of sequence processing. It is well known that one-dimensional CNNs are not sensitive to the order of time steps. Of course, the stacking of multiple layers, one after another, enables the network to learn increasingly complex patterns in data sequences. However, in some cases, this may not be an effective solution. It is also worth mentioning that CNNs are much faster than regular recurrent networks. It should also be noted that LSTM networks are highly sensitive to time steps. Thus, they can be easily used to model time dependencies. As the number of steps increases, their learning process slows down significantly. After considering all these aspects, a sequential model was proposed, the diagram of which is shown in
Figure 9.
In the first step, the model applies a one-dimensional convolutional layer and a pooling layer. This makes it possible to obtain a compressed representation of the input with higher-level functions. Then, this representation is passed on to the next layer, such as the LSTM layer, which is more capable of representing the sequence, preparing it for further processing. After the LSTM layer, the dropout layer is used, which allows for better regularization to reduce the risk of overtraining. The model’s construction is as follows. The input data are a three-dimensional vector (None, 5, 1), where 5 is the time step and 1 represents the time step input dimension features. At first, data are entered into the one-dimensional convolutional layer to extract features and obtain a three-dimensional output vector (None, 5, 256), where 256 is the number of filters (kernels). In the next step, the vector enters the pooling layer. This is a three-dimensional vector (None, 1, 256). The next part of the model is the input of the previously obtained vector to the LSTM layer, where the training takes place. The output data (None, 64) undergoes regularization. Here, another fully connected layer is applied to obtain the output value.
The input is a three-dimensional vector (None, 5, 1), where 5 is the time step and 1 represents the input dimensions. First, data are entered into a one-dimensional convolutional layer to extract features and produce a three-dimensional output vector (None, 5, 256). Moreover, 256 is the number of filters (kernels). In the next step, the vector enters the pooling layer, where a three-dimensional vector is obtained again (None, 1, 256). The next stage of the model is the introduction of the previously obtained vector into the LSTM layer, where training takes place, and the output data (None, 64) after the training stage go through the regularization process, where they later introduce another full connection layer to obtain the output value.
It should be emphasized that the choice of a window size of 5 time steps was guided by the nature of the data, task requirements, and a balance between computational efficiency and model performance. The window sizes were evaluated during the preliminary experiments to assess their impact on the model’s performance. A window of 5 time steps was deemed sufficient to capture relevant short-term trends and patterns in the data while avoiding the inclusion of unnecessary or redundant information. Smaller windows (e.g., 2 or 3 time steps) resulted in insufficient context for the model, leading to suboptimal feature extraction and reduced accuracy. Larger windows (e.g., 10 or 15 time steps) increased the computational cost and complexity of the model without providing significant gains in performance.
4.3. Training, Prediction, and Detection Processes Using the LSTM-CNN Hybrid Model
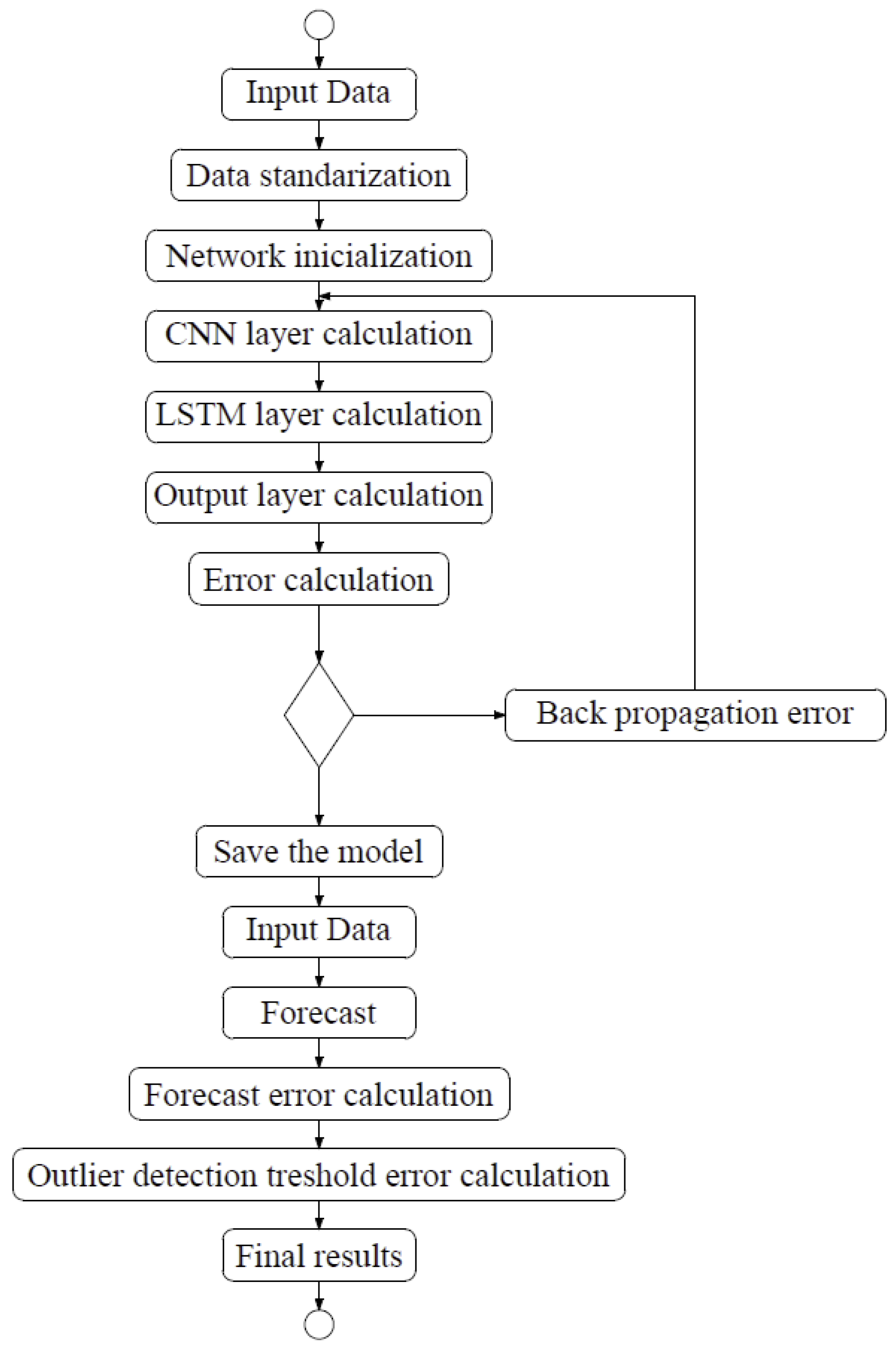
The steps of this algorithm are as follows:
Input data—data used for LSTM-CNN network training.
Data standardization—this process follows according to Formula (20).
Network initialization—initialization of weights and biases on each LSTM-CNN layer.
Calculation of the CNN layer—the input data are successively passed through the convolutional layer and the pooling layer, where features are then extracted and the output value is obtained.
Calculation of the LSTM layer—the data from the previous step are calculated by the current LSTM layer and the output value is obtained.
Calculation of the output layer—the fully connected layer receives data from the LSTM layers to obtain the output value.
Error calculation—data from the full connection layer are compared with the real values and the error is calculated.
Fulfillment of the condition—completion of a certain number of iterations, weight, and forecast error are lower than a certain threshold. If these conditions are met, the algorithm moves on to the next step. Otherwise, it goes to the error backpropagation step.
Backward error propagation—propagate the calculated error backwards, update the weight and bias of each layer. Then, go back to step 4.
Save the model—save the model.
Input—enter data into the forecast process.
Prediction—make predictions.
Calculation of the prediction error—calculate the prediction error.
Calculation of the exception detection threshold—based on the obtained forecasting error from the previous threshold, determine the exception detection threshold.
Final result—list any exceptions found.
The block diagram of the learning process of the proposed modification is shown in
Figure 10.
7. Conclusions
This study has investigated the performance of a hybrid LSTM-CNN approach for outlier detection in data streams. It was shown that the proposed method outperforms the other two models—LSTM and LSTM AE. The
, which was used as a performance indicator, was highest for the hybrid approach. For Set_ 1, the LSTM-CNN model outperforms the LSTM AE method, with the
being higher by as much as 0.49. The value obtained by the LSTM model is only 0.06 lower, which is still a satisfactory result. For Set_2, which turned out to be the easiest to learn, the highest value of
was obtained. It can be seen from
Table 3 that LSTM and LSTM AE achieved the same result
, whereas the value obtained by the LSTM-CNN model was higher by 0.02. For Set_3, LSTM-CNN also outperformed the other methods, with an
higher than LSTM and LSTM AE by 0.10 and 0.05, respectively. The same results were achieved for Set_4. Significant differences were observed in terms of the learning time. The LSTM model, the simplest in construction, was the fastest to learn. The time taken by the algorithm to train on each set did not exceed two seconds. The reconstruction-based LSTM AE was the slowest to learn. The LSTM-CNN model demonstrated a slightly longer learning time as compared to the LSTM algorithm. However, in this case, it should be noted that the hybrid LSTM-CNN model has more layers than the LSTM. In addition, the difference in learning time between the LSTM and LSTM-CNN is very small and does not significantly affect the outlier detection results.
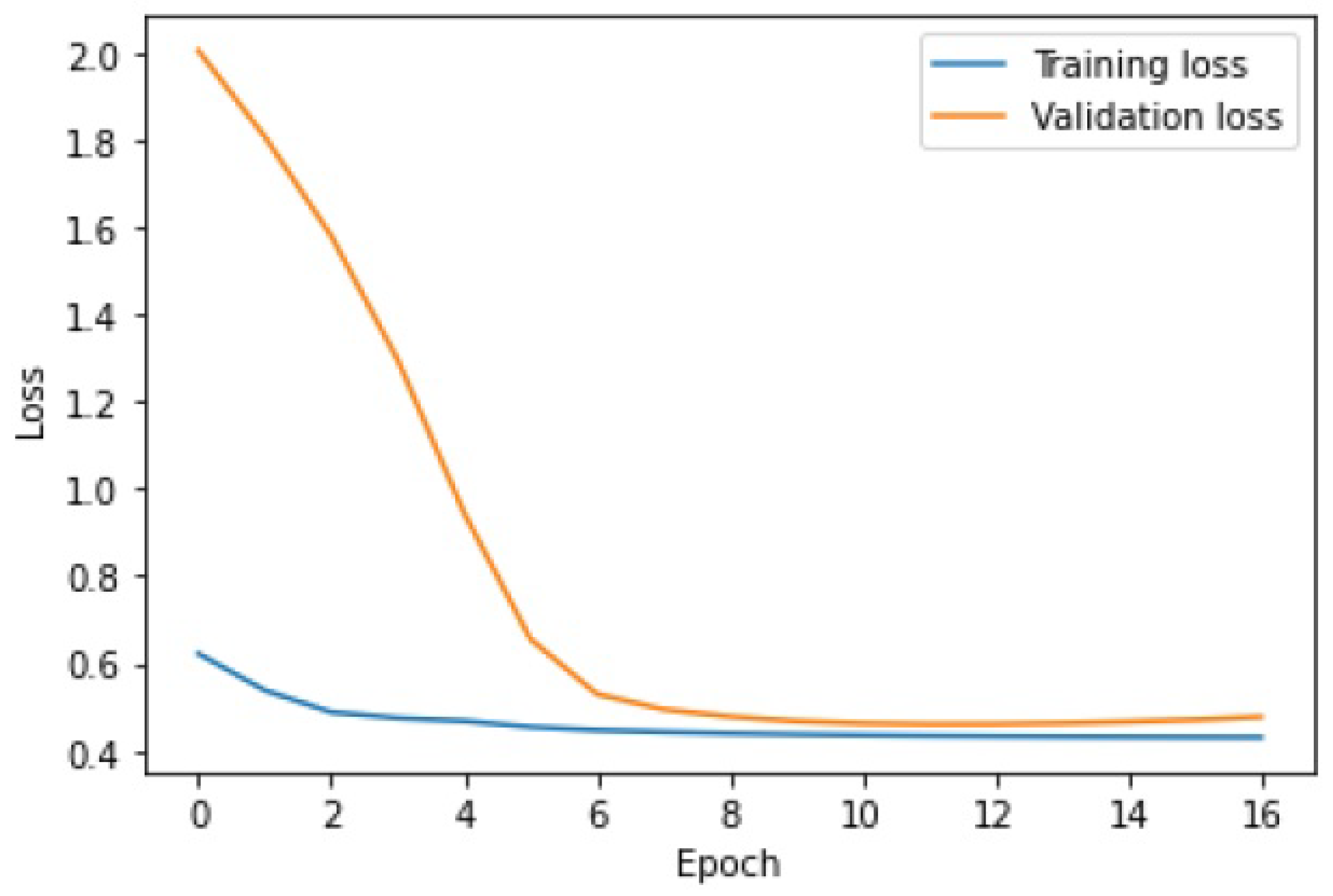
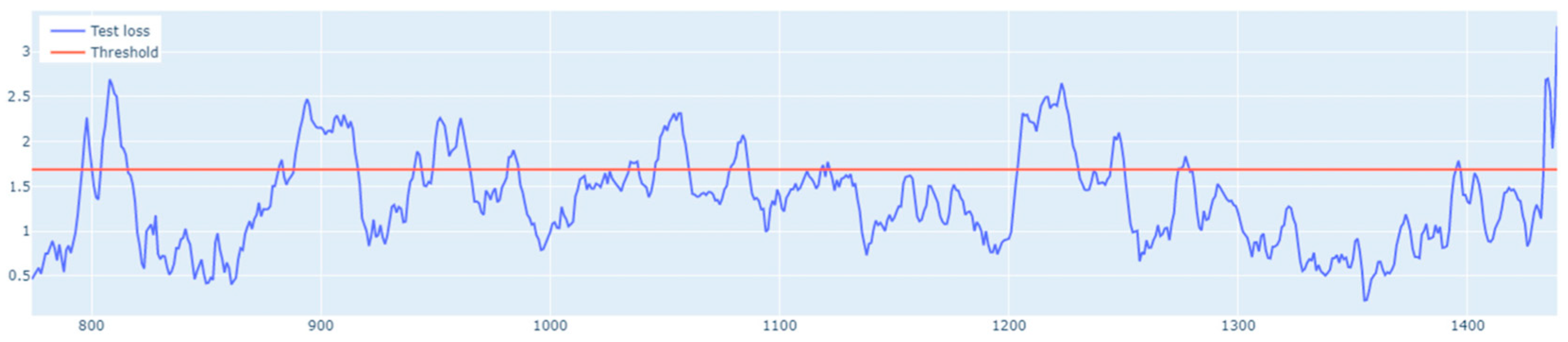
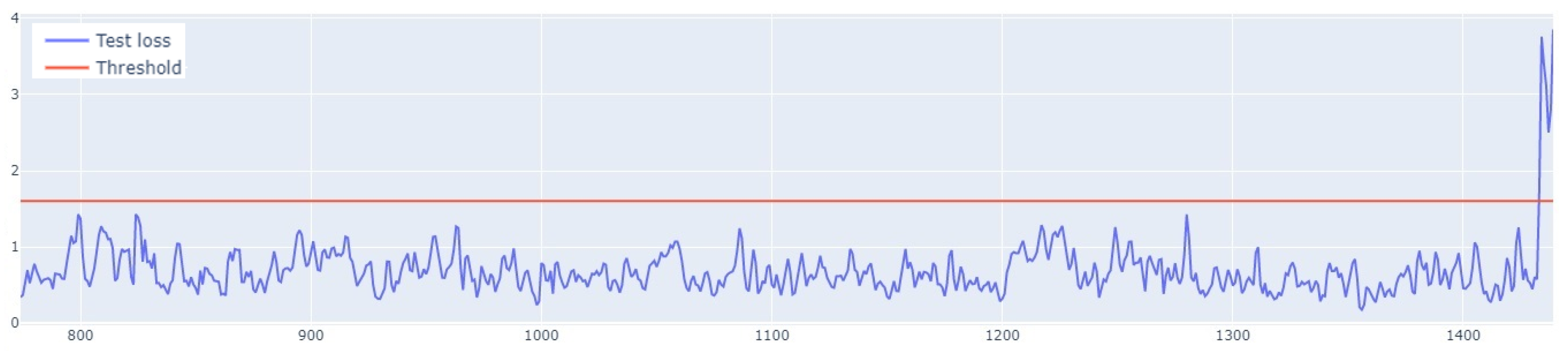
When it comes to the learning performance, LSTM AE produced the least satisfactory results. For Set_2, the training and validation lines were closest to each other and the MSE measurement error was the smallest. In the remaining sets, the LSTM AE model failed to learn the time-series patterns. This is best illustrated by the threshold and outliers graphs, where the number of detected outliers far exceeds the number of real outliers. This is because insufficient learning has lowered the detection threshold. As indicated by the line plots of training and validation loss, the networks LSTM and LSTM-CNN demonstrated a similar learning performance, the new model performing better, as it reached a higher . The novel LSTM-CNN method was able to detect 7 out of 8, 22 out of 19, 6 out of 11, and 5 out of 8 real outliers in Set_1, Set_2, Set_3, and Set_4, respectively. Thus, it may be concluded that the hybrid approach is well suited for outlier detection problems in data streams.
As for the memory requirements of the proposed solution, the LSTM autoencoder primarily consumes memory for network weights and hidden states, typically ranging from 500 kB to several MB. The LSTM-CNN introduces a CNN layer, which increases parameter count but reduces the number of input features to the LSTM. This may lead to lower overall memory consumption depending on the complexity of the input data. Both architectures fall within the same order of magnitude in memory consumption, but LSTM-CNN has the advantage of reducing input dimensionality, which can improve efficiency. Simple statistical techniques such as PCA and regression require significantly less memory, typically in the range of tens to hundreds of kB, as they do not rely on large trainable weight matrices or hidden states. In contrast, both LSTM autoencoders and LSTM-CNN models require hundreds of kB to several MB, making them considerably more memory-intensive. Compared to the LSTM autoencoder, the proposed LSTM-CNN architecture introduces additional parameters from the CNN layer but may reduce overall memory consumption by decreasing the number of input features to the LSTM. While both architectures require significantly more memory than simple statistical methods, the CNN component helps optimize memory usage by reducing redundant input dimensions before they reach the LSTM layer.
In this article, we propose the combination of LSTM and CNN to leverage their complementary strengths for outlier detection in sequential and high-dimensional data. Each individual method has certain limitations that are addressed when used together. LSTMs excel at capturing long-term dependencies and temporal patterns in sequential data, making them ideal for time-series analysis, but they struggle with efficiently modeling spatial or local patterns in high-dimensional data, as their design focuses primarily on sequential dependencies. Furthermore, LSTMs are computationally intensive and prone to overfitting when applied to complex datasets with a high variability. Convolutional Neural Networks are highly effective at extracting local patterns and spatial features due to their convolutional structure, which operates on subsets of the input data. Unfortunately CNNs are less suited for handling sequential dependencies or temporal dynamics because they are primarily designed for fixed-size inputs with a focus on local correlations. The hybrid LSTM-CNN model combines the strengths of both architectures to address their individual limitations as follows: CNNs extract features from the data, which are then processed by LSTMs to capture temporal dependencies. The CNN layer reduces the dimensionality of the input data, feeding only the most relevant features into the LSTM. This reduces overfitting and improves the robustness of the model, especially when dealing with high-dimensional datasets. By combining these methods, the computational inefficiencies of LSTMs and the sequence-insensitivity of CNNs are mitigated. The hybrid approach ensures that the strengths of one architecture compensate for the weaknesses of the other. The combination of the LSTM and CNN is particularly important for outlier detection.
The model proposed in this article has several limitations. The hybrid LSTM-CNN method was applied to labeled data, which may restrict its applicability in scenarios where annotated datasets are scarce or unavailable. The computational demands of the hybrid LSTM-CNN model, while manageable for medium-sized datasets, could become a challenge when working with large-scale datasets, particularly in the context of big data. The model’s sensitivity to hyperparameter selection poses another limitation. Achieving optimal performance may require domain-specific expertise and significant effort in fine-tuning. Despite these limitations, the proposed method demonstrates significant potential in various real-world applications, particularly in anomaly detection systems. For example, for detecting faults or irregularities in industrial systems and IoT sensor networks; for identifying abnormal patterns in physiological signals, such as ECG or EEG data; and for detecting unusual trends or anomalies in financial time-series data, such as stock market trends. These examples illustrate the versatility of the hybrid LSTM-CNN approach in addressing complex, real-world problems involving sequential and high-dimensional data. The proposed comparative analysis of anomaly detection methods based on streaming data can be directly applied in the context of intelligent monitoring systems, IoT sensors, and temporal data analysis. The importance of anomaly detection for sensor systems is of great importance. Modern sensor systems generate huge amounts of streaming data, which require effective methods for analysis and real-time anomaly detection so the models presented in the article (LSTM, LSTM autoencoder, and LSTM-CNN) may be of interest to readers involved in sensor signal processing.