Mechanical Structure Design and Motion Simulation Analysis of a Lower Limb Exoskeleton Rehabilitation Robot Based on Human–Machine Integration
Abstract
1. Introduction
2. Analysis of Human Lower Limb Gait Characteristics and Data Collection
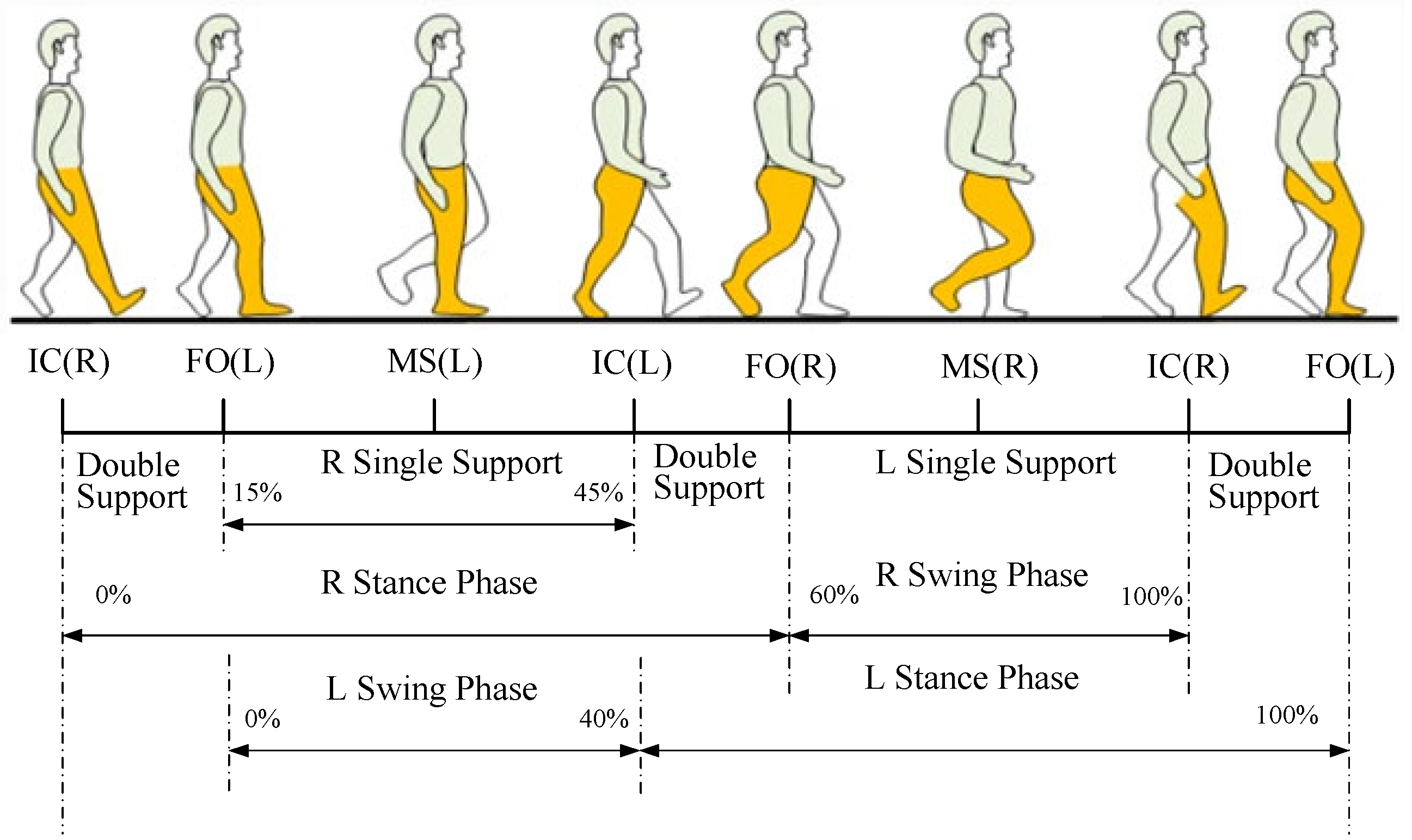
2.1. Analysis of Human Lower Limb Gait Characteristics
2.2. Data Collection of Joint Angles in the Human Lower Limb
2.2.1. Experimental Platform
2.2.2. Experimental Procedure
2.2.3. Data Processing
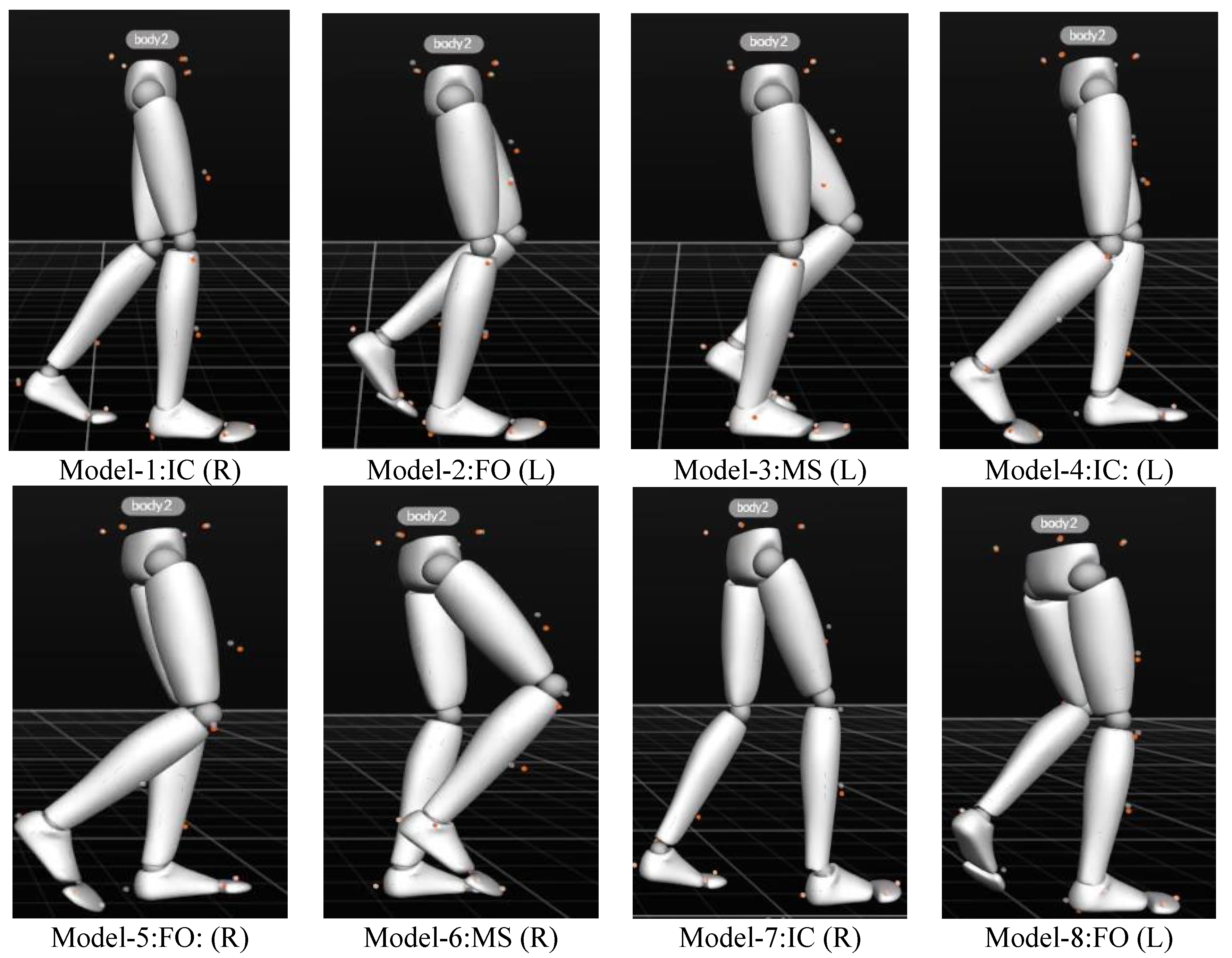
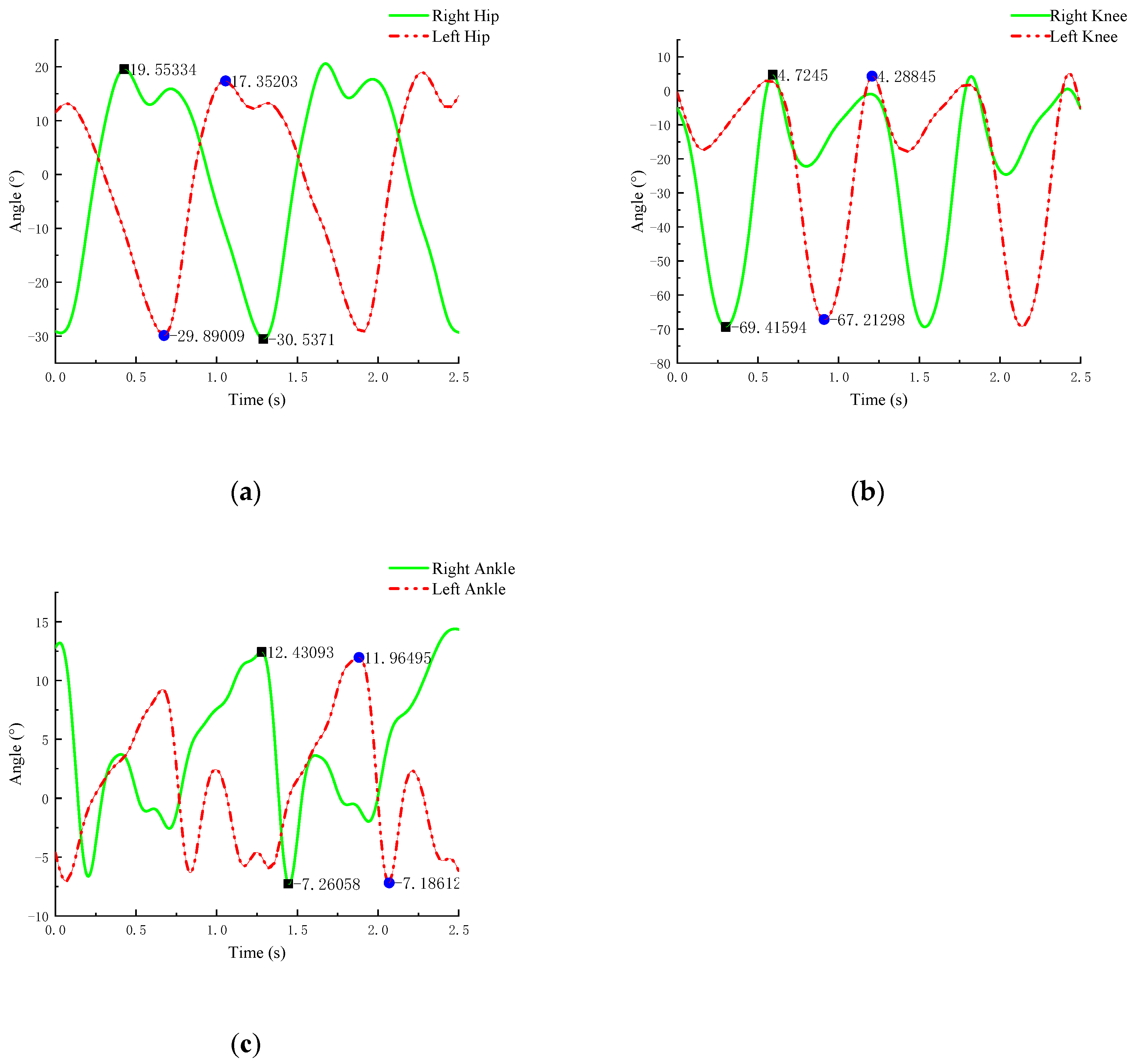
2.2.4. Experimental Results and Analysis
3. Design of Lower Limb Exoskeleton Rehabilitation Robot
3.1. Design Principles of the Lower Limb Exoskeleton Rehabilitation Robot
3.2. Design Standards for the Dimensions of Lower Limb Exoskeleton Rehabilitation Robots
3.3. Joint Design of Lower Limb Exoskeleton Rehabilitation Robot
3.3.1. Mechanism Degree of Freedom Solution
3.3.2. Hip Joint
3.3.3. Knee Joint
3.3.4. Ankle Joint
3.4. Kinematic Analysis of Lower Limb Exoskeleton Rehabilitation Robot
3.4.1. D-H Kinematic Modeling
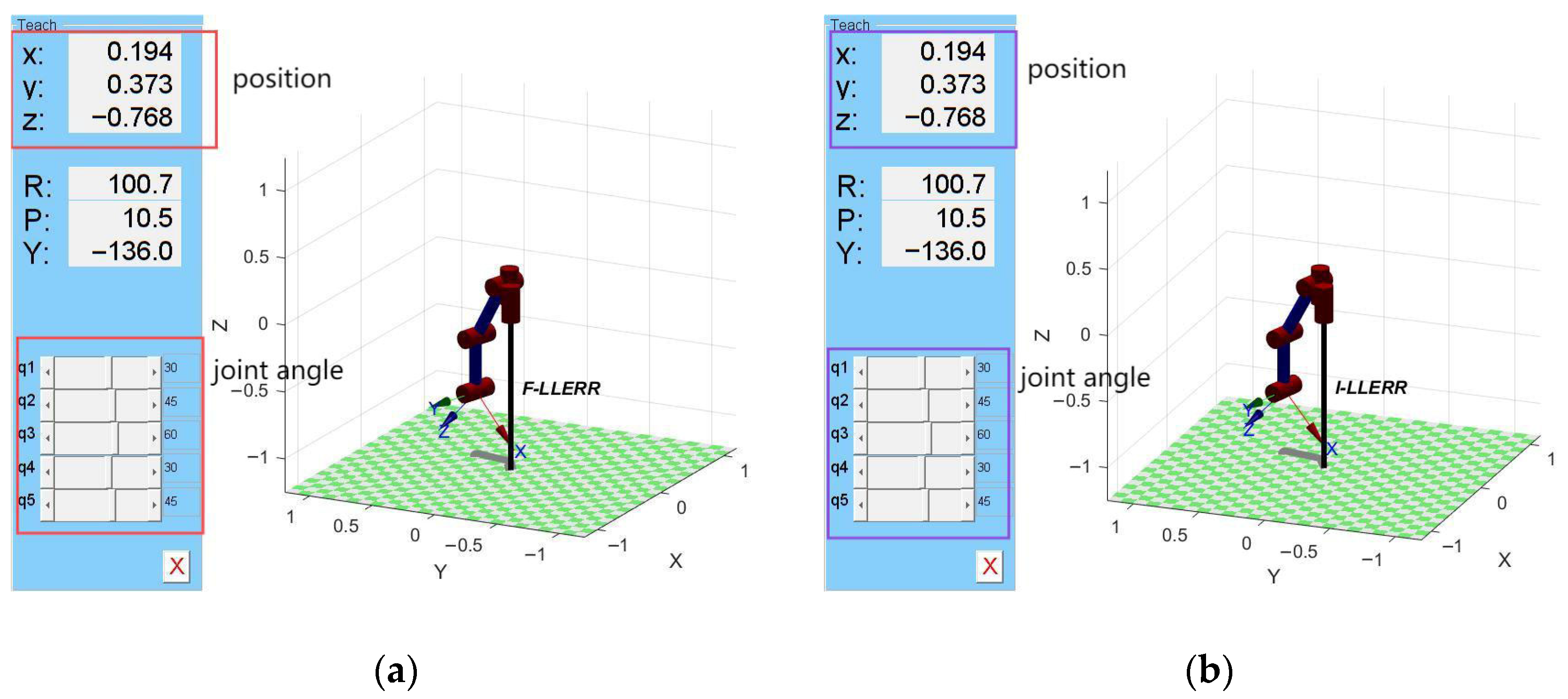
3.4.2. Forward Kinematic Analysis and Simulation of the Lower Limb Exoskeleton Rehabilitation Robot
- Forward Kinematic Analysis
- Based on MATLAB Robotics forward kinematics simulation
- Velocity and Acceleration Calculation
3.4.3. Inverse Kinematic Analysis and Simulation of the Lower Limb Exoskeleton Rehabilitation Robot
- Inverse Kinematic Analysis
- Solve for the joint angle θ1
- Solve for the joint angle θ3
- Solve for the joint angle θ2
- Solve for the joint angle θ4, θ5
- Based on MATLAB Robotics inverse kinematics simulation
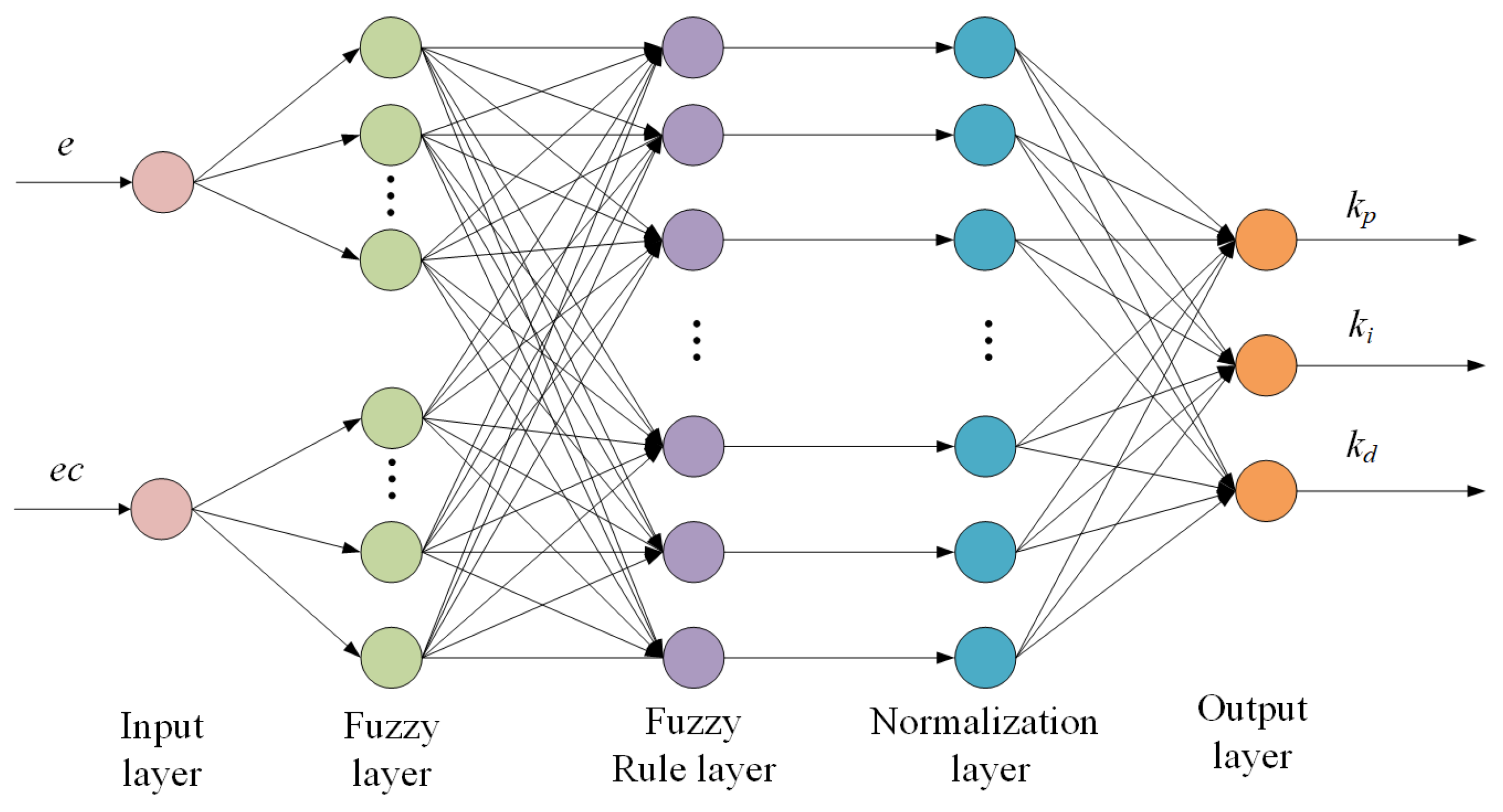
3.5. PID Control Strategy Based on BP Fuzzy Neural Network
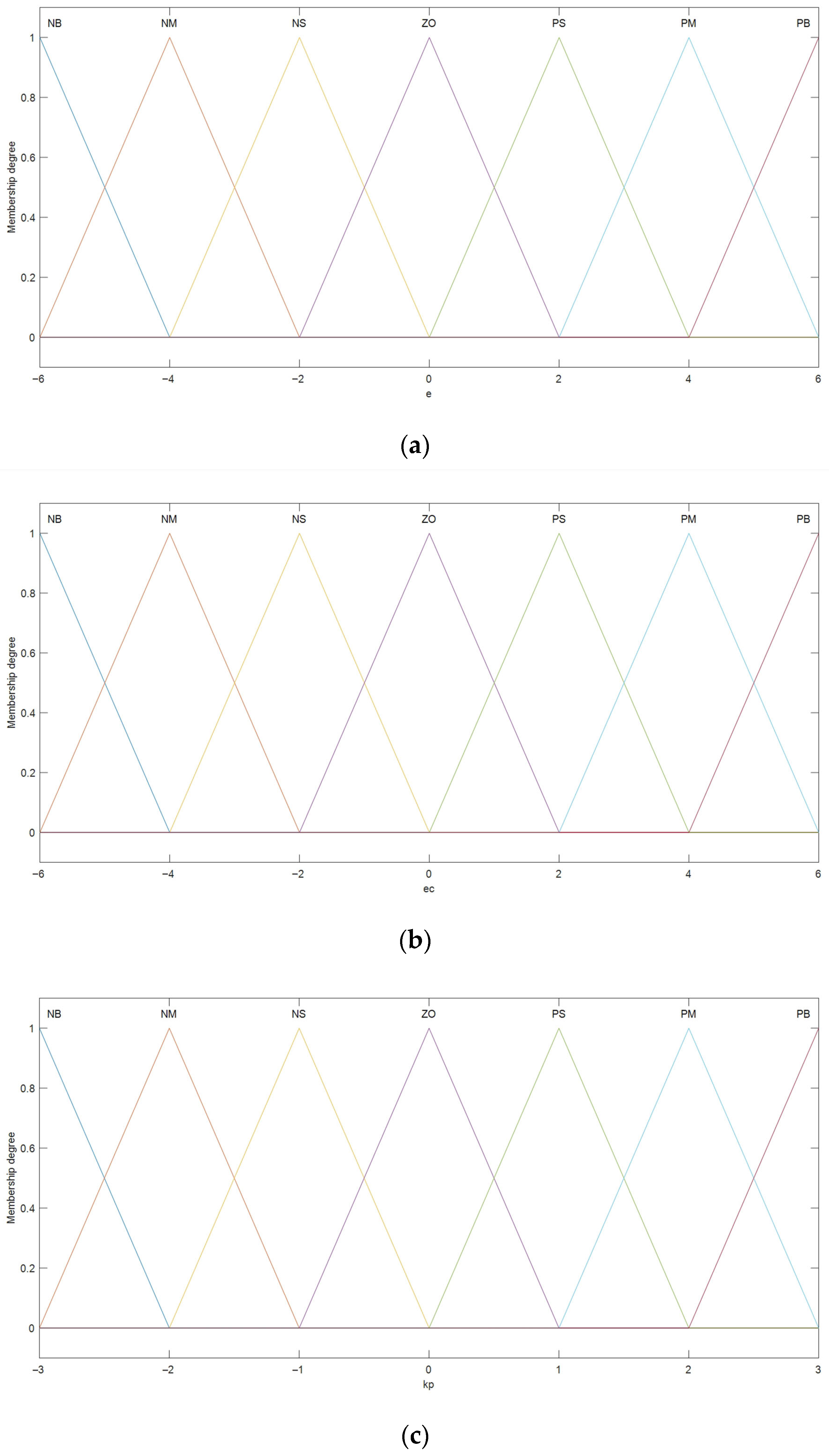
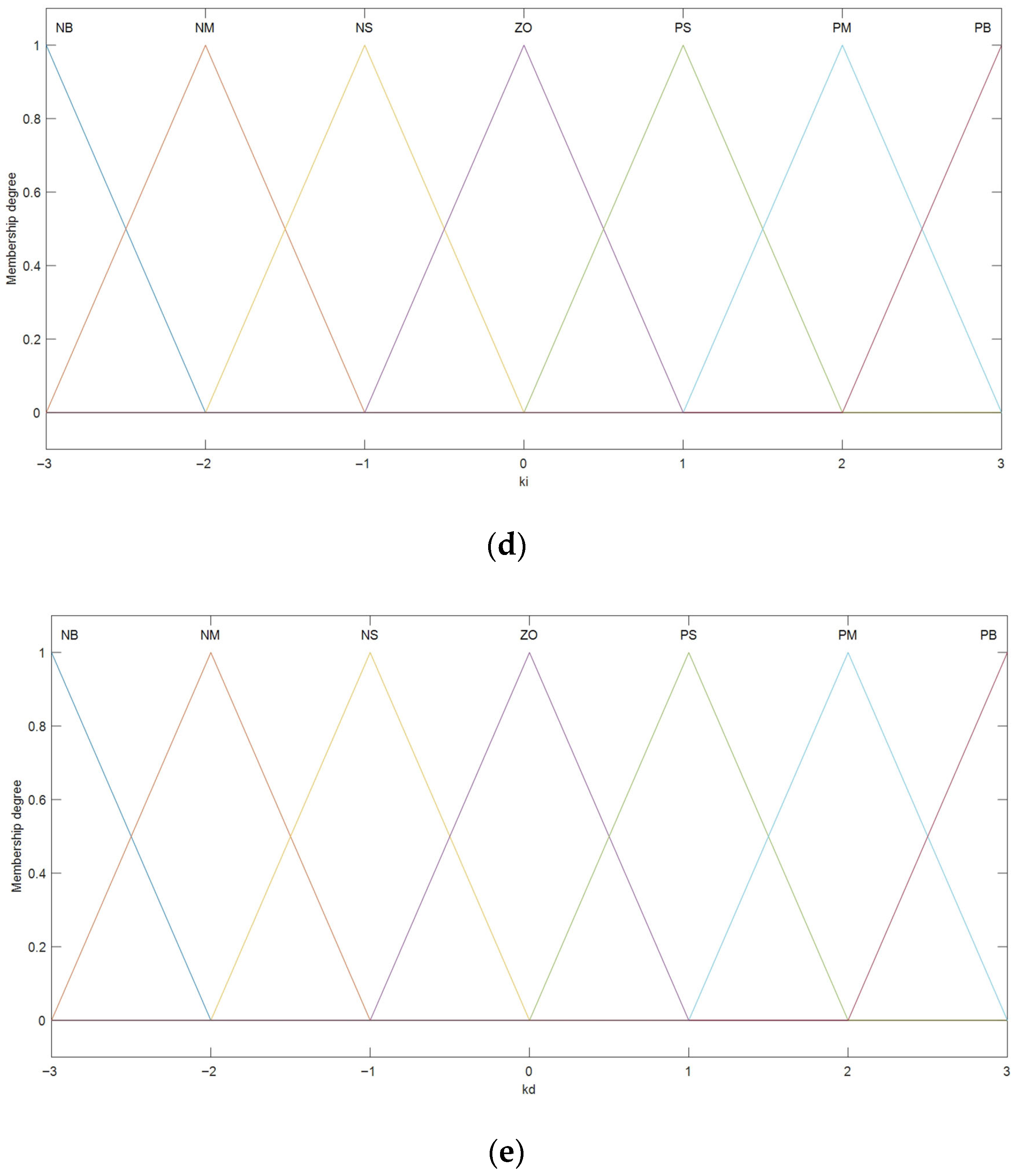
3.5.1. Fuzzy PID Controller’s Domain and Membership Functions
3.5.2. BP Fuzzy Neural Network PID Controller Design
3.5.3. The Calculation of Joint Input and Output Torques
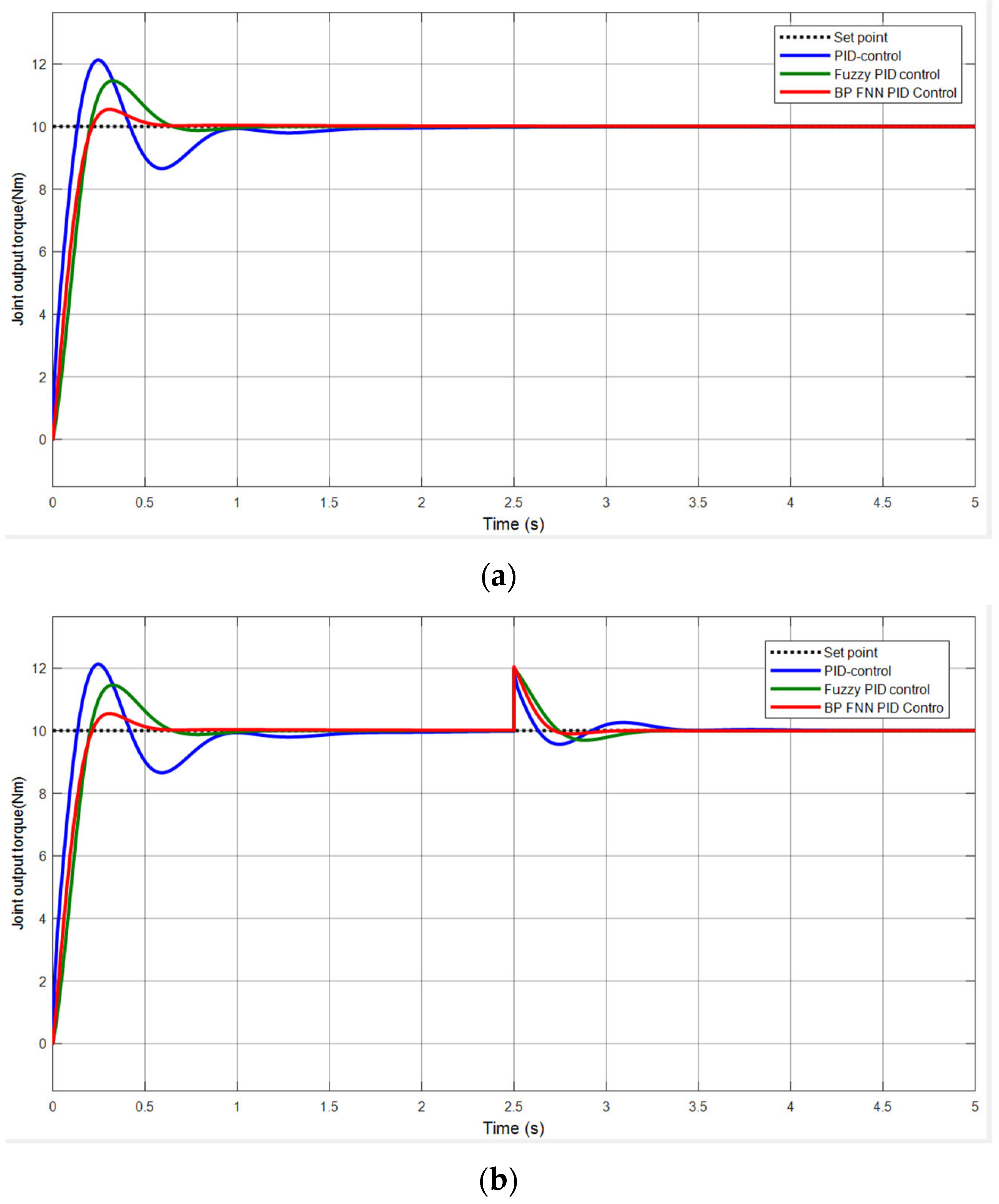
3.5.4. BP Fuzzy Neural Network PID Control Simulation Analysis
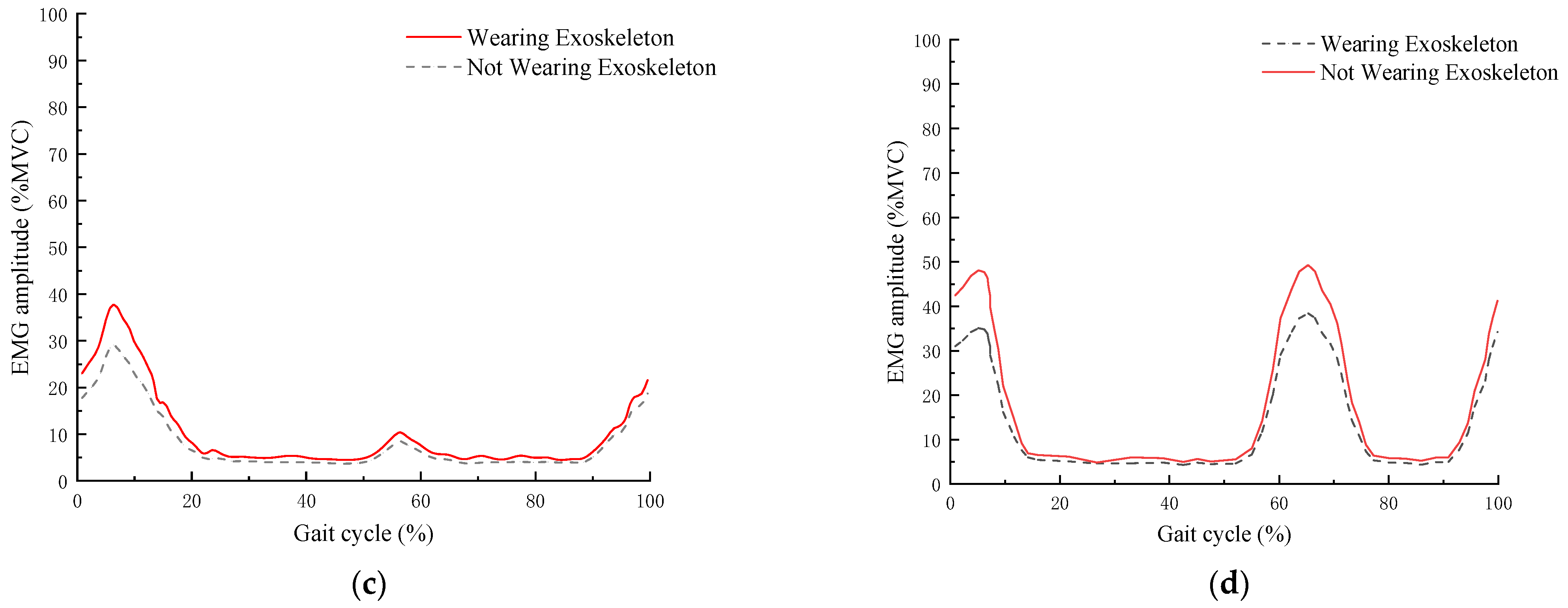
4. Wearable Testing of the Lower Limb Exoskeleton Rehabilitation Robot Prototype
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qiu, S.; Pei, Z.; Wang, C.; Tang, Z. Systematic review on wearable lower extremity robotic exoskeletons for assisted locomotion. J. Bionic Eng. 2023, 20, 436–469. [Google Scholar] [CrossRef]
- Kilichev, I.A.; Matyokubov, M.O.; Adambaev, Z.I.; Khudayberganov, N.Y.; Mirzaeva, N.S. Register of stroke in the desert-steppe zones of Uzbekistan. BIO Web Conf. 2023, 65, 04002. [Google Scholar] [CrossRef]
- Mead, G.E.; Sposato, L.A.; Sampaio Silva, G.; Yperzeele, L.; Wu, S.; Kutlubaev, M.; Cheyne, J.; Wahab, K.; Urrutia, V.C.; Rabinstein, A.A.; et al. A systematic review and synthesis of global stroke guidelines on behalf of the World Stroke Organization. Int. J. Stroke 2023, 18, 499–531. [Google Scholar] [CrossRef] [PubMed]
- MajidiRad, A.; Yihun, Y.; Hakansson, N.; Mitchell, A. The effect of lower limb exoskeleton alignment on knee rehabilitation efficacy. Healthcare 2022, 10, 1291. [Google Scholar] [CrossRef] [PubMed]
- Tigrini, A.; Mobarak, R.; Mengarelli, A.; Khushaba, R.N.; Al-Timemy, A.H.; Verdini, F.; Gambi, E.; Fioretti, S.; Burattini, L. Phasor-Based Myoelectric Synergy Features: A Fast Hand-Crafted Feature Extraction Scheme for Boosting Performance in Gait Phase Recognition. Sensors 2024, 24, 5828. [Google Scholar] [CrossRef]
- Mobarak, R.; Mengarelli, A.; Verdini, F.; Al-Timemy, A.H.; Fioretti, S.; Burattini, L.; Tigrini, A. Neuromechanical-Driven Ankle Angular Position Control During Gait Using Minimal Setup and LSTM Model. In Proceedings of the 2024 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Eindhoven, The Netherlands, 26–28 June 2024; pp. 1–6. [Google Scholar]
- Wu, L.; Xu, G.; Wu, Q. The effect of the Lokomat® robotic-orthosis system on lower extremity rehabilitation in patients with stroke: A systematic review and meta-analysis. Front. Neurol. 2023, 14, 1260652. [Google Scholar] [CrossRef]
- Adhikari, V.; MajidRad, A.H.; Yihun, Y.; Desai, J. Assist-as-needed controller to a task-based knee rehabilitation exoskeleton. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 3212–3215. [Google Scholar]
- Jin, X.; Guo, J. Disturbance rejection model predictive control of lower limb rehabilitation exoskeleton. Sci. Rep. 2023, 13, 19463. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, P.; Hou, Z.; Hu, B.; Sui, C.; Han, J. Kinetostatic analysis of a novel 6-DoF 3UPS parallel manipulator with multi-fingers. Mech. Mach. Theory 2014, 78, 36–50. [Google Scholar] [CrossRef]
- Lu, Y.; Chang, Z.; Lu, Y.; Wang, Y. Development and kinematics/statics analysis of rigid-flexible-soft hybrid finger mechanism with standard force sensor. Robot. Comput.-Integr. Manuf. 2021, 67, 101978. [Google Scholar] [CrossRef]
- Wang, P.; Low, K.H.; Tow, A.; Lim, P.H. Initial system evaluation of an overground rehabilitation gait training robot (NaTUre-gaits). Adv. Robot. 2011, 25, 1927–1948. [Google Scholar] [CrossRef]
- Uehara, A.; Kawamoto, H.; Sankai, Y. Proposal of Period Modulation Control of Wearable Cyborg HAL Trunk-Unit for Parkinson’s Disease/Parkinsonism Utilizing Motor Intention and Dynamics. In Proceedings of the 2023 IEEE/SICE International Symposium on System Integration (SII), Atlanta, GA, USA, 17–20 January 2023; pp. 1–6. [Google Scholar]
- Selfa Aymerich, P. Kinematic Analysis Framework for Smart Exoskeleton Design. Bachelor’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2024. [Google Scholar]
- Jocelyn, S.; Ledoux, É.; Marrero, I.A.; Burlet-Vienney, D.; Chinniah, Y.; Bonev, I.A.; Ben Mosbah, A.; Berger, I. Classification of collaborative applications and key variability factors to support the first step of risk assessment when integrating cobots. Saf. Sci. 2023, 166, 106219. [Google Scholar] [CrossRef]
- Li, X.B.; Sun, L.Y.; Li, J.K.; Li, W.Q.; Zhang, T.; Li, Y.; Xu, Y.J.; Zhang, J.N. Design and application of petrochemical inspection robot. In Proceedings of the 2023 2nd International Symposium on Control Engineering and Robotics (ISCER), Hangzhou, China, 17–19 February 2023; pp. 280–283. [Google Scholar]
- Negishi, T.; Ogihara, N. Regulation of whole-body angular momentum during human walking. Sci. Rep. 2023, 13, 8000. [Google Scholar] [CrossRef]
- Adjel, M. Toward the Development of a Sparse, Multi-Modal and Affordable Motion Analysis System. Applications to clinical motor tests. Ph.D. Thesis, Université de Paris-Est/Créteil, Créteil, France, 2024. [Google Scholar]
- Chen, X.; Liu, W.; Bao, Q.; Liu, X.; Yang, Q.; Dai, R.; Mei, T. Motion Capture from Inertial and Vision Sensors. arXiv 2024, arXiv:2407.16341. [Google Scholar]
- Pradon, D.; Tong, L.; Chalitsios, C.; Roche, N. Development of Surface EMG for Gait Analysis and Rehabilitation of Hemiparetic Patients. Sensors 2024, 24, 5954. [Google Scholar] [CrossRef] [PubMed]
- Best, A.N. The Role of the Trunk in the Stability and Energetics of Locomotion. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2024. [Google Scholar]
- Hasan, M.J.; Bashar, N.; Sarker, S.; Lopa, S.A.; Hamim, T. Harmonic reduction of second order sallen and key lowpass filter and second order MFB lowpass filter through closed loop PID controlled method. Int. J. Inf. Technol. 2024, 16, 2635–2645. [Google Scholar] [CrossRef]
- Yang, Y.J.; Vadivelu, A.K.N.; Hepworth, J.; Zeng, Y.; Pilgrim, C.H.; Kulic, D.; Abdi, E. Experimental evaluation of accuracy and efficiency of two control strategies for a novel foot commanded robotic laparoscope holders with surgeons. Sci. Rep. 2024, 14, 9264. [Google Scholar] [CrossRef] [PubMed]
- Wang, P. On crescent-shaped objects of the early Bronze Age in southern Siberia and the surrounding areas. Chin. Archaeol. 2023, 23, 158–168. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, Z.; Zheng, C.; Zhu, L.; Wang, Y. Research on Mechanical Leg Structure Design and Control System of Lower Limb Exoskeleton Rehabilitation Robot Based on Magnetorheological Variable Stiffness and Damping Actuator. Actuators 2024, 13, 132. [Google Scholar] [CrossRef]
- Bodo, G.; Giannattasio, R.; Ramadoss, V.; Tessari, B.; Laffranchi, M. A Modular, Time-Independent, Path-Based Controller for Assist-as-Needed Rehabilitative Exoskeletons. In Proceedings of the 2024 10th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), Heidelberg, Germany, 1–4 September 2024; pp. 761–766. [Google Scholar]
- Alwardat, M.Y.; Alwan, H.M. Forward and inverse kinematics of a 6-DOF robotic manipulator with a prismatic joint using MATLAB robotics toolbox. Optimization 2024, 2, 3. [Google Scholar]
- Ajayi, O.K.; Arojo, T.A.; Ogunnaike, A.S.; Adeyi, A.J.; Olanrele, O.O. Performance Enhancement with Denavit-Hartenberg (DH) Algorithm and Faster-RCNN for a 5 DOF Sorting Robot. In Mechatronics and Automation Technology, Proceedings of the 2nd International Conference (ICMAT 2023), Wuhan, China, 28–29 October 2023; IOS Press: Amsterdam, The Netherlands, 2024; pp. 459–466. [Google Scholar]
- Zhao, M.; Liu, M.; Ren, B.; Dai, S.; Sebe, N. Denoising Diffusion Probabilistic Models for Action-Conditioned 3D Motion Generation. In Proceedings of the ICASSP 2024-2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 4225–4229. [Google Scholar]
- Chen, P.H.; Fan, R.E.; Lin, C.J. A study on SMO-type decomposition methods for support vector machines. IEEE Trans. Neural Netw. 2024, 17, 893–908. [Google Scholar] [CrossRef]
- Erfanifar, R.; Hajarian, M.; Sayevand, K. A family of iterative methods to solve nonlinear problems with applications in fractional differential equations. Math. Methods Appl. Sci. 2024, 47, 2099–2119. [Google Scholar] [CrossRef]
- Omar, A.; Rabie, A.; Thabet, D.; Abdellatif, I.; Elsayed, K.; Elbadawy, M.; Shalaby, R. Dynamic Modeling and Kinematics Verification for Quadruped Robot. 2024; preprint. [Google Scholar]
- Trica, I.R.; Bahar, A.C. The impact of utilizing technological and robotic system lokomat on balance rehabilitation in post-stroke patients. Acta Marisiensis Ser. Medica 2024, 70, 88. [Google Scholar]
- Feng, C.M.; Botha, E.; Pitt, L. From HAL to GenAI: Optimizing chatbot impacts with CARE. Bus. Horiz. 2024, 67, 537–548. [Google Scholar] [CrossRef]
- Zhou, Z.; Xu, M.; Wang, Z.; Gao, H.; Mai, J.; Wang, Q. Mechatronic Design of a Shank-Free Bilateral Exoskeleton for Loaded Walking. In Proceedings of the 2024 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 15–19 July 2024; pp. 1398–1403. [Google Scholar]
- Zhao, C.; Liu, Z.; Zhu, L. Design and analysis of a lower limb exoskeleton rehabilitation robot based on a series elastic actuator. 2023; preprint. [Google Scholar]
- Wang, L.; Meng, L.; Kang, R.; Liu, B.; Gu, S.; Zhang, Z.; Meng, F.; Ming, A. Design and dynamic locomotion control of quadruped robot with perception-less terrain adaptation. Cyborg Bionic Syst. 2022, 2022, 9816495. [Google Scholar] [CrossRef] [PubMed]
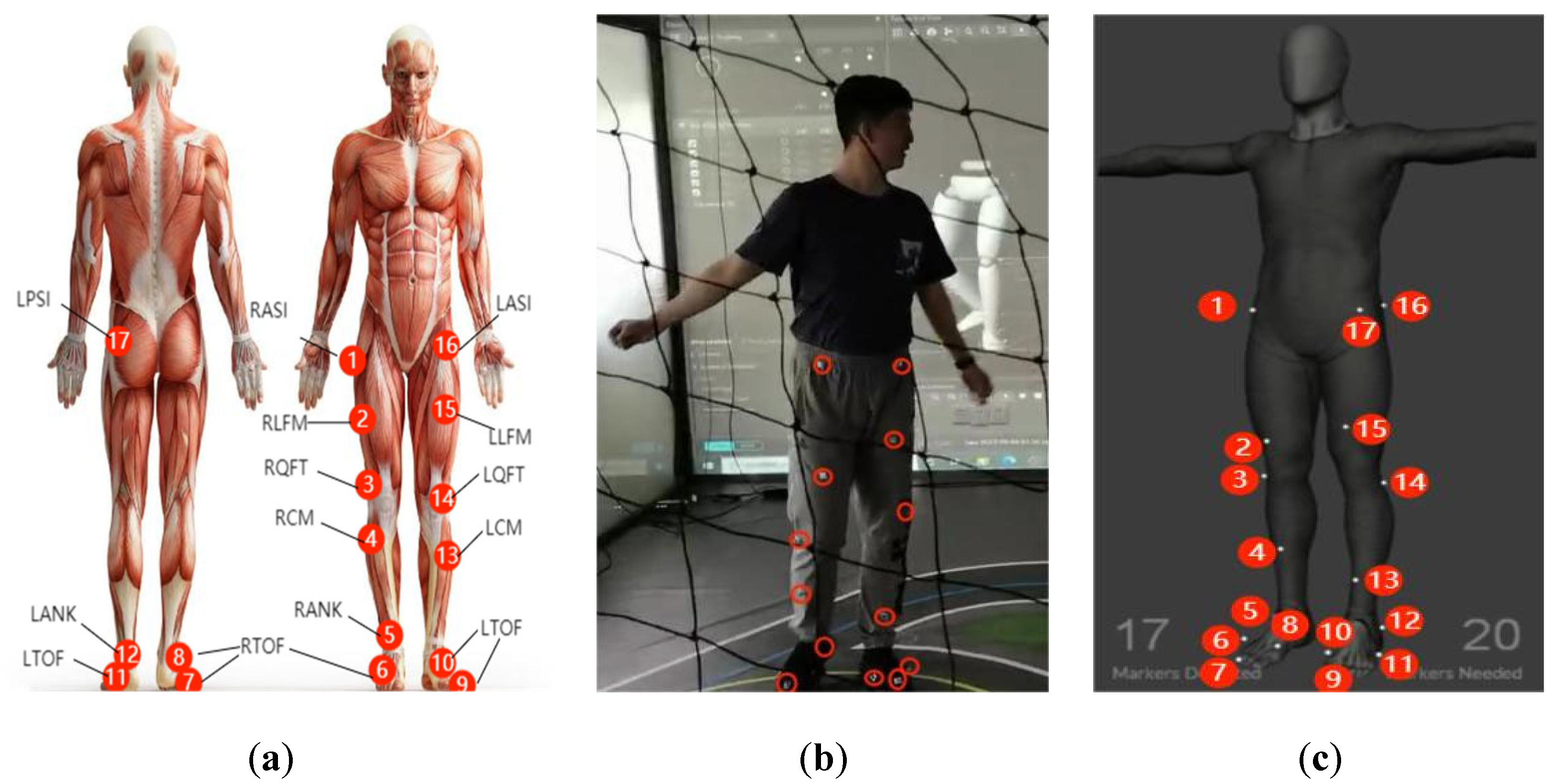


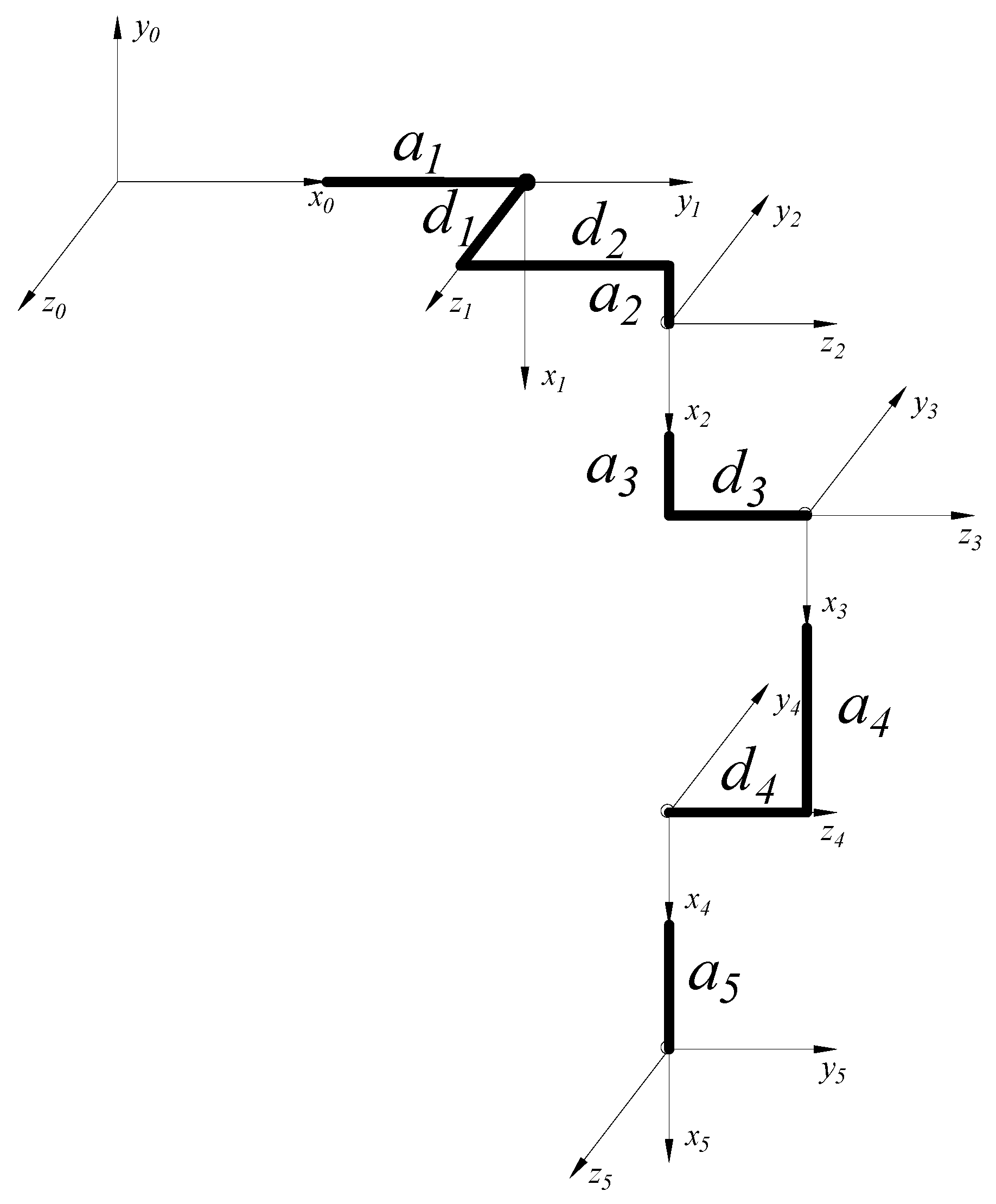




| Number | Marker Label | Definition | Position |
|---|---|---|---|
| 1/16 | RASI/LASI | Right/Left Anterior Auperior Iliac | Front right waist/front left waist |
| 2/15 | RLFM/LLFM | Right/Left Lateral Femoris Muscle | Outer side of the front thigh |
| 3/14 | RQFT/LQFT | Right/Left Quadriceps Femoris Tendon | Front side of the thigh muscles |
| 4/13 | RCM/LCM | Right/Left Calf Muscle | Back side of the calf |
| 5 | RANK | Right Lateral Ankle | Bone prominence on the outer side of the right ankle |
| 6/7/8 | RTOE | Right Toe | Tip of the right toe |
| 9/10/11 | LTOE | Left Toe | Tip of the left toe |
| 12 | LANK | Left Lateral Ankle | Bone prominence on the outer side of the left ankle |
| 17 | LPSI | Left Posterior Spine Iliac | Front outer side of the thigh muscles |
| Lower Limb | Joint | Range of Motion |
|---|---|---|
| Right leg | Hip joint | −31~20° |
| Knee joint | −70~5° | |
| Ankle joint | −8~13° | |
| Left leg | Hip joint | −30~18° |
| Knee joint | −68~5° | |
| Ankle joint | −8~12° |
| Percentage | Male (18–60 Years Old) | Female (18–60 Years Old) | ||||||
|---|---|---|---|---|---|---|---|---|
| Height | Thigh Length | Lower Leg Length | Hip Width | Height | Thigh Length | Lower Leg Length | Hip Width | |
| 1 | 1543 | 413 | 324 | 273 | 1449 | 387 | 300 | 275 |
| 5 | 1583 | 428 | 338 | 282 | 1484 | 402 | 313 | 290 |
| 10 | 1604 | 436 | 344 | 288 | 1503 | 410 | 319 | 296 |
| 50 | 1678 | 465 | 369 | 306 | 1570 | 438 | 344 | 317 |
| 90 | 1754 | 496 | 396 | 327 | 1640 | 467 | 370 | 340 |
| 95 | 1775 | 505 | 403 | 334 | 1659 | 476 | 376 | 346 |
| 99 | 1814 | 523 | 419 | 346 | 1697 | 494 | 390 | 360 |
| i | ai | αi | di | θi |
|---|---|---|---|---|
| 1 | a1 | 0 | d1 | θ1 − π/2 |
| 2 | a2 | −π/2 | d2 | θ2 |
| 3 | a3 | 0 | d3 | θ3 |
| 4 | a4 | 0 | d4 | θ4 |
| 5 | a5 | π/2 | 0 | θ5 |
| Control Method | Overshoot | Settling Time |
|---|---|---|
| PID | 21.2% | 0.96 s |
| Fuzzy PID | 14.6% | 0.66 s |
| BP Neural Network PID | 5.5% | 0.49 s |
| Muscle Name | Exoskeleton Wear Condition | Average EMG Amplitude (%MVC) |
|---|---|---|
| Gastrocnemius | No | 65.5 |
| Yes | 52.4 | |
| Biceps femoris | No | 27.3 |
| Yes | 19.1 | |
| Rectus femoris | No | 34.2 |
| Yes | 28.1 | |
| Tibialis anterior | No | 46.7 |
| Yes | 36.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Liu, Z.; Ou, Y.; Zhu, L. Mechanical Structure Design and Motion Simulation Analysis of a Lower Limb Exoskeleton Rehabilitation Robot Based on Human–Machine Integration. Sensors 2025, 25, 1611. https://doi.org/10.3390/s25051611
Zhao C, Liu Z, Ou Y, Zhu L. Mechanical Structure Design and Motion Simulation Analysis of a Lower Limb Exoskeleton Rehabilitation Robot Based on Human–Machine Integration. Sensors. 2025; 25(5):1611. https://doi.org/10.3390/s25051611
Chicago/Turabian StyleZhao, Chenglong, Zhen Liu, Yuefa Ou, and Liucun Zhu. 2025. "Mechanical Structure Design and Motion Simulation Analysis of a Lower Limb Exoskeleton Rehabilitation Robot Based on Human–Machine Integration" Sensors 25, no. 5: 1611. https://doi.org/10.3390/s25051611
APA StyleZhao, C., Liu, Z., Ou, Y., & Zhu, L. (2025). Mechanical Structure Design and Motion Simulation Analysis of a Lower Limb Exoskeleton Rehabilitation Robot Based on Human–Machine Integration. Sensors, 25(5), 1611. https://doi.org/10.3390/s25051611






