Bipartite Fault-Tolerant Consensus Control for Multi-Agent Systems with a Leader of Unknown Input Under a Signed Digraph
Abstract
1. Introduction
- (1)
- Most existing studies on the consensus control problem of MASs primarily consider unsigned graphs [7,8,9,10,11,12]. In contrast, this paper broadens the scope by analyzing directed networks that include both positive and negative weights. Furthermore, unlike the studies in [17,18,19,20], which achieve bipartite consensus without considering actuator faults, we address the bipartite consensus problem under actuator faults. This consideration aligns more closely with practical scenarios and enhances the robustness of MASs.
- (2)
- Due to the leader’s unknown input signal, the follower agents cannot acquire precise information regarding the leader. In contrast to the common assumption of bounded unknown input signals [30,31,32], this paper examines the unknown input signal and employs parameterization theory to design a distributed leader-state observer. This approach allows follower agents to effectively track the leader’s signal.
- (3)
- This paper designs intermediate observers using auxiliary variables to estimate follower states and time-varying actuator faults simultaneously. Drawing from these observers, a bipartite fault-tolerant consensus control protocol is proposed. Unlike existing studies, this approach eliminates the observer matching condition, significantly broadening its applicability.
2. Preliminaries and Problem Description
2.1. Graph Theory
2.2. Problem Description
3. Main Results
3.1. Fault Estimation Observer Design
3.2. Distributed Consensus Control Protocol
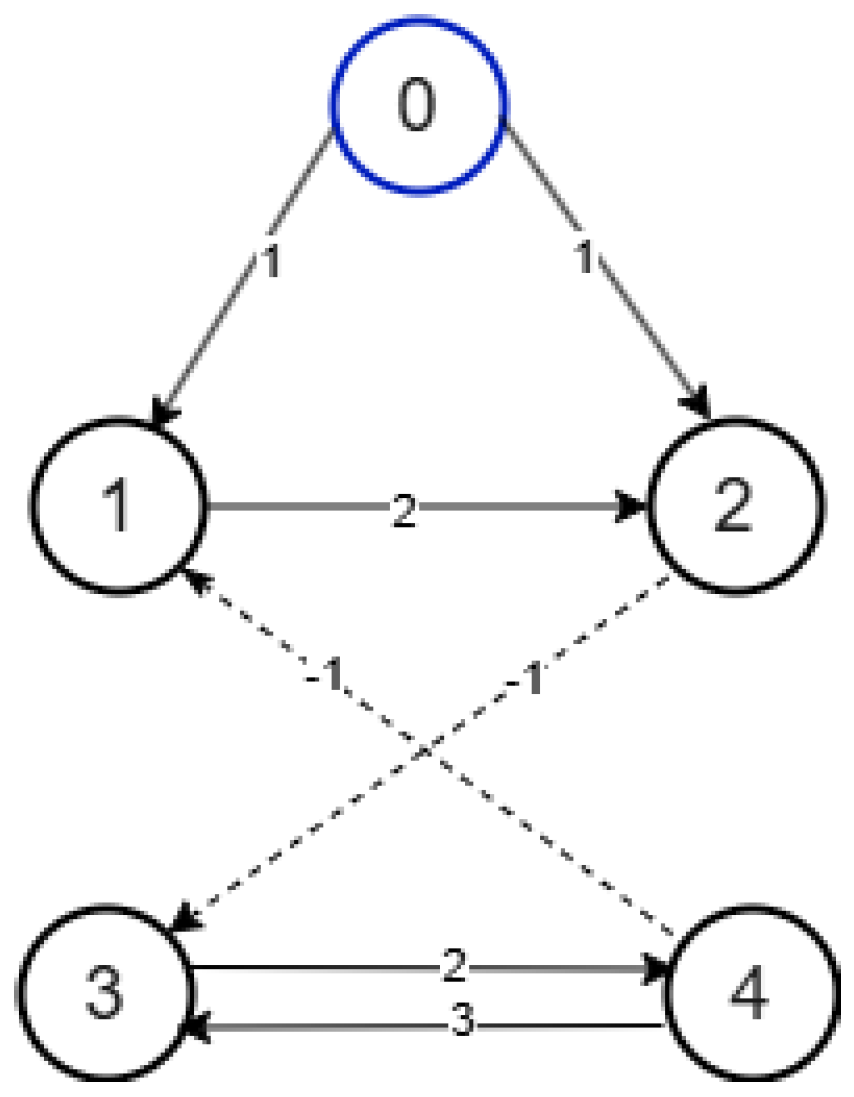
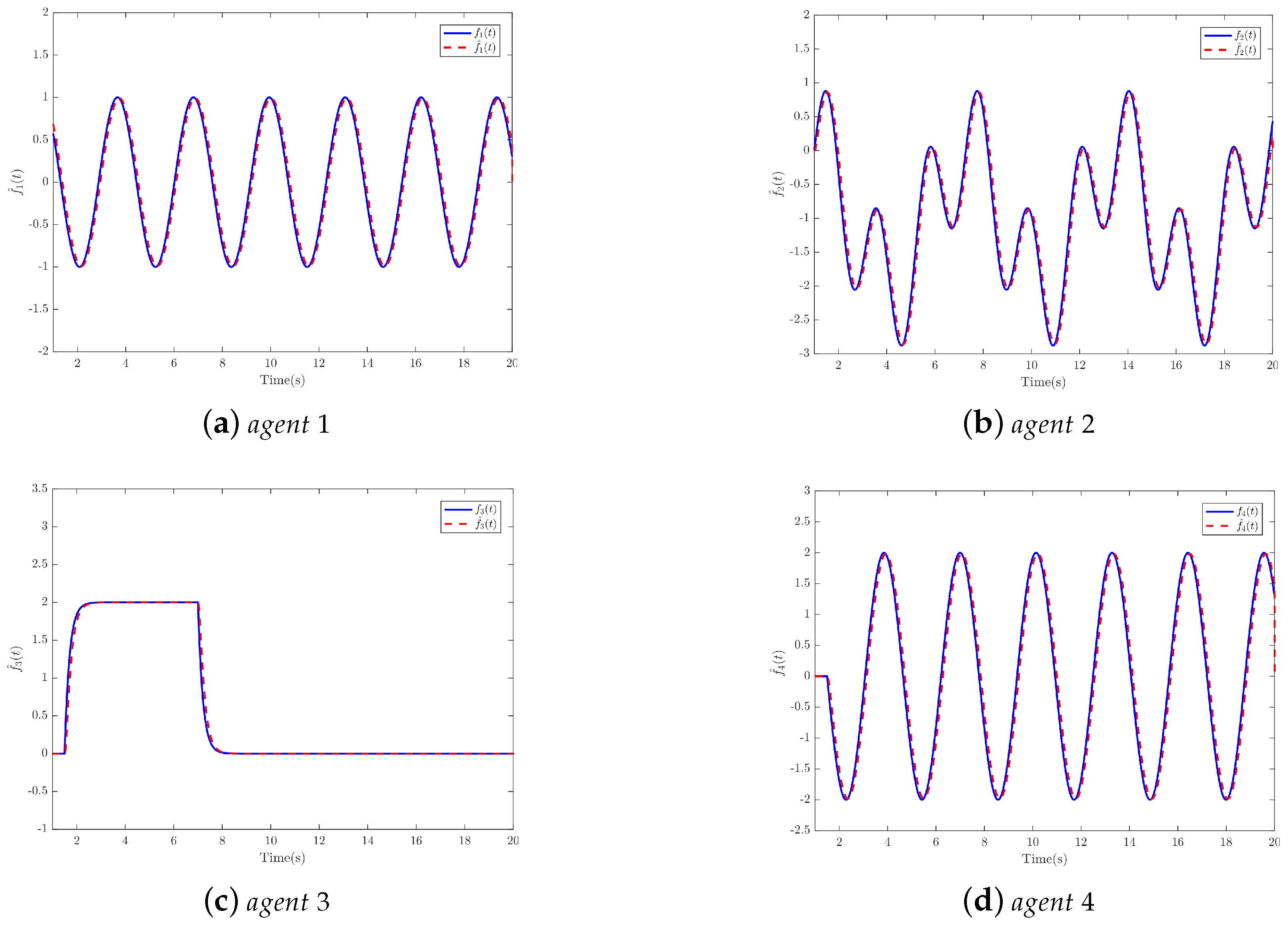
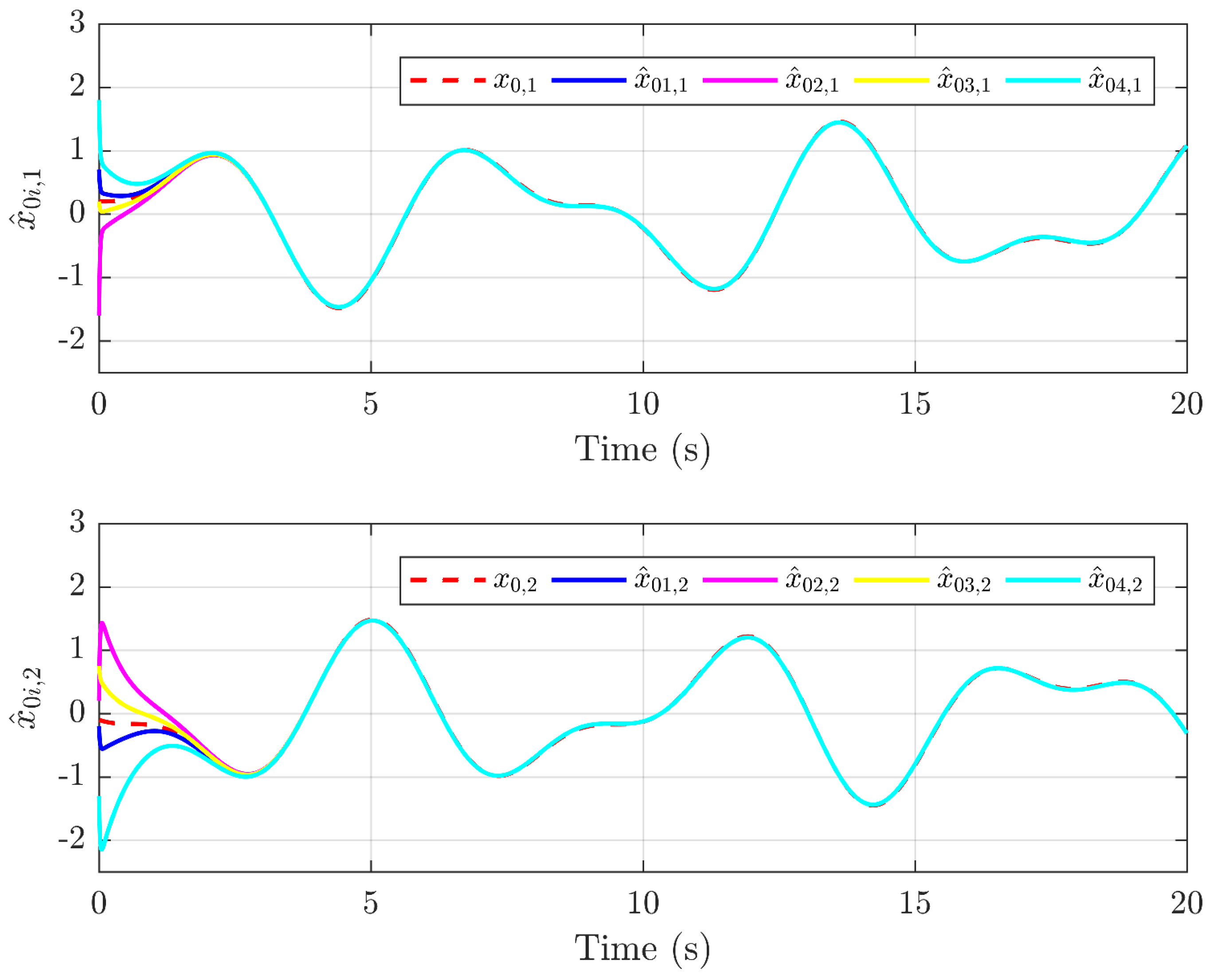
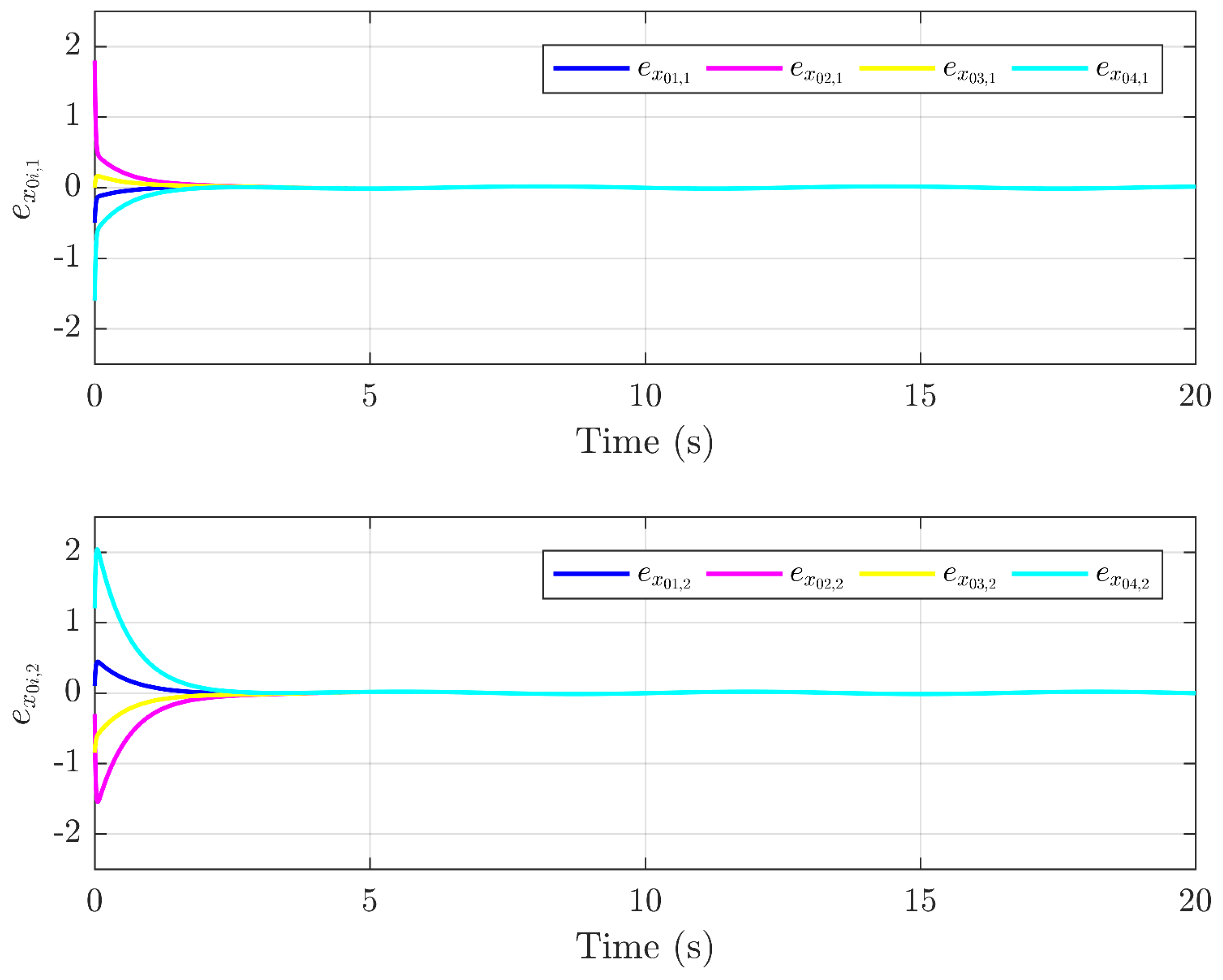
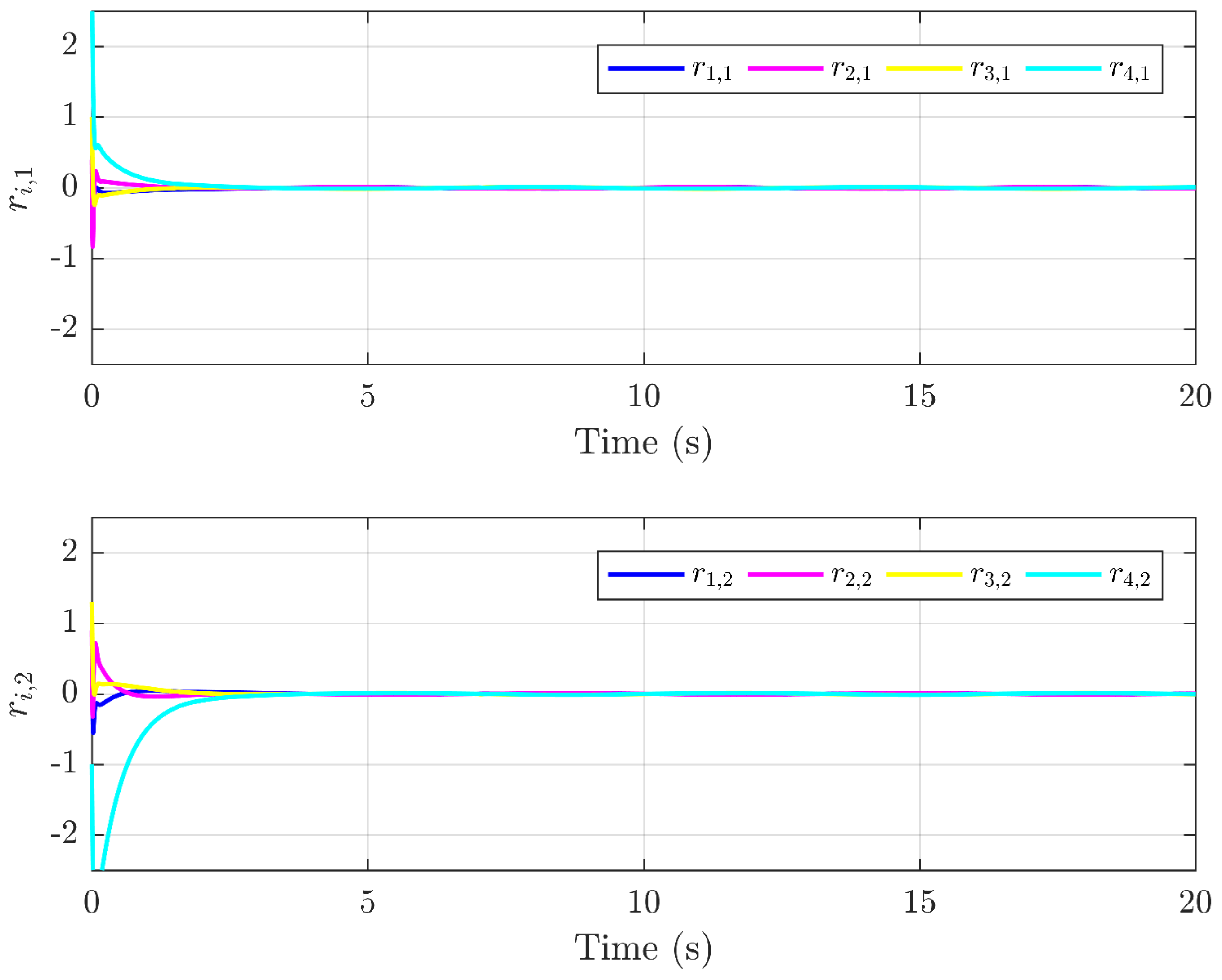
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bhattacharyya, S.; Patra, S. Positive consensus of multi-agent systems with hierarchical control protocol. Automatica 2022, 139, 110191. [Google Scholar] [CrossRef]
- Fan, C.; Lam, J.; Chu, K.F.; Lu, X.; Kwok, K.W. Output Reachable Set-Based Leader-Following Consensus of Positive Agents Over Switching Networks. IEEE Trans. Cybern. 2023, 54, 3918–3930. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Su, H.; Zeng, Z. Resilient interval observer-based coordination control for multi-agent systems under stealthy attacks. Automatica 2024, 167, 111781. [Google Scholar] [CrossRef]
- Guo, H.; Chen, M.; Jiang, Y.; Lungu, M. Distributed adaptive human-in-the-loop event-triggered formation control for QUAVs with quantized communication. IEEE Trans. Ind. Informat. 2022, 19, 7572–7582. [Google Scholar] [CrossRef]
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An overview of recent progress in the study of distributed multi-agent coordination. IEEE Trans. Ind. Informat. 2012, 9, 427–438. [Google Scholar] [CrossRef]
- Liu, P.M.; Guo, X.G.; Wang, J.L.; Xie, X.P.; Yang, F.W. Fully distributed hierarchical ET intrusion-and fault-tolerant group control for MASs with application to robotic manipulators. IEEE Trans. Autom. Sci. Eng. 2023, 21, 2868–2881. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Liao, L. Consensus of high-order discrete-time multiagent systems with switching topology. IEEE Trans. Syst. Man Cybern. Syst. 2018, 51, 721–730. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, D.; Wang, J.; Ahn, C.K. Adaptive memory event-triggered observer-based control for nonlinear multi-agent systems under DoS attacks. IEEE/CAA J. Autom. Sin. 2021, 8, 1644–1656. [Google Scholar] [CrossRef]
- Chai, J.; Lu, Q.; Tao, X.; Peng, D.; Zhang, B. Dynamic event-triggered fixed-time consensus control and its applications to magnetic map construction. IEEE/CAA J. Autom. Sin. 2023, 10, 2000–2013. [Google Scholar] [CrossRef]
- Hong, Y.; Su, Y.; Cai, H. Internal Model Based Cooperative Robust Resilient Control Under DoS Attacks With Application to Vehicles Formation. IEEE Trans. Ind. Informat. 2024, 20, 13124–13134. [Google Scholar] [CrossRef]
- Zhang, K.; Tian, H.; Wang, P.; Huang, T. Observer-Based Dynamic Event-Triggered Consensus of MIMO Linear Multiagent Systems With Directed Topology. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 5834–5843. [Google Scholar] [CrossRef]
- Mao, B.; Wu, X.; Lü, J.; Chen, G. Predefined-time bounded consensus of multiagent systems with unknown nonlinearity via distributed adaptive fuzzy control. IEEE Trans. Cybern. 2022, 53, 2622–2635. [Google Scholar] [CrossRef]
- Ma, L.; Zhu, F. Human-in-the-loop formation control for multi-agent systems with asynchronous edge-based event-triggered communications. Automatica 2024, 167, 111744. [Google Scholar] [CrossRef]
- Parisien, C.; Anderson, C.H.; Eliasmith, C. Solving the problem of negative synaptic weights in cortical models. Neural Comput. 2008, 20, 1473–1494. [Google Scholar] [CrossRef]
- Xia, W.; Cao, M.; Johansson, K.H. Structural balance and opinion separation in trust–mistrust social networks. IEEE Trans. Control Netw. Syst. 2015, 3, 46–56. [Google Scholar] [CrossRef]
- Parsegov, S.E.; Proskurnikov, A.V.; Tempo, R.; Friedkin, N.E. Novel multidimensional models of opinion dynamics in social networks. IEEE Trans. Autom. Control 2016, 62, 2270–2285. [Google Scholar] [CrossRef]
- Wang, X.; Cao, Y.; Niu, B.; Song, Y. A novel bipartite consensus tracking control for multiagent systems under sensor deception attacks. IEEE Trans. Cybern. 2022, 53, 5984–5993. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Chen, L.; Pan, Y.; Lam, H.K. Fuzzy-based robust precision consensus tracking for uncertain networked systems with cooperative–antagonistic interactions. IEEE Trans. Fuzzy Syst. 2022, 31, 1362–1376. [Google Scholar] [CrossRef]
- Cao, Z.; Niu, B.; Zong, G.; Zhao, X.; Ahmad, A.M. Active disturbance rejection-based event-triggered bipartite consensus control for nonaffine nonlinear multiagent systems. Int. J. Robust Nonlinear Control 2023, 33, 7181–7203. [Google Scholar] [CrossRef]
- Xu, C.; Xu, H.; Guan, Z.H.; Ge, Y. Observer-based dynamic event-triggered semiglobal bipartite consensus of linear multi-agent systems with input saturation. IEEE Trans. Cybern. 2022, 53, 3139–3152. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Duan, J.; Zhang, J. Distributed bipartite consensus of linear multiagent systems based on event-triggered output feedback control scheme. IEEE Trans. Syst. Man, Cybern. Syst. 2020, 51, 6743–6756. [Google Scholar] [CrossRef]
- Liu, G.; Liang, H.; Pan, Y.; Ahn, C.K. Antagonistic interaction-based bipartite consensus control for heterogeneous networked systems. IEEE Trans. Syst. Man, Cybern. Syst. 2022, 53, 71–81. [Google Scholar] [CrossRef]
- Tang, Z.; Zhen, Z.; Zhao, Z.; Deconinck, G. Distributed disturbance observer-based nonfragile bipartite consensus of nonlinear multiagent systems with multiple time-varying delays. ISA Trans. 2024, 150, 44–55. [Google Scholar] [CrossRef]
- Sanjuan, A.; Nejjari, F.; Sarrate, R. Actuator fault estimation using optimization-based learning techniques for linear parameter varying systems with unreliable scheduling parameters. Eng. Appl. Artif. Intell. 2024, 127, 107247. [Google Scholar] [CrossRef]
- Liu, J.; Ren, Y. A general transfer framework based on industrial process fault diagnosis under small samples. IEEE Trans. Ind. Informat. 2020, 17, 6073–6083. [Google Scholar] [CrossRef]
- Dhahri, S.; Naifar, O. Fault-Tolerant Tracking Control for Linear Parameter-Varying Systems under Actuator and Sensor Faults. Mathematics 2023, 11, 4738. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Li, W.; Mu, Y.; He, Q. Distributed bipartite adaptive event-triggered fault-tolerant consensus tracking for linear multiagent systems under actuator faults. IEEE Trans. Cybern. 2021, 52, 11313–11324. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Ding, D.W.; Lu, Y.; Deng, C.; Ren, Y. Distributed fault-tolerant bipartite output synchronization of discrete-time linear multiagent systems. IEEE Trans. Cybern. 2022, 53, 1360–1373. [Google Scholar] [CrossRef]
- He, S.; Wang, H.; Yu, W. Distributed fast finite-time tracking consensus of multi-agent systems with a dynamic leader. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 2176–2180. [Google Scholar] [CrossRef]
- Song, W.; Feng, J.; Zhang, H.; Wang, W. Dynamic event-triggered formation control for heterogeneous multiagent systems with nonautonomous leader agent. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9685–9699. [Google Scholar] [CrossRef]
- Wu, Y.; Li, C.; Li, H. Explicit Performance Containment Control for Multi-Agent Systems With Leaders Bounded Unknown Input by Hybrid Time-Event Triggered Mechanism. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 4377–4389. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.L.; Lu, Q. Fixed-time leader-following consensus for multiple wheeled mobile robots. IEEE Trans. Cybern. 2019, 50, 4381–4392. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Wen, G.; Huang, T.; Yu, W.; Ren, Y. Observer-based consensus protocol for directed switching networks with a leader of nonzero inputs. IEEE Trans. Cybern. 2020, 52, 630–640. [Google Scholar] [CrossRef] [PubMed]
- Mei, A.; Wen, G.; Peng, Z.; Rahmani, A.; Huang, T. Vortex formation control for linear multiagent systems with unknown leader input and external disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 636–640. [Google Scholar] [CrossRef]
- Altafini, C. Consensus problems on networks with antagonistic interactions. IEEE Trans. Autom. Control 2012, 58, 935–946. [Google Scholar] [CrossRef]
- Wang, Q.; Dong, X.; Lü, J.; Ren, Z. Fully distributed adaptive formation tracking for directed heterogeneous multi-agent systems with unknown input. IEEE Trans. Circuits Syst. II: Express Briefs 2022, 70, 700–704. [Google Scholar] [CrossRef]
- Zhu, F.; Fu, Y.; Dinh, T.N. Asymptotic convergence unknown input observer design via interval observer. Automatica 2023, 147, 110744. [Google Scholar] [CrossRef]
- Zhu, F.; Li, M. Distributed interval observer and distributed unknown input observer designs. IEEE Trans. Autom. Control 2024, 69, 8868–8875. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, A.; Zhang, W.; Yue, D.; Chen, C.; Shi, J. Bipartite Fault-Tolerant Consensus Control for Multi-Agent Systems with a Leader of Unknown Input Under a Signed Digraph. Sensors 2025, 25, 1556. https://doi.org/10.3390/s25051556
Liu A, Zhang W, Yue D, Chen C, Shi J. Bipartite Fault-Tolerant Consensus Control for Multi-Agent Systems with a Leader of Unknown Input Under a Signed Digraph. Sensors. 2025; 25(5):1556. https://doi.org/10.3390/s25051556
Chicago/Turabian StyleLiu, Anning, Wenli Zhang, Dongdong Yue, Chuang Chen, and Jiantao Shi. 2025. "Bipartite Fault-Tolerant Consensus Control for Multi-Agent Systems with a Leader of Unknown Input Under a Signed Digraph" Sensors 25, no. 5: 1556. https://doi.org/10.3390/s25051556
APA StyleLiu, A., Zhang, W., Yue, D., Chen, C., & Shi, J. (2025). Bipartite Fault-Tolerant Consensus Control for Multi-Agent Systems with a Leader of Unknown Input Under a Signed Digraph. Sensors, 25(5), 1556. https://doi.org/10.3390/s25051556





