4.2. Evaluation Metrics
To scientifically and objectively assess the efficacy of OD methods for ORSIs, it is imperative to employ a range of quantitative evaluation metrics—Precision, Recall, mAP, Intersection over Union (IoU), and Frames Per Second (FPS)—which collectively appraise model performance across various dimensions, including accuracy, localization precision, and processing speed. In practical applications, appropriate assessment metrics can be chosen based on varying requirements and experimental goals with the evaluation criteria utilized in this work being mAP.
Precision is defined as the ratio of accurately predicted positive cases to the total expected positive cases, which was calculated as illustrated in Equation (18):
where TP represents a true positive instance, while FP signifies a false positive instance.
Recall is derived from true samples and is defined as the ratio of correctly predicted positive cases to the total true positive cases, as computed in Equation (19):
where FN signifies a false negative example.
mAP is a crucial metric for evaluating the effectiveness of OD algorithms, as it comprehensively reflects the detector’s accuracy and recall. Calculating mAP often entails multiple steps: initially, for each category, the area under its PR (Precision–Recall) curve, referred to as AP (Average Precision), is computed, as illustrated in Equation (20); subsequently, the AP values across all categories are averaged, culminating in the determination of mAP. mAP for the OD task involving N categories is calculated as demonstrated in Equation (21).
IoU is an index utilized to quantify the extent of overlap between the model’s predicted BBox and the GT box. A larger IoU value indicates a greater overlap between the predicted box and the GT box, resulting in enhanced localization accuracy of the model. The formula for computing the IoU is presented in Equation (22):
FPS is a statistic for assessing the velocity of an OD algorithm, representing the number of image frames processed each second. A higher FPS number indicates a more rapid image processing by the model and enhances real-time performance. The calculation of FPS often relies on the processing duration of an individual image. The result is influenced by various aspects, including model complexity, computational resource performance (e.g., CPU, GPU), and the extent of image processing parallelization.
4.3. Implementation Details
Our experiments are based on the MMRotate [
55] ROD framework (which integrates numerous SOTA ROD algorithms), and the R-RetinaNet detector was chosen as the baseline model.
This study employed the P3 to P7 layers of the FPN to detect multi-scale objects, establishing an anchor at each feature map point for regression purposes. The data augmentation approach solely comprises random flipping and random rotation. During the label assignment phase, the threshold for matching positive examples is established at 0.5 to guarantee the integrity of the detection results.
The ablation experiments employed the mAP measures established by PASCAL VOC 2007 to facilitate a fair comparison with alternative approaches and were conducted on the HRSC2016 dataset. This dataset includes vessels with changes in multi-scale objects and high aspect ratios, which are characteristics that render OD in ORSIs a significant difficulty.
The studies utilized a solitary RTX 2080Ti GPU, with a batch size of 2, employing the AdamW optimizer, an initial learning rate of , and a weight decay coefficient of 0.05. The training duration was 72, and the resolution of the input samples was uniformly set to pixels.
4.4. Ablation Studies
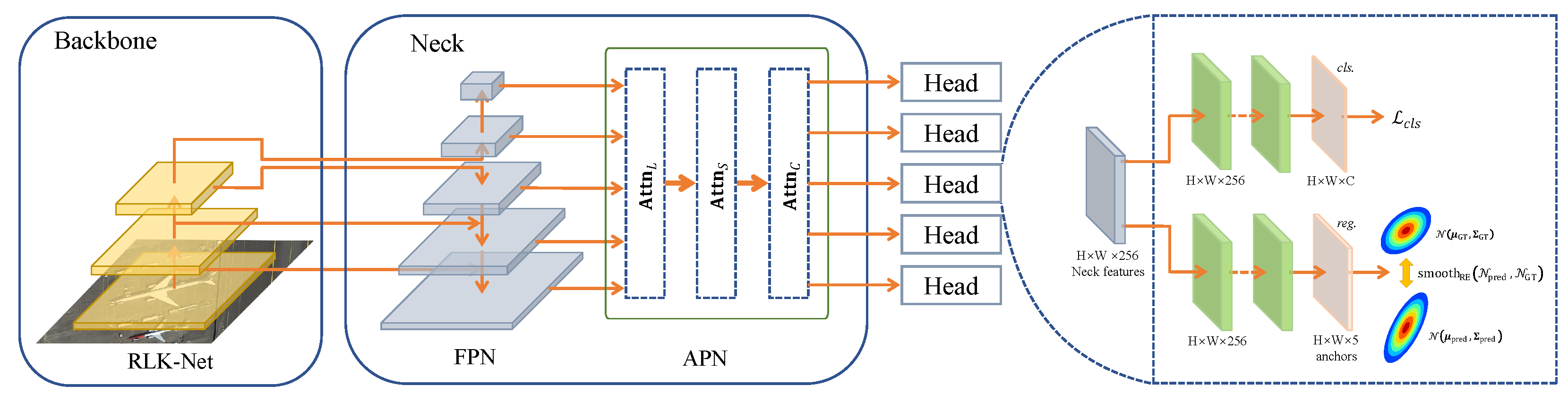
In this study, the baseline architecture we selected covers the ResNet backbone network and the R-RetinaNet detector. Except for the RLK-Net-S/T comparison test, RLK-Net-S is used as the backbone network in all ablation studies.
Then, we conducted an ablation study of various combinations of PSMDet components on detection efficacy.
Table 2 illustrates that the integration of the three elements of RLK-Net, ASN, and
markedly enhances the self-modulation capability throughout the detection process, hence augmenting overall detection performance. The experimental results indicate that the sole use of the baseline model, devoid of a self-modulation mechanism, hampers the high accuracy of RSOD. This yields a map of merely 85.37% for the baseline model.
The implementation of RLK-Net enhances detection performance by 2.17%, demonstrating that the RLK-Net backbone network effectively extracts more robust scale-sensitive features. Moreover, the ASN’s tri-layer adaptive perception system enhances detection performance by 1.22%. The implementation of loss guarantees metric consistency with the loss, enhancing PSMDet’s detection performance by 1.93%, resulting in an overall improvement of 5.32% relative to the baseline model, thereby thoroughly substantiating PSMDet’s efficacy.
Table 3 demonstrates that RLK-Net-S surpasses RLK-Net-T in both depth and width, resulting in a 0.82% advantage in the mAP metric. Consequently, RLK-Net-S was ultimately chosen as the backbone network for this investigation.
Next, we determined the efficacy of the structural reparameterization ablation study. To fairly compare with the SFE block, two variants with the same number of parallel branches and without AC were designed: (A) with the same convolutional kernel size and (B) with the same equivalent convolutional kernel size. The SFE block has the highest mAP, and the mAPs of variants A and B are 0.76% and 0.94% lower, respectively, which indicates that the SFE block can effectively capture different sparse patterns, thereby ensuring the extraction of scale-sensitive features, which is crucial for high-precision detection in the end.
An ablation study of using large convolutional kernels in the middle and upper stages, Stage 2 to Stage 4, is explored. As shown in
Table 4, the best mAP was obtained with K = 13 at 90.69% in the first group of experiments. K = 15 and K = 11 came next, with 90.15% and 89.57%, respectively. This indicates that the features extracted by the lower layers of the backbone network only encode local information so that they can be combined with the high-level features extracted by the final layers of the backbone network to achieve better detection.
In the second group of experiments, when all four stages use LK blocks with K = 13, the mAP is the worst, only 88.93%, which is first because Stage 1 is mainly used for extracting the low-level features such as colors, edges and textures and thus is not suitable for using a fast LK such as K = 13. In remote sensing images, the scale of objects varies greatly, and using an LK block may introduce additional background noise that drowns out relevant features such as colors, edges and textures of small objects. Secondly, the AC layer in the SFE block further makes the space of relevant features such as color, edge and texture sparse.
In addition,
Table 5 also shows that replacing the large convolutional kernels in the last three stages with
kernels in the third set of experiments reduces model performance. Therefore, we use
convolutional kernels by default in the intermediate and advanced stages.
Evaluation of the efficacy of employing SK blocks to regulate network depth scaling. To explore effectiveness, we take a novel perspective and focus on the role of small convolutional kernels in controlling network depth scaling. Traditionally, expanding convolutional networks with large convolutional kernels follows a set pattern: deepening the model by simply stacking more large convolutional kernels, as in ConvNeXt-S. However, we question this and argue that adding more large convolutional kernels does not lead to a consistent performance improvement. To verify this, we designed a set of experiments, as shown in
Table 6, in which we attempted to expand the number of blocks in Stage 3 from 9 to 27 based on ConvNeXt-S and explored whether these additional blocks should continue to use large convolution kernels (LK blocks).
The experimental results show that the depth expansion brings the expected performance improvement, indicating that the nine LK blocks have laid a solid foundation for performance. However, although the configuration of 27 LK blocks has a slight advantage in mAP, its inference speed has dropped significantly. In addition, removing the convolution in the SK block significantly decreases mAP, while the throughput improvement is minimal. These findings highlight the importance of the small convolution kernels in the SK block during depth expansion. Although they may not be as effective as large convolutional kernels in expanding the ERF, small convolutional kernels provide the network with additional performance gains by increasing the spatial pattern’s abstraction level. Therefore, when building deeper convolutional networks with large convolutional kernels, a clever combination of large and small ones is the key to achieving a balance of performance and efficiency.
Next, we conducted an ablation study on the effectiveness of APN. This study incrementally incorporates various attention modules into the baseline model to assess their impact on performance. , , and denote the scale-perception attention module, spatial-perception attention module, and task-perception module, respectively.
Table 7 illustrates that the incorporation of any module markedly enhances the mAP index, with the spatial perception attention module demonstrating the most substantial improvement, yielding a 0.78% increase in mAP. The introduction of both scale-perception and spatial-perception modules results in a further enhancement of mAP by 0.95%. The comprehensive APN module enhanced the mAP of the baseline model by 1.38%. This result illustrates the effective synergy among the modules, which collectively augment the self-modulation capability and enhance the model’s detection performance via feature alignment.
For an ablation study of regression loss functions and associated hyperparameters, this paper examines three kinds of regression loss functions based on RE: the original RE, the nonlinearly transformed f(RE), and the adjusted loss that includes the hyperparameter .
Table 8 illustrates that the performance of RE is suboptimal at 0.58% owing to its heightened sensitivity to significant errors. The implementation of basic nonlinear transformations like
and
markedly enhances performance to 88.32% and 88.86%, respectively. Furthermore, comprehensive hyperparameter optimization experiments are performed for the suggested loss function. With
and
established, the loss function attains optimal performance, yielding an mAP of 90.69%.
Last, we conducted an ablation study of normalization techniques. To mitigate the excessive increase of the regression error and obtain the normalization effect, we implemented Equation (16). Nonetheless, this supplementary normalizing procedure prompts inquiries over whether the RE genuinely enhances the results or simply adds extraneous noise. To validate our method and eliminate potential influence from normalization, we additionally normalized the
loss.
Table 9 illustrates a substantial decline in performance following the normalizing process. This result suggests that the efficacy of RE stems not from the normalization procedure in Equation (16) but from the novel enhancement of our methodology.
4.5. Comparative Experiments
In the comparative trials, we selected RLK-Net-S as the foundational network.
The experimental findings in
Table 10 demonstrate that our strategy achieves the highest mAP score of 90.69% on the HRSC2016 dataset. Initially, we eliminated the strategy of conventionally utilizing numerous redundant preset anchors and instead implemented a streamlined approach by deploying a singular horizontal anchor at each feature grid point. This approach markedly enhances inference speed and illustrates that reducing the number of anchor points can yield better detection results in the OD problem. The detection data presented in
Figure 9 confirm the efficacy of our method. The detection results indicate no substantial center point offset or angular deviation, demonstrating that our suggested
loss function successfully assures the coupling of all parameters, hence achieving improved model convergence. Specifically, in the detection results numbered 3, 5, and 6, multiple scale objects are precisely identified, which can be ascribed to the proficient performance of the backbone network RLK-Net in scale-sensitive feature extraction, which is complemented by the
loss function and the effective feature calibration of the APN across three dimensions. In conclusion, our suggested progressive self-modulation process exhibits exceptional precision in OD and location.
The experimental findings presented in
Table 11 demonstrate that our technique attains a remarkable mAP score of 89.86% on the UCAS-AOD dataset, significantly surpassing previous detectors.
Figure 10 illustrates that our technique excels at recognizing intricate scenes, demonstrating significant resilience and precision. In Results 1 and 6, densely clustered little objects are precisely identified, demonstrating the efficacy and precision of our method in addressing dense objects. In Result 2, the trajectories of all vehicles on the circular lane are precisely tangent to the lane, illustrating the precision and efficacy of our approach in managing intricate traffic situations. Moreover, in Results 3, 4, and 5, our detector demonstrates resilience against leaking, even when individual automobiles are situated in building shadows or partially obscured by trees, further affirming the robustness of our methodology. Particularly in Results 6 to 9, despite encountering aircraft with unique aerodynamic configurations that blend with the background texture, our method consistently demonstrates the capability to accurately ascertain the positions and orientations of all aircraft, thereby reinforcing the robustness of our approach in managing complex objects.
Then, we used the Precision–Recall curves on the HRSC2016 and UCAS-AOD datasets (shown in
Figure 11) to visualize the performance of the PSMDet model in terms of Precision rate under different Recall rates. It can be seen that PSMDet can maintain high Precision (mAP) while ensuring a high Recall rate, thus demonstrating the robustness of PSMDet in processing ORSIs with multiple scales and multiple objects.