A Sub-Pixel Measurement Platform Using Twist-Angle Analysis in Two-Dimensional Planes
Abstract
:1. Introduction
2. Materials and Methods
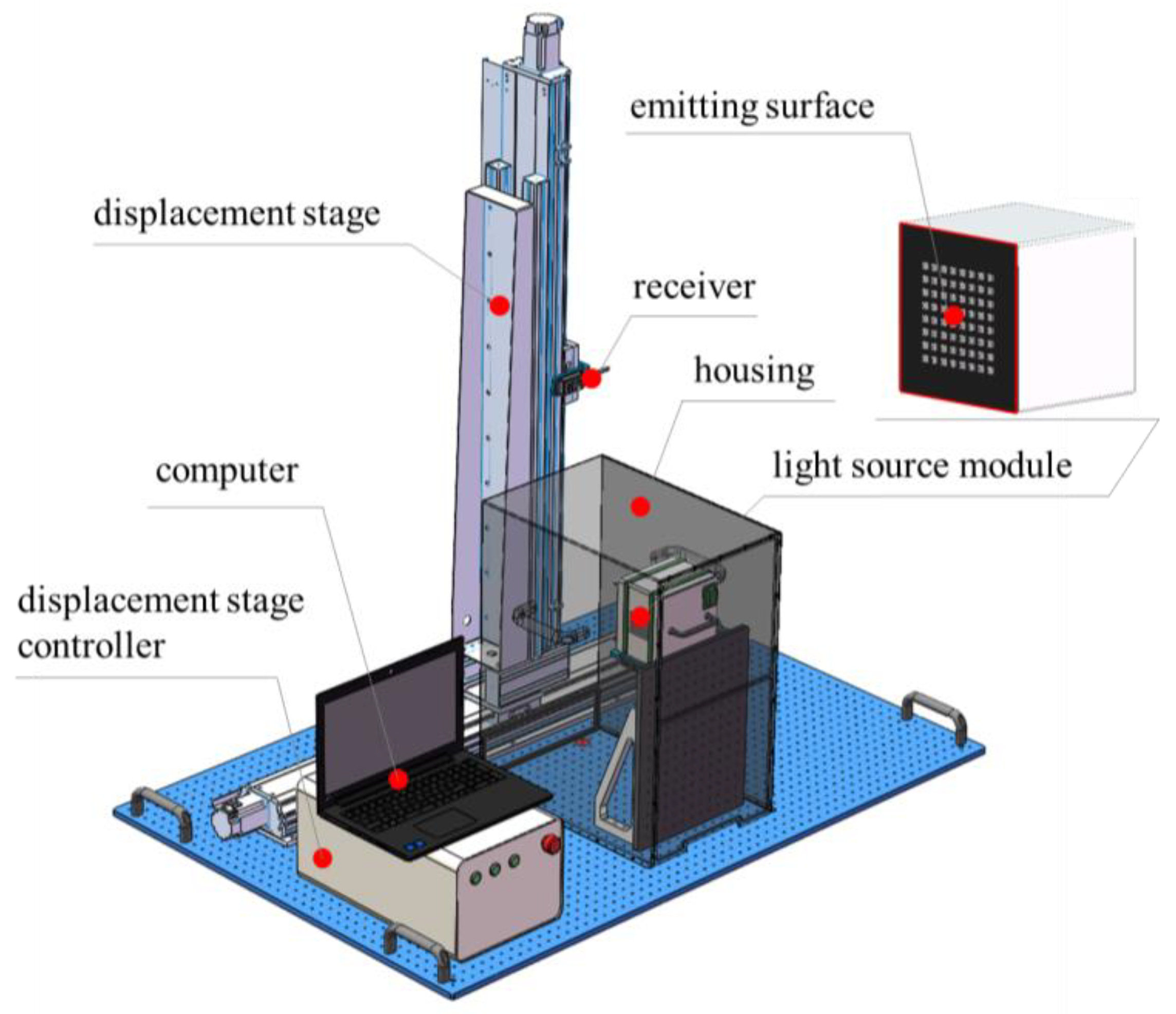
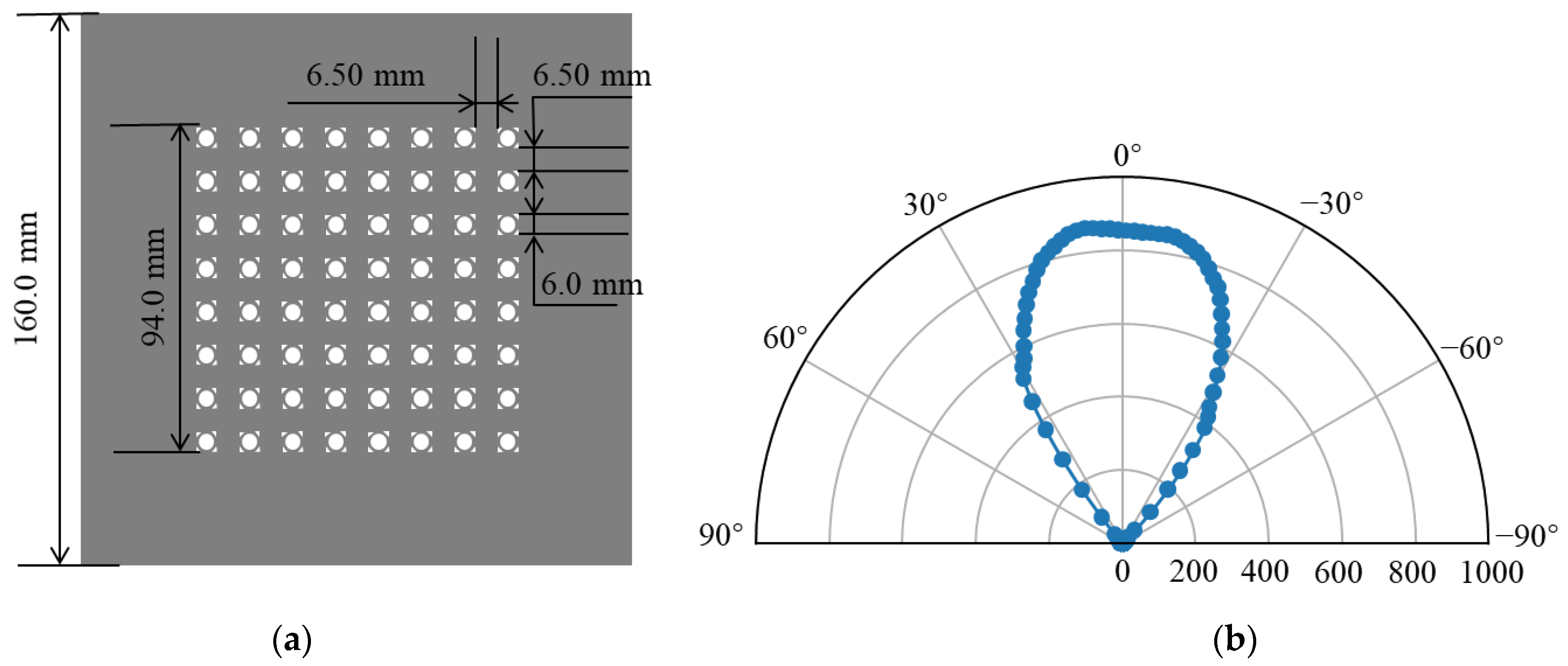
2.1. Measurement Setup
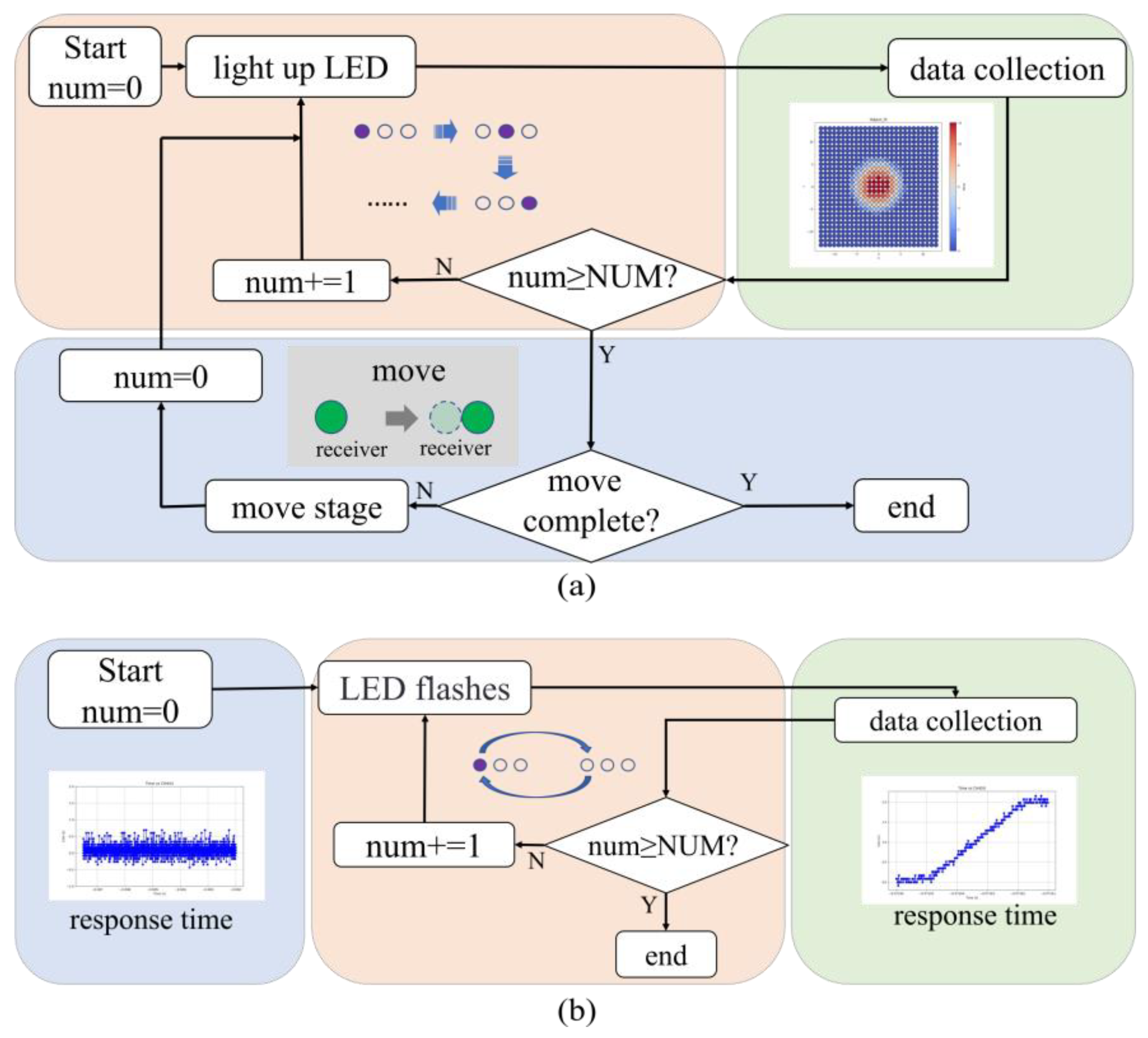
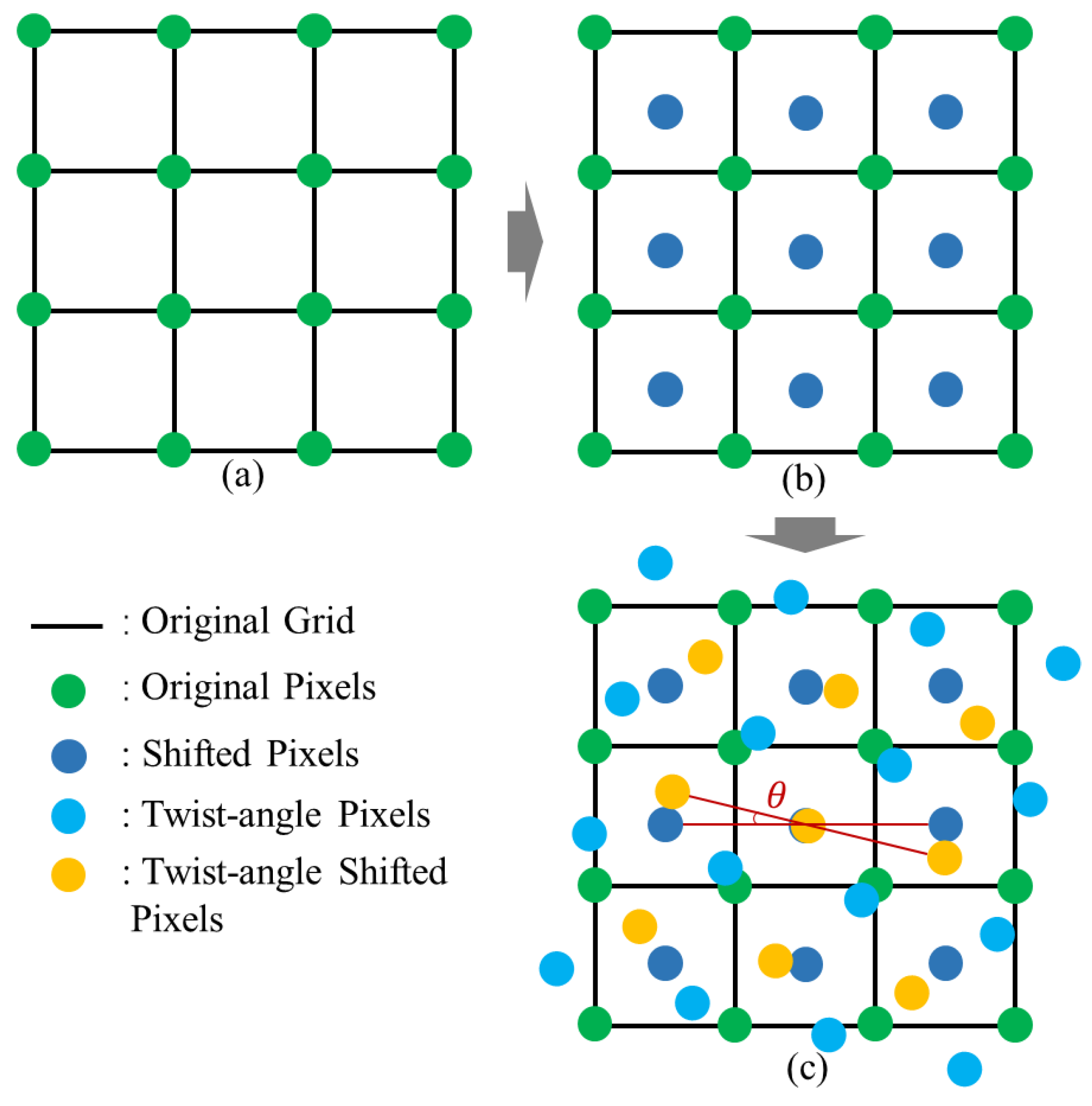
2.2. Testing Methods
3. Results and Discussion
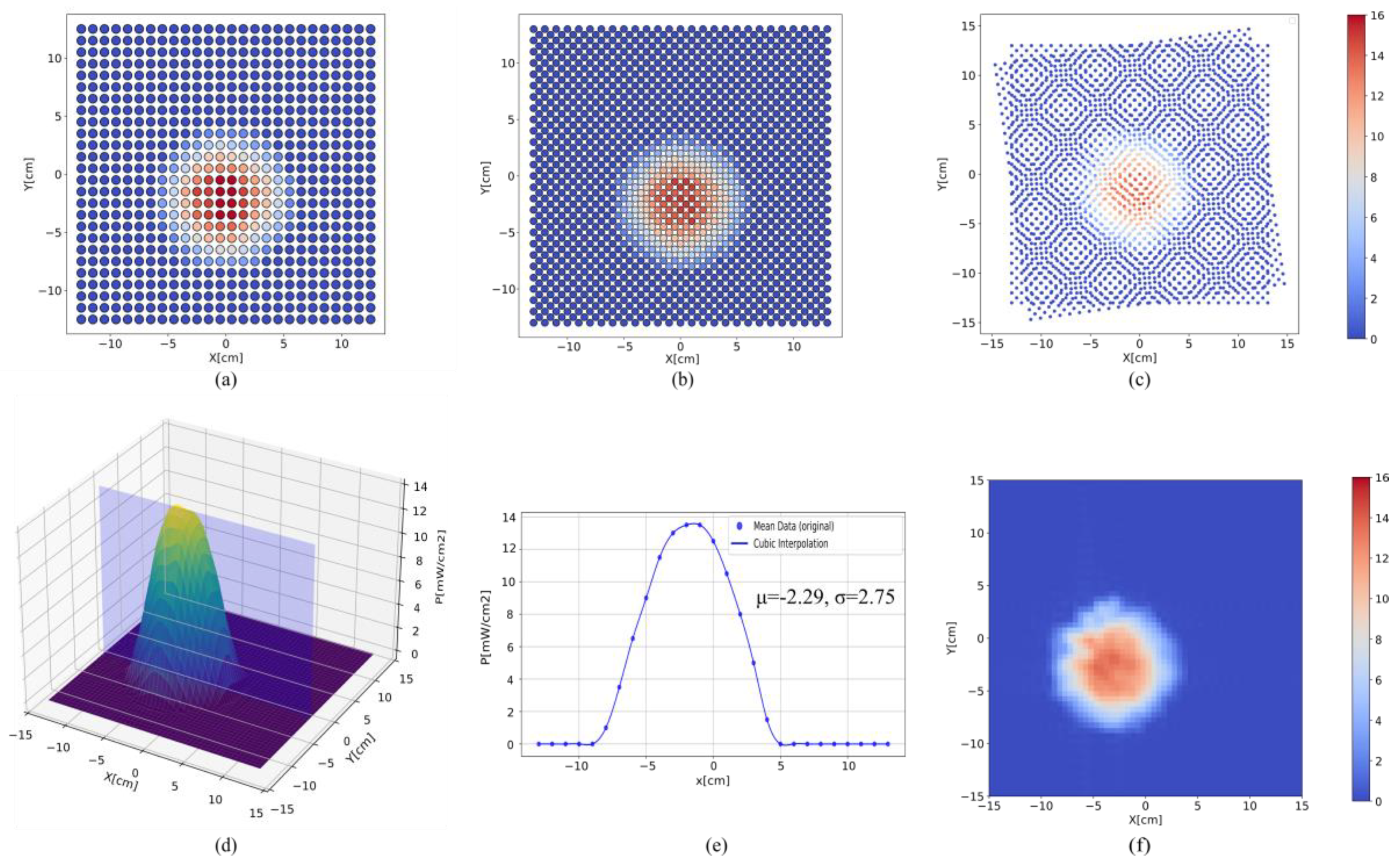
3.1. Spatial Intensity Distribution
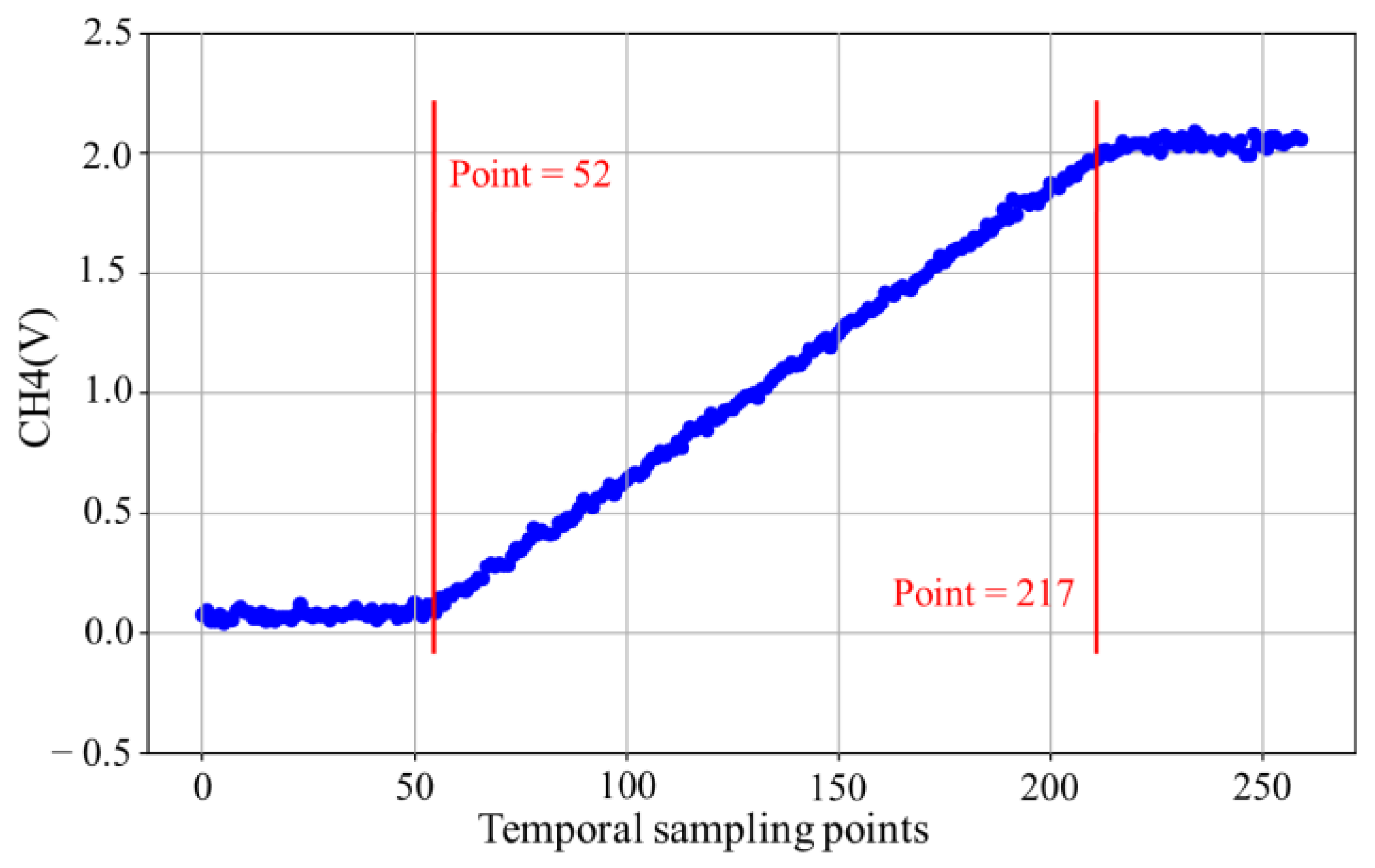
3.2. Response Time Testing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Muramoto, Y.; Kimura, M.; Nouda, S. Development and future of ultraviolet light-emitting diodes: UV-LED will replace the UV lamp. Semicond. Sci. Technol. 2014, 29, 084004. [Google Scholar] [CrossRef]
- Zheng, L.; Birr, T.; Zywietz, U.; Reinhardt, C.; Roth, B. Feature size below 100 nm realized by UVLED-based microscope projection photolithography. Light Adv. Manuf. 2023, 4, 410–419. [Google Scholar]
- Erickstad, M.; Gutierrez, E.; Groisman, A. A low-cost low-maintenance ultraviolet lithography light source based on light-emitting diodes. Lab Chip 2015, 15, 57–61. [Google Scholar] [CrossRef] [PubMed]
- Shiba, S.F.; Jeon, H.; Kim, J.-S.; Kim, J.-E.; Kim, J. 3D microlithography using an integrated system of 5-mm uv-leds with a tilt-rotational sample holder. Micromachines 2020, 11, 157. [Google Scholar] [CrossRef]
- Mudunuri, S.P.; Biswas, S. Low resolution face recognition across variations in pose and illumination. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 1034–1040. [Google Scholar] [CrossRef]
- Yapici, M.K.; Farhat, I. UV-LED exposure system for low-cost photolithography. Opt. Microlithogr. XXVII 2014, 9052, 523–529. [Google Scholar]
- Kim, J.; Yoon, Y.-K.; Allen, M.G. Computer numerical control (CNC) lithography: Light-motion synchronized UV-LED lithography for 3D microfabrication. J. Micromech. Microeng. 2016, 26, 035003. [Google Scholar] [CrossRef]
- Bing, C.Y.; Mohanan, A.A.; Saha, T.; Ramanan, R.N.; Parthiban, R.; Ramakrishnan, N. Microfabrication of surface acoustic wave device using UV LED photolithography technique. Microelectron. Eng. 2014, 122, 9–12. [Google Scholar] [CrossRef]
- Shiba, S.F.; Tan, J.Y.; Kim, J. Multidirectional UV-LED lithography using an array of high-intensity UV-LEDs and tilt-rotational sample holder for 3-D microfabrication. Micro Nano Syst. Lett. 2020, 8, 5. [Google Scholar] [CrossRef]
- Huntington, M.D.; Odom, T.W. A portable, benchtop photolithography system based on a solid-state light source. Small 2011, 7, 3144–3147. [Google Scholar] [CrossRef]
- Zheng, L.; Zywietz, U.; Birr, T.; Duderstadt, M.; Overmeyer, L.; Roth, B.; Reinhardt, C. UV-LED projection photolithography for high-resolution functional photonic components. Microsyst. Nanoeng. 2021, 7, 64. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.H.; Oh, S.S.; Kim, Y.-S.; Choi, C.-G. Fabrication of antireflection nanostructures by hybrid nano-patterning lithography. Microelectron. Eng. 2010, 87, 125–128. [Google Scholar] [CrossRef]
- Kontio, J.M.; Simonen, J.; Tommila, J.; Pessa, M. Arrays of metallic nanocones fabricated by UV-nanoimprint lithography. Microelectron. Eng. 2010, 87, 1711–1715. [Google Scholar] [CrossRef]
- Stuerzebecher, L.; Harzendorf, T.; Vogler, U.; Zeitner, U.D.; Voelkel, R. Advanced mask aligner lithography: Fabrication of periodic patterns using pinhole array mask and Talbot effect. Opt. Express 2010, 18, 19485–19494. [Google Scholar] [CrossRef]
- Dreyer, C.; Mildner, F. Application of LEDs for UV-curing. In III-Nitride Ultraviolet Emitters: Technology and Applications; Springer: Berlin/Heidelberg, Germany, 2016; pp. 415–434. [Google Scholar]
- Shiba, S.F.; Beavers, J.; Laramore, D.; Lindstrom, B.; Brovles, J.; Gaither, C.; Hieber, T.; Kim, J. UV-LED lithography system and characterization. In Proceedings of the 2020 IEEE 15th International Conference on Nano/Micro Engineered and Molecular System (NEMS), San Diego, CA, USA, 27–30 September 2020; pp. 73–76. [Google Scholar]
- Zollner, C.J.; DenBaars, S.; Speck, J.; Nakamura, S. Germicidal ultraviolet LEDs: A review of applications and semiconductor technologies. Semicond. Sci. Technol. 2021, 36, 123001. [Google Scholar] [CrossRef]
- Li, Z.; Ye, X.; Han, Q.; Qi, F.; Luo, H.; Shi, H.; Xiong, W. Research on calibration and data processing method of dynamic target monitoring spectrometer. In Proceedings of the Second Symposium on Novel Technology of X-Ray Imaging, Hefei, China, 26–28 November 2018; pp. 632–637. [Google Scholar]
- Wang, X.; Xiong, J.; Hu, X.; Li, Q. Implementation and uniformity calibration of LED array for photodynamic therapy. J. Innov. Opt. Health Sci. 2022, 15, 2240004. [Google Scholar] [CrossRef]
- Greenspan, H. Super-resolution in medical imaging. Comput. J. 2009, 52, 43–63. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, Y.; Ding, M.; Ghanem, B. Sod-mtgan: Small object detection via multi-task generative adversarial network. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 206–221. [Google Scholar]
- Lobanov, A.P. Resolution limits in astronomical images. arXiv 2005, arXiv:astro-ph/0503225. [Google Scholar]
- Lillesand, T.; Kiefer, R.W.; Chipman, J. Remote Sensing and Image Interpretation; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Region-based convolutional networks for accurate object detection and segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 142–158. [Google Scholar] [CrossRef]
- Swaminathan, A.; Wu, M.; Liu, K.R. Digital image forensics via intrinsic fingerprints. IEEE Trans. Inf. Forensics Secur. 2008, 3, 101–117. [Google Scholar] [CrossRef]
- Bashir, S.M.A.; Wang, Y.; Khan, M.; Niu, Y. A comprehensive review of deep learning-based single image super-resolution. PeerJ Comput. Sci. 2021, 7, e621. [Google Scholar] [CrossRef] [PubMed]
- Tan, R.; Yuan, Y.; Huang, R.; Luo, J. Video super-resolution with spatial-temporal transformer encoder. In Proceedings of the 2022 IEEE International Conference on Multimedia and Expo (ICME), Taipei, Taiwan, 18–22 July 2022; pp. 1–6. [Google Scholar]
- Li, H.; Zhang, P. Spatio-temporal fusion network for video super-resolution. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–9. [Google Scholar]
- Shah, N.R.; Zakhor, A. Resolution enhancement of color video sequences. IEEE Trans. Image Process. 1999, 8, 879–885. [Google Scholar] [CrossRef] [PubMed]
- Thawakar, O.; Patil, P.W.; Dudhane, A.; Murala, S.; Kulkarni, U. Image and video super resolution using recurrent generative adversarial network. In Proceedings of the 2019 16th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Taipei, Taiwan, 18–21 September 2019; pp. 1–8. [Google Scholar]
- Panchenko, E.; Wesemann, L.; Gómez, D.E.; James, T.D.; Davis, T.J.; Roberts, A. Ultracompact camera pixel with integrated plasmonic color filters. Adv. Opt. Mater. 2019, 7, 1900893. [Google Scholar] [CrossRef]
- Pejović, V.; Lee, J.; Georgitzikis, E.; Li, Y.; Kim, J.H.; Lieberman, I.; Malinowski, P.E.; Heremans, P.; Cheyns, D. Thin-film photodetector optimization for high-performance short-wavelength infrared imaging. IEEE Electron Device Lett. 2021, 42, 1196–1199. [Google Scholar] [CrossRef]
- Morimoto, K.; Ardelean, A.; Wu, M.-L.; Ulku, A.C.; Antolovic, I.M.; Bruschini, C.; Charbon, E. A megapixel time-gated SPAD image sensor for 2D and 3D imaging applications. arXiv 2019, arXiv:1912.12910. [Google Scholar] [CrossRef]
- Kim, S.; Bose, N.K. Reconstruction of 2-D bandlimited discrete signals from nonuniform samples. IEE Proc. F (Radar Signal Process.) 1990, 137, 197–204. [Google Scholar] [CrossRef]
- Rogalski, A.; Martyniuk, P.; Kopytko, M. Challenges of small-pixel infrared detectors: A review. Rep. Prog. Phys. 2016, 79, 046501. [Google Scholar] [CrossRef]
- Komatsu, T.; Aizawa, K.; Igarashi, T.; Saito, T. Signal-processing based method for acquiring very high resolution images with multiple cameras and its theoretical analysis. IEE Proc. I (Commun. Speech Vis.) 1993, 140, 19–25. [Google Scholar] [CrossRef]
- Yue, L.; Shen, H.; Li, J.; Yuan, Q.; Zhang, H.; Zhang, L. Image super-resolution: The techniques, applications, and future. Signal Process. 2016, 128, 389–408. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, X.; Tian, Y.; Wang, W.; Xue, J.-H.; Liao, Q. Deep learning for single image super-resolution: A brief review. IEEE Trans. Multimed. 2019, 21, 3106–3121. [Google Scholar] [CrossRef]
- Gibson, G.M.; Johnson, S.D.; Padgett, M.J. Single-pixel imaging 12 years on: A review. Opt. Express 2020, 28, 28190–28208. [Google Scholar] [CrossRef] [PubMed]
- Bishara, W.; Su, T.-W.; Coskun, A.F.; Ozcan, A. Lensfree on-chip microscopy over a wide field-of-view using pixel super-resolution. Opt. Express 2010, 18, 11181–11191. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Chen, Q.; Li, J.; Sun, J.; Ding, T.; Zuo, C. The dynamic super-resolution phase imaging based on low-cost lensfree system. In Proceedings of the Sixth International Conference on Optical and Photonic Engineering (icOPEN 2018), Shanghai, China, 8–11 May 2018; pp. 314–318. [Google Scholar]
- Clark, J.; Palmer, M.; Lawrence, P. A transformation method for the reconstruction of functions from nonuniformly spaced samples. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 1151–1165. [Google Scholar] [CrossRef]
- Shukla, A.; Merugu, S.; Jain, K. A technical review on image super-resolution techniques. In Advances in Cybernetics, Cognition, and Machine Learning for Communication Technologies; Springer: Singapore, 2020; pp. 543–565. [Google Scholar]
- Park, S.C.; Park, M.K.; Kang, M.G. Super-resolution image reconstruction: A technical overview. IEEE Signal Process. Mag. 2003, 20, 21–36. [Google Scholar] [CrossRef]
- Ur, H.; Gross, D. Improved resolution from subpixel shifted pictures. CVGIP Graph. Models Image Process. 1992, 54, 181–186. [Google Scholar] [CrossRef]
- Papoulis, A. Generalized sampling expansion. IEEE Trans. Circuits Syst. 1977, 24, 652–654. [Google Scholar] [CrossRef]
- Brown, J. Multi-channel sampling of low-pass signals. IEEE Trans. Circuits Syst. 1981, 28, 101–106. [Google Scholar] [CrossRef]
- Landweber, L. An iteration formula for Fredholm integral equations of the first kind. Am. J. Math. 1951, 73, 615–624. [Google Scholar] [CrossRef]
- Alam, M.S.; Bognar, J.G.; Hardie, R.C.; Yasuda, B.J. Infrared image registration and high-resolution reconstruction using multiple translationally shifted aliased video frames. IEEE Trans. Instrum. Meas. 2000, 49, 915–923. [Google Scholar] [CrossRef]
- Nguyen, N.; Milanfar, P. An efficient wavelet-based algorithm for image superresolution. In Proceedings of the 2000 International Conference on Image Processing (Cat. No. 00CH37101), Vancouver, BC, Canada, 10–13 September 2000; pp. 351–354. [Google Scholar]
- Park, M.K.; Lee, E.S.; Park, J.Y.; Kang, M.G.; Kim, J. Discrete cosine transform based high-resolution image reconstruction considering the inaccurate subpixel motion information. Opt. Eng. 2002, 41, 370–380. [Google Scholar] [CrossRef]
- Ben-Ezra, M.; Zomet, A.; Nayar, S.K. Video super-resolution using controlled subpixel detector shifts. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 977–987. [Google Scholar] [CrossRef]
- Bishara, W.; Sikora, U.; Mudanyali, O.; Su, T.-W.; Yaglidere, O.; Luckhart, S.; Ozcan, A. Holographic pixel super-resolution in portable lensless on-chip microscopy using a fiber-optic array. Lab Chip 2011, 11, 1276–1279. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, J.; Kong, W.; Zhou, Y.; Pi, Y.; Cao, Z. A Sub-Pixel Measurement Platform Using Twist-Angle Analysis in Two-Dimensional Planes. Sensors 2025, 25, 1081. https://doi.org/10.3390/s25041081
Lyu J, Kong W, Zhou Y, Pi Y, Cao Z. A Sub-Pixel Measurement Platform Using Twist-Angle Analysis in Two-Dimensional Planes. Sensors. 2025; 25(4):1081. https://doi.org/10.3390/s25041081
Chicago/Turabian StyleLyu, Jiangbo, Wenchao Kong, Yan Zhou, Yazhi Pi, and Zizheng Cao. 2025. "A Sub-Pixel Measurement Platform Using Twist-Angle Analysis in Two-Dimensional Planes" Sensors 25, no. 4: 1081. https://doi.org/10.3390/s25041081
APA StyleLyu, J., Kong, W., Zhou, Y., Pi, Y., & Cao, Z. (2025). A Sub-Pixel Measurement Platform Using Twist-Angle Analysis in Two-Dimensional Planes. Sensors, 25(4), 1081. https://doi.org/10.3390/s25041081




