Monte Carlo Guidance for Better Imaging of Boreal Lakes in the Wavelength Region of 400–800 nm
Abstract
1. Introduction
2. Materials and Methods
2.1. Monte Carlo Model
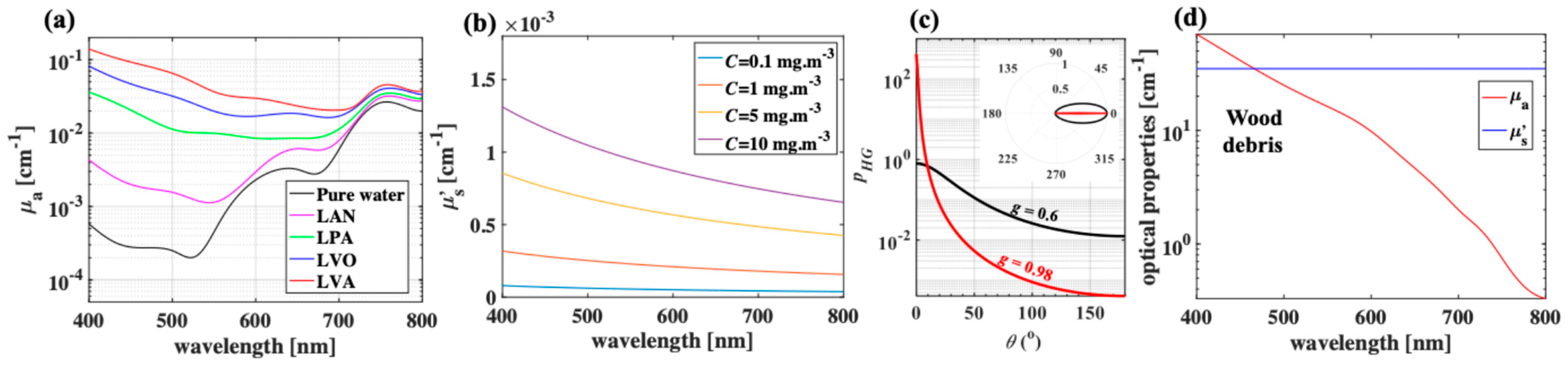
2.2. Optical Properties of Boreal Lake Waters and Woody Debris in the Study Area
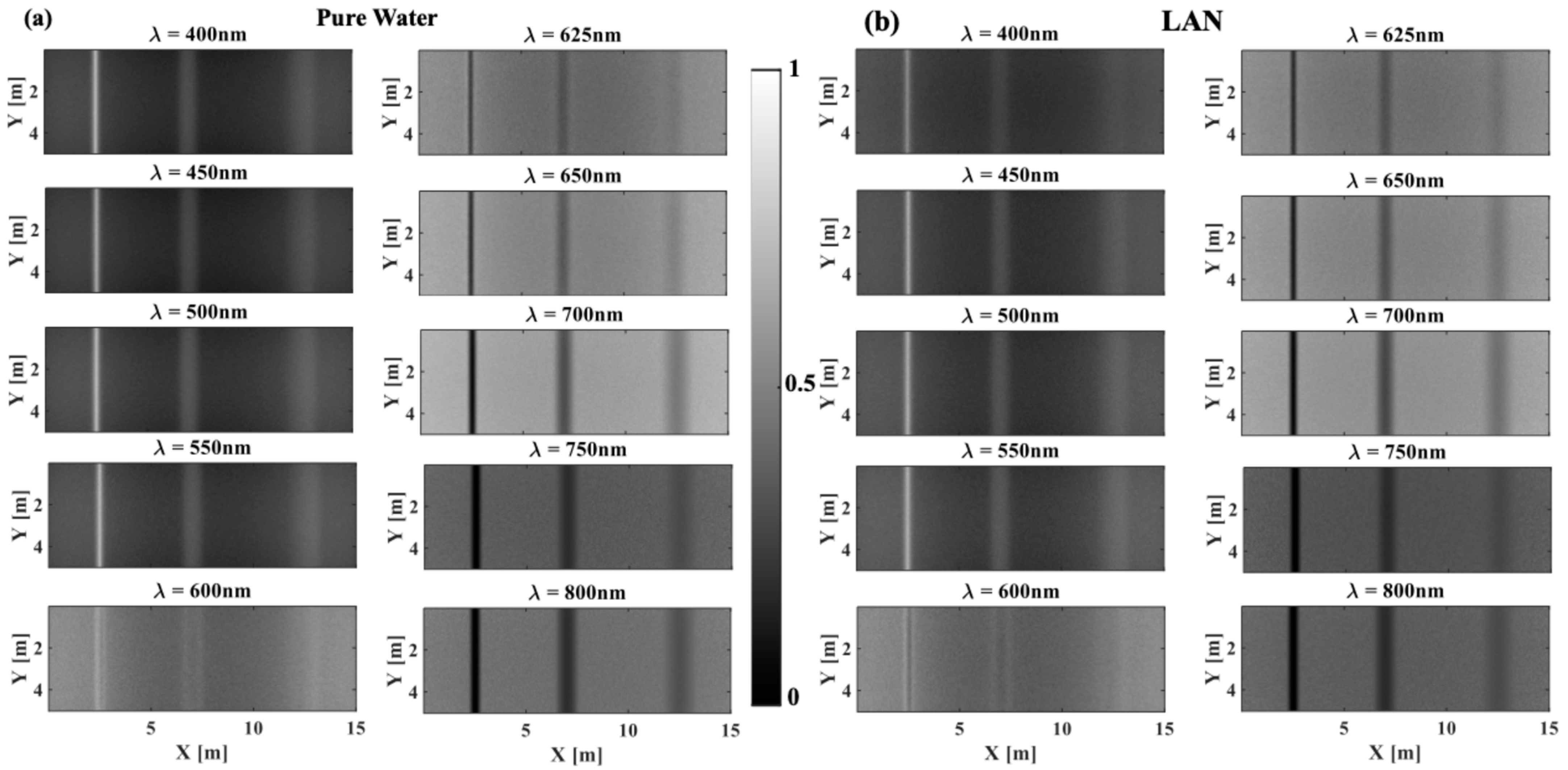
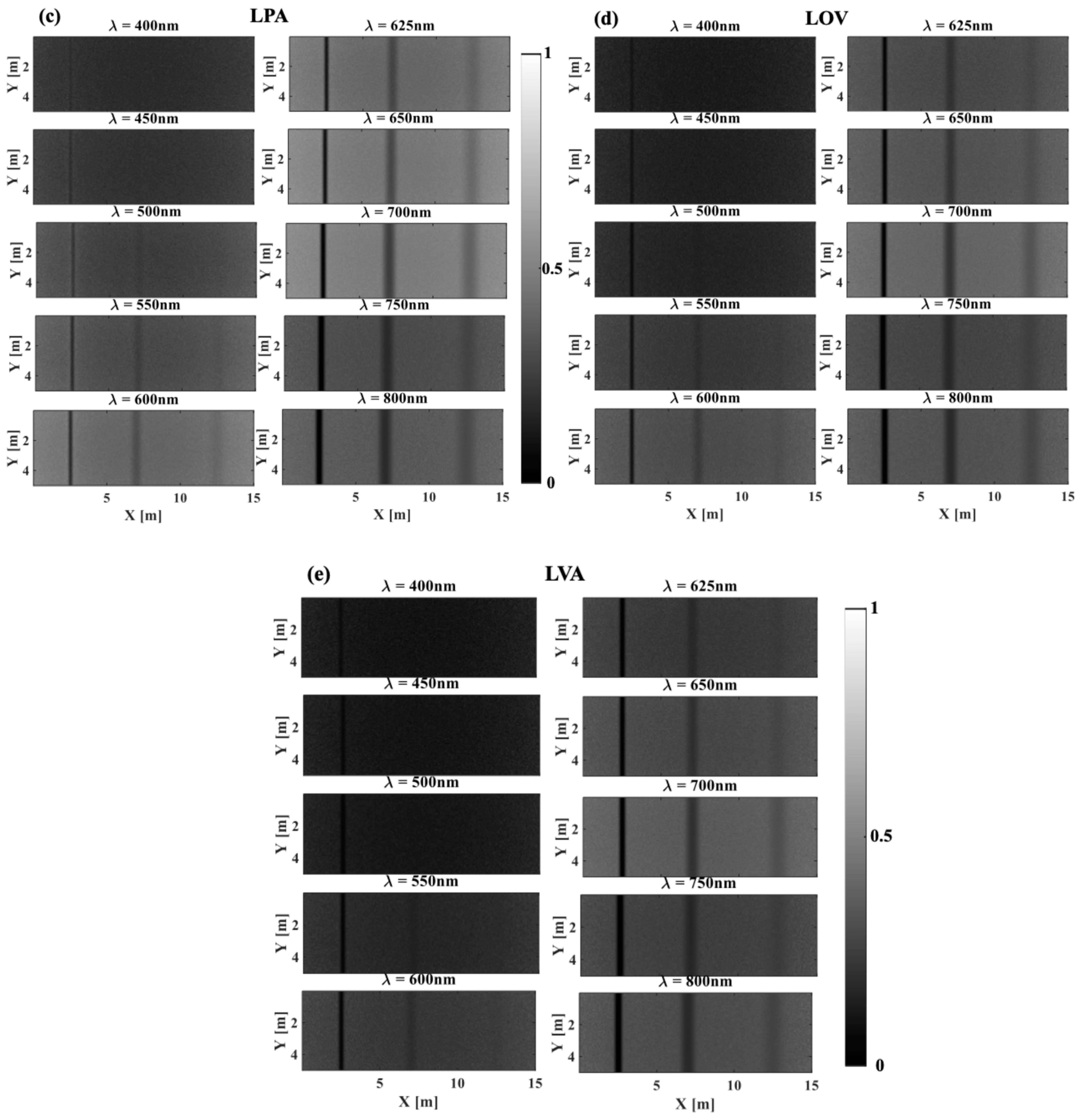
3. Results
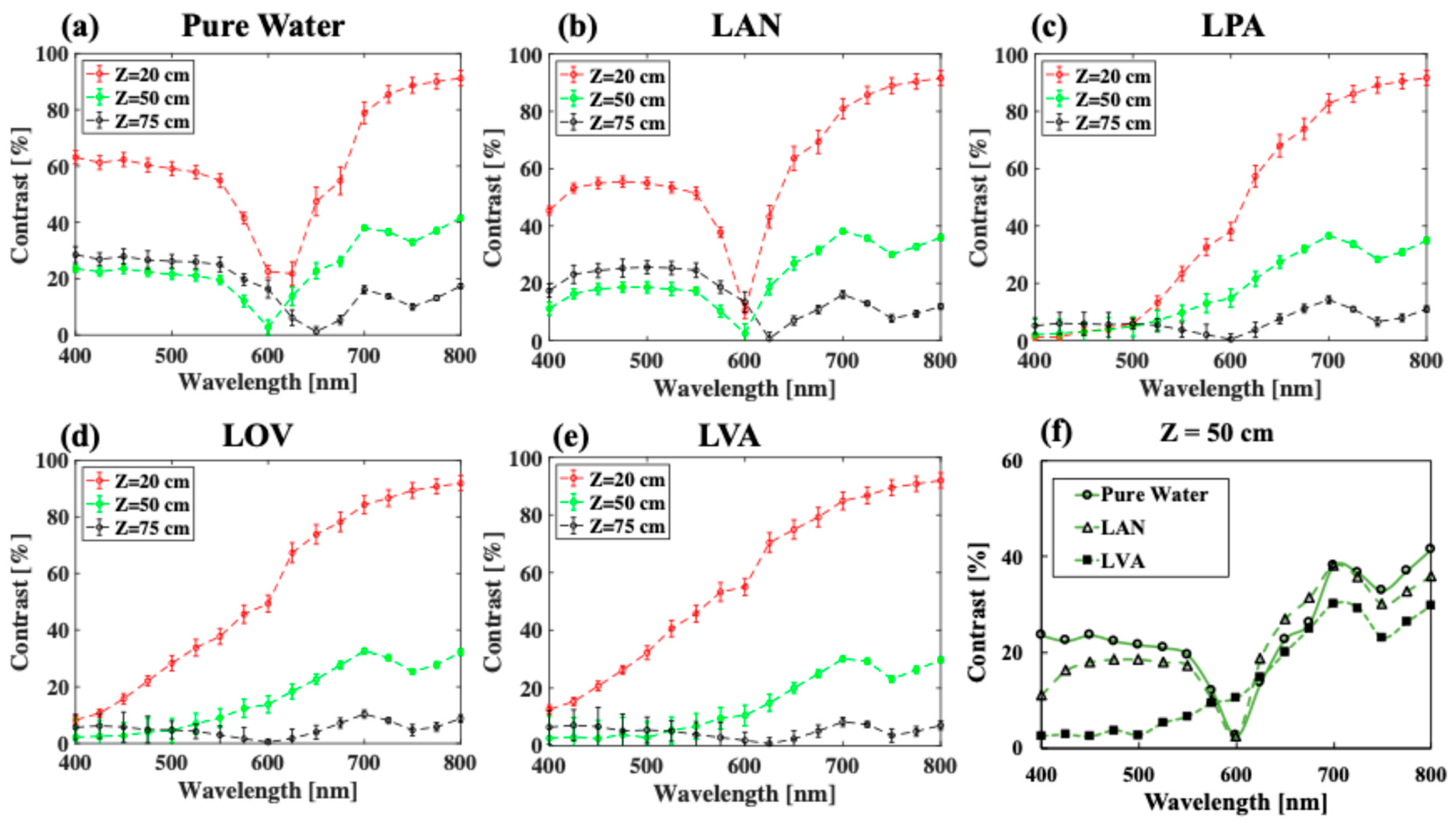
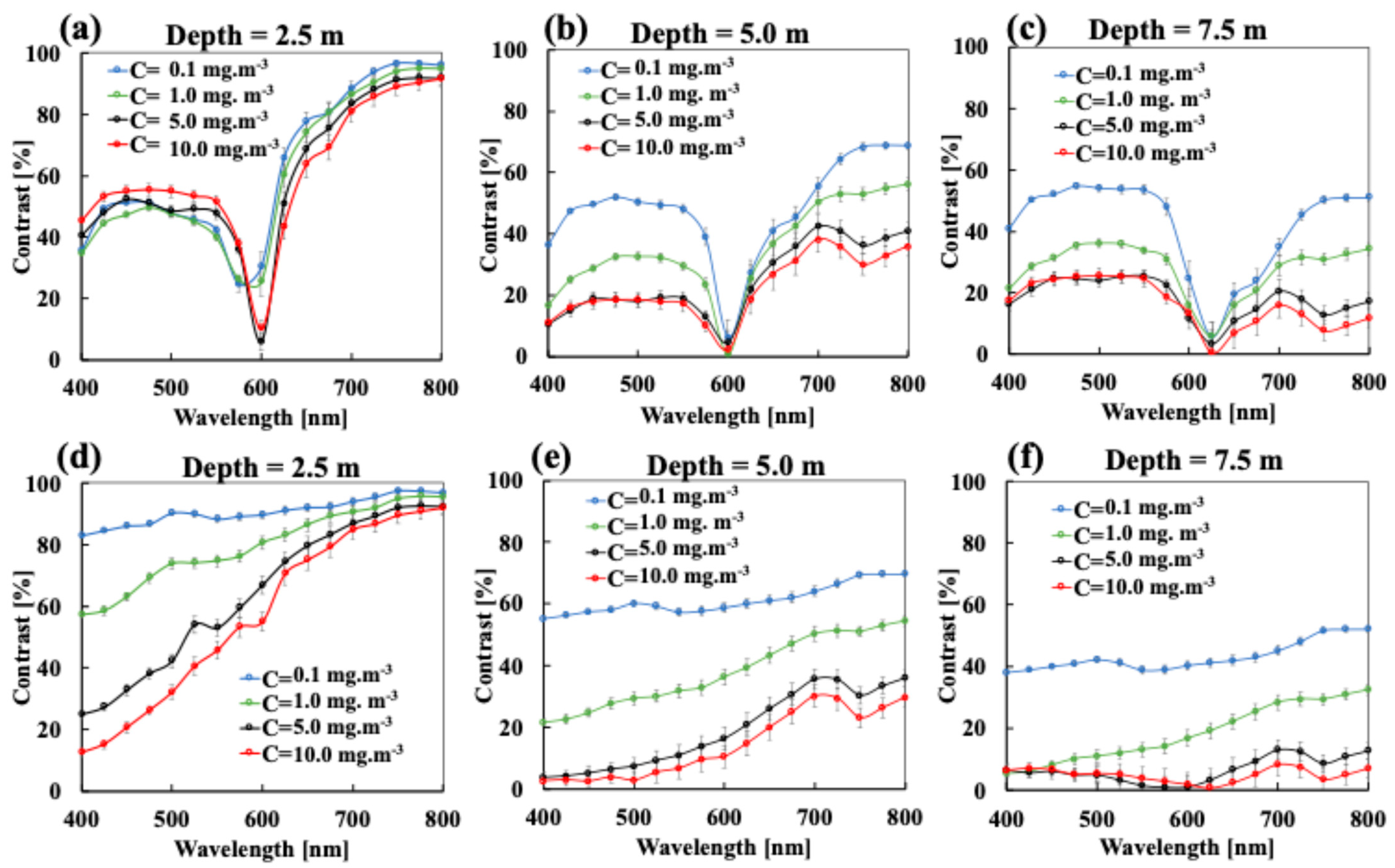
3.1. The Effect of Phytoplankton Absorption on the Spectral Contrast–Depth Dynamics
3.2. The Effect of Chlorophyll Scattering on the Spectral Contrast–Depth Dynamics
4. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Riordan, B.; Verbyla, D.; McGuire, A.D. Shrinking ponds in subarctic Alaska based on 1950–2002 remotely sensed images. J. Geophys. Res. Biogeosci. 2006, 111. [Google Scholar] [CrossRef]
- Roach, J.K.; Griffith, B.; Verbyla, D. Landscape influences on climate–related lake shrinkage at high latitudes. Global Change Biol. 2013, 19, 2276–2284. [Google Scholar] [CrossRef] [PubMed]
- Carroll, M.L.; Townshend, J.; DiMiceli, C.; Loboda, T.; Sohlberg, R. Shrinking lakes of the Arctic: Spatial relationships and trajectory of change. Geophys. Res. Lett. 2011, 38, 286. [Google Scholar] [CrossRef]
- Klein, E.; Berg, E.E.; Dial, R. Wetland drying and succession across the Kenai Peninsula lowlands, south-central Alaska. Can. J. For. Res. 2005, 35, 1931–1941. [Google Scholar] [CrossRef]
- Smith, L.C.; Sheng, Y.; MacDonald, G.; Hinzman, L. Disappearing Arctic lakes. Science 2005, 308, 1429. [Google Scholar] [CrossRef] [PubMed]
- Arnott, S.E.; Keller, B.; Dillon, P.J.; Yan, N.; Paterson, M.; Findlay, D. Using temporal coherence to determine the response to climate change in boreal shield lakes. Environ. Monit. Assess. 2003, 88, 365–388. [Google Scholar] [CrossRef]
- Hinzman, L.D.; Bettez, N.D.; Bolton, W.R.; Chapin, F.S.; Dyurgerov, M.B.; Fastie, C.L.; Griffith, B.; Hollister, R.D.; Hope, A.; Huntington, H.P. Evidence and implications of recent climate change in northern Alaska and other Arctic regions. Clim. Change 2005, 72, 251–298. [Google Scholar] [CrossRef]
- Kaufman, D.S.; Schneider, D.P.; McKay, N.P.; Ammann, C.M.; Bradley, R.S.; Briffa, K.R.; Miller, G.H.; Otto-Bliesner, B.L.; Overpeck, J.T.; Vinther, B.M. Recent warming reverses long-term Arctic cooling. Science 2009, 325, 1236–1239. [Google Scholar] [CrossRef]
- Ruckstuhl, K.E.; Johnson, E.A.; Miyanishi, K. Introduction. The boreal forest and global change. Philos. Trans. R. Soc. B Biol. Sci. 2008, 363, 2243–2247. [Google Scholar] [CrossRef] [PubMed]
- Baulch, H.; Schindler, D.; Turner, M.; Findlay, D.; Paterson, M.; Vinebrooke, R. Effects of warming on benthic communities in a boreal lake: Implications of climate change. Limnol. Oceanogr. 2005, 50, 1377–1392. [Google Scholar] [CrossRef]
- Guzzo, M.M.; Blanchfield, P.J. Climate change alters the quantity and phenology of habitat for lake trout (Salvelinus na- maycush) in small boreal shield lakes. Can. J. Fish. Aquat. Sci. 2017, 74, 871–884. [Google Scholar] [CrossRef]
- Schindler, D.W.; Bayley, S.E.; Parker, B.R.; Beaty, K.G.; Cruikshank, D.R.; Fee, E.J.; Schindler, E.U.; Stainton, M.P. The effects of climatic warming on the properties of boreal lakes and streams at the Experimental Lakes Area, Northwestern Ontario. Limnol. Oceanogr. 1996, 41, 1004–1017. [Google Scholar] [CrossRef]
- Findlay, D.; Kasian, S.; Stainton, M.; Beaty, K.; Lyng, M. Climatic influences on algal populations of boreal forest lakes in the Experimental Lakes Area. Limnol. Oceanogr. 2001, 46, 1784–1793. [Google Scholar] [CrossRef]
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Choulga, M.; Kourzeneva, E.; Zakharova, E.; Doganovsky, A. Estimation of the mean depth of boreal lakes for use in numerical weather prediction and climate modelling. Tellus A: Dyn. Meteorol. Oceanogr. 2014, 66, 21295. [Google Scholar]
- Lehner, B.; Anand, M.; Fluet-Chouinard, E.; Tan, F.; Aires, F.; Allen, G.H.; Bousquet, P.; Canadell, J.G.; Davidson, N.; Finlayson, C.M. Mapping the world’s inland surface waters: An update to the global lakes and wetlands database (GLWD v2). Earth Syst. Sci. Data Discuss. 2024, 1–49. [Google Scholar]
- Lehner, B.; Döll, P. Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geostatistical approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef]
- Verpoorter, C.; Kutser, T.; Seekell, D.A.; Tranvik, L.J. A global inventory of lakes based on high-resolution satellite imagery. Geophys. Res. Lett. 2014, 41, 6396–6402. [Google Scholar] [CrossRef]
- Arst, H.; Erm, A.J.; Herlevi, A.; Kutser, T.; Leppäranta, M.; Reinart, A.; Virta, J. Optical properties of boreal lake waters in Finland and Estonia. BER 2008, 13, 133–158. [Google Scholar]
- Ripoll, J.; Nieto-Vesperinas, M.; Arridge, S.R.; Dehghani, H. Boundary conditions for light propagation in diffusive media with nonscattering regions. J. Opt. Soc. Am. A 2000, 17, 1671–1681. [Google Scholar] [CrossRef]
- Arridge, S.R.; Dehghani, H.; Schweiger, M.; Okada, E. The finite element model for the propagation of light in scattering media: A direct method for domains with nonscattering regions. Med. Phys. 2000, 27, 252–264. [Google Scholar] [CrossRef] [PubMed]
- Martelli, F.; Contini, D.; Taddeucci, A.; Zaccanti, G. Photon migration through a turbid slab described by a model based on diffusion approximation. II. Comparison with Monte Carlo results. Appl. Opt. 1997, 36, 4600–4612. [Google Scholar] [CrossRef] [PubMed]
- Hielscher, A.H.; Alcouffe, R.E.; Barbour, R.L. Comparison of finite-difference transport and diffusion calculations for photon migration in homogeneous and heterogeneous tissues. Phys. Med. Biol. 1998, 43, 1285. [Google Scholar] [CrossRef]
- Custo, A.; Wells, W.M.; Barnett, A.H.; Hillman, E.M.; Boas, D.A. Effective scattering coefficient of the cerebral spinal fluid in adult head models for diffuse optical imaging. Appl. Opt. 2006, 45, 4747–4755. [Google Scholar] [CrossRef] [PubMed]
- Ma, G.; Delorme, J.-F.; Gallant, P.; Boas, D.A. Comparison of simplified Monte Carlo simulation and diffusion approximation for the fluorescence signal from phantoms with typical mouse tissue optical properties. Appl. Opt. 2007, 46, 1686–1692. [Google Scholar] [CrossRef]
- Martinelli, M.; Gardner, A.; Cuccia, D.; Hayakawa, C.; Spanier, J.; Venugopalan, V. Analysis of single Monte Carlo methods for prediction of reflectance from turbid media. Opt. Express 2011, 19, 19627–19642. [Google Scholar] [CrossRef]
- Ren, X.; Chen, H.; Wang, X.; Qu, G.; Wang, J.; Liang, J.; Tian, J. Molecular optical simulation environment (MOSE): A platform for the simulation of light propagation in turbid media. PLoS ONE 2013, 8, e61304. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Wang, G. A tetrahedron-based inhomogeneous Monte Carlo optical simulator. Phys. Med. Biol. 2010, 55, 947. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Wilson, B.C.; Adam, G. A Monte Carlo model for the absorption and flux distributions of light in tissue. Med. Phys. 1983, 10, 824–830. [Google Scholar] [CrossRef]
- Arridge, S.; Schweiger, M.; Hiraoka, M.; Delpy, D. A finite element approach for modeling photon transport in tissue. Med. Phys. 1993, 20, 299–309. [Google Scholar] [CrossRef] [PubMed]
- Ajmal, A.; Boonya-Ananta, T.; Rodriguez, A.J.; Le, V.D.; Ramella-Roman, J.C. Monte Carlo analysis of optical heart rate sensors in commercial wearables: The effect of skin tone and obesity on the photoplethysmography (PPG) signal. Biomed. Opt. Express 2021, 12, 7445–7457. [Google Scholar] [CrossRef] [PubMed]
- Le, V.D.; Wang, Q.; Gould, T.; Ramella-Roman, J.C.; Pfefer, T.J. Vascular contrast in narrow-band and white light imaging. Appl. Opt. 2014, 53, 4061–4071. [Google Scholar]
- Le, V.N.; Srinivasan, V.J. Beyond diffuse correlations: Deciphering random flow in time-of-flight resolved light dynamics. Opt. Express 2020, 28, 11191–11214. [Google Scholar]
- Le, V.N.; Wang, Q.; Ramella-Roman, J.C.; Pfefer, T.J. Monte Carlo modeling of light-tissue interactions in narrow band imag- ing. J. Biomed. Opt. 2012, 18, 010504. [Google Scholar] [CrossRef]
- Wang, Q.; Le, V.N.; Ramella-Roman, J.; Pfefer, J. Broadband ultraviolet-visible optical property measurement in layered turbid media. Biomed. Opt. Express 2012, 3, 1226–1240. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Liu, Q. Review of Monte Carlo modeling of light transport in tissues. J. Biomed. Opt. 2013, 18, 050902. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Boas, D.A. Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units. Opt. Express 2009, 17, 20178–20190. [Google Scholar] [CrossRef]
- Yan, S.; Fang, Q. Hybrid mesh and voxel-based Monte Carlo algorithm for accurate and efficient photon transport modeling in complex bio-tissues. Biomed. Opt. Express 2020, 11, 6262–6270. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Nina-Paravecino, F.; Kaeli, D.; Fang, Q. Scalable and massively parallel Monte Carlo photon transport simulations for heterogeneous computing platforms. J. Biomed. Opt. 2018, 23, 010504. [Google Scholar] [CrossRef]
- Yuan, Y.; Yu, L.; Doğan, Z.; Fang, Q. Graphics processing units-accelerated adaptive nonlocal means filter for denoising three- dimensional Monte Carlo photon transport simulations. J. Biomed. Opt. 2018, 23, 121618. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Yan, S. Graphics processing unit-accelerated mesh-based Monte Carlo photon transport simulations. J. Biomed. Opt. 2019, 24, 115002. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Jeong, S.; Lee, J.-H.; Sun, W.; Choi, N.; Cho, I.-J. 3D high-density microelectrode array with optical stimulation and drug delivery for investigating neural circuit dynamics. Nat. Commun. 2021, 12, 492. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, T.; Takikawa, Y.; Kawagoe, R.; Shibuya, S.; Iwano, T.; Kitazawa, S. Influence of skin blood flow on near-infrared spectroscopy signals measured on the forehead during a verbal fluency task. Neuroimage 2011, 57, 991–1002. [Google Scholar] [CrossRef] [PubMed]
- Vasung, L.; Turk, E.A.; Ferradal, S.L.; Sutin, J.; Stout, J.N.; Ahtam, B.; Lin, P.-Y.; Grant, P.E. Exploring early human brain development with structural and physiological neuroimaging. Neuroimage 2019, 187, 226–254. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Son, Y.; Chae, U.; Kim, J.; Choi, N.; Lee, H.J.; Woo, J.; Cho, Y.; Yang, S.H.; Lee, C.J. Multifunctional multi-shank neural probe for investigating and modulating long-range neural circuits in vivo. Nat. Commun. 2019, 10, 3777. [Google Scholar] [CrossRef]
- Saloranta, T.M.; Andersen, T. MyLake—A multi-year lake simulation model code suitable for uncertainty and sensitivity anal- ysis simulations. Ecol. Model. 2007, 207, 45–60. [Google Scholar] [CrossRef]
- Vachon, D.; Lapierre, J.F.; Del Giorgio, P.A. Seasonality of photochemical dissolved organic carbon mineralization and its relative contribution to pelagic CO2 production in northern lakes. J. Geophys. Res. Biogeosci. 2016, 121, 864–878. [Google Scholar] [CrossRef]
- Grosbois, G.; Del Giorgio, P.A.; Rautio, M. Zooplankton allochthony is spatially heterogeneous in a boreal lake. Freshwater Biol. 2017, 62, 474–490. [Google Scholar] [CrossRef]
- Hastie, A.; Lauerwald, R.; Weyhenmeyer, G.; Sobek, S.; Verpoorter, C.; Regnier, P. CO2 evasion from boreal lakes: Revised estimate, drivers of spatial variability, and future projections. Global Change Biol. 2018, 24, 711–728. [Google Scholar] [CrossRef] [PubMed]
- Wolf, R.; Thrane, J.-E.; Hessen, D.O.; Andersen, T. Modelling ROS formation in boreal lakes from interactions between dis- solved organic matter and absorbed solar photon flux. Water Res. 2018, 132, 331–339. [Google Scholar] [CrossRef] [PubMed]
- Allesson, L.; Koehler, B.; Thrane, J.E.; Andersen, T.; Hessen, D.O. The role of photomineralization for CO2 emissions in boreal lakes along a gradient of dissolved organic matter. Limnol. Oceanogr. 2021, 66, 158–170. [Google Scholar] [CrossRef]
- Street-Perrott, F.A.; Holmes, J.A.; Robertson, I.; Ficken, K.J.; Koff, T.; Loader, N.J.; Marshall, J.D.; Martma, T. The Holocene isotopic record of aquatic cellulose from lake Äntu Sinijärv, Estonia: Influence of changing climate and organic-matter sources. Quat. Sci. Rev. 2018, 193, 68–83. [Google Scholar] [CrossRef]
- Tönno, I.; Kirsi, A.-L.; Freiberg, R.; Alliksaar, T.; Lepane, V.; Koiv, T.; Kisand, A.; Heinsalu, A. Ecosystem changes in large and shallow Vörtsjärv, a lake in Estonia—Evidence from sediment pigments and phosphorus fractions. Boreal Environ. Res. 2013, 18, 1–16. [Google Scholar]
- Karjalainen, L.; Kuuluvainen, T. Amount and diversity of coarse woody debris within a boreal forest landscape dominated by Pinus sylvestris in Vienansalo Wilderness, Eastern Fennoscandia. Silva Fenn. 2002, 36, 147–167. [Google Scholar] [CrossRef]
- Siitonen, J. Forest management, coarse woody debris and saproxylic organisms: Fennoscandian boreal forests as an example. Ecol. Bull. 2001, 11–41. [Google Scholar]
- Sippola, A.L.; Siitonen, J.; Kallio, R. Amount and quality of coarse woody debris in natural and managed coniferous forests near the timberline in Finnish Lapland. Scand. J. Forest Res. 1998, 13, 204–214. [Google Scholar] [CrossRef]
- Hecht, E. Optics; Addison-Wesley: Boston, MA, USA, 2001. [Google Scholar]
- Gordon, H.R.; Morel, A. In-water algorithms. In Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery: A Review; Springer: New York, NY, USA, 1983; pp. 24–67. [Google Scholar]
- Morel, A. Optics of marine particles and marine optics. In Particle Analysis in Oceanography; Springer: Berlin/Heidelberg, Germany, 1991; pp. 141–188. [Google Scholar]
- Hale, G.M.; Querry, M.R. Optical constants of water in the 200-nm to 200-μm wavelength region. Appl. Opt. 1973, 12, 555–563. [Google Scholar] [CrossRef]
- Cuccia, D.J.; Bevilacqua, F.; Durkin, A.J.; Ayers, F.R.; Tromberg, B.J. Quantitation and mapping of tissue optical properties using modulated imaging. J. Biomed. Opt. 2009, 14, 024012–024013. [Google Scholar] [CrossRef]
- O’Sullivan, T.D.; Cerussi, A.E.; Cuccia, D.J.; Tromberg, B.J. Diffuse optical imaging using spatially and temporally modulated light. J. Biomed. Opt. 2012, 17, 071311. [Google Scholar] [CrossRef] [PubMed]
- Le, V.N.; Manser, M.; Gurm, S.; Wagner, B.; Hayward, J.E.; Fang, Q. Calibration of spectral imaging devices with oxygenation-controlled phantoms: Introducing a simple gel-based hemoglobin model. Front. Phys. 2019, 7, 192. [Google Scholar] [CrossRef]
- Le, V.N.; Provias, J.; Murty, N.; Patterson, M.S.; Nie, Z.; Hayward, J.E.; Farrell, T.J.; McMillan, W.; Zhang, W.; Fang, Q. Dual-modality optical biopsy of glioblastomas multiforme with diffuse reflectance and fluorescence: Ex vivo retrieval of optical prop- erties. J. Biomed. Opt. 2017, 22, 27002. [Google Scholar]
- Mobley, C.D.; Gentili, B.; Gordon, H.R.; Jin, Z.; Kattawar, G.W.; Morel, A.; Reinersman, P.; Stamnes, K.; Stavn, R.H. Compar- ison of numerical models for computing underwater light fields. Appl. Opt. 1993, 32, 7484–7504. [Google Scholar] [CrossRef] [PubMed]
- Beechie, T.J.; Sibley, T.H. Relationships between channel characteristics, woody debris, and fish habitat in northwestern Wash- ington streams. Trans. Am. Fish. Soc. 1997, 126, 217–229. [Google Scholar] [CrossRef]
- Bilby, R.E.; Bisson, P.A. Function and distribution of large woody debris. River Ecol. Manag. 1998, 324, 324. [Google Scholar]
- Ehrman, T.P.; Lamberti, G.A. Hydraulic and particulate matter retention in a 3rd-order Indiana stream. J. N. Am. Benthol. Soc. 1992, 11, 341–349. [Google Scholar] [CrossRef]
- D’Andrea, C.; Farina, A.; Comelli, D.; Pifferi, A.; Taroni, P.; Valentini, G.; Cubeddu, R.; Zoia, L.; Orlandi, M.; Kienle, A. Time-resolved optical spectroscopy of wood. Appl. Spectrosc. 2008, 62, 569–574. [Google Scholar] [CrossRef]
- Allisy-Roberts, P.J.; Williams, J. Farr’s Physics for Medical Imaging; Elsevier Health Sciences: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Hari, P.; Pumpanen, J.; Huotari, J.; Kolari, P.; Grace, J.; Vesala, T.; Ojala, A. High-frequency measurements of productivity of planktonic algae using rugged nondispersive infrared carbon dioxide probes. Limnol. Oceanogr. Methods 2008, 6, 347–354. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du Le, V.N. Monte Carlo Guidance for Better Imaging of Boreal Lakes in the Wavelength Region of 400–800 nm. Sensors 2025, 25, 1020. https://doi.org/10.3390/s25041020
Du Le VN. Monte Carlo Guidance for Better Imaging of Boreal Lakes in the Wavelength Region of 400–800 nm. Sensors. 2025; 25(4):1020. https://doi.org/10.3390/s25041020
Chicago/Turabian StyleDu Le, Vinh Nguyen. 2025. "Monte Carlo Guidance for Better Imaging of Boreal Lakes in the Wavelength Region of 400–800 nm" Sensors 25, no. 4: 1020. https://doi.org/10.3390/s25041020
APA StyleDu Le, V. N. (2025). Monte Carlo Guidance for Better Imaging of Boreal Lakes in the Wavelength Region of 400–800 nm. Sensors, 25(4), 1020. https://doi.org/10.3390/s25041020





