Imbalance Fault Detection of Marine Current Turbine Based on GLRT Detector
Abstract
1. Introduction
2. Imbalance Fault Model
2.1. Influence of Wave and Turbulence
2.2. Influence of Blade Imbalance on the Stator Current
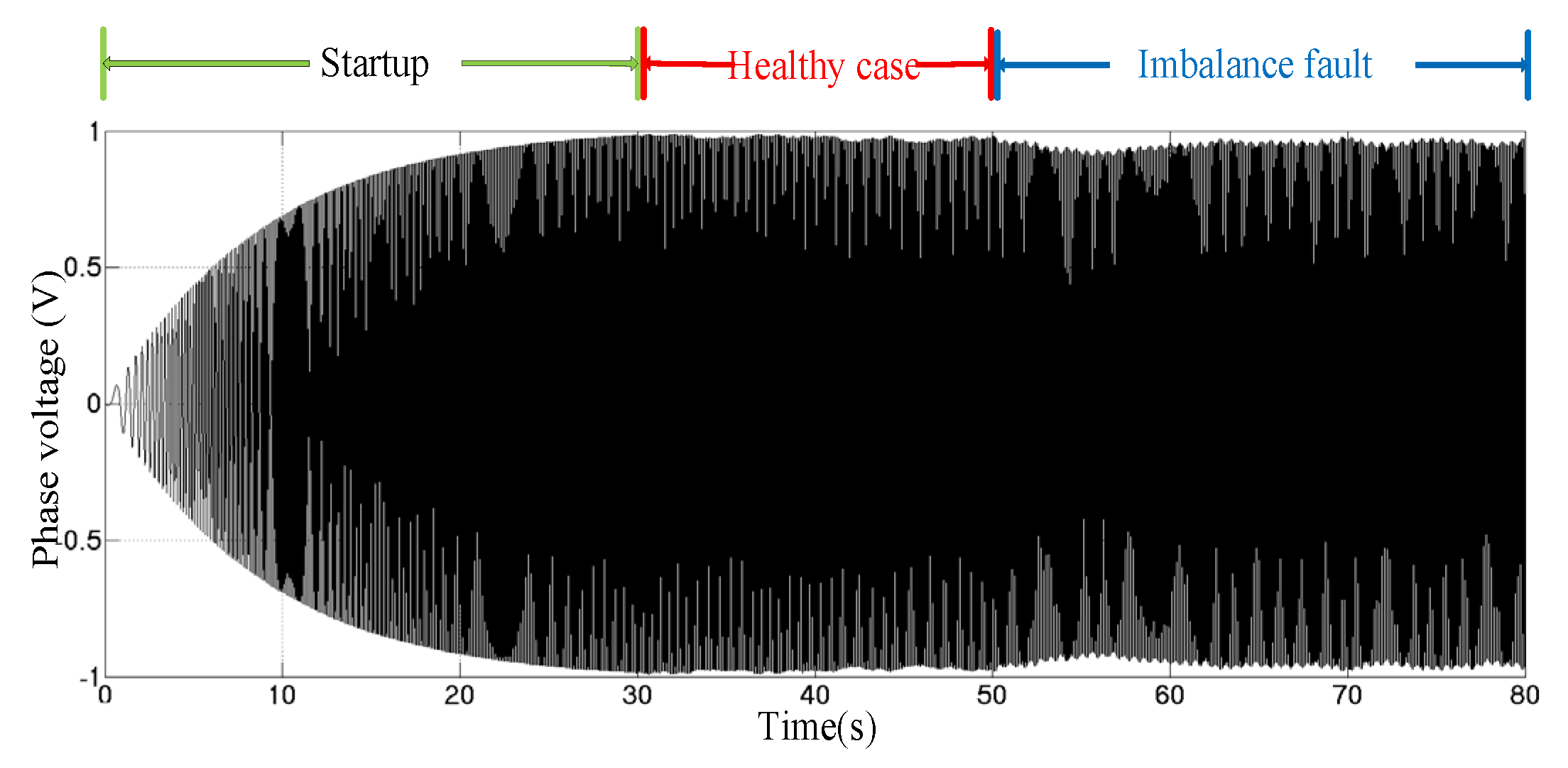
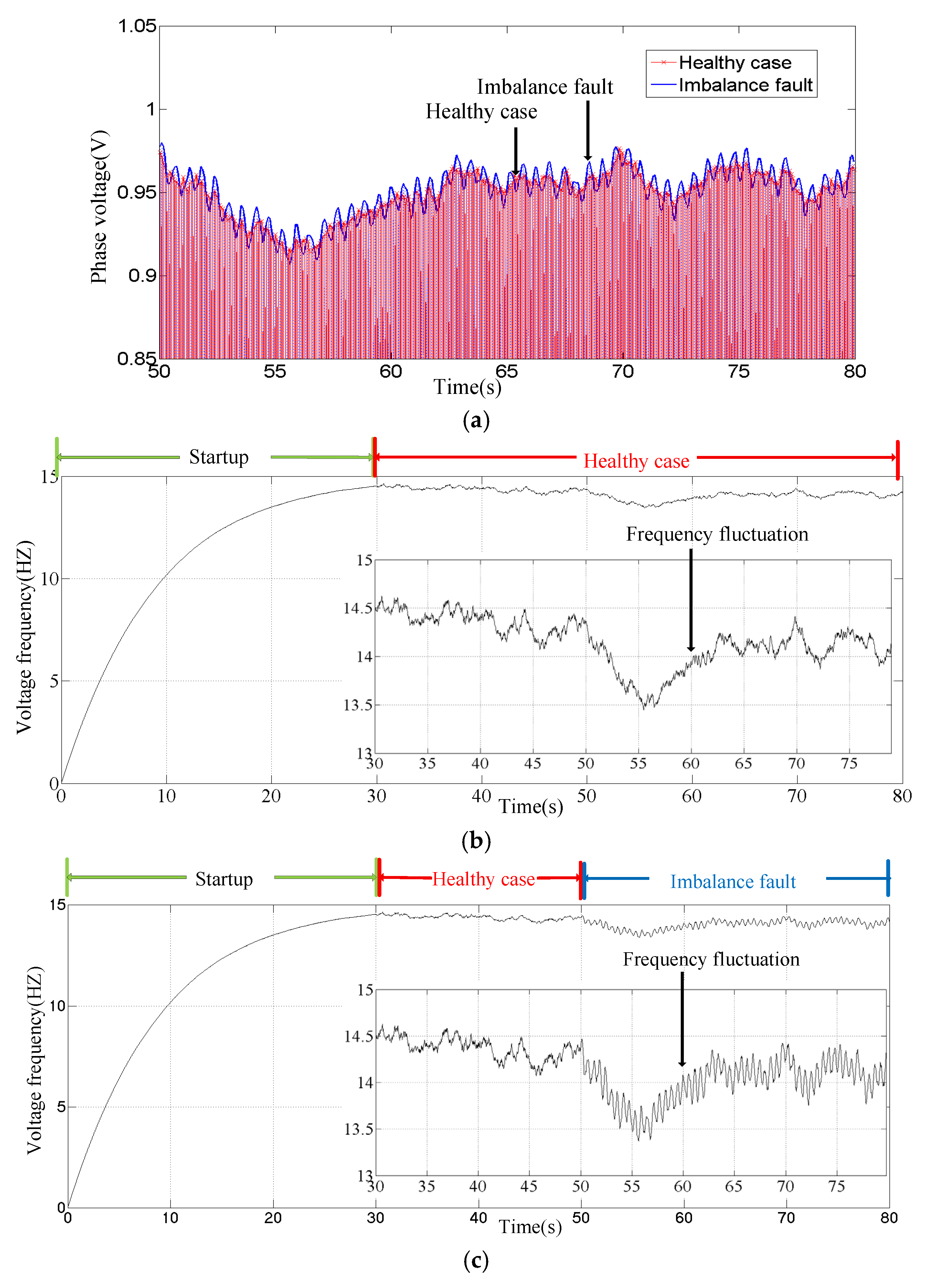
2.3. Simulation Results
3. Fault Detection Method Based on GLRT Detector
3.1. Instantaneous Frequency Estimation Based on MPM
3.2. GLRT Detector
3.3. Data Normalization
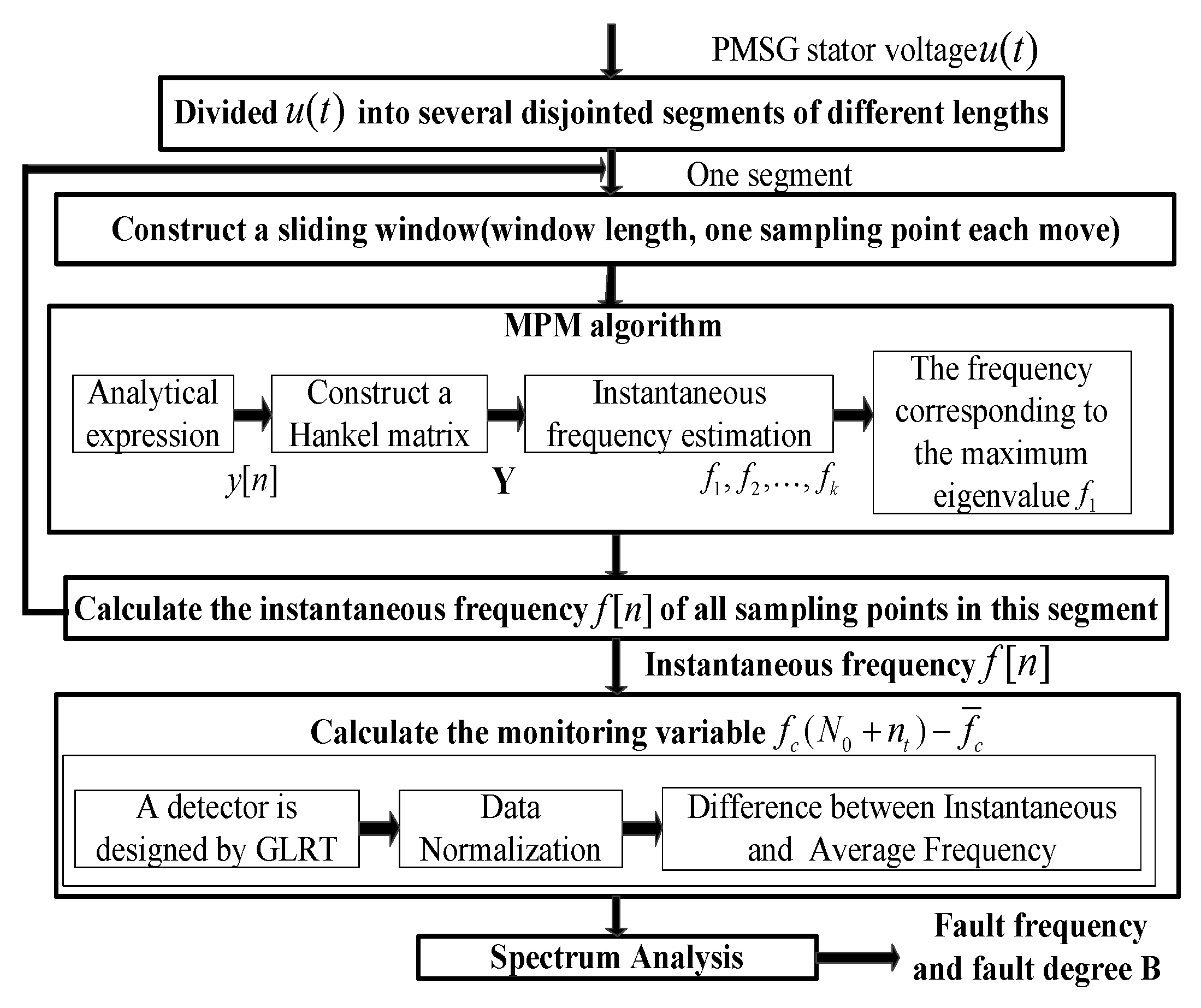
3.4. Process of Fault Detection
- (1)
- It starts with the non-stationary stator voltage signal of length Zero crossing points or extreme points are found to determine the breaking points of The data length is the number of samples in an integer number of mechanical cycles.
- (2)
- The instantaneous frequency is calculated by MPM. The data begin with and end with where is the length of the segment including
- (3)
- The instantaneous frequency is normalized by (28), and the monitoring variable is calculated by (29). The variable is used to measure the fault degree.
- (4)
- The power spectral density of the monitoring variable is analyzed to detect the fault characteristic frequency.
4. Experimental Design and Analysis
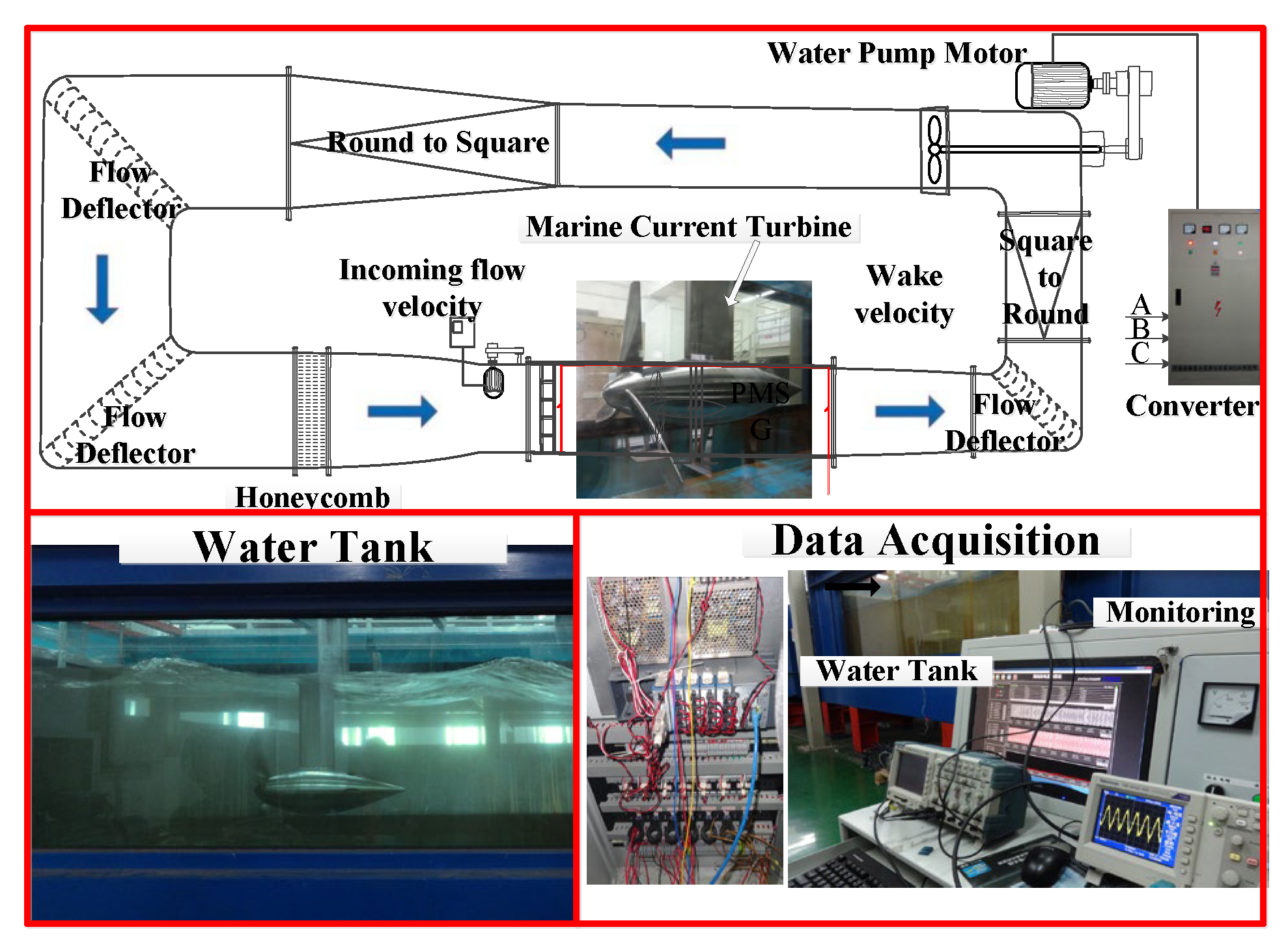
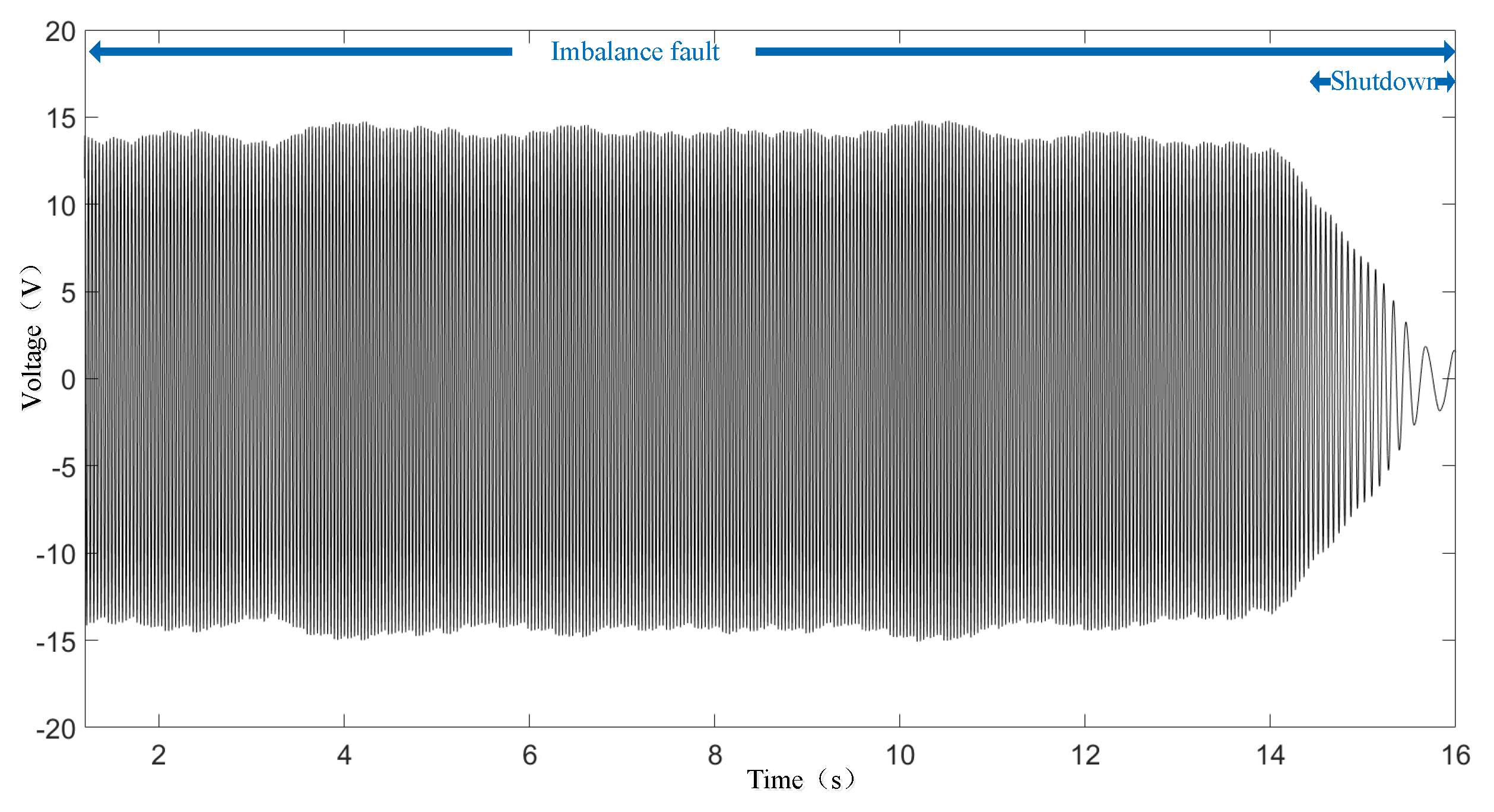
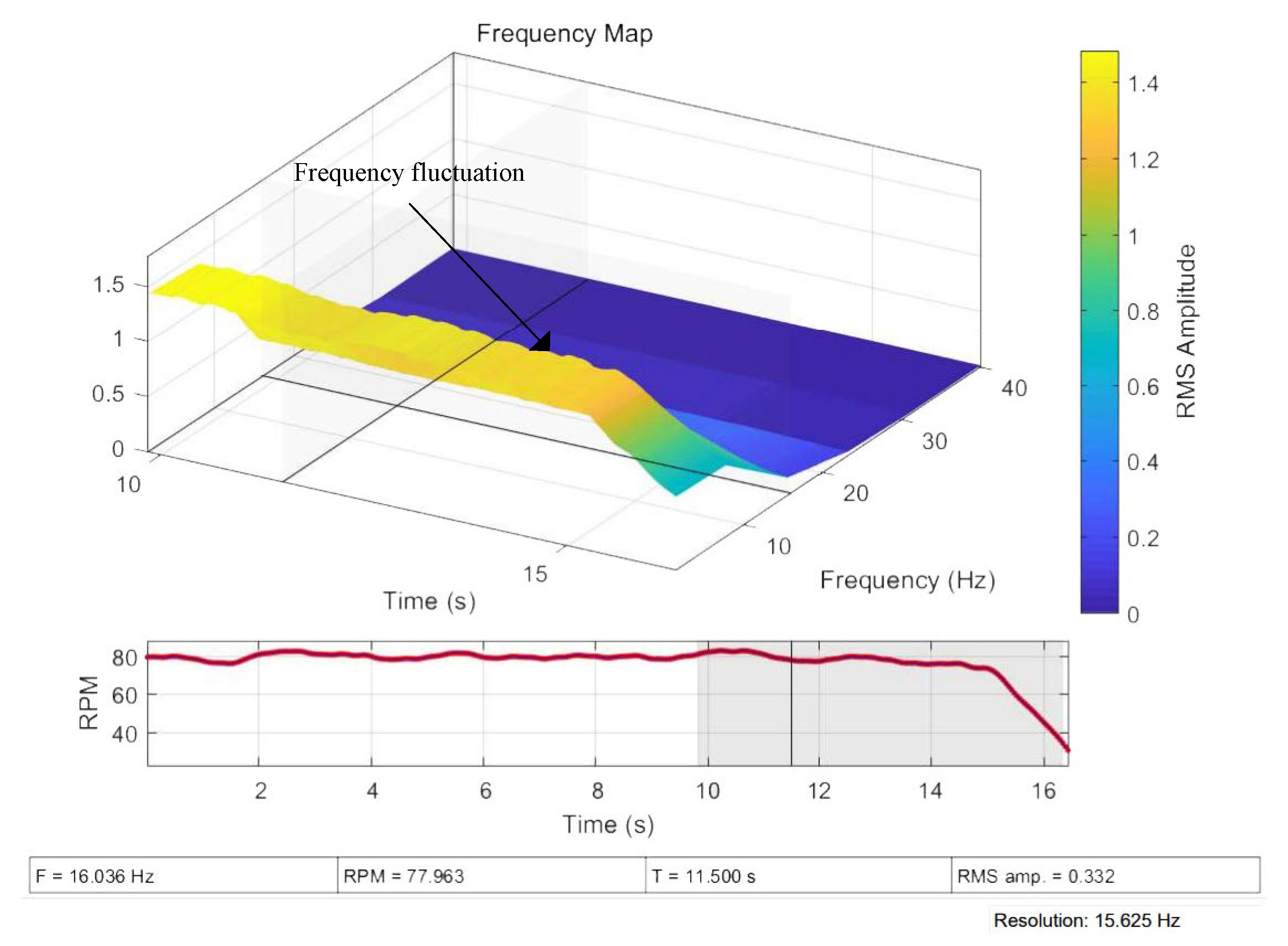
4.1. Experiment System Setup
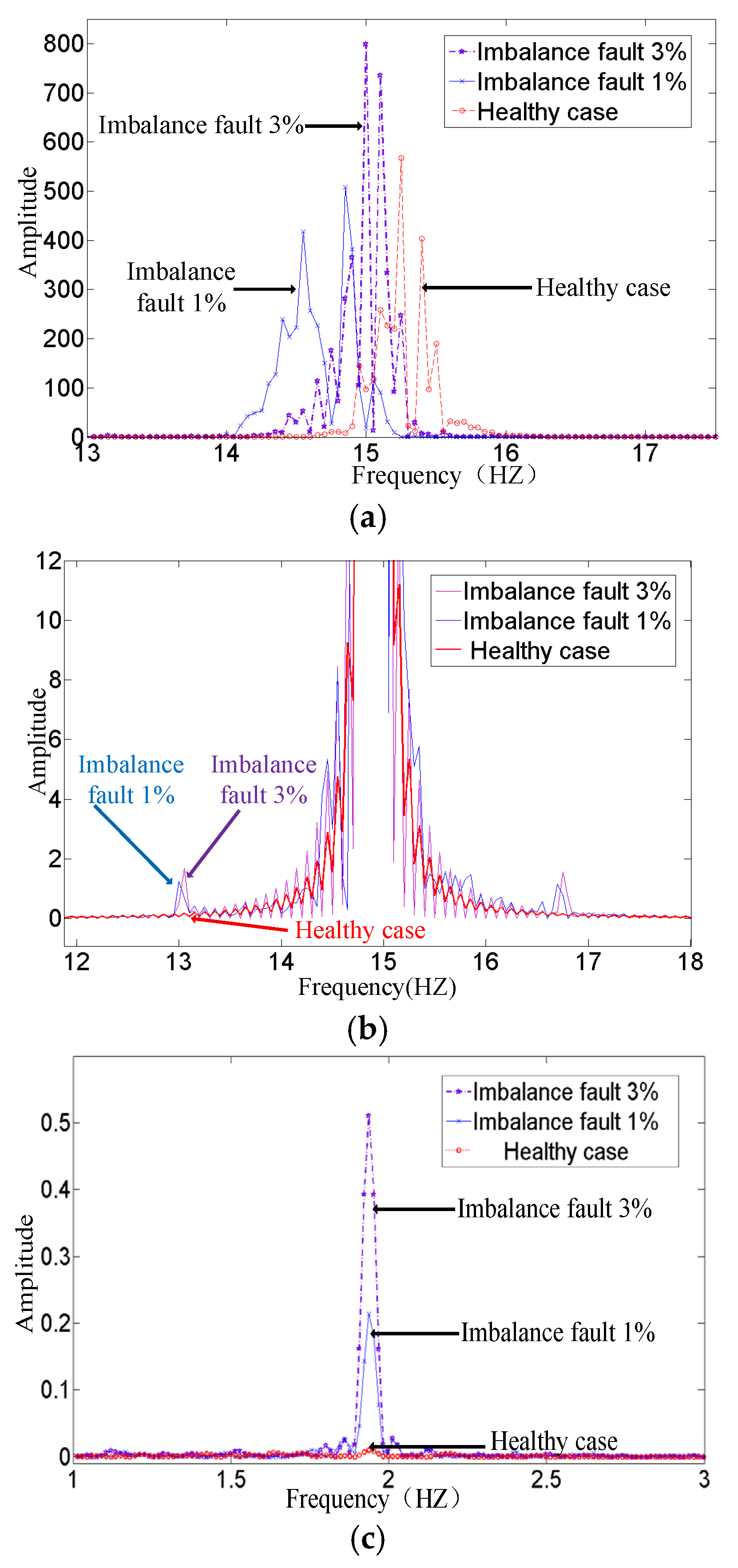
4.2. Fault Detection Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Q.K.; Liu, H.W.; Lin, Y.G.; Yin, X.X.; Li, W.; Gu, Y.J. Development and experiment of a 60 kW horizontal-axis marine current power system. Energy 2015, 88, 149–156. [Google Scholar] [CrossRef]
- Guy, C.; Hart, E.; Vengatesan, V.; Forehand, D. Numerical modeling of a 1.5 MW tidal turbine in realistic coupled wave–current sea states for the assessment of turbine hub-depth impacts on mechanical loads. Ocean Eng. 2024, 292, 116577. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, T.; Tang, T.; Liu, Z.; Claramunt, C. A Synchronous Sampling Based Harmonic Analysis Strategy for Marine Current Turbine Monitoring System under Strong Interference Conditions. Energies 2019, 12, 2117. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, F.; Tang, T. A Mechanical Impact Fault Detection Method Based on PCA for Marine Current Turbine. In Proceedings of the2021 CAA Symposium on Fault Detection, Supervision, and Safety for Technical Processes (SAFEPROCESS), Chengdu, China, 17–18 December 2021; pp. 1–5. [Google Scholar]
- Gao, Y.; Liu, H.; Guo, G.; Lin, Y.; Gu, Y.; Ni, Y. Effect of capitation evolution on power characteristics of tidal current turbine. Phys. Fluids 2023, 35, 307–312. [Google Scholar] [CrossRef]
- Mei, Y.; Jing, F.; Lu, Q.; Guo, B. Experimental study on power characteristics of a horizontal-axis tidal turbine under pitch motion. Ocean Eng. 2024, 307, 118184. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, T.; Tang, T.; Benbouzid, M.; Diallo, D. An imbalance fault detection method based on data normalization and EMD for marine current turbines. ISA Trans. 2017, 68, 302–312. [Google Scholar] [CrossRef]
- Habbouche, H.; Rashid, H.; Amirat, Y.; Banerjee, A.; Benbouzid, M. A 2D VMD video image processing-based transfer learning approach for the detection and estimation of biofouling in tidal stream turbines. Ocean Eng. 2024, 312, 10–21. [Google Scholar] [CrossRef]
- Rashid, H.; Habbouche, H.; Amirat, Y.; Mamoune, A.; Titah-Benbouzid, H.; Benbouzid, M. B-FLOWS: Biofouling Focused Learning and Observation for Wide-Area Surveillance in Tidal Stream Turbines. J. Mar. Sci. Eng. 2024, 12, 1828. [Google Scholar] [CrossRef]
- Rashid, H.; Benbouzid, M.; Titah-Benbouzid, H.; Amirat, Y.; Mamoune, A. Tidal Stream Turbine Biofouling Detection and Estimation: A Review-Based Roadmap. J. Mar. Sci. Eng. 2023, 11, 908. [Google Scholar] [CrossRef]
- Yang, W.; Tavner, P.J.; Court, R. An online technique for condition monitoring the induction generators used in wind and marine turbines. Mech. Syst. Signal Process. 2013, 38, 103–112. [Google Scholar] [CrossRef]
- Diken, H.; Asiri, S. Vibration Analysis of Horizontal Axis Wind Turbine Considering Tower-Nacelle-Foundation Interaction. J. Vib. Eng. Technol. 2024, 12, 27–32. [Google Scholar] [CrossRef]
- He, D.; Zhang, Z.; Jin, Z.; Zhang, F.; Yi, C.; Liao, S. RTSMFFDE-HKRR: A fault diagnosis method for train bearing in noise environment. Measurement 2025, 239, 115417. [Google Scholar] [CrossRef]
- Touti, W.; Salah, M.; Bacha, K.; Chaari, A. Condition monitoring of a wind turbine drivetrain based on generator stator current processing. ISA Trans. 2022, 128, 650–664. [Google Scholar] [CrossRef] [PubMed]
- Issaadi, I.; Hemsas, K.E.; Soualhi, A. Wind Turbine Gearbox Diagnosis Based on Stator Current. Energies 2023, 16, 5286. [Google Scholar] [CrossRef]
- Sandoval, S.; Leon, P.D. Recasting the (Synchro squeezed) Short-Time Fourier Transform as an Instantaneous Spectrum. Entropy 2022, 24, 518. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, D.; Zhang, R.; Li, W. A Method for Detecting LDoS Attacks in SDWSN Based on Compressed Hilbert–Huang Transform and Convolutional Neural Networks. Sensors 2023, 23, 4745. [Google Scholar] [CrossRef]
- Mansourlakouraj, M.; Hosseinpour, H.; Livani, H.; Benidris, M. Waveform Measurement Unit-Based Fault Location in Distribution Feeders via Short-Time Matrix Pencil Method and Graph Neural Network. IEEE Trans. Ind. Appl. 2023, 9, 86–96. [Google Scholar] [CrossRef]
- Wang, L.; Lin, Y.F.; Lo, T.M. Implementation and Measurements of a Prototype Marine-Current Power Generation System on Peng-Hu Island. IEEE Trans. Ind. Appl. 2015, 51, 651–657. [Google Scholar] [CrossRef]
- Zhao, H.; Niu, G. Enhanced order spectrum analysis based on iterative adaptive crucial mode decomposition for planetary gearbox fault diagnosis under large speed variations. Mech. Syst. Signal Process. 2023, 185, 498–509. [Google Scholar] [CrossRef]
- Gong, X.; Qiao, W. Current-Based Mechanical Fault Detection for Direct-Drive Wind Turbines via Synchronous Sampling and Impulse Detection. IEEE Trans. Ind. Electron. 2015, 62, 1693–1702. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, W.; Liu, J.; Dai, L.; Fang, X.; Ge, J. Adaptive radar detection of subspace-based distributed target in power heterogeneous clutter. IEEE Sens. J. 2024, 10, 34–40. [Google Scholar] [CrossRef]
- Hua, Y.; Sarkar, T.K. Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 814–824. [Google Scholar] [CrossRef]






| Turbine | Parameter | Generator | Parameter |
|---|---|---|---|
| Airfoil | Naca0018 | Pole-pair | 8 |
| Pitch angle | 3.4–25.2 deg | Flux | 0.1775 Wb |
| Chord length | 5.68–9.6 cm | Resistance | 3.3 |
| Blade diameter | 0.6 m | d axis inductance | 11.873 mH |
| Water density | 1024 kg/m3 | q axis inductance | 11.873 mH |
| Water velocity | 1.1 m/s | Total inertia | 3.5 kg m2 |
| radial position (r/) | 0.178 | 0.292 | 0.405 | 0.518 | 0.632 | 0.745 | 0.858 | 0.972 |
| Pitch Angle (deg) | 25.23 | 17.83 | 13.70 | 10.85 | 8.61 | 6.71 | 5.02 | 3.47 |
| Chord length (cm) | 9.60 | 9.50 | 9.24 | 8.84 | 8.28 | 7.56 | 6.70 | 5.68 |
| Fault Degree | Average Value B (Measured Under Stable Flow Conditions) | Relative Error of MPM | Relative Error of STFT | Relative Error of HT |
|---|---|---|---|---|
| 0% | 0.007 | 0.211% | 1.032% | 1.725% |
| 1% | 0.278 | 0.173% | 1.218% | 1.531% |
| 3% | 0.837 | 0.165% | 4.735% | 1.592% |
| Fault Degree | Amplitude of the Fault Component | Average Current Frequency | Load Resistance |
|---|---|---|---|
| 0% | 0.012 | 15.56 Hz | 31.5 |
| 1% | 0.104 | 15.72 Hz | 31.5 |
| 3% | 0.518 | 15.36 Hz | 31.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Chen, J.; Yang, L.; Claramunt, C. Imbalance Fault Detection of Marine Current Turbine Based on GLRT Detector. Sensors 2025, 25, 874. https://doi.org/10.3390/s25030874
Zhang M, Chen J, Yang L, Claramunt C. Imbalance Fault Detection of Marine Current Turbine Based on GLRT Detector. Sensors. 2025; 25(3):874. https://doi.org/10.3390/s25030874
Chicago/Turabian StyleZhang, Milu, Jutao Chen, Liu Yang, and Christophe Claramunt. 2025. "Imbalance Fault Detection of Marine Current Turbine Based on GLRT Detector" Sensors 25, no. 3: 874. https://doi.org/10.3390/s25030874
APA StyleZhang, M., Chen, J., Yang, L., & Claramunt, C. (2025). Imbalance Fault Detection of Marine Current Turbine Based on GLRT Detector. Sensors, 25(3), 874. https://doi.org/10.3390/s25030874










