Development of Air Quality Monitoring Systems: Balancing Infrastructure Investment and User Satisfaction Policies
Abstract
1. Introduction
2. Related Works
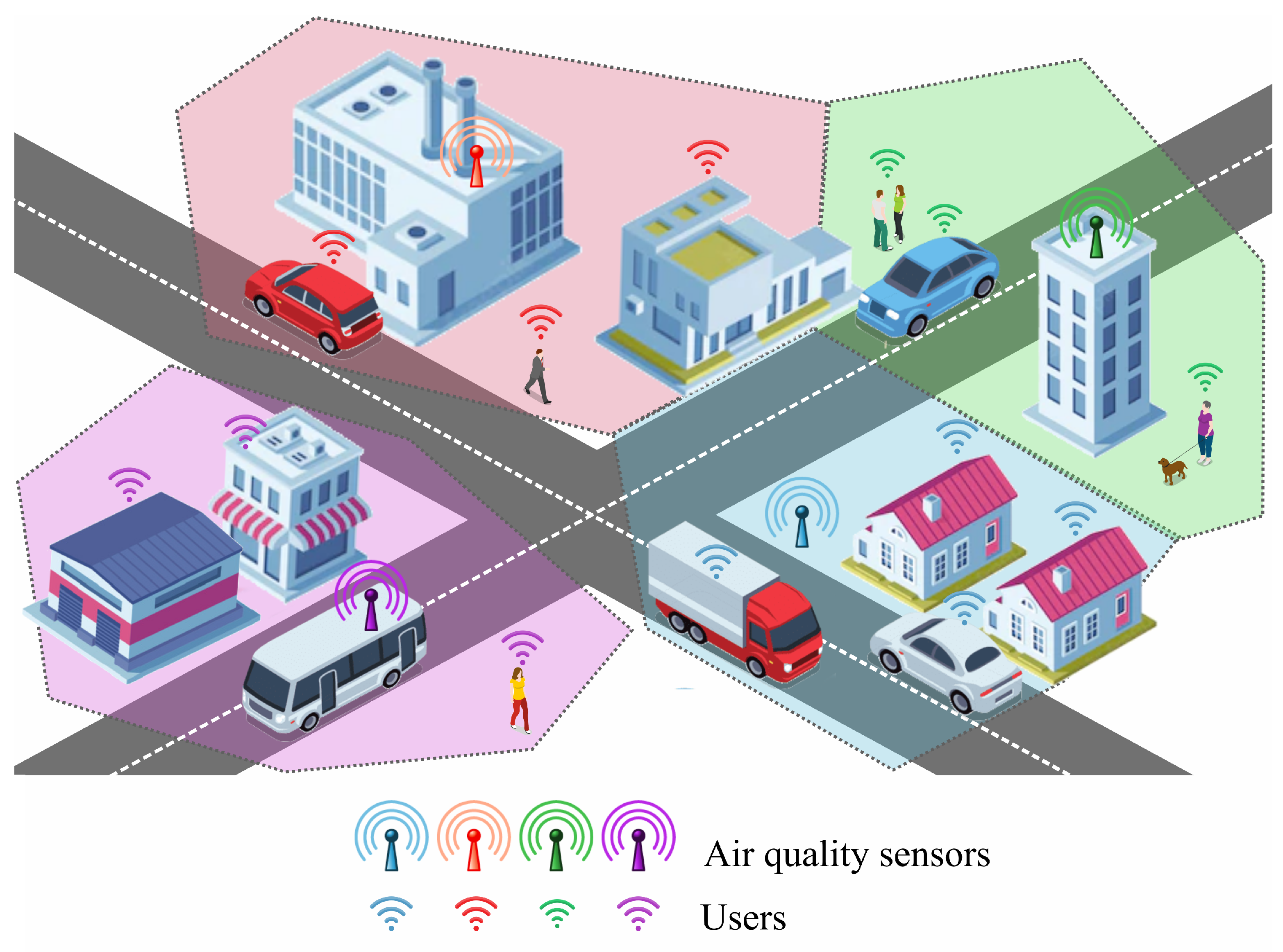
3. Methodology
- Pollution detection delay. The harm caused by a delayed response to pollution increases with the time taken for pollution detection. The delay in detecting contamination can be modeled as a random variable following an exponential distribution with a rate parameter , where characterizes the sensor’s environment and p denotes the probability of detecting air pollution at a specified false negative rate [41].
- Detection cost. The effectiveness of AI-based air pollution detection methods often correlates with their cost, as higher accuracy typically require substantial computational resources. Machine learning enables us to achieve the desired performance even with low-cost sensors [42]. However, improving detection precision involves higher operational costs for training and maintaining AI models.
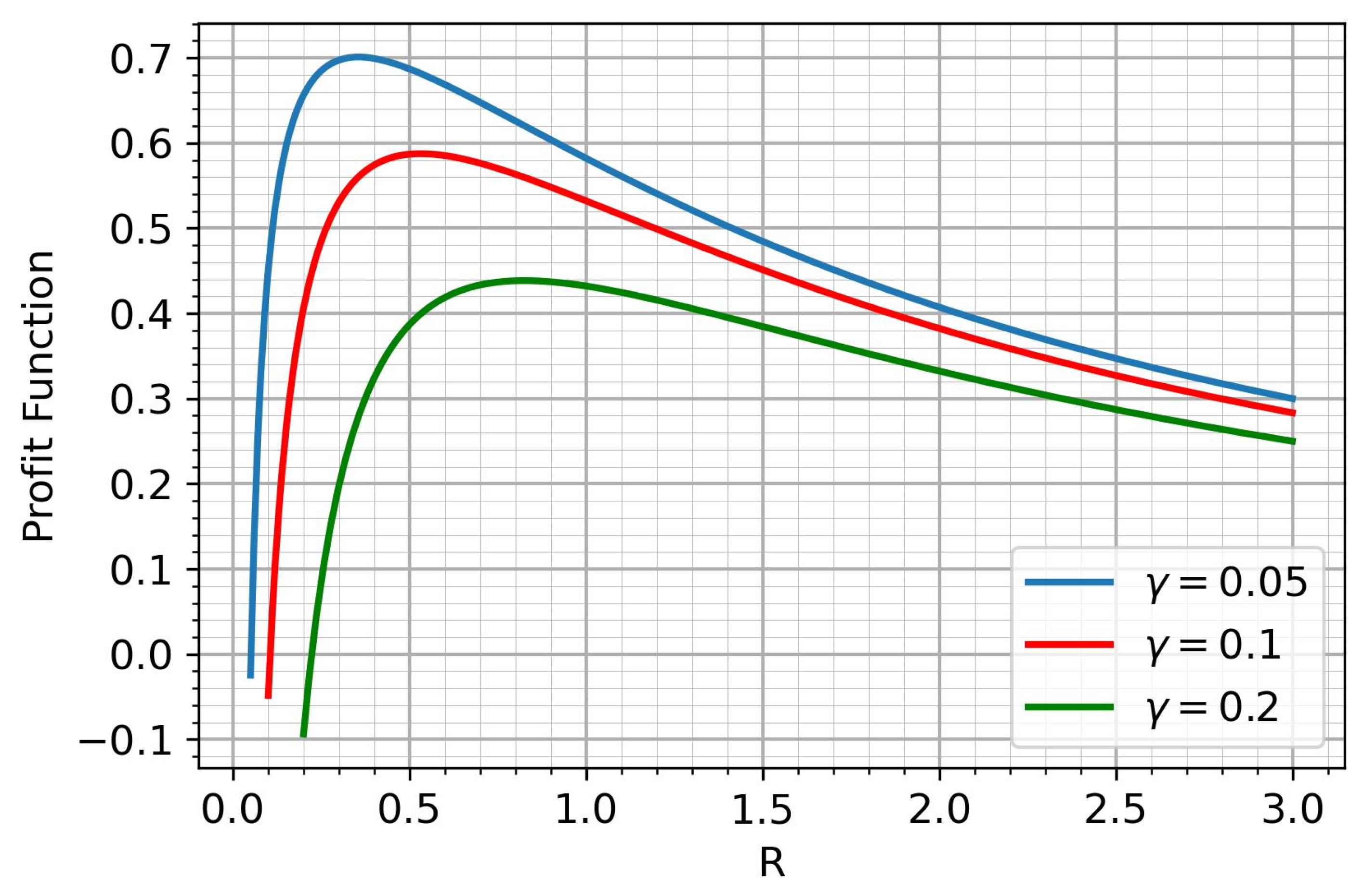
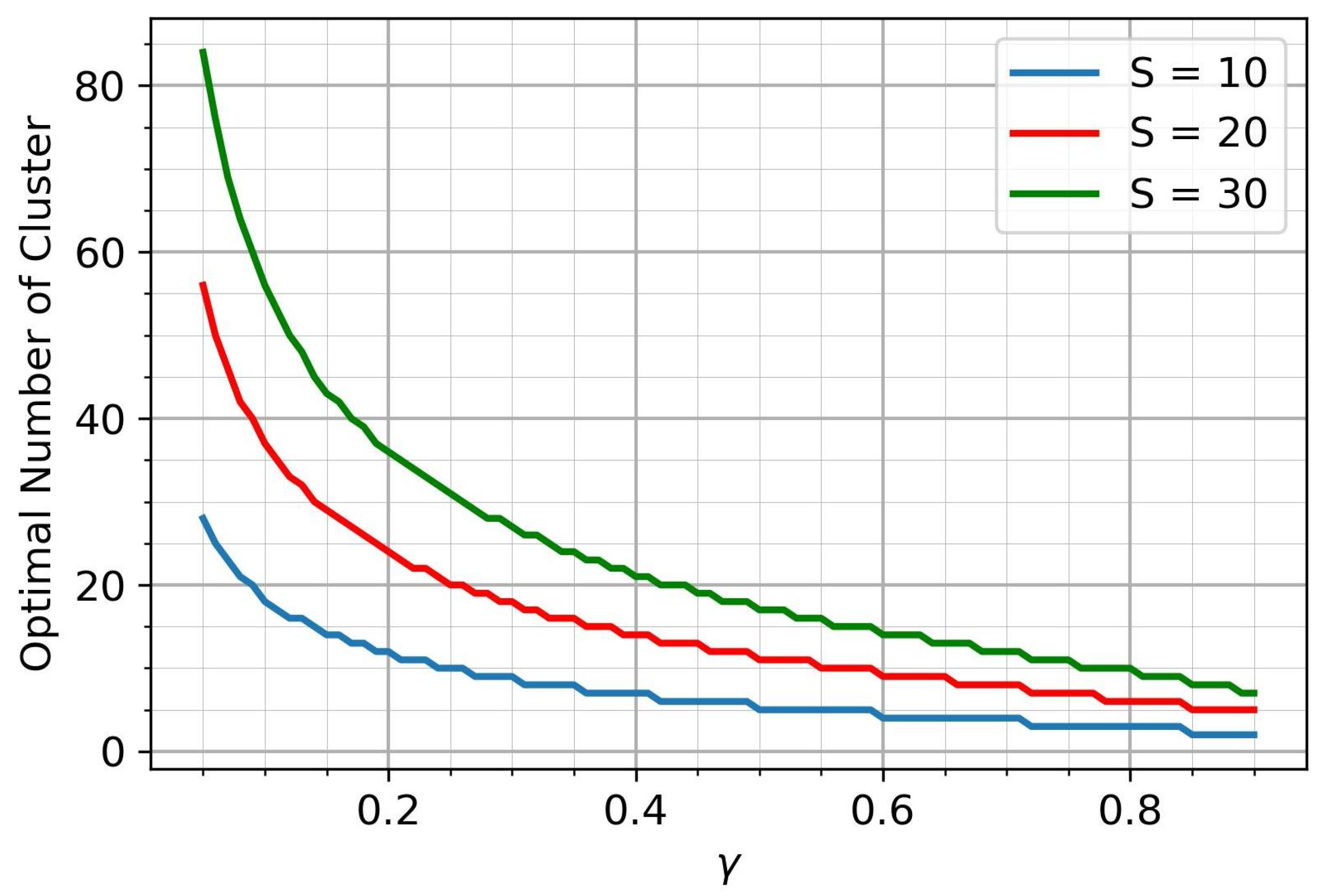
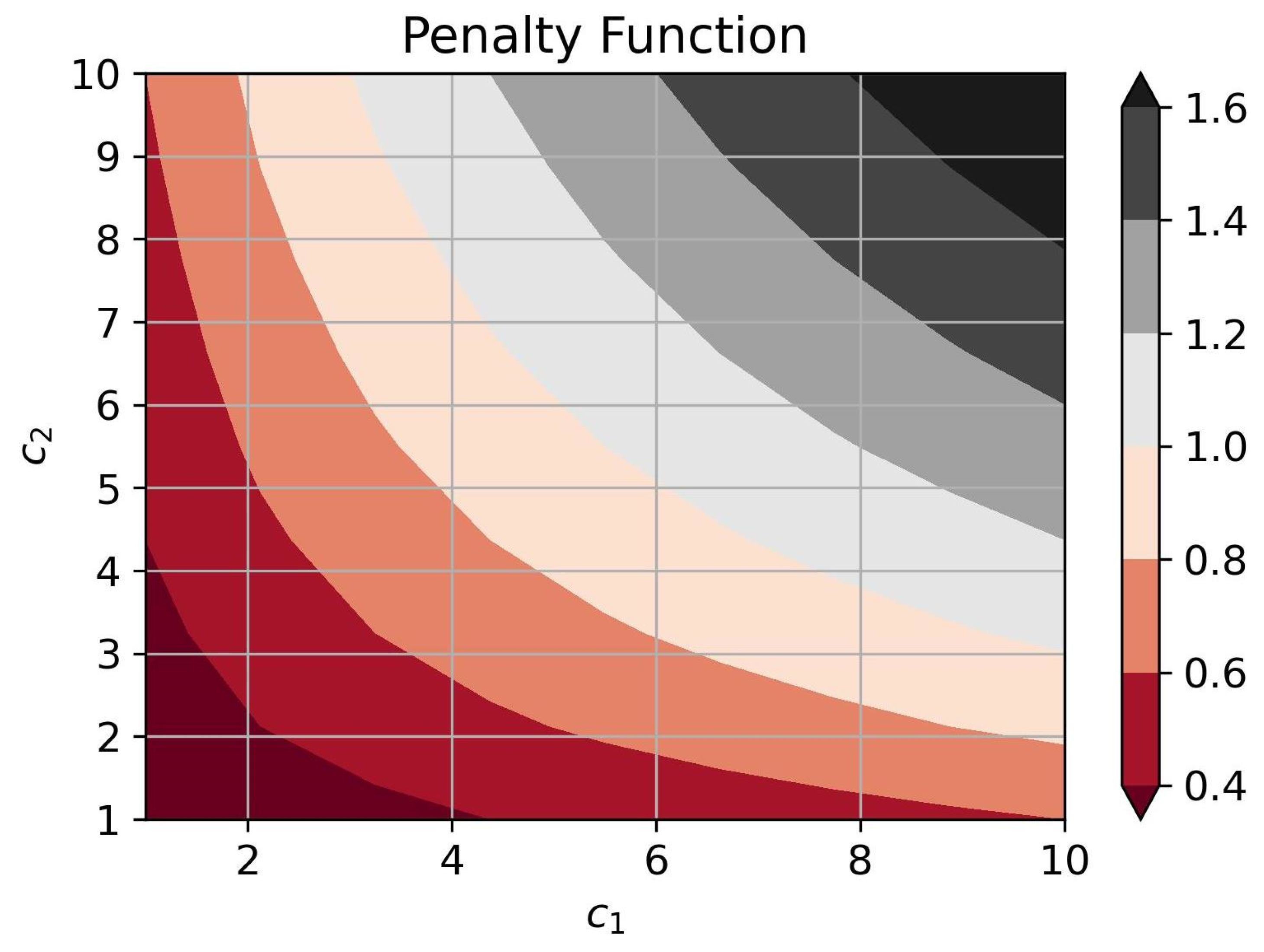
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Ding, D.; Ji, X.; Zhang, X.; Zhou, P.; Dou, Y.; Dan, M.; Shu, M. Construction of Multipollutant Air Quality Health Index and Susceptibility Analysis Based on Mortality Risk in Beijing, China. Atmosphere 2022, 13, 1370. [Google Scholar] [CrossRef]
- Campbell, L.D.; Pruss, U.A. Climate change, air pollution and noncommunicable diseases. Bull. World Health Organ 2019, 97, 160–161. [Google Scholar] [CrossRef] [PubMed]
- Motlagh, N.H.; Lagerspetz, E.; Nurmi, P.; Li, X.; Varjonen, S.; Mineraud, J. Toward massive scale air quality monitoring. IEEE Commun. Mag. 2020, 58, 54–59. [Google Scholar] [CrossRef]
- Mihăiţă, A.S.; Dupont, L.; Chery, O.; Camargo, M.; Cai, C. Evaluating air quality by combining stationary, smart mobile pollution monitoring and data-driven modelling. J. Clean. Prod. 2019, 221, 398–418. [Google Scholar] [CrossRef]
- Sassi, M.S.; Chaari, L. Comprehensive survey on air quality monitoring systems based on emerging computing and communication technologies. Comput. Netw. 2022, 209, 108904. [Google Scholar] [CrossRef]
- Sun, C.; Li, V.O.; Lam, J.C.; Leslie, I. Optimal Citizen-Centric Sensor Placement for Air Quality Monitoring: A Case Study of City of Cambridge, the United Kingdom. IEEE Access 2019, 7, 47390–47400. [Google Scholar] [CrossRef]
- Ajnoti, N.; Gehlot, H.; Tripathi, S.N. Hybrid instrument network optimization for air quality monitoring. Atmos. Meas. Tech. 2024, 17, 1651–1664. [Google Scholar] [CrossRef]
- Williams, D.E.; Henshaw, G.S.; Bart, M.; Laing, G.; Wagner, J.; Naisbitt, S.; Salmond, J.A. Validation of low-cost ozone measurement instruments suitable for use in an air-quality monitoring network. Meas. Sci. Technol. 2013, 24, 065803. [Google Scholar] [CrossRef]
- Mead, M.I.; Popoola, O.A.M.; Stewart, G.B.; Landshoff, P.; Calleja, M.; Hayes, M.; Baldovi, J.J.; McLeod, M.W.; Hodgson, T.F.; Dicks, J.; et al. The use of electrochemical sensors for monitoring urban air quality in low-cost, high-density networks. Atmos. Environ. 2013, 70, 186–203. [Google Scholar] [CrossRef]
- Patel, D.; Kulwant, M.; Shirin, S.; Kumar, A.; Ansari, M.; Yadav, A. Artificial Intelligence for Air Quality and Control Systems. In Modeling and Simulation of Environmental Systems: A Computation Approach; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Motlagh, N.H.; Boor, B.E.; Lu, D.; Nurmi, P.; Petäjä, T. Virtual Sensors: Toward High-Resolution Air Pollution Monitoring using AI and IoT. IEEE Internet Things Mag. 2023, 6, 76–81. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Motlagh, N.H.; Fung, P.L.; Lu, D.; Timonen, H.; Kuula, J. Intelligent Calibration and Virtual Sensing for Integrated Low-Cost Air Quality Sensors. IEEE Sens. J. 2020, 20, 13638–13652. [Google Scholar] [CrossRef]
- Mitreska Jovanovska, E.; Batz, V.; Lameski, P.; Zdravevski, E.; Herzog, M.A.; Trajkovik, V. Methods for Urban Air Pollution Measurement and Forecasting: Challenges, Opportunities, and Solutions. Atmosphere 2023, 14, 1441. [Google Scholar] [CrossRef]
- Jung, Y.J.; Lee, Y.K.; Lee, D.G.; Lee, Y.; Nittel, S.; Beard, K.; Nam, K.W.; Ryu, K.H. Design of Sensor Data Processing Steps in an Air Pollution Monitoring System. Sensors 2011, 11, 11235–11250. [Google Scholar] [CrossRef]
- Samudra, A.A.; Hertasning, B.; Amiro, L. Policy for handling air pollution in Jakarta: Study using System Dynamics Simulation Models. J. Infrastruct. Policy Dev. 2024, 8, 2969. [Google Scholar] [CrossRef]
- Mofarrah, A.; Husain, T. A holistic approach for optimal design of air quality monitoring network expansion in an urban area. Atmos. Environ. 2010, 44, 432–440. [Google Scholar] [CrossRef]
- Henriquez, A.; Osses, A.; Gallardo, L.; Diaz, R.M. Analysis and optimal design of air quality monitoring networks using a variation approach. Tellus B Chem. Phys. Meteorol. 2015, 67, 25385. [Google Scholar] [CrossRef]
- Huang, Z.; Yu, Q.; Liu, Y.; Ma, W.; Chen, L. Optimal Design of Air Quality Monitoring Network for Pollution Detection and Source Identification in Industrial Parks. Atmosphere 2019, 10, 318. [Google Scholar] [CrossRef]
- Gupta, S.; Pebesma, E.; Mateu, J.; Degbelo, A. Air Quality Monitoring Network Design Optimisation for Robust Land Use Regression Models. Sustainability 2018, 10, 1442. [Google Scholar] [CrossRef]
- Gagliardi, G.; Gallelli, V.; Violi, A.; Lupia, M.; Cario, G. Optimal Placement of Sensors in Traffic Networks Using Global Search Optimization Techniques Oriented towards Traffic Flow Estimation and Pollutant Emission Evaluation. Sustainability 2024, 16, 3530. [Google Scholar] [CrossRef]
- Borges, M.; Lopes, P.; Silva, L. Network Optimization of Carbon Monoxide Sensor Nodes in the Metropolitan Region of São Paulo. Electronics 2023, 12, 4647. [Google Scholar] [CrossRef]
- Mano, Z.; Kendler, S.; Fishbain, B. Information Theory Solution Approach to the Air Pollution Sensor Location–Allocation Problem. Sensors 2022, 22, 3808. [Google Scholar] [CrossRef]
- Engel-Cox, J.; Huff, A.; Kanabkaew, T.; Oanh, N.T.K. Satellite Tools for Air Quality Management with Focus on Particulate Matter. In Integrated Air Quality Management; CRC Press: Boca Raton, FL, USA, 2012; Volume 125. [Google Scholar] [CrossRef]
- Liu, B.; Peng, Y.; Wang, W.; Mao, N. Robust optimization for designing air quality monitoring network in coal ports under uncertainty. Atmos. Environ. 2023, 304, 119792. [Google Scholar] [CrossRef]
- Aggoune-Mtalaa, W.; Laib, M. Analyzing Air Pollution and Traffic Data in Urban Areas in Luxembourg. Smart Cities 2023, 6, 929–943. [Google Scholar] [CrossRef]
- Gualtieri, G.; Camilli, F.; Cavaliere, A.; De Filippis, T.; Di Gennaro, F.; Di Lonardo, S.; Gioli, B.; Matese, A.; Rocchi, L.; Toscano, P.; et al. An integrated low-cost road traffic and air pollution monitoring platform to assess vehicles’ air quality impact in urban areas. Transp. Res. Procedia 2017, 27, 609–616. [Google Scholar] [CrossRef]
- Verghese, S.; Nema, A.K. Optimal design of air quality monitoring networks: A systematic review. Stoch. Environ. Res. Risk Assess 2022, 2022 36, 2963–2978. [Google Scholar] [CrossRef]
- Hassan Bhat, T.; Jiawen, G.; Farzaneh, H. Air Pollution Health Risk Assessment (AP-HRA), Principles and Applications. Int. J. Environ. Res. Public Health 2021, 18, 1935. [Google Scholar] [CrossRef]
- Anenberg, S.C.; Belova, A.; Brandt, J.; Fann, N.; Greco, S.; Guttikunda, S.; Heroux, M.-E.; Hurley, F.; Krzyzanowski, M.; Medina, S.; et al. Survey of Ambient Air Pollution Health Risk Assessment Tools. Risk Anal. 2016, 36, 1718–1736. [Google Scholar] [CrossRef] [PubMed]
- Pachoulis, M.; Maggos, T.; Panagopoulos, P.; Dasopoulou, M.; Balla, D.; Stamatelopoulou, A.; Manousakas, M.I.; Eleftheriadis, K.; Saraga, D. Population Health Risks Assessment from Air Pollution Exposure in an Industrialized Residential Area in Greece. Atmosphere 2022, 13, 615. [Google Scholar] [CrossRef]
- Gruszecka-Kosowska, A.; Dajda, J.; Adamiec, E.; Helios-Rybicka, E.; Kisiel-Dorohinicki, M.; Klimek, R.; Pałka, D.; Wąs, J. Human Health Risk Assessment of Air Pollution in the Regions of Unsustainable Heating Sources. Case Study—The Tourist Areas of Southern Poland. Atmosphere 2021, 12, 615. [Google Scholar] [CrossRef]
- Agbehadji, I.E.; Obagbuwa, I.C. Systematic Review of Machine Learning and Deep Learning Techniques for Spatiotemporal Air Quality Prediction. Atmosphere 2024, 15, 1352. [Google Scholar] [CrossRef]
- Gharib, A.; Ibnkahla, M. User Security-Oriented Information-Centric IoT Nodes Clustering With Graph Convolution Networks. IEEE Internet Things J. 2024, 11, 8311–8326. [Google Scholar] [CrossRef]
- Chang, S.; Wu, S.; Huang, N.; Zhang, Y.Y.; Zhu, Y.J.; Wang, C.; Gong, C. Delay Jitter Analysis for VLC Under Indoor Industrial Internet of Things Scenarios. IEEE Photonics J. 2024, 16, 7303315. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, L.; Li, S.; Xiang, Y. Hybrid Multi-Access Method for Space-Based IoT: Adaptive Bandwidth Allocation and Beam Layout Based on User Distribution. Sensors 2024, 24, 6082. [Google Scholar] [CrossRef]
- Boubrima, A.; Bechkit, W.; Rivano, H. Optimal WSN Deployment Models for Air Pollution Monitoring. IEEE Trans. Wirel. Commun. 2017, 16, 2723–2735. [Google Scholar] [CrossRef]
- Fox, J. Applied Regression Analysis, Linear Models, and Related Methods; Sage Publications: Thousand Oaks, CA, USA, 1997. [Google Scholar]
- Senic, A.; Ivanovic, M.; Dobrodolac, M.; Stojadinovic, Z. Prioritization of Preventive Measures: A Multi-Criteria Approach to Risk Mitigation in Road Infrastructure Projects. Mathematics 2025, 13, 278. [Google Scholar] [CrossRef]
- Tessema, B.; Yen, G.G. An adaptive penalty formulation for constrained evolutionary optimization. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum 2009, 39, 565–578. [Google Scholar] [CrossRef]
- Shakhov, V.; Sokolova, O.; Koo, I. On the Suitability of Intrusion Detection System for Wireless Edge Networks. Energies 2021, 14, 5954. [Google Scholar] [CrossRef]
- Shakhov, V.; Materukhin, A.; Sokolova, O.; Koo, I. Optimizing Urban Air Pollution Detection Systems. Sensors 2022, 22, 4767. [Google Scholar] [CrossRef] [PubMed]
- Peltier, R.E.; Castell, N.; Clements, A.L.; Dye, T.; Hüglin, C.; Kroll, J.H.; Lung, S.-C.-C.; Ning, Z.; Parsons, M.; Penza, M.; et al. An Update on Low-Cost Sensors for the Measurement of Atmospheric Composition; World Meteorological Organization (WMO): Geneva, Switzerland, 2020. [Google Scholar]
- Williams, R.W.; Duvall, R.; Kilaru, V.; Hagler, G.; Hassinger, L.; Benedict, K.; Rice, J.; Kaufman, A.; Judge, R.A.; Pierce, G.; et al. Deliberating performance targets workshop: Potential paths for emerging PM2.5 and O3 air sensor progress. Atmos. Environ. X 2019, 2, 100031. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Zhao, Z.; Chen, X.; Palicot, J.; Zhang, H. TACT: A Transfer Actor-Critic Learning Framework for Energy Saving in Cellular Radio Access Networks. IEEE Trans. Wirel. Commun. 2014, 13, 2000–2011. [Google Scholar] [CrossRef]
- Shakhov, V.; Koo, I. Analysis of a Network Stability-Aware Clustering Protocol for Cognitive Radio Sensor Networks. IEEE Internet Things J. 2021, 8, 12476–12477. [Google Scholar] [CrossRef]
- Son, K.; Kim, H.; Yi, Y.; Krishnamachari, B. Base Station Operation and User Association Mechanisms for Energy-Delay Tradeoffs in Green Cellular Networks. IEEE J. Sel. Areas Commun. 2011, 29, 1525–1536. [Google Scholar] [CrossRef]
| References | Description | Technique |
|---|---|---|
| Sun, C., et al. (2019) [6], Ajnoti, N. (2024) [7] | Optimal sensor placement: Citizen-Centric air quality monitoring. Maximizing overall satisfaction from receiving public information about air quality while limiting budget. Assumption of equal distance to the sensor for all cluster users. The statement of the optimization problem appears to be flawed. | Approximate optimization method (greedy algorithm, genetic algorithm). |
| Samudra, A.A., et al. (2024) [15] | Identification of the main sources of air pollution, quantitative assessment of their impact. | Simulation. |
| Mofarrah, A., et al. (2010) [16] | The statement of the optimization problem appears to be flawed. The optimal solution has not been rigorously defined. | Triangular fuzzy numbers. |
| Henriquez, A., et al. (2015) [17] | Three quality indicators are taken into account: accuracy gain, information gain, and degrees of freedom for the signal. The cost factor is not taken into account. | Heuristic optimisation algorithm – simulated annealing. |
| Huang, Z., et al. (2019) [18] | Optimizing an observation performance score that combines averages from both pollution detection effectiveness and source identification accuracy. | Merging Gaussian matching models with source area analysis. |
| Gupta, S., et al. (2018) [19] | Placement of monitoring stations. | Spatial simulated annealing method. |
| Gagliardi, G., et al. (2024) [20] | Problem of selecting a subset of sensors from a pool of potential sensors for monitoring a transportation network. | Simulated annealing heuristic, genetic algorithm. |
| Borges, M., et al. (2023) [21] | The optimization problem is not formalized. The objective function does not include the system cost metric. | Genetic Algorithm. |
| Mano, Z., et al. (2022) [22] | Optimal placement of sensors in known locations. The cost factor is not taken into account. | The Lagrange atmospheric dispersion model under different meteorological conditions. Then, sensors are deployed at the locations that are determined to be the most informative. |
| Liu, B., et al. (2023) [24] | Air quality monitoring network design problem with consideration of uncertain operational efficiency and wind conditions. | Maximum weighted location coverage problem is solved. Then, the linear approximation method is applied to the nonlinear model to improve the computational efficiency. |
| 0.01 | 0.149 |
| 0.1 | 0.532 |
| 0.99 | 6.638 |
| 0.999 | 9.233 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokolova, O.; Yurgenson, A.; Shakhov, V. Development of Air Quality Monitoring Systems: Balancing Infrastructure Investment and User Satisfaction Policies. Sensors 2025, 25, 875. https://doi.org/10.3390/s25030875
Sokolova O, Yurgenson A, Shakhov V. Development of Air Quality Monitoring Systems: Balancing Infrastructure Investment and User Satisfaction Policies. Sensors. 2025; 25(3):875. https://doi.org/10.3390/s25030875
Chicago/Turabian StyleSokolova, Olga, Anastasia Yurgenson, and Vladimir Shakhov. 2025. "Development of Air Quality Monitoring Systems: Balancing Infrastructure Investment and User Satisfaction Policies" Sensors 25, no. 3: 875. https://doi.org/10.3390/s25030875
APA StyleSokolova, O., Yurgenson, A., & Shakhov, V. (2025). Development of Air Quality Monitoring Systems: Balancing Infrastructure Investment and User Satisfaction Policies. Sensors, 25(3), 875. https://doi.org/10.3390/s25030875






