Motion and Inertia Estimation for Non-Cooperative Space Objects During Long-Term Occlusion Based on UKF-GP
Abstract
1. Introduction
- We utilize multi-output GP models to predict projection measurements from a stereo-camera system so that the UKF-GP model can be updated during occlusion. GP models are trained using the projection measurements provided by stereo-camera systems. A product kernel, consisting of two periodic kernels, is designed to capture periodic trends in the non-periodic and noisy training data.
- The initial guesses for the periodicity hyper-parameters are intelligently obtained from the FFT analysis of the training data, enhancing the hyper-parameter training procedure.
- The projection predictions from the GP models and their derivatives obtained from the finite difference method (FDM) are used as pseudo-measurements in the UKF-GP fusion algorithm during long-term occlusion.
- Monte Carlo simulations across multiple tumbling frequencies demonstrate that GP models accurately predict projections for thousands of seconds under occlusion. Furthermore, the UKF-GP algorithm outperforms the conventional UFK in estimating motion and inertia parameters.
2. Methodology
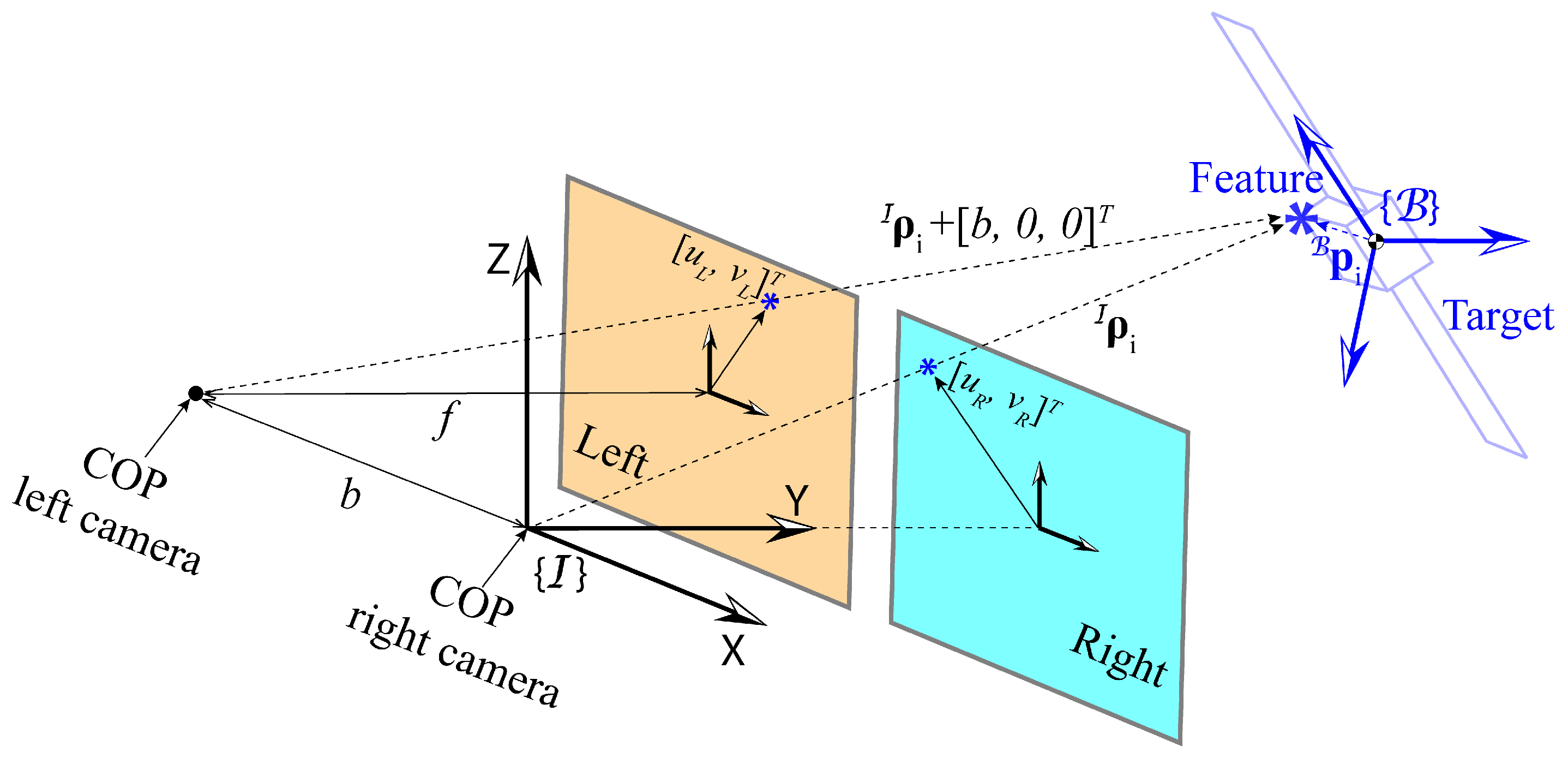
2.1. Problem Scenario
2.2. Unscented Kalman Filter (UKF)
2.2.1. Dynamics Model
2.2.2. Observation Model
2.3. The Gaussian Process (GP)
| Algorithm 1 Periodicity hyper-parameters initial guess determination algorithm for . |
|
2.4. UKF-GP Algorithm
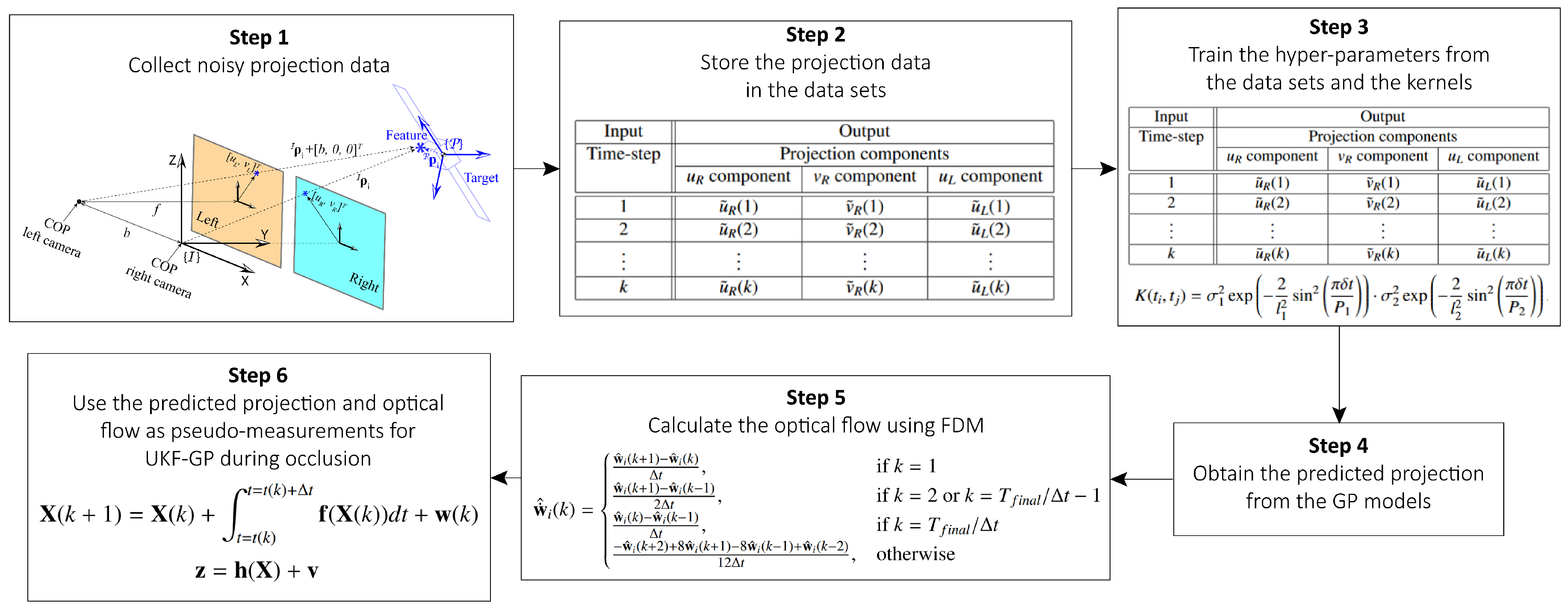
2.5. Simulation Workflow
| Algorithm 2 Simulation workflow. |
|
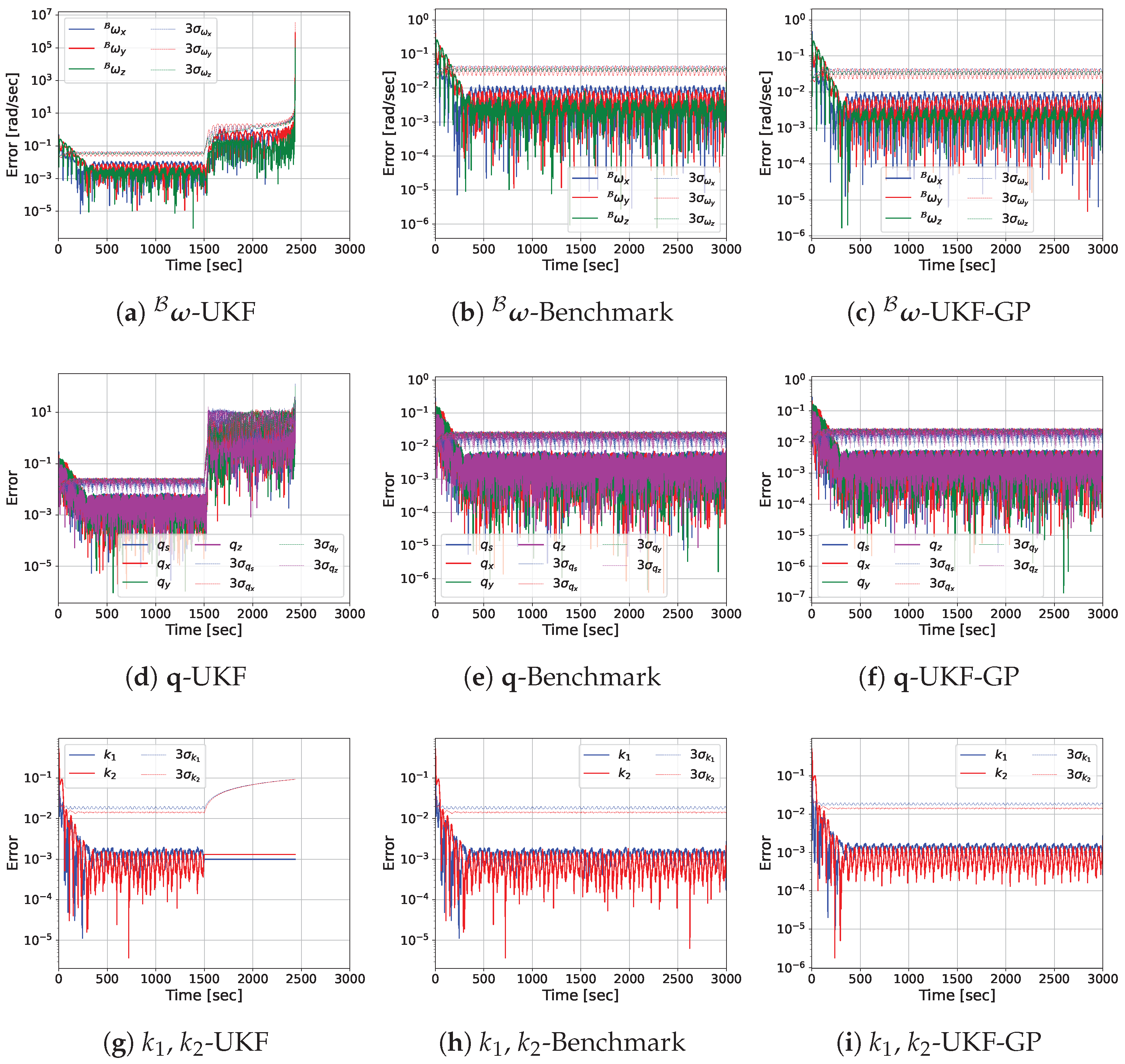
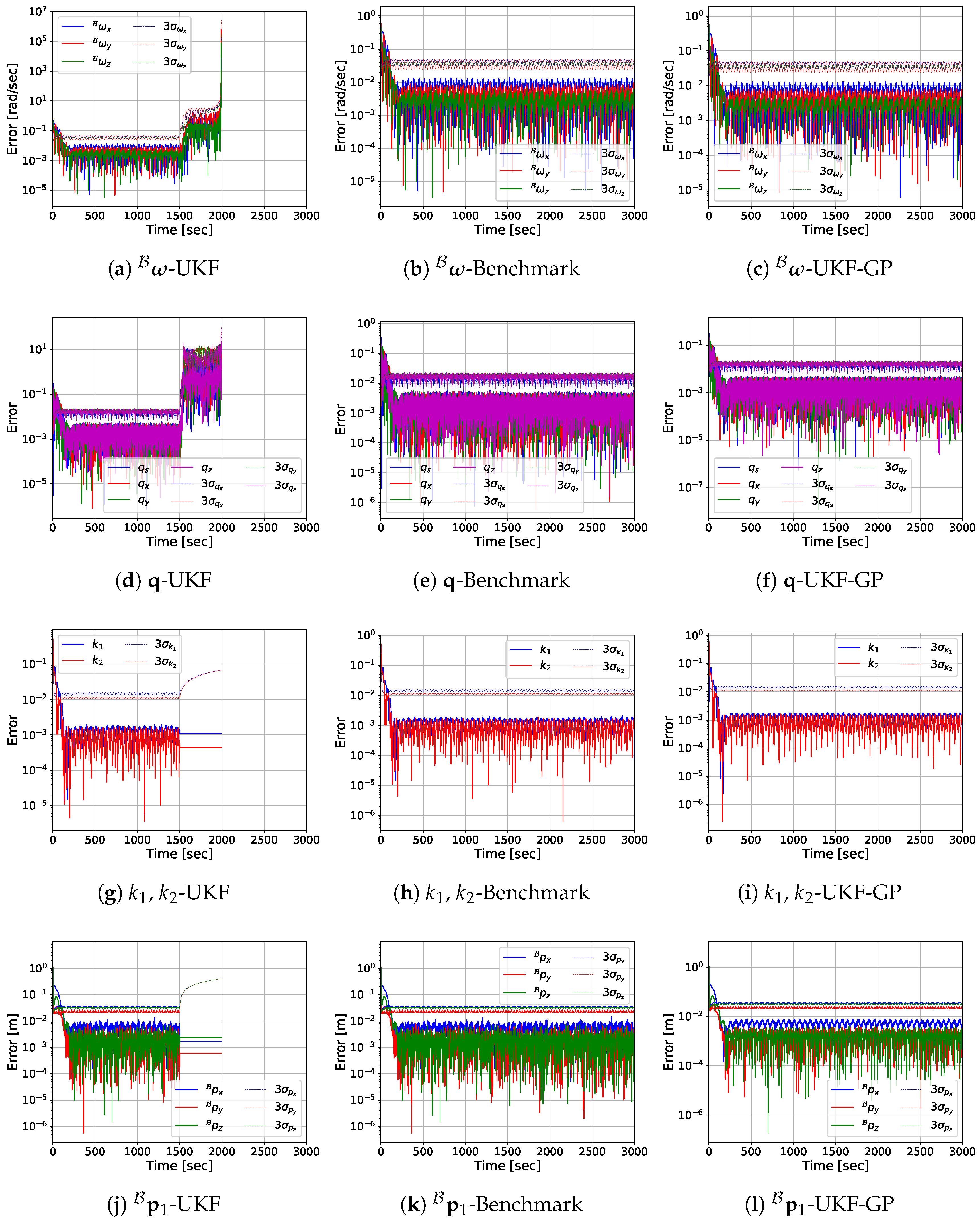
3. Results and Discussion
- Discrete-time intervals: s;
- Sensor measurement sampling rate: Hz;
- Principal axes inertia parameters of the target: , , ;
- Tumbling frequencies: , , , and Hz (the corresponding polhode periods = 441.045 s, 147.015 s, 88.209 s, and 63.006 s, respectively);
- Initial angular velocities in : rad/s;
- Initial attitude quaternion: ;
- Standard deviation of the projection measurement: rad.
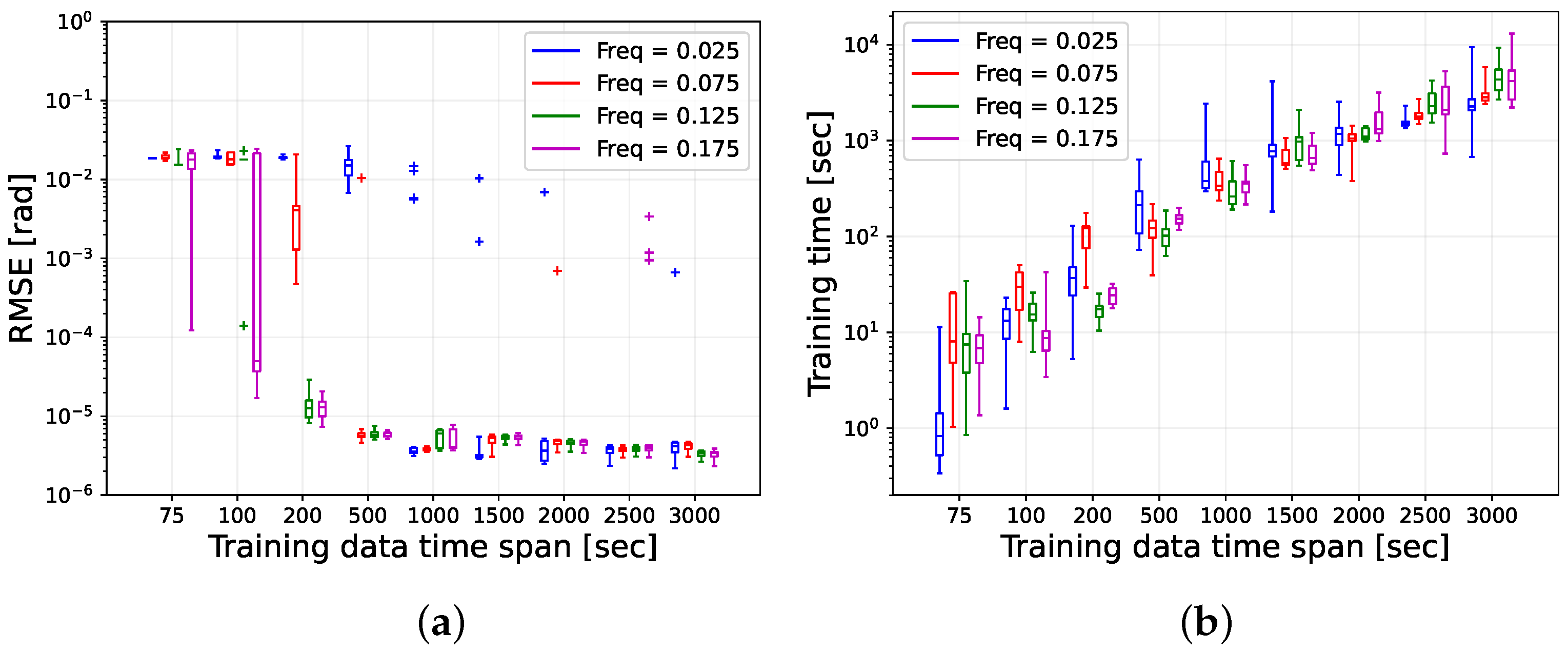
3.1. Prediction Performance of the GP
- Number of features: ;
- Position of the feature in : m;
- Training data time-span: , 100, 200, 500, 1000, 1500, 2000, 2500, and 3000 s;
- Duration of prediction: s;
- Number of runs: .
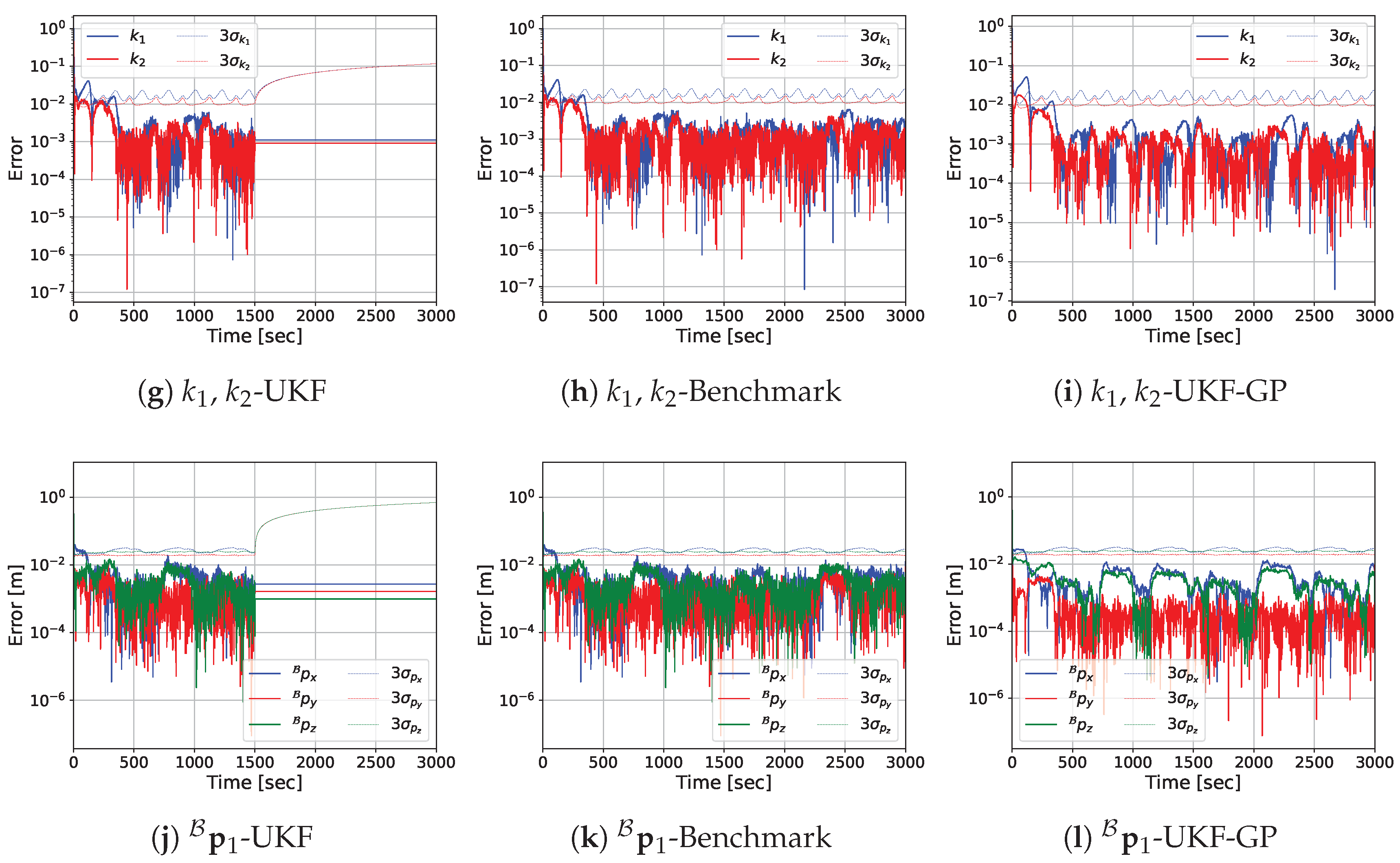
3.2. Prediction Performance of UKF-GP
- Total simulation duration: s.
- Duration of the sensor data availability: s.
- Duration of the occlusion: s.
- Number of features: .
- User-defined constant parameters: , , (from [26]).
- Position of the features in :
- –
- Feature 1: m;
- –
- Feature 2: m;
- –
- Feature 3: m;
- –
- Feature 4: m;
- –
- Feature 5: m.
- Initial guesses of the state variables:
- –
- rad/s;
- –
- ;
- –
- ;
- –
- m.
- Standard deviation of the measurement noise of the optical flow:
- –
- For Hz, rad/s;
- –
- For Hz, rad/s;
- –
- For Hz, rad/s;
- –
- For Hz, rad/s.
- Standard deviation of the measurement noise of the disparity: rad.
- Variances for the initial state error covariance matrix:
- –
- Variance of : ;
- –
- Variance of : ;
- –
- Variance of and : ;
- –
- Variance of : .
- Variances in the process noise covariance matrix:
- –
- Variance in :
- ∗
- For Hz, ;
- ∗
- For Hz, ;
- ∗
- For Hz, ;
- ∗
- For Hz, .
- –
- Variance in :
- ∗
- For Hz, ;
- ∗
- For Hz, ;
- ∗
- For Hz, ;
- ∗
- For Hz, .
- –
- Variance in and : .
- –
- Variance in : .
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UKF | Unscented Kalman filter |
| GP | Gaussian process |
| FFT | Fast Fourier transform |
| LCS | Laser camera system |
| EKF | Extended Kalman filter |
| IEKF | Iterated extended Kalman filter |
| MC | Monte Carlo |
| CoMBiNa | Coarse model-based relative navigation |
| SLAM | Simultaneous localization and mapping |
| ML | Machine learning |
| SPGP | Sparse pseudo-input Gaussian process |
| RBF | Radial basis function |
| DVQ-MANN | Dual-vector quaternion-based mixed artificial neural network |
| DVQ-EKF | Dual-vector quaternion-based extended Kalman filter |
| CM | Center of mass |
| COP | Center of projection |
| SURF | Sped-up robust features |
| SIFT | Scale invariant feature transform |
| L-BFGS | Limited-memory Broyden–Fletcher–Goldfarb–Shanno |
| RMSE | Root mean square error |
Appendix A. Determination of Expressions of and
Appendix B. Determination of the Polhode Period
References
- Aghili, F.; Parsa, K. Motion and parameter estimation of space objects using laser-vision data. J. Guid. Control Dyn. 2009, 32, 538–550. [Google Scholar] [CrossRef]
- Dani, A.; Panahandeh, G.; Chung, S.J.; Hutchinson, S. Image moments for higher-level feature based navigation. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 602–609. [Google Scholar] [CrossRef]
- Meier, K.; Chung, S.J.; Hutchinson, S. Visual-inertial curve simultaneous localization and mapping: Creating a sparse structured world without feature points. J. Field Robot. 2018, 35, 516–544. [Google Scholar] [CrossRef]
- Corke, P.I.; Jachimczyk, W.; Pillat, R. Robotics, Vision and Control: Fundamental Algorithms in MATLAB, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 73, ISBN 978-3-642-20143-1. [Google Scholar] [CrossRef]
- Segal, S.; Carmi, A.; Gurfil, P. Vision-based relative state estimation of non-cooperative spacecraft under modeling uncertainty. In Proceedings of the 2011 Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011; pp. 1–8. [Google Scholar] [CrossRef]
- Segal, S.; Carmi, A.; Gurfil, P. Stereovision-based estimation of relative dynamics between noncooperative satellites: Theory and experiments. IEEE Trans. Control Syst. Technol. 2013, 22, 568–584. [Google Scholar] [CrossRef]
- Pesce, V.; Lavagna, M.; Bevilacqua, R. Stereovision-based pose and inertia estimation of unknown and uncooperative space objects. Adv. Space Res. 2017, 59, 236–251. [Google Scholar] [CrossRef]
- Chang, L.; Liu, J.; Chen, Z.; Bai, J.; Shu, L. Stereo Vision-Based Relative Position and Attitude Estimation of Non-Cooperative Spacecraft. Aerospace 2021, 8, 230. [Google Scholar] [CrossRef]
- Ge, D.; Wang, D.; Zou, Y.; Shi, J. Motion and inertial parameter estimation of non-cooperative target on orbit using stereo vision. Adv. Space Res. 2020, 66, 1475–1484. [Google Scholar] [CrossRef]
- Feng, Q.; Pan, Q.; Hou, X.; Liu, Y.; Zhang, C. A novel parameterization method to estimate the relative state and inertia parameters for non-cooperative targets. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 1675–1681. [Google Scholar]
- Li, Y.; Jia, Y. Stereovision-based relative motion estimation between non-cooperative spacecraft. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 4196–4201. [Google Scholar]
- Mazzucato, M.; Valmorbida, A.; Guzzo, A.; Lorenzini, E.C. Stereoscopic vision-based relative navigation for spacecraft proximity operations. In Proceedings of the 2018 5th IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), Rome, Italy, 20–22 June 2018; pp. 369–374. [Google Scholar]
- De Jongh, W.; Jordaan, H.; Van Daalen, C. Experiment for pose estimation of uncooperative space debris using stereo vision. Acta Astronaut. 2020, 168, 164–173. [Google Scholar] [CrossRef]
- Jiang, C.; Hu, Q. Constrained Kalman filter for uncooperative spacecraft estimation by stereovision. Aerosp. Sci. Technol. 2020, 106, 106133. [Google Scholar] [CrossRef]
- Jixiu, L.; Quan, Y.; Leizheng, S.; Yang, G. Relative Position and Attitude Estimation of Non-cooperative Spacecraft Based on Stereo Camera and Dynamics. J. Phys. Conf. Ser. 2021, 1924, 012025. [Google Scholar] [CrossRef]
- Maestrini, M.; De Luca, M.A.; Di Lizia, P. Relative navigation strategy about unknown and uncooperative targets. J. Guid. Control Dyn. 2023, 46, 1708–1725. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Zhang, Y. Stereovision-based relative states and inertia parameter estimation of noncooperative spacecraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 2489–2502. [Google Scholar] [CrossRef]
- Hillenbrand, U.; Lampariello, R. Motion and parameter estimation of a free-floating space object from range data for motion prediction. In Proceedings of the i-SAIRAS, Munich, Germany, 5–8 September 2005; Available online: https://elib.dlr.de/55779/1/Lampariello-isairas_05.pdf (accessed on 20 January 2025).
- Tweddle, B.E. Computer Vision-Based Localization and Mapping of an Unknown, Uncooperative and Spinning Target for Spacecraft Proximity Operations. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2013. Available online: http://hdl.handle.net/1721.1/85693 (accessed on 20 January 2025).
- Benninghoff, H.; Boge, T. Rendezvous involving a non-cooperative, tumbling target-estimation of moments of inertia and center of mass of an unknown target. In Proceedings of the 25th International Symposium on Space Flight Dynamics, München, Germany, 19–23 October 2015; Available online: https://elib.dlr.de/100186/ (accessed on 20 January 2025).
- Yu, M.; Luo, J.; Wang, M.; Liu, C.; Sun, J. Sparse Gaussian processes for multi-step motion prediction of space tumbling objects. Adv. Space Res. 2023, 71, 3775–3786. [Google Scholar] [CrossRef]
- Hou, X.; Yuan, J.; Ma, C.; Sun, C. Parameter estimations of uncooperative space targets using novel mixed artificial neural network. Neurocomputing 2019, 339, 232–244. [Google Scholar] [CrossRef]
- Barbier, T. Space Debris State Estimation Onboard a Chaser Spacecraft. Ph.D. Thesis, University of Surrey, Guildford, UK, 2023. [Google Scholar] [CrossRef]
- Kamath, A.; Vargas-Hernández, R.A.; Krems, R.V.; Carrington, T.; Manzhos, S. Neural networks vs Gaussian process regression for representing potential energy surfaces: A comparative study of fit quality and vibrational spectrum accuracy. J. Chem. Phys. 2018, 148, 241702. [Google Scholar] [CrossRef] [PubMed]
- Ko, J.; Klein, D.J.; Fox, D.; Haehnel, D. GP-UKF: Unscented Kalman filters with Gaussian process prediction and observation models. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1901–1907. [Google Scholar] [CrossRef]
- Labbe, R. Kalman and Bayesian Filters in Python. Available online: https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python (accessed on 22 November 2024).
- Crassidis, J.L.; Junkins, J.L. Optimal Estimation of Dynamic Systems, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2004; ISBN 9780429211706. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Sharma, S.; DAmico, S. Comparative assessment of techniques for initial pose estimation using monocular vision. Acta Astronautica 2016, 123, 435–445. [Google Scholar] [CrossRef]
- Capuano, V.; Kim, K.; Harvard, A.; Chung, S.J. Monocular-based pose determination of uncooperative space objects. Acta Astronaut. 2020, 166, 493–506. [Google Scholar] [CrossRef]
- Heeger, D.J.; Jepson, A.D. Subspace methods for recovering rigid motion I: Algorithm and implementation. Int. J. Comput. Vis. 1992, 7, 95–117. [Google Scholar] [CrossRef]
- Alvarez, M.A.; Rosasco, L.; Lawrence, N.D. Kernels for vector-valued functions: A review. Found. Trends® Mach. Learn. 2012, 4, 195–266. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; ISBN 026218253X. [Google Scholar] [CrossRef]
- Mecholsky, N.A. Analytic formula for the geometric phase of an asymmetric top. Am. J. Phys. 2019, 87, 245–254. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics, 4th ed.; Springer: Berlin, Germany, 2019; ISBN 978-3-319-99693-6. [Google Scholar] [CrossRef]
- GPy: A Gaussian Process Framework in Python. Available online: http://github.com/SheffieldML/GPy (accessed on 22 November 2024).






| Input | Output | ||
|---|---|---|---|
| Time, t | Projection Components, [rad] | ||
| [sec] | Component | Component | Component |
| ⋮ | ⋮ | ⋮ | ⋮ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kabir, R.H.; Bai, X. Motion and Inertia Estimation for Non-Cooperative Space Objects During Long-Term Occlusion Based on UKF-GP. Sensors 2025, 25, 647. https://doi.org/10.3390/s25030647
Kabir RH, Bai X. Motion and Inertia Estimation for Non-Cooperative Space Objects During Long-Term Occlusion Based on UKF-GP. Sensors. 2025; 25(3):647. https://doi.org/10.3390/s25030647
Chicago/Turabian StyleKabir, Rabiul Hasan, and Xiaoli Bai. 2025. "Motion and Inertia Estimation for Non-Cooperative Space Objects During Long-Term Occlusion Based on UKF-GP" Sensors 25, no. 3: 647. https://doi.org/10.3390/s25030647
APA StyleKabir, R. H., & Bai, X. (2025). Motion and Inertia Estimation for Non-Cooperative Space Objects During Long-Term Occlusion Based on UKF-GP. Sensors, 25(3), 647. https://doi.org/10.3390/s25030647





