Design of a Verification Device of Motor Axle Wheel Load Scales Based on Pump-Controlled Hydraulic Cylinder
Abstract
1. Introduction
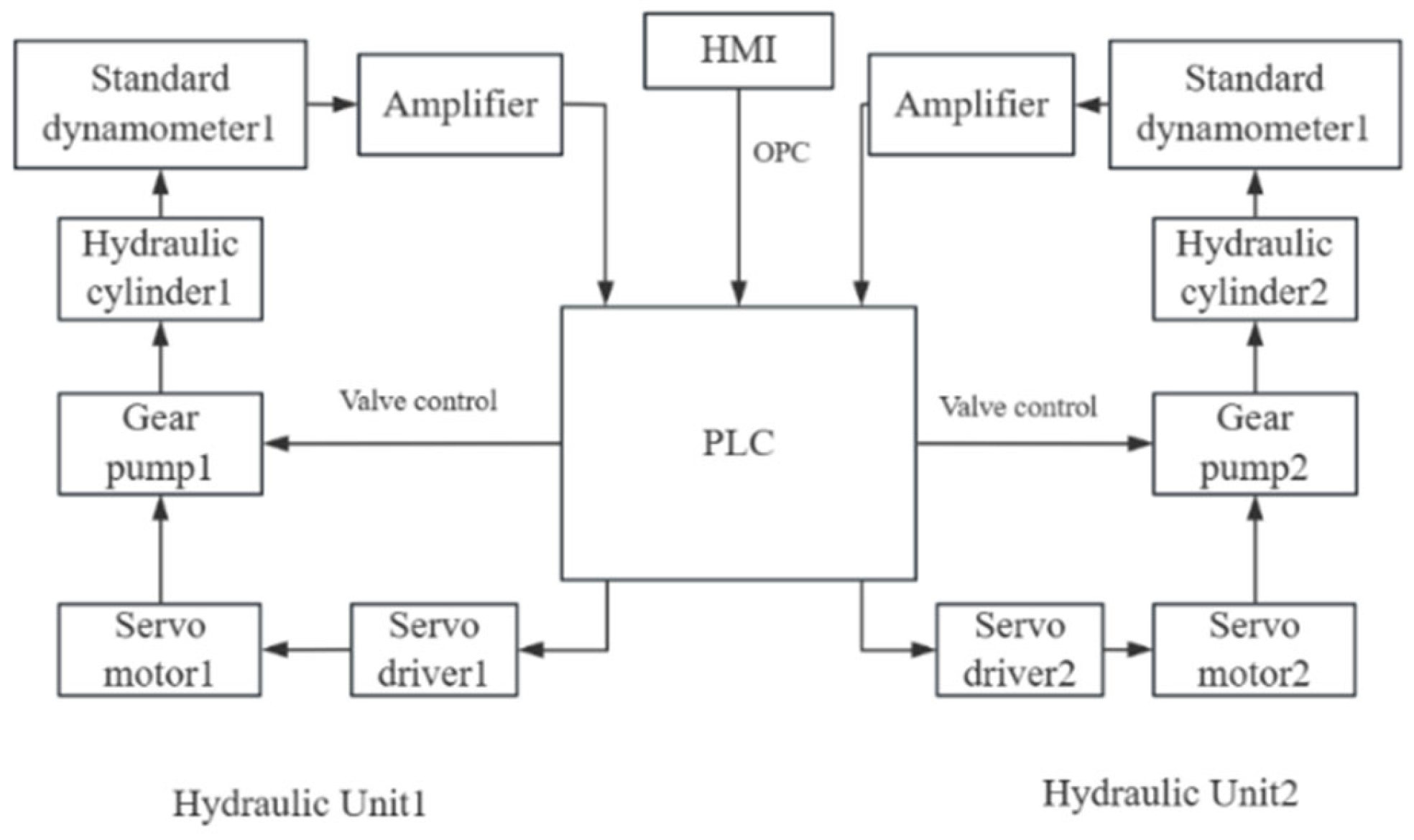
2. Verification Device
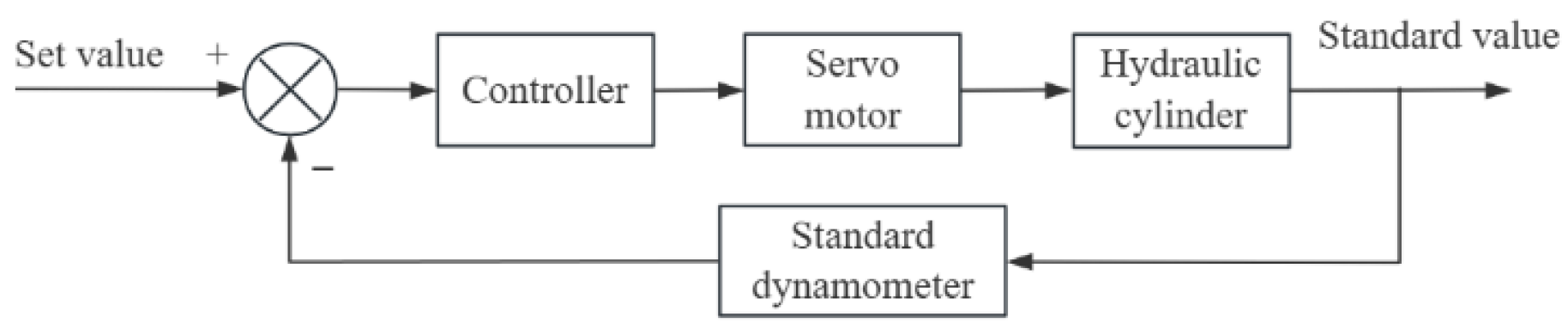
2.1. Working Principle
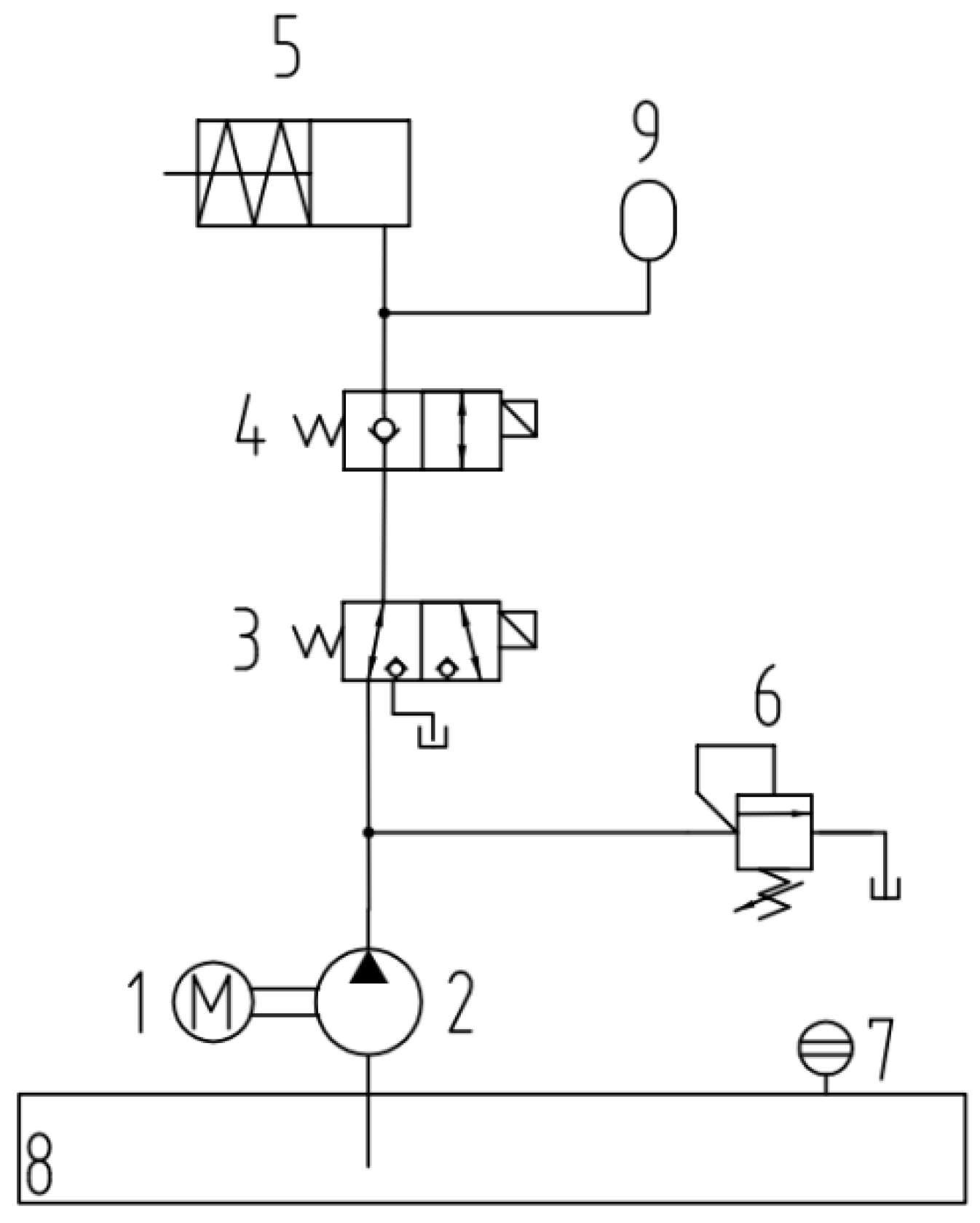
2.2. Hydraulic Unit
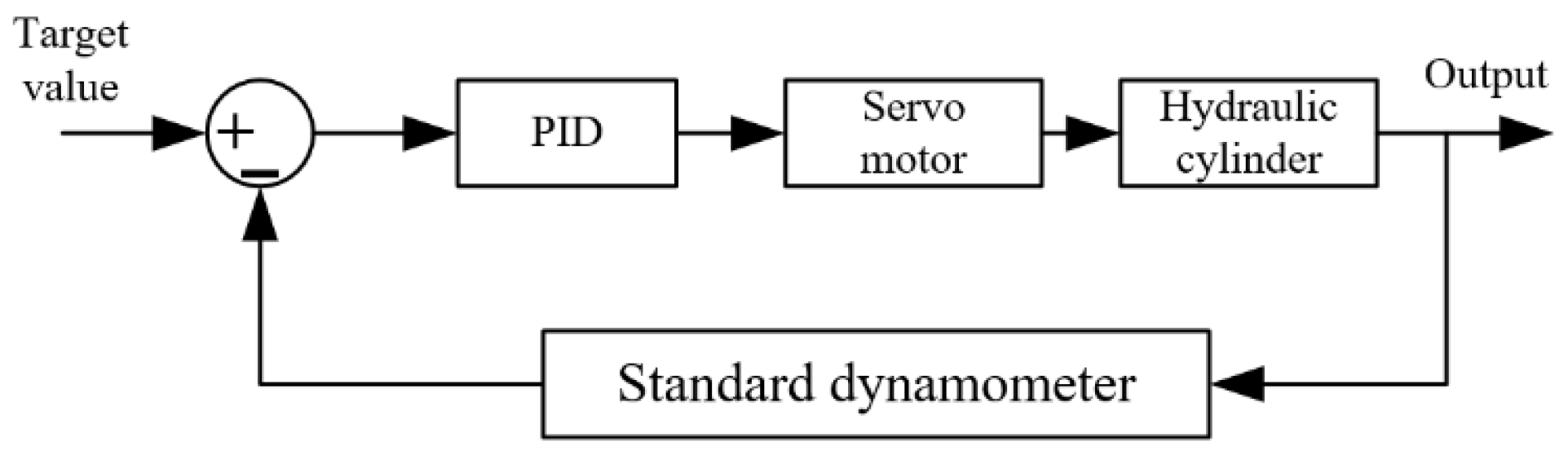
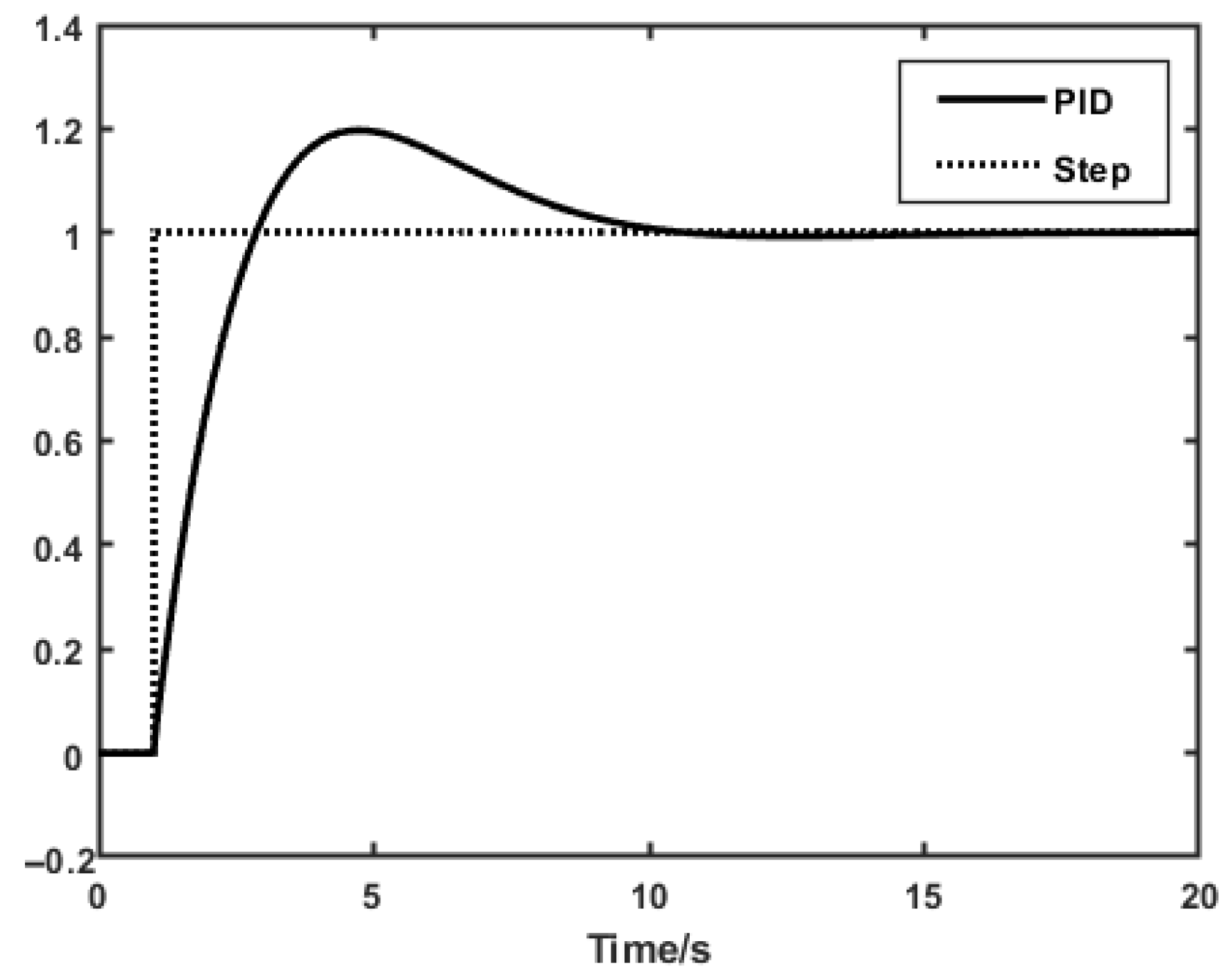
Modeling of Pump-Controlled Hydraulic Unit
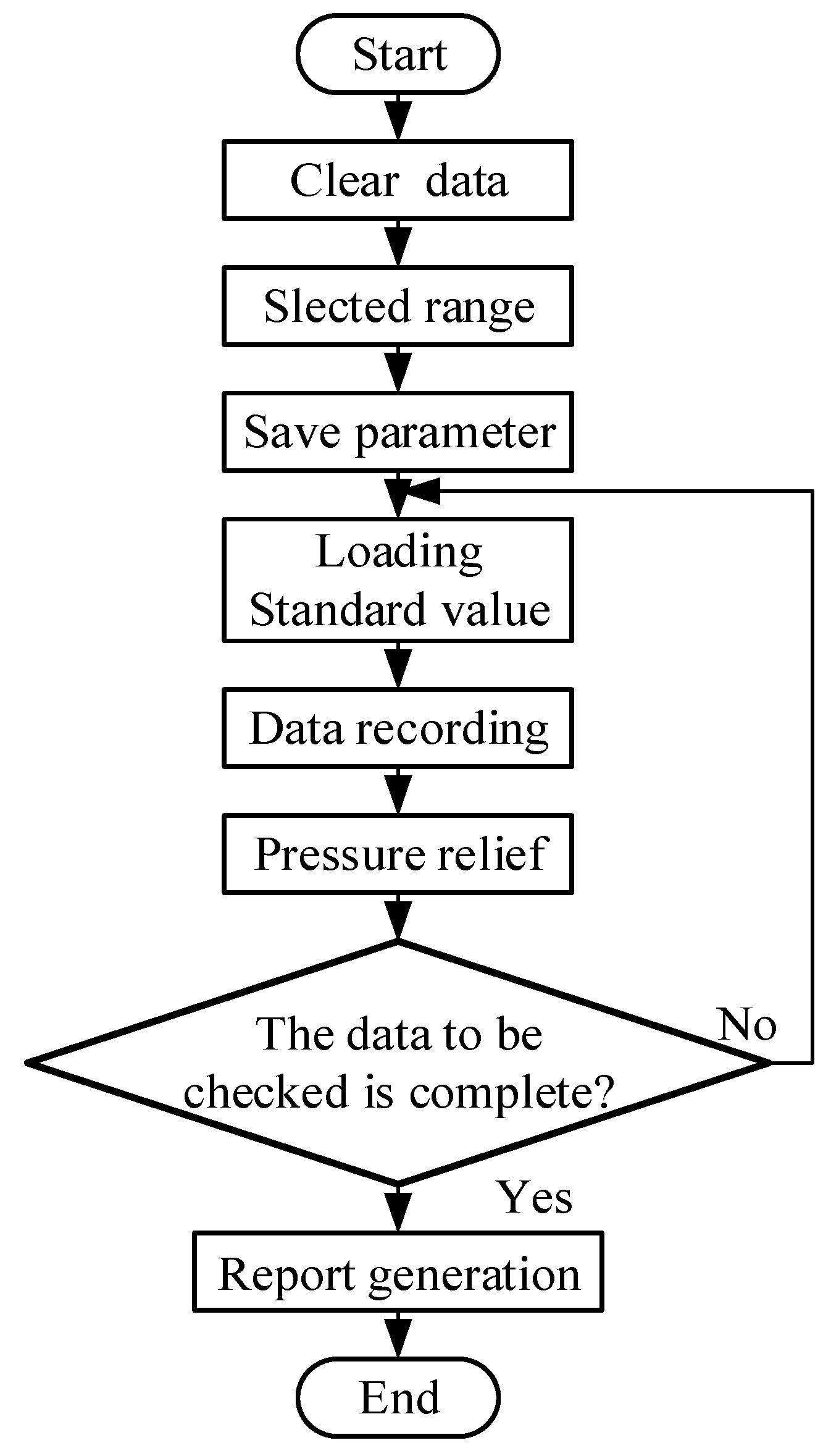
2.3. Control Software
3. Experimental Test and Uncertainty Evaluation
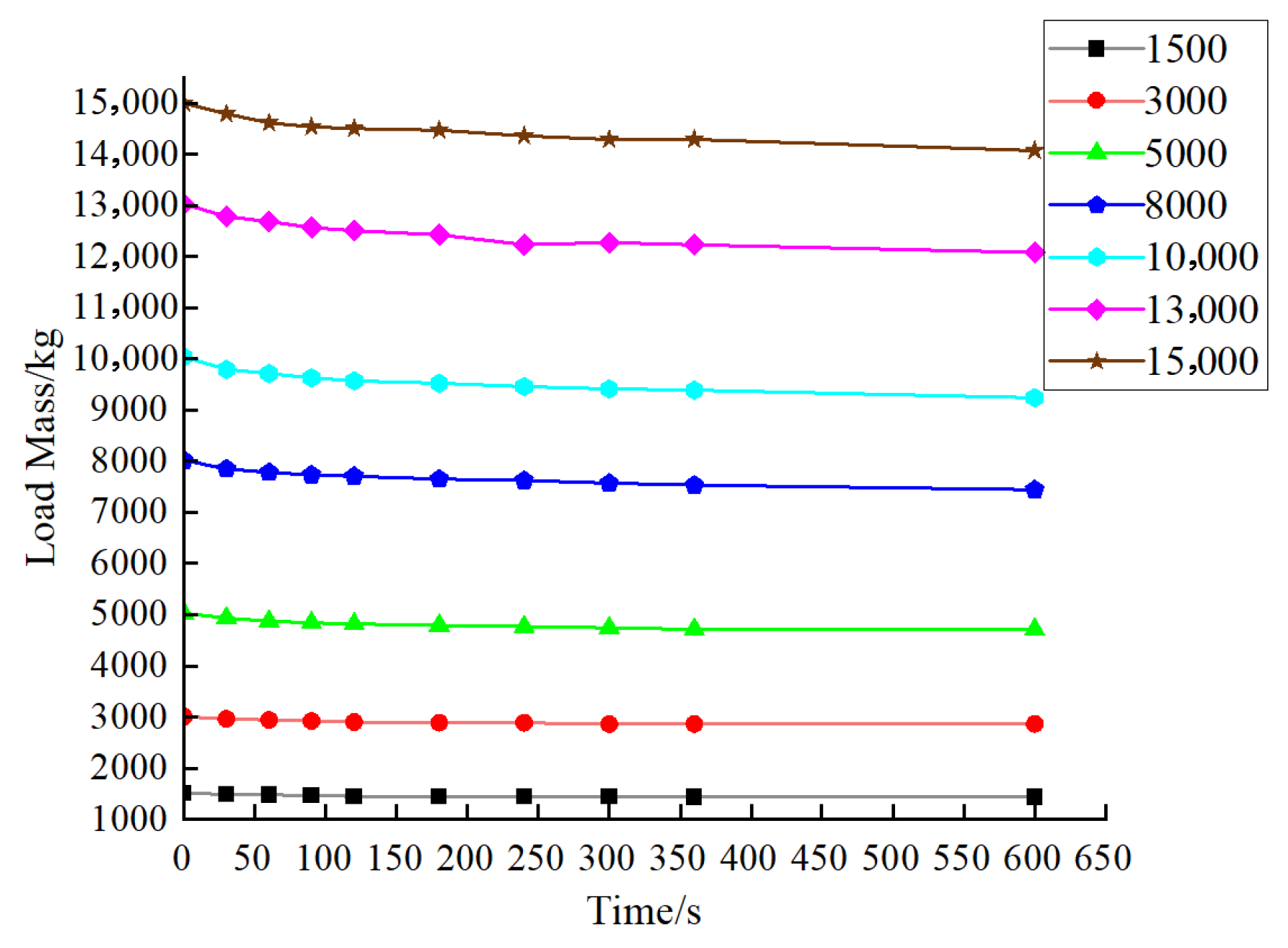
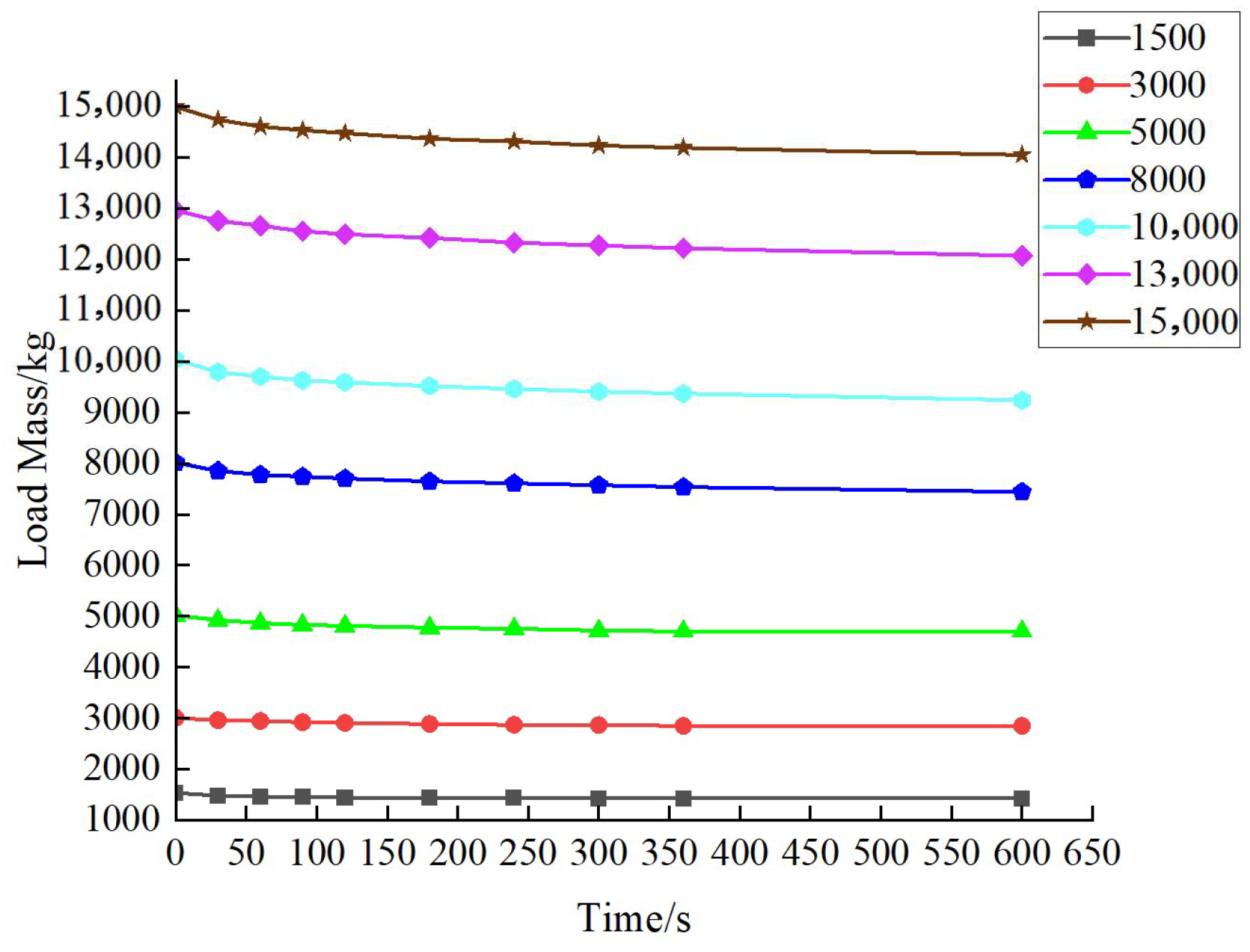
3.1. Experimental Test
3.2. Uncertainty Evaluation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pollaris, H.; Braekers, K.; Caris, A.; Janssens, G.K.; Limbourg, S. Capacitated vehicle routing problem with sequence-based pallet loading and axle weight constraints. EURO J. Transp. Logist. 2016, 5, 231–255. [Google Scholar] [CrossRef]
- Corinna, K.; Jan, F.E. Axle Weights in combined Vehicle Routing and Container Loading Problems. EURO J. Transp. Logist. 2021, 10, 100043. [Google Scholar] [CrossRef]
- Arnold, J.; Ján, O.; Jakub, C. Assessment of the axle loads on the semi-trailer: Case study. Transp. Res. Procedia 2025, 87, 205–216. [Google Scholar] [CrossRef]
- JJG 1014-2019; Verification Regulation of Special Axle (Wheel) Load Scales for Motor Vehicle Test. State Administration for Market Regulation: Beijing, China, 2020. (In Chinese)
- Van Loo, H.; Znidaric, A. Guide for Users of Weigh-in-Motion; ISWIM, International Society for Weigh-in-Motion: Dübendorf, Switzerland; Tiskarna Knjigoveznica Radovljica, Ltd.: Radovljica, Slovenia, 2019. [Google Scholar]
- Burnos, P.; Gajda, J. Optimised Autocalibration Algorithm of Weigh-In-Motion Systems for Direct Mass Enforcement. Sensors 2020, 20, 3049. [Google Scholar] [CrossRef] [PubMed]
- Haider, S.W.; Singh, R.R.; Wang, H. Impact of surface roughness, speed, and sensor configuration on weigh-in-motion (WIM) system accuracy. Int. J. Pavement Res. Technol. 2025, 18, 123–135. [Google Scholar] [CrossRef]
- Hossain, N.; Singh, D.; Zaman, M. Sensitivity of traffic input parameters on rutting performance of a flexible pavement using mechanistic empirical pavement design guide. Int. J. Pavement Res. Technol. 2016, 9, 450–459. [Google Scholar] [CrossRef]
- Burnos, P.; Gajda, J.; Sroka, R. Accuracy Criteria for Evaluation of Weigh-in-Motion Systems. Metrol. Meas. Syst. 2018, 25, 743–754. [Google Scholar] [CrossRef]
- Socha, A.; Izydorczyk, J. Strain Gauge Calibration for High Speed Weight-in-Motion Station. Sensors 2024, 24, 4845. [Google Scholar] [CrossRef] [PubMed]
- Sarnecki, R.; Wiśniewski, W.; Ślusarski, W.; Wiłkojć, P. Traceable calibration of automatic weighing instruments operating in dynamic mode. MATEC Web Conf. 2018, 182, 02005. [Google Scholar] [CrossRef]
- Masud, M.M.; Haider, S.W.; Selezneva, O.; Wolf, D.J. Representative Weigh-In-Motion (WIM) System Accuracy and Guidelines for Equipment Selection Based on Sensor, Site, and Calibration-Related Factors. Int. J. Pavement Res. Technol. 2024, 17, 732–749. [Google Scholar] [CrossRef]
- Masud, M.M.; Haider, S.W. Guidelines for effective weigh-in-motion (WIM) equipment calibration, application for modeling WIM errors, and comparison of the ASTM and LTPP accuracy protocols. Int. J. Pavement Res. Technol. 2024, 17, 1124–1144. [Google Scholar] [CrossRef]
- Sroka, R.; Gajda, J.; Burnos, P.; Daniol, M.; Kania-Markocka, A.; Slusarski, W.; Ziolkowski, R.; Strzalka, P. Calibration of Weigh-In-Motion Systems—Metrological Assessment of Methods for Determining Reference Values. Metrol. Meas. Syst. 2025, 32, 1–15. [Google Scholar] [CrossRef]
- Quan, Z.; Quan, L.; Zhang, J. Review of Energy Efficient Direct Pump Controlled Cylinder Electro-Hydraulic Technology. Renew. Sustain. Energy Rev. 2014, 35, 336–346. [Google Scholar] [CrossRef]
- Yan, Z.; Tang, G.; Wang, A.; Zhao, Z.; Gao, Y. Performance Comparison of Different Motor Pump Controlled Two-Stage Hydraulic Cylinders. Mach. Tool Hydraul. 2025, 53, 141–148. [Google Scholar]
- Zhao, W.; Ebbesen, M.K.; Hansen, M.R.; Andersen, T.O. Mitigating Mode Switching Oscillation in a One-Motor-One-Pump Motor-Controlled Hydraulic Cylinder via System Pressure Control: Simulation Study. Energies 2024, 17, 6334. [Google Scholar] [CrossRef]
- Li, Y.; Ai, C.; Yan, G.; Zhang, T.; Chen, G.; Jia, C.; Chen, W. Flexible Transmission Ratio Theory of Electro-hydraulic Servo Pump Control System. Chin. Hydraul. Pneum. 2021, 45, 10–17. (In Chinese) [Google Scholar]
- Wang, Z.; Yin, C.; Ma, W.; Hu, C.; Da, W. Research on Distributed Pump-Controlled Synchronous System for Tower Cranes Based on Improved BP-PID. Mach. Tool Hydraul. 2025, 53, 79–84. (In Chinese) [Google Scholar]
- Kang, D.; Yokota, K. Analytical Study of Cavitation Surge in a Hydraulic System. ASME J. Fluids Eng. 2014, 136, 101–103. [Google Scholar] [CrossRef] [PubMed]
- Jafar, M.H.; Moayed, W.M. The Effect of Hydraulic Accumulator on the Performance of Hydraulic System. J. Eng. 2014, 20, 174–190. [Google Scholar]
- Dong, J.; Cao, Y.; Chen, Q.; Wu, Y.; Liu, R.G.; Liu, W.; Yang, Y.; Yang, Z. Performance of Single Piezoelectric Vibrator Micropump with Check Valve. J. Intell. Mater. Syst. Struct. 2020, 31, 117–126. [Google Scholar] [CrossRef]
- JJG860-2015; Verification Regulation of Pressure Transducer (Static). State Administration for Market Regulation: Beijing, China, 2015. (In Chinese)



| Component Name | Type Specification |
|---|---|
| Servo Motor | 400 W 3000 RPM |
| Gear Pump | 0.5 cc/r |
| Reversing Valve3 | 20 L/min |
| Reversing Valve4 | 18.9 L/min |
| Overflow Valve | 10 L/min |
| Accumulator | 0.32 L |
| Hydraulic Cylinder | ϕ100 mm |
| Parameters | Data |
|---|---|
| 3 | |
| 7.854 × 10−3 m2 | |
| 7.96 × 10−7 m3/rad | |
| 9.483 × 10−4 m3 | |
| 1.5 × 101 Pa | |
| 2.4 kg | |
| 3.8 × 10−4 N·m·s/rad |
| Standard Value/N | Standard Dynamometer Calibration Value | |
|---|---|---|
| Value1/N | Value2/N | |
| 0 | 0 | 0 |
| 15,000 | 15,027 | 15,040 |
| 30,000 | 30,083 | 30,090 |
| 45,000 | 45,020 | 45,070 |
| 60,000 | 59,967 | 60,050 |
| 75,000 | 74,943 | 75,040 |
| 90,000 | 89,917 | 90,040 |
| 120,000 | 119,860 | 120,000 |
| 150,000 | 149,860 | 149,940 |
| Time/s | Load Mass/kg | ||||||
|---|---|---|---|---|---|---|---|
| 1500 | 3000 | 5000 | 8000 | 10,000 | 13,000 | 15,000 | |
| 0 | 1519.0 | 3006.2 | 5023.0 | 8016.0 | 10,033.0 | 13,020.0 | 14,995.0 |
| 30 | 1486.1 | 2960.6 | 4935.4 | 7849.2 | 9793.0 | 12,779.5 | 14,785.3 |
| 60 | 1475.6 | 2939.5 | 4872.0 | 7779.3 | 9709.0 | 12,680.5 | 14,608.0 |
| 90 | 1470.5 | 2920.5 | 4838.5 | 7732.1 | 9630.5 | 12,563.4 | 14,532.0 |
| 120 | 1448.0 | 2900.3 | 4819.7 | 7705.4 | 9566.2 | 12,503.1 | 14,500.0 |
| 180 | 1448.4 | 2885.4 | 4790.3 | 7649.5 | 9520.5 | 12,420.8 | 14,464.0 |
| 240 | 1448.3 | 2885.4 | 4765.4 | 7621.7 | 9455.0 | 12,231.0 | 14,356.0 |
| 300 | 1448.2 | 2860.5 | 4740.8 | 7570.4 | 9411.5 | 12,269.0 | 14,285.0 |
| 360 | 1430.6 | 2860.8 | 4712.0 | 7532.4 | 9386.4 | 12,224.0 | 14,285.0 |
| 600 | 1430.6 | 2860.8 | 4712.0 | 7443.6 | 9238.0 | 12,080.0 | 14,069.0 |
| Time/s | Load Mass/kg | ||||||
|---|---|---|---|---|---|---|---|
| 1500 | 3000 | 5000 | 8000 | 10,000 | 13,000 | 15,000 | |
| 0 | 1536.2 | 3008.0 | 5017.0 | 8017.0 | 10,035.0 | 12,965.0 | 14,995.0 |
| 30 | 1481.1 | 2962.2 | 4925.1 | 7851.0 | 9794.0 | 12,757.7 | 14,739.0 |
| 60 | 1462.7 | 2943.8 | 4869.8 | 7776.7 | 9702.7 | 12,664.9 | 14,609.0 |
| 90 | 1462.7 | 2925.3 | 4832.4 | 7739.8 | 9628.6 | 12,554.3 | 14,535.0 |
| 120 | 1444.2 | 2906.9 | 4813.9 | 7702.9 | 9591.0 | 12,498.4 | 14,479.0 |
| 180 | 1444.2 | 2888.5 | 4777.0 | 7647.0 | 9517.1 | 12,424.6 | 14,368.0 |
| 240 | 1443.7 | 2870.0 | 4758.6 | 7610.0 | 9461.8 | 12,331.8 | 14,313.0 |
| 300 | 1425.8 | 2865.5 | 4721.7 | 7573.2 | 9406.5 | 12,276.5 | 14,238.0 |
| 360 | 1425.8 | 2851.6 | 4703.2 | 7535.8 | 9369.0 | 12,220.6 | 14,192.0 |
| 600 | 1425.8 | 2851.6 | 4703.2 | 7443.6 | 9239.4 | 12,072.5 | 14,053.0 |
| Hydraulic Unit | Data1/kg | Data2/kg | Data3/kg | Repeatability |
|---|---|---|---|---|
| 1 | 3006.0 | 3005.0 | 3006.0 | 0.033% |
| 2 | 3008.0 | 3008.0 | 3009.0 | 0.033% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, L.; Xu, Z.; Zhou, B.; Zhang, G. Design of a Verification Device of Motor Axle Wheel Load Scales Based on Pump-Controlled Hydraulic Cylinder. Sensors 2025, 25, 7180. https://doi.org/10.3390/s25237180
Hao L, Xu Z, Zhou B, Zhang G. Design of a Verification Device of Motor Axle Wheel Load Scales Based on Pump-Controlled Hydraulic Cylinder. Sensors. 2025; 25(23):7180. https://doi.org/10.3390/s25237180
Chicago/Turabian StyleHao, Long, Zhipeng Xu, Bin Zhou, and Gaoming Zhang. 2025. "Design of a Verification Device of Motor Axle Wheel Load Scales Based on Pump-Controlled Hydraulic Cylinder" Sensors 25, no. 23: 7180. https://doi.org/10.3390/s25237180
APA StyleHao, L., Xu, Z., Zhou, B., & Zhang, G. (2025). Design of a Verification Device of Motor Axle Wheel Load Scales Based on Pump-Controlled Hydraulic Cylinder. Sensors, 25(23), 7180. https://doi.org/10.3390/s25237180






