Takens-Based Kernel Transfer Entropy Connectivity Network for Motor Imagery Classification
Abstract
1. Introduction
2. Mathematical Framework
2.1. Channel-Wise Nonlinear Time Series Embedding from Takens’ Convolutional Layer
2.2. Transfer Entropy from Kernel Matrices
2.3. Transfer Entropy-Based EEG Classification Model
3. Experimental Setup
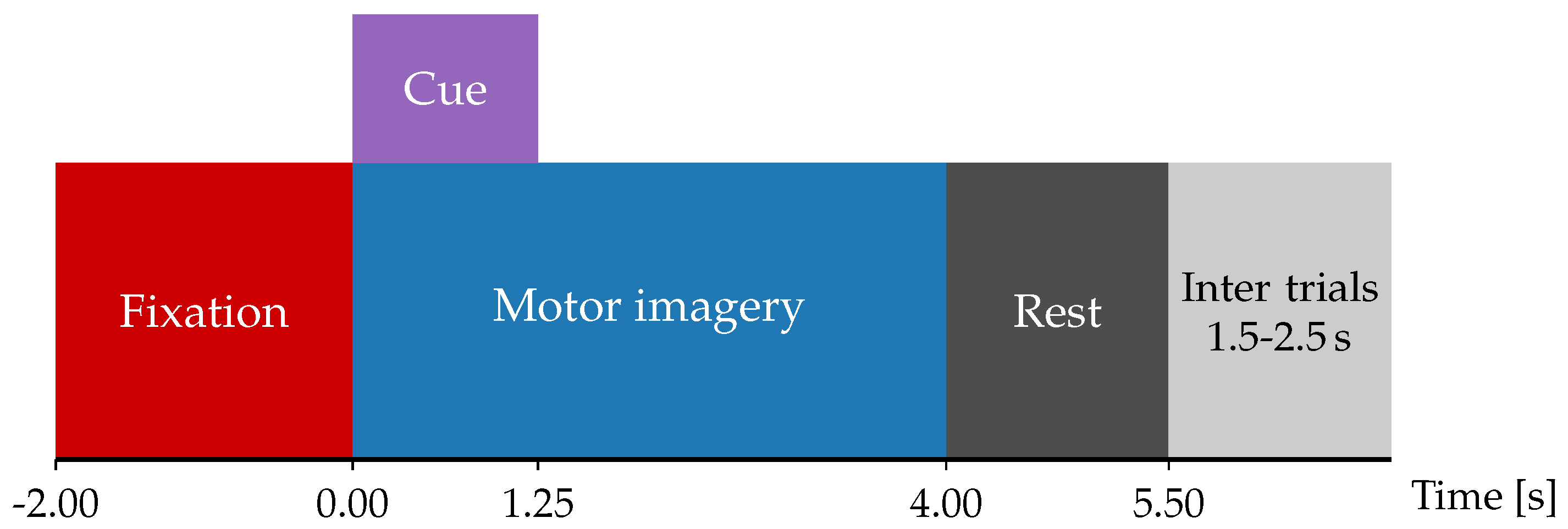
3.1. Dataset and Preprocessing
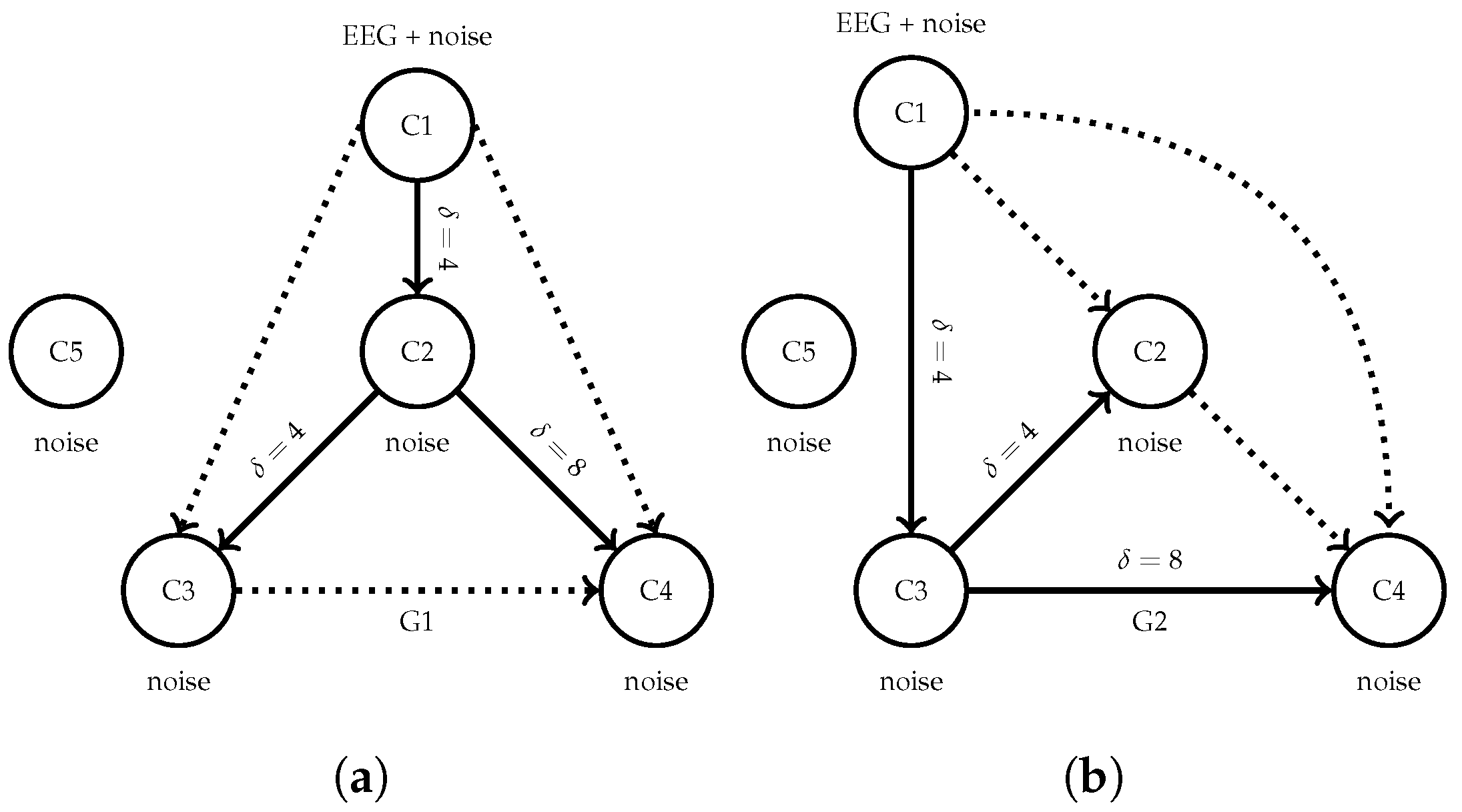
3.2. Semi-Synthetic Causal EEG Benchmark
3.3. Model Setup and Hyperparameter Tuning
4. Results and Discussion
4.1. Performance on Semi-Synthetic Causal EEG Data
4.2. Hyperparameter Tuning
4.3. Interpretability Analysis
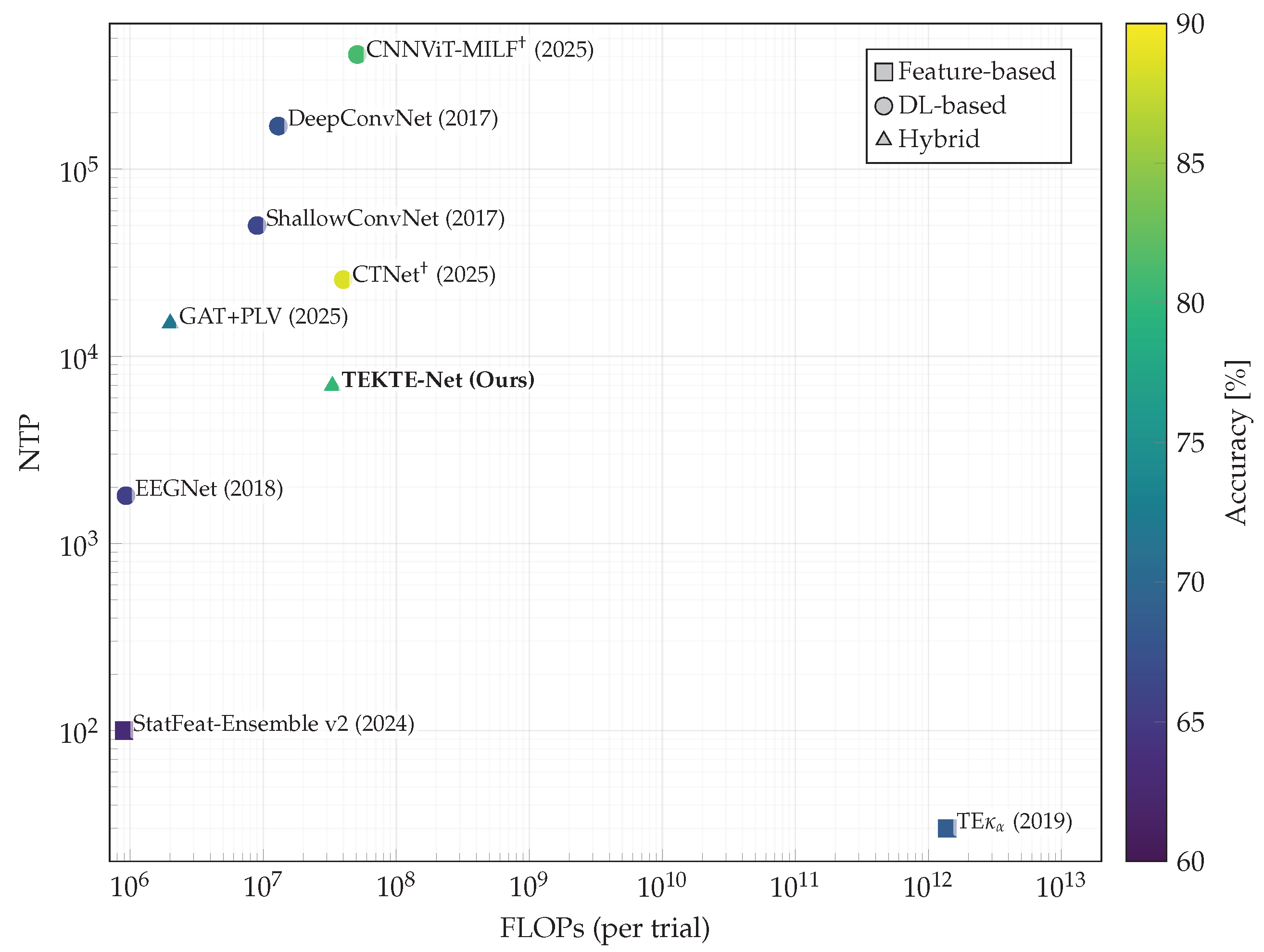
4.4. Performance Assessment
5. Concluding Remarks and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Padfield, N.; Zabalza, J.; Zhao, H.; Masero, V.; Ren, J. EEG-Based Brain-Computer Interfaces Using Motor-Imagery: Techniques and Challenges. Sensors 2019, 19, 1423. [Google Scholar] [CrossRef] [PubMed]
- Fraiwan, M.; Alafeef, M.; Almomani, F. Gauging human visual interest using multiscale entropy analysis of EEG signals. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 2435–2447. [Google Scholar] [CrossRef]
- Kavsaoğlu, A.; Polat, K.; Aygun, A. EEG based brain-computer interface control applications: A comprehensive review. J. Bionic Mem. 2021, 1, 20–33. [Google Scholar] [CrossRef]
- Djamal, C.; Putra, R. Brain-computer interface of focus and motor imagery using wavelet and recurrent neural networks. TELKOMNIKA (Telecommun. Comput. Electron. Control.) 2020, 18, 2748. [Google Scholar] [CrossRef]
- Maya-Piedrahita, M.C.; Herrera-Gomez, P.M.; Berrío-Mesa, L.; Cárdenas-Peña, D.A.; Orozco-Gutierrez, A.A. Supported Diagnosis of Attention Deficit and Hyperactivity Disorder from EEG Based on Interpretable Kernels for Hidden Markov Models. Int. J. Neural Syst. 2022, 32, 2250008. [Google Scholar] [CrossRef] [PubMed]
- Bonnet, C.; Bayram, M.; El Bouzaïdi Tiali, S.; Lebon, F.; Harquel, S.; Palluel-Germain, R.; Perrone-Bertolotti, M. Kinesthetic motor-imagery training improves performance on lexical-semantic access. PLoS ONE 2022, 17, e0270352. [Google Scholar] [CrossRef]
- United Nations, Economic Commission for Latin America and the Caribbean (ECLAC). The 2030 Agenda and the Sustainable Development Goals: An Opportunity for Latin America and the Caribbean. Goals, Targets and Global Indicators; United Nations: Santiago, Chile, 2018. [Google Scholar]
- Miao, M.; Hu, W.; Yin, H.; Zhang, K. Spatial-Frequency Feature Learning and Classification of Motor Imagery EEG Based on Deep Convolution Neural Network. Comput. Math. Methods Med. 2020, 2020, 1981728. [Google Scholar] [CrossRef]
- He, H.; Wu, D. Transfer Learning for Brain-Computer Interfaces: A Euclidean Space Data Alignment Approach. IEEE Trans. Biomed. Eng. 2019, 67, 399–410. [Google Scholar] [CrossRef]
- Marcos-Martínez, D.; Martínez-Cagigal, V.; Santamaría-Vázquez, E.; Pérez-Velasco, S.; Hornero, R. Neurofeedback Training Based on Motor Imagery Strategies Increases EEG Complexity in Elderly Population. Entropy 2021, 23, 1574. [Google Scholar] [CrossRef]
- Arns, M.; Conners, C.; Kraemer, H. A Decade of EEG Theta/Beta Ratio Research in ADHD. J. Atten. Disord. 2013, 17, 374–383. [Google Scholar] [CrossRef]
- Nicolas-Alonso, L.F.; Gomez-Gil, J. Brain Computer Interfaces, a Review. Sensors 2012, 12, 1211–1279. [Google Scholar] [CrossRef] [PubMed]
- Abiri, R.; Borhani, S.; Sellers, E.; Jiang, Y.; Zhao, X. A comprehensive review of EEG-based brain–computer interface paradigms. J. Neural Eng. 2019, 16, 011001. [Google Scholar] [CrossRef] [PubMed]
- Becker, S.; Dhindsa, K.; Mousapour, L.; Dabagh, Y. BCI Illiteracy: It’s Us, Not Them. Optimizing BCIs for Individual Brains. In Proceedings of the 2022 10th International Winter Conference on Brain-Computer Interface (BCI), Gangwon-do, Republic of Korea, 21–23 February 2022; pp. 1–3. [Google Scholar] [CrossRef]
- Shoka, A.; Dessouky, M.; el sherbeny, A.; El-Sayed, A. Literature Review on EEG Preprocessing, Feature Extraction, and Classifications Techniques. Menoufia J. Electron. Eng. Res. 2019, 28, 292–299. [Google Scholar] [CrossRef]
- Cardona-Álvarez, Y.N.; Álvarez Meza, A.M.; Cárdenas-Peña, D.A.; Castaño-Duque, G.A.; Castellanos-Dominguez, G. A Novel OpenBCI Framework for EEG-Based Neurophysiological Experiments. Sensors 2023, 23, 3763. [Google Scholar] [CrossRef]
- Blankertz, B.; Tomioka, R.; Lemm, S.; Kawanabe, M.; Müller, K.R. Optimizing spatial filters for robust EEG single-trial analysis. IEEE Signal Process. Mag. 2007, 25, 41–56. [Google Scholar] [CrossRef]
- Luo, T.; Lv, J.; Chao, F.; Zhou, C. Effect of different movement speed modes on human action observation: An EEG study. Front. Neurosci. 2018, 12, 219. [Google Scholar] [CrossRef]
- Galindo-Noreña, S.; Cárdenas-Peña, D.; Orozco-Gutierrez, A. Multiple Kernel Stein Spatial Patterns for the Multiclass Discrimination of Motor Imagery Tasks. Appl. Sci. 2020, 10, 8628. [Google Scholar] [CrossRef]
- Zhang, L.; Guindani, M.; Vannucci, M. Bayesian models for functional magnetic resonance imaging data analysis. Wiley Interdiscip. Rev. Comput. Stat. 2015, 7, 21–41. [Google Scholar] [CrossRef]
- Rolls, E.; Deco, G.; Huang, C.C.; Feng, J. The Effective Connectivity of the Human Hippocampal Memory System. Cereb. Cortex 2022, 32, 3706–3725. [Google Scholar] [CrossRef]
- Martini, M.; Oermann, E.; Opie, N.; Panov, F.; Oxley, T.; Yaeger, K. Sensor Modalities for Brain-Computer Interface Technology: A Comprehensive Literature Review. Neurosurgery 2019, 86, E108–E117. [Google Scholar] [CrossRef]
- Kundu, S. AI in medicine must be explainable. Nat. Med. 2021, 27, 1328. [Google Scholar] [CrossRef]
- Patel, R.; Zhu, Z.; Bryson, B.; Carlson, T.; Jiang, D.; Demosthenous, A. Advancing EEG classification for neurodegenerative conditions using BCI: A graph attention approach with phase synchrony. Neuroelectronics 2025, 1, 0001. [Google Scholar] [CrossRef]
- García-Murillo, D.G.; Álvarez Meza, A.M.; Castellanos-Dominguez, C.G. KCS-FCnet: Kernel Cross-Spectral Functional Connectivity Network for EEG-Based Motor Imagery Classification. Diagnostics 2023, 13, 1122. [Google Scholar] [CrossRef] [PubMed]
- Staniek, M.; Lehnertz, K. Symbolic Transfer Entropy. Phys. Rev. Lett. 2008, 100, 158101. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.; Barrett, A.; Barnett, L. Granger Causality Analysis in Neuroscience and Neuroimaging. J. Neurosci. Off. J. Soc. Neurosci. 2015, 35, 3293–3297. [Google Scholar] [CrossRef]
- Sanchez Giraldo, L.G.; Rao, M.; Principe, J.C. Measures of Entropy From Data Using Infinitely Divisible Kernels. IEEE Trans. Inf. Theory 2015, 61, 535–548. [Google Scholar] [CrossRef]
- Tangermann, M.; Müller, K.R.; Aertsen, A.; Birbaumer, N.; Braun, C.; Brunner, C.; Leeb, R.; Mehring, C.; Miller, K.J.; Müller-Putz, G.R.; et al. Review of the BCI competition IV. Front. Neurosci. 2012, 6, 55. [Google Scholar] [CrossRef]
- Tenke, C.E.; Kayser, J. Surface Laplacians (SL) and phase properties of EEG rhythms: Simulated generators in a volume-conduction model. Int. J. Psychophysiol. 2015, 97, 285–298. [Google Scholar] [CrossRef]
- Hua, H.; Feng, B.; Yuan, Z.; Xiong, Q.; Shu, L.; Wang, T.; Xu, X. Scalp Surface Laplacian Potential Monitoring System Based on Novel Hydrogel Active Tri-Polar Concentric Ring Electrodes. Sensors Actuators A Phys. 2024, 379, 116003. [Google Scholar] [CrossRef]
- Lu, J.; Mcfarland, D.; Wolpaw, J. Adaptive Laplacian filtering for sensorimotor rhythm-based brain–computer interfaces. J. Neural Eng. 2012, 10, 016002. [Google Scholar] [CrossRef] [PubMed]
- Kapralov, N.; Jamshidi, M.; Stephani, T.; Studenova, A.; Vidaurre, C.; Ros, T.; Villringer, A.; Nikulin, V. Sensorimotor brain–computer interface performance depends on signal-to-noise ratio but not connectivity of the mu rhythm in a multiverse analysis of longitudinal data. J. Neural Eng. 2024, 21, 056027. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Nollo, G.; Porta, A. Information-based detection of nonlinear Granger causality in multivariate processes via a nonuniform embedding technique. Phys. Rev. E 2011, 83, 051112. [Google Scholar] [CrossRef] [PubMed]
- Weber, I.; Ramirez, J.; Schölkopf, B.; Grosse-Wentrup, M. Causal model evaluation in the context of brain-behavior mediation analysis. NeuroImage 2017, 151, 69–83. [Google Scholar] [CrossRef]
- Kus, R.; Kaminski, M.; Blinowska, K. Determination of EEG activity propagation: Pair-wise versus multichannel estimate. IEEE Trans. Biomed. Eng. 2004, 51, 1501–1510. [Google Scholar] [CrossRef]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer Entropy—a model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef]
- Bossomaier, T.; Barnett, L.; Harré, M.; Lizier, J. An Introduction to Transfer Entropy; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Stramaglia, S.; Faes, L.; Cortes, J.M.; Marinazzo, D. Disentangling high-order effects in the Transfer Entropy. Phys. Rev. Res. 2024, 6, L032007. [Google Scholar] [CrossRef]
- Barnett, L.; Barrett, A.; Seth, A. Granger Causality and Transfer Entropy Are Equivalent for Gaussian Variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef]
- De La Pava Panche, I.; Alvarez-Meza, A.M.; Orozco-Gutierrez, A. A Data-Driven Measure of Effective Connectivity Based on Renyi’s α-Entropy. Front. Neurosci. 2019, 13, 1277. [Google Scholar] [CrossRef]
- Penas, D.R.; Hashemi, M.; Jirsa, V.; Banga, J. Parameter estimation in a whole-brain network model of epilepsy: Comparison of parallel global optimization solvers. bioRxiv 2023. [Google Scholar] [CrossRef]
- Rijn, E.; Widge, A. Failure modes and mitigations for Bayesian optimization of neuromodulation parameters. J. Neural Eng. 2025, 22. [Google Scholar] [CrossRef]
- Roy, S.; Chowdhury, A.; McCreadie, K.; Prasad, G. Deep learning based inter-subject continuous decoding of motor imagery for practical brain-computer interfaces. Front. Neurosci. 2020, 14, 918. [Google Scholar] [CrossRef]
- Ashburner, J.; Klöppel, S. Multivariate models of inter-subject anatomical variability. NeuroImage 2011, 56, 422–439. [Google Scholar] [CrossRef]
- Gaur, P.; Gupta, H.; Chowdhury, A.; McCreadie, K.; Pachori, R.; Wang, H. A Sliding Window Common Spatial Pattern for Enhancing Motor Imagery Classification in EEG-BCI. IEEE Trans. Instrum. Meas. 2021, 70, 4002709. [Google Scholar] [CrossRef]
- Huang, G.; Zhao, Z.; Zhang, S.; Hu, Z.; Fan, J.; Fu, M.; Chen, J.; Xiao, Y.; Wang, J.; Dan, G. Discrepancy between inter- and intra-subject variability in EEG-based motor imagery brain-computer interface: Evidence from multiple perspectives. Front. Neurosci. 2023, 17, 1122661. [Google Scholar] [CrossRef] [PubMed]
- Abdullah Almohammadi, Y.K.W. Revealing brain connectivity: Graph embeddings for EEG representation learning and comparative analysis of structural and functional connectivity. Front. Neurosci. 2024, 17, 1288433. [Google Scholar] [CrossRef] [PubMed]
- Leeuwis, N.; Yoon, S.; Alimardani, M. Functional connectivity analysis in motor-imagery brain computer interfaces. Front. Hum. Neurosci. 2021, 15, 732946. [Google Scholar] [CrossRef] [PubMed]
- Vidaurre, C.; Haufe, S.; Jorajuría, T.; Müller, K.R.; Nikulin, V.V. Sensorimotor functional connectivity: A neurophysiological factor related to BCI performance. Front. Neurosci. 2020, 14, 575081. [Google Scholar] [CrossRef]
- Angulo-Sherman, I.N.; León-Domínguez, U.; Martinez-Torteya, A.; Fragoso-González, G.A.; Martínez-Pérez, M.V. Proficiency in motor imagery is linked to the lateralization of focused ERD patterns and beta PDC. J. NeuroEngineering Rehabil. 2025, 22, 30. [Google Scholar] [CrossRef]
- Lasaponara, S.; Pinto, M.; Scozia, G.; Pellegrino, M.; D’Onofrio, M.; Doricchi, F. Pre-motor deficits in left spatial neglect: An EEG study on Contingent Negative Variation (CNV) and response-related beta oscillatory activity. Neuropsychologia 2020, 147, 107572. [Google Scholar] [CrossRef]
- Capotosto, P.; Babiloni, C.; Romani, G.L.; Corbetta, M. Differential Contribution of Right and Left Parietal Cortex to the Control of Spatial Attention: A Simultaneous EEG–rTMS Study. Cereb. Cortex 2011, 22, 446–454. [Google Scholar] [CrossRef] [PubMed]
- Bakhtiari, A.; Petersen, J.; Urdanibia Centelles, O.; Mehdipour Ghazi, M.; Fagerlund, B.; Mortensen, E.; Osler, M.; Lauritzen, M.; Benedek, K. Power and distribution of evoked gamma oscillations in brain aging and cognitive performance. GeroScience 2023, 45, 1523–1538. [Google Scholar] [CrossRef] [PubMed]
- Avital, N.; Nahum, E.; Levi, G.; Malka, D. Cognitive State Classification Using Convolutional Neural Networks on Gamma-Band EEG Signals. Appl. Sci. 2024, 14, 8380. [Google Scholar] [CrossRef]
- Degirmenci, M.; Yuce, Y.K.; Perc, M.; Isler, Y. EEG channel and feature investigation in binary and multiple motor imagery task predictions. Front. Hum. Neurosci. 2024, 17, 1525139. [Google Scholar] [CrossRef]
- Degirmenci, M.; Yuce, Y.K.; Perc, M.; Isler, Y. Statistically significant features improve binary and multiple Motor Imagery task predictions from EEGs. Front. Hum. Neurosci. 2023, 17, 1223307. [Google Scholar] [CrossRef]
- Schirrmeister, R.; Springenberg, J.; Fiederer, L.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization: Convolutional Neural Networks in EEG Analysis. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef]
- Lawhern, V.; Solon, A.; Waytowich, N.; Gordon, S.; Hung, C.; Lance, B. EEGNet: A compact convolutional neural network for EEG-based brain–computer interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef]
- Zhao, W.; Jiang, X.; Zhang, B.; Xiao, S.; Weng, S. CTNet: A convolutional transformer network for EEG-based motor imagery classification. Sci. Rep. 2024, 14, 20237. [Google Scholar] [CrossRef]
- Zhao, Z.; Cao, Y.; Yu, H.; Yu, H.; Huang, J. CNNViT-MILF-a: A Novel Architecture Leveraging the Synergy of CNN and ViT for Motor Imagery Classification. IEEE J. Biomed. Health Inform. 2025, early access. [Google Scholar] [CrossRef]
- Maksimenko, V.; Kurkin, S.; Pitsik, E.; Musatov, V.; Runnova, A.; Efremova, T.; Hramov, A.; Pisarchik, A. Artificial Neural Network Classification of Motor-Related EEG: An Increase in Classification Accuracy by Reducing Signal Complexity. Complexity 2018, 2018, 9385947. [Google Scholar] [CrossRef]
- Hramov, A.E.; Maksimenko, V.A.; Pisarchik, A.N. Physical principles of brain–computer interfaces and their applications for rehabilitation, robotics and control of human brain states. Phys. Rep. 2021, 918, 1–133. [Google Scholar] [CrossRef]
- Gordleeva, S.; Grigorev, N.; Pitsik, E.; Kurkin, S.; Kazantsev, V.; Hramov, A. Detection and rehabilitation of age-related motor skills impairment: Neurophysiological biomarkers and perspectives. Ageing Res. Rev. 2025, 113, 102923. [Google Scholar] [CrossRef]
- Chepurova, A.; Hramov, A.; Kurkin, S. Motor Imagery: How to Assess, Improve Its Performance, and Apply It for Psychosis Diagnostics. Diagnostics 2022, 12, 949. [Google Scholar] [CrossRef]
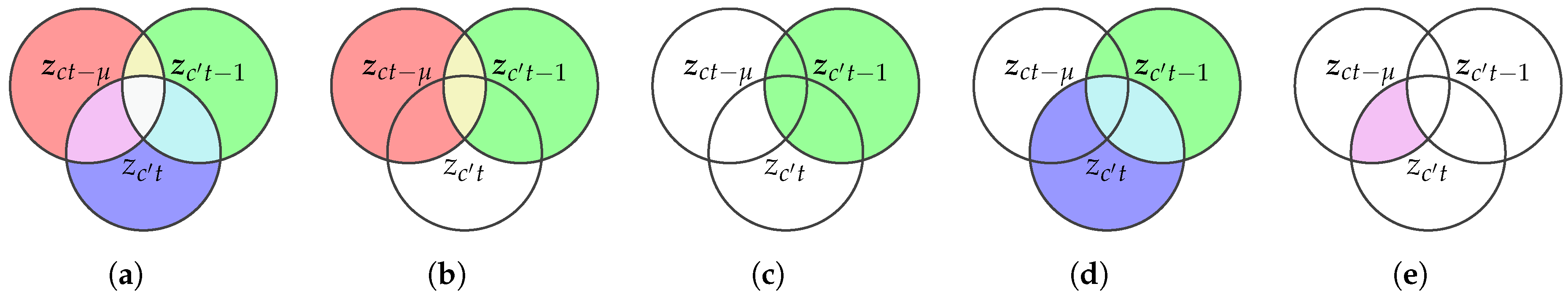
 Frontal left,
Frontal left,  Frontal,
Frontal,  Frontal right,
Frontal right,  Central left,
Central left,  Central right,
Central right,  Centro-parietal left,
Centro-parietal left,  Centro-parietal right,
Centro-parietal right,  Parietal left,
Parietal left,  Parietal right,
Parietal right,  Posterior.
Posterior.
 Frontal left,
Frontal left,  Frontal,
Frontal,  Frontal right,
Frontal right,  Central left,
Central left,  Central right,
Central right,  Centro-parietal left,
Centro-parietal left,  Centro-parietal right,
Centro-parietal right,  Parietal left,
Parietal left,  Parietal right,
Parietal right,  Posterior.
Posterior.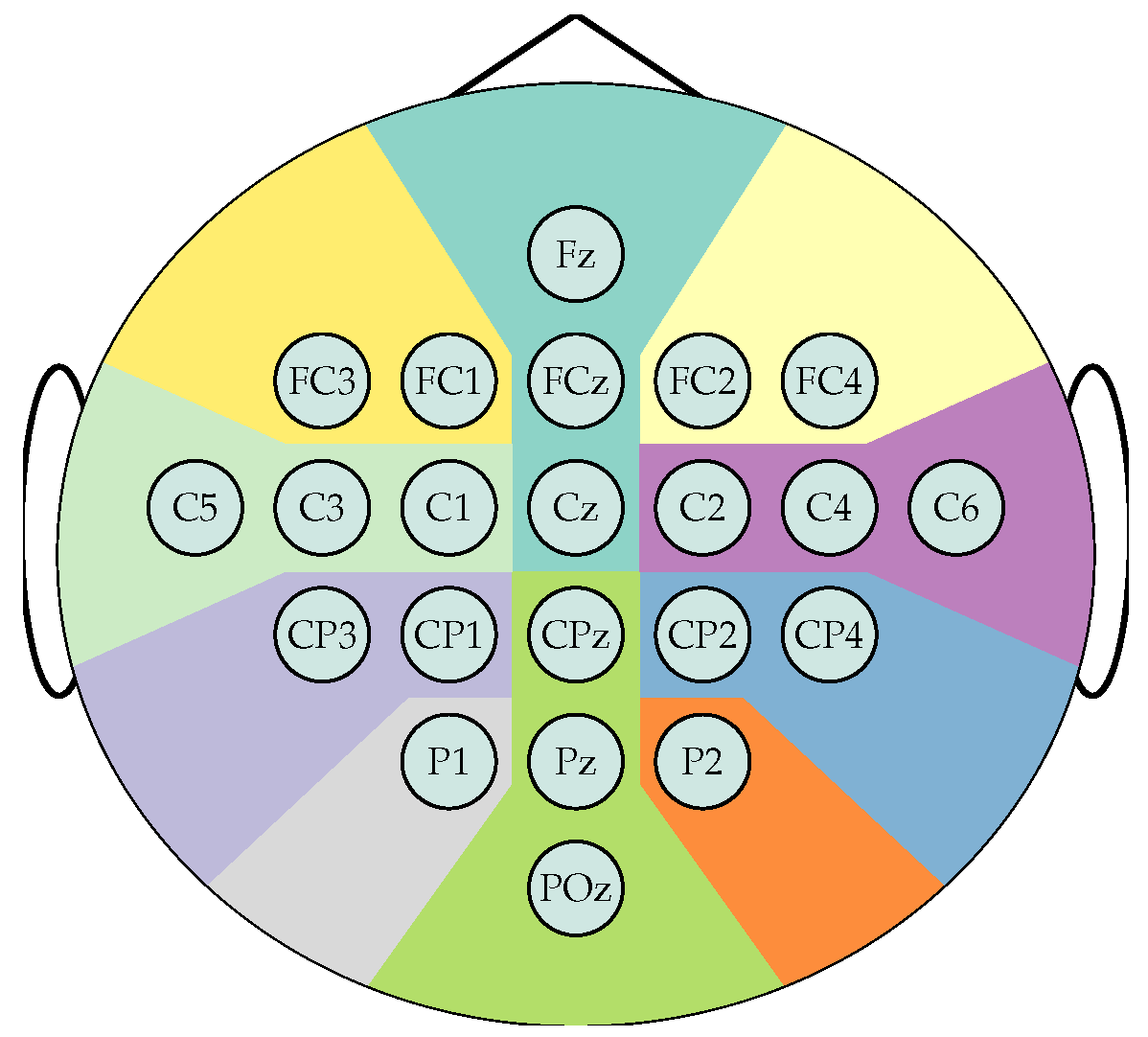
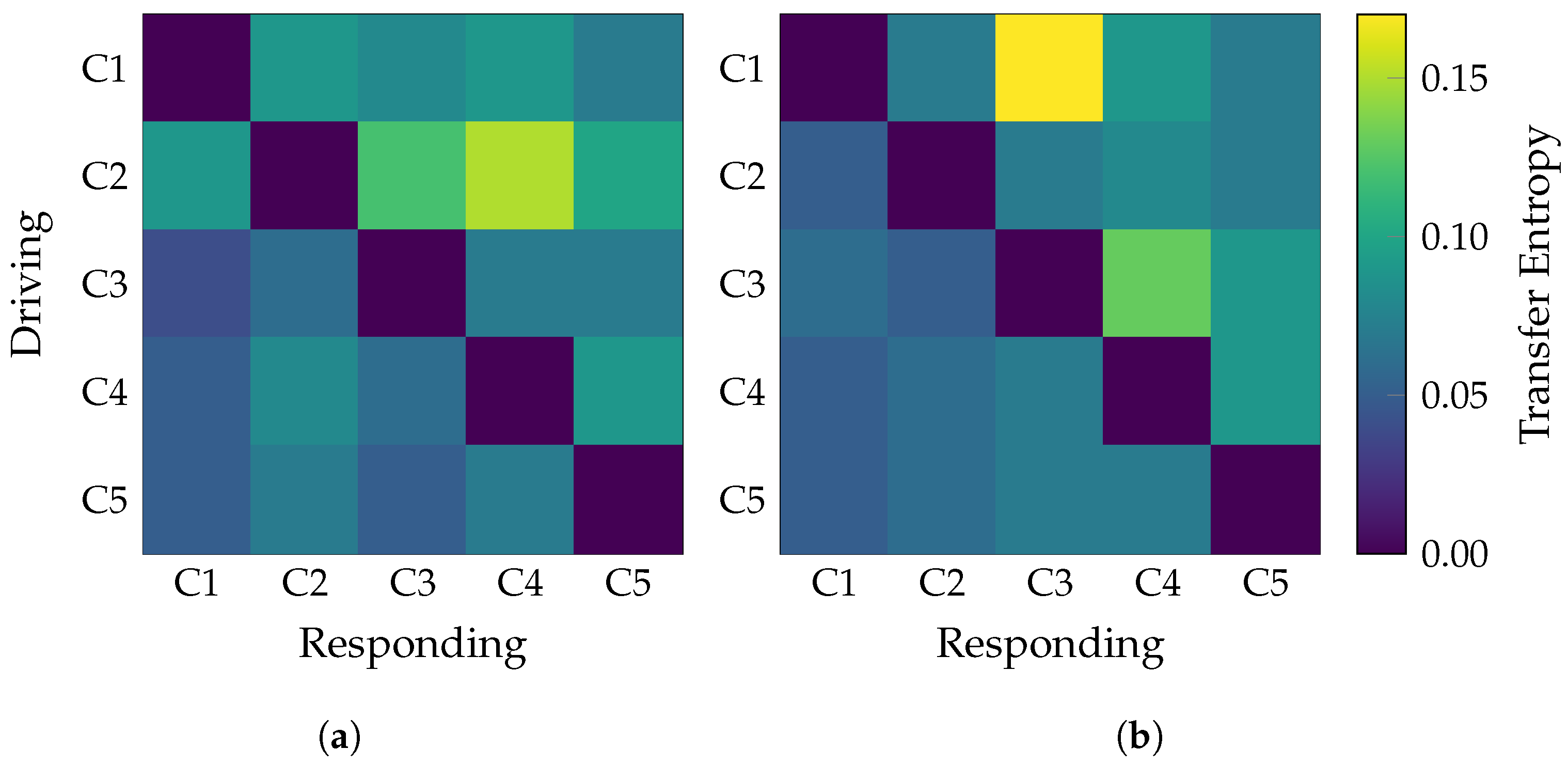
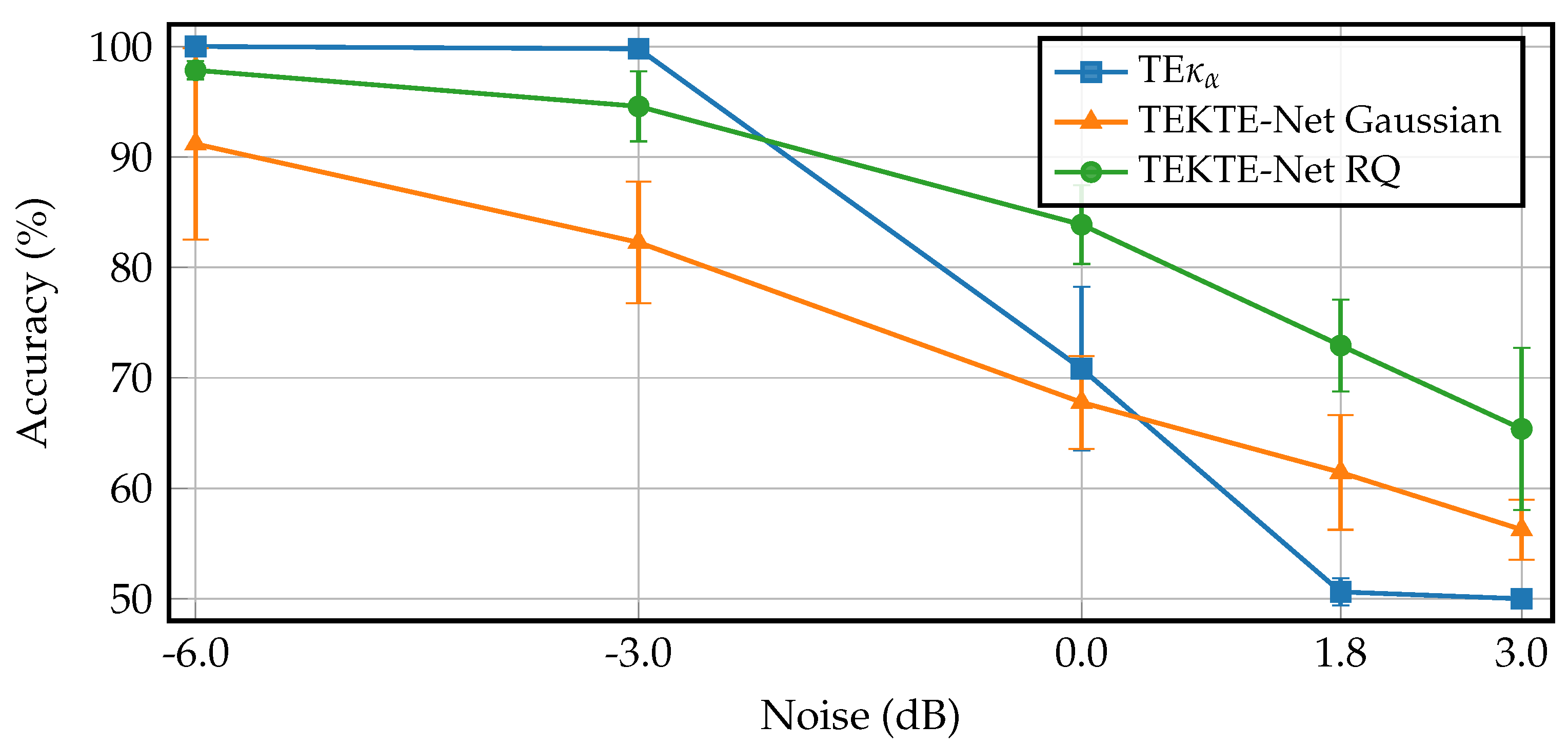
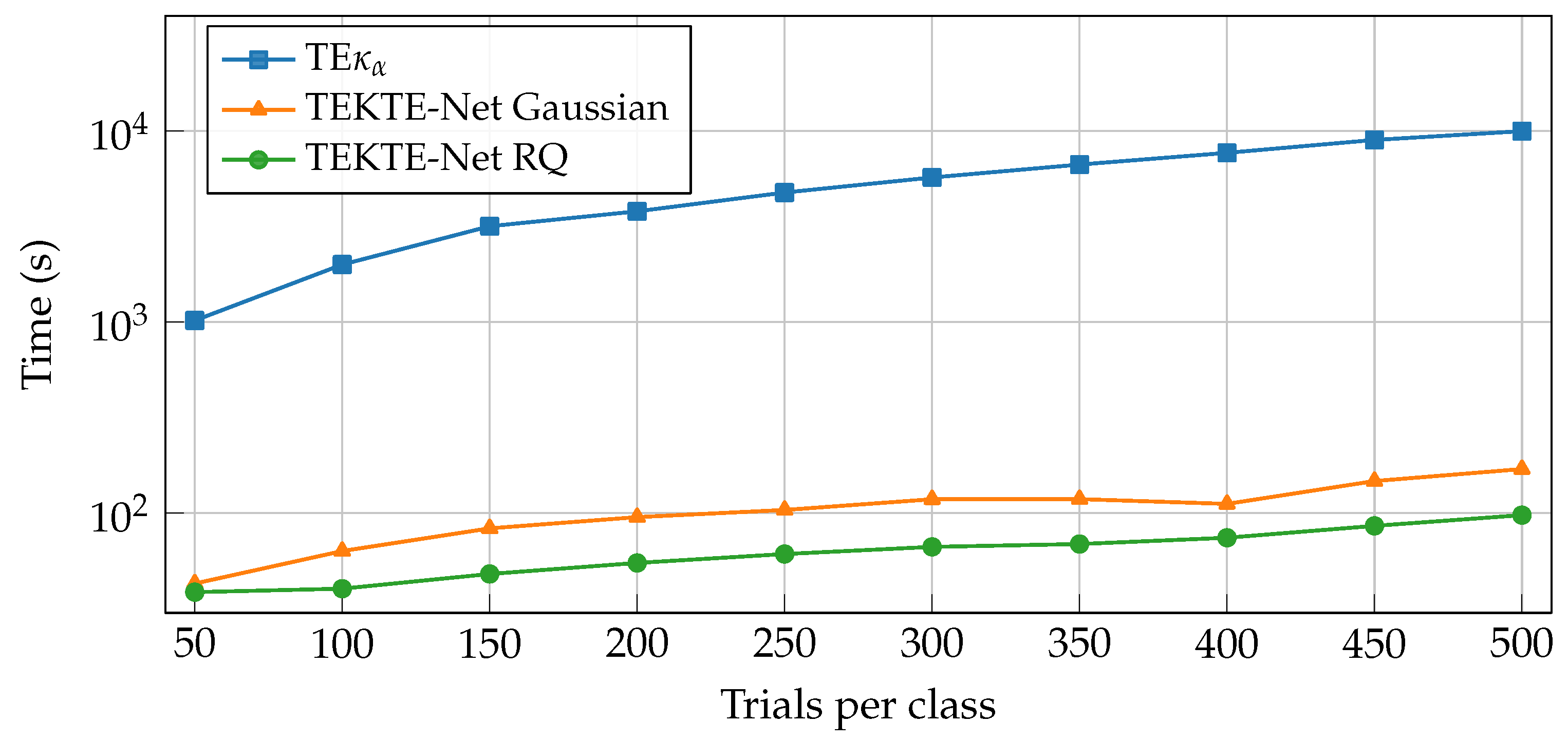
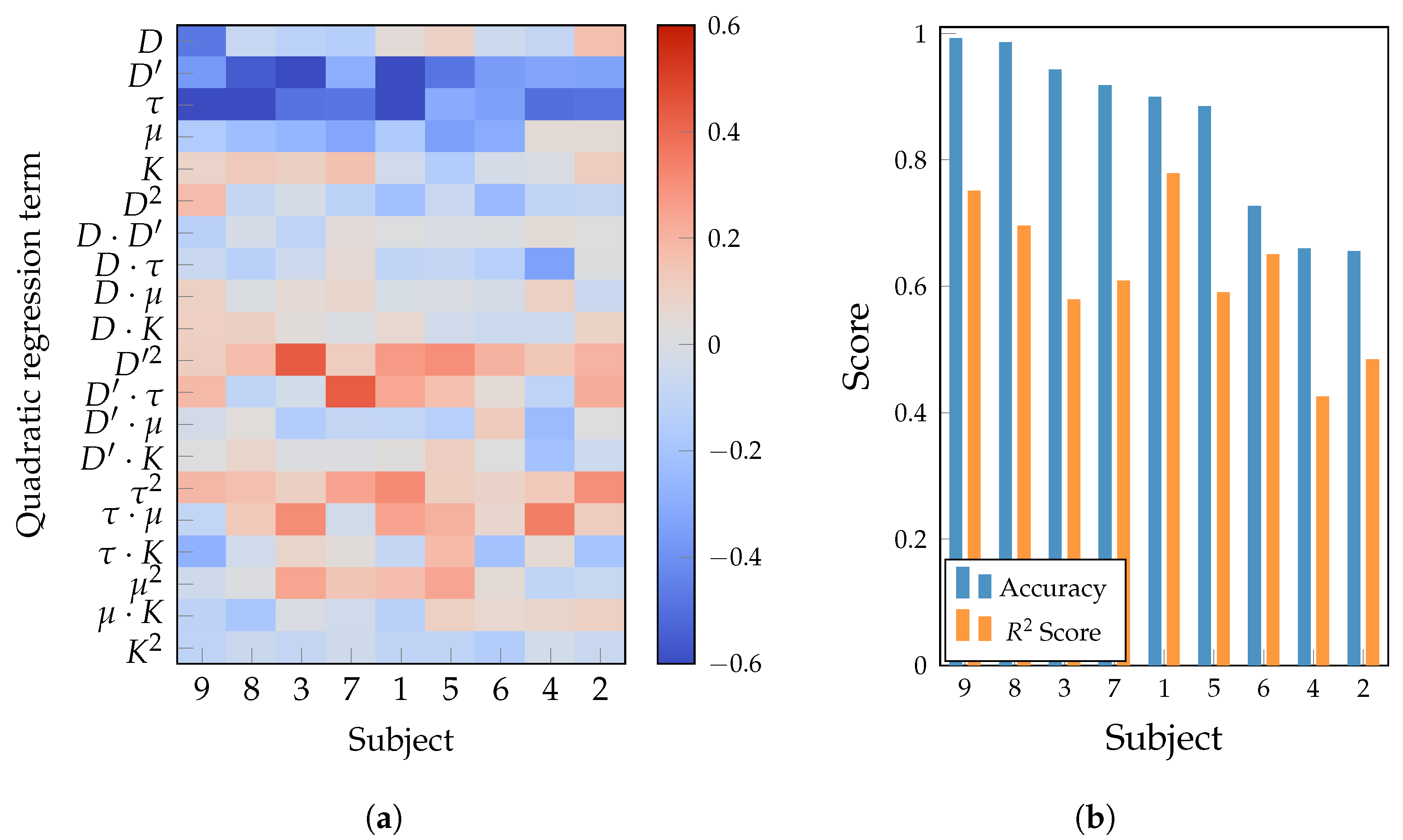
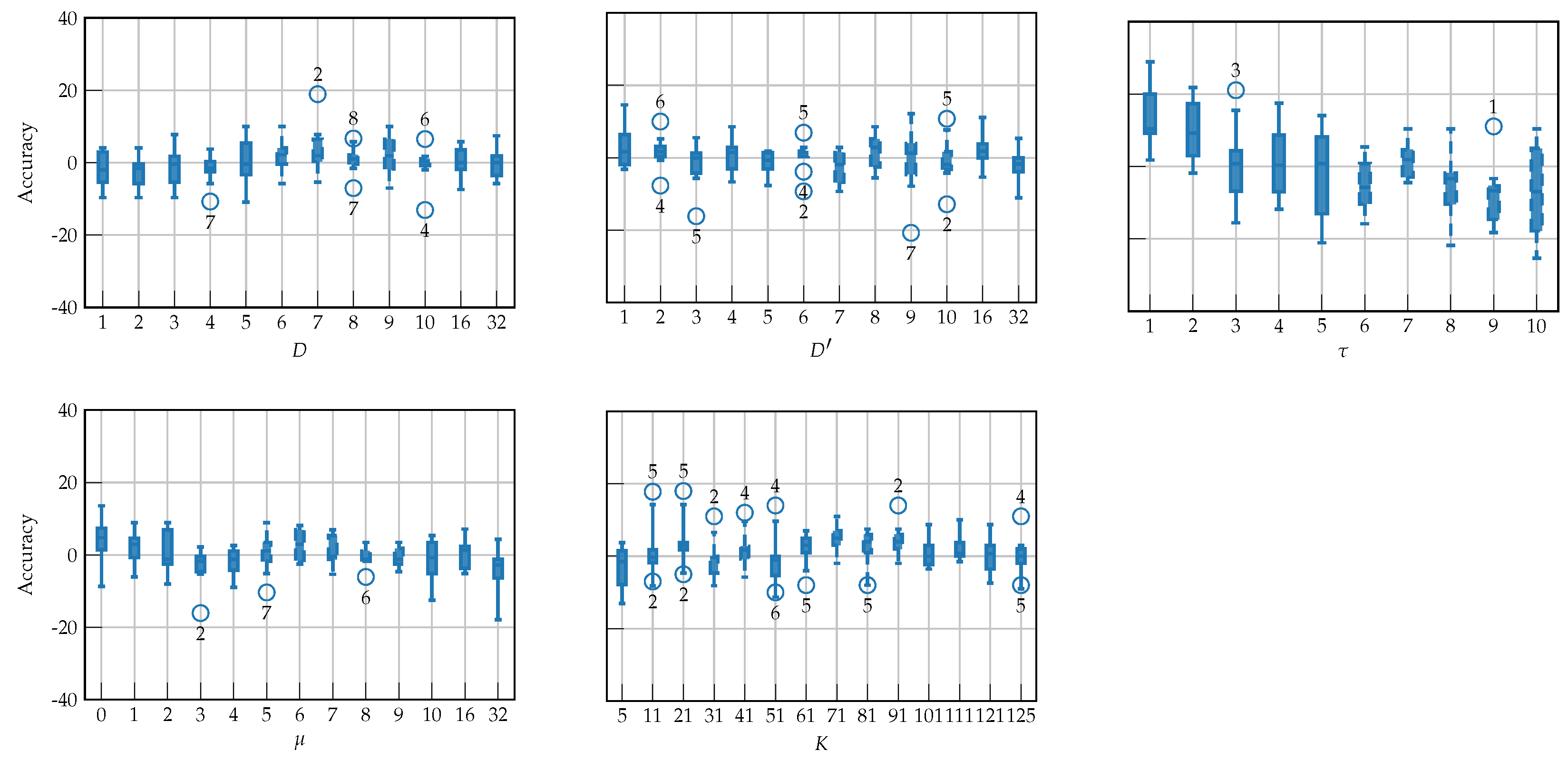
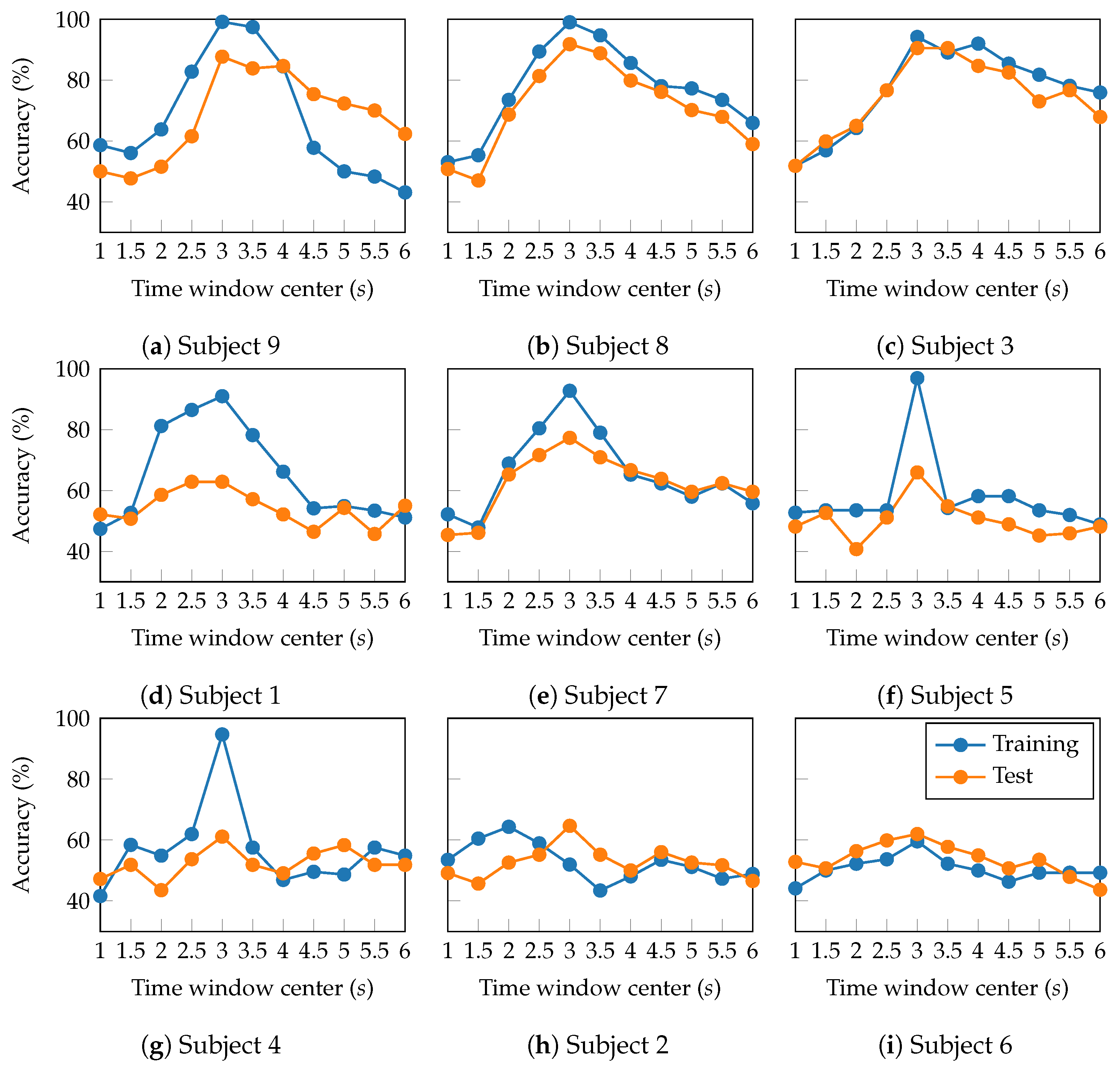
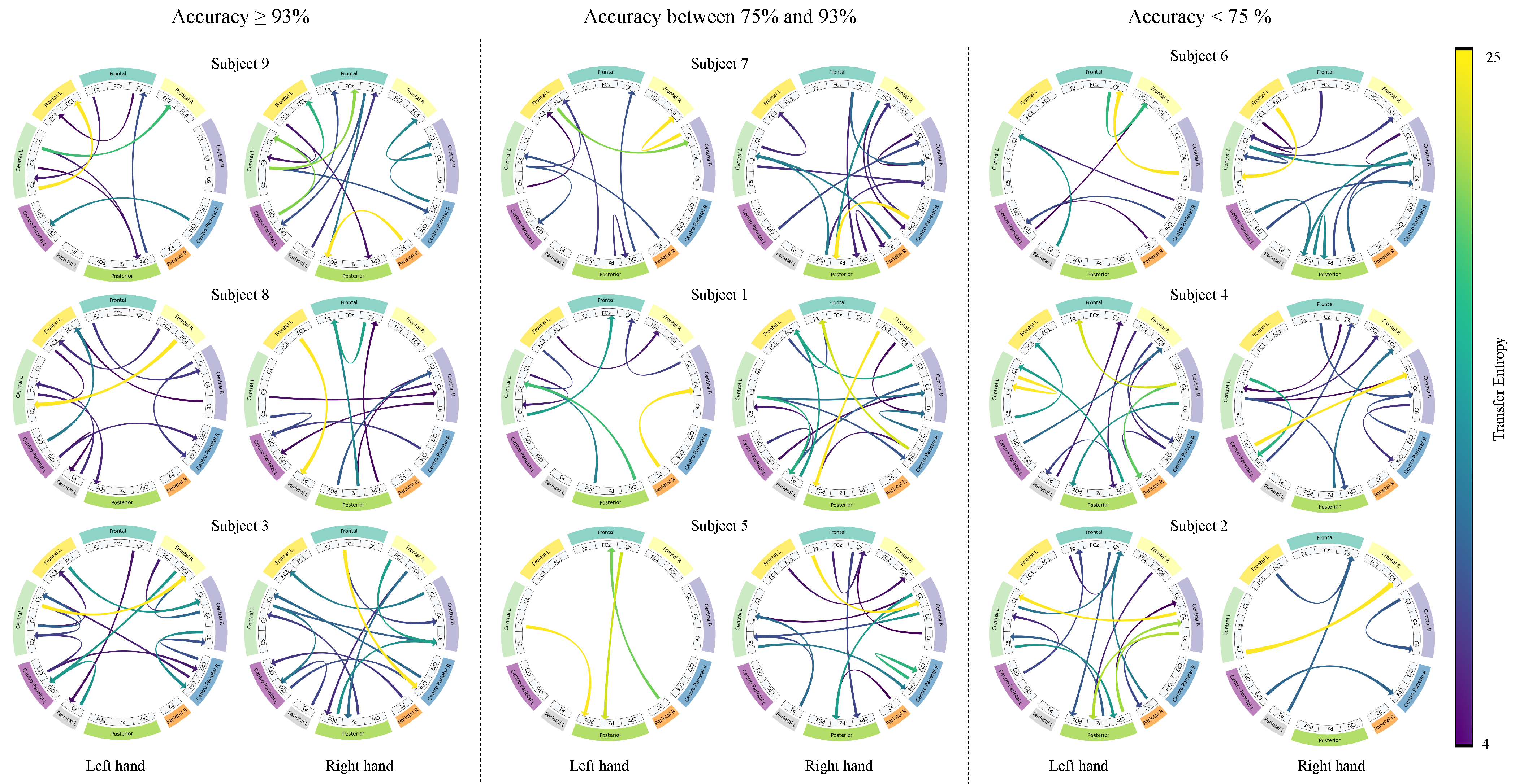
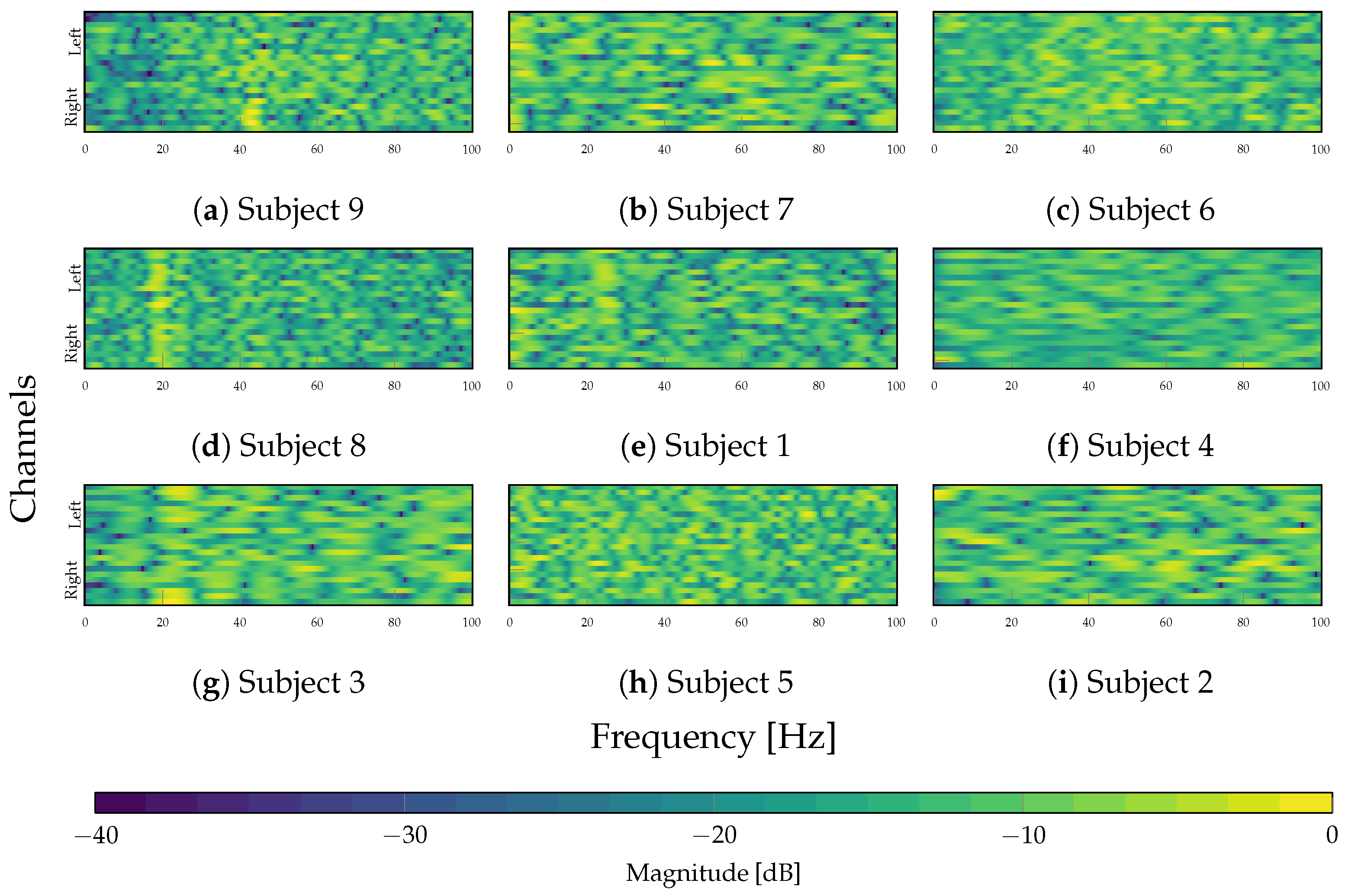
| Layer | Variable | Dimension | Hyperparameters |
|---|---|---|---|
| Input | – | ||
| DepthwiseConv1D | Kernel size K Stride = 1 ReLU activation | ||
| AveragePooling1D | Pool size = 4 Stride = 4 | ||
| TakensConv1D | – | ||
| Order | |||
| Order D Stride Delayed interaction | |||
| RationalQuadratic Kernel | Scale mixture rate | ||
| TransferEntropy | – | ||
| Flatten | – | ||
| Dense | H | Hidden units ReLU activation | |
| Dense | O | Output units Sigmoid activation |
| Group | Subject | D | K | |||
|---|---|---|---|---|---|---|
| High | 9 | 3 | 2 | 1 | 5 | 125 |
| 8 | 1 | 3 | 1 | 3 | 123 | |
| 3 | 3 | 8 | 2 | 0 | 63 | |
| Mid | 7 | 5 | 1 | 1 | 3 | 81 |
| 1 | 1 | 1 | 1 | 8 | 91 | |
| 5 | 6 | 6 | 5 | 9 | 121 | |
| Low | 6 | 5 | 5 | 4 | 10 | 99 |
| 4 | 4 | 3 | 2 | 8 | 51 | |
| 2 | 10 | 2 | 1 | 0 | 57 |
| Subject | Val. Acc (%) | Acc. (%) | F1 (%) | Sens. (%) | Spec. (%) |
|---|---|---|---|---|---|
| 9 | |||||
| 8 | |||||
| 3 | |||||
| 7 | |||||
| 1 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 2 | |||||
| Avg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez-Rivera, A.; Álvarez-Meza, A.M.; Cárdenas-Peña, D.; Orozco-Gutierrez, A. Takens-Based Kernel Transfer Entropy Connectivity Network for Motor Imagery Classification. Sensors 2025, 25, 7067. https://doi.org/10.3390/s25227067
Gomez-Rivera A, Álvarez-Meza AM, Cárdenas-Peña D, Orozco-Gutierrez A. Takens-Based Kernel Transfer Entropy Connectivity Network for Motor Imagery Classification. Sensors. 2025; 25(22):7067. https://doi.org/10.3390/s25227067
Chicago/Turabian StyleGomez-Rivera, Alejandra, Andrés M. Álvarez-Meza, David Cárdenas-Peña, and Alvaro Orozco-Gutierrez. 2025. "Takens-Based Kernel Transfer Entropy Connectivity Network for Motor Imagery Classification" Sensors 25, no. 22: 7067. https://doi.org/10.3390/s25227067
APA StyleGomez-Rivera, A., Álvarez-Meza, A. M., Cárdenas-Peña, D., & Orozco-Gutierrez, A. (2025). Takens-Based Kernel Transfer Entropy Connectivity Network for Motor Imagery Classification. Sensors, 25(22), 7067. https://doi.org/10.3390/s25227067






