Remote Americium Detection Using an Optical Sensor: A D-Optimal Strategy for Efficient PLS-Based Modeling
Abstract
1. Introduction
2. Methods and Materials
2.1. General Materials
2.2. Absorption Spectroscopy
2.3. Experimental Design
2.4. Chemometrics
2.5. E: Statistical Comparison
3. Results and Discussion
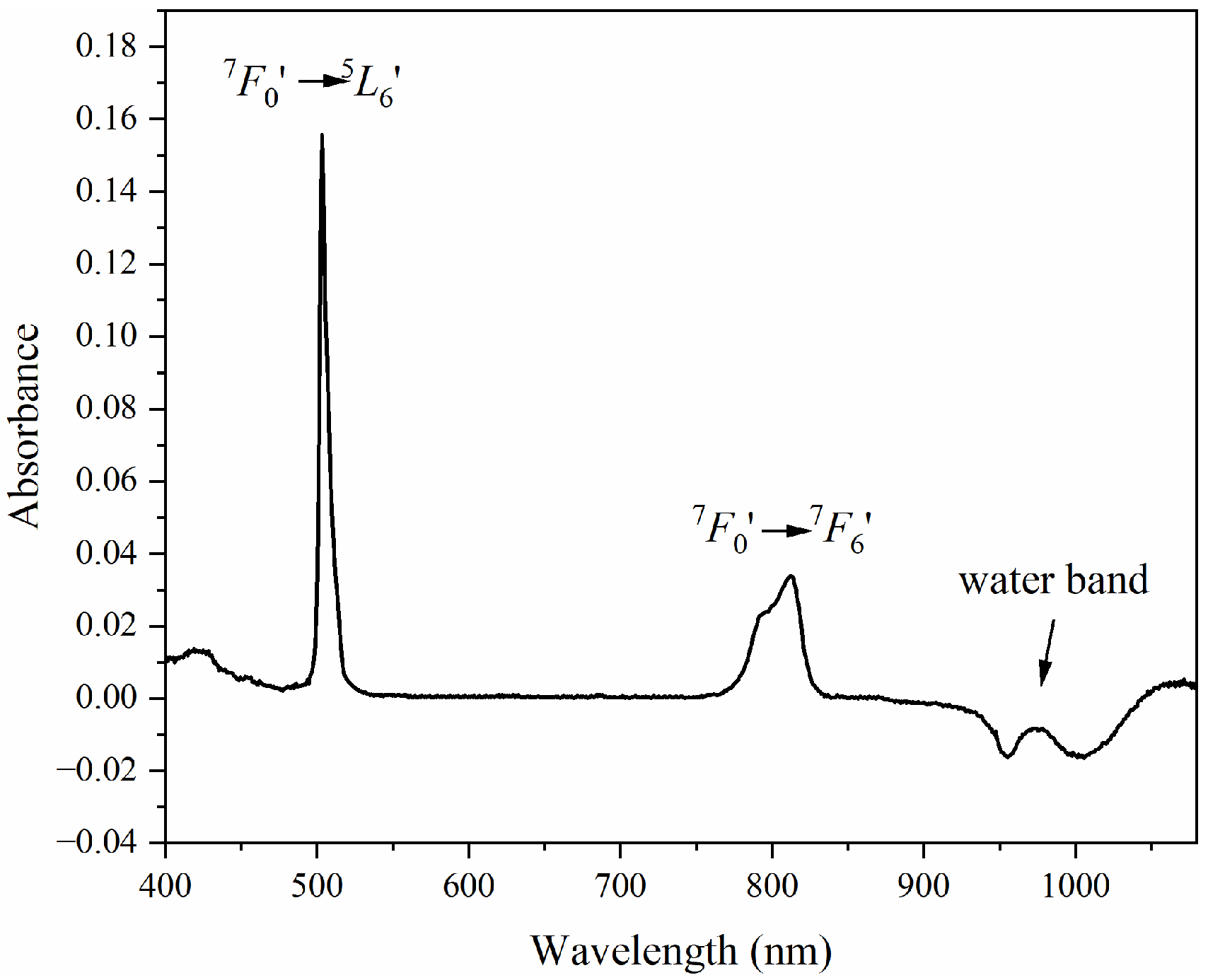
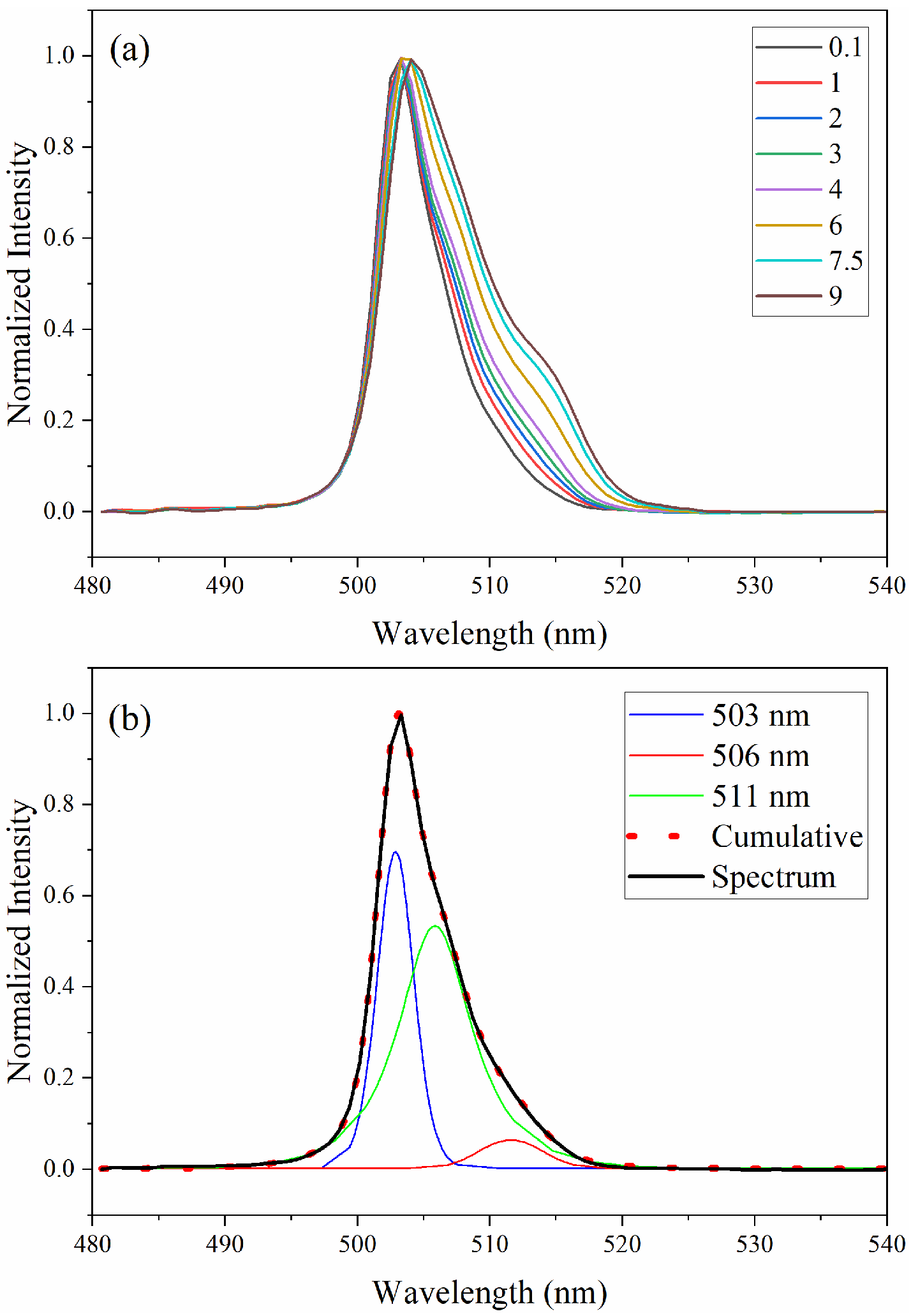
3.1. Absorption Spectra
3.2. Limits of Detection
3.3. D-Optimal Design
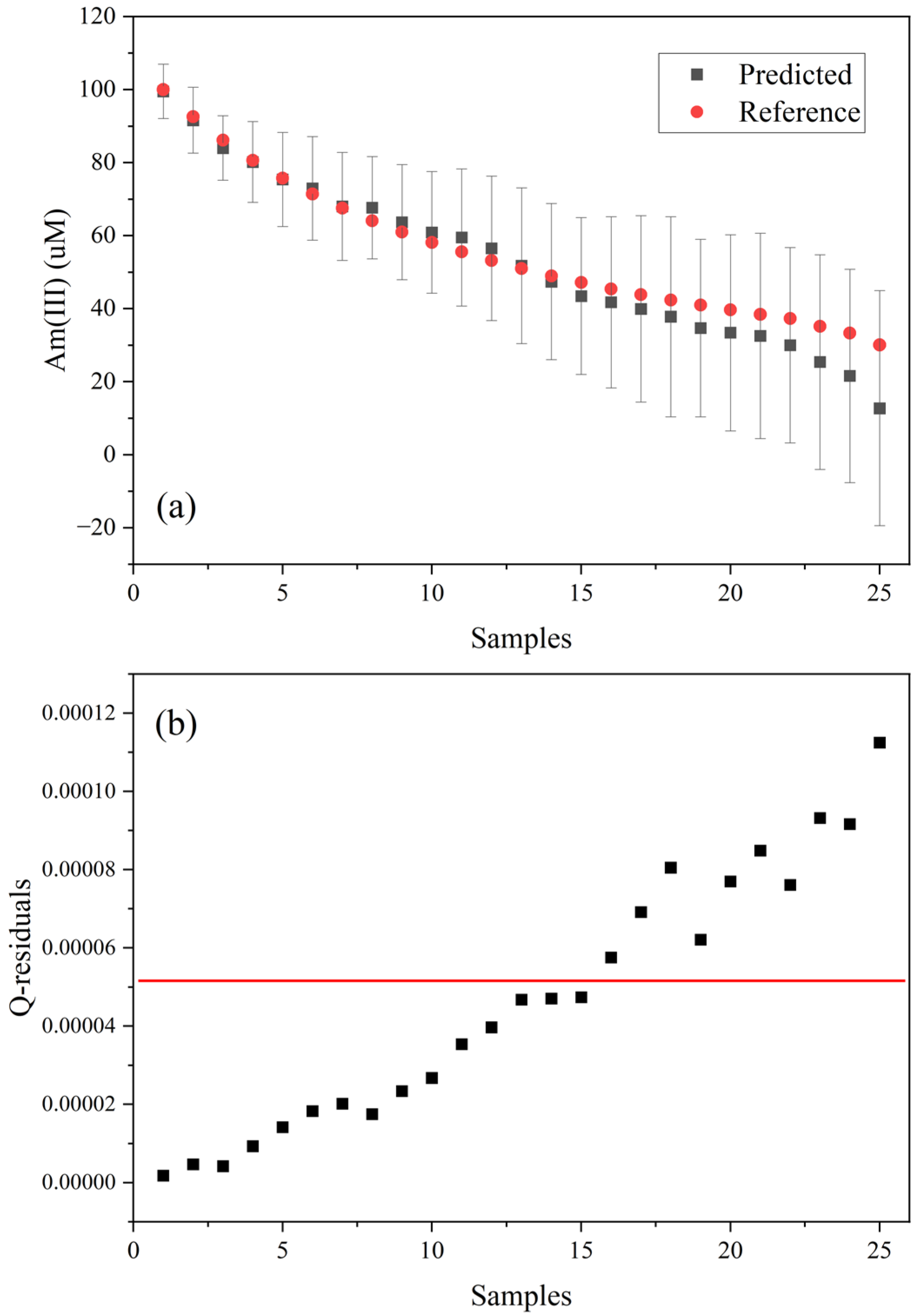
3.4. Partial Least Squares Regression
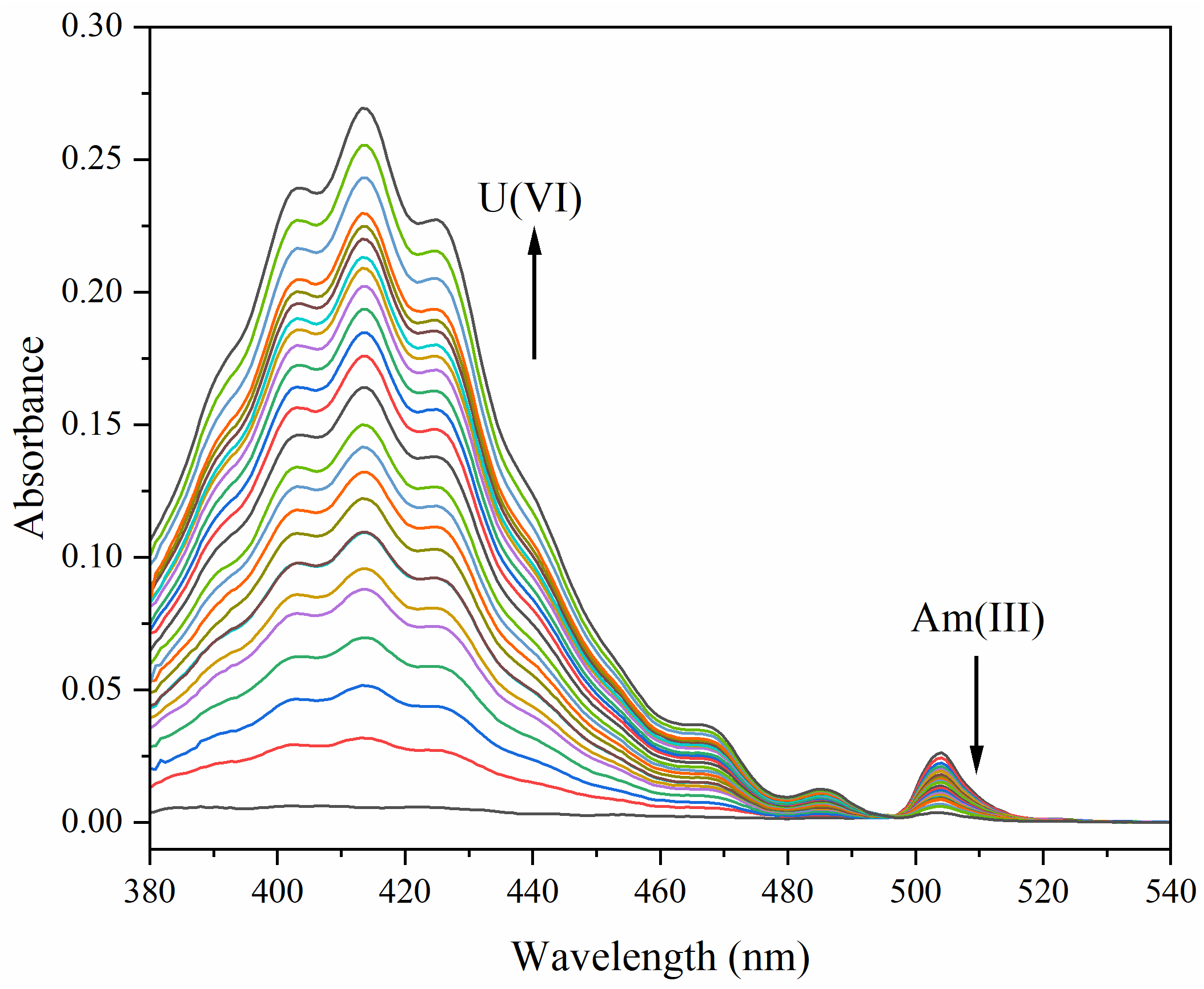
3.5. Performance in the Presence of U
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bryan, S.A.; Levitskaia, T.G.; Johnsen, A.M.; Orton, C.R.; Peterson, J.M. Spectroscopic monitoring of spent nuclear fuel reprocessing streams: An evaluation of spent fuel solutions via Raman, visible, and near-infrared spectroscopy. Radiochim. Acta 2011, 99, 563–571. [Google Scholar] [CrossRef]
- Tsotsou, G.E.; Potiriadi, I. A UV/Vis spectrophotometric methodology for quality control of stevia-based extracts in the food industry. Food Control 2022, 137, 108932. [Google Scholar] [CrossRef]
- Chew, W.; Sharratt, P. Trends in process analytical technology. Anal. Methods 2010, 2, 1412–1438. [Google Scholar] [CrossRef]
- Kirsanov, D.; Rudnitskaya, A.; Legin, A.; Babain, V. UV–Vis Spectroscopy with Chemometric Data Treatment: An Option for On-Line Control in Nuclear Industry. J. Radioanal. Nucl. Chem. 2017, 312, 461–470. [Google Scholar] [CrossRef]
- Aggarwai, S.K. A review on the mass spectrometric studies of americium: Present status and future perspective. Mass Spectrom. Rev. 2018, 37, 43–56. [Google Scholar] [CrossRef] [PubMed]
- Sadergaski, L.R.; Depaoli, D.W.; Myhre, K.G. Monitoring the Caustic Dissolution of Aluminum Alloy in a Radiochemical Hot Cell Using Raman Spectroscopy. Appl. Spectrosc. 2020, 74, 1252–1262. [Google Scholar] [CrossRef]
- Lascola, R.; O’Rourke, P.E.; Kyser, E.A. A Piecewise Local Partial Least Squares (PLS) Method for the Quantitative Analysis of Plutonium Nitrate Solutions. Appl. Spectrosc. 2017, 7, 2579–2594. [Google Scholar] [CrossRef]
- Tse, P.; Shafer, J.; Bryan, S.A.; Nelson, G.L.; Lines, A.M. Measuring Nd (III) Solution Concentration in the Prescence of Interfering Er (III) and Cu (II) Ions: A Partial Least Squares Analysis of Ultraviolet–Visible Spectra. Appl. Spectrosc. 2022, 76, 173–183. [Google Scholar] [CrossRef]
- Kumar, S.; Maji, S.; Sundararajan, K. Nd (III) Hypersensitive Peak as an Optical Absorption Probe for Determining Nitric Acid in Aqueous Solution: An Application to Aqueous Raffinate Solutions in Nuclear Reprocessing. Talanta 2021, 231, 122398. [Google Scholar] [CrossRef] [PubMed]
- Lackey, H.E.; Sell, R.L.; Nelson, G.L.; Bryan, T.A.; Lines, A.M.; Bryan, S.A. Practical Guide to Chemometric Analysis of Optical Spectroscopic Data. J. Chem. Educ. 2023, 100, 2608–2626. [Google Scholar] [CrossRef]
- Despagne, F.; Massart, D.-L.; Noord, O.E. Optimization of Partial-Least-Squares Calibration Models by Simulation of Instrumental Perturbations. Anal. Chem. 1997, 69, 3391–3399. [Google Scholar] [CrossRef]
- Wold, S.; Sjostrom, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Sadergaski, L.R.; Myhre, K.G.; Delmau, L.H. Multivariate chemometric methods and Vis-NIR spectrophotometry for monitoring plutonium-238 anion exchange column effluent in a radiochemical hot cell. Talanta Open 2022, 5, 100120. [Google Scholar] [CrossRef]
- Czitrom, V. One-factor-at-a-time versus designed experiments. Am. Stat. 1999, 53, 126–131. [Google Scholar] [CrossRef]
- Faber, N.K.M. A Closer Look at the Bias-Variance Trade-Off in Multivariate Calibration. J. Chemom. 1999, 13, 185–192. [Google Scholar] [CrossRef]
- Beleites, C.; Salzer, R. Assessing and Improving the Stability of Chemometric Models in Small Sample Size Situations. Anal. Bioanal. Chem. 2008, 390, 1261–1271. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Josefson, M.; Gottfries, J.; Linusson, A. The Utility of Multivariate Design in PLS Modeling. J. Chemom. 2004, 18, 156–165. [Google Scholar] [CrossRef]
- Smucker, B.; Krzywinski, M.; Altman, N. Optimal experimental design. Nat. Methods 2018, 15, 559–560. [Google Scholar] [CrossRef]
- Johnson, R.T.; Montgomery, D.C.; Jones, B.A. An Expository Paper on Optimal Design. Qual. Eng. 2011, 23, 287–301. [Google Scholar] [CrossRef]
- Sadergaski, L.R.; Andrews, H.B.; Wilson, B.A. Comparing sensor fusion and multimodal chemometric models for monitoring U(VI) in complex environments representative of irradiated nuclear fuel. Anal. Chem. 2024, 96, 1759–1766. [Google Scholar] [CrossRef]
- Andrews, H.B.; Sadergaski, L.R.; Cary, S.K. Pursuit of the Ultimate Regression Model for Samarium (III), Europium (III), and LiCl Using Laser-Induced Fluorescence, Design of Experiments, and a Genetic Algorithm for Feature Selection. ACS Omega 2023, 8, 2281–2290. [Google Scholar] [CrossRef] [PubMed]
- Bondi, R.W., Jr.; Igne, B.; Drennen, J.K., III; Anderson, C.A. Effect of Experimental Design on the Prediction Performance of Calibration Models Based on Near-Infrared Spectroscopy for Pharmaceutical Applications. Appl. Spectrosc. 2012, 66, 1442–1453. [Google Scholar] [CrossRef]
- Andrews, H.B.; Sadergaski, L.R. Leveraging Visible and Near-Infrared Spectroelectrochemistry to Calibrate a Robust Model for Vanadium (IV/V) in Varying Nitric Acid and Temperature Levels. Talanta 2023, 259, 124554. [Google Scholar] [CrossRef]
- Sadergaski, L.R.; Hager, T.J.; Andrews, H.B. Design of Experiments, Chemometrics, and Raman Spectroscopy for the Quantification of Hydroxylammonium, Nitrate, and Nitric Acid. ACS Omega 2022, 7, 7287–7296. [Google Scholar] [CrossRef] [PubMed]
- Sadergaski, L.R.; Andrews, H.B.; Rai, D., II; Anagnostopoulos, V.A. Comparing Designed Training Sets to Optimize Multivariate Regression Models for Pr, Nd, and Nitric Acid Using Spectrophotometry. Appl. Spectrosc. Pract. 2024, 2, 27551857241243083. [Google Scholar] [CrossRef]
- Carnall, W.T. A systematic view of optical absorption spectra in the actinide series. J. Less Common Met. 1986, 122, 1–17. [Google Scholar] [CrossRef]
- Duma, T.; Guillaumont, D.; Fillaux, C.; Scheinost, A.; Moisy, P.; Petit, S.; Shuh, D.K.; Tyliszczak, T.; Den Auwer, C. The nature of chemical bonding in actinide and lanthanide ferrocyanides determined by X-ray absorption spectroscopy and density functional theory. Phys. Chem. Chem. Phys. 2016, 18, 2887–2895. [Google Scholar] [CrossRef] [PubMed]
- Hiyama, T.; Sugaya, S.; Kageyama, T.; Kamimura, K. Determination of Americium in a Nitric Acid Medium Using a Second-Order Derivative Spectrophotometry. Anal. Sci. 1996, 12, 427–430. [Google Scholar] [CrossRef][Green Version]
- Grimes, T.S.; Mincher, B.J.; Schmitt, N.C. Reduction Rates for Higher Americium Oxidation States in Nitric Acid; INL/EXT-15-36767; Idaho National Laboratory: Idaho Falls, ID, USA, 2015.
- Robinson, S.M.; Benker, D.E.; Collins, E.D.; Ezold, J.G.; Garrison, J.R.; Hogle, S.L. Production of Cf-252 and other transplutonium isotopes at Oak Ridge National Laboratory. Radiochem. Acta 2020, 108, 737–746. [Google Scholar] [CrossRef]
- Brown, J.; Campbell, C.; Carrigan, C.; Carrott, M.; Greenough, K.; Maher, C.; Tinsley, T. Americium and Plutonium Purification by Extraction (the AMPPEX process): Development of a new method to separate 241Am from aged plutonium dioxide for use in space power systems. Prog. Nucl. Energy 2018, 106, 396–416. [Google Scholar] [CrossRef]
- Cunningham, B.B.; Asprey, L.B. The First Isolation of Americium in the Form of Pure Compounds—The Specific Alpha-Activity and Half-Life of Am-241; UCRL-810; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1950.
- Shukla, J.P.; Subramanian, M.S. Extractive-spectrophotometric determination of americium at trace levels with arsenazo-III. Anal. Chim. Acta 1982, 138, 413–417. [Google Scholar] [CrossRef]
- Schnable, D.; Reinhart, E.D.; Veleta, J.M.; Arteaga, A.; Surbella, R.G., III. Spectroscopic Properties of Americium (III) in Mineral Acid Media. Inorg. Chem. 2025, 64, 14172–14181. [Google Scholar] [CrossRef]
- Zalupski, P.R.; Grimes, T.S.; Heathman, C.R.; Peterman, D.R. Optical Absorption Characteristics For 7F0′-5L6′ and 7F0′-7F6′ Transition of Trivalent Americium Ion in Aqueous Electrolyte Mixtures, INL/JOU-17-40932. Appl. Spectrosc. 2017, 71, 2608–2615. [Google Scholar] [CrossRef]
- Picayo, G.A.; Etz, B.D.; Vyas, S.; Jensen, M.P. Characterization of the ALSEP Process at Equilibrium: Speciation and Stoichiometry of the Extracted Complex. ACS Omega 2020, 5, 8076–8089. [Google Scholar] [CrossRef]
- Zsabka, P.; Wilden, A.; Van Hecke, K.; Modolo, G.; Verweft, M.; Cardinaels, T. Beyond U/Pu separation: Separations of americium from the highly active PUREX raffinate. J. Nucl. Mater. 2023, 581, 154445. [Google Scholar] [CrossRef]
- Ortiz, M.C.; Sarabia, L.A.; Herrero, A.; Sánchez, M.S.; Sanz, M.B.; Giménez, D.; Meléndez, M.E. Capability of detection of an analytical method evaluating false positive and falst negative (ISO 11843) with partial least squares. Chemom. Intell. Lab. Syst. 2003, 69, 21–33. [Google Scholar] [CrossRef]
- Allegrini, F.; Olivieri, A.C. IUPAC-Consistent Approach to the Limit of Detection in Partial Least-Squares Calibration. Anal. Chem. 2014, 86, 7858–7866. [Google Scholar] [CrossRef]
- Chang, K.; Shinzawa, H.; Chung, H. Concentration Determination of Inorganic Acids that Do Not Absorb Near-Infrared (NIR) Radiation Through Recognizing Perturbed NIR Water Bands by Them and Investigation of Accuracy Dependency on Their Acidities. Microchem. J. 2018, 139, 443–449. [Google Scholar] [CrossRef]
- Sadergaski, L.R.; Einkauf, J.D.; Delmau, L.H.; Burns, J.D. Leveraging design of experiments to build chemometric models for the quantification of uranium (VI) and HNO3 by Raman Spectroscopy. Front. Nucl. Eng. 2024, 3, 1411840. [Google Scholar] [CrossRef]
- Andrews, H.B.; Sadergaski, L.R. Hierarchical Modeling to Enhance Spectrophotometry Measurements–Overcoming Dynamic Range Limitations for Remote Monitoring of Neptunium. Chemosensors 2023, 11, 274. [Google Scholar] [CrossRef]
- Lackey, H.E.; Nelson, G.L.; Felmy, H.M.; Guo, X.; Bryan, S.A.; Lines, A.M. PCA and PLS Analysis of Lanthanides Using Absorbance and Single-Beam Visible Spectra. ACS Omega 2024, 9, 33662–33670. [Google Scholar] [CrossRef] [PubMed]
- Workman, J.J. A Review of Calibration Transfer Practices and Instrument Differences in Spectroscopy. Appl. Spectrosc. 2018, 72, 340–365. [Google Scholar] [CrossRef] [PubMed]


| Sample | A | B | Am(III) (µM) | HNO3 (M) | Space Type | Build Type |
|---|---|---|---|---|---|---|
| 1 | 0.000 | 1.000 | 0.0 | 9.0 | Vertex | Model |
| 2 | 1.000 | 0.850 | 500.0 | 7.7 | Vertex | Model |
| 3 | 0.200 | 0.345 | 100.0 | 3.2 | Interior | Model |
| 4 | 0.365 | 1.000 | 182.5 | 9.0 | Edge | Model |
| 5 | 0.331 | 0.670 | 165.7 | 6.1 | Interior | Lack of fit |
| 6 | 0.000 | 0.640 | 0.0 | 5.8 | Interior | Lack of fit |
| 7 | 1.000 | 0.000 | 500.0 | 0.1 | CentEdge | Lack of fit |
| 8 | 1.000 | 0.425 | 500.0 | 3.9 | Edge | Lack of fit |
| 9 | 0.695 | 0.975 | 347.5 | 8.8 | Edge | Model |
| 10 | 0.575 | 0.000 | 287.5 | 0.1 | Vertex | Model |
| 11 | 0.145 | 0.000 | 72.5 | 0.1 | Interior | Lack of fit |
| 12 | 0.570 | 0.125 | 285.0 | 1.2 | Interior | Lack of fit |
| HNO3 (M) | LOD (µM) | LOQ (µM) | Peak Maximum (nm) | Slope (m) | Extinction Coefficient (cm−1 M−1) |
|---|---|---|---|---|---|
| 0.1 | 2.4 | 8 | 503.3 | 3.28 × 10−4 | 327 |
| 1 | 2.5 | 8.3 | 503.3 | 3.19 × 10−4 | 319 |
| 2 | 2.5 | 8.4 | 503.3 | 3.13 × 10−4 | 314 |
| 3 | 2.6 | 8.7 | 503.3 | 3.03 × 10−4 | 302 |
| 4 | 2.7 | 9.1 | 503.3 | 2.88 × 10−4 | 290 |
| 6 | 3.2 | 10.7 | 503.3 | 2.46 × 10−4 | 243 |
| 7.5 | 3.6 | 11.9 | 504.0 | 2.21 × 10−4 | 221 |
| 9 | 3.7 | 12.2 | 504.0 | 2.15 × 10−4 | 216 |
| Variables | PLS2 | PLS1 Am(III) | PLS1 HNO3 |
|---|---|---|---|
| LVs | 3 | 2 | 3 |
| Region (nm) | 460–1080 | 480–530 | 900–1080 |
| Preprocessing | First derivative | Smooth/baseline offset | First derivative |
| Am(III) | — | — | — |
| RMSEC | 10 | 5.4 | — |
| RMSECV | 18 | 10 | — |
| RMSEP | 9.9 | 0.87 | — |
| RMSEP% | 4.0 | 3.5 | — |
| SEP | 10 | 9.3 | — |
| Bias | −0.17 | 0.86 | — |
| HNO3 | — | — | — |
| RMSEC | 0.32 | — | 0.12 |
| RMSECV | 0.52 | — | 0.16 |
| RMSEP | 0.41 | — | 0.17 |
| RMSEP% | 9.2 | — | 3.8 |
| SEP | 0.37 | — | 0.15 |
| Bias | 0.18 | — | 0.097 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadergaski, L.R.; Einkauf, J.D.; Pyles, J.M.; Delmau, L.H.; Burns, J.D. Remote Americium Detection Using an Optical Sensor: A D-Optimal Strategy for Efficient PLS-Based Modeling. Sensors 2025, 25, 7022. https://doi.org/10.3390/s25227022
Sadergaski LR, Einkauf JD, Pyles JM, Delmau LH, Burns JD. Remote Americium Detection Using an Optical Sensor: A D-Optimal Strategy for Efficient PLS-Based Modeling. Sensors. 2025; 25(22):7022. https://doi.org/10.3390/s25227022
Chicago/Turabian StyleSadergaski, Luke R., Jeffrey D. Einkauf, Jennifer M. Pyles, Laetitia H. Delmau, and Jonathan D. Burns. 2025. "Remote Americium Detection Using an Optical Sensor: A D-Optimal Strategy for Efficient PLS-Based Modeling" Sensors 25, no. 22: 7022. https://doi.org/10.3390/s25227022
APA StyleSadergaski, L. R., Einkauf, J. D., Pyles, J. M., Delmau, L. H., & Burns, J. D. (2025). Remote Americium Detection Using an Optical Sensor: A D-Optimal Strategy for Efficient PLS-Based Modeling. Sensors, 25(22), 7022. https://doi.org/10.3390/s25227022






