High-Precision Waveform Stacking Location Method for Microseismic Events Based on S-Transform
Abstract
1. Introduction
2. Methods
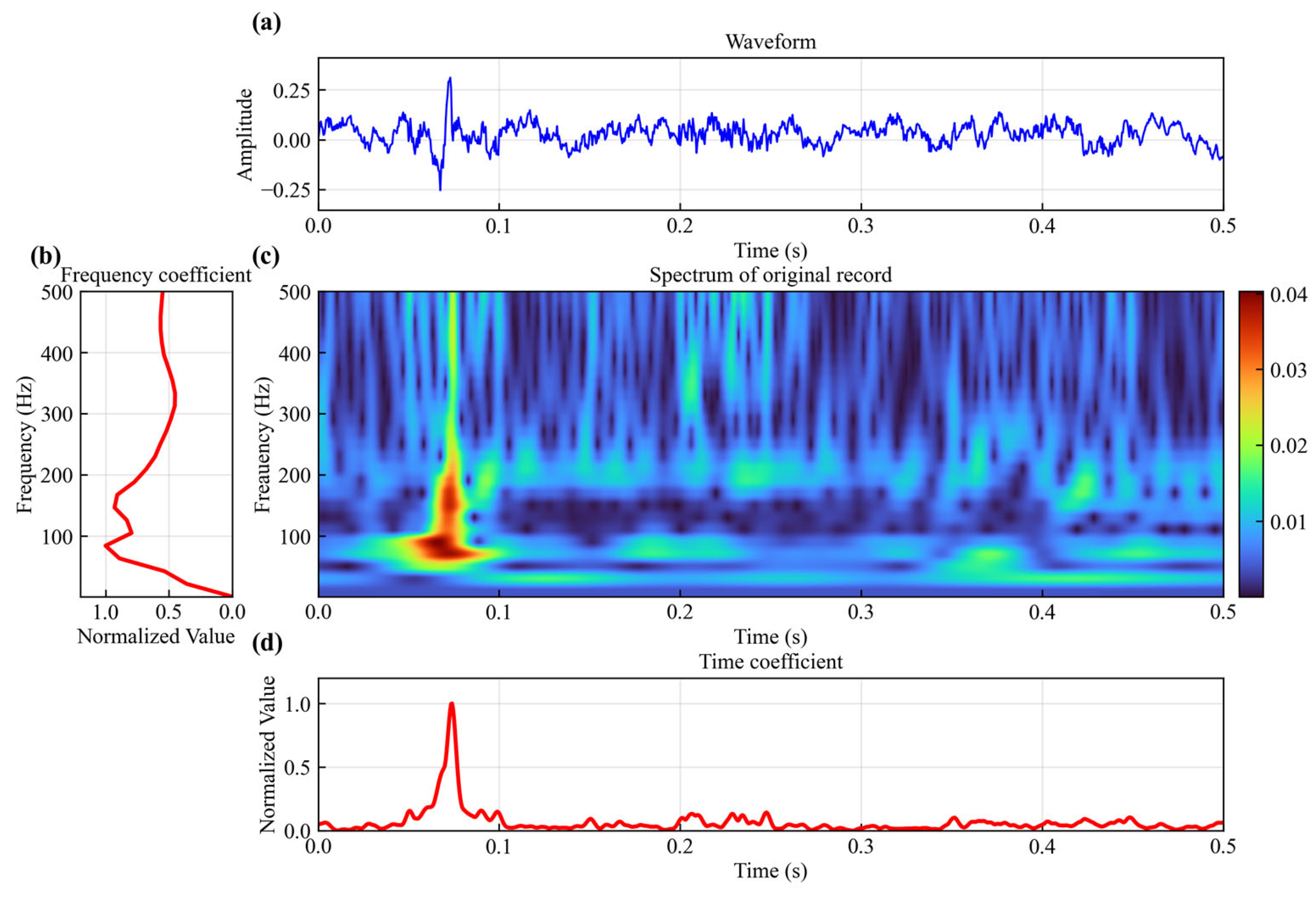
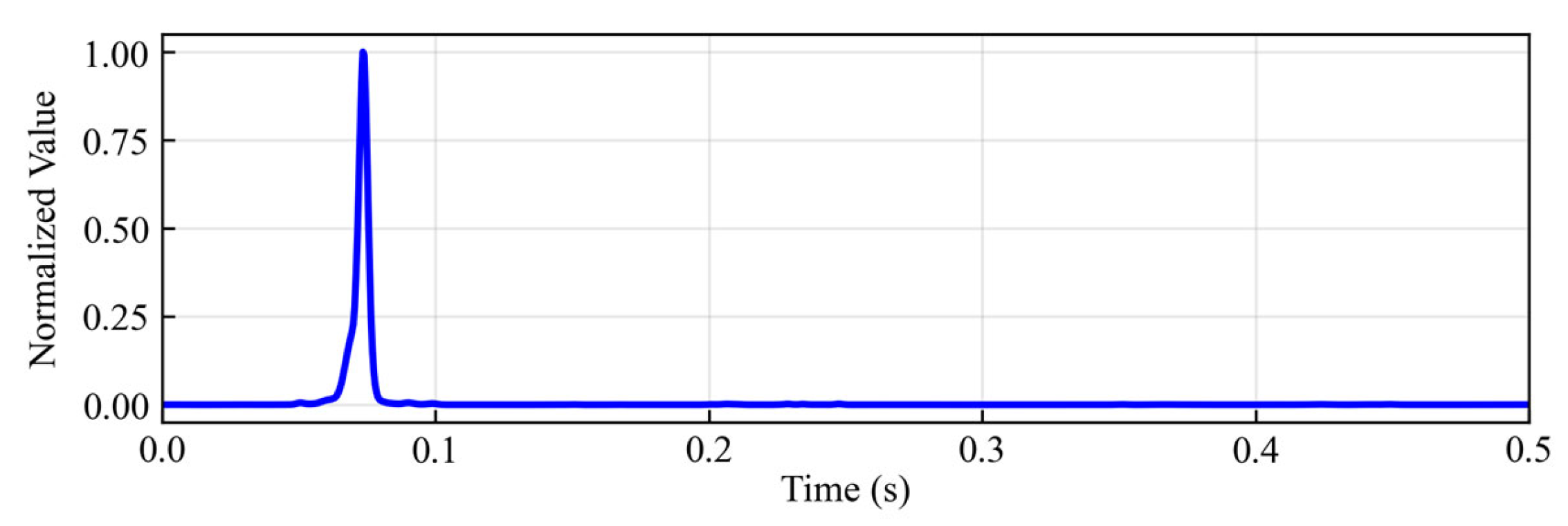
2.1. Construction of Characteristic Function
2.2. Multiple-Cross-Correlation Stacking Method
3. Results
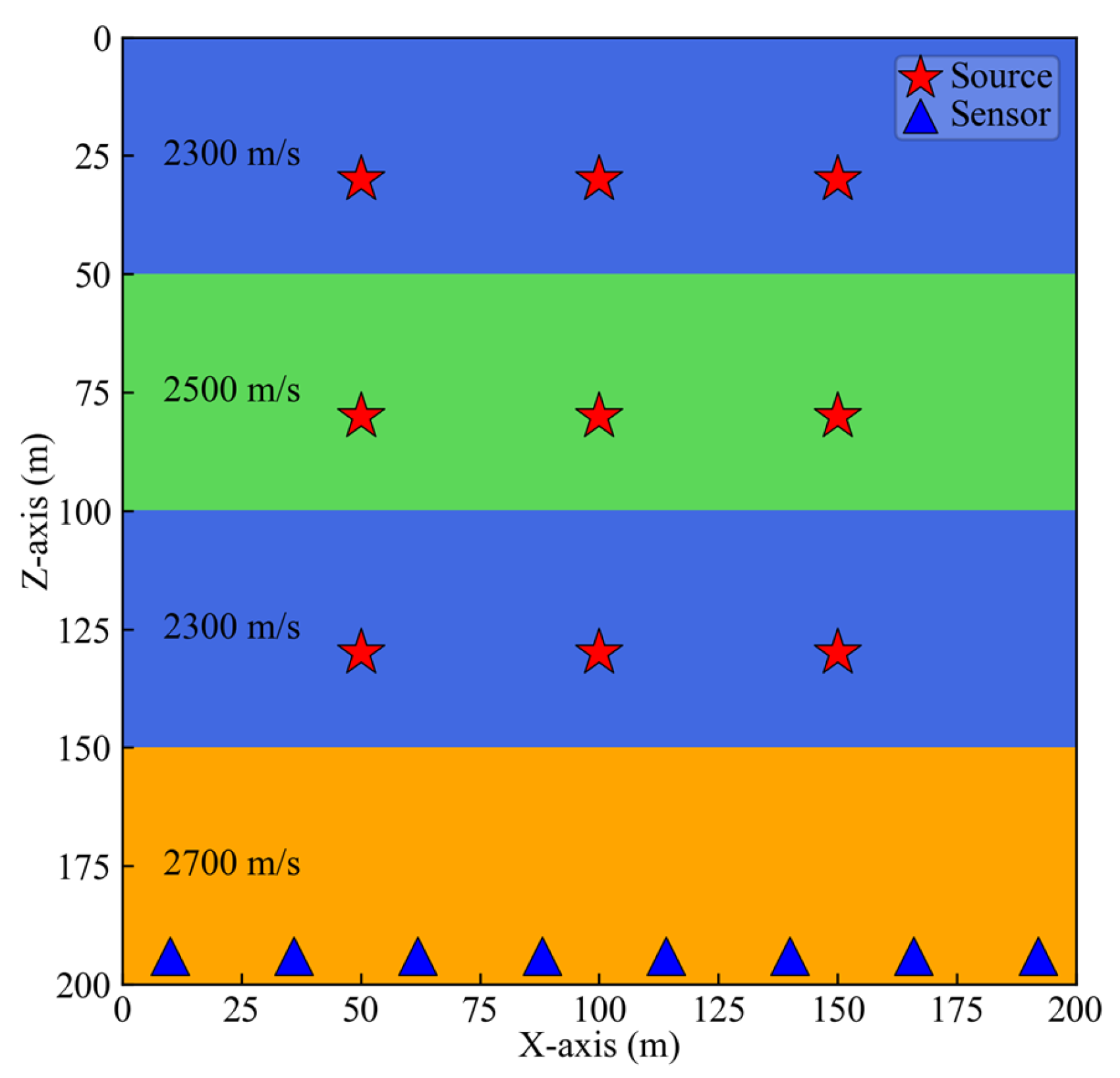
3.1. Application on Synthetic Model
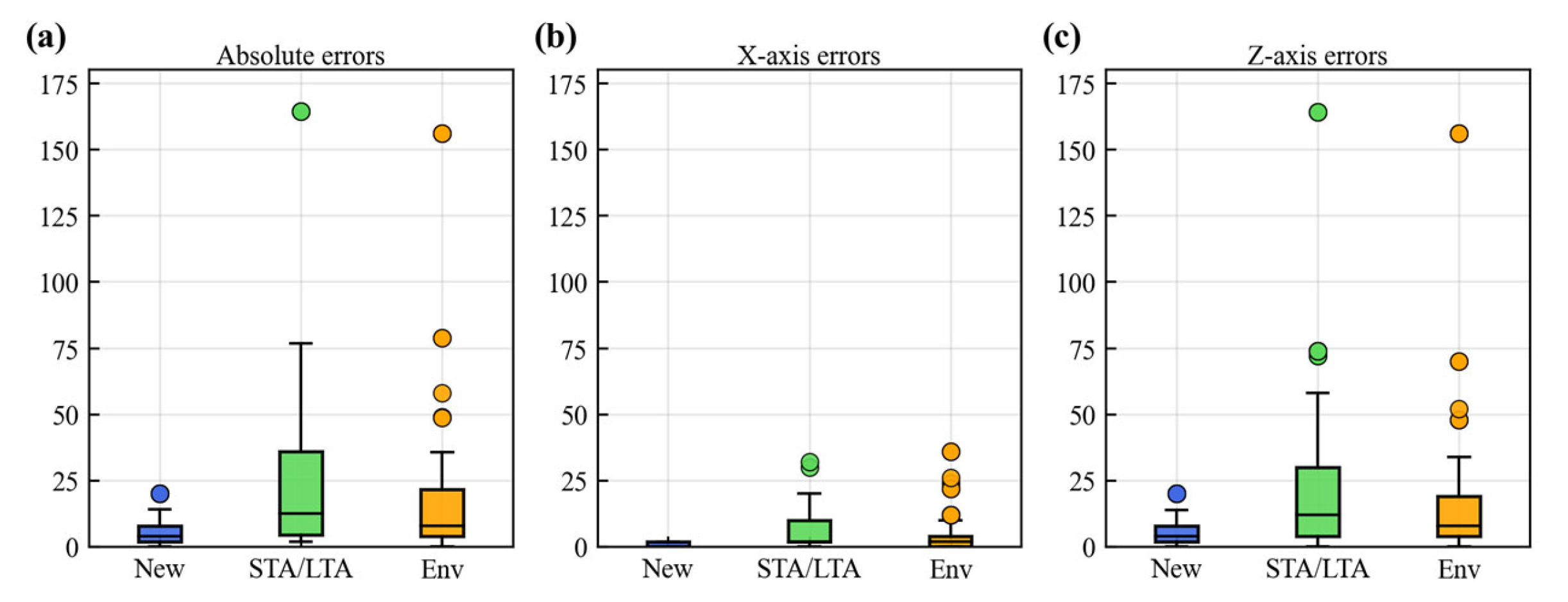
3.2. Error Statistics
3.3. Comparison of Time Cost
3.4. Non-Uniform Sensor Arrays
3.5. Velocity Error Analysis
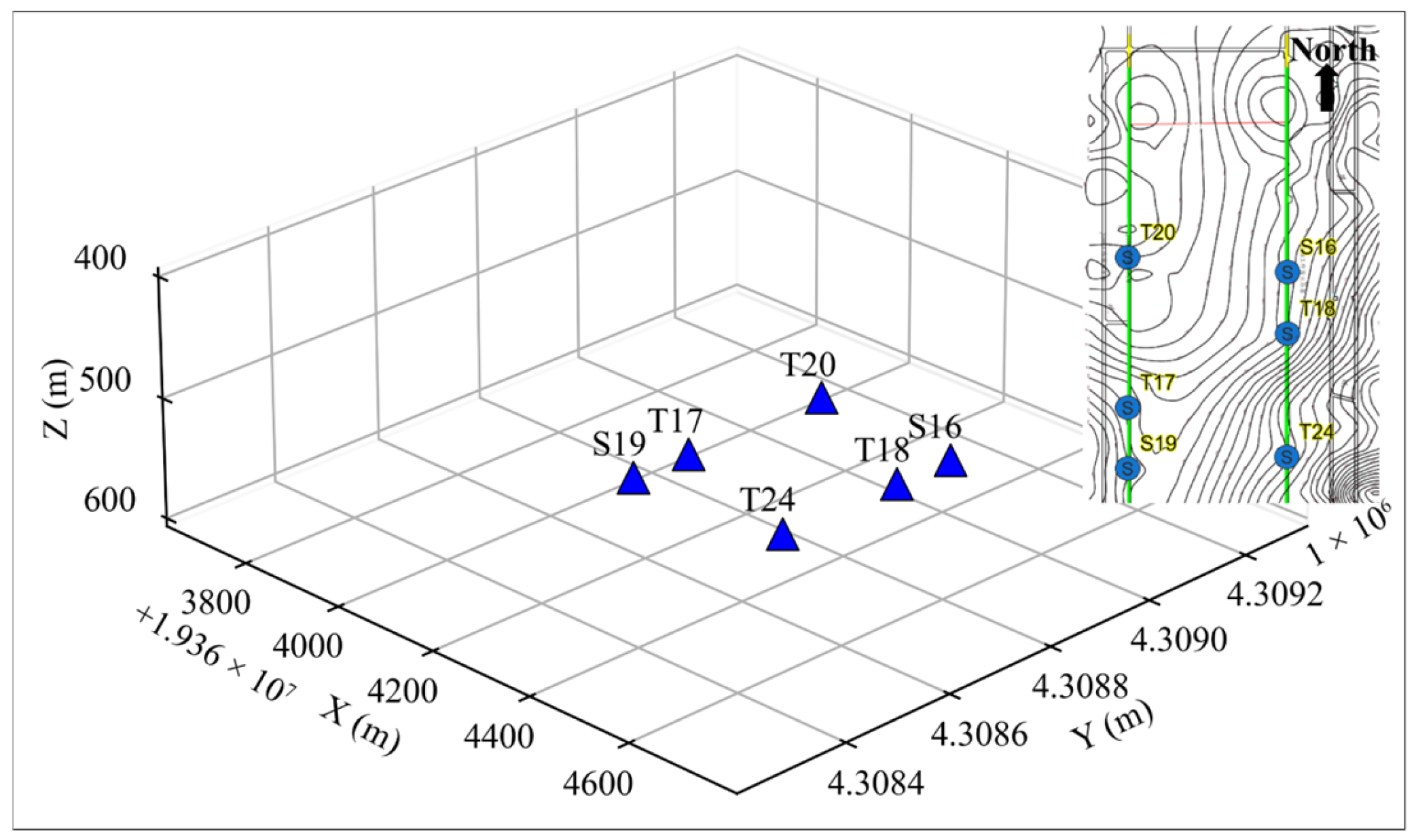
3.6. Application on Real Microseismic Record
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, Z.; Liu, X.; Xu, Q.; Li, C.; Qin, P. Stability Evaluation of Deep-Buried Tbm Construction Tunnel Based on Microseismic Monitoring Technology. Tunn. Undergr. Space Technol. 2018, 81, 512–524. [Google Scholar] [CrossRef]
- Ma, C.; Li, T.; Zhang, H.; Jiang, Y.; Song, T. A Method for Numerical Simulation Based on Microseismic Information and the Interpretation of Hard Rock Fracture. J. Appl. Geophys. 2019, 164, 214–224. [Google Scholar] [CrossRef]
- Kumar, V.; Jha, P.C.; Singh, N.P.; Cherukuri, S. Dynamic Stability Evaluation of Underground Powerhouse Cavern Using Microseismic Monitoring. Geotech. Geol. Eng. 2021, 39, 1795–1815. [Google Scholar] [CrossRef]
- Geiger, L.C. Probability Method for the Determination of Earthquake Epicentres from the Arrival Time Only. Bull. St. Louis Univ. 1912, 8, 60–71. [Google Scholar]
- Juan, C.-W.; Hu, J.-S. Single-Object Localization Using Multiple Ultrasonic Sensors and Constrained Weighted Least-Squares Method. Asian J. Control 2021, 23, 1171–1184. [Google Scholar] [CrossRef]
- Bing, Z.; Greenhalgh, S.A.; Sinadinovski, C. Iterative Algorithm for the Damped Minimum Norm, Least-Squares and Constrained Problem in Seismic Tomography. Explor. Geophys. 1992, 23, 497–505. [Google Scholar] [CrossRef]
- Peng, K.; Guo, H.; Shang, X. Data Field Application in Removing Large P-Phase Arrival Picking Errors and Relocating a Mine Microseismic Event. Soil Dyn. Earthq. Eng. 2020, 139, 106359. [Google Scholar] [CrossRef]
- Cheng, J.; Song, G.; Liu, T.; Hu, B.; Wang, J.; Wang, J. High Precision Location of Micro-Seismic Sources in Underground Coal Mine. Chin. J. Geophys. 2016, 59, 4513–4520. (In Chinese) [Google Scholar] [CrossRef]
- Ge, Q.; Han, L.; Cai, Z. Reverse Travel Time Imaging of Microseismic Location. Explor. Geophys. 2019, 50, 281–296. [Google Scholar] [CrossRef]
- Li, H.; Yang, Z.; Yan, W. An Improved Aic Onset-Time Picking Method Based on Regression Convolutional Neural Network. Mech. Syst. Signal Process. 2022, 171, 108867. [Google Scholar] [CrossRef]
- Cheng, J.; Song, G.; Sun, X.; Wen, L.; Li, F. Research Developments and Prospects on Microseismic Source Location in Mines. Engineering 2018, 4, 653–660. [Google Scholar] [CrossRef]
- Abdullin, A.; Waheed, U.B.; Suleymanli, K.; Stanek, F. Microseismic Source Localization Using Fourier Neural Operator with Application to Field Data from Utah Forge. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–10. [Google Scholar] [CrossRef]
- Ahn, H.; Hu, M.; Park, J.; You, K. Reweighted Partial Least Squares and Deep Learning-Based Rdoa/Aoa Estimation for Seismic Epicenter. IEEE Signal Process. Lett. 2025, 32, 946–950. [Google Scholar] [CrossRef]
- Noor, U.A. Machine Learning Innovations in Revolutionizing Earthquake Engineering: A Review. Arch. Comput. Methods Eng. 2025. [Google Scholar] [CrossRef]
- Wu, S.; Wang, Y.; Xie, F.; Chang, X. Crosscorrelation Migration of Microseismic Source Locations with Hybrid Imaging Condition. Geophysics 2022, 87, KS17–KS31. [Google Scholar] [CrossRef]
- Singha Roy, K.; Arrowsmith, S.; Stump, B.; Hayward, C.; Park, J. Exploiting Signal Coherence to Simultaneously Detect and Locate Earthquakes. Seismol. Res. Lett. 2024, 96, 219–230. [Google Scholar] [CrossRef]
- Li, L.; Tan, J.; Schwarz, B.; Staněk, F.; Poiata, N.; Shi, P.; Diekmann, L.; Eisner, L.; Gajewski, D. Recent Advances and Challenges of Waveform-Based Seismic Location Methods at Multiple Scales. Rev. Geophys. 2020, 58, e2019RG000667. [Google Scholar] [CrossRef]
- Kao, H.; Shan, S.-J. The Source-Scanning Algorithm: Mapping the Distribution of Seismic Sources in Time and Space. Geophys. J. Int. 2004, 157, 589–594. [Google Scholar] [CrossRef]
- Gajewski, D.; Anikiev, D.; Kashtan, B.; Tessmer, E.; Vanelle, C. Localization of Seismic Events by Diffraction Stacking. In Proceedings of the 2007 SEG Annual Meeting, San Antonio, TX, USA, 23–28 September 2007; pp. 1287–1291. [Google Scholar]
- Li, L.; Chen, H.; Wang, X.-M. Weighted-Elastic-Wave Interferometric Imaging of Microseismic Source Location. Appl. Geophys. 2015, 12, 221–234. [Google Scholar] [CrossRef]
- Schuster, G.T.; Yu, J.; Sheng, J.; Rickett, J. Interferometric/Daylight Seismic Imaging. Geophys. J. Int. 2004, 157, 838–852. [Google Scholar] [CrossRef]
- Gharti, H.N.; Oye, V.; Roth, M.; Kühn, D. Automated Microearthquake Location Using Envelope Stacking and Robust Global Optimization. Geophysics 2010, 75, MA27–MA46. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, H.; Zhang, X.; Wang, H.; Zhang, Y.; Liu, Q. Surface Microseismic Monitoring of Hydraulic Fracturing of a Shale-Gas Reservoir Using Short-Period and Broadband Seismic Sensors. Seismol. Res. Lett. 2014, 85, 668–677. [Google Scholar] [CrossRef]
- Staněk, F.; Anikiev, D.; Valenta, J.; Eisner, L. Semblance for Microseismic Event Detection. Geophys. J. Int. 2015, 201, 1362–1369. [Google Scholar] [CrossRef]
- Zhang, C.; Qiao, W.; Che, X.; Lu, J.; Men, B. Automated Microseismic Event Location by Amplitude Stacking and Semblance. Geophysics 2019, 84, KS191–KS210. [Google Scholar] [CrossRef]
- Drew, J.; White, R.S.; Tilmann, F.; Tarasewicz, J. Coalescence Microseismic Mapping. Geophys. J. Int. 2013, 195, 1773–1785. [Google Scholar] [CrossRef]
- Grigoli, F.; Cesca, S.; Krieger, L.; Kriegerowski, M.; Gammaldi, S.; Horalek, J.; Priolo, E.; Dahm, T. Automated Microseismic Event Location Using Master-Event Waveform Stacking. Sci. Rep. 2016, 6, 25744. [Google Scholar] [CrossRef]
- Li, L.; Becker, D.; Chen, H.; Wang, X.; Gajewski, D. A Systematic Analysis of Correlation-Based Seismic Location Methods. Geophys. J. Int. 2017, 212, 659–678. [Google Scholar] [CrossRef]
- Langet, N.; Maggi, A.; Michelini, A.; Brenguier, F. Continuous Kurtosis-Based Migration for Seismic Event Detection and Location, with Application to Piton De La Fournaise Volcano, La Réunion. Bull. Seismol. Soc. Am. 2014, 104, 229–246. [Google Scholar] [CrossRef]
- Poiata, N.; Satriano, C.; Vilotte, J.-P.; Bernard, P.; Obara, K. Multiband Array Detection and Location of Seismic Sources Recorded by Dense Seismic Networks. Geophys. J. Int. 2016, 205, 1548–1573. [Google Scholar] [CrossRef]
- Li, K.L.; Sgattoni, G.; Sadeghisorkhani, H.; Roberts, R.; Gudmundsson, O. A Double-Correlation Tremor-Location Method. Geophys. J. Int. 2016, 208, 1231–1236. [Google Scholar] [CrossRef]
- Yuan, C.; Zhang, J.; Zhang, W. Automatic Microseismic Stacking Location with a Multi-Cross-Correlation Condition. In Proceedings of the 2017 Workshop: Microseismic Technologies and Applications, Hefei, China, 4–6 June 2017; pp. 120–123. [Google Scholar]
- Shi, P.; Angus, D.; Rost, S.; Nowacki, A.; Yuan, S. Automated Seismic Waveform Location Using Multichannel Coherency Migration (Mcm)—I: Theory. Geophys. J. Int. 2018, 216, 1842–1866. [Google Scholar] [CrossRef]
- Shi, P.; Nowacki, A.; Rost, S.; Angus, D. Automated Seismic Waveform Location Using Multichannel Coherency Migration (Mcm)—II. Application to Induced and Volcano-Tectonic Seismicity. Geophys. J. Int. 2018, 216, 1608–1632. [Google Scholar] [CrossRef]
- Wang, H.; Chen, T.; Xu, G. Characteristics of Micro-Seismic Events Induced by Ground Collapse—A Case Study in the Rongxing Gypsum Mine in Hubei Province, China. Sensors 2024, 24, 1309. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Yu, S.; Yin, H.; Sun, Z. Microseismic Time Delay Estimation Method Based on Continuous Wavelet. Sensors 2022, 22, 2845. [Google Scholar] [CrossRef]
- Tan, M.; Hu, Q.; Ohno, S. Method for Seismic Signal Denoising Based on Generalized S-Transform and Nonlinear Complex Diffusion. J. Appl. Geophys. 2023, 215, 105095. [Google Scholar] [CrossRef]
- Chen, H.; Xue, S.; Zheng, X. Multi-Master Event Waveform Stacking Microseismic Location Method Based on Time-Frequency Transformation. J. Appl. Geophys. 2024, 220, 105267. [Google Scholar] [CrossRef]
- Pingping, B.; Yabin, M.; Zichun, W.; Yetao, J.; Wei, L. Stft-Based Multisynchrosqueezing Transform Using a Second-Order Signal Model for Seismic Data Analysis. Sci. Rep. 2025, 15, 35476. [Google Scholar] [CrossRef]
- Shalby, E.M.; Abdelaziz, A.Y.; Ahmed, E.S.; Abd-Elhamed Rashad, B. A Comprehensive Guide to Selecting Suitable Wavelet Decomposition Level and Functions in Discrete Wavelet Transform for Fault Detection in Distribution Networks. Sci. Rep. 2025, 15, 1160. [Google Scholar] [CrossRef]
- Sun, X.; Yang, X.; Zhao, R.; Wang, Z.; Chen, M.; Zheng, T.Q. S-Transform Based Time–Frequency Evaluation of Dynamic Stray Current in Zero-Resistance Converter System. Energies 2025, 18, 1594. [Google Scholar] [CrossRef]
- Zhang, L. A Novel Time-frequency Domain Reflectometry Method Based on S-transform for Power Cable Defect Localization. Recent Adv. Electr. Amp; Electron. Eng. 2025, 18, 563–574. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Sheng, G.; Zhang, Z.; Tang, X.; Xie, K. A First Arrival Picking Method of Microseismic Signals Based on Semi-Supervised Learning Using Freematch and Ms-Picking. Comput. Geosci. 2025, 196, 105844. [Google Scholar] [CrossRef]
- Zhao, H. Fast Sweeping Method for Eikonal Equations. Math. Comput. 2005, 74, 603–627. [Google Scholar] [CrossRef]
- Zeng, Z.; Lu, T.; Han, P.; Zhang, D.; Yang, X.-H.; Shi, Y.; Chang, Y.; Zhang, J.; Dai, R.; Ji, H. Microseismic Data Denoising in the Sychrosqueezed Domain by Integrating the Wavelet Coefficient Thresholding and Pixel Connectivity. Geophys. J. Int. 2022, 232, 1113–1128. [Google Scholar] [CrossRef]
- Lei, J.; Fang, H.; Zhu, Y.; Chen, Z.; Wang, X.; Xue, B.; Yang, M.; Wang, N. Gpr Detection Localization of Underground Structures Based on Deep Learning and Reverse Time Migration. NDT E Int. 2024, 143, 103043. [Google Scholar] [CrossRef]
- Yang, H.; Li, S.; Shu, J.; Yu, H.; Liu, H.; Xu, Y.; Wang, X. Data-Driven High-Resolution Total Focus Imaging from Array Ultrasonic Time-Domain Signals of Reinforced Concrete Material. Constr. Build. Mater. 2025, 492, 143048. [Google Scholar] [CrossRef]



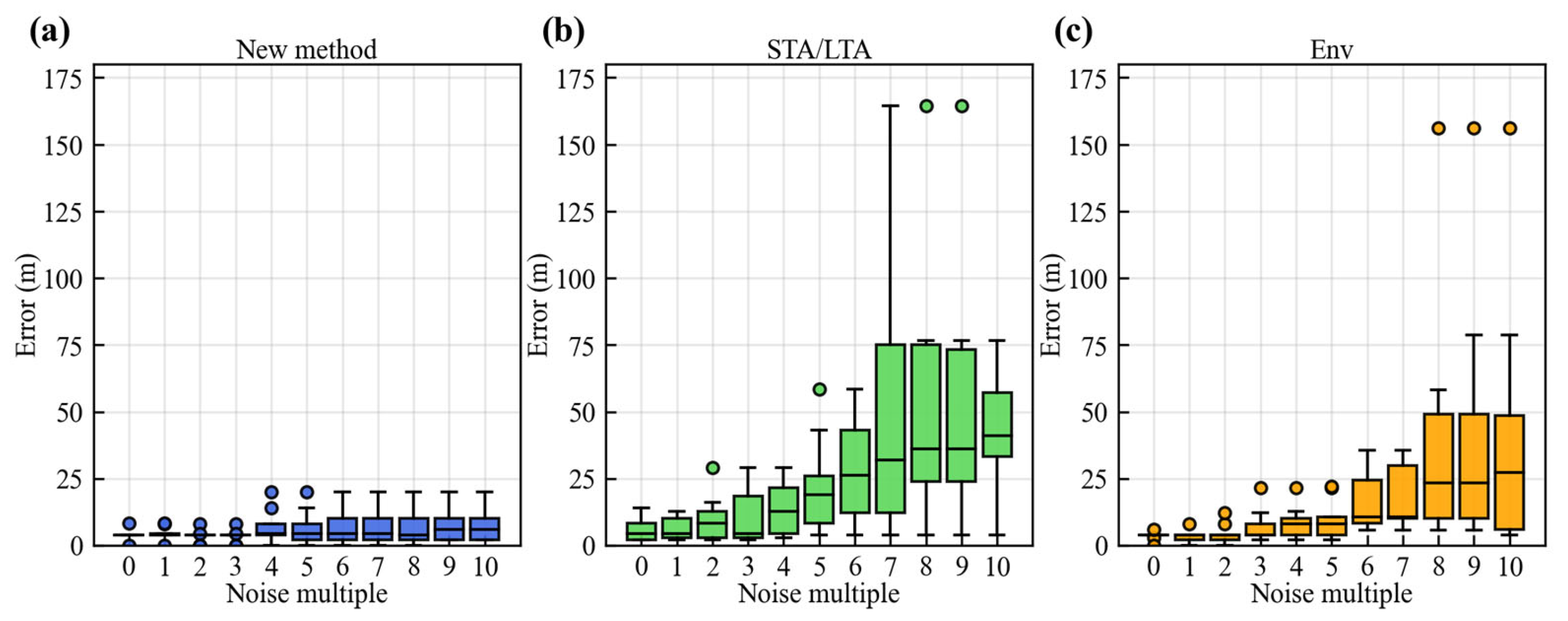


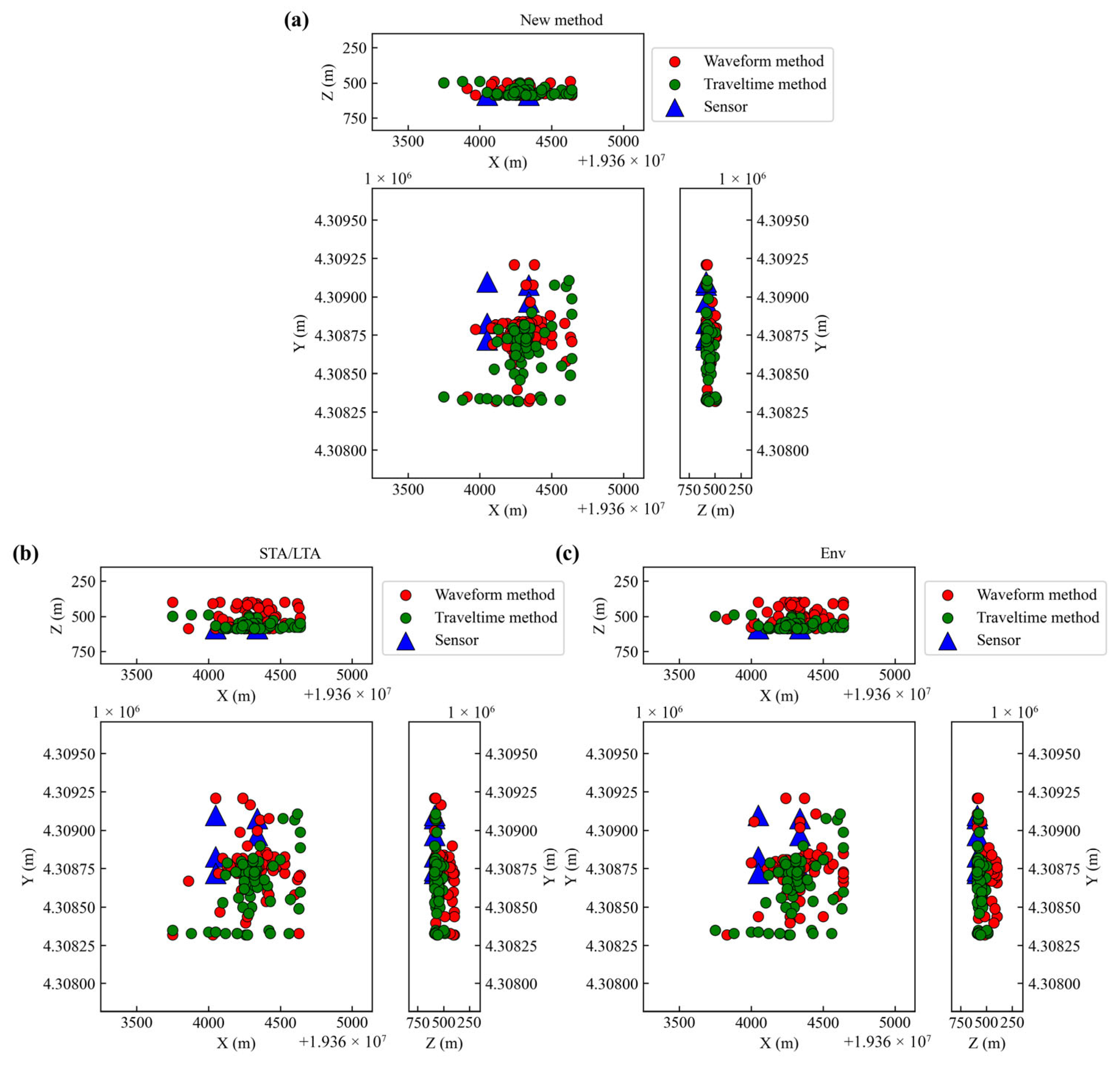
| New Method | STA/LTA | Env | |
|---|---|---|---|
| Time (s) | 0.177 | 0.018 | 0.020 |
| New Method | STA/LTA | Env | |
|---|---|---|---|
| Error of uniform array (m) | 5.97 | 26.77 | 17.63 |
| Error of Array a (m) | 8.67 | 30.82 | 12.44 |
| Error of Array b (m) | 10.30 | 24.82 | 14.68 |
| Method | +15% | +10% | +5% | −5% | −10% | −15% |
|---|---|---|---|---|---|---|
| Error of New (m) | 31.82 | 24.60 | 13.92 | 9.04 | 17.76 | 27.49 |
| Error of STA/LTA (m) | 34.59 | 32.80 | 27.91 | 27.59 | 28.75 | 34.02 |
| Error of Env (m) | 35.03 | 25.20 | 19.81 | 19.63 | 23.91 | 26.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Cheng, J.; Lizurek, G.; Wang, C.; Li, Y.; He, D.; Xu, Z. High-Precision Waveform Stacking Location Method for Microseismic Events Based on S-Transform. Sensors 2025, 25, 6965. https://doi.org/10.3390/s25226965
Zhao H, Cheng J, Lizurek G, Wang C, Li Y, He D, Xu Z. High-Precision Waveform Stacking Location Method for Microseismic Events Based on S-Transform. Sensors. 2025; 25(22):6965. https://doi.org/10.3390/s25226965
Chicago/Turabian StyleZhao, Hongpeng, Jiulong Cheng, Grzegorz Lizurek, Chuanpeng Wang, Yan Li, Dengke He, and Zhongzhong Xu. 2025. "High-Precision Waveform Stacking Location Method for Microseismic Events Based on S-Transform" Sensors 25, no. 22: 6965. https://doi.org/10.3390/s25226965
APA StyleZhao, H., Cheng, J., Lizurek, G., Wang, C., Li, Y., He, D., & Xu, Z. (2025). High-Precision Waveform Stacking Location Method for Microseismic Events Based on S-Transform. Sensors, 25(22), 6965. https://doi.org/10.3390/s25226965







