Figure 2.
Symmetry cases: (a) Agricultural machinery symmetrical structure. (b) Symmetrical structure at bridge construction site.
Figure 2.
Symmetry cases: (a) Agricultural machinery symmetrical structure. (b) Symmetrical structure at bridge construction site.
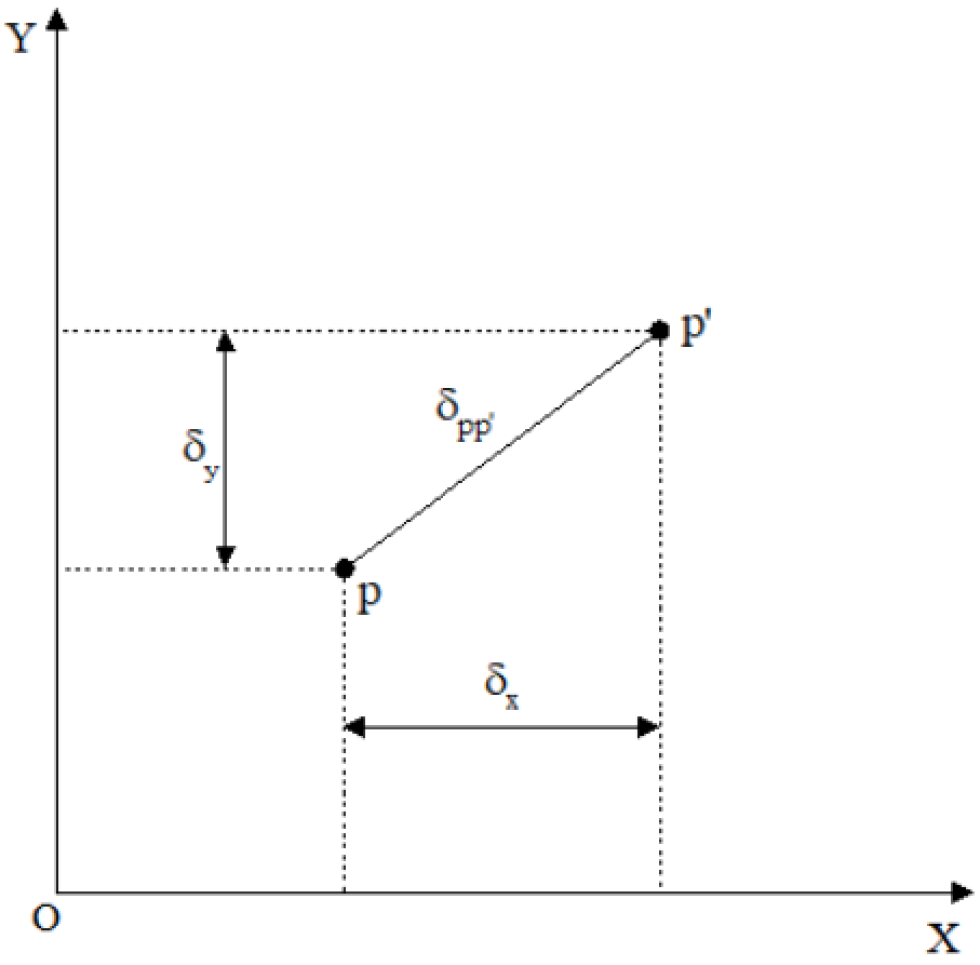
Figure 3.
Spatial positional relationship within the image plane coordinate system.
Figure 3.
Spatial positional relationship within the image plane coordinate system.
Figure 4.
Schematic diagram of the distance between the target point and the pointer points.
Figure 4.
Schematic diagram of the distance between the target point and the pointer points.
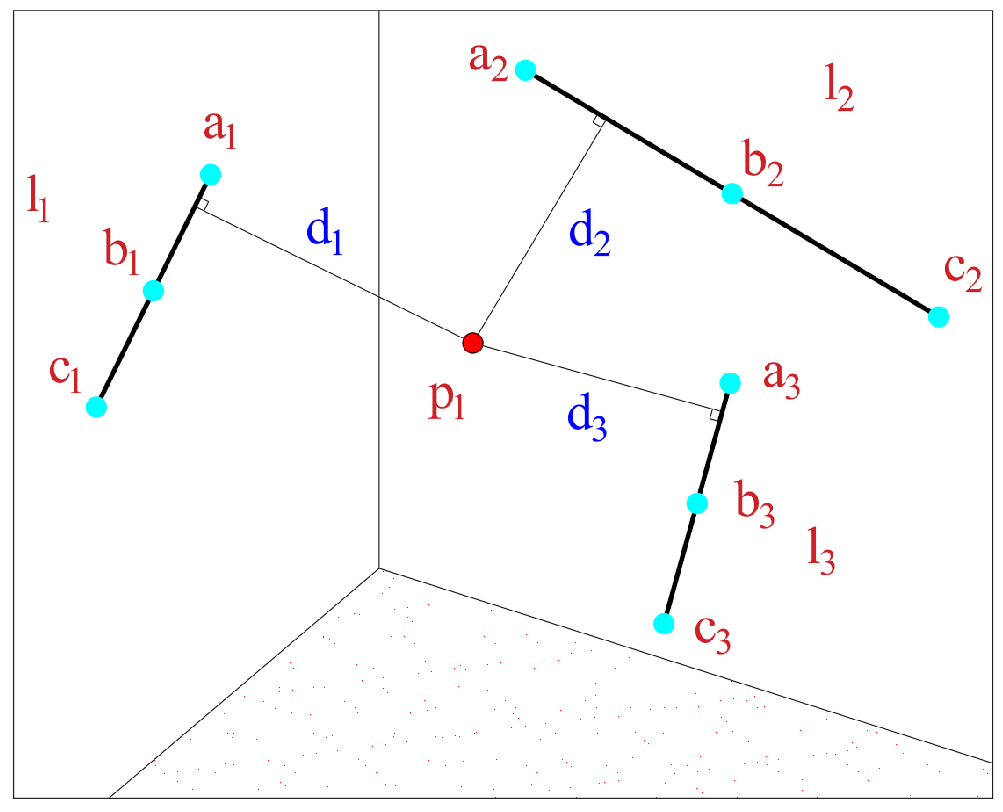
Figure 5.
Schematic diagram of the distance from the target point to the pointer points’ line.
Figure 5.
Schematic diagram of the distance from the target point to the pointer points’ line.
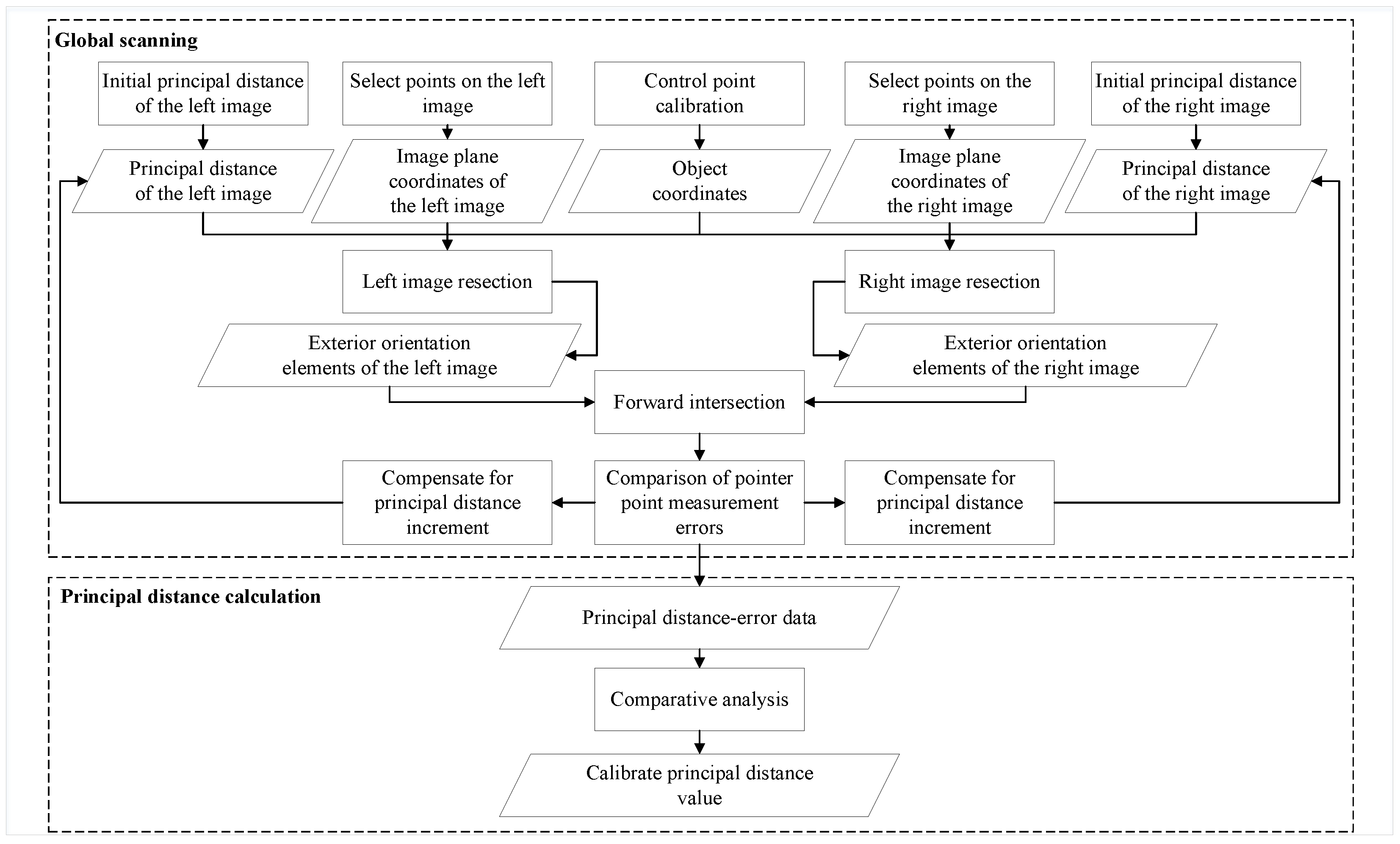
Figure 6.
Schematic diagram of the experimental procedure.
Figure 6.
Schematic diagram of the experimental procedure.
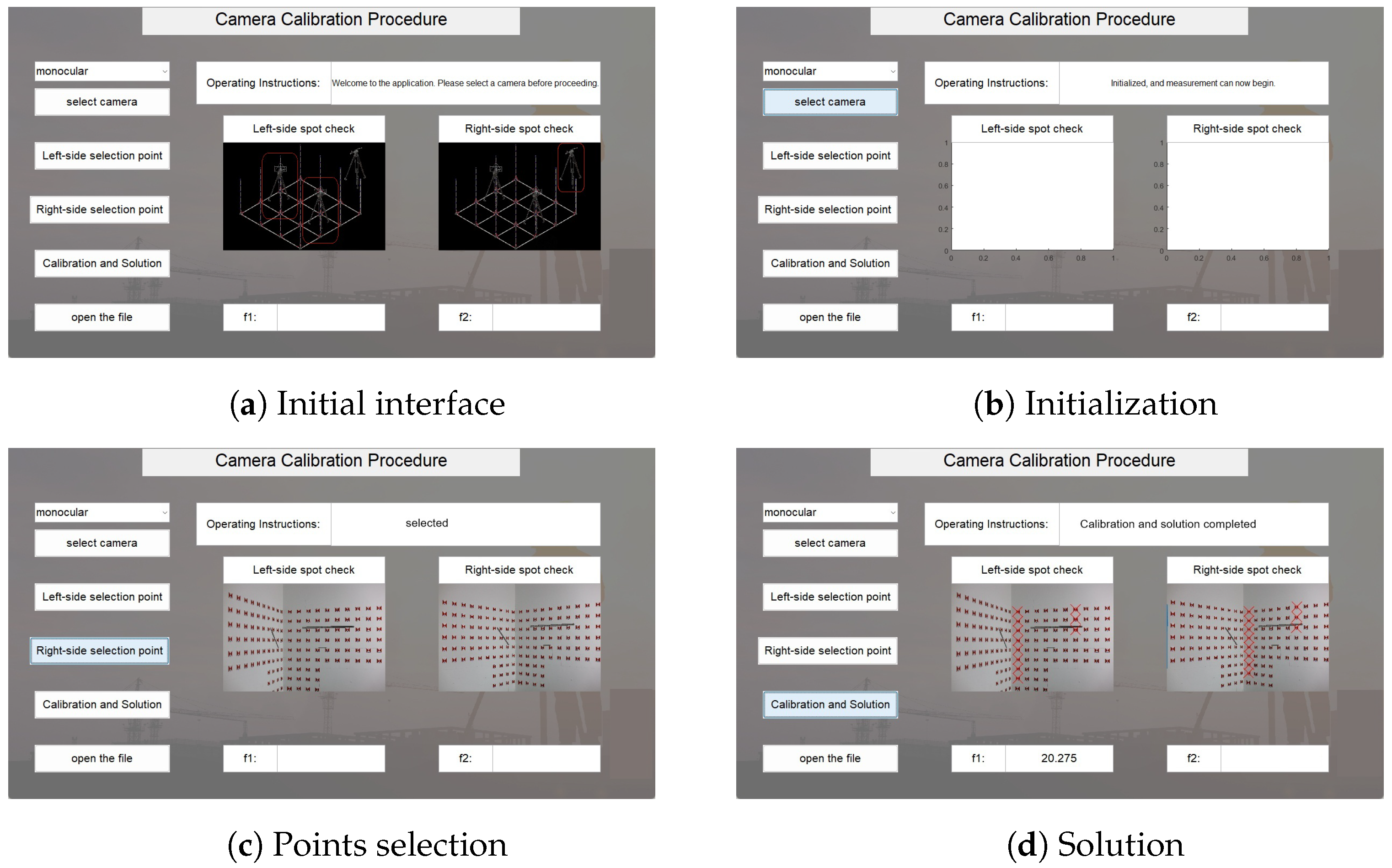
Figure 7.
GUI of the MATLAB2015b program.
Figure 7.
GUI of the MATLAB2015b program.
Figure 8.
Indoor control field.
Figure 8.
Indoor control field.
Figure 9.
Guidelines for selecting test points.
Figure 9.
Guidelines for selecting test points.
Figure 10.
Image pairs from Experiment Group 1, pair 1.
Figure 10.
Image pairs from Experiment Group 1, pair 1.
Figure 11.
Image pairs from Experiment Group 1, pair 2.
Figure 11.
Image pairs from Experiment Group 1, pair 2.
Figure 12.
Bar chart of mean errors.
Figure 12.
Bar chart of mean errors.
Figure 13.
Box plot of mean errors.
Figure 13.
Box plot of mean errors.
Table 1.
Table of symbols.
Table 1.
Table of symbols.
| Name | Explanation | Unit |
|---|
| image point coordinate corrections | mm |
| exterior orientation elements (orientation angles) | ° |
| image-plane coordinates of the image point | mm |
| image-plane coordinates of the principal point | mm |
| object-space coordinates of the camera center | mm |
| image-space coordinates of the object point | mm |
| approximate value from the previous iteration | mm |
| f | focal length | mm |
| object-space coordinates of the object point | mm |
| correction operator | |
Table 2.
Technical specifications of the test camera.
Table 2.
Technical specifications of the test camera.
| Parameter | Value | Unit |
|---|
| CCD resolution | 8688 × 5792 | pixels |
| Pixel size | 4.14 | μm |
Table 3.
Calibration results of the test camera.
Table 3.
Calibration results of the test camera.
| Parameter | Value | Parameter | Value |
|---|
| f(mm) | 54.39 | | −0.0007295 |
| (mm) | 17.97 | | −0.0007047 |
| (mm) | 11.30 | | 0 |
| −0.1495 | | 0 |
| −0.1458 | | |
Table 4.
Object-space coordinates of control points, indicator points, and test points.
Table 4.
Object-space coordinates of control points, indicator points, and test points.
| Number | x (mm) | y (mm) | z (mm) | Number | x (mm) | y (mm) | z (mm) |
|---|
| 1-L12 | −1157 | 8496 | 1690 | d-R17 | −1758 | 8319 | 1489 |
| 2-L20 | −897 | 8166 | 890 | e-R8 | −1602 | 8449 | 887 |
| 3-R34 | −2215 | 7935 | 1290 | A-L16 | −1287 | 8645 | 1287 |
| 4-L34 | −635 | 7861 | 1291 | B-R11 | −1604 | 8448 | 1488 |
| 5-R24 | −1909 | 8192 | 1689 | C-L30 | −763 | 8014 | 1690 |
| 6-R19 | −1907 | 8191 | 688 | D-R28 | −2062 | 8063 | 1289 |
| a-L4 | −1287 | 8645 | 1287 | E-R2 | −1450 | 8577 | 886 |
| b-L17 | −1027 | 8339 | 1492 | F-R32 | −2213 | 7934 | 889 |
| c-L9 | −1602 | 8449 | 887 | | | | |
Table 5.
First set of images, first group of image plane coordinates for the first experiment.
Table 5.
First set of images, first group of image plane coordinates for the first experiment.
| No. | (Pixel) | (Pixel) | (Pixel) | (Pixel) |
|---|
| 1 | 2915.304446 | 4268.459152 | 3685.612012 | 4167.712359 |
| 2 | 2465.555500 | 2057.042761 | 3021.638436 | 2260.264324 |
| 3 | 6177.994276 | 3223.974262 | 6409.409706 | 3311.038932 |
| 4 | 1895.839224 | 3310.269331 | 2239.116946 | 3295.281711 |
| 5 | 5092.168316 | 4271.782926 | 5531.238414 | 4264.914888 |
| 6 | 5111.900364 | 1575.940862 | 5549.529875 | 1778.117378 |
| a | 3126.264742 | 3158.992650 | 4003.131816 | 3211.693944 |
| b | 2694.859231 | 3784.187451 | 3358.225485 | 3732.738076 |
| c | 2923.355872 | 2642.612996 | 3695.018932 | 2757.767444 |
| d | 4583.215765 | 3717.948734 | 5139.344651 | 3740.670620 |
| e | 4077.974894 | 2117.578605 | 4761.096607 | 2288.814240 |
Table 6.
First set of images, second group of image plane coordinates for the first experiment.
Table 6.
First set of images, second group of image plane coordinates for the first experiment.
| No. | (Pixel) | (Pixel) | (Pixel) | (Pixel) |
|---|
| 1 | 3014.894649 | 4174.054300 | 3534.511674 | 4105.041802 |
| 2 | 2568.849625 | 2151.149045 | 2920.416528 | 2246.963792 |
| 3 | 6006.319048 | 3206.436374 | 6220.335682 | 3250.511088 |
| 4 | 2028.906022 | 3285.729541 | 2204.155340 | 3261.390220 |
| 5 | 5019.210222 | 4177.894540 | 5355.045035 | 4175.430140 |
| 6 | 5024.626975 | 1690.513664 | 5363.001270 | 1778.841921 |
| a | 2663.243038 | 3271.599343 | 3052.664024 | 3263.793174 |
| b | 2854.251687 | 2811.443880 | 3316.293994 | 2845.845069 |
| c | 3035.032060 | 2371.887933 | 3565.704843 | 2448.340542 |
| d | 4295.433220 | 3336.269728 | 4748.092594 | 3354.009166 |
| e | 5462.684269 | 3364.295773 | 5743.590179 | 3396.980181 |
| f | 6698.026736 | 3392.742845 | 6847.065216 | 3445.642024 |
| g | 5089.444733 | 2319.666372 | 5420.034036 | 2384.448572 |
| h | 5260.355646 | 2321.877909 | 5566.425056 | 2384.534010 |
| i | 5431.061551 | 2323.431701 | 5715.034374 | 2385.162602 |
Table 7.
Focal length.
| No. | | | | | | | | | | |
|---|
| 1 | | 61.45 | 58.46 | 55.47 | 53.65 | 53.39 | 53.54 | 53.39 | 53.25 | 53.05 |
| 2 | | 61.23 | 52.45 | 53.09 | 53.42 | 53.09 | 53.33 | 53.09 | 53.26 | 53.09 |
| 3 | 50 | 52.98 | 52.74 | 52.67 | 53.42 | 52.49 | 53.31 | 52.49 | 52.84 | 52.68 |
| 4 | | 59.76 | 51.09 | 50.96 | 51.16 | 51.08 | 51.09 | 51.00 | 50.58 | 50.40 |
| 5 | | 60.52 | 53.70 | 53.70 | 53.27 | 53.83 | 53.70 | 53.86 | 53.49 | 53.50 |
Table 8.
External orientation element for the 1st group using the traditional algorithm.
Table 8.
External orientation element for the 1st group using the traditional algorithm.
| No. | X (mm) | Y (mm) | Z (mm) | (°) | (°) | (°) |
|---|
| Left | 408.18 | 3217.88 | 1020.24 | −1.19 | −4.79 | −6.36 |
| Right | −1385.05 | 2261.01 | 993.19 | −1.55 | 0.28 | −1.30 |
Table 9.
External orientation elements for the 1st group using the geometric constraint algorithm.
Table 9.
External orientation elements for the 1st group using the geometric constraint algorithm.
| No. | X (mm) | Y (mm) | Z (mm) | (°) | (°) | (°) |
|---|
| Left | 325.63 | 2979.92 | 1031.79 | −1.21 | 1.50 | −62.90 |
| Right | −1058.38 | 2369.11 | 1013.67 | −1.65 | 877.75 | 945.29 |
Table 10.
External orientation elements for the 1st group using the optical distortion algorithm.
Table 10.
External orientation elements for the 1st group using the optical distortion algorithm.
| No. | X (mm) | Y (mm) | Z (mm) | (°) | (°) | (°) |
|---|
| Left | 267.29 | 3266.47 | 1046.40 | −1.21 | 1.51 | −69.18 |
| Right | −1054.23 | 2667.91 | 1036.63 | −1.49 | 1.30 | −63.11 |
Table 11.
External orientation elements of left and right images for test points A to F in the 1st group using composite weighting.
Table 11.
External orientation elements of left and right images for test points A to F in the 1st group using composite weighting.
| Test Point | No. | X (mm) | Y (mm) | Z (mm) | (°) | (°) | (°) |
|---|
| A | Left | 233.06 | 3438.14 | 1055.77 | −1.94 | 23.50 | −34.62 |
| Right | −1051.07 | 2846.57 | 1049.27 | −1.49 | 1.33 | −69.36 |
| B | Left | 228.12 | 3462.93 | 1057.11 | −1.20 | 1.51 | −44.04 |
| Right | −1050.58 | 2872.35 | 1051.08 | −1.65 | 61.03 | −3.38 |
| C | Left | 231.08 | 3448.06 | 1056.31 | −1.20 | 1.51 | −69.18 |
| Right | −1050.87 | 2856.88 | 1050.00 | −1.49 | 1.33 | −69.36 |
| D | Left | 228.10 | 3463.03 | 1057.12 | −1.94 | 4.65 | −34.62 |
| Right | −1050.57 | 2872.45 | 1051.08 | −1.65 | 73.59 | 9.19 |
| E | Left | 225.48 | 3476.20 | 1057.83 | −1.20 | 7.79 | −56.61 |
| Right | −1050.31 | 2886.16 | 1052.04 | −1.65 | −14.37 | −85.06 |
| F | Left | 221.73 | 3495.05 | 1058.85 | −1.20 | 3777.71 | 3725.87 |
| Right | −1049.93 | 2905.76 | 1053.41 | 4.80 | −42.64 | −245.28 |
Table 12.
Calculation errors of test points using traditional algorithm in the first experiment.
Table 12.
Calculation errors of test points using traditional algorithm in the first experiment.
| No. | X | Y | Z | Distance Error | X Error | Y Error | Z Error |
|---|
| A-L16 | −1026.45 | 8327.16 | 1291.06 | 6.30 | 3.45 | 5.16 | 1.06 |
| B-R11 | −1604.33 | 8460.12 | 1488.49 | 12.13 | 0.33 | 12.12 | 0.49 |
| C-L30 | −764.41 | 8012.07 | 1696.20 | 6.64 | 1.41 | 1.93 | 6.20 |
| D-R28 | −2064.24 | 8067.13 | 1289.43 | 4.72 | 2.24 | 4.13 | 0.43 |
| E-R2 | −1451.61 | 8594.38 | 891.37 | 18.26 | 1.61 | 17.38 | 5.37 |
| F-R32 | −2216.75 | 7937.13 | 889.17 | 4.89 | 3.75 | 3.13 | 0.17 |
| Average error (mm) | 8.82 | 2.13 | 7.31 | 2.29 |
Table 13.
Calculation errors of test points using traditional algorithm in the first experiment (simulated zoom).
Table 13.
Calculation errors of test points using traditional algorithm in the first experiment (simulated zoom).
| No. | X | Y | Z | Distance Error | X Error | Y Error | Z Error |
|---|
| A-L16 | −991.56 | 8077.33 | 1270.39 | 247.46 | 31.44 | 244.67 | 19.61 |
| B-R11 | −1522.72 | 8233.91 | 1449.41 | 232.23 | 81.28 | 214.09 | 38.59 |
| C-L30 | −760.57 | 7832.44 | 1638.94 | 188.62 | 2.43 | 181.56 | 51.06 |
| D-R28 | −1986.06 | 8013.03 | 1273.37 | 92.24 | 75.94 | 49.97 | 15.63 |
| E-R2 | −1371.11 | 8303.76 | 910.50 | 285.46 | 78.89 | 273.24 | 24.50 |
| F-R32 | −2142.74 | 7934.28 | 899.75 | 71.08 | 70.26 | 0.28 | 10.75 |
| Average error (mm) | 186.18 | 56.71 | 160.64 | 26.69 |
Table 14.
Calculation errors of test points using geometry-constrained algorithm in the first experiment.
Table 14.
Calculation errors of test points using geometry-constrained algorithm in the first experiment.
| No. | X | Y | Z | Distance Error | X Error | Y Error | Z Error |
|---|
| A-L16 | −1025.03 | 8327.97 | 1290.68 | 6.35 | 2.03 | 5.97 | 0.68 |
| B-R11 | −1604.55 | 8460.66 | 1488.69 | 12.69 | 0.55 | 12.66 | 0.69 |
| C-L30 | −763.66 | 8013.00 | 1693.72 | 3.91 | 0.66 | 1.00 | 3.72 |
| D-R28 | −2063.52 | 8066.67 | 1289.00 | 3.97 | 1.52 | 3.67 | 0.00 |
| E-R2 | −1451.55 | 8595.64 | 889.82 | 19.09 | 1.55 | 18.64 | 3.82 |
| F-R32 | −2214.84 | 7935.82 | 888.86 | 2.59 | 1.84 | 1.82 | 0.14 |
| Average error (mm) | 8.10 | 1.36 | 7.29 | 1.51 |
Table 15.
Calculation errors of test points using optical-distortion-incorporated geometry-constrained algorithm in the first experiment.
Table 15.
Calculation errors of test points using optical-distortion-incorporated geometry-constrained algorithm in the first experiment.
| No. | X | Y | Z | Distance Error | X Error | Y Error | Z Error |
|---|
| A-L16 | −1024.44 | 8327.76 | 1290.30 | 5.95 | 1.44 | 5.76 | 0.30 |
| B-R11 | −1606.11 | 8462.07 | 1489.08 | 14.27 | 2.11 | 14.07 | 1.08 |
| C-L30 | −763.65 | 8014.35 | 1692.00 | 2.13 | 0.65 | 0.35 | 2.00 |
| D-R28 | −2063.33 | 8065.94 | 1289.00 | 3.23 | 1.33 | 2.94 | 0.00 |
| E-R2 | −1452.85 | 8595.86 | 887.93 | 19.17 | 2.85 | 18.86 | 1.93 |
| F-R32 | −2213.00 | 7932.98 | 889.18 | 1.04 | 0.00 | 1.02 | 0.18 |
| Average error (mm) | 7.63 | 1.40 | 7.17 | 0.92 |
Table 16.
Calculation errors of test points using composite weighted algorithm incorporating geometric constraints, optical distortion and spatial distance metrics in the first experiment.
Table 16.
Calculation errors of test points using composite weighted algorithm incorporating geometric constraints, optical distortion and spatial distance metrics in the first experiment.
| No. | X | Y | Z | Distance Error | X Error | Y Error | Z Error |
|---|
| A-L16 | −1024.04 | 8327.46 | 1289.88 | 5.56 | 1.04 | 5.46 | 0.12 |
| B-R11 | −1607.24 | 8463.10 | 1489.25 | 15.49 | 3.24 | 15.10 | 1.25 |
| C-L30 | −763.58 | 8014.70 | 1690.49 | 1.03 | 0.58 | 0.70 | 0.49 |
| D-R28 | −2062.95 | 8065.08 | 1289.06 | 2.29 | 0.95 | 2.08 | 0.06 |
| E-R2 | −1453.32 | 8595.11 | 886.32 | 18.41 | 3.32 | 18.11 | 0.32 |
| F-R32 | −2212.54 | 7935.71 | 889.20 | 1.78 | 0.46 | 1.71 | 0.20 |
| Average error (mm) | 7.43 | 1.60 | 7.19 | 0.40 |