Aeromagnetic Compensation for UAVs Using Transformer Neural Networks
Abstract
1. Introduction
2. Aeromagnetic Compensation Model and Methodology
2.1. Tolles and Lawson Model
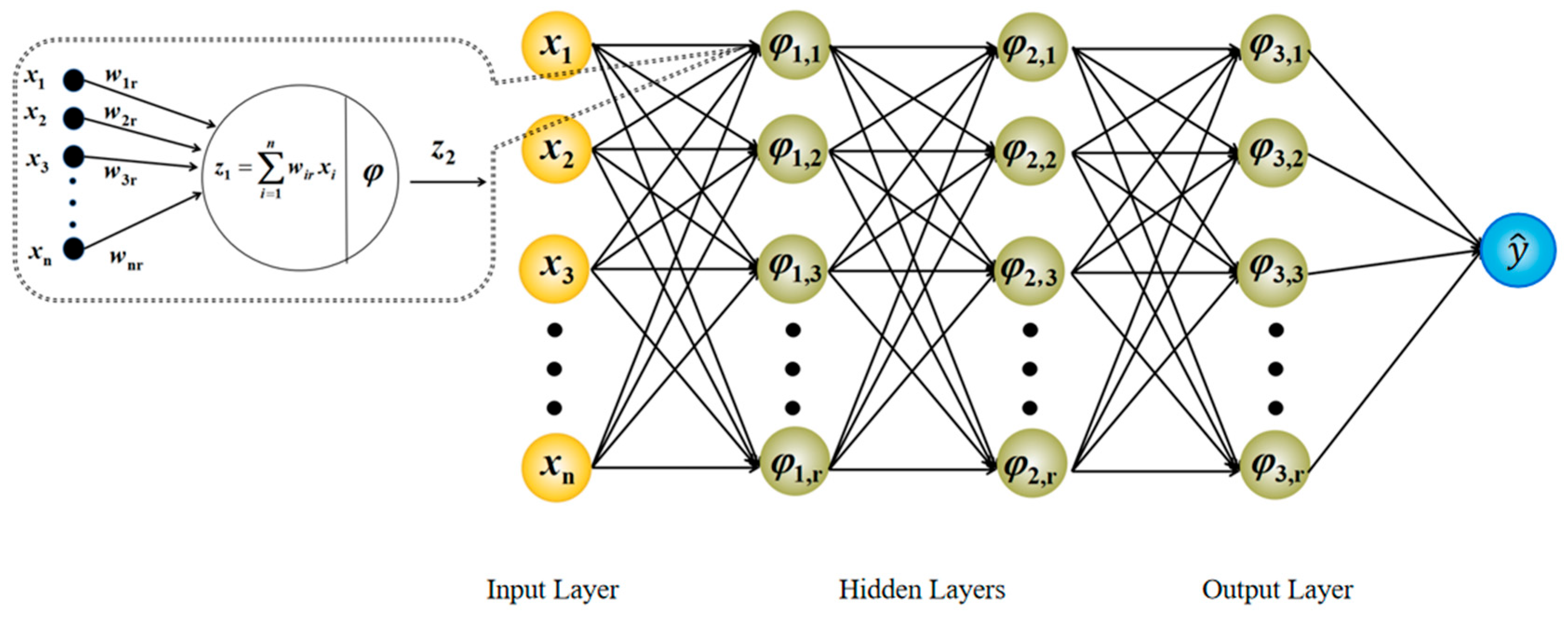
2.2. MLP Neural Networks
2.2.1. Multilayer Perceptron
2.2.2. Forward Propagation
2.2.3. Backpropagation
2.3. Transformer Neural Networks
2.3.1. Forward Propagation
2.3.2. Backpropagation
3. Simulation and Compensation
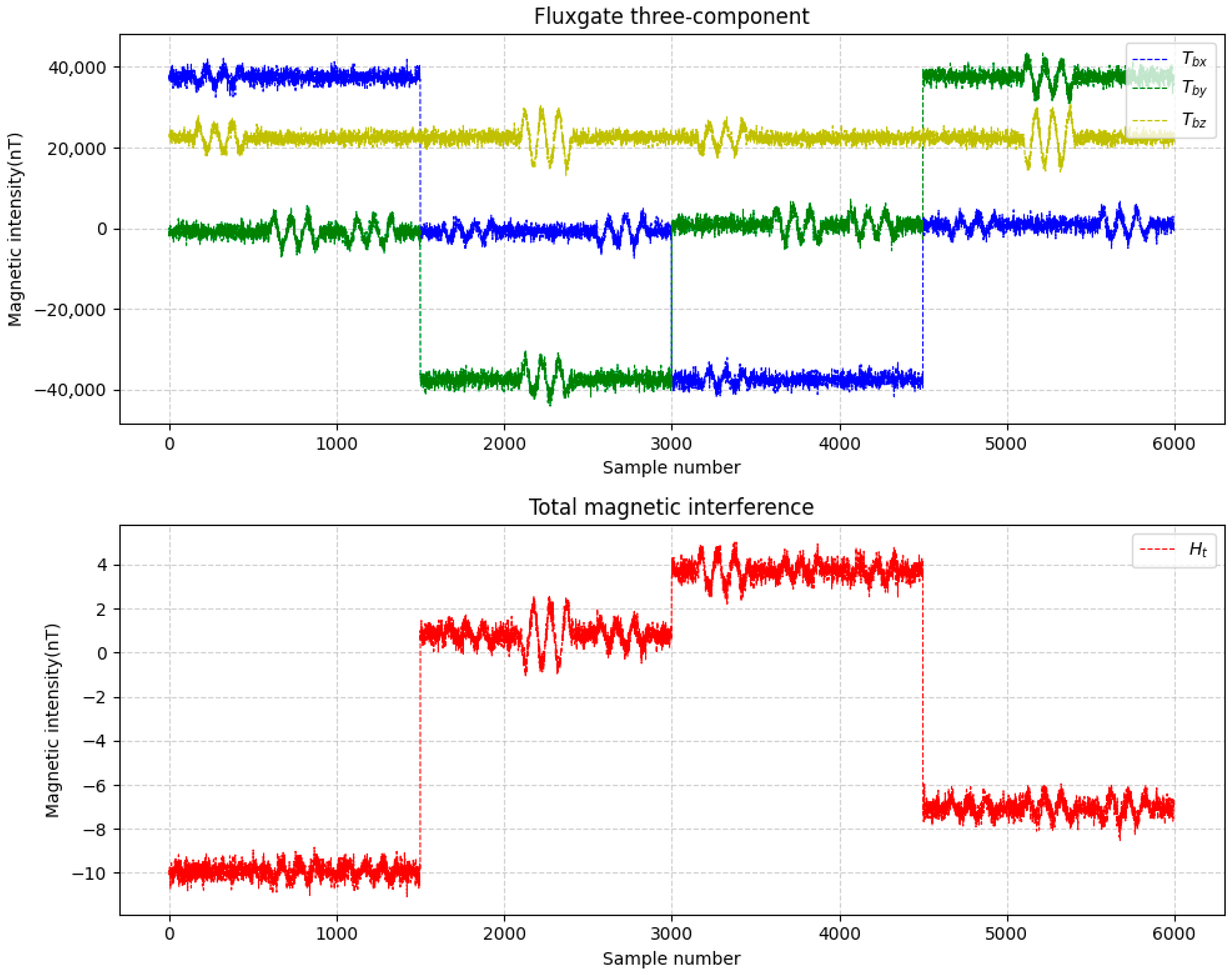
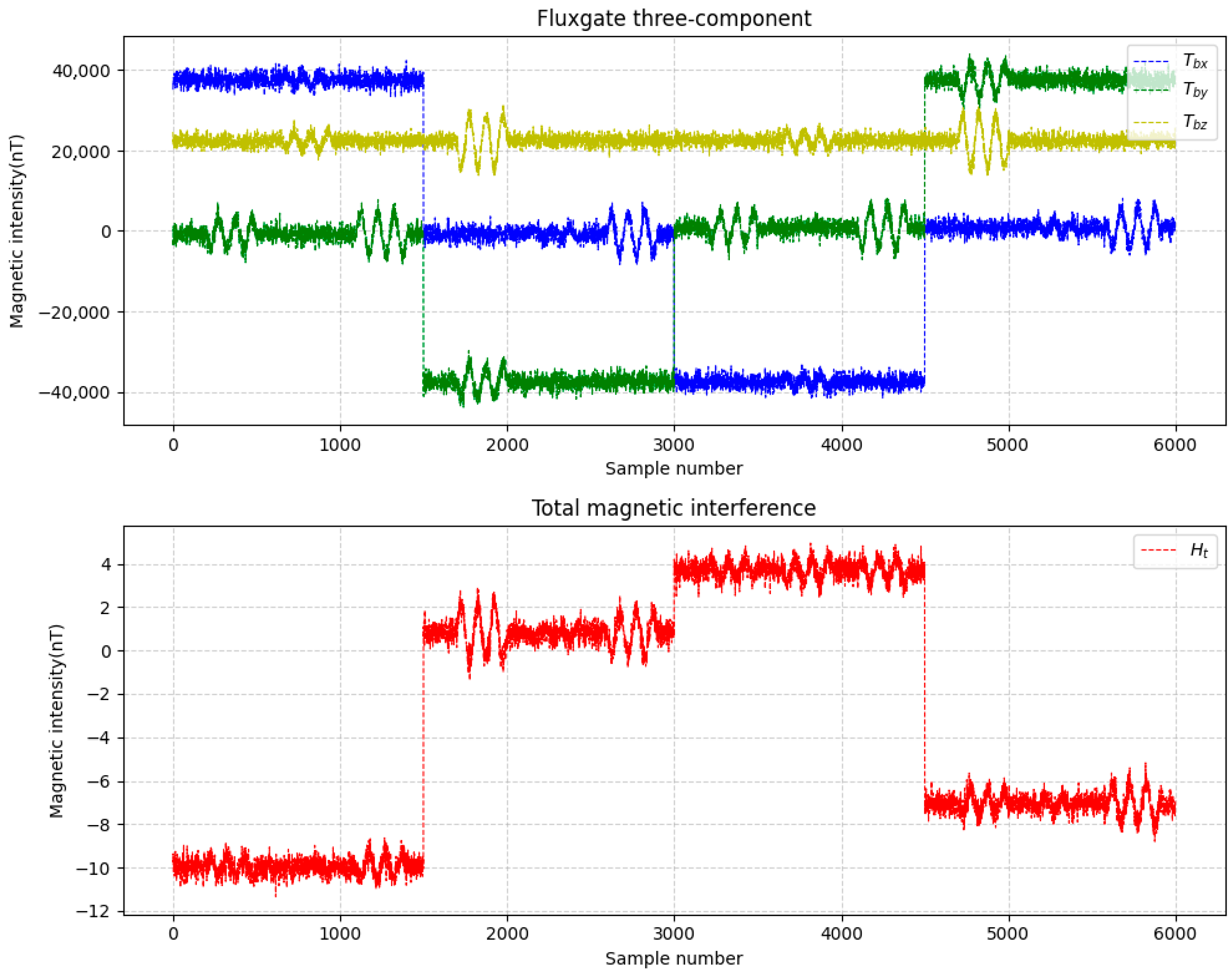
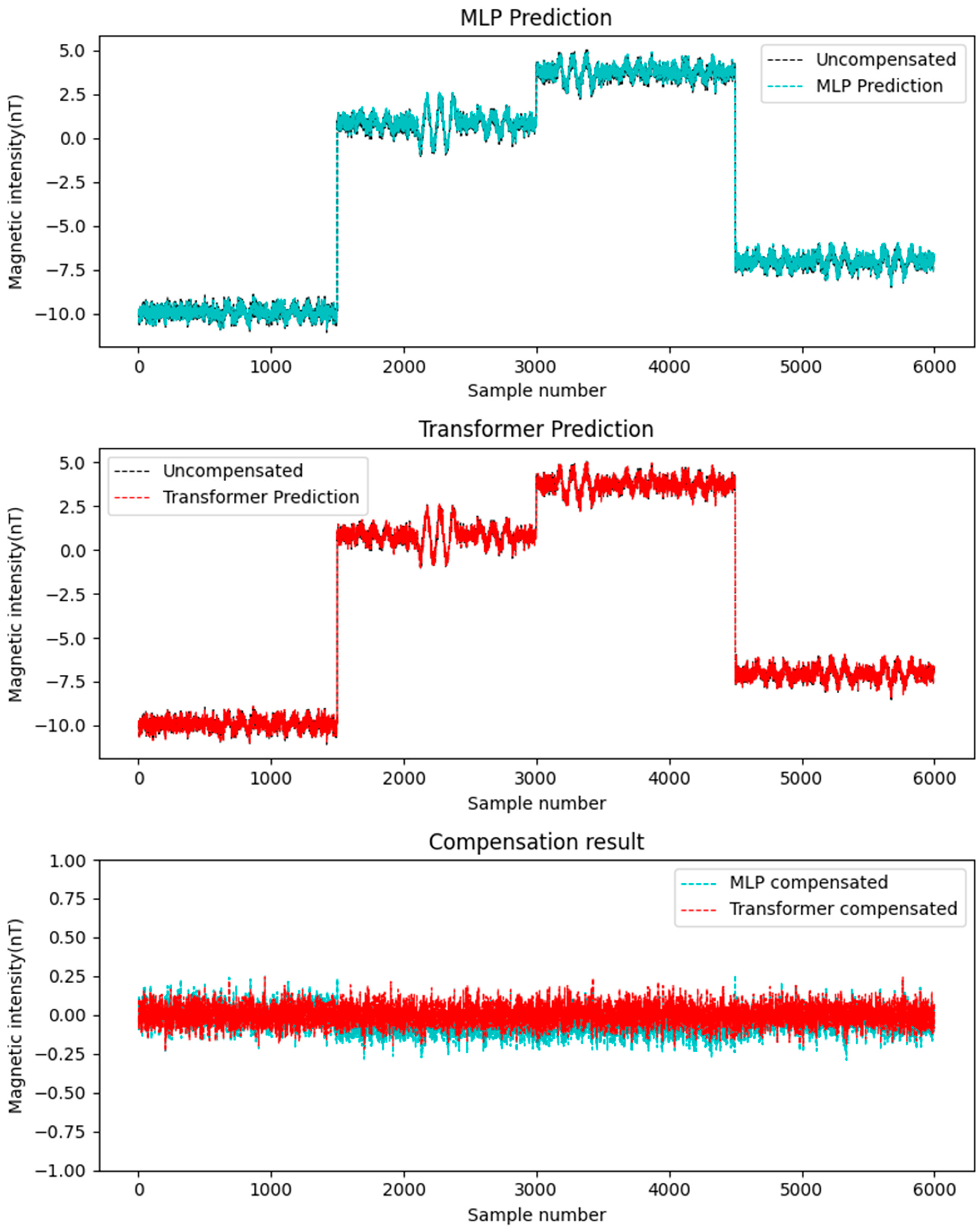
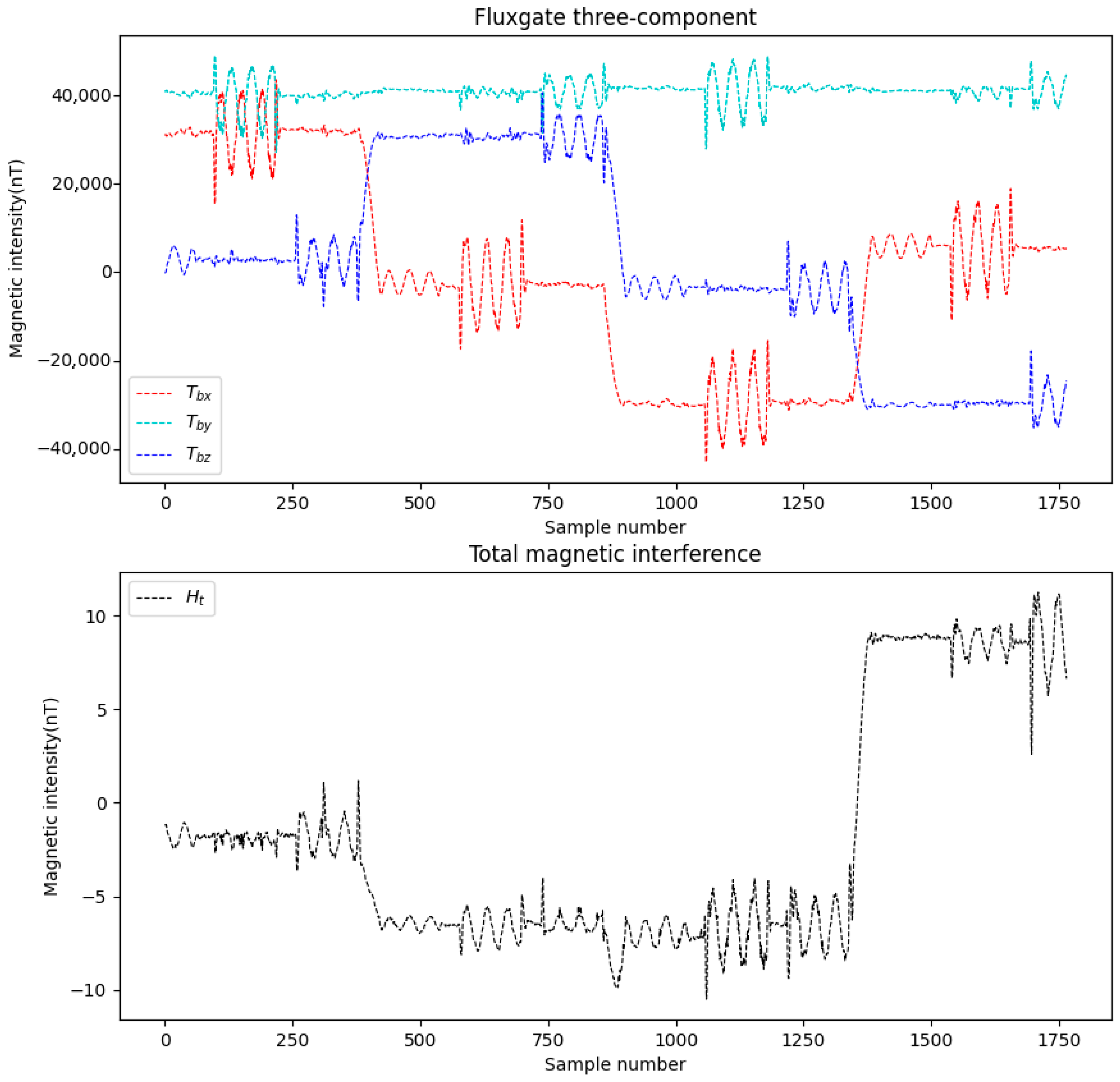
3.1. Experiment of Simulation
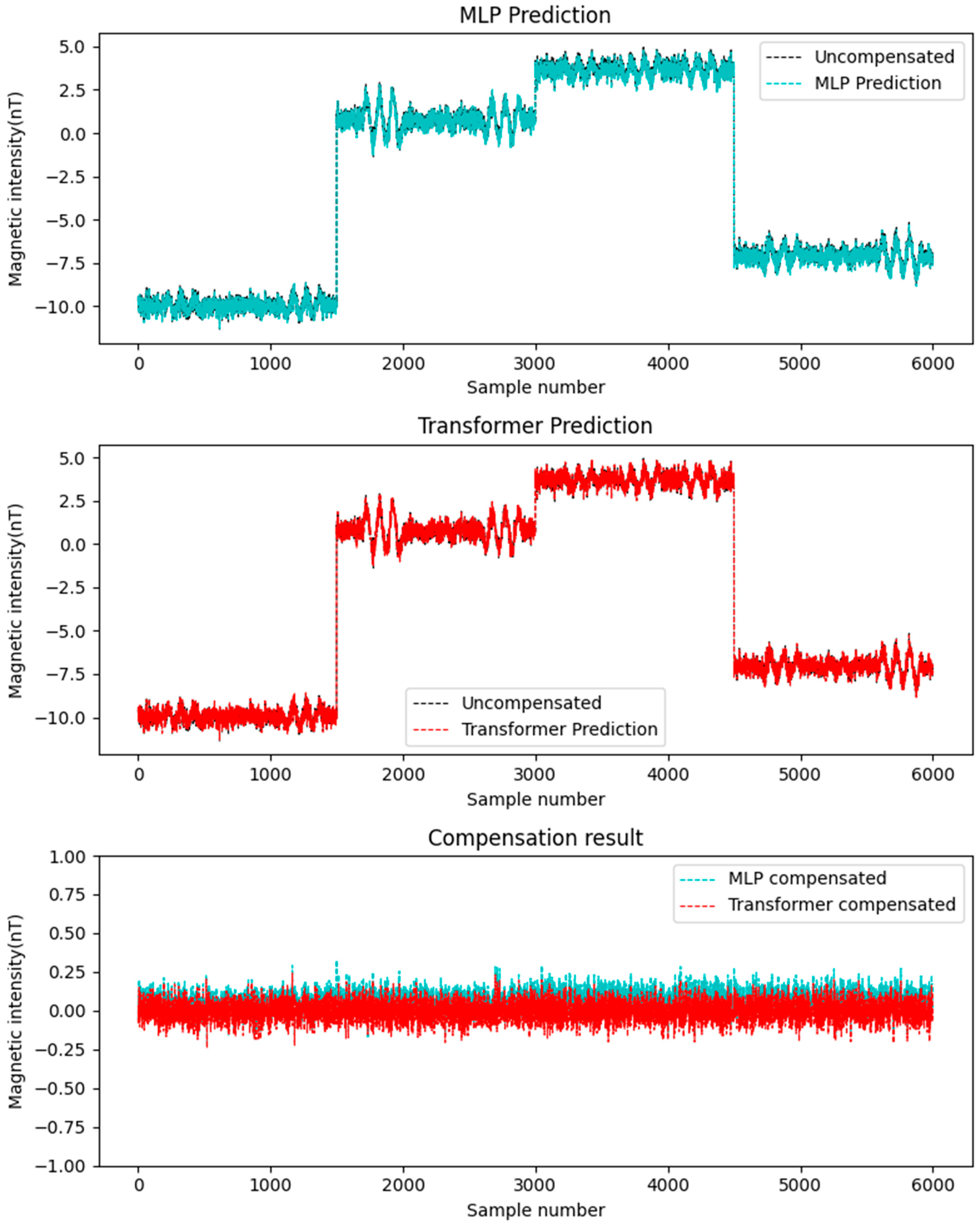
3.2. Compensation Results
4. Field-Measured Data Compensation
4.1. Flight of Compensation
4.2. Compensation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, J.; Chen, J.; Yang, Z. EnergyEfficient UAV Communication with Trajectory Optimization. In Proceedings of the 2021 2nd International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE), Zhuhai, China, 24–26 September 2021; pp. 508–514. [Google Scholar]
- Zheng, Y.; Li, S.; Xing, K.; Zhang, X. Unmanned Aerial Vehicles for Magnetic Surveys: A Review on Platform Selection and Interference Suppression. Drones 2021, 5, 93. [Google Scholar] [CrossRef]
- Yang, S.L.; Li, F.L.; Huang, J.J.; Wang, J.; Huang, M.N.; Wang, X.; Zhou, Q. History and Prospects of Aeromagnetic Compensation Technologies Used in China and Abroad. Geophys. Geochem. Explor. 2017, 41, 694–699. [Google Scholar]
- Xiong, S.Q. Innovation and application of airborne geophysical exploration technology. J. Geomech. 2020, 26, 791–818. [Google Scholar]
- Tolles, W.E.; Lawson, J.D. Magnetic Compensation of MAD Equipped Aircraft; Airborne Instruments Lab. Inc.: Mineola, NY, USA, 1950; pp. 201–211. [Google Scholar]
- Bickel, S. Small Signal Compensation of Magnetic Fields Resulting from Aircraft Maneuvers. IEEE Trans. Aerosp. Electron. Syst. 1979, AES-15, 518–525. [Google Scholar] [CrossRef]
- Leach, B.W. Aeromagnetic compensation as a linear regression problem. In Information Linkage Between Applied Mathematics and Industry II; Academic Press: London, UK, 1980; pp. 139–161. [Google Scholar]
- Wu, P.; Zhang, Q.; Chen, L.; Zhu, W.; Guangyou, F. Aeromagnetic Compensation Algorithm Based on Principal Component Analysis. J. Sens. 2018, 2018, 5798287. [Google Scholar] [CrossRef]
- Newcome, L.R. Unmanned Aviation: A Brief History of Unmanned Aerial Vehicles; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. [Google Scholar]
- Everett, H.R. Unmanned Systems of World Wars I and II; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Wagner, W. Lightning Bugs and Other Reconnaissance Drones. Armed Forces J. Int. 1982, 120, 45–52. [Google Scholar]
- Gertler, J.U.S. Unmanned Aerial Systems; R42136; Congressional Research Service Report for Congress: Washington, DC, USA, 2012.
- Nonami, K.; Kendoul, F.; Suzuki, S.; Wang, W.; Nakazawa, D. Autonomous Flying Robots: Unmanned Aerial Vehicles and Micro Aerial Vehicles, 1st ed.; Springer: Tokyo, Japan, 2010. [Google Scholar] [CrossRef]
- Floreano, D.; Wood, R.J. Science, Technology and the Future of Small Autonomous Drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef]
- Clothier, R.A.; Greer, D.A.; Greer, D.G.; Mehta, A.M. Risk Perception and the Public Acceptance of Drones. Risk Anal. 2015, 35, 1167–1183. [Google Scholar] [CrossRef]
- Sánchez-Soriano, J.; Rojo-Gala, M.Á.; Pérez-Pérez, G.; Bemposta Rosende, S.; Gordo-Herrera, N. Optimized Autonomous Drone Navigation Using Double Deep Q-Learning for Enhanced Real-Time 3D Image Capture. Drones 2024, 8, 725. [Google Scholar] [CrossRef]
- Guo, A.; Huang, W.; Dong, Y.; Ye, H.; Ma, H.; Liu, B.; Wu, W.; Ren, Y.; Ruan, C.; Geng, Y. Wheat Yellow Rust Detection Using UAV-Based Hyperspectral Technology. Remote Sens. 2021, 13, 123. [Google Scholar] [CrossRef]
- Zuo, L.; Gao, S.; Li, Y.; Li, L.; Li, M.; Lu, X. A Fast and Robust Algorithm with Reinforcement Learning for Large UAV Cluster Mission Planning. Remote Sens. 2022, 14, 1304. [Google Scholar] [CrossRef]
- Subbarayalu, V.; Vensuslaus, M.A. An Intrusion Detection System for Drone Swarming Utilizing Timed Probabilistic Automata. Drones 2023, 7, 248. [Google Scholar] [CrossRef]
- Perikleous, D.; Margariti, K.; Velanas, P.; Blazquez, C.S.; Gonzalez-Aguilera, D. Aerial Drones for Geophysical Prospection in Mining: A Review. Drones 2025, 9, 383. [Google Scholar] [CrossRef]
- Williams, P.M. Aeromagnetic Compensation Using Neural Networks. Neural Comput. Appl. 1993, 1, 207–214. [Google Scholar] [CrossRef]
- Ma, M.; Zhou, Z.; Cheng, D. A Dual Estimate Method for Aeromagnetic Compensation. Meas. Sci. Technol. 2017, 28, 115904. [Google Scholar] [CrossRef]
- Yu, P.; Bi, F.; Jiao, J.; Zhao, X.; Zhou, S.; Su, Z. An Aeromagnetic Compensation Algorithm Based on a Residual Neural Network. Appl. Sci. 2022, 12, 10759. [Google Scholar] [CrossRef]
- Jiao, J.; Yu, P.; Zhao, X.; Bi, F. Real-Time Aeromagnetic Compensation With Compressed and Accelerated Neural Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8025905. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, C.; Su, Z.; Yu, P.; Jiao, J. An Aeromagnetic Compensation Algorithm Based on Radial Basis Function Artificial Neural Network. Appl. Sci. 2023, 13, 136. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 2–6 December 2024; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. In Proceedings of the 35th International Conference on Neural Information Processing Systems, Los Angeles, CA, USA, 6–14 December 2021; p. 1717. [Google Scholar]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic Flow Prediction With Big Data: A Deep Learning Approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Qin, Y.; Song, D.; Cheng, H.; Cheng, W.; Jiang, G.; Cottrell, G.W. A dual-stage attention-based recurrent neural network for time series prediction. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 2627–2633. [Google Scholar]
- Leliak, P. Identification and evaluation of magnetic-field sources of magnetic airborne detector equipped aircraft. IRE Trans. Aerosp. Navig. Electr. 1961, 3, 95–105. [Google Scholar] [CrossRef]






| Test Set | Training Set | Method | IR | ||
|---|---|---|---|---|---|
| Data A | Data B | MLP | 5.59 | 0.069 | 82.45 |
| Transformer | 0.065 | 86.40 | |||
| Data B | Data A | MLP | 5.58 | 0.074 | 75.38 |
| Transformer | 0.065 | 86.38 |
| Measuring Range | 1000~100,000 nT |
| Gradient Capacity | 100 nT/cm |
| Ground Static Noise Level | ≤0.01 nT |
| Resolution | 0.0001 nT |
| Sensitivity | 0.02 nT/ |
| Power Consumption | ≤3 W |
| Operating Remperature | −30~+60 °C |
| Test Set | Training Set | Method | IR | ||
|---|---|---|---|---|---|
| Data D | Data C | MLP | 6.21 | 0.17 | 31.13 |
| Transformer | 0.13 | 36.43 | |||
| Data C | Data D | MLP | 6.42 | 0.16 | 40.94 |
| Transformer | 0.14 | 46.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, W.; Yang, C.; Zhou, S. Aeromagnetic Compensation for UAVs Using Transformer Neural Networks. Sensors 2025, 25, 6852. https://doi.org/10.3390/s25226852
Dai W, Yang C, Zhou S. Aeromagnetic Compensation for UAVs Using Transformer Neural Networks. Sensors. 2025; 25(22):6852. https://doi.org/10.3390/s25226852
Chicago/Turabian StyleDai, Weiming, Changcheng Yang, and Shuai Zhou. 2025. "Aeromagnetic Compensation for UAVs Using Transformer Neural Networks" Sensors 25, no. 22: 6852. https://doi.org/10.3390/s25226852
APA StyleDai, W., Yang, C., & Zhou, S. (2025). Aeromagnetic Compensation for UAVs Using Transformer Neural Networks. Sensors, 25(22), 6852. https://doi.org/10.3390/s25226852






