Domain-Adaptive Graph Attention Semi-Supervised Network for Temperature-Resilient SHM of Composite Plates
Abstract
1. Introduction
1.1. Temperature-Induced Variability and Conventional Compensation Methods
1.2. Data-Driven Methods for Temperature Compensation
1.3. Transfer Learning for Mitigating EOVs in SHM
1.4. The Need for Explainability in ML-Based SHM
1.5. Main Contributions
- Combines multiple temperature domains into a single target domain, improving generalisation and reflecting real-world variability for greater robustness and practicality.
- Integrates CORAL and MMD losses to align feature distributions across temperatures, explores CORAL’s effectiveness in SHM, and employs GATs to capture complex spatial-temporal dependencies in UGW data for accurate damage detection.
- Uses GAT attention weights to visualise and quantify sensor contributions, enhancing model transparency and providing valuable insights into sensor importance for both theoretical and practical SHM applications.
2. Materials and Methods
2.1. Overview of the Proposed Framework
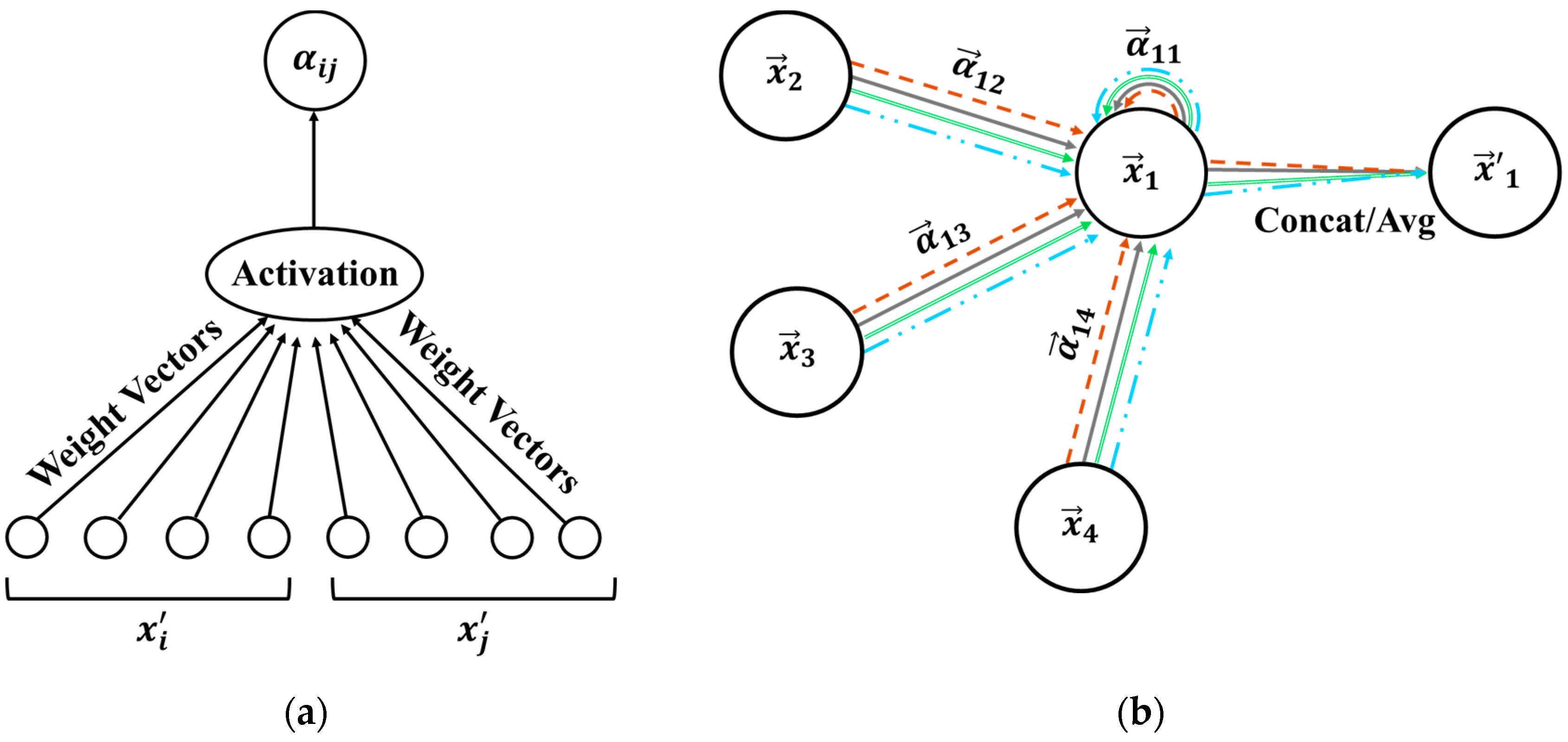
2.2. Graph Attention Networks
- Feature transformation: Each node’s input feature vectors and undergo a shared linear transformation:
- 2.
- Computation of importance scores: A self-attention mechanism computes unnormalised importance scores , quantifying the relevance of the -th node’s features to the -th node:
- 3.
- Normalisation of attention coefficients: The scores are normalised using the softmax function to produce attention coefficients :
- 4.
- Feature aggregation: Each node’s output feature is computed as a weighted sum of its neighbours’ transformed features:
- 5.
- Multi-head attention: To improve stability and expressiveness, multiple attention mechanisms (heads) are employed. Each head independently computes its own set of attention coefficients and aggregated features:
2.3. Domain Adaptation
2.3.1. Domain-Adversarial Neural Network
2.3.2. Maximum Mean Discrepancy
2.3.3. Correlation Alignment
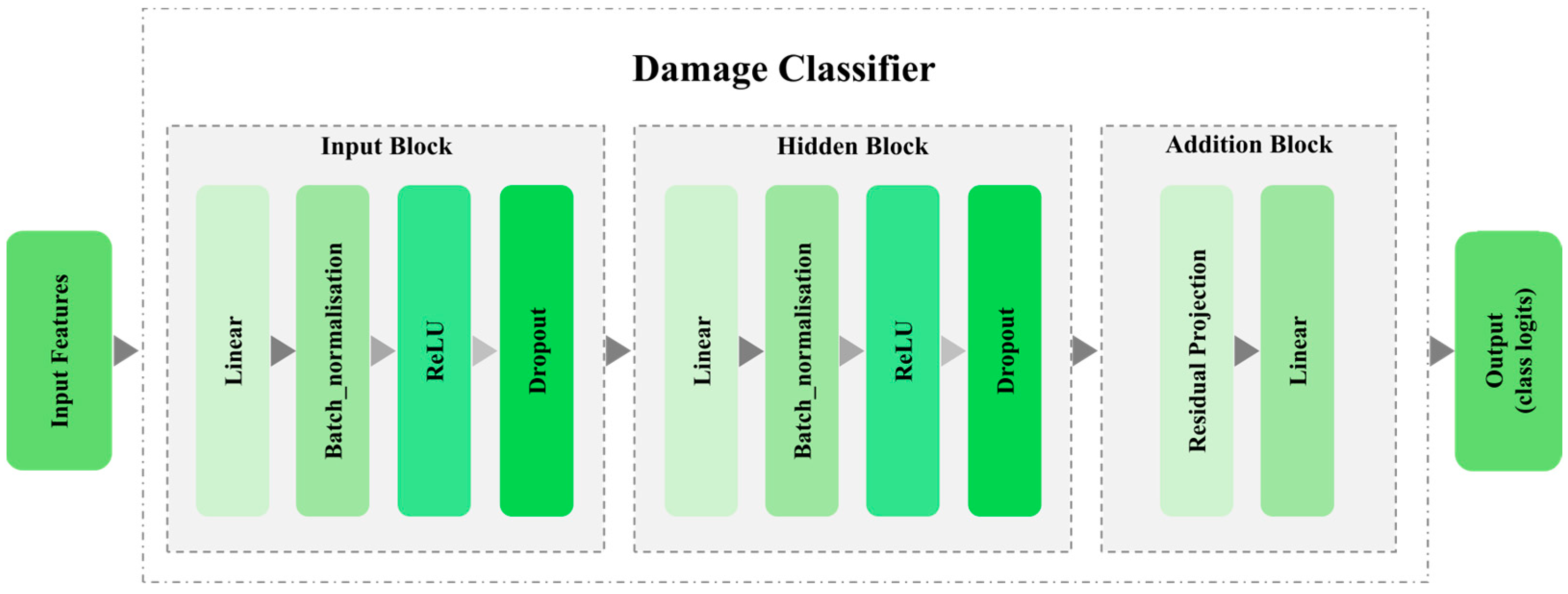
2.4. Training Process of GAT-CAMDA
| Algorithm 1. GAT-CAMDA framework for SHM. |
| Input: Source domain data and labels, target domain data, target domain labels (held out for the validation and testing). Output: Trained GAT-CAMDA model, feature-space alignment and sensor-importance visualisations, final classification performance on source test and target test. 1. Configuration and Setup 1.1 Set the device to GPU if available. 1.2 Initialise random seeds for reproducibility. 1.3 Define global configuration (e.g., hidden dimensions, batch size). 2. Data Preprocessing 2.1 Load source and target data. 2.2 Split source data into training, validation, and testing sets. 2.3 Split target data into training, validation, and testing sets, supporting stratification. 2.4 Convert labels to tensors and create graph-based representations of the data. 3. Model Initialisation 3.1 Define the GNN-based feature extractor using GAT. 3.2 Define the discriminator for domain classification. 3.3 Define the classifier for damage classification. 3.4 Initialise the DANN. 4. Training the Model 4.1 For each epoch: 4.1.1 Compute the adaptive weight for domain-adversarial loss. 4.1.2 For each batch of source and target data: a. Forward pass through the feature extractor, classifier, and discriminator. b. Compute classification loss, domain loss, MMD loss, and CORAL loss. c. Backpropagate the combined loss and update model parameters. 4.2 Perform early stopping based on validation loss. 5. Hyperparameter Optimisation 5.1 Use Optuna for hyperparameter tuning with a defined search space. 5.2 Optimise learning rate, weight decay, loss weights, and model architecture based on validation set of target domain. 5.3 Train and evaluate the final model with the best hyperparameters. 6. Model Evaluation 6.1 Evaluate the model on the source test set for classification accuracy. 6.2 Evaluate the model on the target validation set for domain adaptation performance. 6.3 Generate confusion matrices and classification reports. 7. Feature-Space Visualisation 7.1 Extract feature embeddings using the trained model. 7.2 Apply t-SNE for dimensionality reduction. 7.3 Visualise embeddings before and after domain alignment. 8. Sensor Importance Analysis 8.1 Compute attention scores for each sensor from the GAT layers. 8.2 Normalise and visualise sensor importance scores. 9. Final Outputs 9.1 Trained GAT-CAMDA model. 9.2 Visualisations of feature alignment and sensor importance. |
2.5. Data Synthesising
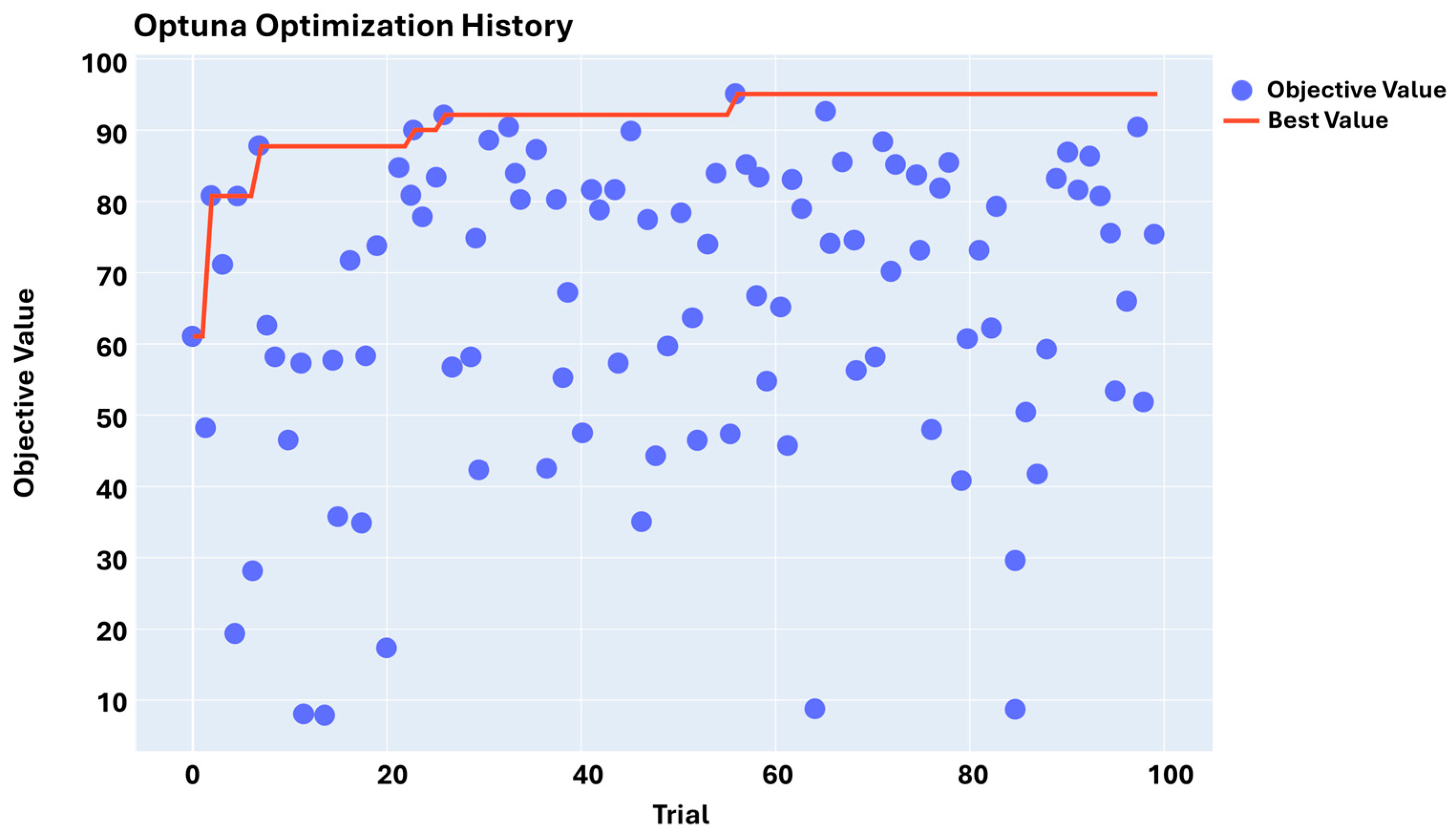
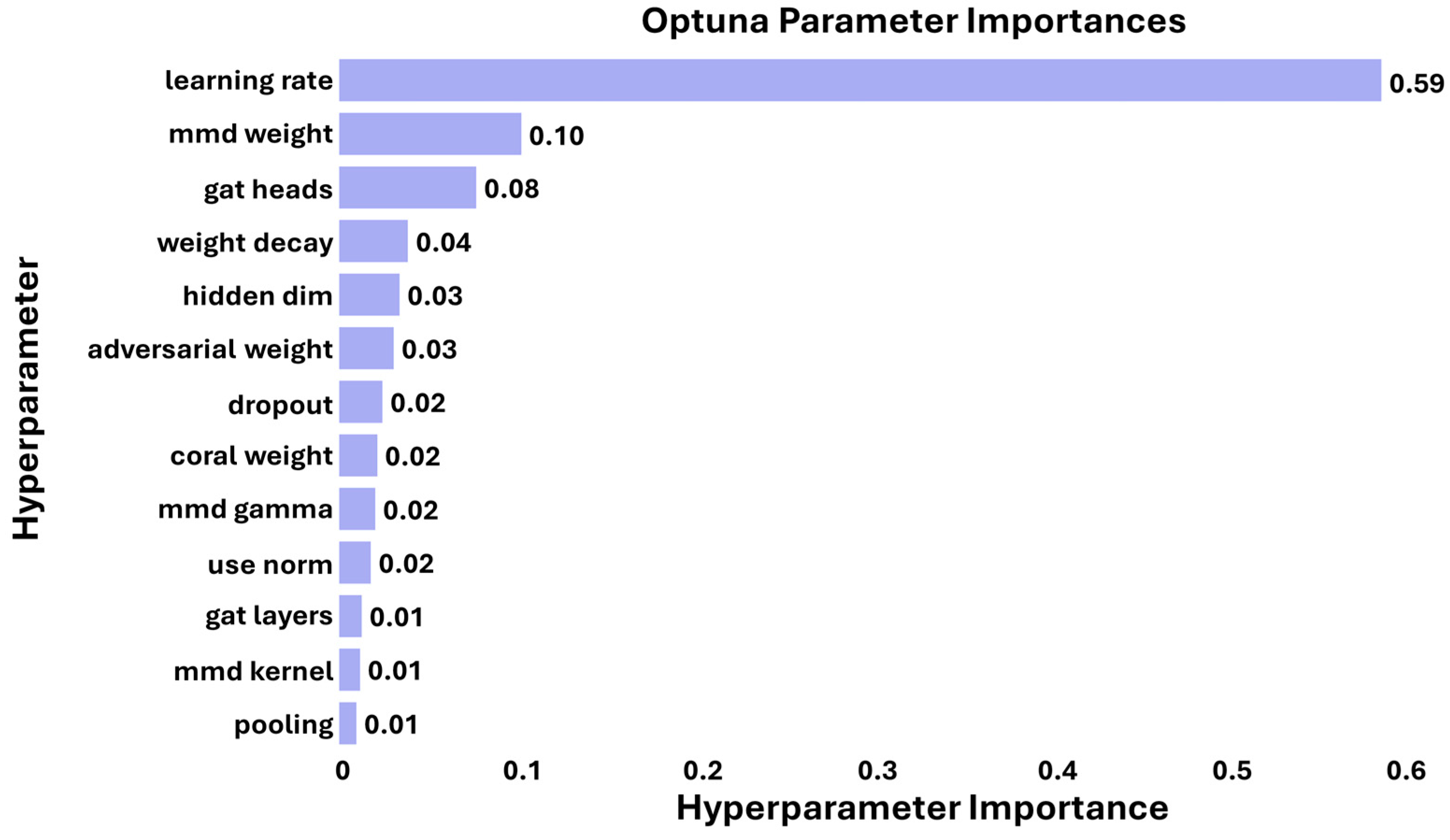
2.6. Hyperparameter Optimisation
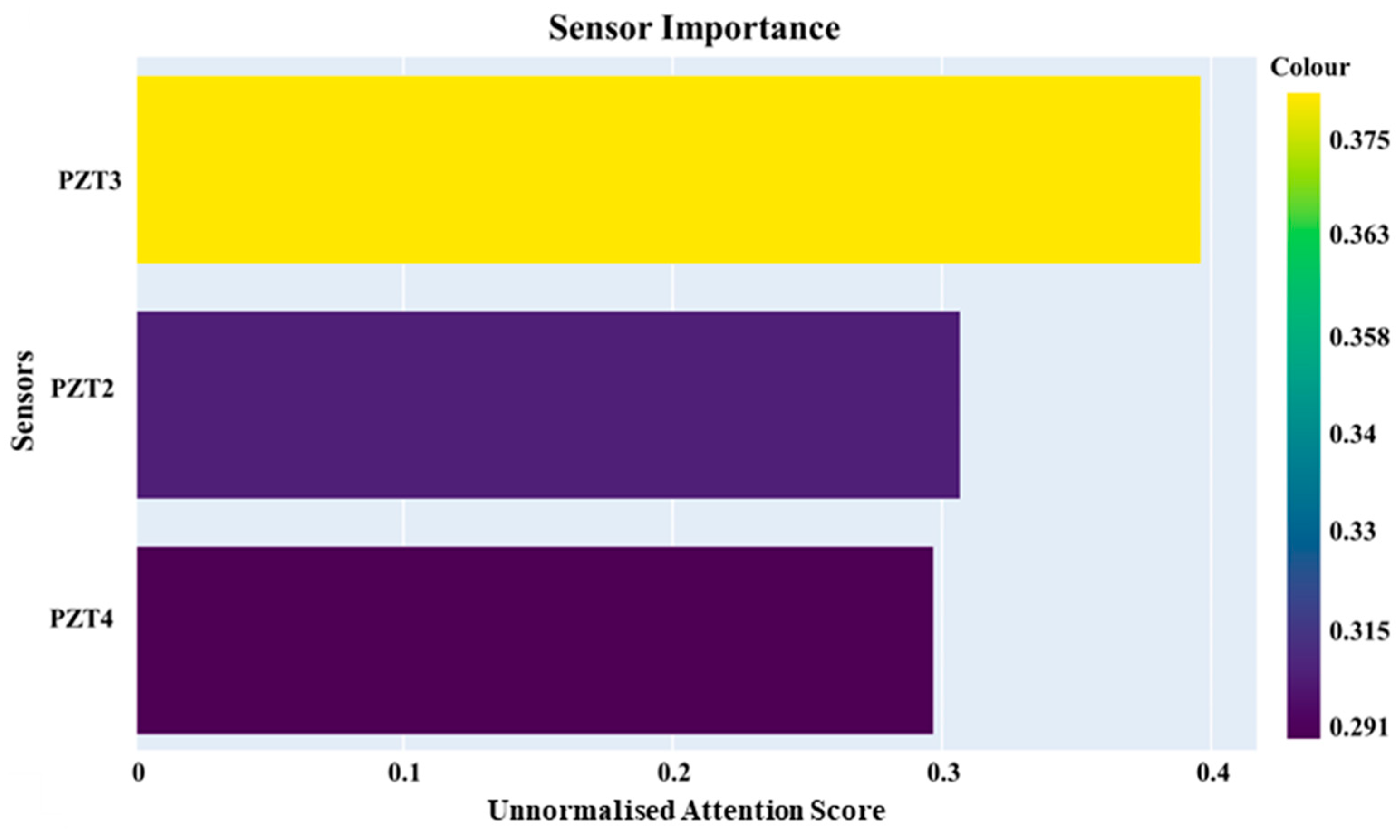
2.7. Computing Sensor Importance
3. Case Study
4. Result and Discussion
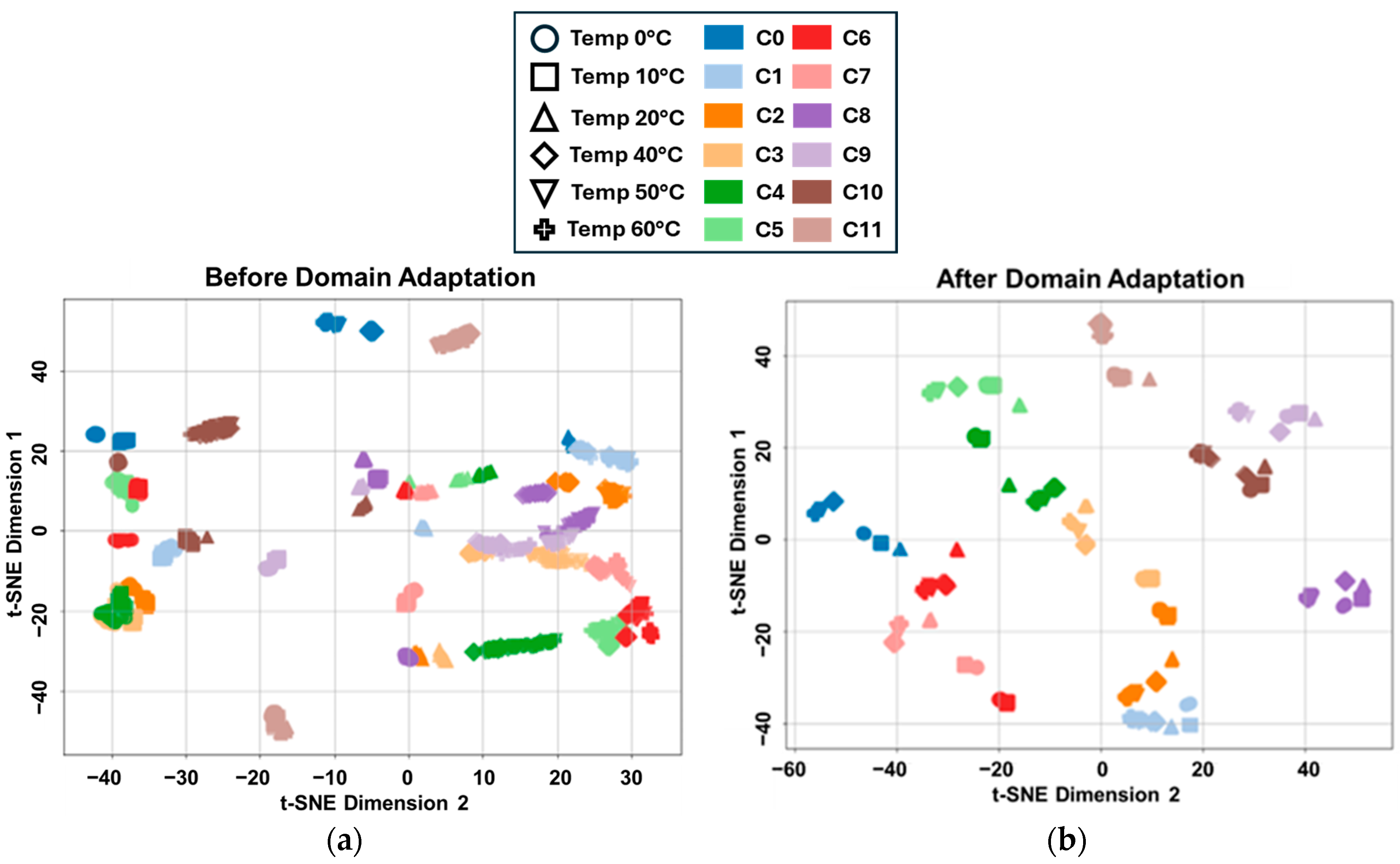
4.1. Dataset Complementation
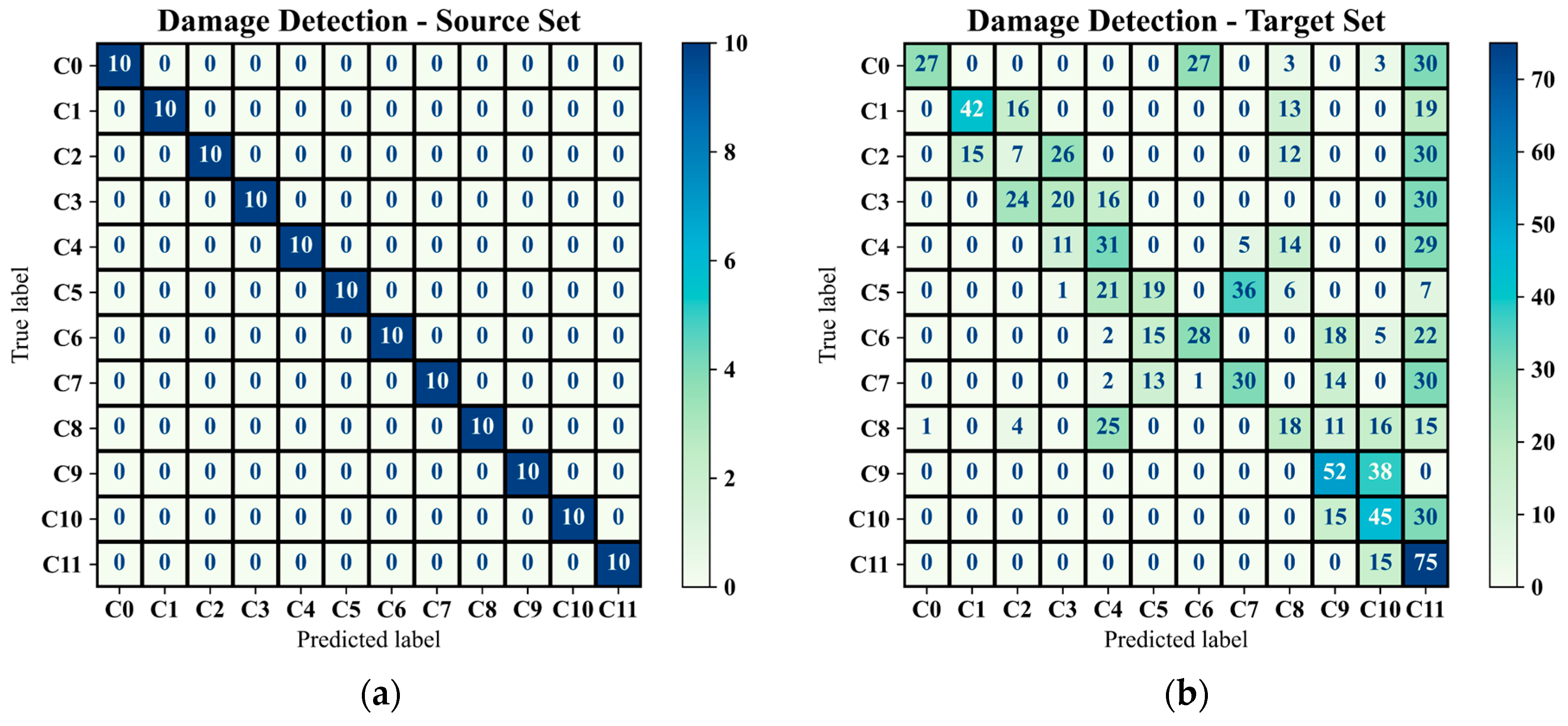
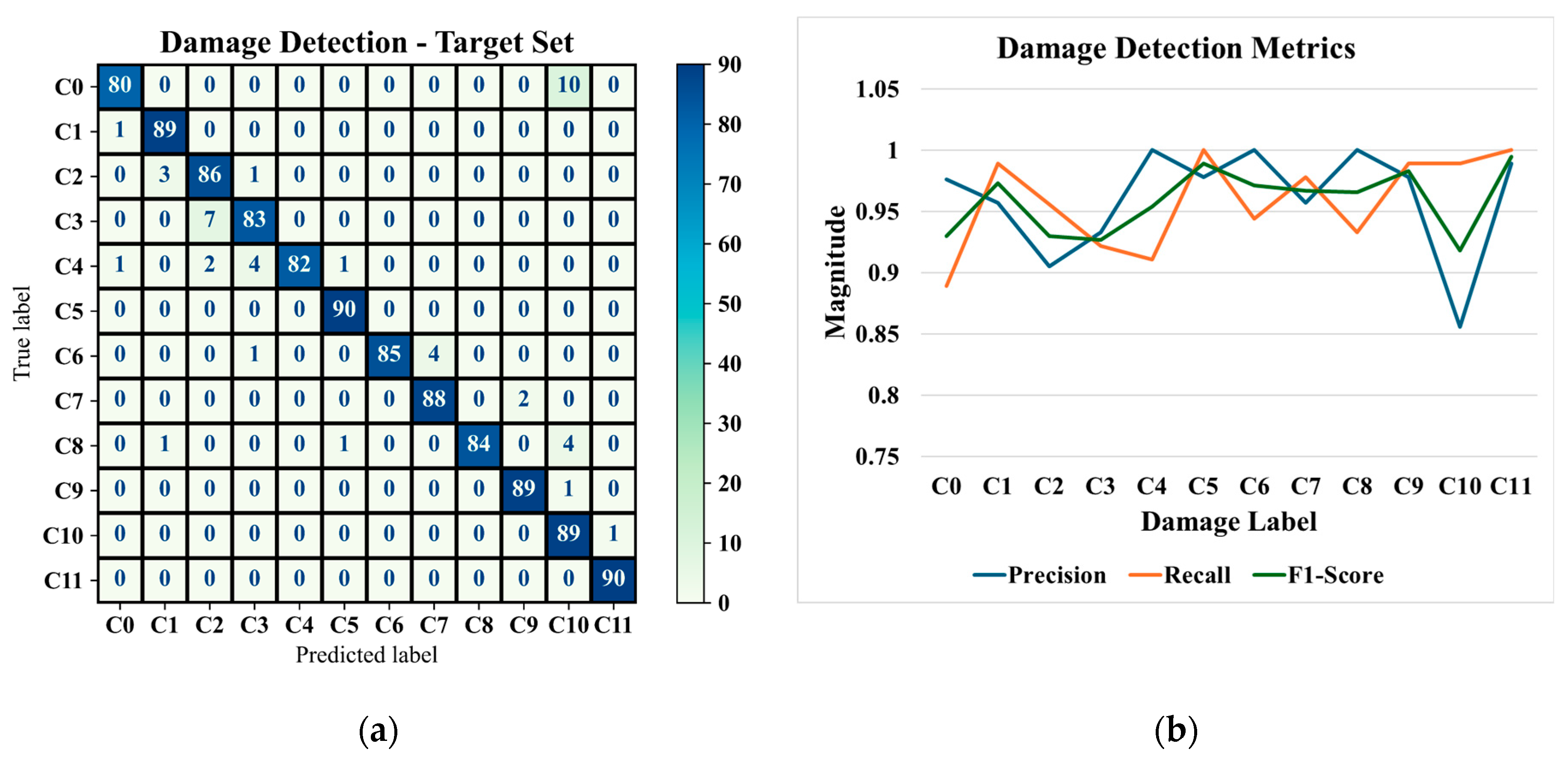
4.2. Damage Detection
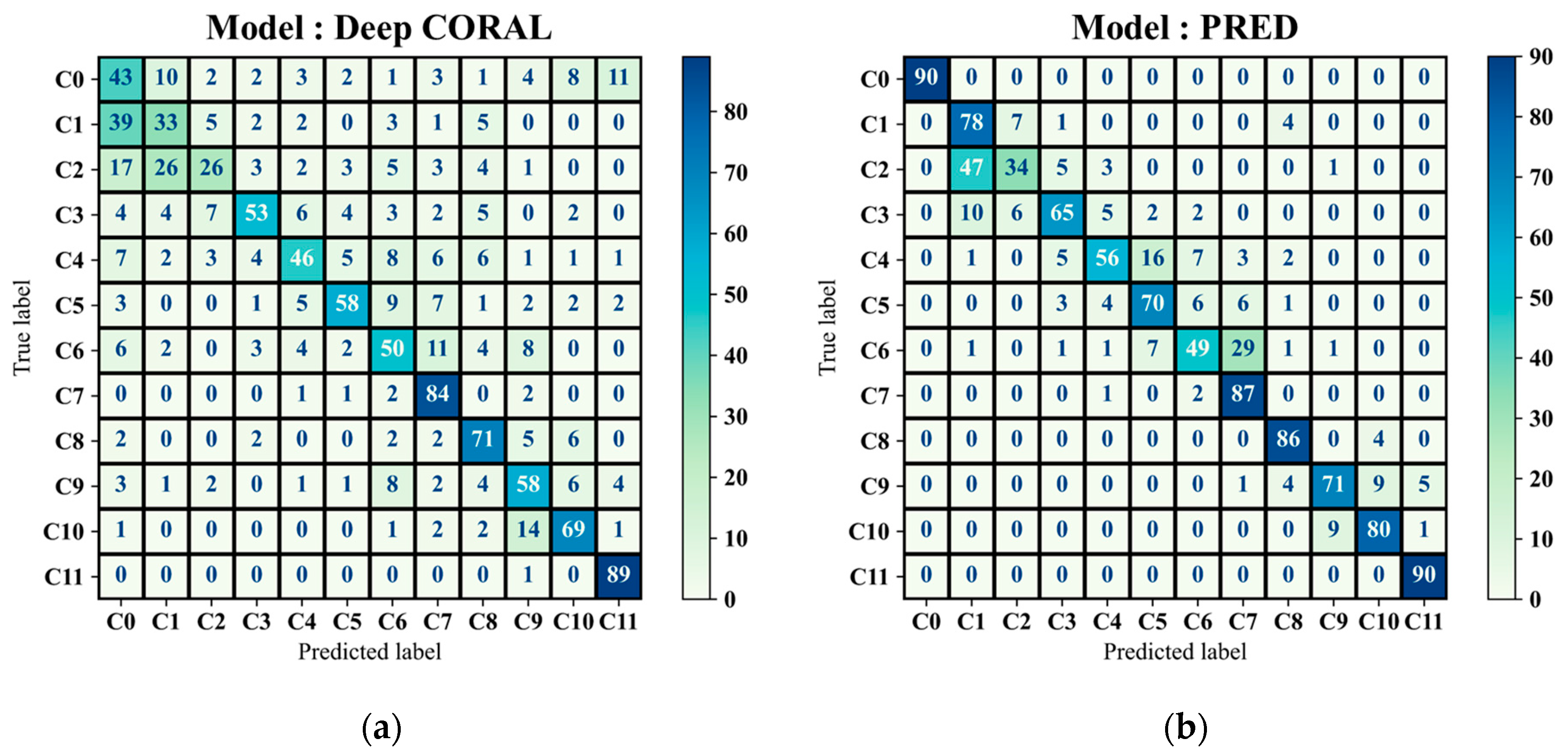
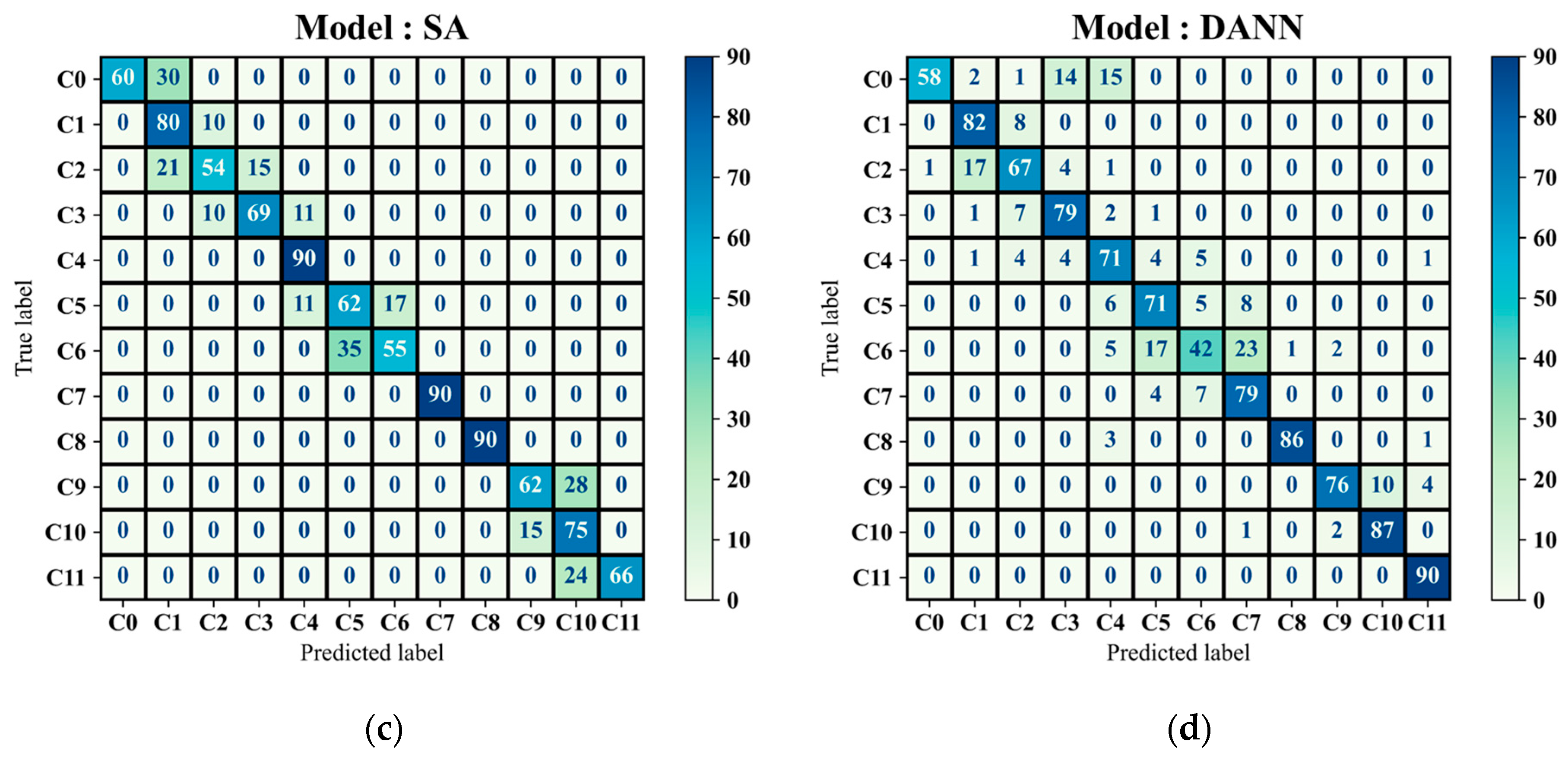
4.3. Comparative Study
4.4. Hyperparameter Importance
4.5. Sensor Importance
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BAR | Balanced Adaptation Regularisation-based Transfer Learning |
| CC | Cross-Correlation |
| CFRP | Carbon Fibre-Reinforced Polymer |
| CORAL | Correlation Alignment |
| DANN | Domain-Adversarial Training of Neural Networks |
| DA | Domain Adaptation |
| DTW | Dynamic Time Warping |
| DUA | Dynamic Unsupervised Adaptation |
| EOVs | Environmental and Operational Variabilities |
| FE | Finite Element |
| fMMD | Feature Selection with MMD |
| GATs | Graph Attention Networks |
| GRL | Gradient Reversal Layer |
| ML | Machine Learning |
| MMD | Maximum Mean Discrepancy |
| PRED | SrcOnly Prediction |
| PZT | Lead Zirconate Titanate |
| RBF | Radial Basis Function |
| ReLU | Rectified Linear Unit |
| SA | Subspace Alignment |
| SHM | Structural Health Monitoring |
| TCA | Transfer Component Analysis |
| TL | Transfer learning |
| t-SNE | t-distributed Stochastic Neighbour Embedding |
| TPE | Tree-structured Parzen Estimator |
| UDA | Unsupervised Domain Adaptation |
References
- Cawley, P. Guided Waves in Long Range Nondestructive Testing and Structural Health Monitoring: Principles, History of Applications and Prospects. NDT E Int. 2024, 142, 103026. [Google Scholar] [CrossRef]
- Gorgin, R.; Luo, Y.; Wu, Z. Environmental and Operational Conditions Effects on Lamb Wave Based Structural Health Monitoring Systems: A Review. Ultrasonics 2020, 105, 106114. [Google Scholar] [CrossRef] [PubMed]
- De Luca, A.; Greco, A.; Rezazadeh, N.; Perfetto, D.; Aversano, A. Guided Waves Propagation in Additively Manufactured GF30-PA6 Panel. Macromol. Symp. 2024, 413, 2400042. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors–Predictive Modeling and Simulation. INCAS Bull. 2010, 2, 31–44. [Google Scholar] [CrossRef]
- De Luca, A.; Perfetto, D.; Polverino, A.; Aversano, A.; Caputo, F. Finite Element Modeling Approaches, Experimentally Assessed, for the Simulation of Guided Wave Propagation in Composites. Sustainability 2022, 14, 6924. [Google Scholar] [CrossRef]
- Zheng, S.; Luo, Y.; Xu, C.; Xu, G. A Review of Laser Ultrasonic Lamb Wave Damage Detection Methods for Thin-Walled Structures. Sensors 2023, 23, 3183. [Google Scholar] [CrossRef]
- Yin, Z.; Tie, Y.; Duan, Y.; Li, C. Optimization of Nonlinear Lamb Wave Detection System Parameters in Cfrp Laminates. Materials 2021, 14, 3186. [Google Scholar] [CrossRef]
- Rezazadeh, N.; Perfetto, D.; Polverino, A.; De Luca, A.; Lamanna, G. Guided Wave-Driven Machine Learning for Damage Classification with Limited Dataset in Aluminum Panel. Struct. Health Monit. 2024, 24, 3138–3161. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, X.; Yan, J.; Yu, Y.; Zhao, B.; Qing, X. Lamb Wave-Based Damage Localization and Quantification Algorithms for CFRP Composite Structures. Compos. Struct. 2022, 295, 115849. [Google Scholar] [CrossRef]
- Zou, L.; Gong, Y.; Tian, D.; Zhao, L.; Zhang, J.; Hu, N. Effect of Interface Angle on Mode I Delamination Damage Behavior of Multidirectional Fully Isotropic Laminates with the Same Global Stiffness. Thin-Walled Struct. 2023, 182, 110211. [Google Scholar] [CrossRef]
- Konstantinidis, G.; Wilcox, P.D.; Drinkwater, B.W. An Investigation into the Temperature Stability of a Guided Wave Structural Health Monitoring System Using Permanently Attached Sensors. IEEE Sens. J. 2007, 7, 905–912. [Google Scholar] [CrossRef]
- Moll, J.; Kexel, C.; Pötzsch, S.; Rennoch, M.; Herrmann, A.S. Temperature Affected Guided Wave Propagation in a Composite Plate Complementing the Open Guided Waves Platform. Sci. Data 2019, 6, 191. [Google Scholar] [CrossRef]
- Rezazadeh, N.; De Luca, A.; Perfetto, D.; Salami, M.R.; Lamanna, G. Systematic Critical Review of Structural Health Monitoring under Environmental and Operational Variability: Approaches for Baseline Compensation, Adaptation, and Reference-Free Techniques. Smart Mater. Struct. 2025, 34, 073001. [Google Scholar] [CrossRef]
- Scheerer, M.; Lager, D. Validation of Temperature Compensation Techniques for Impact Damage Detection and Localization Using Ultrasonic Sparse Arrays. In Proceedings of the 7th European Workshop on Structural Health Monitoring, EWSHM 2014—2nd European Conference of the Prognostics and Health Management (PHM) Society, Nantes, France, 8–11 July 2014. [Google Scholar]
- da Silva, S.; Paixão, J.; Rébillat, M.; Mechbal, N. Extrapolation of AR Models Using Cubic Splines for Damage Progression Evaluation in Composite Structures. J. Intell. Mater. Syst. Struct. 2021, 32, 284–295. [Google Scholar] [CrossRef]
- Ren, F.; Giannakeas, I.N.; Sharif Khodaei, Z.; Aliabadi, M.H.F. Sensitivity Analysis of Temperature Effects on Guided Wave-Based Damage Detection. Mech. Syst. Signal Process 2023, 196, 110322. [Google Scholar] [CrossRef]
- Ren, F.; Giannakeas, I.N.; Sharif Khodaei, Z.; Aliabadi, M.H.F. Theoretical and Experimental Investigation of Guided Wave Temperature Compensation for Composite Structures with Different Thicknesses. Mech. Syst. Signal Process 2023, 200, 110594. [Google Scholar] [CrossRef]
- Perfetto, D.; Sharif Khodaei, Z.; De Luca, A.; Aliabadi, M.H.; Caputo, F. Experiments and Modelling of Ultrasonic Waves in Composite Plates under Varying Temperature. Ultrasonics 2022, 126, 106820. [Google Scholar] [CrossRef]
- Rezazadeh, N.; Annaz, F.; Jabbar, W.A.; Vieira Filho, J.; De Oliveira, M. A Transfer Learning Approach for Mitigating Temperature Effects on Wind Turbine Blades Damage Diagnosis. Struct. Health Monit. 2025. [Google Scholar] [CrossRef]
- de Ferreira, L.P.S.; de Teloli, R.O.; da Silva, S.; Figueiredo, E.; Maia, N.; Cimini, C.A. Bayesian Data-Driven Framework for Structural Health Monitoring of Composite Structures under Limited Experimental Data. Struct. Health Monit. 2024, 24, 738–760. [Google Scholar] [CrossRef]
- Giannakeas, I.N.; Sharif Khodaei, Z.; Aliabadi, M.H. An Up-Scaling Temperature Compensation Framework for Guided Wave–Based Structural Health Monitoring in Large Composite Structures. Struct. Health Monit. 2023, 22, 777–798. [Google Scholar] [CrossRef]
- Cheng, X.; Sharif Khodaei, Z. Temperature Calibration for Guided Wave Hybrid System with FBG-Based Fabry-Perot Sensor. J. Intell. Mater. Syst. Struct. 2023, 34, 766–784. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Moustafa, N.; Hawash, H.; Tari, Z. Responsible Graph Neural Networks; Chapman and Hall/CRC: New York, NY, USA, 2023. [Google Scholar]
- Vrahatis, A.G.; Lazaros, K.; Kotsiantis, S. Graph Attention Networks: A Comprehensive Review of Methods and Applications. Future Internet 2024, 16, 318. [Google Scholar] [CrossRef]
- Niu, J.; Li, S.; Li, Z. Restoration of Missing Structural Health Monitoring Data Using Spatiotemporal Graph Attention Networks. Struct. Health Monit. 2022, 21, 2408–2419. [Google Scholar] [CrossRef]
- Zhao, M.; Taal, C.; Baggerohr, S.; Fink, O. Virtual Sensor for Real-Time Bearing Load Prediction Using Heterogeneous Temporal Graph Neural Networks. PHM Soc. Eur. Conf. 2024, 8, 8. [Google Scholar] [CrossRef]
- Rezazadeh, N.; Perfetto, D.; de Oliveira, M.; De Luca, A.; Lamanna, G. A Fine-Tuning Deep Learning Framework to Palliate Data Distribution Shift Effects in Rotary Machine Fault Detection. Struct. Health Monit. 2024. [Google Scholar] [CrossRef]
- Ozdagli, A.; Koutsoukos, X. Domain Adaptation for Structural Health Monitoring. Annu. Conf. PHM Soc. 2020, 12, 9. [Google Scholar] [CrossRef]
- Zhuojun, X.; Hao, L.; Jianbo, Y.; Jingwen, Y. A Transfer Learning Approach for Data-Driven Localization of Damage Areas in Plate-like Structures of CFRP Materials. Eng. Struct. 2024, 314, 118352. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, X.; Liu, Q.; Zhao, B.; Liao, Y.; Qing, X. An Adaptive Damage Monitoring Method Based on Transfer Features Mapped for Advanced Composite Structures. Compos. Struct. 2024, 329, 117742. [Google Scholar] [CrossRef]
- Poole, J.; Gardner, P.; Dervilis, N.; Bull, L.; Worden, K. On Statistic Alignment for Domain Adaptation in Structural Health Monitoring. Struct. Health Monit. 2023, 22, 1581–1600. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should i Trust You?” Explaining the Predictions of Any Classifier. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Schnur, C.; Goodarzi, P.; Lugovtsova, Y.; Bulling, J.; Prager, J.; Tschöke, K.; Moll, J.; Schütze, A.; Schneider, T. Towards Interpretable Machine Learning for Automated Damage Detection Based on Ultrasonic Guided Waves. Sensors 2022, 22, 406. [Google Scholar] [CrossRef] [PubMed]
- Salih, A.M.; Raisi-Estabragh, Z.; Galazzo, I.B.; Radeva, P.; Petersen, S.E.; Lekadir, K.; Menegaz, G. A Perspective on Explainable Artificial Intelligence Methods: SHAP and LIME. Adv. Intell. Syst. 2024, 7, 2400304. [Google Scholar] [CrossRef]
- Tiwari, A.; Gupta, A.K.; Gupta, T. A Robust Approach to Shear Strength Prediction of Reinforced Concrete Deep Beams Using Ensemble Learning with SHAP Interpretability. Soft Comput. 2024, 28, 6343–6365. [Google Scholar] [CrossRef]
- Azad, M.M.; Kim, H.S. An Explainable Artificial Intelligence-based Approach for Reliable Damage Detection in Polymer Composite Structures Using Deep Learning. Polym. Compos. 2024, 46, 1536–1551. [Google Scholar] [CrossRef]
- Li, X.; Xu, L.; Guo, H.; Yang, L. Application of Graph Convolutional Neural Networks Combined with Single-Model Decision-Making Fusion Neural Networks in Structural Damage Recognition. Sensors 2023, 23, 9327. [Google Scholar] [CrossRef]
- Veličković, P.; Casanova, A.; Liò, P.; Cucurull, G.; Romero, A.; Bengio, Y. Graph Attention Networks. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018—Conference Track Proceedings, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. J. Mach. Learn. Res. 2016, 17, 2096–3030. [Google Scholar]
- Huang, J.; Guan, D.; Xiao, A.; Lu, S. RDA: Robust Domain Adaptation via Fourier Adversarial Attacking. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8968–8979. [Google Scholar]
- Kim, B.; Pineau, J. Maximum Mean Discrepancy Imitation Learning. In Proceedings of the Robotics: Science and systems, Ann Arbor, MI, USA, 18–22 June 2016. [Google Scholar]
- Sun, B.; Feng, J.; Saenko, K. Return of Frustratingly Easy Domain Adaptation. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, AAAI 2016, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- da Silva, S. Data-Driven Model Identification of Guided Wave Propagation in Composite Structures. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 543. [Google Scholar] [CrossRef]
- de Almeida, E.F.; Chavarette, F.R.; Merizio, I.F.; Gonçalves, A.C. Artificial Immune System for Fault Detection and Localization in a Composite Material Plate with Temperature Variation. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 717. [Google Scholar] [CrossRef]
- de Ferreira, L.P.S.; de Teloli, R.O.; da Silva, S.; Figueiredo, E.; Moldovan, I.D.; Maia, N.; Cimini, C.A. Bayesian Calibration for Lamb Wave Propagation on a Composite Plate Using a Machine Learning Surrogate Model. Mech. Syst. Signal Process 2024, 208, 111011. [Google Scholar] [CrossRef]
- Senin, P. Dynamic Time Warping Algorithm Review. Science 2008, 855, 40. [Google Scholar]
- Habermehl, S.; Schlesinger, C.; Prill, D. Comparison and Evaluation of Pair Distribution Functions, Using a Similarity Measure Based on Cross-Correlation Functions. J. Appl. Crystallogr. 2021, 54, 612–623. [Google Scholar] [CrossRef]
- Rezazadeh, N.; De Oliveira, M.; Lamanna, G.; Perfetto, D.; De Luca, A. WaveCORAL-DCCA: A Scalable Solution for Rotor Fault Diagnosis Across Operational Variabilities. Electronics 2025, 14, 3146. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G. Visualizing Data Using T-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain Adaptation via Transfer Component Analysis. IEEE Trans. Neural Netw. 2011, 22, 199–210. [Google Scholar] [CrossRef]
- Uguroglu, S.; Carbonell, J. Feature Selection for Transfer Learning; Springer: Berlin/Heidelberg, Germany, 2011; pp. 430–442. [Google Scholar]
- Sun, B.; Saenko, K. Deep CORAL: Correlation Alignment for Deep Domain Adaptation. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Amsterdam, The Netherlands, 11–14 October 2016; Volume 9915. LNCS. [Google Scholar]
- Daumé, H., III. Frustratingly Easy Domain Adaptation. In Proceedings of the 45th Annual Meeting of the Association of Computational Linguistics, Prague, Czech Republic, 23–30 June 2007. [Google Scholar]
- Fernando, B.; Habrard, A.; Sebban, M.; Tuytelaars, T. Unsupervised Visual Domain Adaptation Using Subspace Alignment. In Proceedings of the Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Mirza, M.J.; Micorek, J.; Possegger, H.; Bischof, H. The Norm Must Go On: Dynamic Unsupervised Domain Adaptation by Normalization. In Proceedings of the Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Hu, Q.; Si, X.; Qin, A.; Lv, Y.; Liu, M. Balanced Adaptation Regularization Based Transfer Learning for Unsupervised Cross-Domain Fault Diagnosis. IEEE Sens. J. 2022, 22, 12139–12151. [Google Scholar] [CrossRef]






| Category | Parameter | Value |
|---|---|---|
| Laminate plate | Dimensions (L × W × T) | 500 mm × 500 mm × 2 mm |
| Number of Plies | 10 | |
| Transducers | Type | PZT |
| Diameter | 6.35 mm | |
| Configuration | One actuator, three sensors | |
| Mounting conditions | Boundary condition | Free–Free |
| Temperature control | Range | 0 °C to 60 °C |
| Increment | 10 °C | |
| Excitation signal | Type | Five-cycle sinusoidal tone burst |
| Frequency | 250 kHz | |
| Data sampling | Sampling rate | 5 MHz |
| Duration per measurement | 100 ms | |
| Data acquisition | Generation system | NI USB 6353 |
| Measurement system | Keysight DSO7034B | |
| Control software | LabVIEW |
| Damage Scenario | Severity (Area Covered) | Class Label | Description | Temperature (Degree Celsius) | Temperature Label |
|---|---|---|---|---|---|
| Healthy | 0% | C0 | No damage | 0 | 0 |
| 10 | 1 | ||||
| 20 | 2 | ||||
| 30 | 3 | ||||
| 40 | 4 | ||||
| 50 | 5 | ||||
| 60 | 6 | ||||
| Damaged D1 | 0.196% | C1 | Industrial putty | 30 | 3 |
| Damaged D2 | 0.282% | C2 | Increased coverage of putty | ||
| Damaged D3 | 0.384% | C3 | Further increase in coverage | ||
| Damaged D4 | 0.502% | C4 | Progressive increase | ||
| Damaged D5 | 0.785% | C5 | Larger area covered | ||
| Damaged D6 | 1.13% | C6 | Substantial coverage | ||
| Damaged D7 | 1.53% | C7 | Continued increase | ||
| Damaged D8 | 1.95% | C8 | Different progression pattern | ||
| Damaged D9 | 2.01% | C9 | Extensive coverage | ||
| Damaged D10 | 2.27% | C10 | High severity | ||
| Damaged D11 | 2.54% | C11 | Maximum simulated severity |
| Domain | Number of Observations per Class | ||
|---|---|---|---|
| Training | Validation | Testing | |
| Source | 63 | 27 | 10 |
| Target | 420 | 90 | 90 |
| Hyperparameter | Value | Hyperparameter | Value |
|---|---|---|---|
| Learning rate | ) | Number of GAT heads | 1, 2, 4 |
| Weight decay | ) | Pooling option | Max, Mean, Sum |
| Adversarial weight | (0, 0.3) | Normalisation | True, False |
| MMD weight | (0, 0.3) | MMD kernel | Linear, RBF |
| CORAL weight | (0, 0.3) | Gamma parameter | (0.1, 10) |
| Hidden dimension | 128, 256, 512 | Number of GAT layers | 4, 8 |
| Dropout rate | (0.1, 0.5) | Batch size | 32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezazadeh, N.; De Luca, A.; Perfetto, D.; Lamanna, G.; Annaz, F.; De Oliveira, M. Domain-Adaptive Graph Attention Semi-Supervised Network for Temperature-Resilient SHM of Composite Plates. Sensors 2025, 25, 6847. https://doi.org/10.3390/s25226847
Rezazadeh N, De Luca A, Perfetto D, Lamanna G, Annaz F, De Oliveira M. Domain-Adaptive Graph Attention Semi-Supervised Network for Temperature-Resilient SHM of Composite Plates. Sensors. 2025; 25(22):6847. https://doi.org/10.3390/s25226847
Chicago/Turabian StyleRezazadeh, Nima, Alessandro De Luca, Donato Perfetto, Giuseppe Lamanna, Fawaz Annaz, and Mario De Oliveira. 2025. "Domain-Adaptive Graph Attention Semi-Supervised Network for Temperature-Resilient SHM of Composite Plates" Sensors 25, no. 22: 6847. https://doi.org/10.3390/s25226847
APA StyleRezazadeh, N., De Luca, A., Perfetto, D., Lamanna, G., Annaz, F., & De Oliveira, M. (2025). Domain-Adaptive Graph Attention Semi-Supervised Network for Temperature-Resilient SHM of Composite Plates. Sensors, 25(22), 6847. https://doi.org/10.3390/s25226847










