A Gradient-Penalized Conditional TimeGAN Combined with Multi-Scale Importance-Aware Network for Fault Diagnosis Under Imbalanced Data
Abstract
1. Introduction
- (1)
- A time-series data augmentation method named the CTGAN network is proposed in this paper. It introduces Wasserstein distance with gradient penalty as the loss function, effectively mitigating the mode collapse issue commonly encountered in traditional TimeGAN network training. By injecting category labels into both the generator and discriminator, this approach effectively overcomes the limitations of uncontrollable outputs in original TimeGAN. It enables the controlled generation of multi-source fault samples, providing a precise data augmentation solution for fault diagnosis.
- (2)
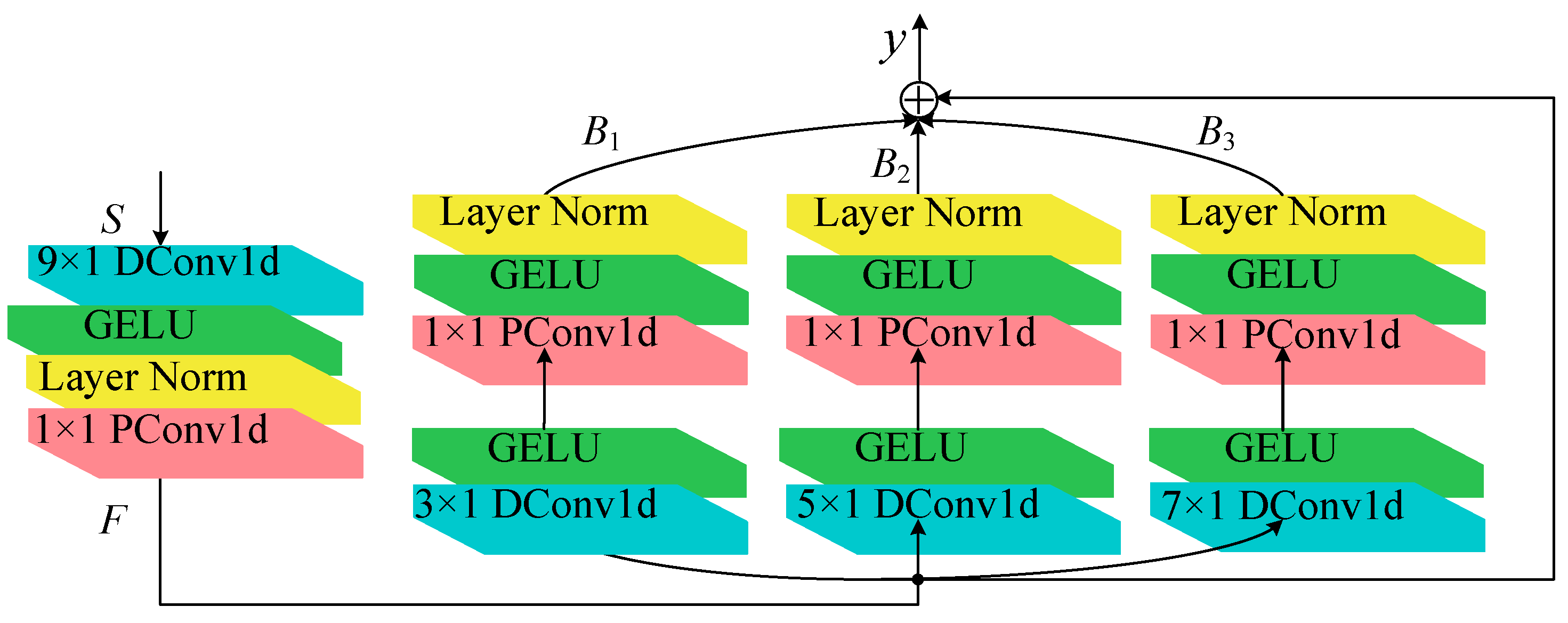
- The MDSR block is proposed to efficiently capture multi-scale feature representations. This module employs multiple branches of depthwise separable convolutions, which significantly reduce computational complexity while accurately capturing multi-scale features. Additionally, MDSR incorporates a residual connection mechanism that effectively preserves the integrity of original features while mitigating gradient vanishing.
- (3)
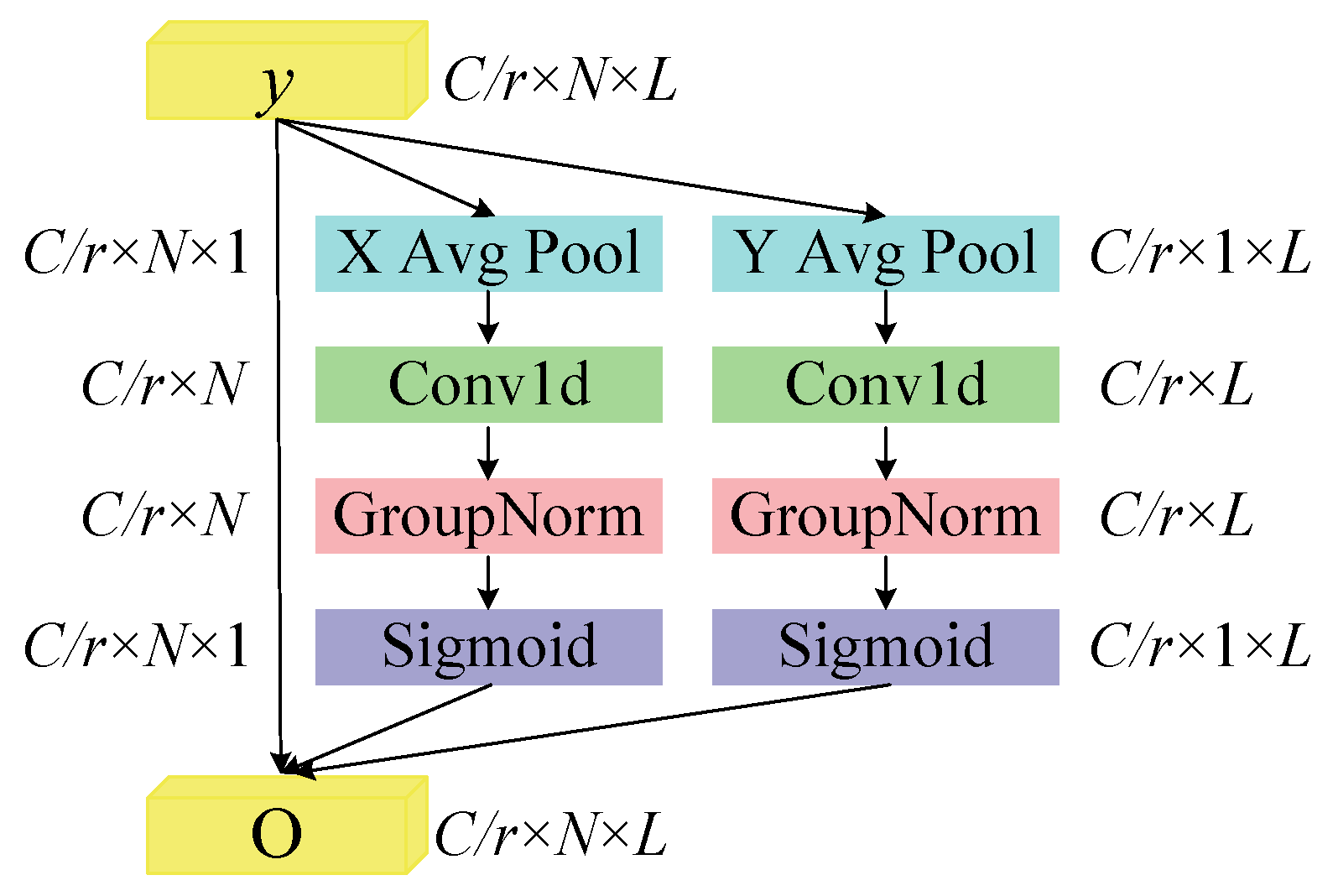
- To address the issue of low diagnostic accuracy caused by differences in the importance of features across different scales, a Scale Enhanced Local Attention (SELA) module is proposed. The SELA module enhances the expressive capability of features across positional and scale dimensions, enabling the model to precisely focus on the most discriminative scale features. This has significantly improved both recognition accuracy and robustness.
- (4)
- This paper proposes the CTGAN-MSIN network from the perspectives of data augmentation and classification. CTGAN resolves the issues of unstable training and uncontrollable generation outcomes in TimeGAN, effectively accomplishing data augmentation tasks. The MSIN integrates both MDSR and SELA modules to extract comprehensive and highly discriminative features. This model effectively addresses the issue of low diagnostic accuracy in classical MSCNN, which arises from its neglect of the important differences among features at different scales. Practicality and effectiveness of the CTGAN-MSIN are validated using both the public bearing dataset and the self-collected axial piston pump dataset.
2. Preliminaries
2.1. Time-Series Generative Adversarial Network
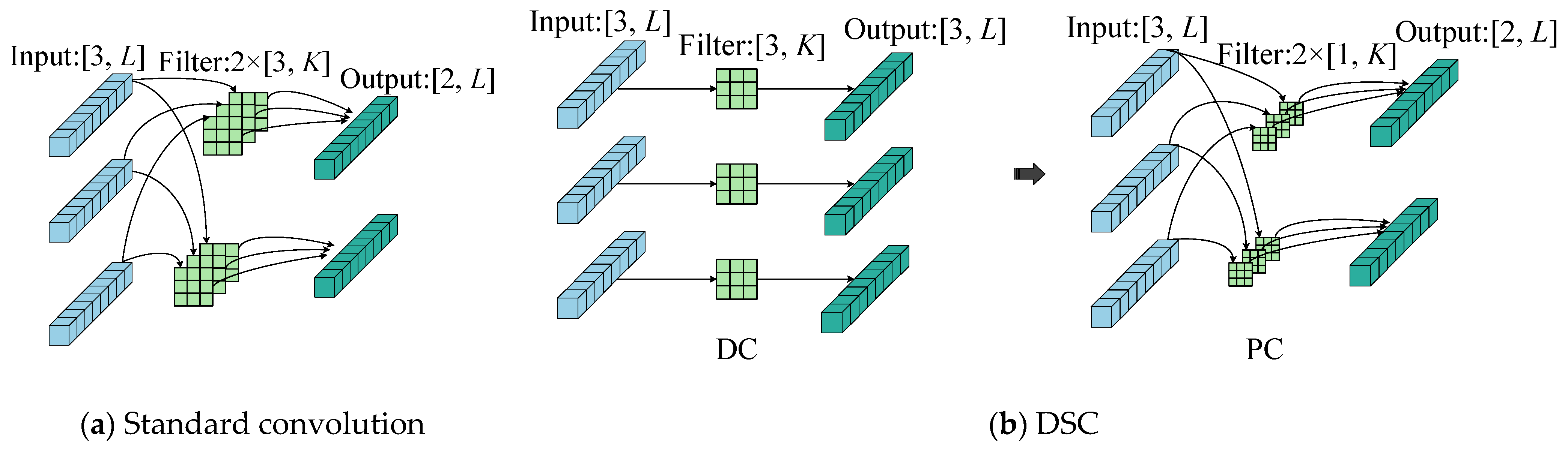
2.2. Depthwise Separable Convolutional Network
2.3. Efficient Local Attention Module
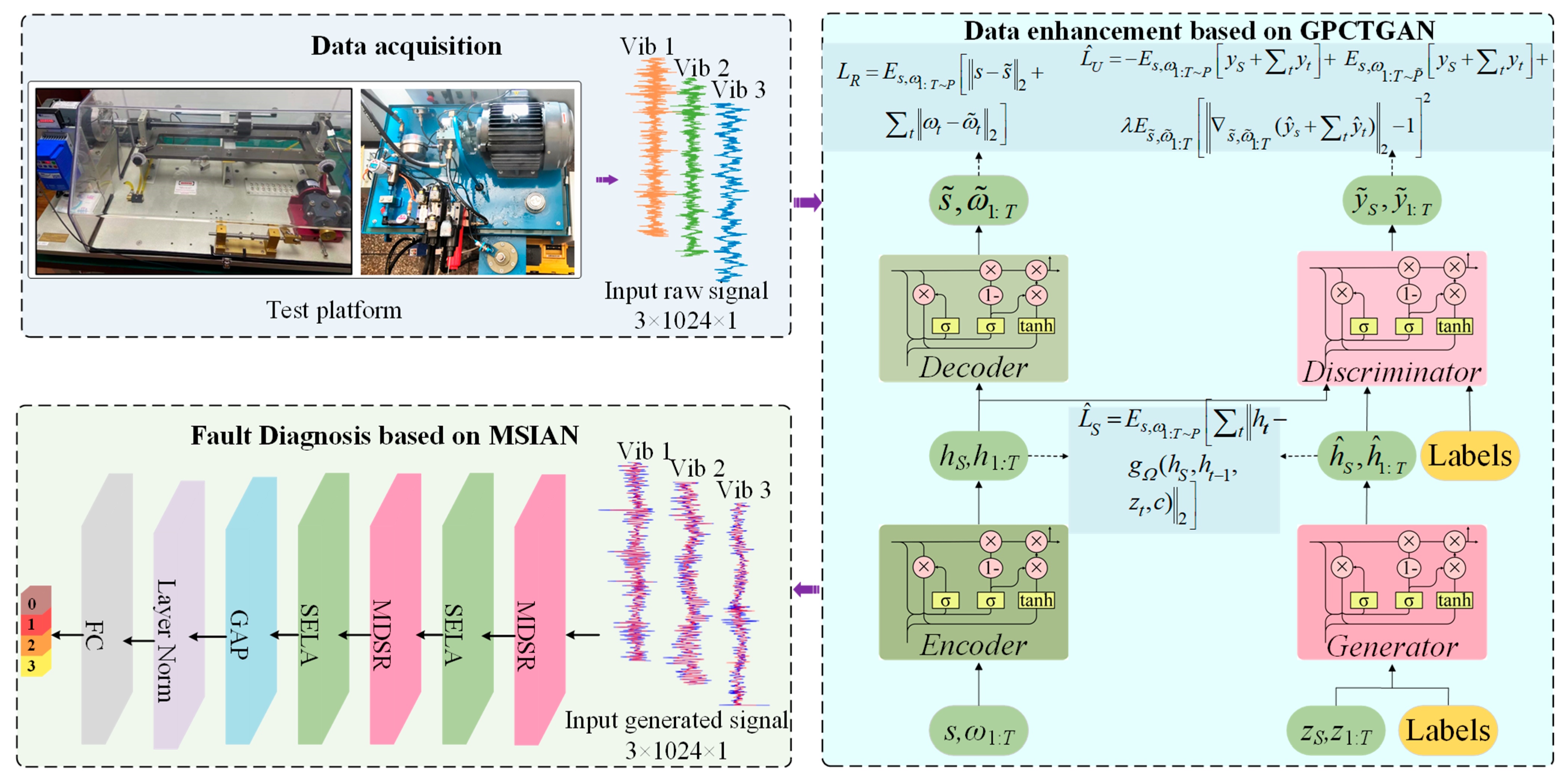
3. Proposed Method
3.1. Gradient-Penalized Conditional Time-Series Generative Adversarial Network
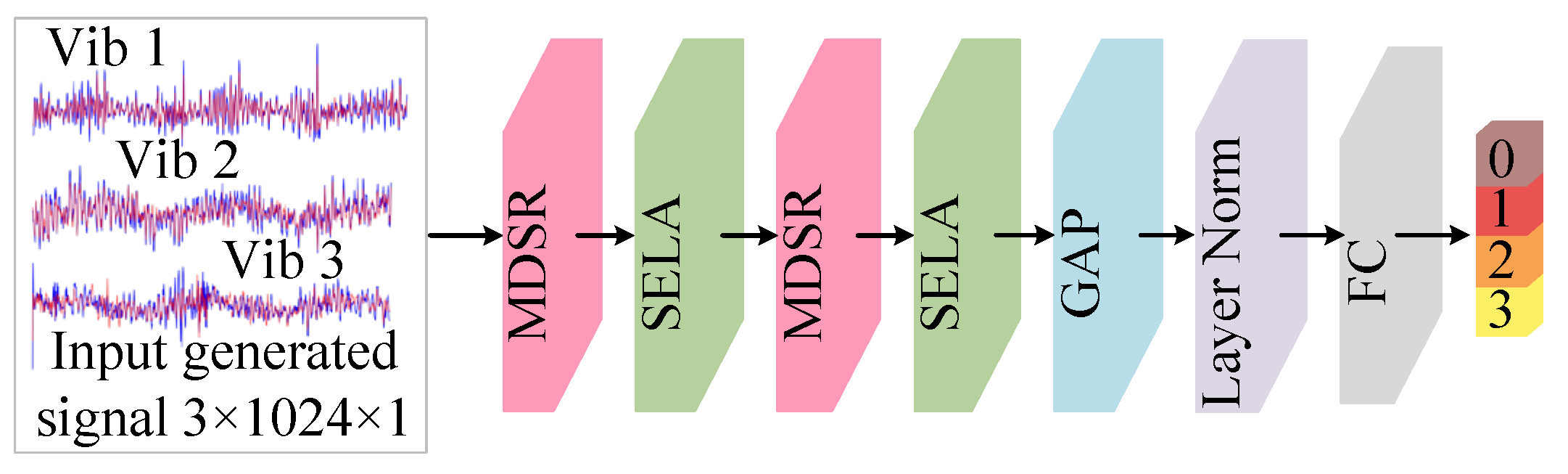
3.2. Multi-Scale Importance-Aware Network
4. Case Studies
4.1. Case 1: HUST Bearing Dataset
4.1.1. Description of HUST Bearing Test
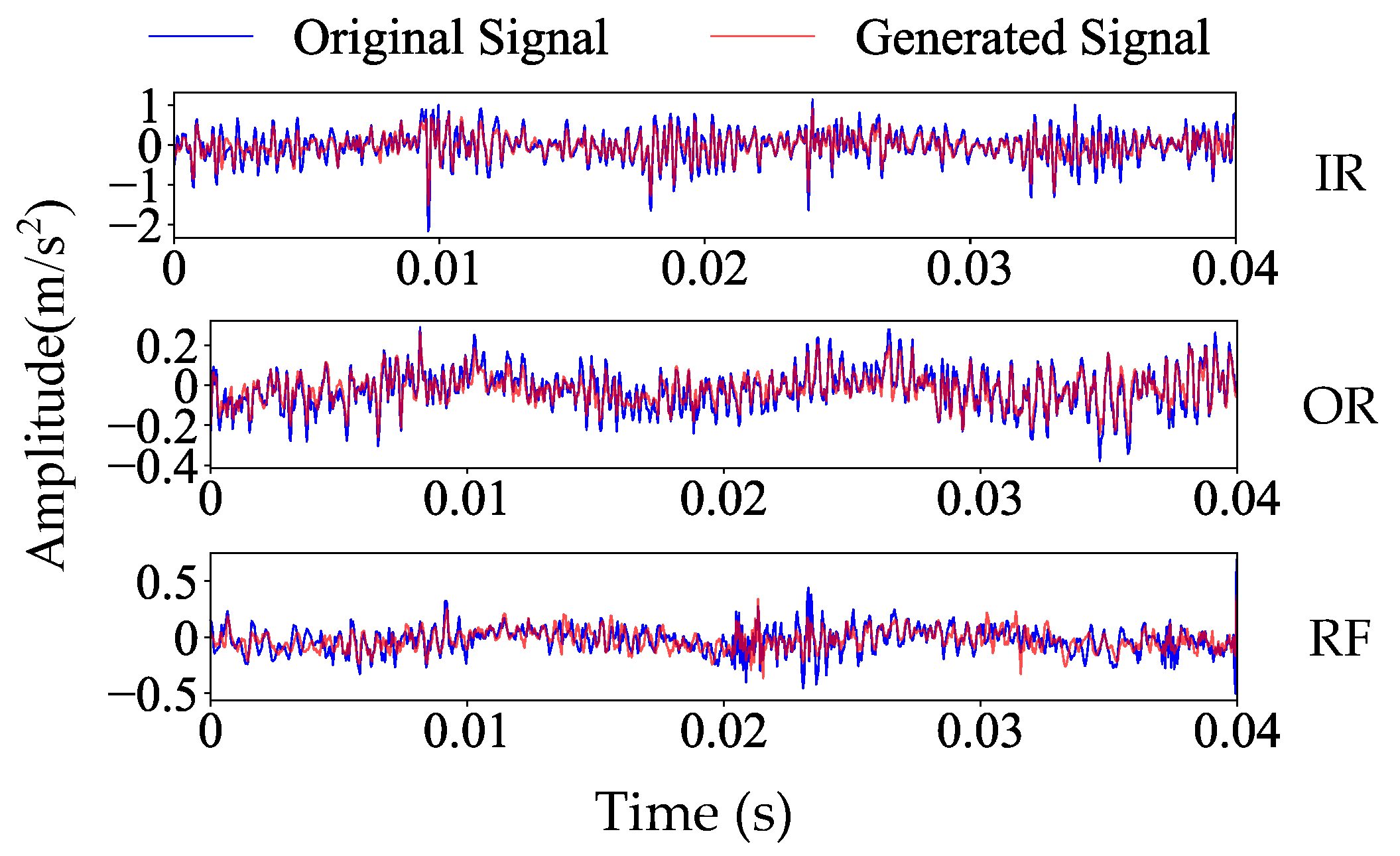
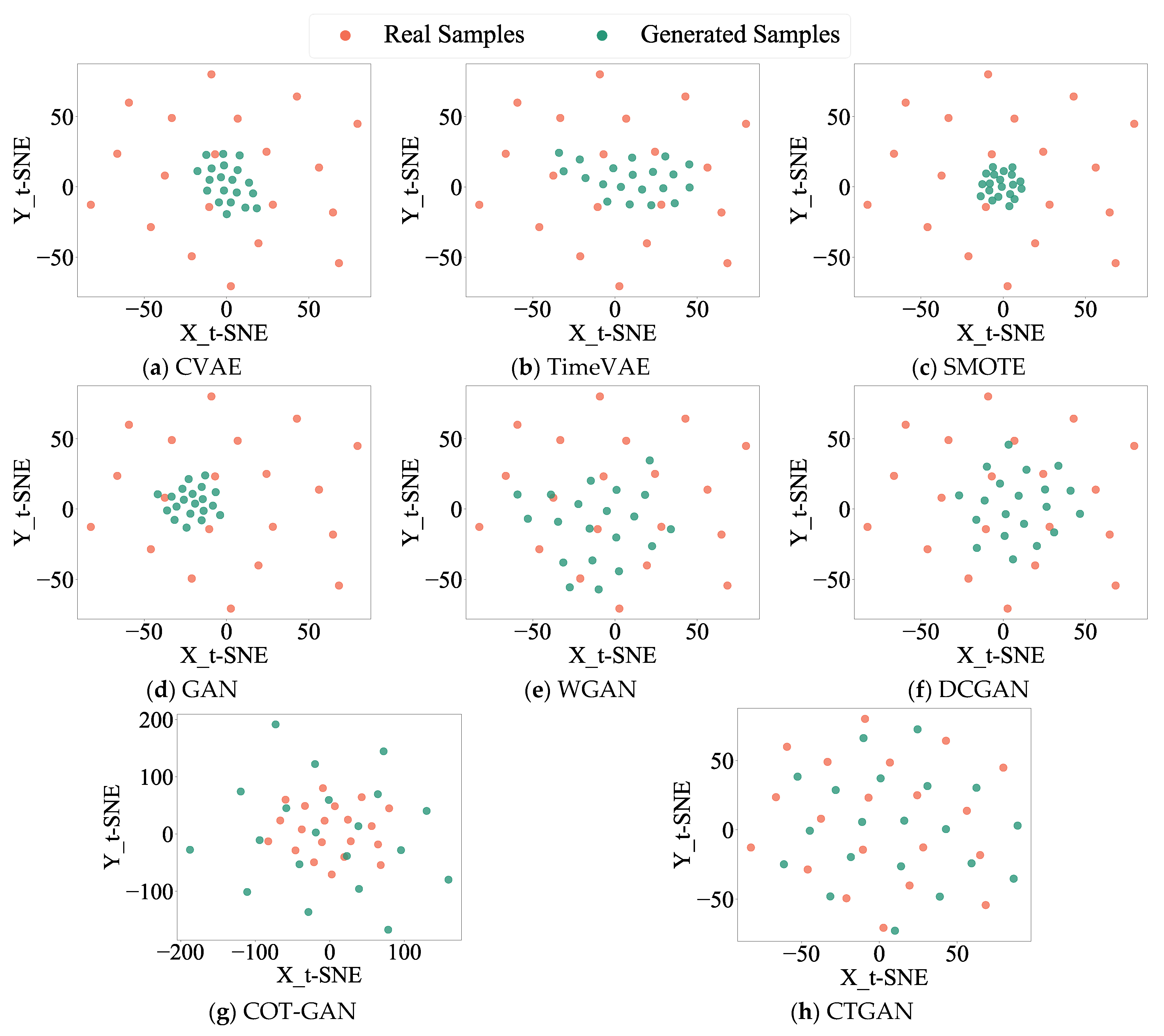
4.1.2. Data Generation and Evaluation in the HUST Bearing Dataset
4.1.3. Ablation Experiment in the HUST Bearing Dataset
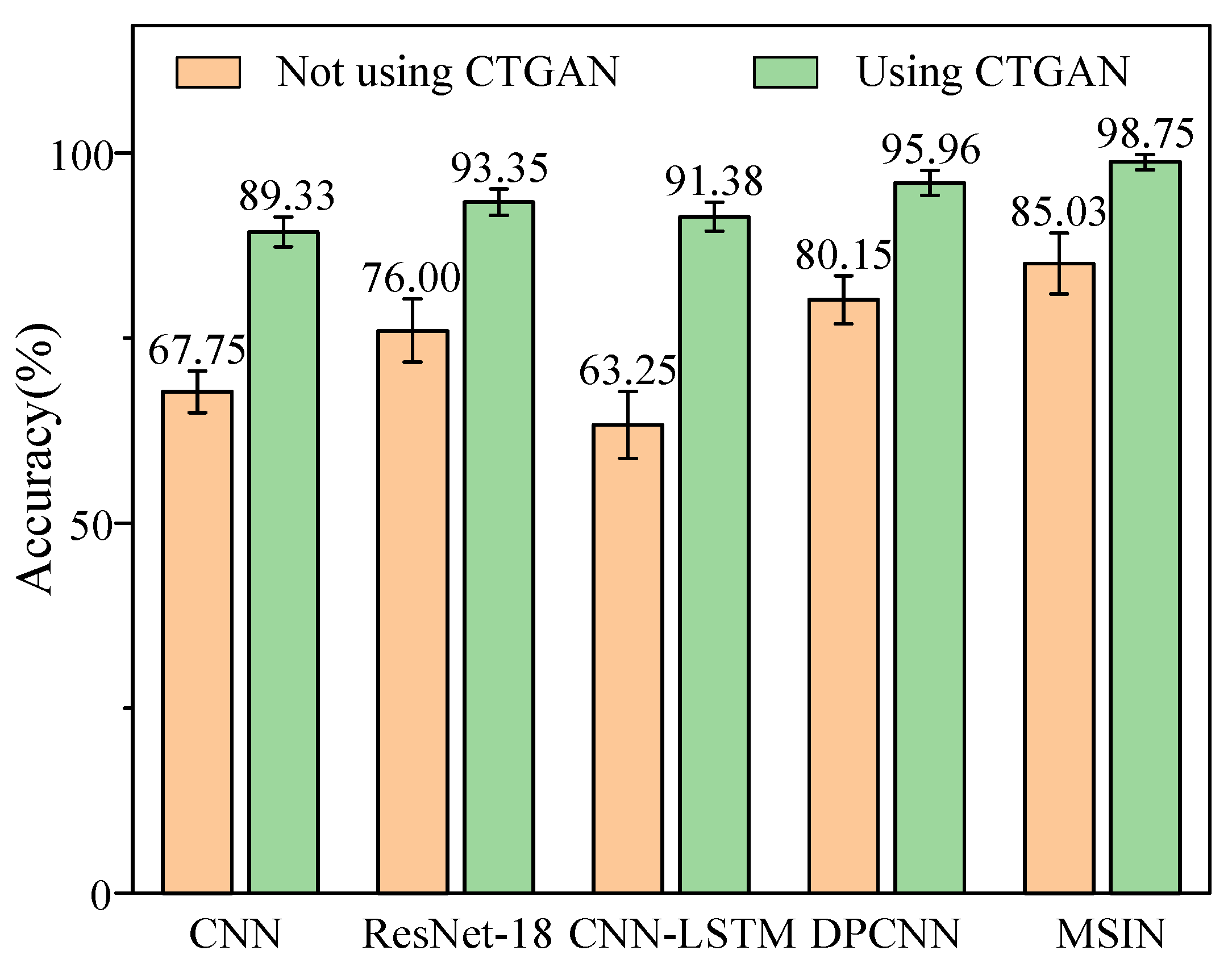
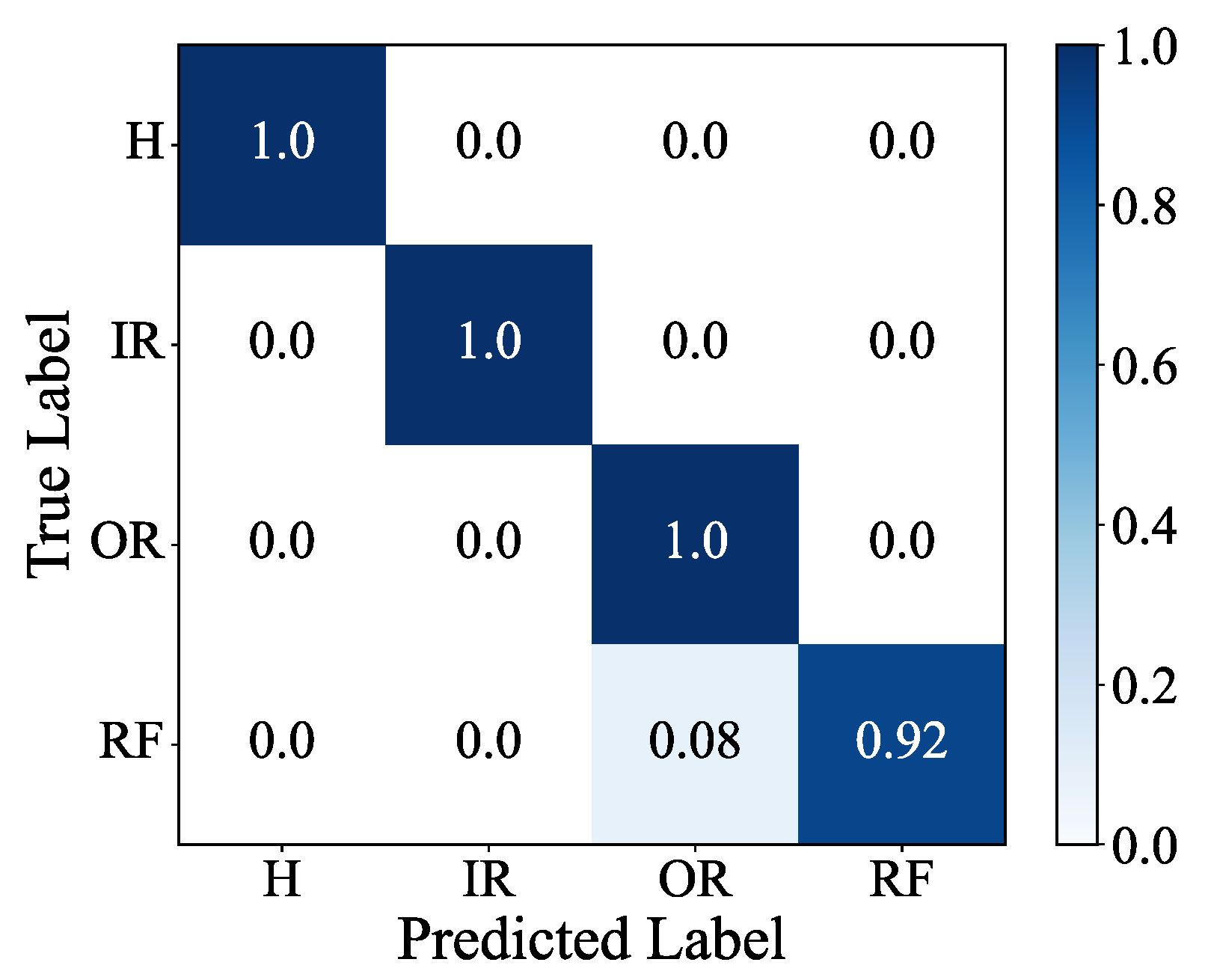
4.1.4. Diagnostic Results Analysis in the HUST Bearing Dataset
4.2. Case 2: Axial Piston Pump Dataset
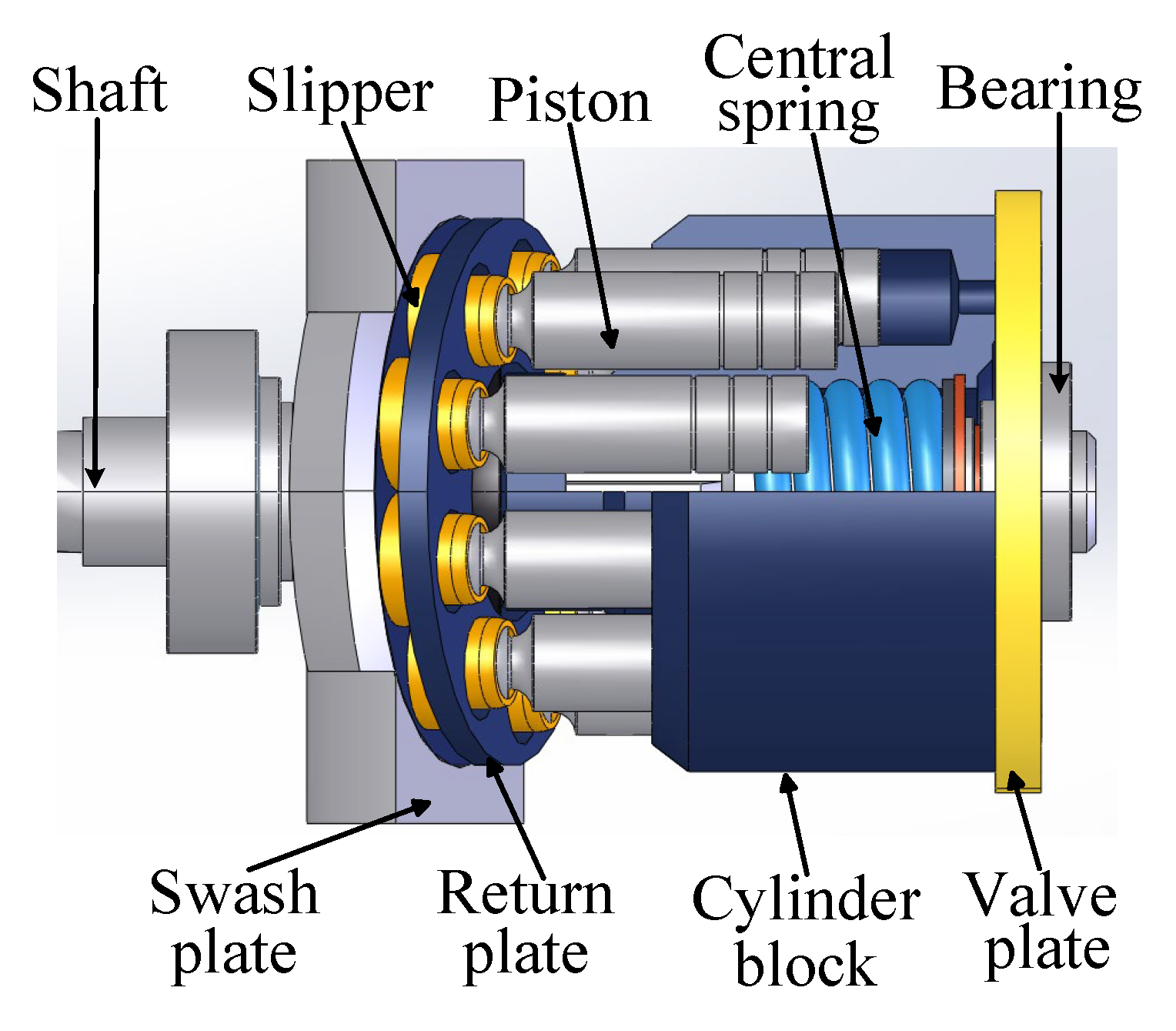
4.2.1. Description of Axial Piston Pump Test
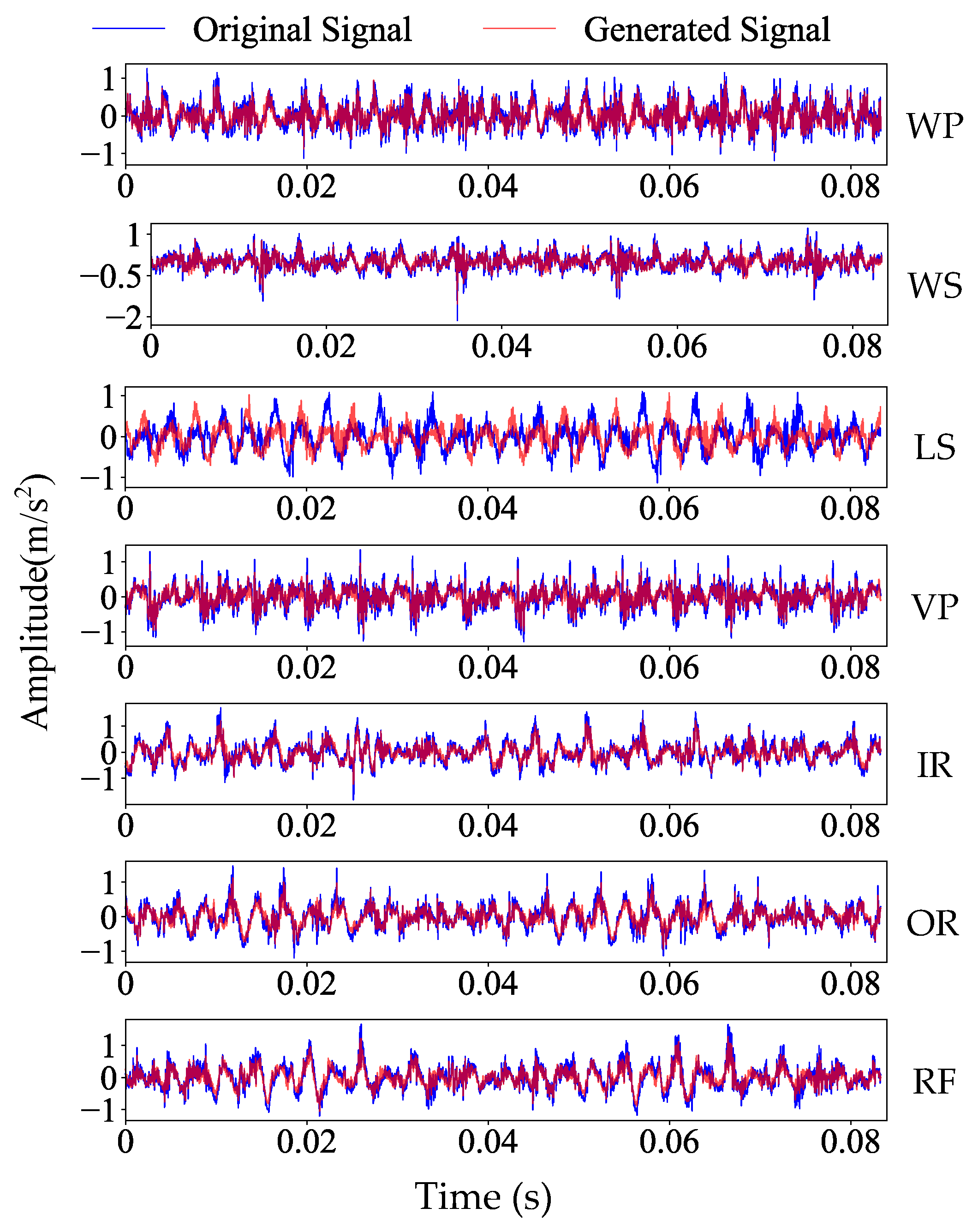
4.2.2. Data Generation and Evaluation in the Axial Piston Pump Dataset
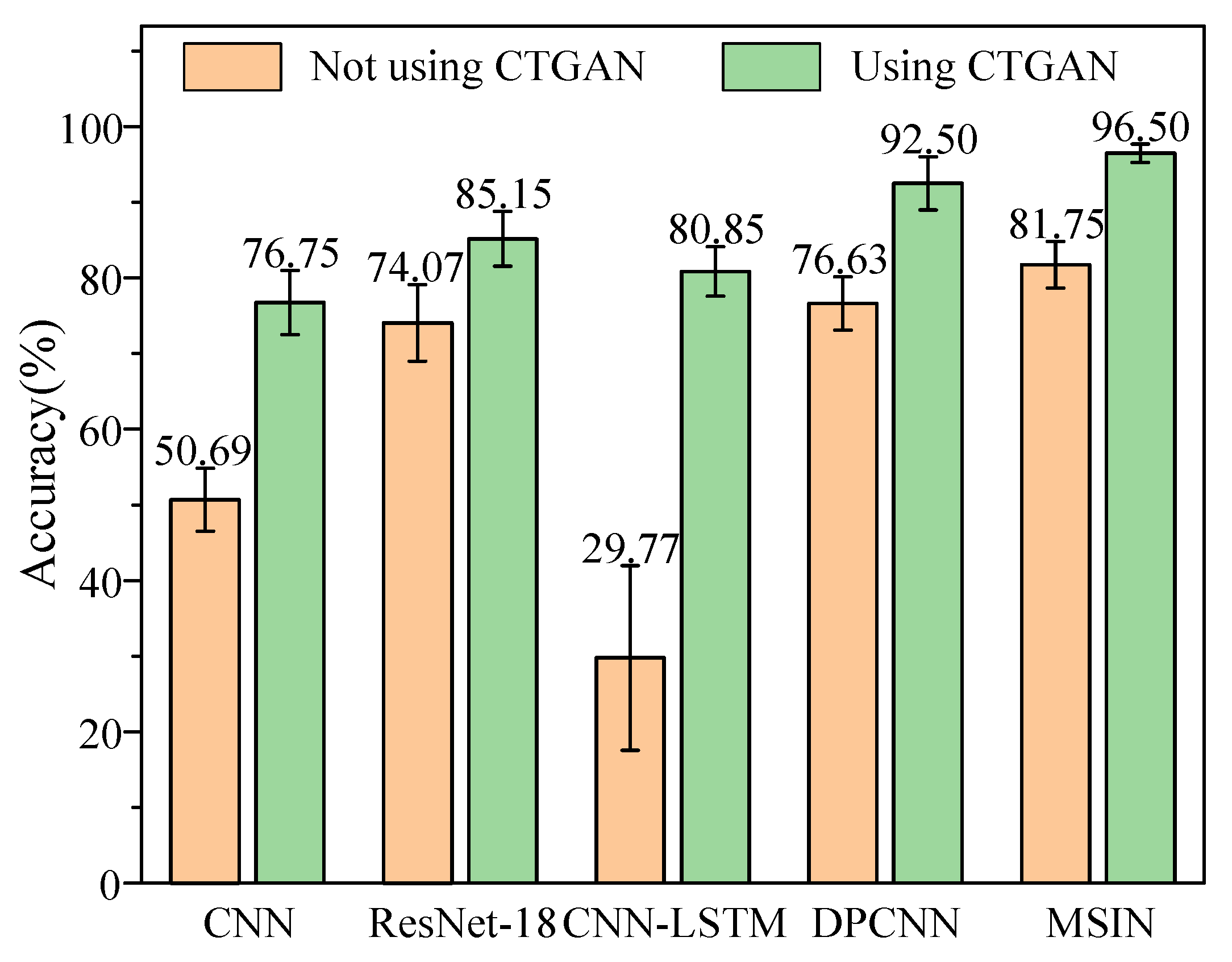
4.2.3. Ablation Experiment in the Axial Piston Pump Dataset
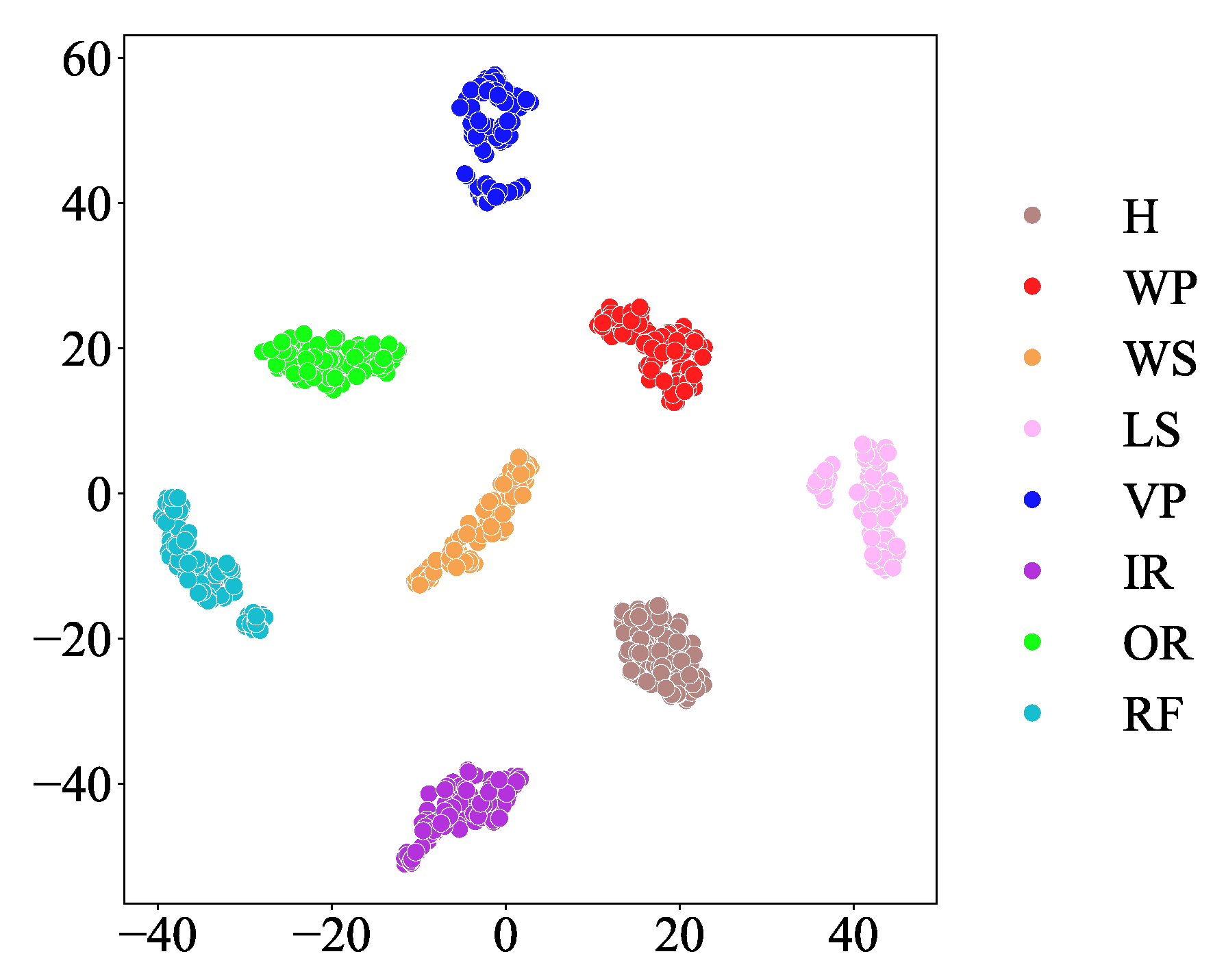
4.2.4. Diagnostic Results Analysis in the Axial Piston Pump Dataset
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, J.; Huang, J.; Liu, S.; Luo, J.; Jing, L. A self-attention Legendre graph convolution network for rotating machinery fault diagnosis. Sensors 2024, 24, 5475. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Zhang, D.; Wu, J.; Wang, Y.; Zhou, Q.; Hu, J. A limited annotated sample fault diagnosis algorithm based on nonlinear coupling self-attention mechanism. Eng. Fail. Anal. 2025, 174, 109474. [Google Scholar] [CrossRef]
- Wang, G.; Liu, D.; Xiang, J.; Cui, L. Attention guided partial domain adaptation for interpretable transfer diagnosis of rotating machinery. Adv. Eng. Inf. 2024, 62, 102708. [Google Scholar] [CrossRef]
- Zhuo, S.; Bai, X.; Han, J.; Ma, J.; Sun, B.; Li, C.; Zhan, L. A novel rolling bearing fault diagnosis method based on the NEITD-ADTL-JS algorithm. Sensors 2024, 25, 873. [Google Scholar] [CrossRef]
- Chen, W.; Yang, K.; Yu, Z.; Shi, Y.; Chen, C. A survey on imbalanced learning: Latest research, applications and future directions. Artif. Intell. Rev. 2024, 57, 137. [Google Scholar] [CrossRef]
- Alimoradia, M.; Sadeghi, R.; Daliri, A.; Zabihimayvan, M. Statistic deviation mode balancer (SDMB): A novel sampling algorithm for imbalanced data. Neurocomputing 2025, 624, 129484. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Z.; Liu, J.; Tan, S.; Liu, C. Application of generative AI-based data augmentation technique in transformer winding deformation fault diagnosis. Eng. Fail. Anal. 2024, 159, 108115. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, H.; Sun, W.; Song, W.; Li, Q. Multivariate time series generation based on dual-channel Transformer conditional GAN for industrial remaining useful life prediction. Knowl.-Based Syst. 2025, 308, 112749. [Google Scholar] [CrossRef]
- Chen, L.; Wan, S.; Dou, L. Improving diagnostic performance of high-voltage circuit breakers on imbalanced data using an oversampling method. IEEE Trans. Power Deliv. 2022, 37, 2704–2716. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, D.; Lee, S.; Hsu, C.; Liu, Y. A boosting resampling method for regression based on a conditional variational autoencoder. Inf. Sci. 2022, 590, 90–105. [Google Scholar] [CrossRef]
- Wan, D.; Lu, R.; Xu, T.; Shen, S.; Lang, X.; Ren, Z. Random Interpolation Resize: A free image data augmentation method for object detection in industry. Expert Syst. Appl. 2023, 228, 120355. [Google Scholar] [CrossRef]
- Vega-Bayo, M.; Perez-Aracil, J.; Prieto-Godino, L.; Salcedo-Sanz, S. Improving the prediction of extreme wind speed events with generative data augmentation techniques. Renew. Energy 2024, 221, 119769. [Google Scholar] [CrossRef]
- Shen, Z.; Kong, X.; Cheng, L.; Wang, R.; Zhu, Y. Fault diagnosis of the rolling bearing by a multi-task deep learning method based on a classifier generative adversarial network. Sensors 2024, 24, 1290. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Pei, Y.; Li, J. A comprehensive survey on design and application of autoencoder in deep learning. Appl. Soft Comput. 2023, 138, 110176. [Google Scholar] [CrossRef]
- Odena, A.; Olah, C.; Shlens, J. Conditional image synthesis with auxiliary classifier GANs. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 2642–2651. [Google Scholar]
- Yang, Z.; Han, Y.; Zhang, C.; Xu, Z.; Tang, S. Research on transformer transverse fault diagnosis based on optimized LightGBM model. Measurement 2025, 244, 116499. [Google Scholar] [CrossRef]
- Wang, R.; Jia, X.; Liu, Z.; Dong, E.; Li, S.; Cheng, Z. Conditional generative adversarial network based data augmentation for fault diagnosis of diesel engines applied with infrared thermography and deep convolutional neural network. Eksploat. Niezawodn.–Maint. Reliab. 2023, 26, 175291. [Google Scholar] [CrossRef]
- Li, Y.; Zou, W.; Jiang, L. Fault diagnosis of rotating machinery based on combination of Wasserstein generative adversarial networks and long short term memory fully convolutional network. Measurement 2022, 191, 110826. [Google Scholar] [CrossRef]
- Chen, G.; Sheng, B.; Fu, G.; Chen, X.; Zhao, G. A GAN-based method for diagnosing bodywork spot welding defects in response to small sample condition. Appl. Soft Comput. 2024, 157, 111544. [Google Scholar] [CrossRef]
- Li, X.; Wu, X.; Wang, T.; Xie, Y.; Chu, F. Fault diagnosis method for imbalanced data based on adaptive diffusion models and generative adversarial networks. Eng. Appl. Artif. Intell. 2025, 147, 110410. [Google Scholar] [CrossRef]
- Yoon, J.; Jarrett, D.; van der Schaar, M. Time-series generative adversarial networks. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; Volume 32, pp. 1–9. [Google Scholar]
- Shi, Y.; Li, J.; Li, H.; Yang, B. An imbalanced data augmentation and assessment method for industrial process fault classification with application in air compressors. IEEE Trans. Instrum. Meas. 2023, 72, 3521510. [Google Scholar] [CrossRef]
- Sim, Y.; Lee, C.; Hwang, J.; Kwon, G.; Chang, S. AI-based remaining useful life prediction for transmission systems: Integrating operating conditions with TimeGAN and CNN-LSTM networks. Electr. Power Syst. Res. 2025, 238, 111151. [Google Scholar] [CrossRef]
- Ye, L.; Zhang, K.; Jiang, B. Synergistic feature fusion with deep convolutional GAN for fault diagnosis in imbalanced rotating machinery. IEEE Trans. Ind. Inform. 2024, 21, 1901–1910. [Google Scholar] [CrossRef]
- Wang, C.; Yang, J.; Jie, H.; Tao, Z.; Zhao, Z. A lightweight progressive joint transfer ensemble network inspired by the Markov process for imbalanced mechanical fault diagnosis. Mech. Syst. Sig. Process. 2025, 224, 111994. [Google Scholar] [CrossRef]
- Guo, H.; Ping, D.; Wang, L.; Zhang, W.; Wu, J.; Ma, X.; Xu, Q.; Lu, Z. Fault diagnosis method of rolling bearing based on 1d multi-channel improved convolutional neural network in noisy environment. Sensors 2025, 25, 2286. [Google Scholar] [CrossRef]
- Choi, J.; Lee, S. RNN-based integrated system for real-time sensor fault detection and fault-informed accident diagnosis in nuclear power plant accidents. Nucl. Eng. Technol. 2023, 55, 814–826. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale, Internation Conference on Learning Representations (ICLR). arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Liu, X.; Lu, J.; Li, Z. Multiscale fusion attention convolutional neural network for fault diagnosis of aero-engine rolling bearing. IEEE Sens. J. 2023, 23, 19918–19934. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Z.; Chen, Y.; Jin, Y.; Bai, G. Selective kernel convolution deep residual network based on channel-spatial attention mechanism and feature fusion for mechanical fault diagnosis. ISA Trans. 2023, 133, 369–383. [Google Scholar] [CrossRef]
- Liu, R.; Wang, F.; Yang, B.; Qin, S. Multiscale kernel based residual convolutional neural network for motor fault diagnosis under nonstationary conditions. IEEE Trans. Ind. Inform. 2020, 16, 3797–3806. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, J.; Huang, W.; Yu, B.; Lyu, F.; Zhang, X.; Xu, B. The loose slipper fault diagnosis of variable-displacement pumps under time-varying operating conditions. Reliab. Eng. Syst. Saf. 2024, 252, 110448. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Liang, W.; He, F. Research on rolling bearing fault diagnosis based on parallel depthwise separable ResNet neural network with attention mechanism. Expert Syst. Appl. 2025, 286, 128105. [Google Scholar] [CrossRef]
- Xu, W.; Wan, Y. ELA: Efficient local attention for deep convolutional neural networks. arXiv 2024, arXiv:2403.01123. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar] [CrossRef]
- Zhao, C.; Zio, E.; Shen, W. Domain generalization for cross-domain fault diagnosis: An application-oriented perspective and a benchmark study. Reliab. Eng. Syst. Saf. 2024, 245, 109964. [Google Scholar] [CrossRef]
- Desai, A.; Freeman, C.; Beaver, I.; Wang, Z. Timevae: A variational auto-encoder for multivariate time series generation. arXiv 2021, arXiv:2111.08095. [Google Scholar] [CrossRef]
- Chawla, N.; Bowyer, K.; Hall, L.; Kegelmeyer, W. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Goodfellow, I.; Xu, B.; Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Advances in Neural Information Processing Systems 27 (NIPS 2014), Proceedings of the Annual Conference on Neural Information Processing Systems 2014, Montreal, QC, Canada, 8–13 December 2014; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014. [Google Scholar]
- Xu, T.; Li, W.; Munn, M.; Acciaio, B. COT-GAN: Generating sequential data via causal optimal transport. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; Volume 33, pp. 8798–8809. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, Q.; Tang, X.; Zhao, S.; Lu, X. A novel fault diagnosis method based on CNN and LSTM and its application in fault diagnosis for complex systems. Artif. Intell. Rev. 2022, 55, 1289–1315. [Google Scholar] [CrossRef]
- Qin, N.; You, Y.; Huang, D.; Jia, X.; Zhang, Y.; Du, J.; Wang, T. AttGAN-DPCNN: An extremely imbalanced fault diagnosis method for complex signals from multiple sensors. IEEE Sens. J. 2024, 24, 38270–38285. [Google Scholar] [CrossRef]








| Fault Type | Operating Condition | Label | Sample Number |
|---|---|---|---|
| Health | 3900 rpm | H | 150 |
| Inner ring fault | 3900 rpm | IR | 10 |
| Outer ring fault | 3900 rpm | OR | 10 |
| Rolling element fault | 3900 rpm | RF | 10 |
| Network | Structure | Parameter | |
|---|---|---|---|
| Embedder | GRU | Hidden_dim = 24 | Optimizer = Adam Initial learning rate = 0.0001 Decay steps = 100 Decay rate = 0.96 Epochs = 2000 |
| Dropout | Dropout rate = 0.2 | ||
| GRU | Hidden_dim = 24 | ||
| Dense | Units = 24 | ||
| Layer Norm | β = 0, γ = 1 | ||
| Recovery | GRU | Hidden_dim = 24 | |
| Dropout | Dropout rate = 0.2 | ||
| GRU | Hidden_dim = 24 | ||
| Dense | Units = 24 | ||
| Layer Norm | β = 0, γ = 1 | ||
| Dense1 | Units = 3 | ||
| Generator | GRU | Hidden_dim = 24 | |
| Dropout | Dropout rate = 0.2 | ||
| Dense1 | Units = 3 | ||
| Discriminator | GRU | Hidden_dim = 24 | |
| Dropout | Dropout rate = 0.2 | ||
| Dense | Units = 24 | ||
| Layer Norm | β = 0, γ = 1 | ||
| Dense2 | Units = 1 | ||
| Model | TimeGAN | Condition Label | Wasserstein Distance with Gradient Penalty | Accuracy (%) |
|---|---|---|---|---|
| TimeGAN | √ | × | × | 92.00 |
| CTGAN (without GP) | √ | √ | × | 96.86 |
| GPTGAN | √ | × | √ | 95.50 |
| CTGAN | √ | √ | √ | 98.75 |
| Model | 1D-CNN | MDSR | ELA | SELA | Accuracy (%) |
|---|---|---|---|---|---|
| MDSR | × | √ | × | × | 94.73 |
| CNN-ELA | √ | × | √ | × | 93.26 |
| 1D-CNN | √ | × | × | × | 89.33 |
| MSIN | × | √ | × | √ | 98.75 |
| Model | CTGAN | MSIN | CNN | Accuracy (%) |
|---|---|---|---|---|
| MSIN-only | × | √ | × | 85.03 |
| CTGAN-CNN | √ | × | √ | 89.33 |
| CTGAN-MSIN | √ | √ | × | 98.75 |
| Main Parameters | Values |
|---|---|
| Batch size | 16 |
| Optimizer | Adam |
| Learning rate | 0.0001 |
| Training epochs | 100 |
| Method | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Time (s) |
|---|---|---|---|---|---|
| CNN | 67.75 ± 2.82 | 73.56 ± 3.69 | 67.75 ± 2.82 | 65.61 ± 3.75 | —— |
| CVAE | 88.75 ± 8.56 | 90.93 ± 6.77 | 88.75 ± 8.56 | 87.04 ± 10.99 | 0.0215 |
| TimeVAE | 89.86 ± 4.59 | 91.63 ± 2.40 | 89.86 ± 4.59 | 89.07 ± 5.83 | 0.0070 |
| SMOTE | 92.45 ± 3.32 | 92.82 ± 3.37 | 92.45 ± 3.32 | 92.35 ± 3.37 | —— |
| GAN | 91.39 ± 5.35 | 93.14 ± 3.45 | 91.39 ± 5.35 | 90.10 ± 6.55 | 0.3119 |
| WGAN | 94.25 ± 3.89 | 95.30 ± 3.1 | 94.25 ± 3.89 | 94.19 ± 4.10 | 3.0125 |
| DCGAN | 96.75 ± 1.45 | 96.83 ± 2.12 | 96.75 ± 1.45 | 96.72 ± 2.16 | 0.6826 |
| COT-GAN | 92.08 ± 4.91 | 92.74 ± 5.45 | 92.08 ± 4.91 | 92.70 ± 3.73 | 5.4786 |
| CTGAN | 98.75 ± 1.19 | 98.66 ± 1.30 | 98.75 ± 1.19 | 98.48 ± 1.46 | 5.8146 |
| Fault Type | Label | Sample Number |
|---|---|---|
| Health | H | 150 |
| Wear of piston | WP | 10 |
| Wear of slipper | WS | 10 |
| Loose slipper | LS | 10 |
| Wear of valve plate | VP | 10 |
| Inner ring fault | IR | 10 |
| Outer ring fault | OR | 10 |
| Rolling element fault | RF | 10 |
| Model | TimeGAN | Condition Label | Wasserstein Distance with Gradient Penalty | Accuracy (%) |
|---|---|---|---|---|
| TimeGAN | √ | × | × | 90.86 |
| CTGAN (without GP) | √ | √ | × | 94.50 |
| GPTGAN | √ | × | √ | 93.25 |
| CTGAN | √ | √ | √ | 96.50 |
| Model | 1D-CNN | MDSR | ELA | SELA | Accuracy (%) |
|---|---|---|---|---|---|
| MDSR | × | √ | × | × | 91.50 |
| CNN-ELA | √ | × | √ | √ | 88.68 |
| 1D-CNN | √ | × | × | × | 76.75 |
| MSIN | × | √ | × | √ | 96.50 |
| Model | CTGAN | MSIN | CNN | Accuracy (%) |
|---|---|---|---|---|
| MSIN-only | × | √ | × | 81.75 |
| CTGAN-CNN | √ | × | √ | 76.75 |
| CTGAN-MSIN | √ | √ | × | 96.50 |
| Method | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Time (s) |
|---|---|---|---|---|---|
| CNN | 50.69 ± 4.16 | 61.23 ± 2.78 | 50.69 ± 4.16 | 48.06 ± 4.12 | —— |
| CVAE | 73.47 ± 5.83 | 75.94 ± 7.99 | 73.47 ± 5.83 | 70.93 ± 5.61 | 0.0378 |
| TimeVAE | 90.63 ± 4.78 | 91.02 ± 5.48 | 90.63 ± 4.78 | 90.76 ± 4.20 | 0.0191 |
| SMOTE | 89.69 ± 5.46 | 91.44 ± 5.08 | 89.69 ± 5.46 | 89.42 ± 5.72 | —— |
| GAN | 67.00 ± 7.75 | 61.90 ± 9.42 | 67.00 ± 7.75 | 61.37 ± 10.23 | 0.3777 |
| WGAN | 88.75 ± 6.10 | 92.59 ± 5.78 | 88.75 ± 6.10 | 85.78 ± 6.12 | 3.5187 |
| DCGAN | 91.75 ± 4.83 | 93.19 ± 2.12 | 91.75 ± 4.83 | 91.33 ± 5.12 | 0.8125 |
| COT-GAN | 87.75 ± 3.53 | 88.40 ± 4.60 | 87.75 ± 3.53 | 88.37 ± 2.80 | 6.0504 |
| CTGAN | 96.50 ± 1.22 | 96.84 ± 0.82 | 96.50 ± 1.22 | 96.37 ± 1.59 | 6.3361 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, R.; Chen, D.; Yao, C.; Hu, D.; Xian, Q.; Zhang, S. A Gradient-Penalized Conditional TimeGAN Combined with Multi-Scale Importance-Aware Network for Fault Diagnosis Under Imbalanced Data. Sensors 2025, 25, 6825. https://doi.org/10.3390/s25226825
Deng R, Chen D, Yao C, Hu D, Xian Q, Zhang S. A Gradient-Penalized Conditional TimeGAN Combined with Multi-Scale Importance-Aware Network for Fault Diagnosis Under Imbalanced Data. Sensors. 2025; 25(22):6825. https://doi.org/10.3390/s25226825
Chicago/Turabian StyleDeng, Ranyang, Dongning Chen, Chengyu Yao, Dongbo Hu, Qinggui Xian, and Sheng Zhang. 2025. "A Gradient-Penalized Conditional TimeGAN Combined with Multi-Scale Importance-Aware Network for Fault Diagnosis Under Imbalanced Data" Sensors 25, no. 22: 6825. https://doi.org/10.3390/s25226825
APA StyleDeng, R., Chen, D., Yao, C., Hu, D., Xian, Q., & Zhang, S. (2025). A Gradient-Penalized Conditional TimeGAN Combined with Multi-Scale Importance-Aware Network for Fault Diagnosis Under Imbalanced Data. Sensors, 25(22), 6825. https://doi.org/10.3390/s25226825






