A Novel Fixed-Time Super-Twisting Control with I&I Disturbance Observer for Uncertain Manipulators
Abstract
1. Introduction
- (1)
- The conventional super-twisting control algorithm ensures finite-time convergence; however, the maximum convergence time depends on the initial states and control parameters, making it uncontrollable and unpredictable. Although Tran et al. [25] proposed a fixed-time super-twisting algorithm whose upper bound of convergence time depends only on control parameters, this method is applicable only to single-input single-output (SISO) systems and cannot be directly extended to multi-input multi-output (MIMO) cases.
- (2)
- Fuzzy logic, neural network, and adaptive control approaches are commonly employed to estimate composite disturbances in complex control systems. However, these methods often suffer from non-vanishing estimation errors, that is, the estimation error of composite disturbances does not asymptotically converge to zero.
- (3)
- The majority of existing sliding mode surfaces exhibit asymptotic or finite-time convergence characteristics, lacking fixed-time convergence properties. Sliding mode controllers designed under the fixed-time convergence framework typically ensure that only the sliding surface reaches zero within a fixed time, without guaranteeing that the tracking error confined to the surface also converges to zero within the same fixed time. Consequently, the system tracking error cannot be guaranteed to vanish absolutely within a fixed time.
- (1)
- The fixed-time super-twisting algorithm for single-input single-output (SISO) systems described in [25] is extended to multi-input multi-output (MIMO) systems using a fixed-time convergence approach. A fixed-time adaptive super-twisting sliding mode controller is developed for the MIMO robotic arm dynamic system with parameter perturbations. The proposed controller enables the end-effector to achieve fast and accurate trajectory tracking under complex operating conditions while effectively suppressing high-frequency chattering.
- (2)
- An Immersion and Invariance (I&I) disturbance observer is designed to estimate external composite disturbances with minimal estimation error. The observer features a simple structure and guarantees exponential convergence of the estimation error to zero, thereby overcoming the non-convergence issues of conventional composite disturbance estimators and mitigating the impact of external disturbances on trajectory tracking accuracy.
- (3)
- A sliding mode surface with fixed-time convergence characteristics is constructed, ensuring that tracking errors on the surface converge to zero within a fixed time. Consequently, the trajectory tracking error of the overall system achieves global fixed-time convergence, further enhancing the precision and robustness of the control performance.
2. Problem Formulation and Model Description
- (1)
- Disturbances satisfy , where
- (2)
- Let , . There exists a positive definite matrix and any positive number , such that the symmetric positive definite matrix satisfies
3. Design of the Fixed-Time Super-Twisting Sliding Mode Controller
4. Stability Analysis
5. Numerical Simulation Analysis
5.1. Control and Simulation Parameters
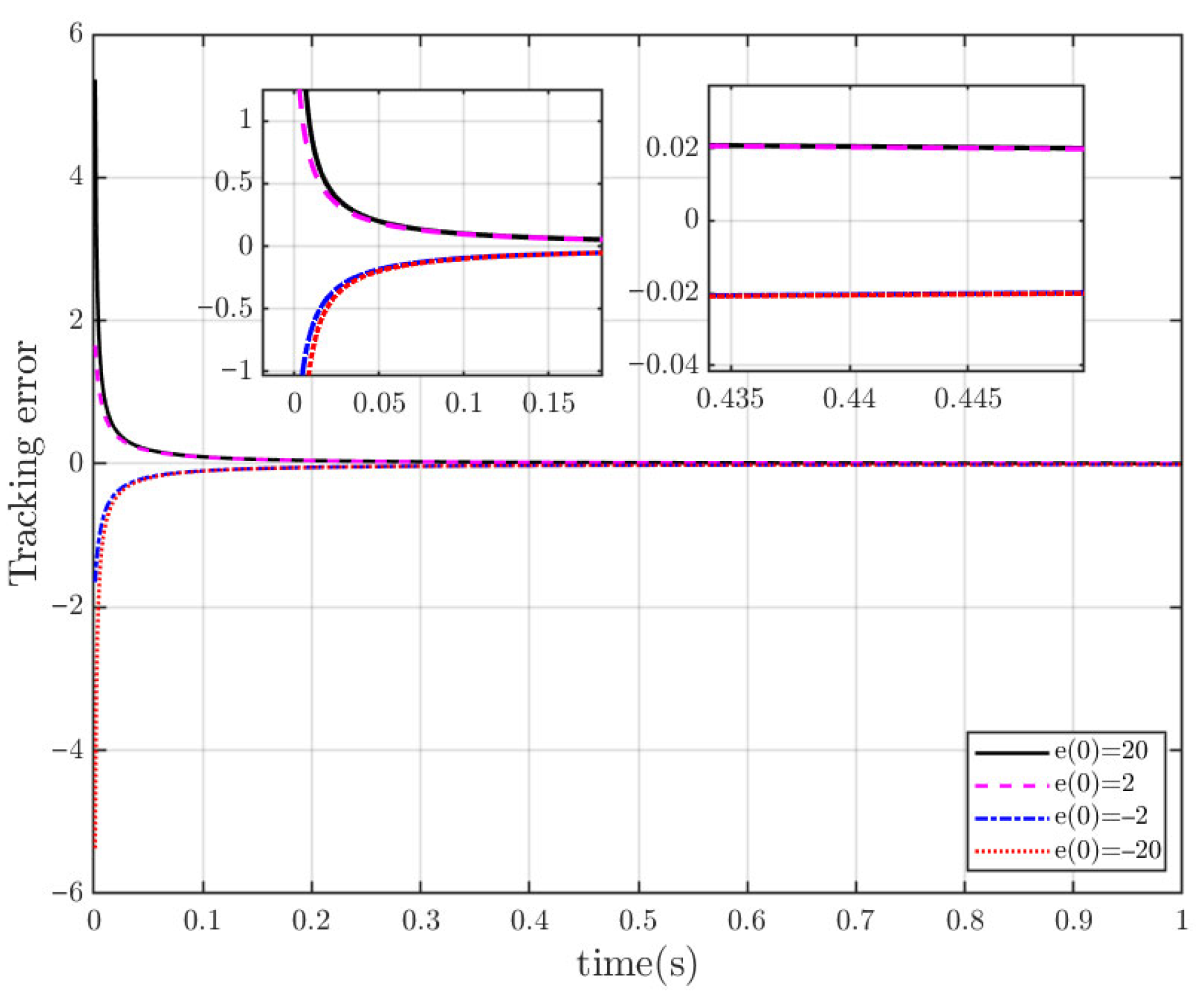
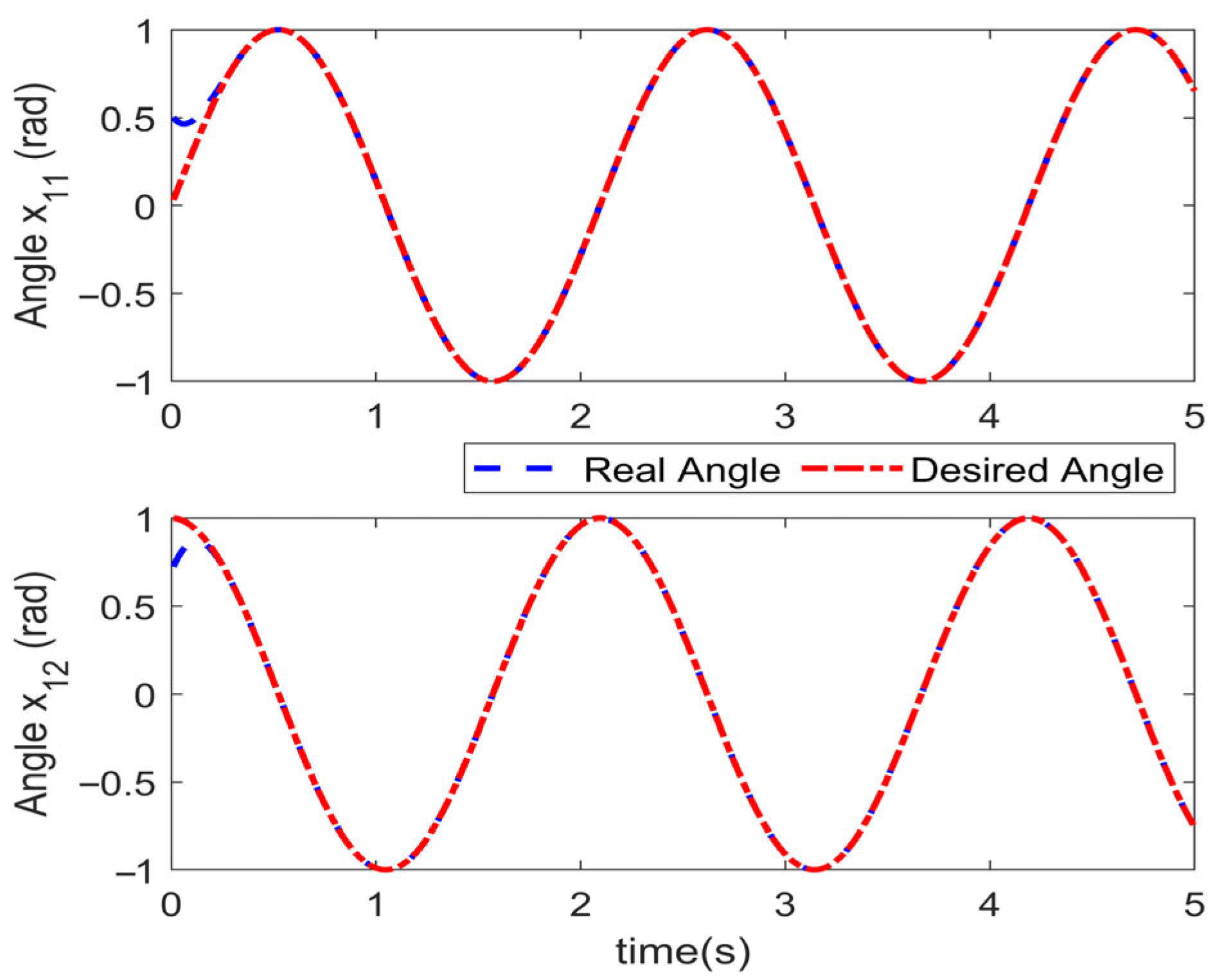
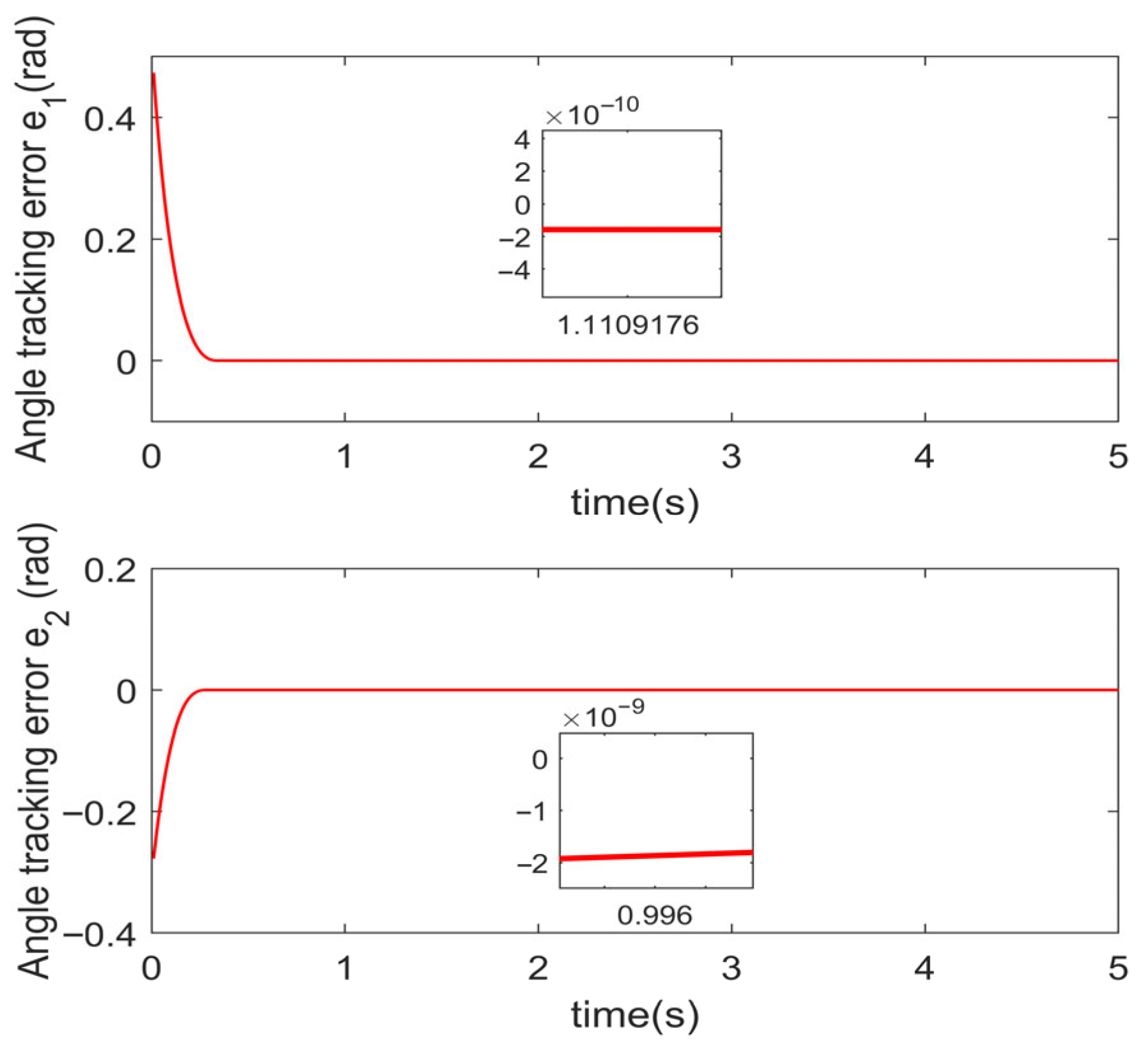
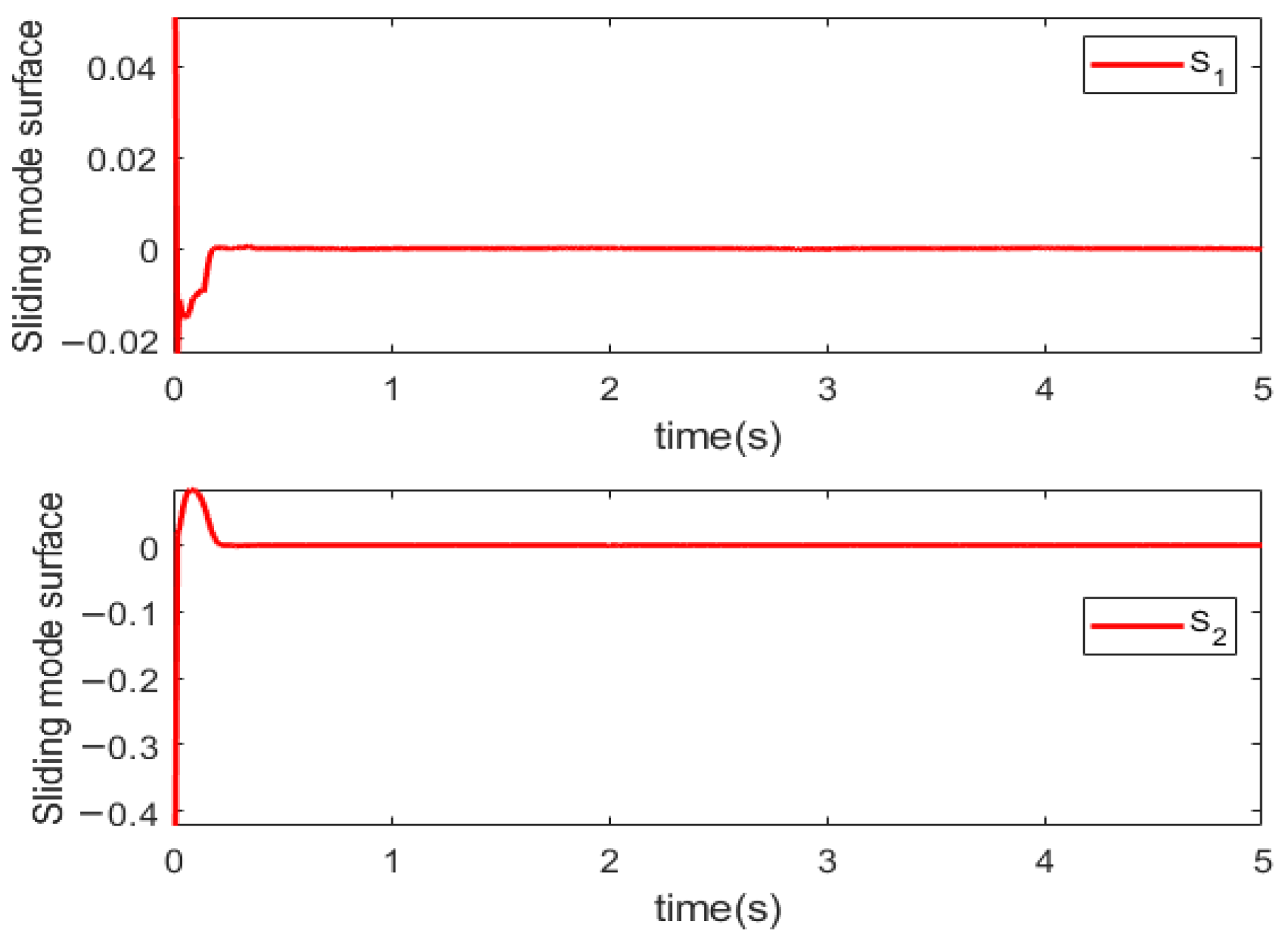
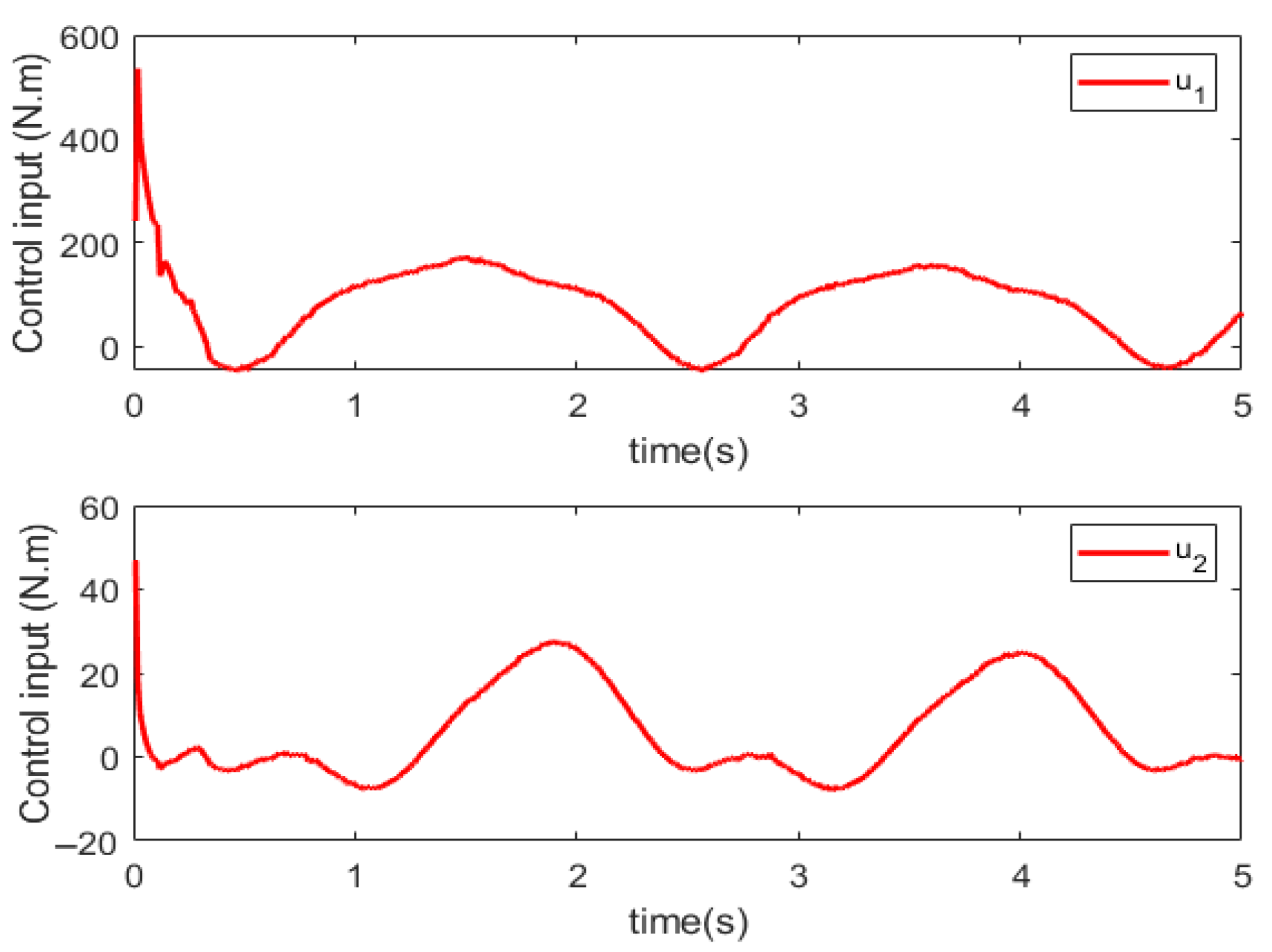
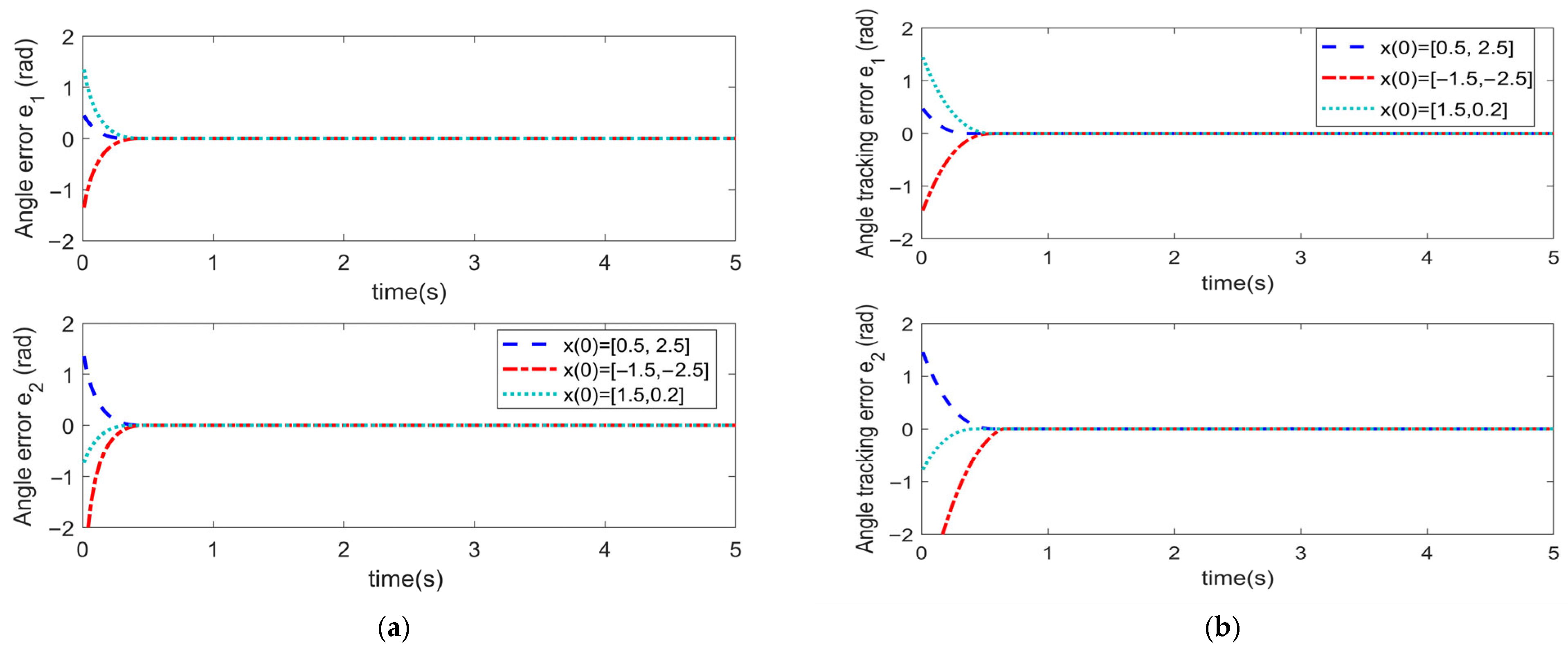
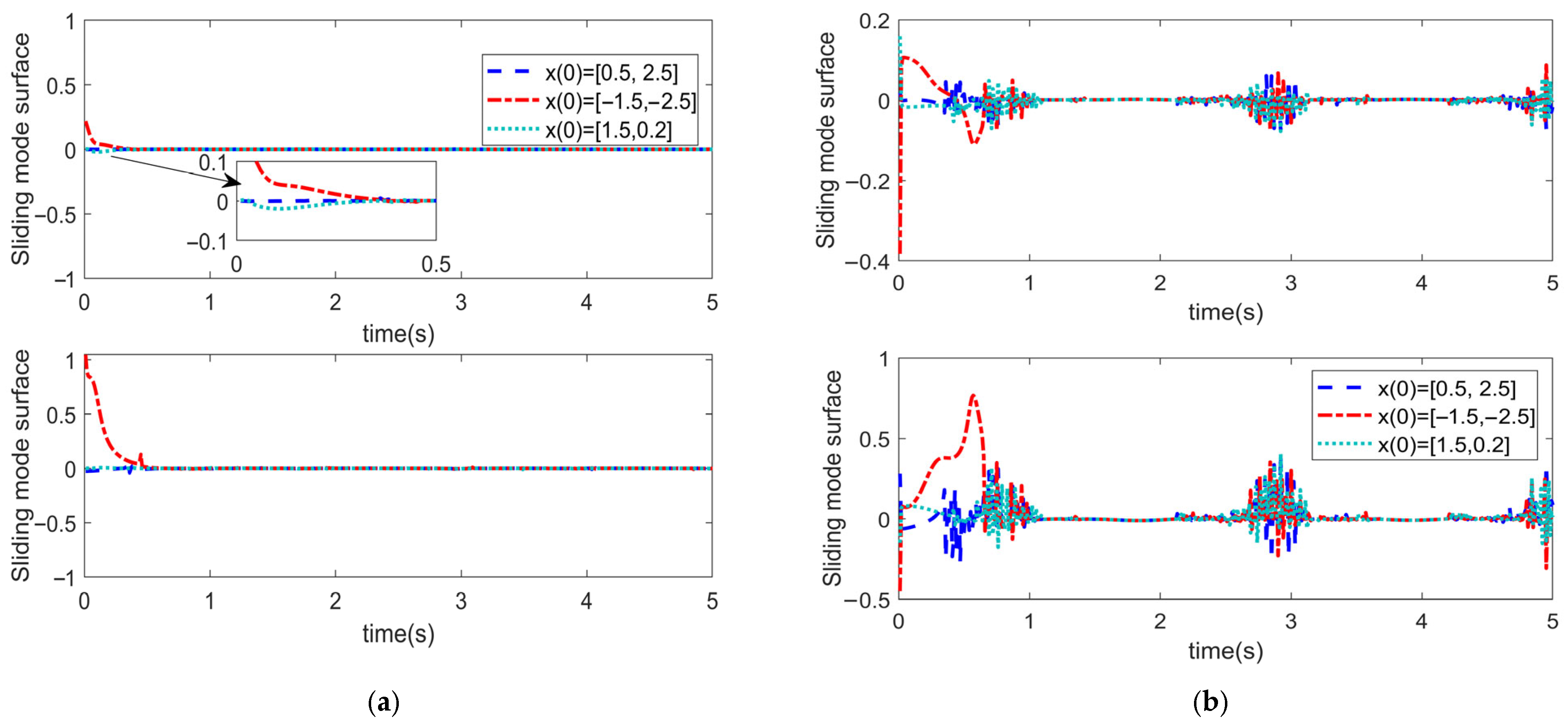
5.2. Effectiveness Analysis
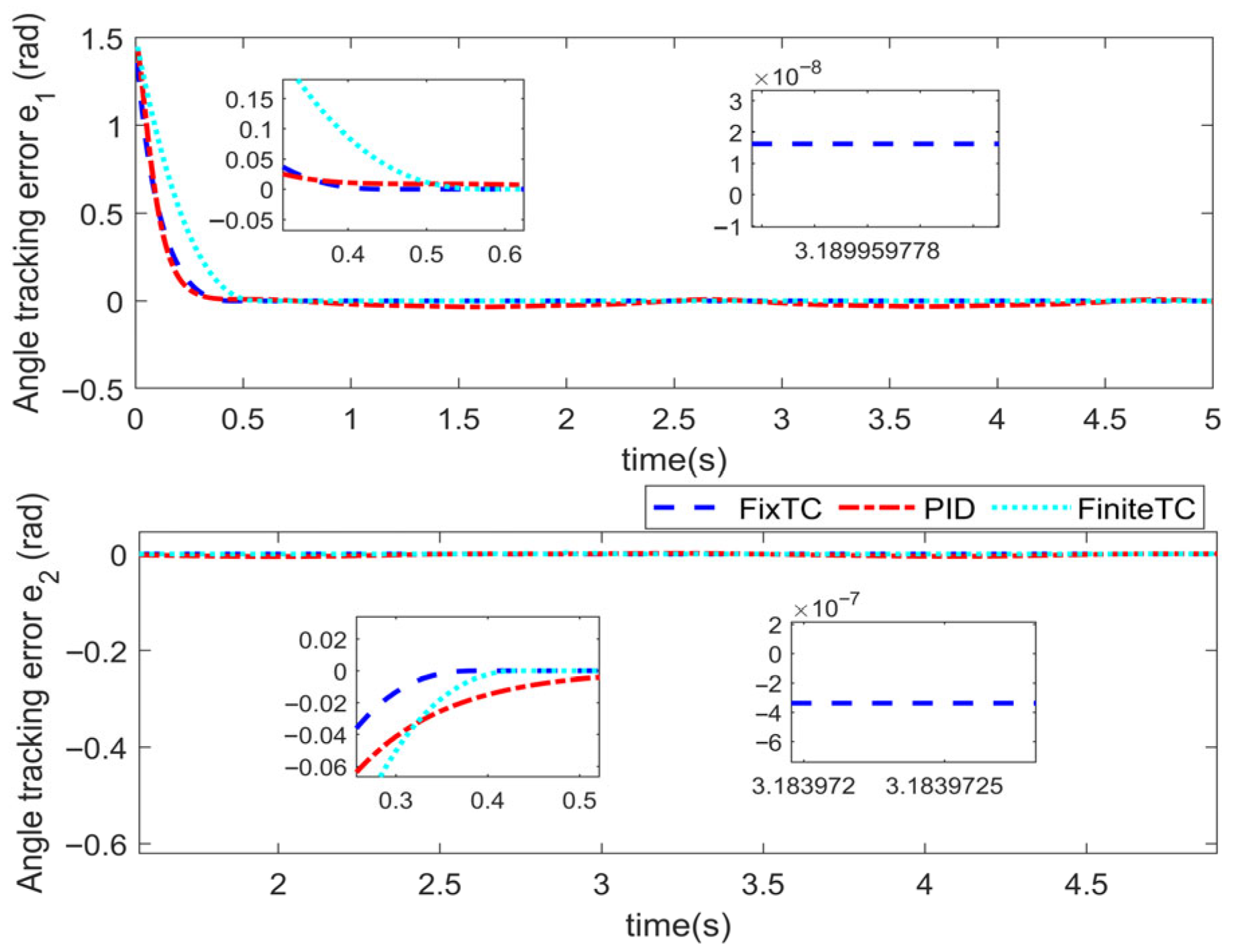
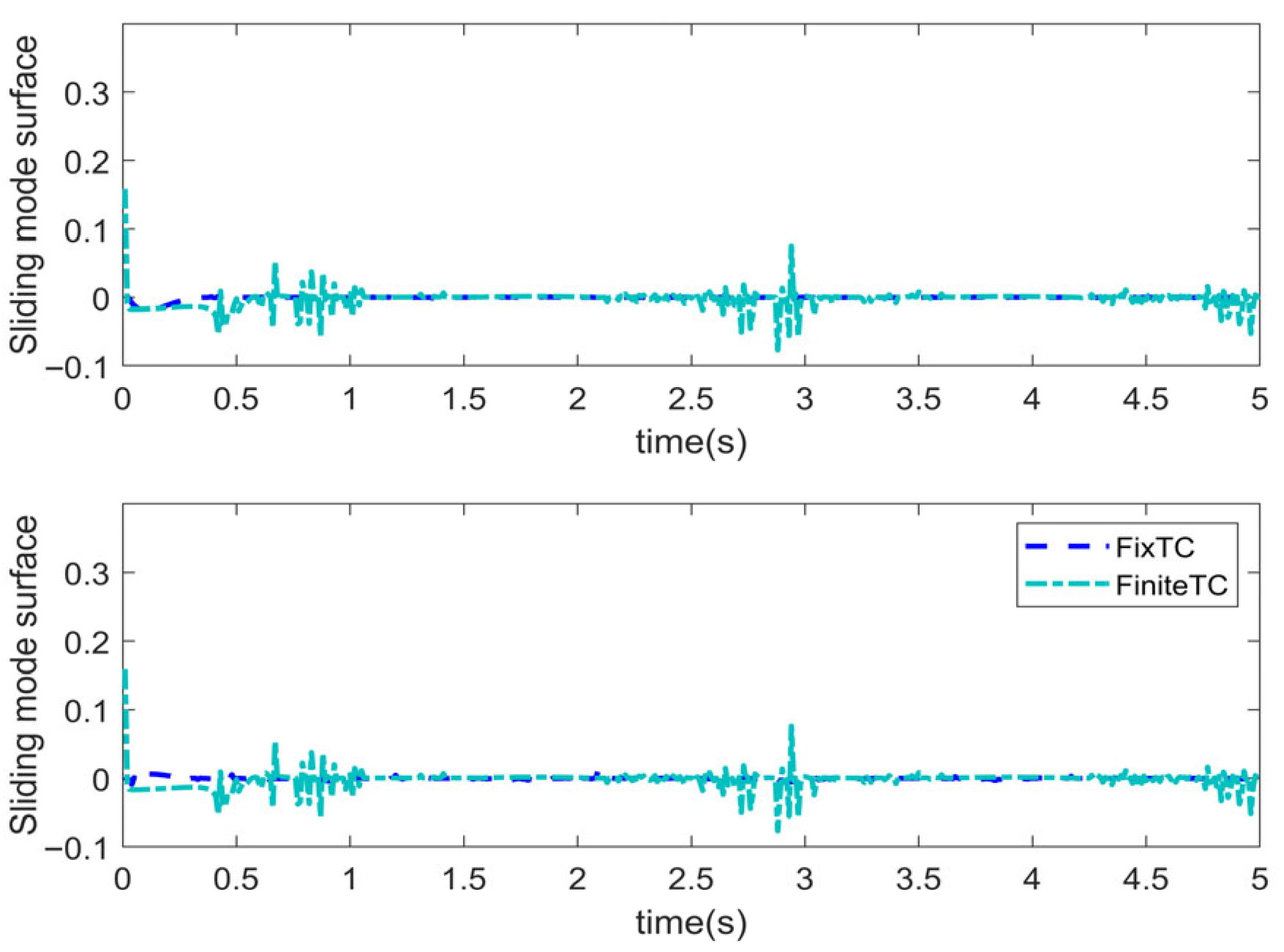
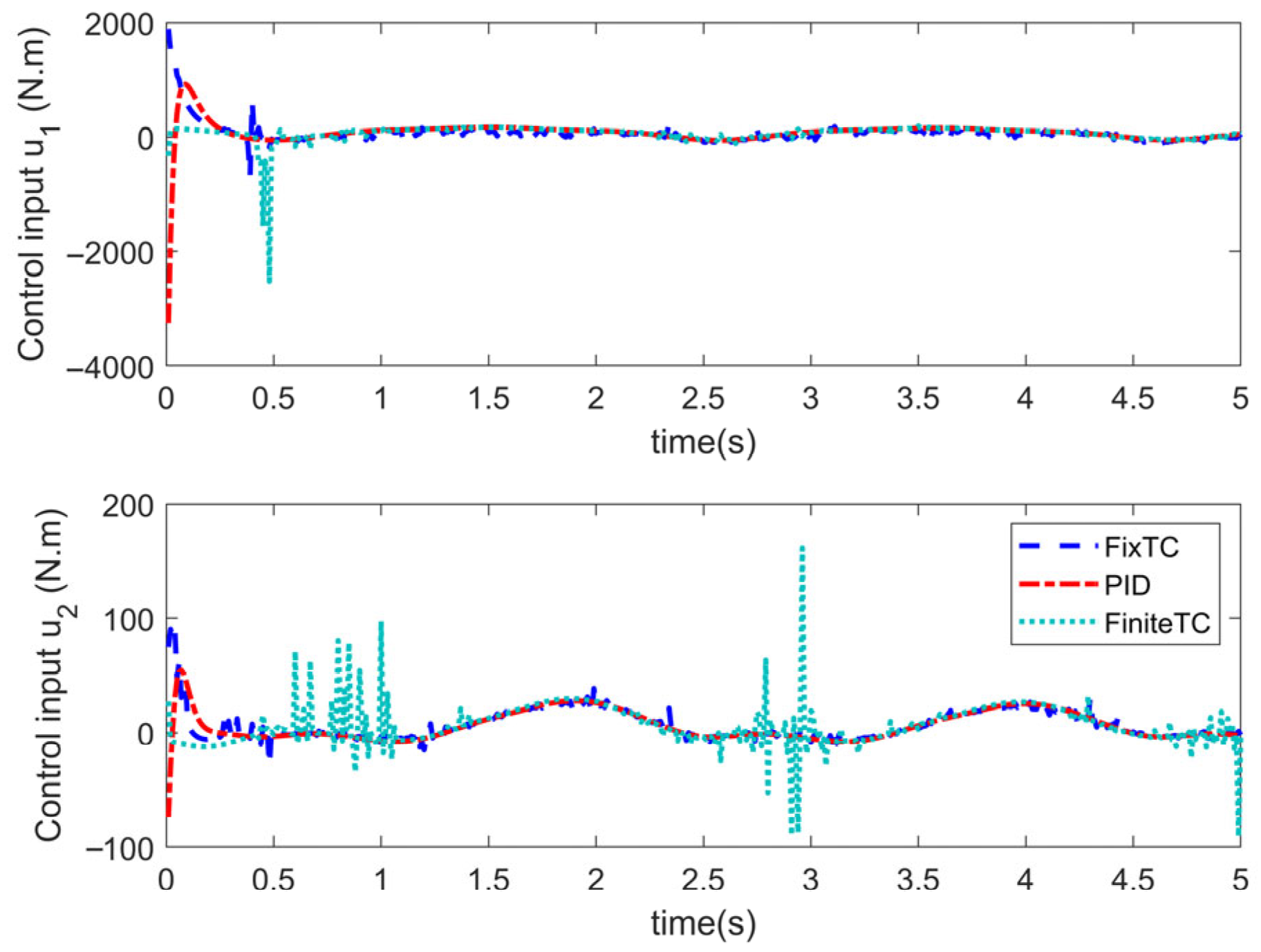
5.3. Comparative Analysis of Different Controllers
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yin, C.W.; Riaz, S. Novel adaptive predefined-time complete tracking control of nonlinear systems via ELM. Appl. Intell. 2025, 55, 337. [Google Scholar] [CrossRef]
- Yin, C.W. Predefined time convergence guaranteed performance control for uncertain systems based on reinforcement learning. Eng. Appl. Artif. Intell. 2025, 40, 109734. [Google Scholar] [CrossRef]
- Saleem, O.; Abbas, F.; Iqbal, J. Complex fractional-order LQIR for inverted-pendulum-type robotic mechanisms—Design and experimental validation. Mathematics 2023, 11, 913. [Google Scholar] [CrossRef]
- Yin, C.; Yi, P.; Bu, X.W. Neural network-based intelligent perception guaranteed performance control for mechanical arm. Robot. Auton. Syst. 2025, 190, 104991. [Google Scholar] [CrossRef]
- Harvey, D.R.; John, C.; Herbert, E. Active disturbance rejection control based on a cascade estimator composed of reduced-order and full-order extended state observers. ISA Trans. 2024, 151, 296–311. [Google Scholar]
- Yin, C.W.; Ding, Y.P.; Sun, H. Nonsingular Fast Predefined Time Convergence Sliding Mode Control for Construction Robot. ISA Trans. 2025, 161, 109–121. [Google Scholar] [CrossRef]
- Ahmad, S.; Uppal, A.A.; Azam, M.R.; Iqbal, J. Chattering free sliding mode control and state dependent Kalman filter design for underground coal gasification energy conversion process. Electronics 2023, 12, 876. [Google Scholar] [CrossRef]
- Ullah, N.; Mehmood, Y.; Aslam, J.; Ali, A.; Iqbal, J. UAVs-UGV leader follower formation using adaptive non-singular terminal super twisting sliding mode control. IEEE Access 2021, 5, 74385–74405. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, H.; Wang, S.-Q.; Xu, J.; Su, H.; Zhang, J. Adaptive neural network H∞ control for offshore platform with input delay and nonlinearity. IET Control Theory Appl. 2024, 18, 384–398. [Google Scholar] [CrossRef]
- Kang, J. Neural network-based model predictive tracking control of an uncertain robotic manipulator with input constraints. ISA Trans. 2021, 109, 89–101. [Google Scholar] [CrossRef]
- Yin, C.W.; Riaz, S.; Uppal, A.A.; Iqbal, J. Fuzzy fault-tolerant controller with guaranteed performance for MIMO systems under uncertain initial state. Int. J. Control Autom. Syst. 2024, 22, 2038–2054. [Google Scholar] [CrossRef]
- Zhou, G. Fuzzy logic-based adaptive tracking control of manipulator actuated by dc motor. Int. J. Robot. Autom. 2021, 36, 34–51. [Google Scholar] [CrossRef]
- Anjum, M.; Khan, Q.; Ullah, S.; Hafeez, G.; Fida, A.; Iqbal, J.; Albogamy, F.R. Maximum power extraction from a standalone photo voltaic system via neuro-adaptive arbitrary order sliding mode control strategy with high gain differentiation. Appl. Sci. 2023, 12, 2773. [Google Scholar] [CrossRef]
- Zhu, D.C.; Du, B.L.; Zhu, P.C.; Wu, W. Adaptive backstepping sliding mode control of trajectory tracking for robotic manipulators. Complexity 2020, 3, 3156787. [Google Scholar]
- Ren, B.; Wang, Y.; Chen, J. Trajectory-Tracking-Based Adaptive Neural Network Sliding Mode Controller for Robot Manipulators. J. Comput. Inf. Sci. Eng. 2020, 20, 031009. [Google Scholar] [CrossRef]
- Bing, Z.; Liang, Y.; Wang, C.; Lai, G.; Chen, Y. Adaptive finite-time tracking control of robot manipulators with multiple uncertainties based on a low-cost A neural approximator. J. Frankl. Inst. 2022, 359, 4938–4958. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Cheng, Y. Model free based finite time fault-tolerant control of robot manipulators subject to disturbances and input saturation. Int. J. Robust Nonlinear Control 2022, 32, 5281–5303. [Google Scholar] [CrossRef]
- Su, Y.X.; Zheng, C.H. A New Nonsingular Integral Terminal Sliding Mode Control for Robot Manipulators. Int. J. Syst. Sci. 2020, 51, 1418–1428. [Google Scholar] [CrossRef]
- Gao, W.B. Variable Structure Control for Nonlinear Systems. Autom. Sin. 1989, 15, 408–415. [Google Scholar]
- Liao, Y.; Yang, Y.; Wang, Y. Novel double power combination function reaching law foe sliding mode control. J. Natl. Univ. Def. Technol. 2017, 39, 105–110. [Google Scholar]
- Pan, J.; Li, W.; Zhang, H.P. Control algorithms of magnetic suspension systems based on the improved double exponential reaching law of sliding mode control. Int. J. Control Autom. Syst. 2018, 16, 2878–2887. [Google Scholar] [CrossRef]
- Shtessel, Y.; Taleb, M.; Plestan, F. A novel adaptive-gain supertwisting sliding mode controller: Methodology and application. Automatica 2012, 48, 759–769. [Google Scholar] [CrossRef]
- Evangelista, C.; Puleston, P.; Valenciaga, F.; Fridman, L. Lyapunov-Designed Super-Twisting Sliding Mode Control for Wind Energy Conversion Optimization. IEEE Trans. Ind. Electron. 2013, 60, 538–545. [Google Scholar] [CrossRef]
- Salgado, I.; Chairez, I.; Camacho, O.; Yañez, C. Super-twisting sliding mode differentiation for improving PD controllers performance of second order systems. ISA Trans. 2014, 53, 1096–1106. [Google Scholar] [CrossRef]
- Tran, X.T.; Oh, H. A modified generic second order algorithm with fixed-time stability. ISA Trans. 2021, 109, 72–80. [Google Scholar] [CrossRef]
- Chen, M.; An, S. Fixed-time tracking control for strict-feedback nonlinear systems based on backstepping algorithm. Control Decis. 2021, 36, 173–179. [Google Scholar]
- Polyakov, A. Nonlinear feedback design for fifixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2016–2110. [Google Scholar] [CrossRef]
- Astolfi, A.; Ortega, R. Immersion and invariance: A new tool for stabilization and adaptive control of nonlinear systems. IEEE Trans. Autom. Control 2003, 48, 590–606. [Google Scholar] [CrossRef]
- Xia, D.; Yue, X. Anti-Unwinding Immersion and Invariance Adaptive Attitude Control of Rigid Spacecraft with Inertia Uncertainties. J. Aerosp. Eng. 2022, 35, 35–46. [Google Scholar] [CrossRef]
- Peng, X.; Shi, X.; Gong, Y. Immersion and invariance-based adaptive pose tracking control under disturbances and input saturation. IET Control Theory Appl. 2022, 16, 829–845. [Google Scholar] [CrossRef]
- Liu, J.K. Robot Control System Design and MATLAB Simulation: The Basic Design Method; Tsinghua University Press: Beijing, China, 2016. [Google Scholar]



| Symbol | Description | Value | Unit |
|---|---|---|---|
| Mass of manipulator | 10 | kg | |
| Mass of manipulator | 5 | kg | |
| I1 | moment of inertia | 0.83 | kg·m2 |
| I2 | moment of inertia | 0.83 | kg·m2 |
| l1 | joint length | 1 | m |
| l2 | joint length | 0.5 | m |
| lc1 | joint length | 0.5 | m |
| lc2 | joint length | 0.25 | m |
| g | gravitational acceleration | 9.81 | kg·m2 |
| Mass perturbation | kg | ||
| Mass perturbation | kg | ||
| Inertia moment perturbation | kg·m2 | ||
| Inertia moment perturbation | kg·m2 | ||
| d1(t) | External disturbance | 3sin(0.1 t) | N·m |
| d2(t) | External disturbance | (1-exp(−0.1 t)) | N·m |
| Category | Symbol | Value |
|---|---|---|
| I&I disturbance observer | 10 | |
| Sliding mode surface | 5 | |
| 5 | ||
| 5 | ||
| 3 | ||
| 5 | ||
| 3 | ||
| Super-twisting sliding mode control | ||
| 0.5 | ||
| 1 | ||
| 1 | ||
| 0.7 | ||
| 1.6 |
| Angle Convergence Time | Angle Tracking Accuracy | Total Energy Consumption | ||||
|---|---|---|---|---|---|---|
| e1 | e2 | e1 | e2 | u1 | u2 | |
| FixTC | 0.42 s | 0.40 s | ||||
| PID | 0.44 s | 0.55 s | ||||
| Finite TC | 0.55 s | 0.43 s | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Zhang, J.; Yin, C.; Dai, R. A Novel Fixed-Time Super-Twisting Control with I&I Disturbance Observer for Uncertain Manipulators. Sensors 2025, 25, 6723. https://doi.org/10.3390/s25216723
Xu L, Zhang J, Yin C, Dai R. A Novel Fixed-Time Super-Twisting Control with I&I Disturbance Observer for Uncertain Manipulators. Sensors. 2025; 25(21):6723. https://doi.org/10.3390/s25216723
Chicago/Turabian StyleXu, Lin, Jiahao Zhang, Chunwu Yin, and Rui Dai. 2025. "A Novel Fixed-Time Super-Twisting Control with I&I Disturbance Observer for Uncertain Manipulators" Sensors 25, no. 21: 6723. https://doi.org/10.3390/s25216723
APA StyleXu, L., Zhang, J., Yin, C., & Dai, R. (2025). A Novel Fixed-Time Super-Twisting Control with I&I Disturbance Observer for Uncertain Manipulators. Sensors, 25(21), 6723. https://doi.org/10.3390/s25216723








