WAWA: Wavelet Analysis-Based Watermarking Authentication for GNSS Civil Signal with Immediate Symbol-Level Verification
Abstract
1. Introduction
- Novel Authentication Architecture for Immediate Verification: We introduce the WAWA scheme, which integrates public-key cryptography with wavelet-domain watermarking. This architecture facilitates the transmission of a complete digital signature within the physical signal layer, thereby eliminating the verification delay and time-synchronization dependency that are inherent weaknesses of TESLA-based protocols.
- Low-Memory, Dual-Mode Verification Framework: We design a flexible, dual-path verification framework adaptable to diverse receiver capabilities. It features a “slow path” for fully standalone receivers and a “fast path” for network-assisted receivers, enabling the architecture to support a wide range of resource-constrained devices without the need for large data buffers.
- Comprehensive Performance Modeling and Simulation Verification: We develop theoretical models to evaluate the scheme’s detection performance and its impact on the primary GNSS signal and validate the models through simulation. This analysis quantifies the trade-offs between key system parameters, providing a clear framework for system design and optimization.
2. Materials and Methods
2.1. Foundations of the WAWA Scheme
2.1.1. GNSS Baseband Signal Model
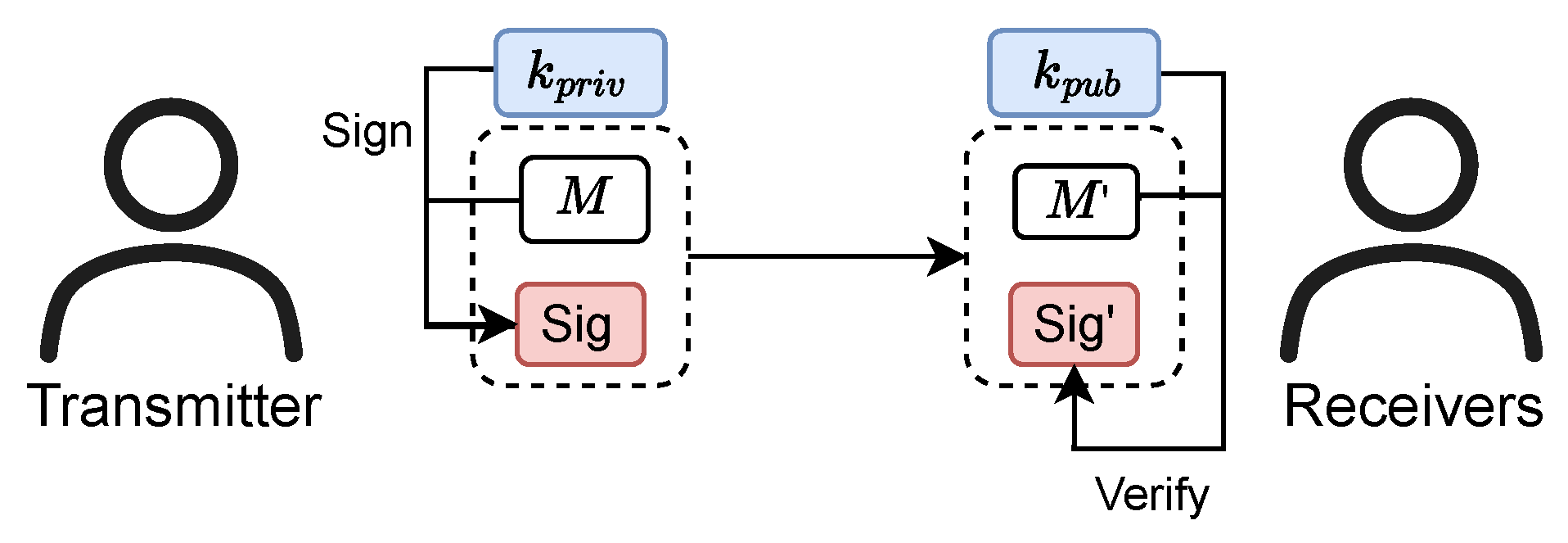
2.1.2. Cryptographic Cornerstone: Public Key Cryptography for Immediate Authentication
2.1.3. Embedding Strategy: Digital Watermarking
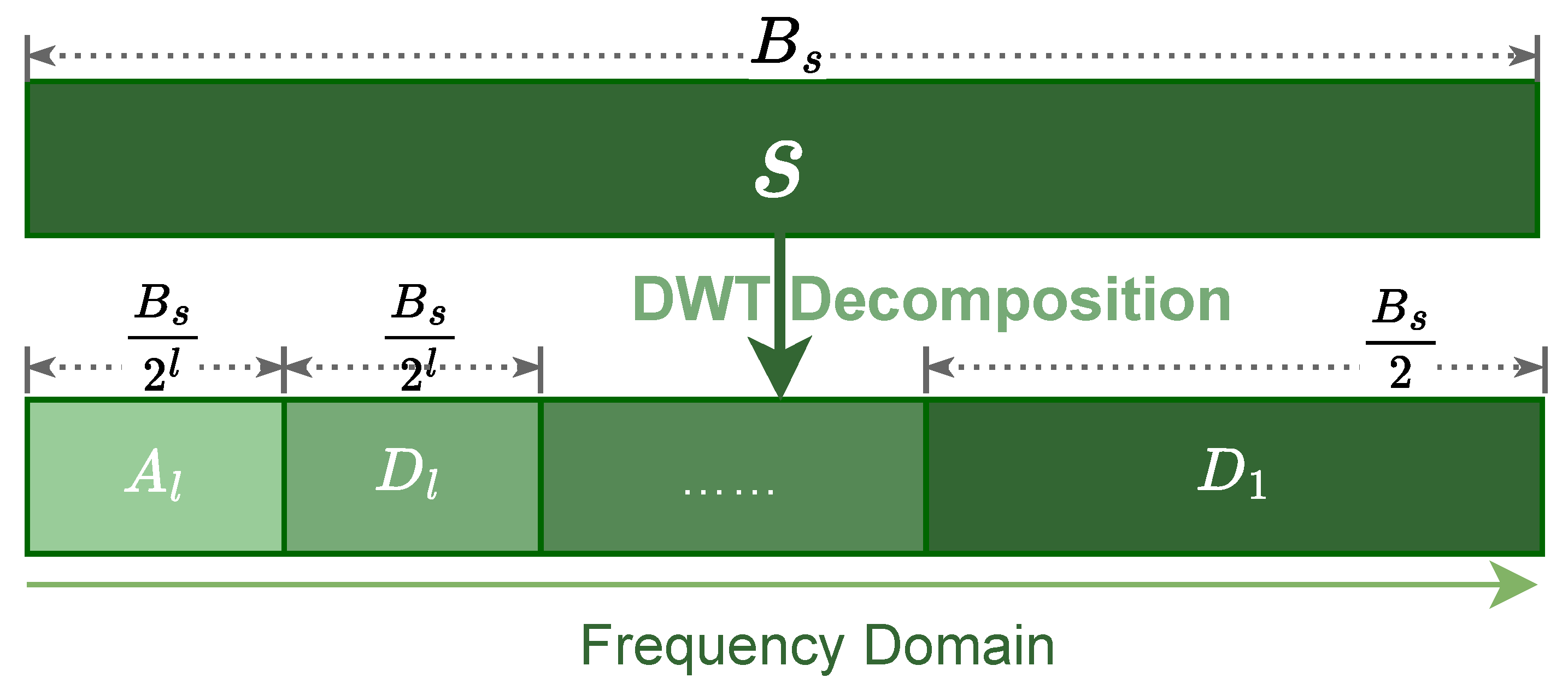
2.1.4. Embedding Domain: Discrete Wavelet Transform (DWT)
2.2. Design of the WAWA Scheme
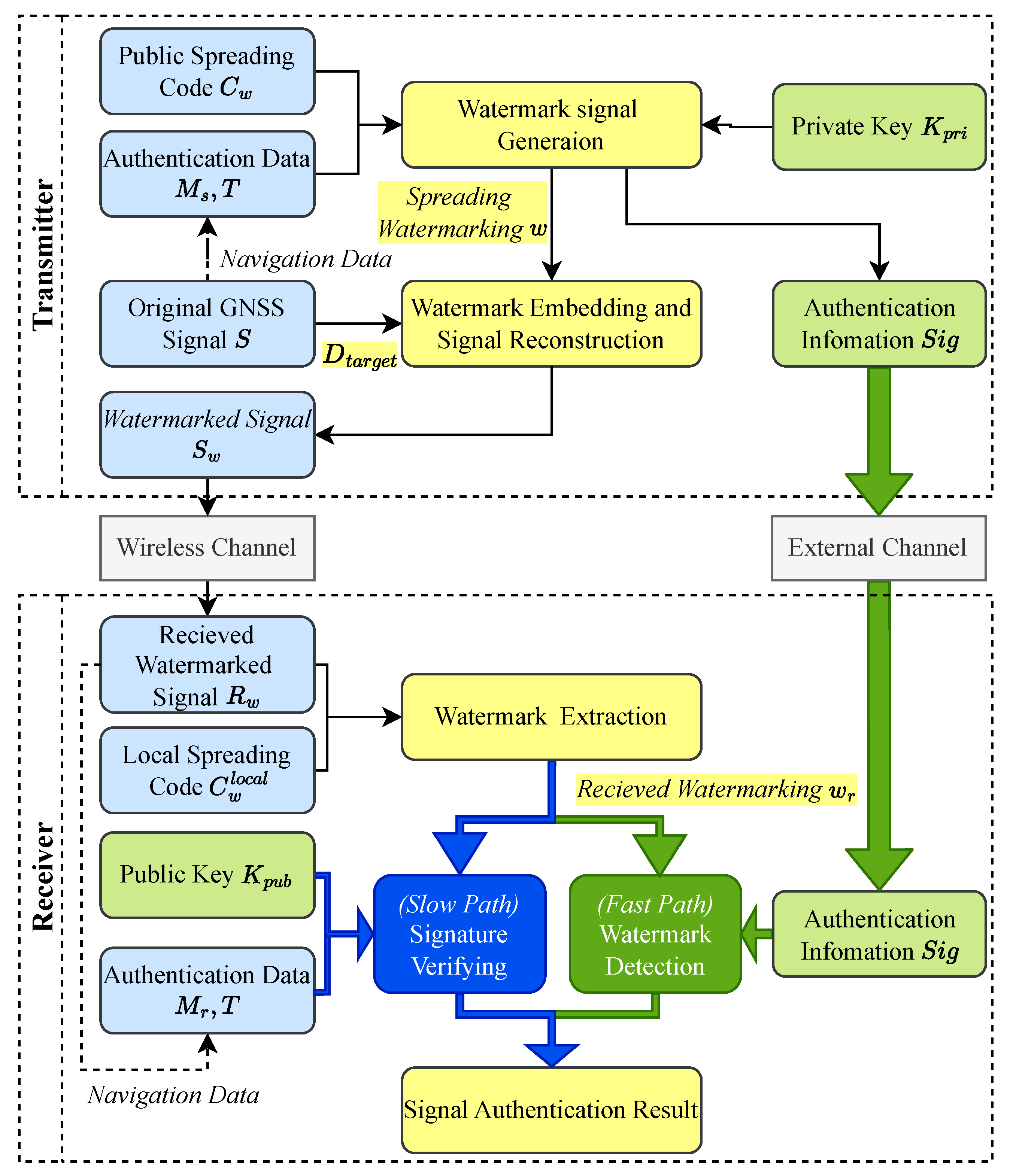
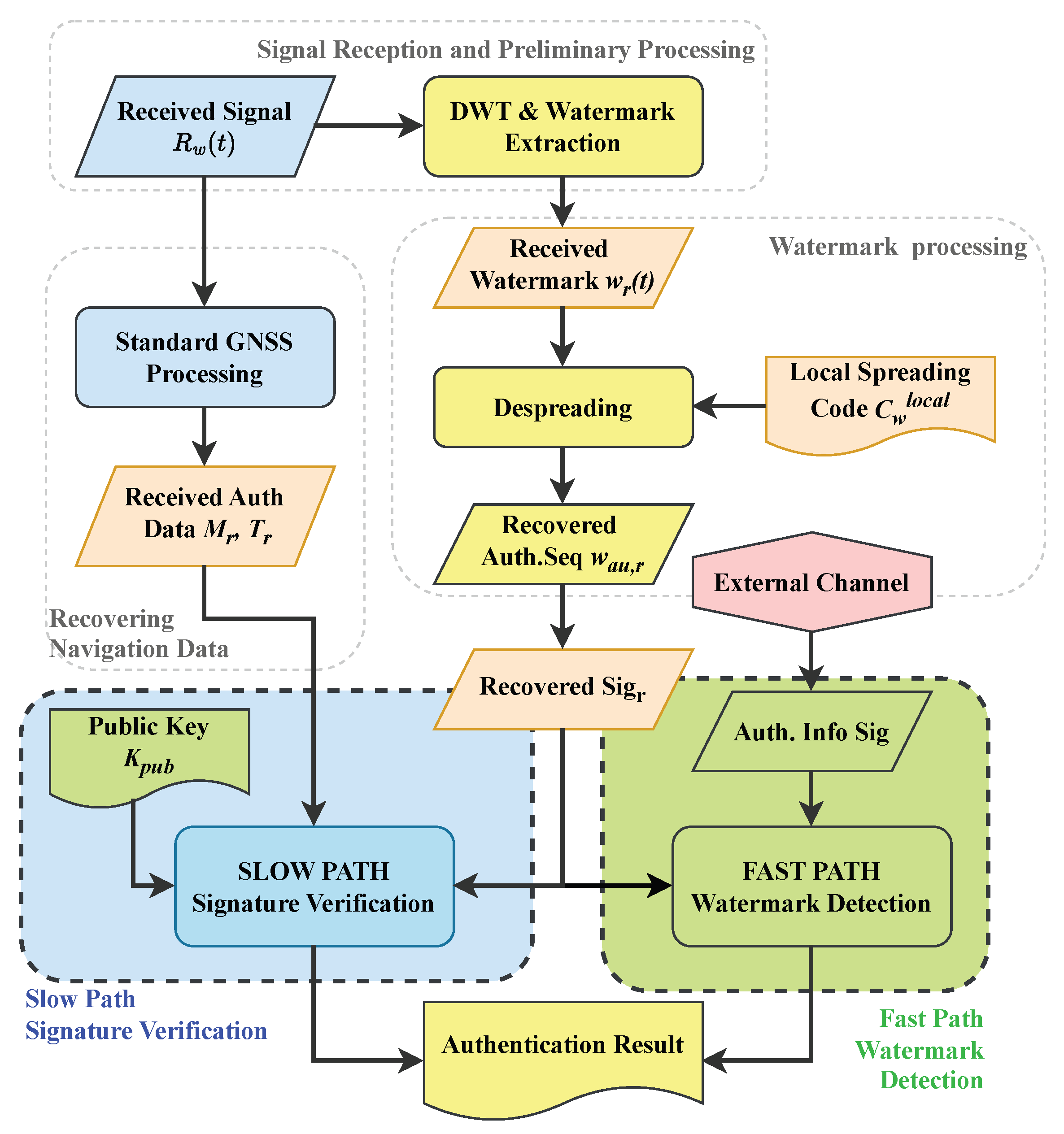
2.2.1. System Architecture
- The slow path is designed for fully autonomous, standalone receivers. It performs a hard-decision decoding on the extracted watermark to reconstruct the full digital signature, which is then verified using the public key . This path guarantees authentication without reliance on any external communication.
- The fast path is designed for network-assisted receivers that prioritize speed. In this mode, the receiver obtains the authentic signature in advance from a trusted, high-speed channel, e.g., a cellular network. It then uses this authentic signature as a local template for a rapid correlation detection against the soft-decision values of the extracted watermark , enabling near real-time authentication.
2.2.2. Wavelet Domain Embedding Process
2.2.3. Authentication Watermark Sequence Design
2.2.4. Receiver Watermark Extraction and Dual-Path Verification
- (1)
- Slow Path Verification: Standalone Signature Check
- (2)
- Fast Path Verification: Assisted Correlation Detection
3. Results
3.1. Watermark Detection Performance
3.1.1. Slow Path: Bit Error Rate (BER) Analysis
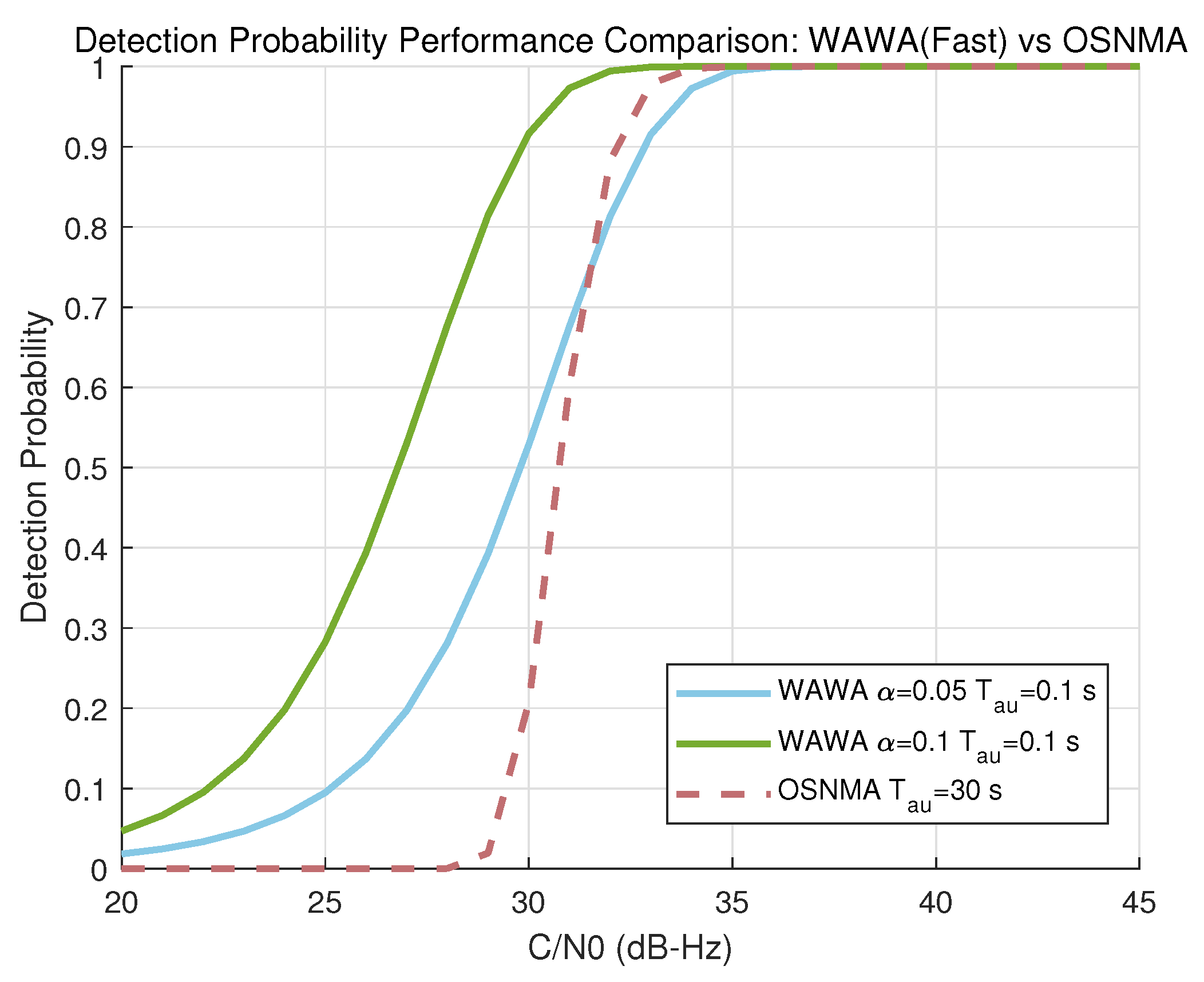
3.1.2. Fast Path: Correlation Detection Performance
3.1.3. Performance Evaluation
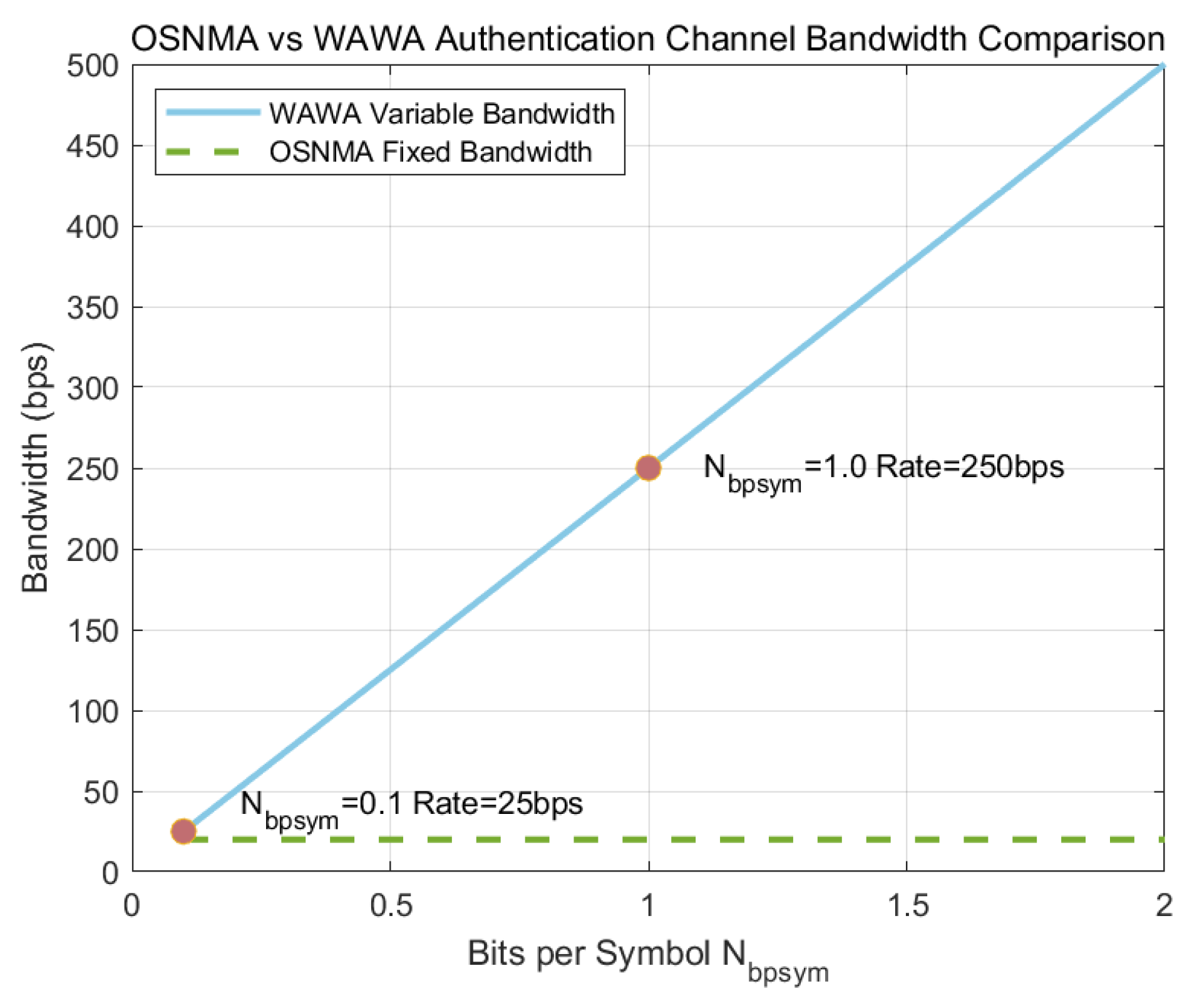
3.2. Effective Channel Bandwidth
3.3. Impact on Legacy GNSS Receivers
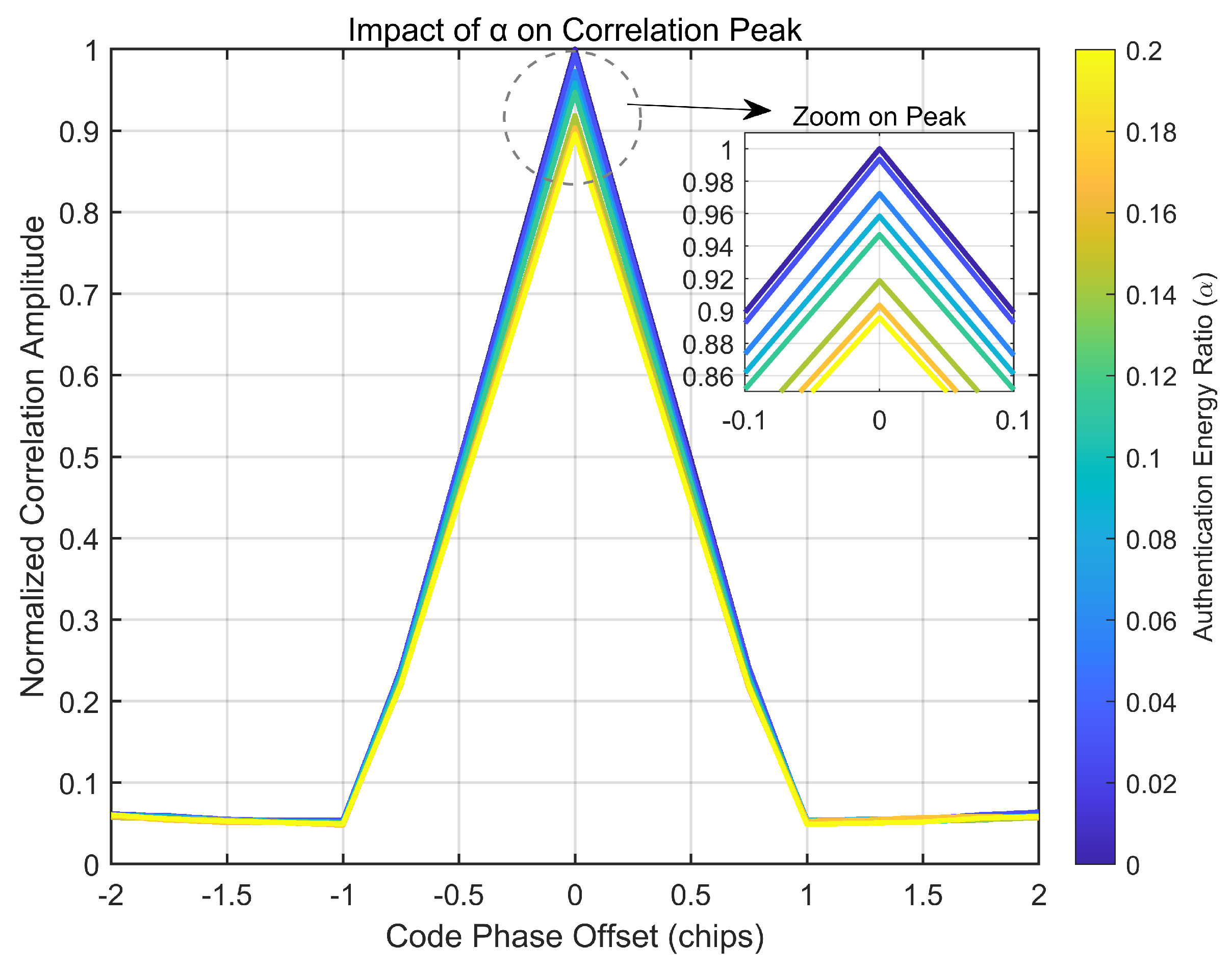
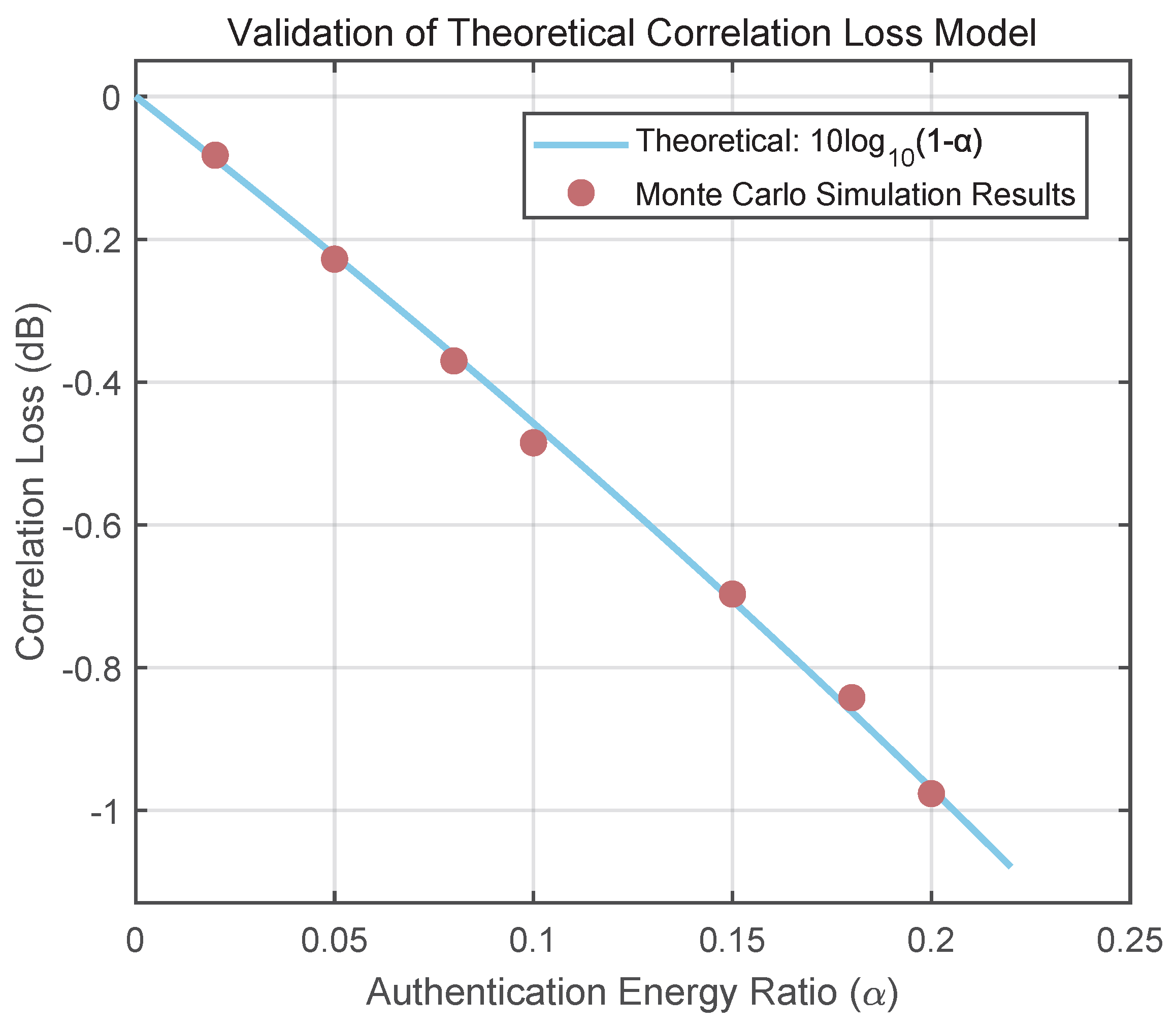
3.3.1. Correlation Loss: Theory and Validation
3.3.2. Impact on Code Tracking Precision
4. Discussion
4.1. Immediacy of Verification and Its Implications
4.2. Bandwidth as a Key Enabler for Stronger Cryptography
4.3. Resource Efficiency: Overcoming the Memory Barrier
4.4. Security Considerations, Limitations, and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BER | Bit Error Rate |
| DLL | Delay-Locked Loop |
| DWT | Discrete Wavelet Transform |
| GNSS | Global Navigation Satellite System |
| IDWT | Inverse Discrete Wavelet Transform |
| NMA | Navigation Message Authentication |
| OSNMA | Open Service Navigation Message Authentication |
| SCA | Spreading Code Authentication |
| SNR | Signal-to-Noise Ratio |
| TESLA | Timed Efficient Stream Loss-tolerant Authentication |
| PNT | Positioning, Navigation, and Timing |
| PKC | Public Key Cryptography |
| PKI | Public Key Infrastructure |
| WAWA | Wavelet Analysis based Watermarking Authentication |
References
- Dovis, F.; Ruotsalainen, L.; Toledo-Moreo, R.; Kassas, Z.Z.M.; Gikas, V. Recent Advancement on the Use of Global Navigation Satellite System-Based Positioning for Intelligent Transport Systems [Guest Editorial]. IEEE Intell. Transp. Syst. Mag. 2020, 12, 6–9. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, G.; Nie, Z.; Ferreira, V.; Casula, G. High-Precision and High-Reliability Positioning, Navigation, and Timing: Opportunities and Challenges. Remote Sens. 2024, 16, 4403. [Google Scholar] [CrossRef]
- Jin, S.; Camps, A.; Jia, Y.; Wang, F.; Martin-Neira, M.; Huang, F.; Yan, Q.; Zhang, S.; Li, Z.; Edokossi, K.; et al. Remote Sensing and Its Applications Using GNSS Reflected Signals: Advances and Prospects. Satell. Navig. 2024, 5, 19. [Google Scholar] [CrossRef]
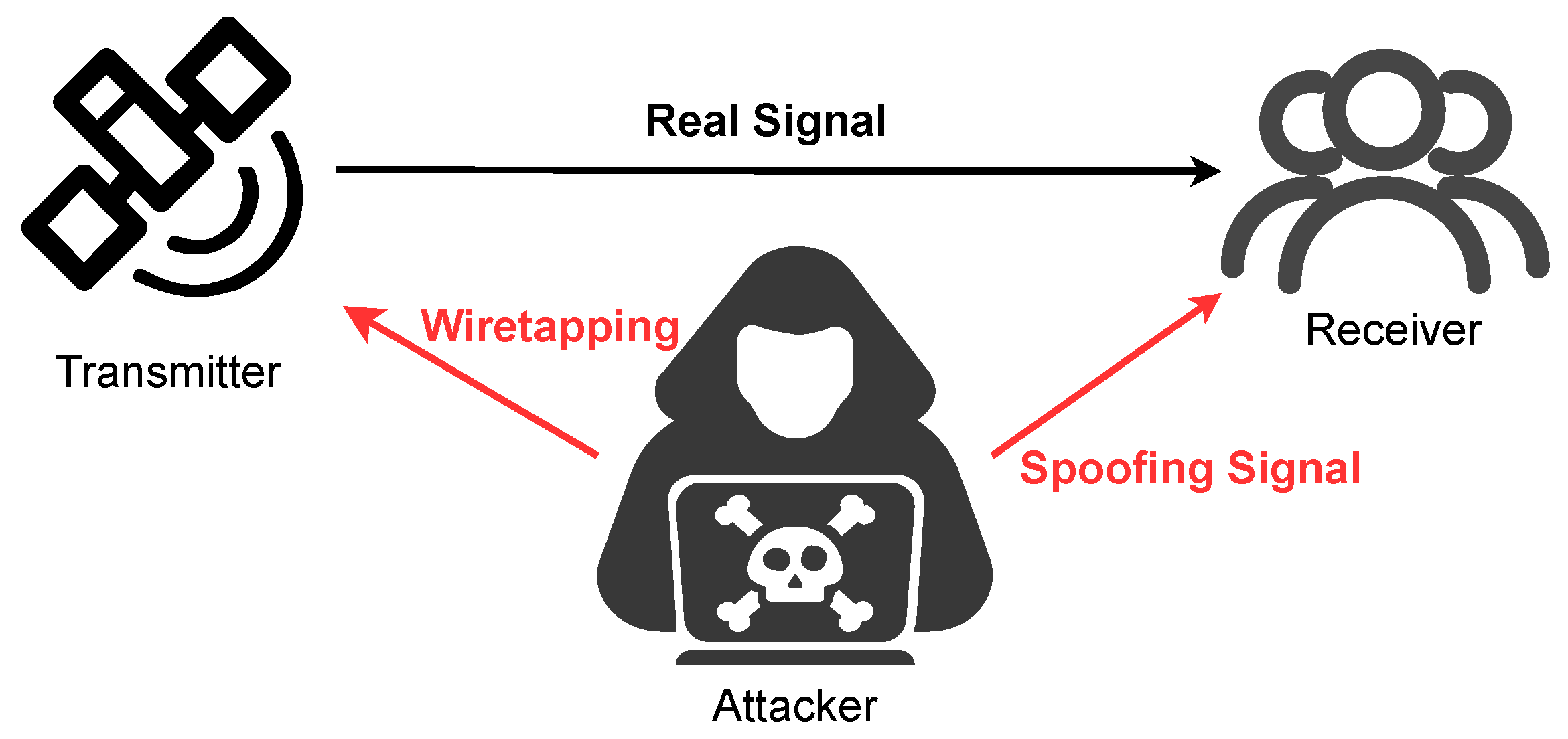
- Meng, L.; Yang, L.; Yang, W.; Zhang, L. A Survey of GNSS Spoofing and Anti-Spoofing Technology. Remote Sens. 2022, 14, 4826. [Google Scholar] [CrossRef]
- Radoš, K.; Brkić, M.; Begušić, D. Recent Advances on Jamming and Spoofing Detection in GNSS. Sensors 2024, 24, 4210. [Google Scholar] [CrossRef]
- Psiaki, M.; Humphreys, T. GNSS Spoofing and Detection. Proc. IEEE 2016, 104, 1258–1270. [Google Scholar] [CrossRef]
- Fernández-Hernández, I.; Châtre, E.; Dalla Chiara, A.; Da Broi, G.; Pozzobon, O.; Fidalgo, J.; Odriozola, M.; Moreno, G.; Sturaro, S.; Caparra, G.; et al. Impact Analysis of SBAS Authentication. Navigation 2018, 65, 517–532. [Google Scholar] [CrossRef]
- UK Government. The Economic Impact on the UK of a Disruption to GNSS: Executive Summary. Technical Report, Cabinet Office; 2017. Available online: https://www.gov.uk/government/publications/the-economic-impact-on-the-uk-of-a-disruption-to-gnss (accessed on 24 October 2025).
- Wang, L.; Chen, L.; Li, B.; Liu, Z.; Li, Z.; Lu, Z. Development Status and Challenges of Anti-Spoofing Technology of GNSS/INS Integrated Navigation. Front. Phys. 2024, 12, 1425084. [Google Scholar] [CrossRef]
- Esswein, M.C.; Psiaki, M.L. Classification of Authentic and Spoofed GNSS Signals Using a Calibrated Antenna Array. Navigation 2025, 72. [Google Scholar] [CrossRef]
- Wesson, K.D.; Gross, J.N.; Humphreys, T.E.; Evans, B.L. GNSS Signal Authentication via Power and Distortion Monitoring. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 739–754. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Yang, Y.; Liang, C.; Liu, R. Spoofing and Anti-Spoofing Technologies of Global Navigation Satellite System: A Survey. IEEE Access 2020, 8, 165444–165496. [Google Scholar] [CrossRef]
- Gallardo, F.; Pérez-Yuste, A.; Konovaltsev, A. Satellite Fingerprinting Methods for GNSS Spoofing Detection. Sensors 2024, 24, 7698. [Google Scholar] [CrossRef]
- Chen, X.; Luo, R.; Liu, T.; Yuan, H.; Wu, H. Satellite Navigation Signal Authentication in GNSS: A Survey on Technology Evolution, Status, and Perspective for BDS. Remote Sens. 2023, 15, 1462. [Google Scholar] [CrossRef]
- Fernández-Hernández, I.; Rijmen, V.; Seco-Granados, G.; Simon, J.; Rodríguez, I.; Calle, J.D. A Navigation Message Authentication Proposal for the Galileo Open Service. Navigation 2016, 63, 85–102. [Google Scholar] [CrossRef]
- Perrig, A.; Canetti, R.; Tygar, J.D.; Song, D. The TESLA Broadcast Authentication Protocol. RSA CryptoBytes Tech. Newsl. 2002, 5, 2–13. [Google Scholar]
- Hammarberg, T.; García, J.M.V.; Alanko, J.N.; Bhuiyan, M.Z.H. An Experimental Performance Assessment of Galileo OSNMA. Sensors 2024, 24, 404. [Google Scholar] [CrossRef]
- Anderson, J.; Lo, S.; Walter, T. Time Synchronization for TESLA-based GNSS-enabled Systems. In Proceedings of the 35th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2022), Denver, CO, USA, 19–23 September 2022; pp. 3408–3417. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Zhu, X.; He, J.; Zhao, S.; Shen, Y.; Jiang, X. Practical Spoofing Attacks on Galileo Open Service Navigation Message Authentication. arXiv 2025, arXiv:2501.09246. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Shen, Y.; Zhu, J.; Chen, Y.; Jiang, X. Novel Replay Attacks against Galileo Open Service Navigation Message Authentication. In Proceedings of the International Technical Meeting of the Satellite Division of The Instituteof Navigation (ION GNSS+ 2023), Denver, CO, USA, 11–15 September 2023; pp. 3897–3907. [Google Scholar] [CrossRef]
- Ardizzon, F.; Crosara, L.; Tomasin, S.; Laurenti, N. On the Limits of Cross-Authentication Checks for GNSS Signals. IEEE Trans. Inf. Forensics Secur. 2024, 19, 4480–4493. [Google Scholar] [CrossRef]
- Anderson, J.; Carroll, K.; DeVilbiss, N.; Gillis, J.; Hinks, J.; O’Hanlon, B.; Rushanan, J.; Scott, L. Chips-Message Robust Authentication (Chimera) for GPS Civilian Signals. Navig. J. Inst. Navig. 2017, 2017, 2388–2416. [Google Scholar]
- So, H.; Gunawardena, S.; Hebert, J. Required Memory Analysis of a GPS Receiver for Implementing CHIMERA SCA. In Proceedings of the 2023 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 24–27 April 2023; pp. 905–910. [Google Scholar] [CrossRef]
- Nicola, M.; Motella, B.; Gamba, M.T. The Chimera Solution: Performance Assessment. In Proceedings of the 2020 European Navigation Conference (ENC), Dresden, Germany, 23–24 November 2020; pp. 1–10. [Google Scholar] [CrossRef]
- Wu, Z.; Bai, Y.; Zhang, Y.; Liu, L.; Yue, M. TrustCNAV: Certificateless Aggregate Authentication of Civil Navigation Messages in GNSS. Comput. Secur. 2024, 148, 104172. [Google Scholar] [CrossRef]
- Liu, H.; Mo, Y.; Yan, J.; Xie, L.; Johansson, K.H. An Online Approach to Physical Watermark Design. IEEE Trans. Autom. Control 2020, 65, 3895–3902. [Google Scholar] [CrossRef]








| Parameter | Symbol | Value |
|---|---|---|
| Symbol Duration | 4 ms | |
| Signature Length | 672 bits | |
| Bits per Symbol | 1 | |
| False Alarm Probability (Fast Path) | ||
| Authentication Interval (Fast Path) | 1 s |
| Feature | OSNMA (NMA Example) | Chimera (SCA Example) | WAWA (This Work) |
|---|---|---|---|
| Authentication Level | Navigation Message | Spreading Code/Physical Layer | Navigation Message via Physical Layer |
| Typical Verification Latency | High ( 30 s) | High (waits for NMA key) | Immediate (Slow/Fast Path) |
| Receiver Memory Req. | Low | Very High (MBs) | Low |
| Receiver Comp. Complexity | Low | Moderate | Moderate (DWT) |
| Correlation Loss | None | High: dB | Moderate: dB |
| Time Sync. Dependency | High (Vulnerable) | High (via NMA) | None |
| Primary Advantages | Backward compatibility | Chip-level protection | Immediacy, Low Memory, No Sync. Risk |
| Primary Disadvantages | Latency, Sync. Risk, Low BW | High Memory, High Corr. Loss | Introduces Corr. Loss, PKI Management, Space Segment Mod. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Tang, X.; Lin, H.; Wu, Y.; Sun, G. WAWA: Wavelet Analysis-Based Watermarking Authentication for GNSS Civil Signal with Immediate Symbol-Level Verification. Sensors 2025, 25, 6615. https://doi.org/10.3390/s25216615
Tang X, Tang X, Lin H, Wu Y, Sun G. WAWA: Wavelet Analysis-Based Watermarking Authentication for GNSS Civil Signal with Immediate Symbol-Level Verification. Sensors. 2025; 25(21):6615. https://doi.org/10.3390/s25216615
Chicago/Turabian StyleTang, Xinyu, Xiaomei Tang, Honglei Lin, Yi Wu, and Guangfu Sun. 2025. "WAWA: Wavelet Analysis-Based Watermarking Authentication for GNSS Civil Signal with Immediate Symbol-Level Verification" Sensors 25, no. 21: 6615. https://doi.org/10.3390/s25216615
APA StyleTang, X., Tang, X., Lin, H., Wu, Y., & Sun, G. (2025). WAWA: Wavelet Analysis-Based Watermarking Authentication for GNSS Civil Signal with Immediate Symbol-Level Verification. Sensors, 25(21), 6615. https://doi.org/10.3390/s25216615






